Temperature-Fermion Number Correlations in Finite Paired Systems

Abstract

We investigate finite systems of N paired fermions, common in atomic nuclei, for example. These systems exhibit quantum mechanical features akin to those of superconductors. We discover, however, some specific N dependent effects that can not be attained in the thermodynamics limit of ordinary superconductivity. In particular, an important fact is uncovered: there is a strong correlation between the temperature T and the number of fermions N. A certain temperature increase $\Delta T$ produces, in thermal quantifiers (such as the entropy), quite different effects if $N=4$ or $N=25$. In fact, whether a given temperature value should be regarded as high or low can not be ascertained independent of the N value.

1. Introduction

Long ago, Bohr, Mottelson, and Pines [1], and also Belyaev [2], successfully applied and adapted to atomic nuclei the ideas and methods of the superconductivity theory developed by Barden, Cooper, and Schrieffer [3,4]. Since then, nuclear superconductivity based on nuclear fermion-pairing has become a standard ingredient in the study of nuclear structure [5] and there is a well known manner of adapting the usual theory of superconductivity to a finite system of fermions [5].

In this effort, we uncover some peculiar, temperature T dependent effects exhibited by finite $N\text{-}$fermion systems endowed with a fermion–fermion pairing interaction identical to the one employed in nuclear physics and reported in Equation (4.140) of the celebrated book by Ring and Schuck on nuclear theory [5]. Amongst several hundreds of accompanying references, see also, for example [6,7,8].

These peculiar pairing effects strongly correlate N with T and are best appreciated in a context based on the Gibbs canonical ensemble. We employ an exactly solvable model for pairing-interacting fermions [9] for which the BCS treatment of superconductivity becomes exact, so that our results are not based on approximate treatments. We begin our labors below by describing this model below.

2. Many-Fermions Solvable Models

2.1. Preliminaries: Lipkin Model

The Lipkin Model (LM) [10,11] has been seen to be extraordinarily useful in theoretical investigations with regard to the validity and usefulness of variegated approaches, designed so as to scrutinize the manifold facets of the quantum many body problem.

The model is based on an SU2 algebra corresponding to special operators, called quasi-spin operators. It yields easily obtainable exact solutions to the pertinent Schrödinger equation (SE), which, in turn, are to be confronted with results found by appealing to diverse types of theoretical approximations to the many body SE. The relevant Casimir operator [10] has attached several multiplets, and only the one associated to the unperturbed ground state of the system is usually the focus of concern.

Cambiaggio and Plastino (CP) [9] advanced a simple LM-extension to deal with excited multiplets and this allowed for the formulation, in quasi-spin language, of a BCS-like theory which mimics superconductivity, providing us with exact solutions. This was a generalization of the LM to the case of a variable particle number, requiring only an SU2 × SU2 algebra for dealing with the SE.

2.2. Cambiaggio–Plastino Exactly Solvable SU2 × SU2 Model of Paired Fermions

The model [9,12] considers N fermions distributed in two (2 $\mathsf{\Omega }$)-fold degenerate single-particle levels, separated by an energy gap $ϵ$ ($N=2$$\mathsf{\Omega }$). One characterizes the 2 $\mathsf{\Omega }$ lower states by the quantum numbers $p,\mu$ with $p=1,\dots ,2$$\mathsf{\Omega }$ and $\mu =\pm 1$. One has the usual SU2 quasi-spin operators [10]

$$J_z=(1/2)\sum _{p,\mu }\mu C_{p,\mu }^{+}{C}_{p,\mu },$$

(1)

$$J_{+}=\sum _p{C}_{p,+}^{+}{C}_{p,-},$$

(2)

$$J_{-}=\sum _p{C}_{p,-}^{+}{C}_{p,+},$$

(3)

to which CP add the SU2 angular momentum-like “pairing” operators

$$Q_0=(1/2)\sum _{p,\mu }{C}_{p,\mu }^{+}{C}_{p,\mu }-\mathsf{\Omega },$$

(4)

$$Q_{+}=\sum _p{C}_{p,+}^{+}{C}_{p,-}^{+},$$

(5)

$$Q_{-}=\sum _p{C}_{p,-}{C}_{p,+}.$$

(6)

Obviously, $Q_{+}$ creates, and $Q_{-}$ destroys, two particles which yield zero contribution to the $J_z$-value, and which could then be said to “couple” to $J_z=0$. Any Q-operator commutes with all J-operators, and vice versa (SU2 × SU2). Accordingly, one can construct a complete orthonormal basis characterized by the eigenvalues of the operators $J^2,J_z,Q^2,Q_0$—i.e., $|J,Q,J_z,Q_0\rangle$. A “pairing” Hamiltonian, which commutes with the number the operator would read, mimics the nuclear pairing one [5] (and with $ϵ=1$) as

$$H=J_z-(G/2)Q_{+}{Q}_{-},$$

(7)

with G the pairing-strength.

Note that the pairing interaction in the last equation has exactly the same form as that used in nuclear theory (see [5], Equation (4.140)). CP next introduce the quasi-spin seniority number $\nu$

$$\nu =2(\mathsf{\Omega }-Q),$$

(8)

which indicates the number of particles not “paired” to $J_z=0$—that is, $\nu$ is the number of “unpaired" particles in a Q-multiplet. We have also [9]

$$J=\nu /2,$$

(9)

$$J+Q=\mathsf{\Omega }.$$

(10)

In the case of the Lipkin model, $N=2\mathsf{\Omega }$, $Q_0=0$, relations that we use here [9]. The unperturbed ground state (no interaction) has $J=\mathsf{\Omega },J_z=-\mathsf{\Omega },Q=Q_0=0$ and belongs to the multiplet $J=\mathsf{\Omega },Q=Q_0=0.$ The exact eigenvalues of H are [9]

$$E(J,Q,J_z,Q_0)=J_z-(G/2)\left[Q(Q+1)-Q_0(Q_0-1)\right].$$

(11)

The energy of the unperturbed ground state ($\nu =N,Q=Q_0)$ is [9]

$$E_0=-\mathsf{\Omega }.$$

(12)

The state of quasi-spin seniority zero, in which all particles are “paired” to $J_z=0$ mimics a nuclear “superconducting” state [9,13]. It is characterized by $\nu =0$ and $Q=\mathsf{\Omega }$. In general, its ”superconducting” energy is

$$E_s=-(G/2)\left[\mathsf{\Omega }(\mathsf{\Omega }+1)-Q_0(Q_0-1)\right],$$

(13)

$$E_s=-(G/2)\left[\mathsf{\Omega }(N-\nu )+\frac{\nu }{2}\left(\frac{\nu }{2}-1\right)-\frac{N}{2}\left(\frac{N}{2}-1\right)\right].$$

(14)

The associated state becomes the superconducting state of the pairing-interacting system for

$$G=G_{crit}\ge (4\mathsf{\Omega }/N)\frac{1}{2\mathsf{\Omega }+1-N/2}=\frac{2}{\mathsf{\Omega }+1},$$

(15)

(the last equality in the r.h.s. holds just for the Lipkin case in which $Q_0=0$) while if the coupling constant is smaller than the critical one the system remains in the unperturbed ground state (UGS). We see that the greater N, the less ”effort” it takes, measured in G-units, to make the system a superconductor, a nice fact that was not duly emphasized in [9].

A phase-transition ensues at $G=G_{crit}$ from the UGS to the superconducting state, belonging to another multiplet. It is essential to realize that, as N grows, $G_{crit}$ diminishes. It is shown in [9] that, in this model, the BCS solution coincides with the exact one. Additionally, it is easy to see that the energy difference between a system with N fermions and one with $N+2$ ones is

$$E_D=[E_s(\mathsf{\Omega }+1)-E_s\left(\mathsf{\Omega }\right)]=-G(\mathsf{\Omega }+1).$$

(16)

Thus, in the exponential Boltzmann factor of the partition function, N ”works” in opposite fashion, as T does. The preceding considerations were made at temperature zero. We proceed to the statistical treatment for finite T’s next.

2.3. The Cambiaggio–Plastino Model af Finite Temperature T

At finite temperature T, with $\beta =1/T$, the ensuing remnants of $T=0$-phase-transitions are called cross-overs [14]. For our present model, the pertinent treatment was devised and implemented in [13].

For investigating ground states, only the $J+Q=\mathsf{\Omega }$ “band” requires consideration. For non-zero temperatures, though, a multitude of states belonging to other bands becomes “accessible” as one builds up the pertinent statistical ensemble. Defining the degeneracy $Y(J,Q)$ (deduced in [13])

$$Y(J,Q)=\frac{(2\mathsf{\Omega }+2)!\left(2\mathsf{\Omega }\right)!(2J+1)(2\mathsf{\Omega }+1)}{(\mathsf{\Omega }+J+Q+2)!(\mathsf{\Omega }+J-Q+1)!(\mathsf{\Omega }-J+Q+1)!(\mathsf{\Omega }-J-Q)!},$$

(17)

the pseudo partition function $Z_M$ is seen to be [13] [see also Equation (11)]

$$Z_M=\sum _{M=-J}^{M=J}exp[-\beta (M-\frac{G}{2}Q(Q+1))],$$

(18)

and the system’s partition function Z reads as

$$Z=\sum _{J,Q}Y(J,Q)Z_M,$$

(19)

where J and Q run over all the values permitted by the following restrictions [13,15]

$$0\le J\le \mathsf{\Omega },$$

(20)

$$0\le Q\le \mathsf{\Omega },$$

(21)

$$0\le J+Q\le \mathsf{\Omega }.$$

(22)

Once in possession of Z, all statistical quantifiers become available.

2.4. Our Main Finite Temperature Quantifiers

So as to properly present our results, we will slightly modify (22) in the fashion

$$0\le J+Q=s\le \mathsf{\Omega }.$$

(23)

To perform the double sum over J, Q, it is better to sum over $J+Q=s$ and over J, leaving Q fixed at $Q=s-J$, with

$$0\le s\le \mathsf{\Omega },$$

(24)

and $s=0,1,2,3,\dots ,\mathsf{\Omega }$ and $J=0,1,2,.\dots ,s$. Thus,

$$Z=\sum _{J,Q}Y(J,Q)Z_M=\sum _{s=0}^{\mathsf{\Omega }}\sum _{J=0}^{s}Y(J,Q)Z_M.$$

(25)

Let us insist that, once we have Z, all statistical quantifiers become available.

As usual [10], we fix the number of particles in the fashion $N=2\mathsf{\Omega }$. The canonical probability distribution (CPD) is now

$$P(M,Q,J)=\frac{Y(J,Q)exp[-\beta (M-\frac{G}{2}Q(Q+1))]}{Z}.$$

(26)

Two very important, finite temperature quantifiers are (1) the effective superconductivity index X (Cf. Equation (8))

$$X=\sum _{J,Q}\sum _{M=-J}^{M=J}P(M,Q)[(N-\nu )/N],$$

(27)

which is unity for a perfect superconductor and vanishes for the unperturbed system (no pairing interaction), and (2) the mean quasi-spin seniority $<\nu >$

$$<\nu >=<1-X>=\sum _{J,Q}\sum _{M=-J}^{M=J}P(M,Q)\nu ,$$

(28)

which yields the average number of unpaired fermions. Remember that the critical coupling constant is $G_{crit}=2/(\mathsf{\Omega }+1)$.

Our probability distribution is given by Equation (24) with Z given by (23). For its evaluation we need the Y degeneracy of Equation (15). Our goal is to compute the quantifier X (Equations (25) and (26)), the average number of paired fermions. This equals unity for full pairing. We appeal to Equations (25) and (26), that use the definitions given in Equations (15), (16), (23) and (24).

3. Main Results

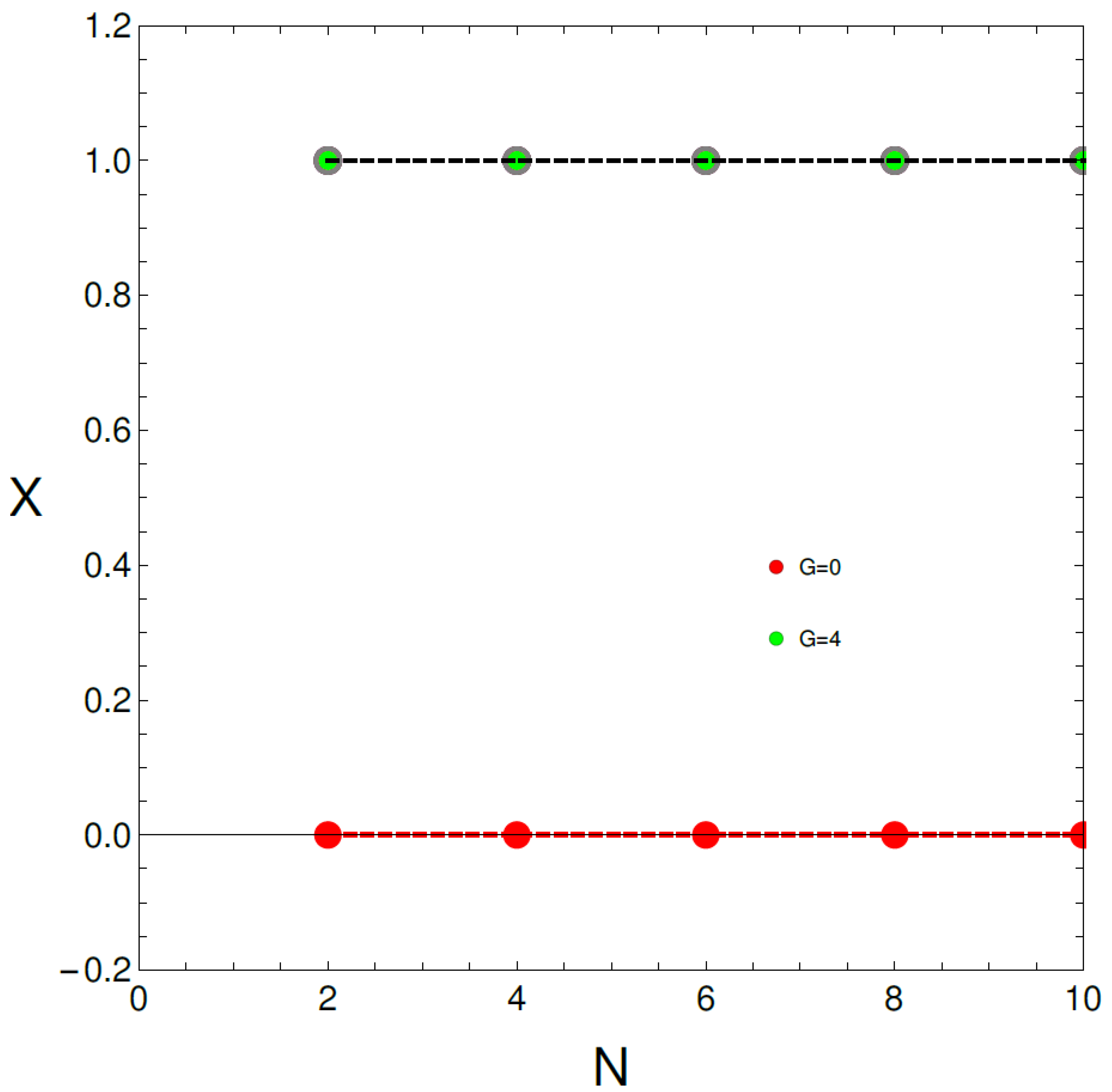
3.1. X vs. N

Figure 1 depicts X vs. N (using Equation (25)) for fixed $G=0$ and $G=4$ at a very low temperature. In the first case, $G<G_{critical}$, there are no paired fermions up to $N=10$ (they would eventually emerge at sufficiently high N, which is surprising enough, as we will discuss below). In the second case, $G>G_{critical}$, all fermions are paired. Figure 2 displays again X vs. N for several values of G, both larger and smaller than $G_{critical}$.

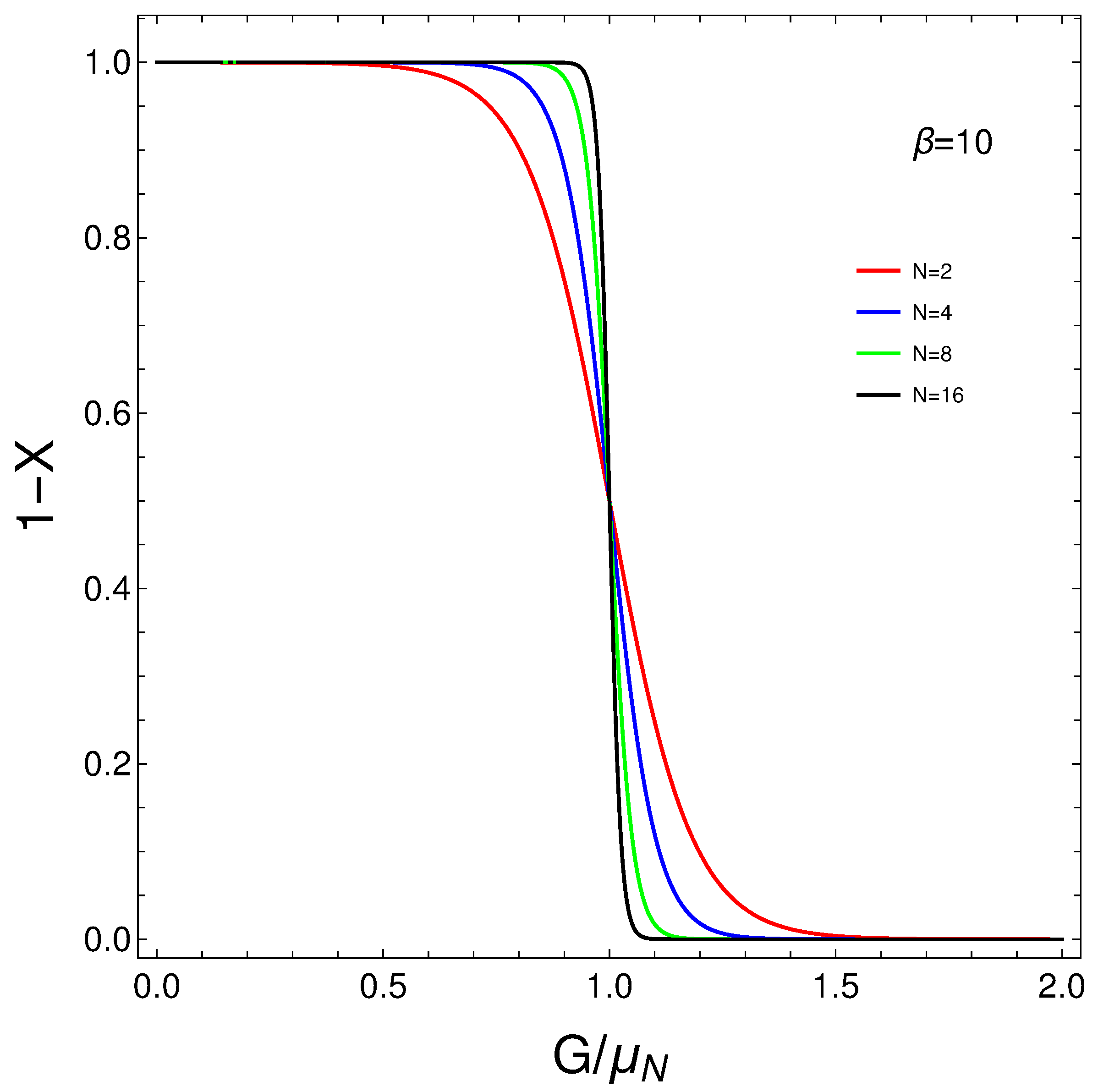
• A phenomenon that we wish to emphasize is that temperature-induced partial superconductivity emerges and is clearly appreciated, even for $G=0$.
• A second phenomenon to be highlighted is that the degree of partial superconductivity increases with N for a fixed G.

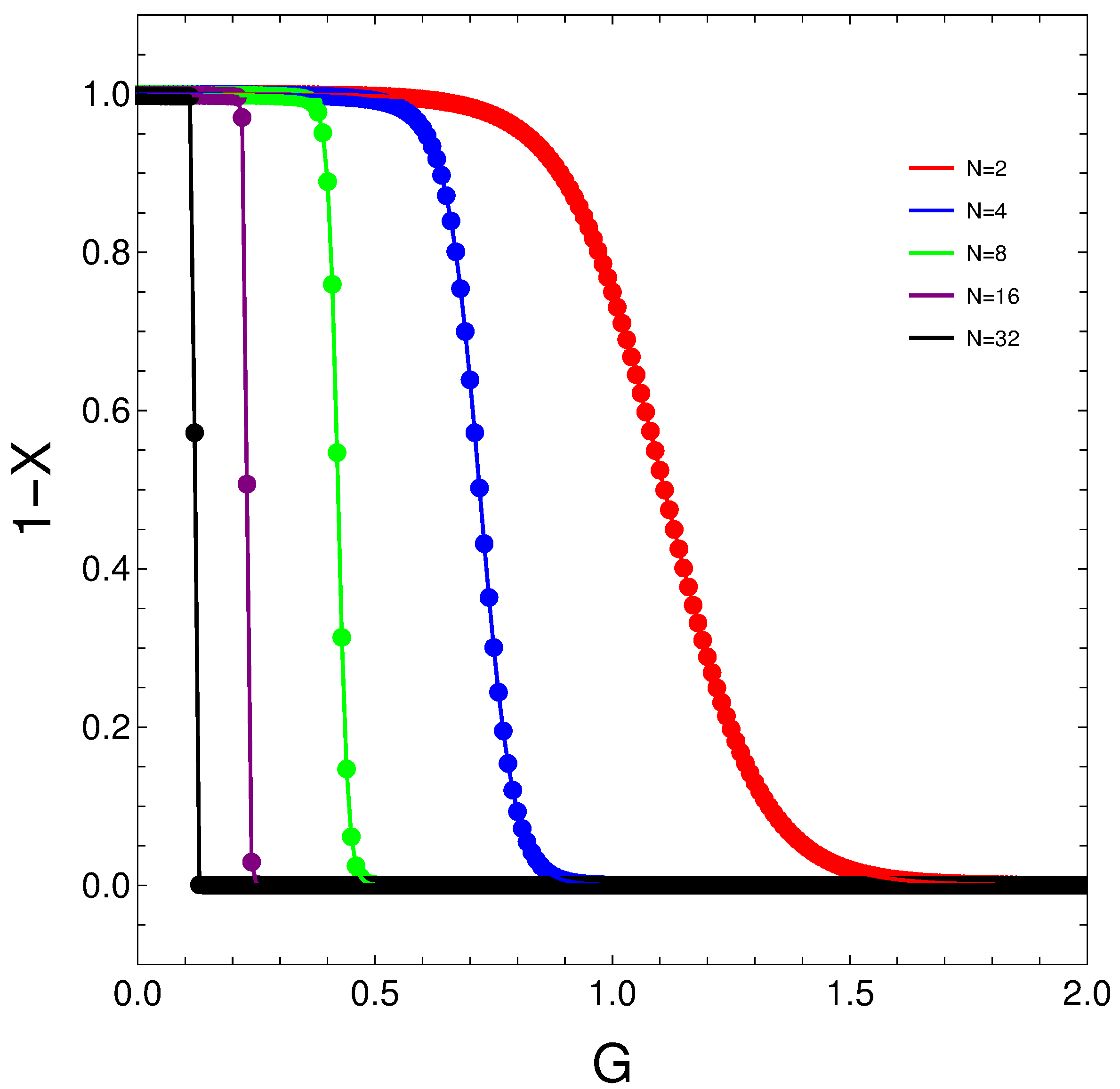
3.2. Average Number of Unpaired Fermions $<\nu >$

We plot in Figure 3 the mean number of unpaired fermions (or average quasi-spin seniority) $<\nu >=1-X$ vs. N for $G=0.5$ and several values of $\beta$. At very low temperatures ($\beta =10,20,\mathrm{and}100$), the corresponding lines superpose themselves. The circles are data, the lines guide the eye.

For a fully superconducting state we have, of course, $<\nu >=1-X=0$. Absolute lack of superconductivity entails $<\nu >=1-X=N$. Partial superconductors (PS) have intermediate values for $1-X=<\nu >$.

• A crucial point to be highlighted is that increasing the fermion number, per se, produces pairing.
• This is seen in the upper dark curve, in which PS emerges just by adding two fermions to the system.
• Of course, the rest of the curves are an evidence of the same rather extraordinary phenomenon that we believe to have discovered here.
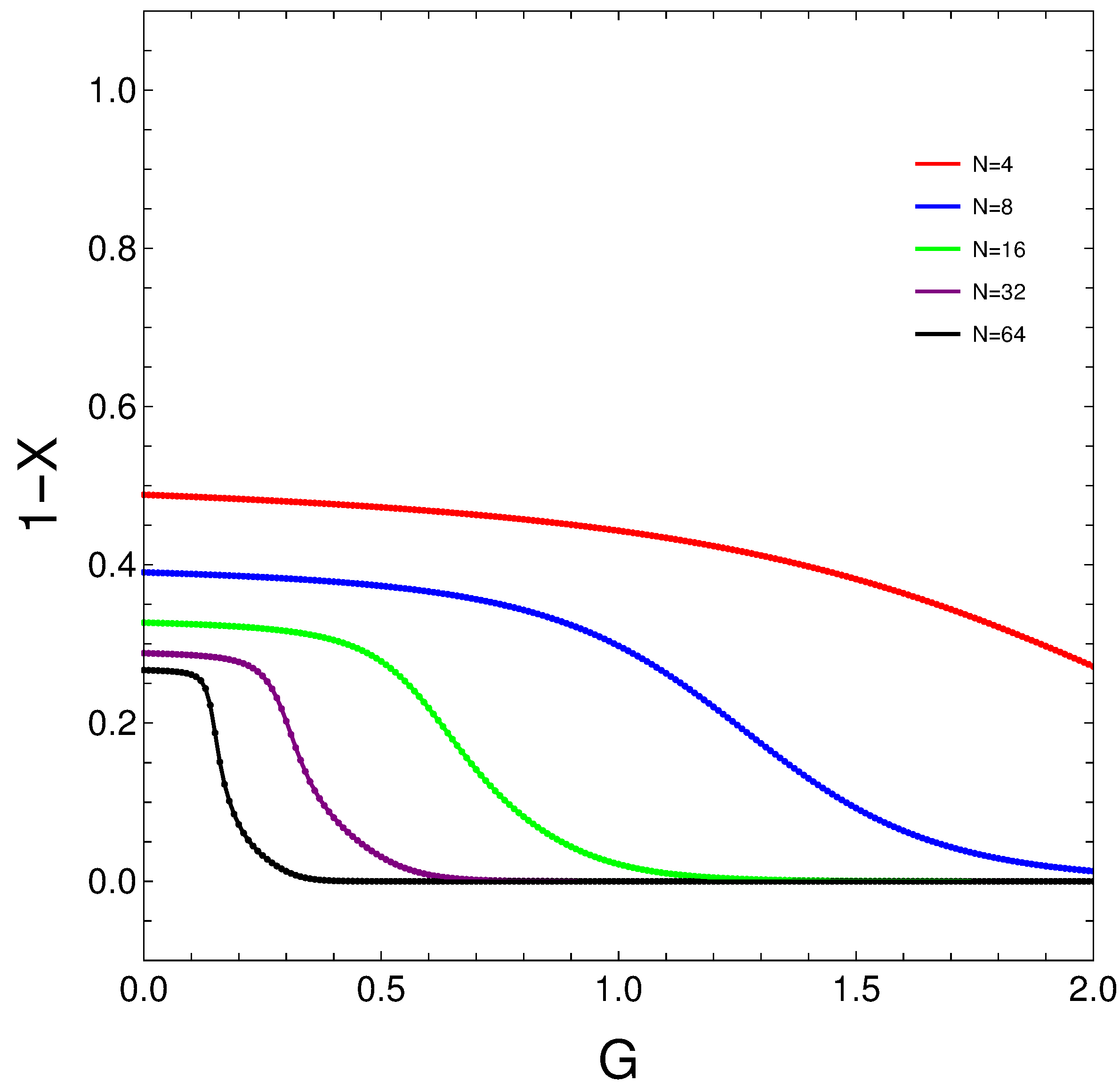
• Note also, as another point, that at very high T, there seems to be a limiting curve.
• Evidence for this assertion is the similarity between the curves for $\beta =0.1$ and $\beta =0.5$ .
• However, this is explained via a simple underlying motive. For $T\to \infty$ all possible fermions’ configurations have equal statistical weight.
• Thus, one should obviously have $<\nu >=1-X=1/2$ for any values of either G or N.

3.3. Enter Sigmoids

We will explore now the phenomenon of achieving, in drawing appropriate quantifiers versus G, the Fermi-Dirac sigmoid function (at low enough T) just by increasing the fermion-number. In Figure 4, we plot $1-X=<\nu >$, the average number of unpaired fermions, versus G for several N values and see that, as N grows, the critical coupling constant G , at which the sigmoid begins displaying a quasi-step shape, steadily diminishes. It takes less and less ”pairing effort” (smaller G’s) to generate superconductivity the larger N becomes.

Continuing with our exploration, Figure 5 shows an instance in which the shape of the quantifier $1-X$ versus G displays significant changes according to the N-value. This implies that it is legitimate to assert that whether T should be regarded as high or low depends upon the value of N. For $N=$ 2, up to $N=16$, the temperature is high enough to erase the typical Fermi Dirac sigmoid shape. However, for $N=32$, the ”effective” T, that results from augmenting N, is low enough so that the sigmoid shape reappears. Thus a new idea is at play here: the effective operating temperature effects that depend upon N.

Abounding on this theme, for given $\beta$ and G-values, there should exist then a high enough $N=N_{crit}$ such that $<\nu >$ becomes arbitrarily small—say $1-X=<\nu ><{10}^{-4}$. Figure 6 depicts $N_{crit}$ versus $\beta$ for several coupling constants.

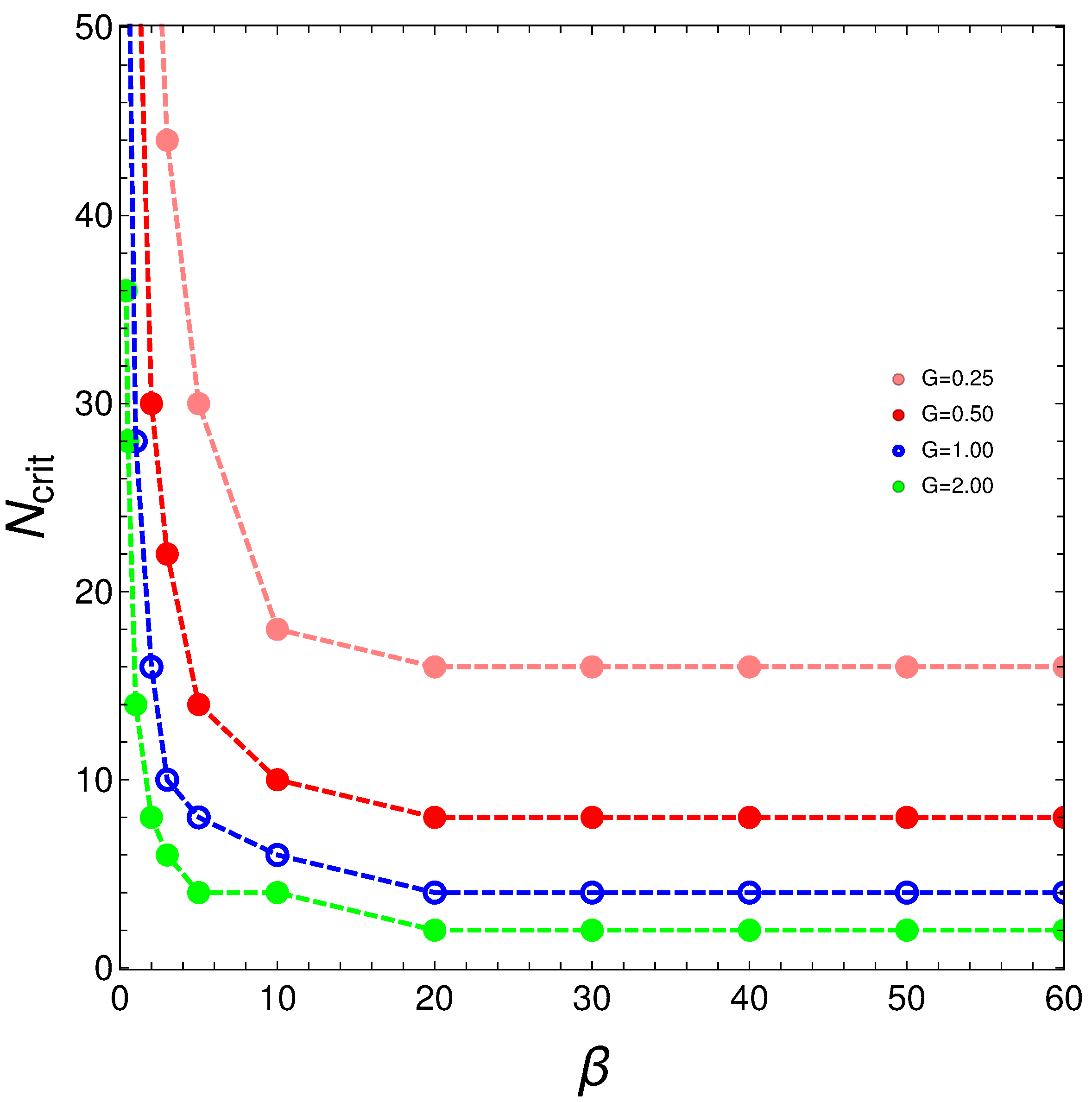
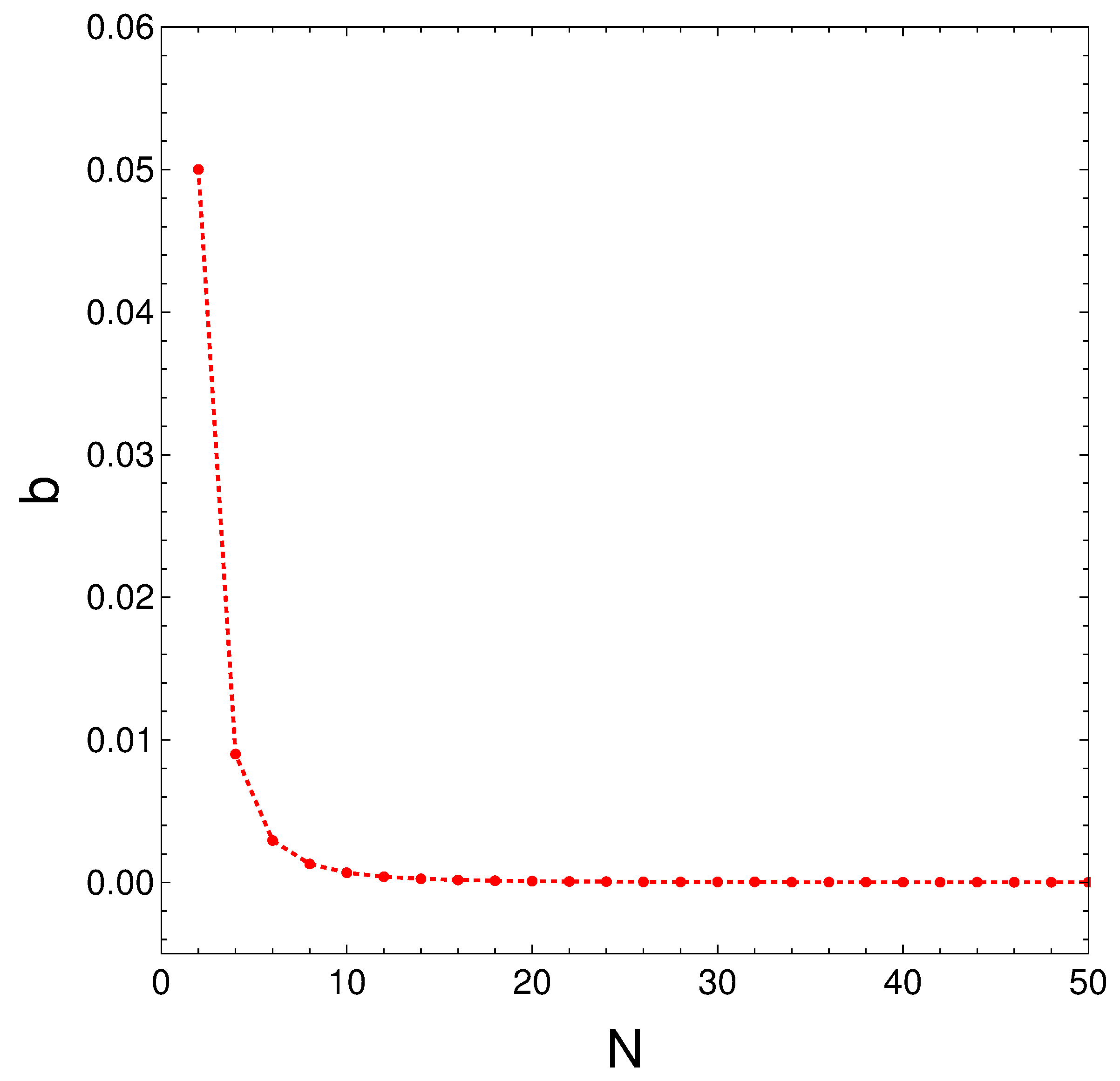
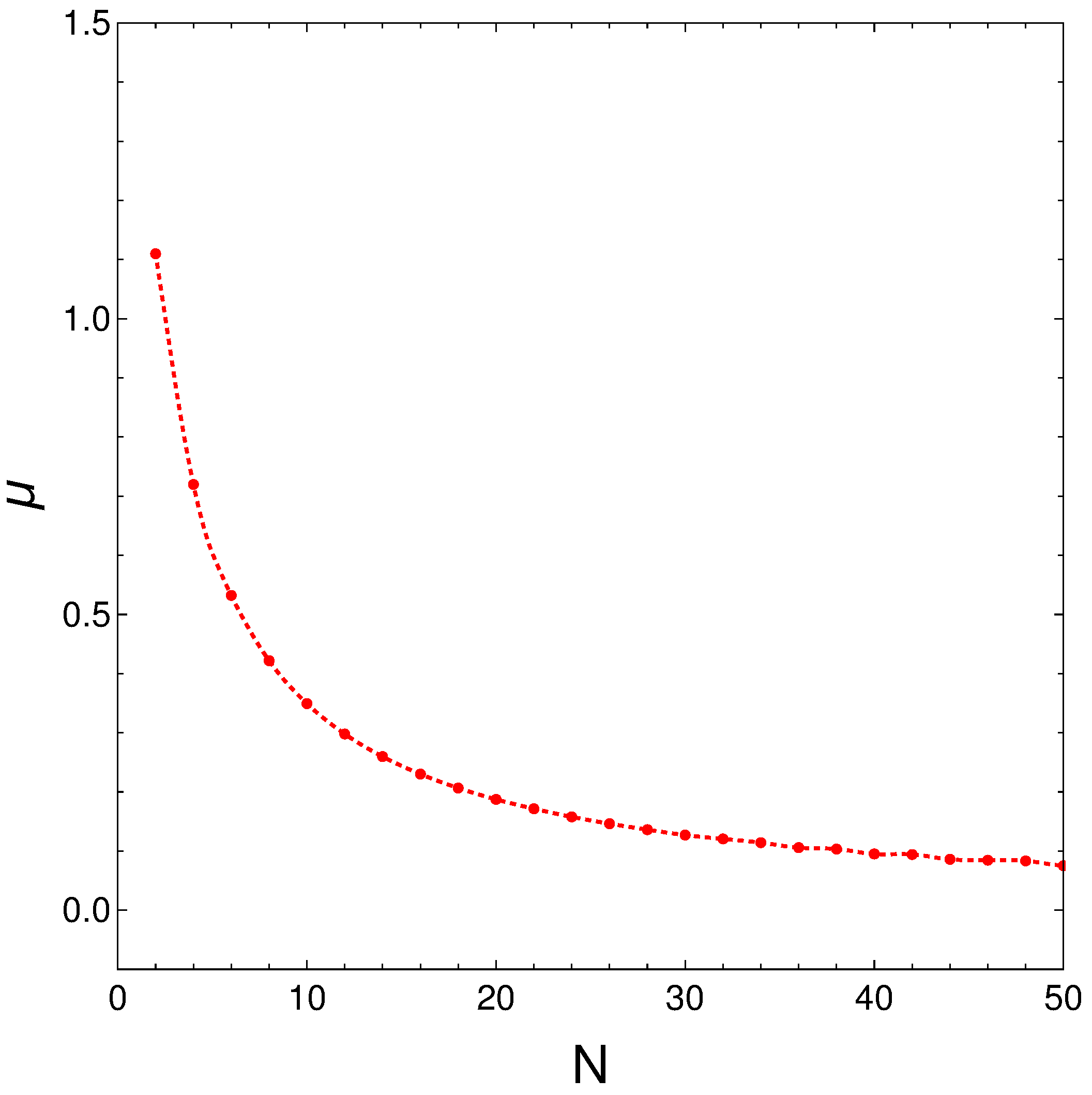
4. Sigmoid-Fitting Quantities ${\mu }_N\left(T\right)$ and $b_N\left(T\right)$

This sigmoid representation constitutes our main present achievement. We wish to show that the average number of unpaired fermions $1-X=<\nu >$ is adequately (and exactly) represented by the typical sigmoid shape of the Fermi Dirac distribution (FDD). This typical FDD is, in text-books, drawn against T. Here we do it against N.

For a system of identical fermions in thermodynamic equilibrium, the average number of fermions $<n_i>$ in a single-particle state i of energy ${ϵ}_i$ is given by the sigmoid ($\mu$ is the Fermi energy and $\beta =1/k_{B}T$)

$$<n_i>=\frac{1}{1+exp[({ϵ}_i-\mu )/\left(k_{B}T\right)]}.$$

(29)

We illustrate in what follows that, in our problem, it is possible to exactly fit $1-X=<\nu >$ values in the fashion

$$1-X=\frac{1}{1+exp[\frac{(G-{\mu }_N\left(T\right))}{b_N\left(T\right)N}]},$$

(30)

where ${\mu }_N\left(T\right)$ and $b_N\left(T\right)$ are, at every pair $T,N$, suitable quantities (see plots below). The following mappings ensue, comparing these two last equations.

• $b_{N}N\to k_{B}T,$
• $G-{\mu }_N\to {ϵ}_i-\mu .$

Figure 7 displays, for $beta=10$, an example of our sigmoids.

The behavior of our ”Fermi coupling ${\mu }_N$” as N changes is depicted in Figure 8 for $\beta =10$. It rapidly vanishes as N grows. We see that in our pairing model, N plays the role of a pseudo-temperature, in comparison with the Fermi Dirac sigmoid. This is one of our main conclusions in this work.

The behavior of our factor $b_N\left(T\right)$ is displayed in Figure 9 for $\beta =10$. We see clearly that $X\to 1$ rapidly as N grows, since $b_N$ goes to zero in fast fashion when that happens.

5. Conclusions

The theoretical machinery of superconductivity [4] was adapted for describing fermion-pairing in finite systems of N particles more than 60 years ago [5]. Here we have described apparently unreported N-dependent effects in these finite fermions systems. We have worked with a well known SU2 × SU2 exactly solvable superconductivity model [9], so that our results are exact. Note that in such a model the pairing interaction has exactly the same form as that used in nuclear theory (see [5], Equation (4.140)).

• The point of the novelty is that, for these systems, N growth mimics temperature changes.
• The greater N, the less interaction strength it takes, as measured by the $G-$value, to make the system a superconductor.
• Additionally, in the exponential Boltzmann factor of the partition function, N ”works” in exactly the opposite fashion, as does T (see Equation (16)), a fact not highlighted before, as far as we know.

Further aspects of our work to be emphasized are

• Figure 2 teaches us that temperature-induced partial superconductivity may exist even for a pairing coupling constant $G=0$.
• A second phenomenon to be highlighted is that the degree of partial superconductivity increases with N for a fixed G.
• Figure 3 displays the mean number of unpaired fermions $<\nu >$ versus N for several temperatures T.
• We see that at low temperatures $<\nu >$ eventually vanishes for high enough N.
• The larger T, the larger the N value necessary to achieve this null result.
• Figure 4 and Figure 5 plot $<\nu >$ versus G for several N’s. The first for a low temperature, the second for an intermediate one.
• Note that in the second graph, the temperature erases ”sigmoidal” features for low enough N, but they eventually appear at $N=32$.
• The N dependent effects are duly highlighted in these two graphs.
• Our main result is that we can exactly match the behavior of the mean value of the number of unpaired fermions $<\nu >=1-X$ with that of the mean occupation number of free fermions of single particle energies ${ϵ}_i$ (see Equations (29) and (30)), as depicted by Figure 6 and Figure 7.
• Two parameters ${\mu }_N\left(T\right)$ and $b_N\left(T\right)$ are needed for this fitting.
• Their behaviors are illustrated by Figure 8 and Figure 9, respectively.
• Note that it is the product $b_{N}N$ that plays a temperature role, and that $b_N$ itself strongly depends upon N, as seen in Figure 9, so that, in the fitting process, $N\to \infty$ ”works” as if $\beta \to \infty$ .

In summary, some peculiar N-dependent effects of interacting (finite) paired fermions have been illustrated in this effort. Note that, in nature, the heaviest nuclei (transuranic ones) are all superconductors if they are even–even [5]. Additionally, the rare earth nuclei are rather heavy, in which the same occurs [5].