Assessing the Precision of Quantum Simulation of Many-Body Effects in Atomic Systems Using the Variational Quantum Eigensolver Algorithm
Abstract
1. Introduction
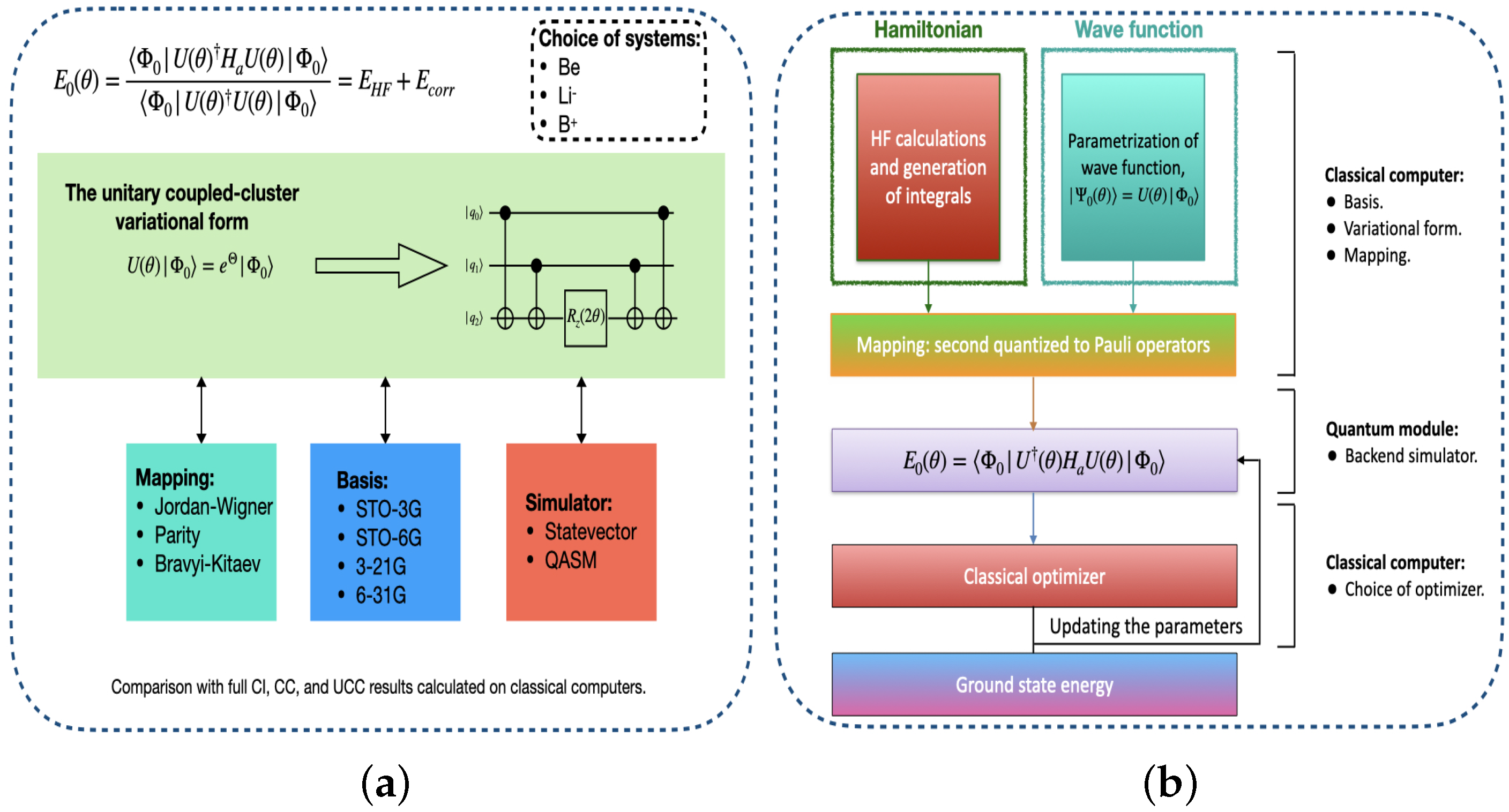
2. Theory
2.1. The Variational Quantum Eigensolver Algorithm
2.2. Many-Body Methods
3. Methodology
4. Results and Discussion
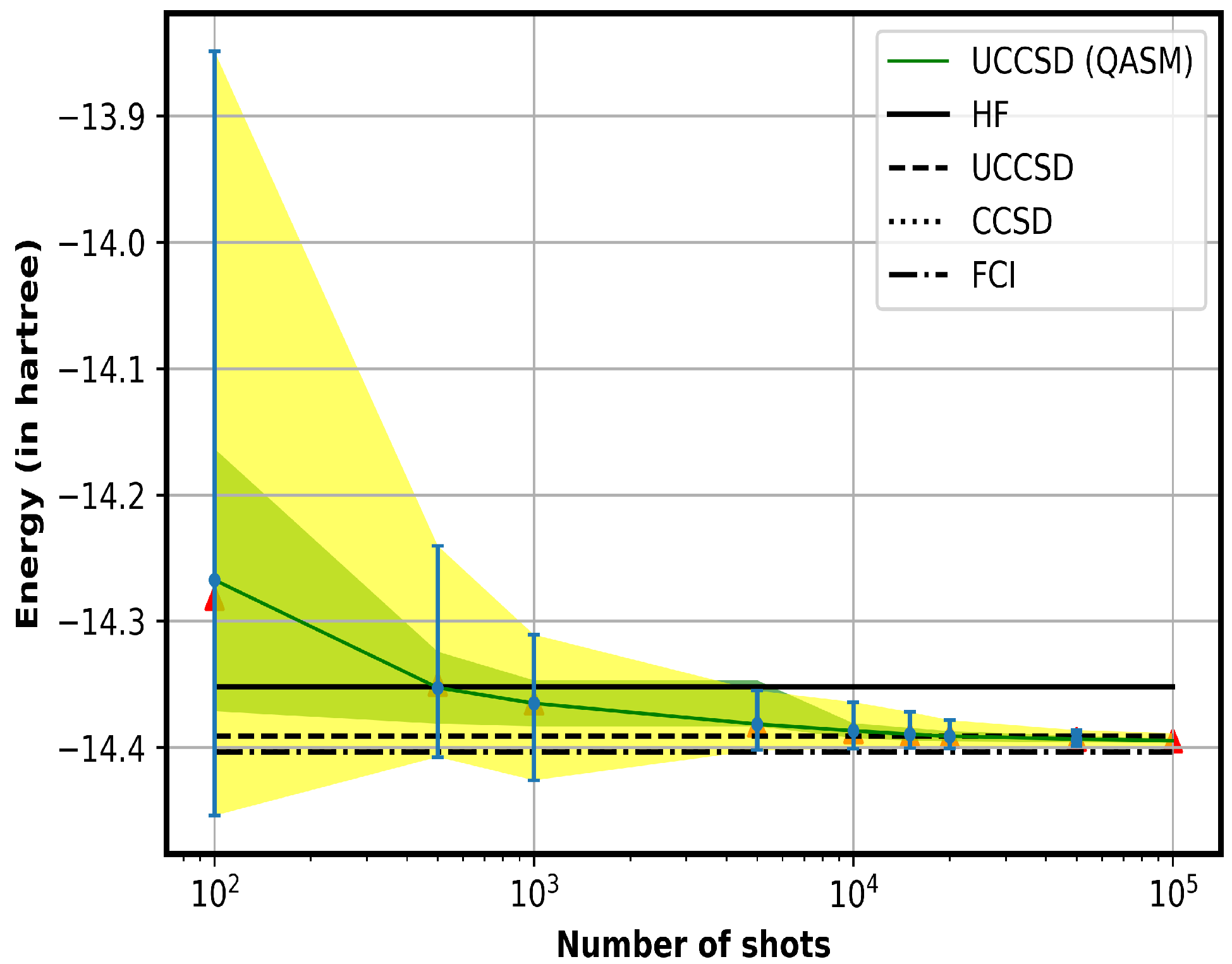
4.1. Analysis of the Required Number of Shots for QASM Calculations
4.2. Analysis of Errors Due to Trotter Number
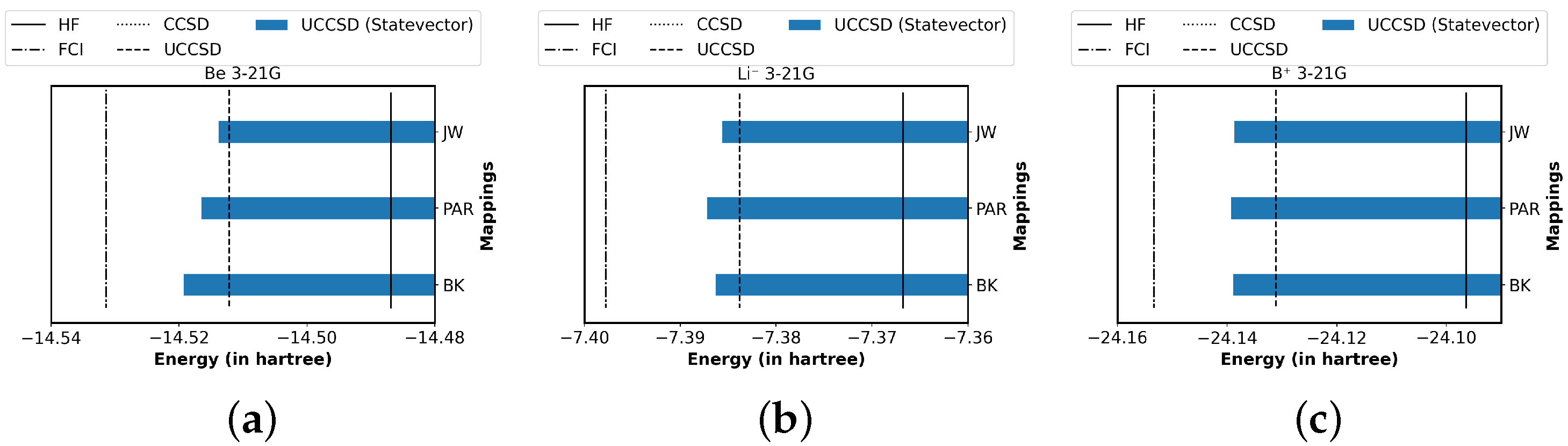
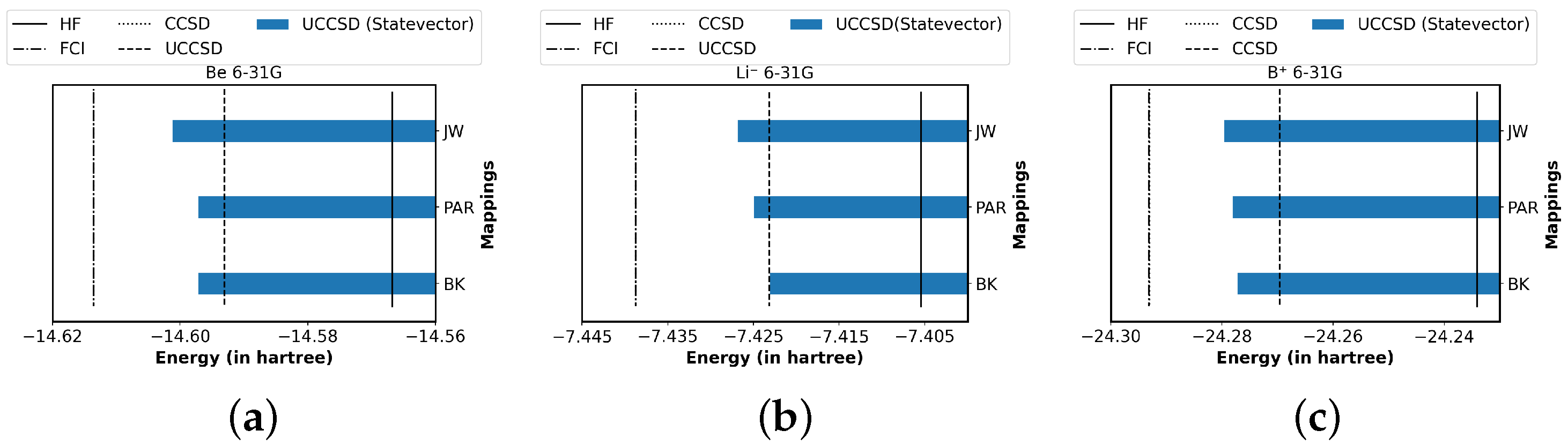
4.3. Main Results and Analysis
4.4. Further Findings from Obtained Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deutsch, I.H. Harnessing the Power of the Second Quantum Revolution. Phys. Rev. X Quantum 2020, 1, 020101. [Google Scholar] [CrossRef]
- McArdle, S.; Endo, S.; Aspuru-Guzik, A.; Benjamin, S.C.; Yuan, X. Quantum Computational Chemistry. Rev. Mod. Phys. 2020, 92, 015003. [Google Scholar] [CrossRef]
- Cade, C.; Mineh, L.; Montanaro, A.; Stanisic, S. Strategies for Solving the Fermi-Hubbard Model on Near-Term Quantum Computers. Phys. Rev. B 2020, 102, 235122. [Google Scholar] [CrossRef]
- Nam, Y.; Chen, J.S.; Pisenti, N.C.; Wright, K.; Delaney, C.; Maslov, D.; Kim, J. Ground-State Energy Estimation of the Water Molecule on a Trapped-Ion Quantum Computer. Nature J. Phys. Q. Info. 2020, 6, 33. [Google Scholar] [CrossRef]
- Takeshita, T.; Rubin, N.C.; Jiang, Z.; Lee, E.; Babbush, R.; McClean, J.R. Increasing the Representation Accuracy of Quantum Simulations of Chemistry without Extra Quantum Resources. Phys. Rev. X 2020, 10, 011004. [Google Scholar] [CrossRef]
- Low, G.H.; Chuang, I.L. Hamiltonian Simulation by Qubitization. Quantum 2019, 3, 163. [Google Scholar] [CrossRef]
- Sawaya, N.P.D.; Menke, T.; Kyaw, T.H.; Johri, S.; Aspuru-Guzik, A.; Guerreschi, G.G. Resource-Efficient Digital Quantum Simulation of d-Level Systems for Photonic, Vibrational, and Spin-s Hamiltonians. Nature J. Phys. Q. Info. 2020, 6, 49. [Google Scholar] [CrossRef]
- Chivilikhin, D.; Samarin, A.; Ulyantsev, V.; Iorsh, I.; Oganov, A.R.; Kyriienko, O. MoG-VQE: Multiobjective Genetic Variational Quantum Eigensolver. arXiv 2020, arXiv:2007.04424. [Google Scholar]
- Abrams, D.S.; Lloyd, S. Simulation of Many-Body Fermi Systems on a Universal Quantum Computer. Phys. Rev. Lett. 1997, 79, 2586. [Google Scholar] [CrossRef]
- Abrams, D.S.; Lloyd, S. Quantum Algorithm Providing Exponential Speed Increase for Finding Eigenvalues and Eigenvectors. Phys. Rev. Lett. 1999, 83, 5162. [Google Scholar] [CrossRef]
- Saue, T.; Bast, R.; Gomes, A.S.P.; Jensen, H.J.A.; Visscher, L.; Aucar, I.A.; van Stralen, J.N. The DIRAC Code for Relativistic Molecular Calculations. J. Chem. Phys. 2020, 152, 204104. [Google Scholar] [CrossRef] [PubMed]
- Aspuru-Guzik, A.; Dutoi, A.D.; Love, P.J.; Gordon, M.H. Simulated Quantum Computation of Molecular Energies. Science 2005, 309, 1704. [Google Scholar] [CrossRef] [PubMed]
- Lanyon, B.P.; Whitfield, J.D.; Gillett, G.G.; Goggin, M.E.; Almeida, M.P.; Kassal, I.; White, A.G. Towards Quantum Chemistry on a Quantum Computer. Nat. Chem. 2010, 2, 106. [Google Scholar] [CrossRef]
- Mohammadbagherpoor, H.; Oh, Y.H.; Dreher, P.; Singh, A.; Yu, X.; Rindos, A.J. An Improved Implementation Approach for Quantum Phase Estimation on Quantum Computers. arXiv 2019, arXiv:1910.11696. [Google Scholar]
- Paesani, S.; Gentile, A.A.; Santagati, R.; Wang, J.; Wiebe, N.; Tew, D.P.; O’Brien, J.L.; Thompson, M.G. Experimental Bayesian Quantum Phase Estimation on a Silicon Photonic Chip. Phys. Rev. Lett. 2017, 118, 100503. [Google Scholar] [CrossRef]
- Yung, M.H.; Casanova, J.; Mezzacapo, A.; McClean, J.R.; Lamata, L.; Aspuru-Guzik, A.; Solano, E. From Transistor to Trapped-Ion Computers for Quantum Chemistry. Sci. Rep. 2014, 4, 3589. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.R.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A Variational Eigenvalue Solver on a Photonic Quantum Processor. Nat. Comm. 2014, 5, 4213. [Google Scholar] [CrossRef]
- Clarke, J.; Wilhelm, K.F. Superconducting Quantum Bits. Nature 2008, 453, 1031. [Google Scholar] [CrossRef]
- Cirac, J.I.; Zoller, P. Quantum Computations with Cold Trapped Ions. Phys. Rev. Lett. 1995, 74, 4091. [Google Scholar] [CrossRef]
- Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-Efficient Variational Quantum Eigensolver for Small Molecules and Quantum Magnets. Nature 2017, 549, 242. [Google Scholar] [CrossRef]
- Wang, H.; Kais, S.; Aspuru-Guzik, A.; Hoffmann, M.R. Quantum Algorithm for Obtaining the Energy Spectrum of Molecular Systems. Phys. Chem. Chem. Phys. 2008, 10, 5388. [Google Scholar] [CrossRef] [PubMed]
- Colless, J.I.; Ramasesh, V.V.; Dahlen, D.; Blok, M.S.; Kimchi-Schwartz, M.E.; McClean, J.R.; Carter, J.; de Jong, W.A.; Siddiqi, I. Computation of Molecular Spectra on a Quantum Processor with an Error-Resilient Algorithm. Phys. Rev. X 2018, 8, 011021. [Google Scholar] [CrossRef]
- Wang, Y.; Dolde, F.; Biamonte, J.; Babbush, R.; Bergholm, V.; Yang, S.; Wrachtrup, J. Quantum Simulation of Helium Hydride Cation in a Solid-State Spin Register. Am. Chem. Soc. Nano 2015, 9, 7769. [Google Scholar] [CrossRef] [PubMed]
- Romero, J.; Babbush, R.; McClean, J.R.; Hempel, C.; Love, P.J.; Aspuru-Guzik, A. Strategies for Quantum Computing Molecular Energies using the Unitary Coupled Cluster Ansatz. Quantum Sci. Technol. 2019, 4, 014008. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, R.P.; Behera, B.K.; Panigrahi, P.K. Quantum Simulation of Negative Hydrogen Ion using Variational Quantum Eigensolver on IBM Quantum Computer. arXiv 2019, arXiv:1903.03454v1. [Google Scholar]
- Schmidt-Kaler, F.; Pfau, T.; Schmelcher, P.; Schleich, W. Focus on Atom Optics and its Applications. New J. Phys. 2010, 12, 065014. [Google Scholar] [CrossRef]
- Chou, C.W.; Hume, D.B.; Rosenband, T.; Wineland, D.J. Optical Clocks and Relativity. Science 2010, 329, 1630. [Google Scholar] [CrossRef]
- Wansbeek, L.W.; Sahoo, B.K.; Timmermans, R.G.E.; Jungmann, K.; Das, B.P.; Mukherjee, D. Atomic Parity Nonconservation in Ra+. Phys. Rev. A 2008, 78, 050501. [Google Scholar] [CrossRef]
- Tiecke, T.G.; Thompson, J.D.; De Leon, N.P.; Liu, L.R.; Vuletic, V.; Lukin, M.D. Nanophotonic Quantum Phase Switch with a Single Atom. Nature 2014, 508, 241. [Google Scholar] [CrossRef]
- Fortson, N. Possibility of Measuring Parity Nonconservation With a Single Trapped Atomic Ion. Phys. Rev. Lett. 1993, 70, 2383. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Das, B.P. Relativistic Normal Coupled-Cluster Theory for Accurate Determination of Electric Dipole Moments of Atoms: First Application to the 199Hg Atom. Phys. Rev. Lett. 2018, 120, 203001. [Google Scholar] [CrossRef] [PubMed]
- Sur, C.; Latha, K.V.P.; Sahoo, B.K.; Chaudhuri, R.K.; Das, B.P.; Mukherjee, D. Electric Quadrupole Moments of the D States of Alkaline-Earth-Metal Ions. Phys. Rev. Lett. 2006, 96, 193001. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, B.K.; Das, B.P.; Spiesberger, H. New Physics Constraints from Atomic Parity Violation in 133Cs. Phys. Rev. D 2021, 103, L111303. [Google Scholar] [CrossRef]
- Kastberg, A.; Aoki, A.; Sahoo, B.K.; Sakemi, Y.; Das, B.P. Optical-Lattice-Based Method for Precise Measurements of Atomic Parity Violation. Phys. Rev. A 2019, 100, 050101. [Google Scholar] [CrossRef]
- Sakurai, A.; Sahoo, B.K.; Asahi, K.; Das, B.P. Relativistic Many Body Theory of the Electric Dipole Moment of 129Xe and its Implications for Probing New Physics Beyond the Standard Model. Phys. Rev. A 2019, 100, 020502. [Google Scholar] [CrossRef]
- Prasannaa, V.S.; Mitra, R.; Sahoo, B.K. Reappraisal of P, T-Odd Parameters from the Improved Calculation of Electric Dipole Moment of 225Ra Atom. J. Phys. B 2020, 53, 195004. [Google Scholar] [CrossRef]
- Guo, X.T.; Yu, Y.-M.; Liu, Y.; Suo, B.B.; Sahoo, B.K. Electric dipole and quadrupole properties of Cd atom for atomic clock applications. Phys. Rev. A 2021, 103, 013109. [Google Scholar] [CrossRef]
- Oskay, W.H.; Itano, W.M.; Bergquist, J.C. Measurement of the 199Hg+ 5d9 6s22D5/2 Electric Quadrupole Moment and a Constraint on the Quadrupole Shift. Phys. Rev. Lett. 2006, 94, 163001. [Google Scholar]
- Rosenband, T.; Schmidt, P.O.; Hume, D.B.; Itano, W.M.; Fortier, T.M.; Stalnaker, J.E.; Kim, K.; Diddams, S.A.; Koelemeij, J.C.J.; Bergquist, J.C.; et al. Observation of the 1S0 to 3P0 Clock Transition in 27Al+. Phys. Rev. Lett. 2007, 98, 220801. [Google Scholar] [CrossRef]
- Wilpers, G.; Oates, C.W.; Diddams, S.A.; Bartels, A.; Fortier, T.M.; Oskay, W.H.; Hollberg, L. Absolute frequency measurement of the neutral 40Ca optical frequency standard at 657 nm based on microkelvin atoms. Metrologia 2007, 44, 146. [Google Scholar] [CrossRef][Green Version]
- Barber, Z.W.; Hoyt, C.; Oates, C.; Hollberg, L.; Taichenachev, A.; Yudin, V. Direct Excitation of the Forbidden Clock Transition in Neutral 174Yb Atoms Confined to an Optical Lattice. Phys. Rev. Lett. 2006, 96, 083002. [Google Scholar] [CrossRef] [PubMed]
- Ludlow, A.D.; Zelevinsky, T.; Campbell, G.K.; Blatt, S.; Boyd, M.M.; de Miranda, M.H.G.; Martin, M.J.; Thomsen, J.W.; Foreman, S.M.; Ye, J.; et al. Sr Lattice Clock at 1 × 1016 Fractional Uncertainty by Remote Optical Evaluation with a Ca Clock. Science 2008, 319, 1805. [Google Scholar] [CrossRef] [PubMed]
- Jefferts, S.R.; Shirley, J.; Parker, T.E.; Heavner, T.P.; Meekhof, D.M.; Nelson, C.; Walls, F.L. Accuracy evaluation of NIST-F1. Metrologia 2002, 39, 321. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Ohayon, B. Benchmarking Many-body Approaches for the Determination of Isotope Shift Constants: Application to the Li, Be+ and Ar15+ Isoelectronic Systems. Phys. Rev. A 2021, 103, 052802. [Google Scholar] [CrossRef]
- Koszorús, Á; Yang, X.F.; Jiang, W.G.; Novario, S.J.; Bai, S.W.; Billowes, J.; Wilkins, S.G. Charge radii of exotic potassium isotopes challenge nuclear theory and the magic character of N=32. Nature Phys. 2021, 17, 439. [Google Scholar]
- Yu, Y.-M.; Sahoo, B.K.; Suo, B.B. Ground state gj factors of the Cd+, Yb+ and Hg+ ions. Phys. Rev. A 2020, 102, 062824. [Google Scholar] [CrossRef]
- Lindgren, I.; Morrison, J. Atomic Many-Body Theory; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Kellö, V.; Urban, M.; Sadlej, A.J. Electric Dipole Polarizabilities of Negative Ions of the Coinage Metal Atoms. Chem. Phys. Lett. 1996, 253, 383. [Google Scholar] [CrossRef]
- Sahoo, B.K. Determination of the Dipole Polarizability of the Alkali-metal Negative Ions. Phys. Rev. A 2020, 102, 022820. [Google Scholar] [CrossRef]
- Andersen, T. Low-energy Outer-shell Photodetachment of the Negative Ion of Boron. Phys. Reps. 2004, 394, 157. [Google Scholar]
- Massey, H.S.W. Negative Ions, 3rd ed.; Cambridge University Press: London, UK; Cambridge University Press: New York, NY, USA, 1976. [Google Scholar]
- Dudinikov, V. Development and Applications of Negative Ion Sources; Springer Series on Atomic, Optical, and Plasma Physics, v. 110, Switzerland; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Lim, I.S.; Schwerdtfeger, P. Four-component and Scalar Relativistic Douglas-Kroll Calculations for Static Dipole Polarizabilities of the Alkaline-earth-metal Elements and their Ions from Can to Ran (n=0,+1,+2). Phys. Rev. A 2004, 70, 062501. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Das, B.P. Relativistic Coupled-cluster Studies of Dipole Polarizabilities in Closed-shell Atoms. Phys. Rev. A 2008, 77, 062516. [Google Scholar] [CrossRef]
- Singh, Y.; Sahoo, B.K.; Das, B.P. Correlation Trends in the Ground-state Static Electric Dipole Polarizabilities of Closed-shell Atoms and Ions. Phys. Rev. A 2013, 88, 062504. [Google Scholar] [CrossRef]
- Puchalski, M.; Komasa, J.; Pachucki, K. Testing Quantum Electrodynamics in the Lowest Singlet States of the Beryllium Atom. Phys. Rev. A 2013, 87, 030502. [Google Scholar] [CrossRef]
- Cook, E.C.; Vira, A.D.; Patterson, C.; Livernois, E.; Williams, W.D. Testing Quantum Electrodynamics in the Lowest Singlet State of Neutral Beryllium-9. Phys. Rev. Lett. 2018, 121, 053001. [Google Scholar] [CrossRef]
- Puchalski, M.; Pachucki, K.; Komasa, J. Isotope Shift in a Beryllium Atom, Phys. Rev. A 2014, 89, 012506. [Google Scholar] [CrossRef]
- McGeoch, M.W.; Sclier, R.E. Generation of Lithium Negative Ions in a Volume Source with Optical Pumping. J. Appl. Phys. 1987, 61, 4955. [Google Scholar] [CrossRef]
- Das, B.P.; Idrees, M. Some Theoretical Aspects of the Group-IIIA-ion Atomic Clocks: Intercombination Transition Probabilities. Phys. Rev. A 1990, 42, 6900. [Google Scholar] [CrossRef]
- Wineland, D.J.; (Department of Radiology and Nuclear Medicine, University Hospital Basel, Basel, Switzerland). Personal Communication, 2014.
- Gao, Q.; Nakamura, H.; Gujarati, T.P.; Jones, G.O.; Rice, J.E.; Wood, S.P.; Yamamoto, N. Computational Investigations of the Lithium Superoxide Dimer Rearrangement on Noisy Quantum Devices. arXiv 2019, arXiv:1906.10675. [Google Scholar] [CrossRef]
- Lolur, P.; Rahm, M.; Skogh, M.; Garcia-Alvarez, L.; Wendin, G. Benchmarking the Variational Quantum Eigensolver through Simulation of the Ground State Energy of Prebiotic Molecules on High-Performance Computers. arXiv 2021, arXiv:2010.1357. [Google Scholar]
- Zha, X.H.; Zhang, C.; Fan, D.; Xu, P.; Du, S.; Zhang, R.-Q.; Fu, C. The Impacts of Optimization Algorithm and Basis Size on the Accuracy and Efficiency of Variational Quantum Eigensolver. arXiv 2021, arXiv:2006.15852. [Google Scholar]
- Armaos, V.; Badounas, D.A.; Deligiannis, P.; Lianos, K. Computational Chemistry on Quantum Computers: Ground State Estimation. Appl. Phys. A 2020, 126, 625. [Google Scholar] [CrossRef]
- Tavares, C.; Oliveira, S.; Fernes, V.; Postnikov, A.; Vasilevskiy, M.I. Calculation of the Ground-state Stark Effect in Small Molecules Using the Variational Quantum Eigensolver. arXiv 2021, arXiv:2103.11743. [Google Scholar]
- Jones, N.C.; Whitfield, J.D.; McMahon, P.L.; Yung, M.H.; Meter, R.V.; Aspuru-Guzik, A.; Yamamoto, Y. Faster Quantum Chemistry Simulation on Fault-Tolerant Quantum Computers. N. J. Phys. 2012, 14, 115023. [Google Scholar]
- Seeley, J.T.; Richard, M.J.; Love, P.J. The Bravyi–Kitaev Transformation for Quantum Computation of Electronic Structure. J. Chem. Phys. 2012, 137, 224109. [Google Scholar] [CrossRef]
- Bravyi, S.; Gambetta, J.M.; Mezzacapo, A.; Temme, K. Tapering off Qubits to Simulate Fermionic Hamiltonians. arXiv 2017, arXiv:1701.08213. [Google Scholar]
- Bartlett, R.J.; Musial, M. Coupled-Cluster Theory in Quantum Chemistry. Revs. Mod. Phys. 2007, 79, 291. [Google Scholar] [CrossRef]
- Das, B.P.; Nayak, M.K.; Abe, M.; Prasannaa, V.S. Relativistic Many-Body Aspects of the Electron Electric Dipole Moment Searches Using Molecules. In Handbook of Relativistic Quantum Chemistry; Liu, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kutzelnigg, W. Quantum chemistry in Fock space. I. The universal wave and energy operators. J. Chem. Phys. 1982, 77, 3081. [Google Scholar] [CrossRef]
- Sun, Q.; Berkelbach, T.C.; Blunt, N.S.; Booth, G.H.; Guo, S.; Li, Z.; Chan, G.K.L. PySCF: The Python-Based Simulations of Chemistry Framework, Wiley Interdisciplinary Reviews: Computational Molecular. Science 2017, 8, e1340. [Google Scholar]
- McClean, J.R.; Rubin, N.C.; Sung, K.J.; Kivlichan, I.D.; Bonet-Monroig, X.; Cao, Y.; Babbush, R. OpenFermion: The Electronic Structure Package for Quantum Computers. arXiv 2017, arXiv:1710.07629. [Google Scholar] [CrossRef]
- Boys, S.F. Electronic Wave Functions - I. A General Method of Calculation for the Stationary States of Any Molecular System. Proc. R. Soc. Lond. A 1950, 200, 542. [Google Scholar]
- Hehre, W.J.; Stewart, R.F.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. I. Use of Gaussian Expansions of Slater-Type Atomic Orbitals. J. Chem. Phys. 1969, 51, 2657. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724. [Google Scholar] [CrossRef]
- Powell, M. Direct Search Algorithms for Optimization Calculations. Acta Numer. 1998, 7, 287. [Google Scholar] [CrossRef]
- Rattew, A.G.; Hu, S.; Pistoia, M.; Chen, R.; Wood, S. A Domain-agnostic, Noise-resistant, Hardware-efficient Evolutionary Variational Quantum Eigensolver. arXiv 2020, arXiv:1910.09694. [Google Scholar]
- Bös, J. Numerical Optimization of the Thickness Distribution of Three-Dimensional Structures With Respect to their Structural Acoustic Properties. Struct. Multidiscip. Optim. 2006, 32, 30. [Google Scholar] [CrossRef]
- Abraham, H. Qiskit: An Open-source Framework for Quantum Computing. 2019. Available online: https://zenodo.org/record/2562111#.YlamE-hBxPY (accessed on 1 December 2021). [CrossRef]
- Gokhale, P.; Angiuli, O.; Ding, Y.; Gui, K.; Tomesh, T.; Suchara., M.; Martonosi, M.; Chong, F.T. O(N3) Measurement Cost for Variational Quantum Eigensolver on Molecular Hamiltonians. IEEE Trans. Quantum Eng. IEEE Trans. Quantum Eng. 2020, 1, 1. [Google Scholar]
- Izmaylov, A.F.; Yen, T.C.; Ryabinkin, I.G. Revising the Measurement Process in the Variational Quantum Eigensolver: Is It Possible to Reduce the Number of Separately Measured Operators? Chem. Sci. 2019, 10, 3746. [Google Scholar] [CrossRef]
- Verteletskyi, V.; Yen, T.C.; Izmaylov, A.F. Measurement Optimization in the Variational Quantum Eigensolver using a Minimum Clique Cover. J. Chem. Phys. 2020, 152, 124114. [Google Scholar] [CrossRef]
- Zhao, A.; Tranter, A.; Kirby, W.M.; Ung, S.F.; Miyake, A.; Love, P.J. Measurement Reduction in Variational Quantum Algorithms. Phys. Rev. A 2020, 101, 062322. [Google Scholar] [CrossRef]
- Al-Mohy, A.H.; Higham, N.J. Computing the Action of the Matrix Exponential, with an Application to Exponential Integrators. SIAM J. Sci. Comput. 2011, 33, 488. [Google Scholar] [CrossRef]
- Gambetta, J.M. IBM’s Roadmap for Scaling Quantum Technology. Available online: https://www.ibm.com/blogs/research/2020/09/ibm-quantum-roadmap/ (accessed on 1 December 2021).



| Map | Method | Backend | Be | Li | B |
|---|---|---|---|---|---|
| HF | −14.351880 | −7.213273 | −23.948470 | ||
| ClC | FCI | −14.403655 (−0.051775) | −7.253791 (−0.040518) | −24.009814 (−0.061344) | |
| CCSD | −14.403651 (−0.051771) | −7.253786 (−0.040513) | −24.009811 (−0.061341) | ||
| UCCSD | −14.391028 (−0.039148) | −7.244008 (−0.030735) | −23.994757 (−0.046287) | ||
| UCCSD | QASM | −14.388109 (−0.036229) | −7.244270 (−0.030997) | −24.002041 (−0.053571) | |
| JW | ( in %) | () | () | () | |
| UCCSD | SV | −14.403490 (−0.05161) | −7.253682 (−0.040409) | −24.009652 (−0.061182) | |
| ( in %) | () | () | () | ||
| UCCSD | QASM | −14.394762 (−0.042882) | −7.243156 (−0.029883) | −23.992675 (−0.044205) | |
| PAR | ( in %) | () | () | () | |
| UCCSD | SV | −14.403446 (−0.051566) | −7.253611 (−0.040338) | −24.009631 (−0.061161) | |
| ( in %) | () | () | () | ||
| UCCSD | QASM | −14.392365 (−0.040485) | −7.243775 (−0.030502) | −23.998311 (−0.049841) | |
| BK | ( in %) | () | () | () | |
| UCCSD | SV | −14.403539 (−0.051659) | −7.253681 (−0.040408) | −24.009500 (−0.06103) | |
| ( in %) | () | () | () |
| Map | Method | Backend | Be | Li | B |
|---|---|---|---|---|---|
| HF | −14.503361 | −7.295246 | −24.190562 | ||
| ClC | FCI | −14.556088 (−0.052727) | −7.336640 (−0.041394) | −24.252889 (−0.062327) | |
| CCSD | −14.556083 (−0.052722) | −7.336635 (−0.041389) | −24.252884 (−0.062322) | ||
| UCCSD | −14.543257 (−0.039896) | −7.326677 (−0.031431) | −24.237615 (−0.047053) | ||
| UCCSD | QASM | −14.544091 (−0.04073) | −7.326529 (−0.031283) | −24.227757 (−0.037195) | |
| JW | ( in %) | () | () | () | |
| UCCSD | SV | −14.555940 (−0.052579) | −7.336485 (−0.041239) | −24.252614 (−0.062052) | |
| ( in %) | () | () | () | ||
| UCCSD | QASM | −14.541160 (−0.037799) | −7.321997 (−0.026751) | −24.222150 (−0.031588) | |
| PAR | ( in %) | () | () | () | |
| UCCSD | SV | −14.555943 (−0.052582) | −7.336510 (−0.041264) | −24.252623 (−0.062061) | |
| ( in %) | () | () | () | ||
| UCCSD | QASM | −14.548048 (−0.044687) | −7.321989 (−0.026743) | −24.241578 (−0.051016) | |
| BK | ( in %) | () | () | () | |
| UCCSD | SV | −14.555848(−0.052487) | −7.336462 (−0.041216) | −24.252669 (−0.062107) | |
| ( in %) | () | () | () |
| Map | Method | Backend | Be | Li | B |
|---|---|---|---|---|---|
| HF | −14.486820 | −7.366760 | −24.096376 | ||
| ClC | FCI | −14.531444 (−0.044624) | −7.397779 (−0.031019) | −24.153344 (−0.056968) | |
| CCSD | −14.531416 (−0.044596) | −7.397757 (−0.030997) | −24.153311 (−0.056935) | ||
| UCCSD | −14.512130 (−0.02531) | −7.383818 (−0.017058) | −24.131129 (−0.034753) | ||
| JW | UCCSD | SV | −14.513922 (−0.027102) | −7.385692 (−0.018932) | −24.138757 (−0.042381) |
| ( in %) | () | () | () | ||
| PAR | UCCSD | SV | −14.516600 (−0.02978) | −7.387247 (−0.020487) | −24.139378 (−0.043002) |
| ( in %) | () | () | () | ||
| BK | UCCSD | SV | −14.519369 (−0.032549) | −7.386396 (−0.019636) | −24.139013 (−0.042637) |
| ( in %) | () | () | () |
| Map | Method | Backend | Be | Li | B |
|---|---|---|---|---|---|
| HF | −14.566764 | −7.405387 | −24.234041 | ||
| ClC | FCI | −14.613545 (−0.046781) | −7.438753 (−0.033366) | −24.293125 (−0.059084) | |
| CCSD | −14.613518 (−0.046754) | −7.438739 (−0.033352) | −24.293096 (−0.059055) | ||
| UCCSD | −14.593071 (−0.026307) | −7.423171 (−0.017784) | −24.269635 (−0.035594) | ||
| JW | UCCSD | SV | −14.601323 (−0.034559) | −7.426886 (−0.021499) | −24.279715 (−0.045674) |
| ( in %) | () | () | () | ||
| PAR | UCCSD | SV | −14.597296 (-0.111) | −7.425017 (-0.185) | −24.278157 (-0.061) |
| ( in %) | (−0.030532) | (−0.01963) | (−0.044116) | ||
| BK | UCCSD | SV | −14.597296 (−0.030532) | −7.423154 (−0.017767) | −24.277312 (−0.043271) |
| ( in %) | () | () | () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sumeet; Prasannaa V, S.; Das, B.P.; Sahoo, B.K. Assessing the Precision of Quantum Simulation of Many-Body Effects in Atomic Systems Using the Variational Quantum Eigensolver Algorithm. Quantum Rep. 2022, 4, 173-192. https://doi.org/10.3390/quantum4020012
Sumeet, Prasannaa V S, Das BP, Sahoo BK. Assessing the Precision of Quantum Simulation of Many-Body Effects in Atomic Systems Using the Variational Quantum Eigensolver Algorithm. Quantum Reports. 2022; 4(2):173-192. https://doi.org/10.3390/quantum4020012
Chicago/Turabian StyleSumeet, Srinivasa Prasannaa V, Bhanu Pratap Das, and Bijaya Kumar Sahoo. 2022. "Assessing the Precision of Quantum Simulation of Many-Body Effects in Atomic Systems Using the Variational Quantum Eigensolver Algorithm" Quantum Reports 4, no. 2: 173-192. https://doi.org/10.3390/quantum4020012
APA StyleSumeet, Prasannaa V, S., Das, B. P., & Sahoo, B. K. (2022). Assessing the Precision of Quantum Simulation of Many-Body Effects in Atomic Systems Using the Variational Quantum Eigensolver Algorithm. Quantum Reports, 4(2), 173-192. https://doi.org/10.3390/quantum4020012






