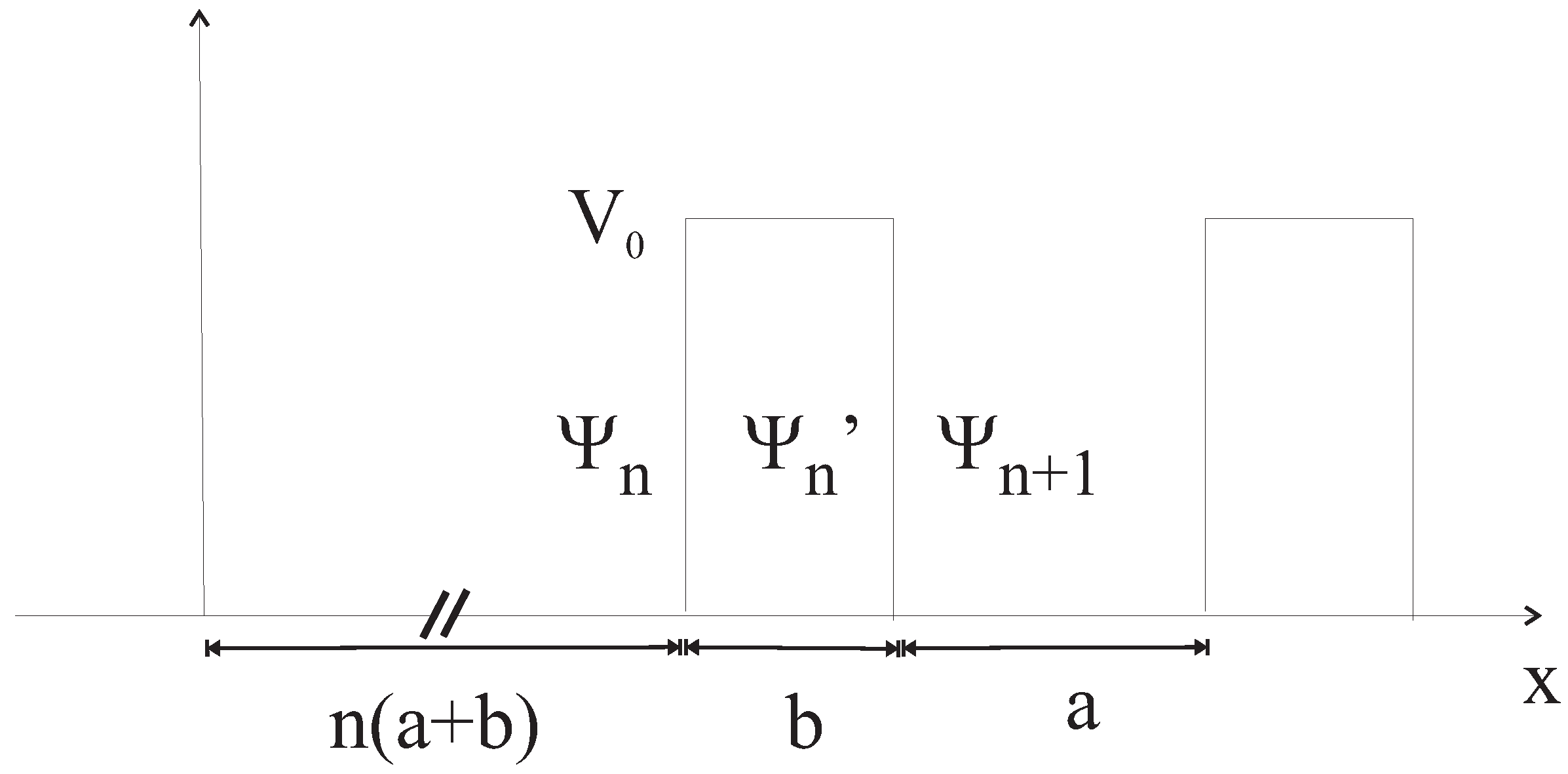1. Introduction
The tunneling effect is one of the most typical features of quantum mechanics, and a clear demonstration of the wavelike behavior of matter at a microscopic scale (at least in the context of the standard Copenhagen interpretation). Historically, it was first observed in the decay of nuclei [
1] and in field-effect emission of electrons from metals [
2]. Later it was exploited, among many other applications, in Zener diodes [
3,
4] and in scanning tunneling microscopes [
5]. Tunneling processes involving macroscopic wavefunctions in superconductors give rise to the Josephson effect [
6], which has been applied to SQUIDs (super quantum interference devices), frequency standards, quantum circuits and q-bits. Long-range tunneling has an important role in chemistry and biology [
7].
When the tunneling effect involves single particles or multiple incoherent particles, it can be usually described by theoretical models based on a Schrödinger equation and its exact or approximate solutions. We thus have a theory in which the wavefunction in the barrier is known and we can evaluate in principle the probability for the tunneling particles to be located at any position in the classically forbidden region. At the same time, we can compute the probability density and the probability current , which satisfy the continuity relation thanks to a general property of the solutions of the Schrödinger equation.
By inserting the source into the Maxwell equations we can then compute in principle the e.m. field generated by the tunneling current. In most cases this field is not detectable, because the number of tunneling particles is small, and their current too. Actually, for tunneling processes at the atomic level, e.m. emissions are more properly evaluated with quantum perturbation theory than by solving Maxwell equations.
On the other hand, when the tunneling involves a large number of particles, it cannot be described by a simple Schrödinger equation. This is the case of tunneling in condensed matter, be it incoherent or coherent (for coherent matter with a macroscopic wavefunction there are some further specifications, see below). In this case we do not know the wavefunction in the barrier and we usually cannot locate the particles in the barrier with a definite probability as a function of space and time; we only know a tunneling probability, or more generally a tunneling Hamiltonian operator that can be applied between initial and final states on the two sides of the barrier.
For condensed matter systems it is generally possible to define a quantum field theory with local interactions, which includes charge and current operators satisfying a local conservation relation analogous to
. The next step, however, is often to introduce approximations and effective models with non-local interactions. Furthermore, even in the original local theory, quantum anomalies may occur after renormalization, spoiling the symmetry and conservation properties of the original Hamiltonian [
8,
9,
10]. In most approaches to quantum transport there is no attempt to compute the wavefunction of tunneling particles in the barrier. The issue of tunneling time has been lively debated, and it is both based on experimental results and theoretical models; according to some authors, in certain cases the tunneling time cannot be distinguished from zero [
11,
12,
13].
A recent series of sophisticated numerical first-principles calculations of the local current density in organic molecular chains and carbon wires [
14,
15,
16,
17] confirm the existence of discontinuities in the stationary local flux, which are not eliminated by an enlargement of the wavefunctions eigenbasis employed. Already in 2008, Wang et al. [
18] had shown that in such cases the Landauer-Büttiker formalism leads to restore conservation by the introduction of a non-local secondary current of the form
, where
, with our notation, in the stationary case. The applications treated by Wang et al. concerned some idealized materials and graphene [
19], while Gardner et al. [
16,
17] compute explicitly the part of the flux that does not follow molecular bonds for specific saturated molecules.
Nozaki et al. [
20] point out that a precise knowledge of magnetic field patterns in molecular devices can be important for applications to molecular magnets. This leads us to ask a logical theoretical question (but also with possible practical implications): how should one compute the e.m. field of a microscopic current that is not locally conserved? A first answer can be, that since the non-local extension of the current proposed by Wang restores conservation, the Maxwell equations can be applied to such a “completed” current.
A more complete and powerful approach, however, consists of extending Maxwell’s theory along the lines originally proposed by Aharonov and Bohm [
21] and by Ohmura [
22]. This theory allows us to compute e.m. fields, compatibly with Special Relativity, even when charge is not locally conserved, avoiding the need to impose a “taboo on teleportation”, at least in phenomenological models. It also applies to generalized microscopic models with fractional dimensions and non-local potentials. There has been much work on this extended theory over the last years, and many technical aspects have been clarified [
21,
23,
24,
25,
26,
27,
28,
29]. The final recipe is unique and relatively simple, considering that some non-local expressions involving the sources are unavoidable. In
Section 2 of this work we recall the extended equations for the e.m. fields and their far-field solution in the oscillating dipole approximation. We also recall the relations concerning the extended Lorenz force and energy-momentum conservation.
In
Section 3 we introduce a simple model for discontinuous microscopic currents in a metal. We show that the effective/averaged consequence of the microscopic discontinuities is to generate an extra-source whose moment
is proportional to the average macroscopic density
:
. The coefficient
is in turn proportional to the number of discontinuities per unit volume, to their average length and average current affected. This method is applied to a resonating cavity with a mode TM
and allows to compute the anomalous longitudinal electric field
in the far-field region along the axis of the cavity.
In
Section 4 we introduce a 1-D model for resonant tunneling in a metal based on the Kronig-Penney 1-D model of a crystal lattice consisting in square potential barriers. This simple model can be solved exactly and allows to interpret at least part of the conduction current as due to long-range resonant tunneling of valence electrons, with transmission coefficient
.
Section 5 and
Section 6 are devoted to macroscopic quantum systems described by a collective wavefunction. In
Section 5 we consider the effect of quantum fluctuations in a Josephson junction oscillating at its plasma frequency. Due to the uncertainty on the product
, the expectation value of the anomaly
I cannot be exactly zero and in a semiclassical approximation this generates in general a random longitudinal electric field in the radiation region.
In
Section 6 we consider solutions of the Ginzburg-Landau equation describing a superconducting weak link and we check the claim, often found in the literature, that such solutions can contain points at which
and the quantum phase can “slip” freely. We conclude that this is not possible if the local conservation of charge holds exactly.
2. Extended Field Equations and Energy-Momentum Relations
In the Aharonov-Bohm theory of extended electrodynamics the gauge invariance of the four-potentials is reduced to transformations of the form , where . (Here we define , being the electric potential and the vector potential. The metric has signature , with coordinates and .)
The four-divergence of
is promoted to a dynamical field
S (
), obeying the equation
where
often called “extra-current” or “extra-source”, is zero in standard classical situations where charge is locally conserved but can be different from zero in more general settings, for example in fractional quantum mechanics or in the presence of non-local potentials in the Schrödinger equation.
The extended first and fourth Maxwell equations are in SI units
where one recognizes additional sources
and
which, due to Equation (
1), can be spread out in space, far away from the physical sources
and
.
The second and third Maxwell equations remain valid in their familiar form, and also the wave equations for
and
retain their usual form
Nevertheless, due to the appearance of
S in Equations (
3) and (
4) the wave solutions of (
5) and (
6) can contain a longitudinal electric field which for a spherical wave in the dipole approximation has the expression
being
is the dipole moment of the extra-current
I:
If we apply Equation (
6) to a stationary current with some interruptions (due to “instant tunneling” or other failures of local conservation of charge), the Biot-Savart law predicts an effect of “missing
” from the regions with
; the prediction is confirmed by full integration of (
6). An experiment proposed for the detection of this effect is described in [
30], while in
Section 3 of this work we discuss the case of high-frequency currents circulating in the walls of a resonant cavity.
A complex calculation [
31] shows that the energy-momentum tensor of the e.m. field in Aharonov-Bohm theory is given by the usual Maxwell tensor
plus a term depending on
S:
By imposing the conservation of the total energy-momentum of field and matter, namely
one obtains equations for the power
w exerted by the field on matter, and for the force
per unit volume on matter (extended Lorenz force):
We thus see that the potentials have a direct effect on matter where . Since gauge invariance is strongly reduced, under suitable boundary conditions at infinity for the potentials, w and can be in principle computed without any ambiguities.
3. A Simple Model for Discontinuous Currents in a Conductor
In this section we give a first example of a possible application of the Aharonov-Bohm extended electrodynamics in a phenomenological model of condensed matter physics.
We start with the assumption that when current circulates in a conductor part of it is due to resonant tunneling of bound electrons close to the Fermi level, and that this tunneling can be interpreted as a discontinuous transport of those electrons across the classically forbidden zones.
If there is an electron current of value
that discontinuously crosses from the point
to the point
, the corresponding extra source is
This can be easily seen if one considers the integral over an arbitrary volume
V
where
represents the discontinuous component of the current density. By choosing
V to include either
, or
, expression (
15) is then established.
In this way, if one considers a small volume
, in which a number of these extra sources exist, the corresponding moment is
Following the previous ideas, we consider that the
’s amount to a fraction of the current circulating in
, that is
, while the
’s amount to a fraction of the distance
traversed by the current
in
. Since
, a simple model reflecting these ideas is given by
In this expression models the fractions previously considered, and is the macroscopic current in the material.
Considering that it is expected that
, one can determine
using Maxwell equations, and then evaluate the anomalous effects due to the dipolar moments of the extra sources by adding up the effect of each elementary dipole, given by [
31]
with
. We have in this way
For the expressions of the Fourier transforms in time we have
As an important case, let us consider the anomalous effects predicted by this model in the case of resonant EM cavities. Once the EM fields in the cavity had been determined from Maxwell equations, the current circulating in the cavity walls are determined from the condition
evaluated at the wall, with
the (external) unit vector normal to the wall surface considered. In this expression
is the surface current density, so that, correspondingly, in expressions (19) one makes the replacement
and extends the integral to the internal surface of the cavity.
As a relatively simple example let us consider the
generated by the TM
mode of a cylindrical cavity of radius
a and height
d. The corresponding frequency is
, and the magnetic field, in cylindrical coordinates (
r,
,
z), is given in terms of the Bessel function of the first kind as
where
is the electric field on the axis of the cavity.
The expression of
is then given by
with
In particular, along the
z axis
that for
,
d can be approximated by
The advantage of considering a closed cavity is that usual transverse electromagnetic radiation is confined to the inside of the cavity. On the other hand, the longitudinal component, that according to the proposed model would be generated inside the cavity walls, is transmitted without decay inside the conductor (see Appendix A in [
28]), so that it could in principle be detected outside the cavity, and its characteristics, as predicted by Equation (26), tested. For instance the
decay, the
dependence of the intensity, etc. Additionally, if a high-Q cavity is employed, intense values of
can be obtained, so as to facilitate detection of
for small values of
.
4. Kronig-Penney 1-D Model and Resonant Tunneling
In order to qualitatively justify the assumption of long range tunneling in a metal, we consider the Kronig-Penney 1-D model of a crystal lattice consisting in square barriers of height
, width
b and separation
a as shown in
Figure 1. This potential is not meant to represent that of the bare ion lattice, but the effective, Hartree-Fock potential valid for the electrons in the highest energy levels, that includes the screening of the ion lattice potential by the lowest energy electrons.
Given the barrier at
, the wavefunction at its left, corresponding to the energy
E, is
the one inside the barrier
and that at its immediate right is
where,
with
The boundary conditions at each side of the barrier are
Solving these boundary conditions for
and
in terms of
and
results in
with a matrix
whose explicit expression can be readily computed. Considering now Bloch theorem:
with
p the quasi-momentum, one has for a generic barrier at
that the wavefunctions at its left and right must be related by
that, together with the general relation (28) results in a linear, homogeneous system of equations for the coefficients
,
,
, and
, the zero of whose determinant determines the allowed values, or bands, of
k, and the value of
p corresponding to each allowed
k.
Alternatively, one can study the related problem of the transmission across a finite number of barriers. For this, one considers that for
there is an “incident” wave given by
while for
(after
N barriers) there is an “emerging” wave
Using the relations (28) we can write
with (
at the farthest right)
In this way, to obtain the reflection (
R) and transmission (
T) coefficients across the
N barriers, we put
,
,
,
, to have
and
so that one has a resonant tunneling with perfect transmission across the
N barriers when
.
As one can reasonably expect, the energy levels with zero transmission (), are found inside the forbidden bands as determined by Bloch theorem. However, the relevant point is that when solving the condition for perfect transmission across N barriers one obtains solutions distributed all across each allowed band. This means that bound electrons () with the appropriate energy could in principle tunnel freely across a large number of barriers. Of course, the exclusion principle forbids this unless there is an available state with the same energy to tunnel to.
Moreover, in a metal the conduction electrons belong in general to an allowed band that includes energy levels with
and
, that fill the levels up to the Fermi energy
. A sketch of the obtained solution for five barriers is shown in
Figure 2, in which the Fermi level, allowed bands and energy levels with perfect transmission across the whole lattice are shown.
Since the conduction band is not completely filled, a small energy perturbation, as produced by an applied electric field, can promote electrons with energy close to to higher levels. The assumption is that this effect can work on a small number of electrons in bound energy levels (close to ) so as to free levels for other bound electrons to resonantly tunnel to, resulting in a fraction of the electric current to be due to electrons that tunnel across a considerable distance.
5. Josephson Junctions as Random Sources of a Longitudinal Electric Field
In our work [
31] we have shown that in macroscopic quantum systems for which the phase-number uncertainty relation
holds, one can derive from it an uncertainty relation between charge and current in a given state:
We have proven this formula for a Josephson junction, re-obtaining the same relation given by Devoret [
32,
33] and by Chen et al. [
34] for Josephson junctions and more generally for quantum circuits. Then we have applied it to the quantity
(in 1D) that we call “anomaly” because classically it is always zero. (
I is also called “extra-current” in the jargon of extended electrodynamics and fractional quantum mechanics.) Focusing on a simple 1D case with time dependence
and a dependence of
on space as
, we have written the operator
as a linear combination of the operators
and
. Considering that these operators do not have common eigenstates and satisfy (29), we have derived an estimate of the uncertainty
.
The conclusion is that
displays quantum fluctuations for any state
and the classical conservation relation
cannot be exactly satisfied everywhere at the quantum level. We have evaluated the magnitude order of the fluctuations for the case of a specific Josephson junction operating at a resonant frequency
GHz with a current of the order of
A [
35]. It turns out that
A/m
.
The high frequency emission of Josephson junctions is well known; usually the emitted power does not exceed a few
W, but there have been several attempts to improve it by building arrays of synchronized junctions [
36,
37]. Now we hypothesize that besides the standard emission of the oscillating super-current, an anomalous emission described by extended electrodynamics could be present, namely we regard
as the stochastic source of a field
S which is itself stochastic and can have a role in the extended Maxwell equations, in particular giving rise to a fluctuating longitudinal electric radiation field
.
In order to estimate the magnitude order of this field we recall the Equation (
7) for the anomalous dipole emission. This formula is exact for a classical mono-chromatic field proportional to
, but we can use it as an approximation for a stochastic field. We know that the quantum noise of an harmonic oscillator has a spectrum peaked at its frequency [
38,
39]. Admitting that there can be some spread in frequency and a random superposition of modes with frequency
, we still can assume the time derivative of
P to be of the order of
.
P itself is of order
, where
V is the effective volume of one electrode,
d is the distance between the electrodes (thickness of the junction) and
is the magnitude order of the fluctuations of
I on each electrode, as given above.
Actually we suppose that when there is a random unbalance
in one electrode (i.e., an unbalance between
and
, implying failure of local conservation), this will be compensated by an opposite variation on the other electrode, in such a way that the total charge on the junction is constant and not fluctuating (see
Figure 3).
V is the effective volume of the electrodes in the sense that it is the volume occupied by the oscillating charge. For the example above
V can be estimated at ∼
m
, being the oscillating charge ∼
C and its density ∼
C/m
. The thickness
d of the oxide layer is of the order of 10 nm. In conclusion, the anomalous longitudinal random field strength at distance
r will be quite small, of order
V/m. It could increase if the distance between the electrodes is increased, like for instance in configurations with more junctions or superconducting islands [
40].
6. Tunneling Solutions of the Ginzburg-Landau Equation in a Long Superconducting Bridge
In this Section we consider quantum phase slip points in weak superconducting links and we prove that they cannot be exactly described by solutions of a (current-conserving) Ginzburg-Landau equation.
Mathematically, the Ginzburg-Landau (GL) equation can be seen as an extension of the Schrödinger equation through a non-linear term. It is widely used to compute the collective wavefunction of pairs in a superconductor. It can be derived by minimizing the free energy of a general phenomenological model able to describe not only low-T
superconductors with Cooper pairs bound by virtual phonons, but also e.g. ceramic high-T
materials in which the microscopic mechanism behind superconductivity is still unclear. Improving upon London’s theory, the GL equation allows to model cases in which the absolute value of the wavefunction is space-dependent, like border effects and magnetic vortexes. A time-dependent version also exists, but here we shall consider the stationary equation, applied to a “weak link”, namely a narrow superconducting bridge connecting two bulk superconductors. In such links, as well as in superconducting nanowires, a 1D version of the GL equation can be applied. It takes the form [
41]
where
,
is the macroscopic wavefunction,
is a constant that we take equal to the amplitude of the wavefunction in the bulk and
is the coherence length of the superconductor (for example
m in a Type-I superconductor like Pb). We solve the equation in an interval
where
L can range from a fraction of
(short links) to a multiple of
L (long links).
According to some phenomenological models, weak links can exhibit the phenomenon of quantum phase slips [
42]: these are points where the absolute value
of the macroscopic wavefunction vanishes and thus the phase becomes indefinite and can jump by multiples of
. As a consequence, in the presence of slip points the phase/current relation becomes multi-valued, deviating from the usual Josephson relation. This can be observed experimentally [
43,
44].
Phase slips can occur due to thermal fluctuations which make
vanish locally, but in the absence of relevant thermal fluctuations they have been traditionally explained based on particular solutions of the GL equation. In these solutions
takes equal values at the extremes of the weak link, but there is a phase shift
across the link (like in any Josephson junction). At one or more points in the link one can reportedly have
and thus a phase slip point. The calculation is particularly simple in the Aslamazov-Larkin model, in which the GL equation is linearized (this is valid only for very narrow links, such that
[
45]). However, according to Likharev and Yacobson [
43,
46] phase slips can also occur for long links. In that case the complete non-linear GL equation must be considered and formal solutions are obtained through series expansions, or numerical integration can be performed.
What we found in our accurate numerical solutions (see details in
Appendix A and
Appendix B) is the following: the absolute value
may approach zero at certain points, but due to local conservation of charge it never becomes exactly zero, therefore the quantum phase
is always well-defined and one can conclude that the 1D GL equation does not predict any phase slip in weak links.
It is possible to prove this property in general in analytical form. Let us write the wavefunction as
. The current density is given, in the absence of magnetic field, by the familiar expression
with
. In order to transform the GL equation into a system of equations of the first order, we write
The equation then becomes
We split the real and imaginary parts and call
; the resulting system is
The
x-dependent part of the current density can be written as
and the derivative is
By replacing it into Equations (36) and (37) one immediately finds the conservation property .
Now, suppose that at some point . If J must stay finite and non-zero when , we must have from (31) that at least one among the first derivatives u and v must diverge as . But from the GL Equation (30) we also have that , which is inconsistent with such a behavior of the first derivatives.
Intuitively, we can also notice that when the density of the superfluid tends to zero at some point, its velocity v (proportional to the gradient of ) should tend to infinity in order to keep constant the current density . In a non-relativistic theory this is possible in principle, but requires a huge acceleration in a very short space, which looks unphysical.
In conclusion, if a phase slip is actually present at some point, this means that the GL equation is not exactly satisfied at that point, and therefore we cannot guarantee the exact local conservation of the current. In fact, we are not aware of any other wave equation with locally conserved current which has stationary solutions such that at some point. It might well exist, but the belief that the GL equation can describe phase slips is in our opinion unjustified.
Clearly, being the GL theory an effective theory, it is not supposed to hold in general at the microscopic level. In that case the same applies to the associated local conservation of current.