Cyclic Six-Atomic Boron-Nitrides: Quantum-Chemical Consideration by Ab Initio CCSD(T) Method
1
Kazan Department of Joint Supercomputer Center of Russian Academy of Sciences–Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS”, Lobachevskii Street 2/31, Kazan 420111, Russia
2
Department of Analytical Chemistry, Certification and Quality Management, Kazan National Research Technological University, K. Marx Street 68, Kazan 420015, Russia
*
Author to whom correspondence should be addressed.
Quantum Rep. 2022, 4(3), 351-361; https://doi.org/10.3390/quantum4030025
Submission received: 13 August 2022
/
Revised: 25 August 2022
/
Accepted: 14 September 2022
/
Published: 16 September 2022
(This article belongs to the Special Issue Fundamentals and Applications in Quantum Chemistry)
Abstract
:By means of the CCSD(T)/6-311++G(df,p) and G4 quantum-chemical calculation methods, the calculation of the molecular and electronic structures of boron–nitrogen compounds having the B3N3 composition was carried out and its results were discussed. It was noted that seven isomeric forms with different space structures can exist; wherein, the most stable form is a distorted flat hexagon with alternating B and N atoms, with both B and N atoms forming regular triangles, but with different side lengths. The values of geometric parameters of molecular structures in each of these compounds are presented. Also, the key thermodynamic parameters of formation (enthalpy ΔfH0, entropy S0, Gibbs’ energy ΔfG0) and relative total energies of these compounds are calculated.
1. Introduction
At present, a very significant number of chemical compounds containing boron and nitrogen atoms are described in the literature (see, for example, early publications [1,2,3,4,5,6,7] and recent works [8,9,10,11,12,13,14,15]). Despite this, one compound is known to contain atoms of only these two elements, namely, boron nitride BN, for which a number of polymorphic modifications have been found [16,17,18,19,20,21,22,23,24], the most famous of which are α-BN (hexagonal) and β-BN (cubic). α-BN has a structure similar to that of graphite; β-BN, known by the names “elbor”, “borazon”, “cubonite” et al., has a diamond-like structure and a very high hardness, almost no different from that of diamond. Due to this high hardness, it is widely used in industry in grinding tools for processing various steels and alloys. Unlike diamond, it is non-combustible, withstands high thermal loads and retains the sharpness of its crystals (grains) for a longer time, which makes it possible to intensify the modes of grinding materials. Also, a number of other modifications of boron nitride resembling allotropes of carbon are described in the literature, f.e., nanotubes and nanolayers; however, all these modifications of boron nitride can be considered inorganic polymers and contain a very significant number of atoms. There is no information in the literature about any other boron nitrides, including those with a small (less than 10) number of atoms in the structural unit (molecule). One of the most interesting compounds of boron with nitrogen is borazine B3H6N3 (Figure 1), which has also been studied in many works (see in particular, [25,26,27,28,29,30,31,32,33,34]) and which, along with B and N atoms, also contains hydrogen atoms. This compound is isoelectronic to benzene C6H6 and in its physical properties resembles it in many respects (although it differs quite a lot from it in chemical properties—for example, in B3H6N3, only hydrogen atoms bonded to B atoms can be replaced without breaking the cycle, while H atoms at N atoms are not able to enter into substitution reactions). A chemical compound close to borazine is the triboron trinitride B3N3 which, in principle, could be obtained as a result of the mild oxidation of B3H6N3, but, as far as we know, has not been obtained in experiment yet, and has not even been considered theoretically (in any case, we could not find works devoted to this compound). Nevertheless, this compound is of rather great interest not only for expanding understanding of the chemistry of boron, but also in practical terms, since it can serve, for example, as a precursor for obtaining various compounds of this element and creating promising materials based on boron-containing compounds. This compound is, in principle, capable of existing in the form of a number of isomeric forms having a cyclic structure, and their identification seems to be very interesting. Taking into account all the above, this article is devoted to establishing the possibility of the existence of this compound and, in the case of a positive answer to this question, to identifying its isomers and the specifics of their molecular and electronic structures, as well as their thermodynamic characteristics.
2. Method
The initial structures of the cyclic B3N3` (Figure 2) molecules for carrying out quantum-chemical calculations were as follows:
The choice of these initial structures was determined by the following two factors: first, the valence possibilities of the boron and nitrogen atoms (each of which is capable of binding with one, two or three neighboring atoms by means of three chemical bonds according to the exchange mechanism of chemical bond formation); and, second, the greatest typicality of these structures compared with other structures with a corresponding number of atoms. For these reasons, possible polyhedra such as the regular octahedron and the pentagonal pyramid were not included in the number of initial structures. The calculation of parameters of molecular and electronic structures of B3N3 molecules was carried out by means of the CCSD(T)/6-311++G(df,p) method combined with the coupled cluster method, using both single and double substitutions, including triple excitations non-iteratively–CCSD(T) [35,36,37,38] with the basis set 6-311++G(df,p) [39,40,41,42]. The given method is one of the most accurate and reliable quantum-chemical methods for calculating the molecular structures of various chemical compounds (in particular, p-elements) and takes into account electron correlation very well. Calculations were performed with the Gaussian09 program package [43]. To visualize the results of our calculations, we used the ChemCraft software, Version 1.8. The correspondence of the found stationary points to energy minima was proved in all cases by the calculation of the second derivatives of energy with respect to the atom coordinates; all equilibrium structures corresponding to the minima on the potential energy surfaces have only positive frequencies. The values of the standard enthalpies and Gibbs’ energies of the nitrogen-containing compounds under study were calculated using the G4 method described in detail in [44].
3. Results and Discussion
According to the results of our calculations, there are seven minima on the potential energy surface of the B3N3 system, and, therefore, in principle, there can be seven structures of polyatomic nitrogen molecules B3N3: B3N3 (I), B3N3 (II) and B3N3 (III)—in the form of flat distorted hexagons but with a different alternation of boron and nitrogen atoms, B3N3 (IV)—a non-planar distorted hexagon, B3N3 (V)—in the form of an “open book”, B3N3 (VI)—in the form where the atoms of the above elements are at the vertices of a distorted trigonal prism and B3N3 (VII)—in a shape that can be seen as a combination of a highly distorted pentagon and triangle. The images of the molecular structures of these B3N3 modifications are shown in Figure 3.
Thus, out of the 12 initial structures of B3N3 presented above, slightly more than half are implemented. That is characteristic, B3N3 acyclic structures or hybrid structures containing cyclic and acyclic fragments (in particular, a combination of a triangle and a triatomic linear fragment) are not realized. The key geometric parameters of these structures (bond lengths, valence and torsion (dihedral) angles) are given in Table 1. Data on the relative stability of all these forms are presented in Table 2; as can be seen, according to the values of the total energy (E0), they are arranged as E0[B3N3 (I)] < E0[B3N3 (II)] < E0[B3N3 (IV)] < E0[B3N3 (V)] < E0[B3N3 (III)] < E0[B3N3 (VI)] < E0[B3N3 (VII)]. So, the most stable of these modifications is B3N3 (I) and the least stable is B3N3 (VII). In this regard, it should be noted that according to the data of [45,46], in the case of the homonuclear N6 molecule, the modification with the molecular structure in the form of an “open book” turns out to be the most stable among all cyclic modifications of N6. The most stable modification of B3N3 (I) not only has a significantly lower energy (by more than 400 kJ∙mole−1) compared to that of other modifications of B3N3 but also a significantly larger set of symmetry elements (D3h symmetry group, one third order axis, three second order axes, four planes of symmetry and a center of symmetry). The remaining modifications of B3N3 either have only one plane of symmetry and belong to the Cs symmetry group (B3N3 (II), B3N3 (III), B3N3 (VII)) or are completely devoid of any symmetry elements (B3N3 (IV), B3N3 (V), B3N3 (VI)). The B3N3 (I) structure can be considered the result of a combination (overlapping) of two regular triangles, (B1B2B3) and (N1N2N3), in which the interatomic distances are 189.9 and 264.8 pm, respectively. This structure contains only B–N bonds, the lengths of which are equal to 136.5 pm. A similar situation takes place in the B3N3 (V) structure, however, there, all these relationships are different from each other (Table 1). In the remaining five modifications, all three possible types of chemical bonds, B–N, B–B and N–N are present. Taking into account the larger covalent radius of the boron atom compared to that of the nitrogen atom (82 and 75 pm, respectively), one would expect that, on average, the N–N bonds will be the shortest, the B–B bonds the longest, and the B–N bonds will occupy an intermediate position. This expectation in the case of the compounds under consideration is generally justified, but the lengths of the shortest bonds are slightly inconsistent with it since the N–N bond has a length of 130.5 pm (in B3N3 (III)), the shortest B–N bond is 129.5 pm (in B3N3 (II)), and the shortest B–B bond is 154.5 pm (in B3N3 (III)). The longest chemical bonds between these atoms are 154.7 (in B3N3 (IV)), 156.6 (in B3N3 (VI)), and 171.8 (in B3N3 (VI)) pm, respectively. In this connection it is worth noting that, in five of these seven modifications, all bond lengths between atoms turn out to be different. The exceptions are B3N3 (I), where all bond lengths are the same, and, oddly enough, the most “high-energy” modification of B3N3 (VII), where pairwise equality of bond lengths takes place (Table 1). As for the bond angles, they, as one would expect, taking into account the above asymmetry and differences in the bond lengths between atoms, in most cases also turn out to be different. The exceptions are B3N3 (I) and B3N3 (VII), where these structural parameters are pairwise equal.
The NBO analysis data for each of the seven B3N3 modifications obtained with using ideas outlined in [47] (version NBO3 inbuilt in Gaussian09) are presented in Table 3. As should be expected, the charges on different atoms of the same element (both B and N) are different, since, in all B3N3 modifications except for B3N3 (I), the atoms of any of these two elements are not equivalent to each other. In addition, since nitrogen is a more electronegative element than boron, one would also expect that in all these compounds the charges on the boron atoms would be positive and on the nitrogen atoms they would be negative. In general, this prediction is justified, but there are two exceptions among them, namely, B3N3 (III) and B3N3 (VII), in each of which one of the three boron atoms has a negative (albeit a very small) charge. In this regard, it is noteworthy that in each of these modifications there are two B–B chemical bonds, while in the remaining five modifications there is either one such bond (in B3N3 (II), B3N3 (IV) and B3N3 (VI)), or they are absent altogether (in B3N3 (I) and B3N3 (V)). Perhaps (and even very likely) these two facts are somehow connected, but how, namely, remains unclear, and further research is needed. It should also be noted that the effective charges on the B and N atoms differ quite significantly from +3.00 and −3.00, respectively, which, in turn, indicates a rather pronounced degree of covalence of the B–N bonds. The highest degree of polarization of these bonds takes place in the most stable modification of triboron trinitride, B3N3 (I), whereas the lowest its degree occurs in the least stable B3N3 (VII) (Table 3).
The values of the standard enthalpy ΔfH0, the standard entropy S0 and the standard Gibbs energy ΔfG0 for various modifications of B3N3 are given in Table 4. As can be seen from it, the values of ΔfG0 for each of these modifications are positive, and therefore, none of them can be obtained from simple substances formed by these elements (i.e., in the interaction between solid boron and molecular nitrogen N2). In this connection, it is necessary to consider the possibility of synthesis at least the most energetically favorable modification of triboron trinitride, namely, B3N3 (I) from other starting compounds. The most interesting and logical among them is the preparation of B3N3 (I) as a result of the oxidation of borazine B3N3H6 with molecular oxygen in the gas or liquid phase according to the general Schemes (1) or (2), respectively
by analogy with the long and well-known oxidation reaction of benzene C6H6, which is isoelectronic to borazine, according to the general Scheme (3)
2 B3H6N3 (gas) + 3 O2 (gas) → 2 B3N3 (gas) + 6 H2O (gas)
2 B3H6N3 (liq) + 3 O2 (gas) → 2 B3N3 (gas) + 6 H2O (gas)
2 C6H6 + 3 O2 → 12 C + 6 H2O
The standard thermodynamic parameters of formation for substances participating in Reaction (1) are presented in Table 5.
Using these data, one can easily calculate the standard thermodynamic parameters of Reaction (1) ΔH0 = −32.0 kJ∙mol−1, ΔS0 = 472.6 J∙mol∙K−1, ΔG0 = −172.5 kJ∙mol−1 (see Supplementary Materials). In accordance with the classical Gibbs–Helmholtz equation ΔG (T) = ΔH0 − TΔS0, and the indicated values ΔH0 and ΔS0, the temperature dependence of the Gibbs energy ΔG (T) for Reaction (1) is described by Expression (4)
ΔG (T) = ΔH0 − TΔS0 = −32.0 − 0.4726T
A similar calculation, but using the known experimental values for B3H6N3 (liq), O2 (gas) and H2O (gas), gives the standard thermodynamic parameters of Reaction (2) ΔH0 = 15.4 kJ∙mol−1, ΔS0 = 731.6 J∙mol∙K−1, ΔG0 = −204.2 kJ∙mol−1 (see Supplementary Materials) and temperature dependence ΔG (T) (5)
ΔG (T) = ΔH0 − TΔS0 = 15.4 − 0.7316T
As is easy to see from the given data, according to the results of the calculation by the G4 method, Reaction (1) is exothermic, but with only a small release of thermal energy, while Reaction (2) is endothermic, but with a small absorption of thermal energy. However, in both the first and second variants, it is accompanied by a very significant increase in the entropy of the reaction system. A direct consequence of these two factors is that, in principle, both Reaction (1) and Reaction (2)—as can be easily calculated from Formulas (4) and (5)—can proceed at least starting from T = 22 K, i.e., even at very low temperatures. Since the values of ΔG (T) for this reaction decrease with increasing temperature, therefore, it can and should be carried out under standard conditions (by the way, this possibility is directly indicated by the negative values of ΔG0 equal to (−172.7) kJ∙mol−1 and (−204.2) kJ∙mol−1 presented above). In this way the synthesis of triboron trinitride (at least its most thermodynamically stable form B3N3 (I)) using Reaction (1) or Reaction (2) seems to be quite realistic. It only remains to carry out this synthesis experimentally. As for the other six modifications, it is easy to show that for each of them the value of ΔG0 in Reactions (1) and (2) is positive, so that under standard conditions none of them can be obtained (although in principle it remains possible to obtain them at high temperatures, since both of these reactions in any case proceed with an increase in the entropy of the reaction system).
4. Conclusions
As can be seen from the aforementioned, the presented data of quantum chemical calculations using the CCSD (T) functional and the 6-311++G(df,p) basis set confirm the possibility of the existence of seven different modifications of triboron trinitride B3N3; any minima on the potential energy surface of this compound corresponding to other molecular structures (including acyclic ones) are not detected. At the same time, the most energetically favorable among them is a structure in the form of a distorted hexagon with a regular (every atom) alternation of boron and nitrogen atoms and the largest number of symmetry elements (point group D3h), while other structures have, comparatively, a significantly higher total energy (400 kJ∙mole−1 and more). Despite this, all these seven compounds are, in principle, capable of independent existence as isolated molecules. Although none of the modifications of B3N3 can in principle be obtained by direct interaction of boron and nitrogen, at least one of them, the most stable modification indicated above, can be obtained as a result of the oxidation reaction of borazine with molecular oxygen in the gas or liquid phase and, perhaps, even under standard (i.e., relatively soft) conditions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/quantum4030025/s1, Table S1: Energy differences between LUMO and HOMO (ΔLUMO-HOMO) for various modifications of B3N3.
Author Contributions
Conceptualization, O.V.M.; Methodology, O.V.M. and D.V.C.; Software, D.V.C.; Validation, O.V.M. and D.V.C.; Formal Analysis, O.V.M. and D.V.C.; Investigation, O.V.M. and D.V.C.; Resources, D.V.C.; Data Curation, D.V.C.; Writing—Original Draft Preparation, O.V.M. and D.V.C.; Writing—Review & Editing, O.V.M.; Visualization, O.V.M. and D.V.C.; Supervision, O.V.M.; Project Administration, O.V.M.; Funding Acquisition, D.V.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study did not require institutional approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
No unpublished data was created or analyzed in this article.
Acknowledgments
All quantum-chemical calculations were performed at the Joint Supercomputer Center of Russian Academy of Sciences–Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS” (http://www.jscc.ru, accessed on 1 January 2005). Contribution of author Chachkov D.V. was funded by the state assignment to the Federal State Institution “Scientific Research Institute for System Analysis of the Russian Academy of Sciences” for scientific research. Also, this study was carried out using the equipment of the Center for Collective Use “Nanomaterials and Nanotechnology” of the Kazan National Research Technological University with the financial support of the Ministry of Science and Higher Education of the Russian Federation under agreement No. 075-15-2021-699.
Conflicts of Interest
The authors declare that they have no conflict of interest, financial or otherwise.
References
- Coursen, D.I.; Hoard, J.L. The Structure of B-Trichloroborazole. J. Am. Chem. Soc. 1952, 74, 1742–1750. [Google Scholar] [CrossRef]
- Hughes, E.W. The crystal structure of ammonia-borane, H3NBH3. J. Am. Chem. Soc. 1956, 78, 502–503. [Google Scholar] [CrossRef]
- Lippert, E.L.; Lipscomb, W.N. The structure of H3NBH3. J. Am. Chem. Soc. 1956, 78, 503–504. [Google Scholar] [CrossRef]
- Harshbarger, W.; Lee, G.H.; Porter, R.F.; Bauer, S.H. Structure of B-monoamino-borazine. J. Am. Chem. Soc. 1969, 91, 551–555. [Google Scholar] [CrossRef]
- Chang, C.-H.; Porter, R.F.; Bauer, S.H. Molecular structure of dimethyl-cyclotetrazenoborane, (CH3)2N4BH. Inorg. Chem. 1969, 8, 1677–1683. [Google Scholar] [CrossRef]
- Harshbarger, W.; Lee, G.H.; Porter, R.F.; Bauer, S.H. Structure of borazine. Inorg. Chem. 1969, 8, 1683–1689. [Google Scholar] [CrossRef]
- Gopinathan, M.S.; Whitehead, M.A.; Coulson, C.A.; Carruthers, J.R.; Rollett, J.S. A reinvestigation of the crystal and molecular structure of hexachloroborazine. Acta Cryst. B 1974, 30, 731–737. [Google Scholar] [CrossRef]
- Kar, T.; Scheiner, S.; Roy, A.K. Structure and Properties of [8]BN-Circulenes: Inorganic Analogues of [8]Circulenes. J. Phys. Chem. C 2015, 119, 15541–15546. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Pandey, S.K.; Misra, N. Stability versus aromaticity in mono-hydroxylated borazine, 1,2-azaborine and 1,3,2,4-diazadiborine. Mol. Phys. 2016, 114, 1763–1770. [Google Scholar] [CrossRef]
- Li, D.-Z.; Feng, L.-Y.; Pei, L.; Zhang, L.-J.; Wu, S.-G.; Zhai, H.-J. Pentagonal five-center four-electron π bond in ternary B3N2H5 cluster: An extension of the concept of three-center four-electron ω bond. Phys. Chem. Chem. Phys. 2017, 19, 2479–2486. [Google Scholar] [CrossRef]
- Less, R.J.; Hanf, S.; García-Rodríguez, R.; Bond, A.D.; Wright, D.S. A [HN(BH═NH)2]2– Dianion, Isoelectronic with a β-Diketiminate. Organometallics 2018, 37, 628–631. [Google Scholar] [CrossRef]
- Anafcheh, M.; Ahmadi, E.; Zahedi, M. Addition of borazine to boron nitride nanotubes: [2+2] cycloaddition or bond cleavage. Monatsh. Chem. 2019, 150, 1019–1024. [Google Scholar] [CrossRef]
- Prieschl, D.; Bélanger-Chabot, G.; Guo, X.; Dietz, M.; Müller, M.; Krummenacher, I.; Lin, Z.; Braunschweig, H. Synthesis of Complex Boron–Nitrogen Heterocycles Comprising Borylated Triazenes and Tetrazenes Under Mild Conditions. J. Am. Chem. Soc. 2020, 142, 1065–1076. [Google Scholar] [CrossRef] [PubMed]
- Ota, K.; Kinjo, R. Inorganic Benzene Valence Isomers. Chem. Asian J. 2020, 15, 2558–2574. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Espinosa, Y.; Méndez-Sánchez, R.A.; Sadurní, E. On the electronic structure of benzene and borazine: An algebraic description. J. Phys. B Atomic. Mol. Opt. Phys. 2020, 53, 105101. [Google Scholar] [CrossRef]
- Vel, L.; Demazeau, G.; Etourneau, J. Cubic Boron Nitride: Synthesis, Physicochemical Properties and Applications. Mater. Sci. Eng. B 1991, 10, 149–164. [Google Scholar] [CrossRef]
- Rubio, A.; Corkill, J.L.; Cohen, M.L. Theory of Graphitic Boron Nitride Nanotubes. Phys. Rev. B 1994, 49, 5081–5084. [Google Scholar] [CrossRef]
- Zedlitz, R. Properties of Amorphous Boron Nitride Thin Films. J. Non-Cryst. Solids 1996, 198–200, 403–410. [Google Scholar] [CrossRef]
- Golberg, D.; Bando, Y.; Tang, C.C.; Zhi, C.Y. Boron Nitride Nanotubes. Adv. Mater. 2007, 19, 2413–2432. [Google Scholar] [CrossRef]
- Goriachko, A.; He, Y.; Knapp, M.; Over, H.; Corso, M.; Brugger, T.; Berner, S.; Osterwalder, J.; Greber, T. Self-Assembly of a Hexagonal Boron Nitride Nanomesh on Ru(0001). Langmuir 2007, 23, 2928–2931. [Google Scholar] [CrossRef]
- Kawaguchi, M.; Kuroda, S.; Muramatsu, Y. Electronic Structure and Intercalation Chemistry of Graphite-Like Layered Material with a Composition of BC6N. J. Phys. Chem. Solids 2008, 69, 1171–1178. [Google Scholar] [CrossRef]
- Cai, Q.; Scullion, D.; Gan, W.; Falin, A.; Zhang, S.; Watanabe, K.; Taniguchi, T.; Chen, Y.; Santos, E.J.C. High thermal conductivity of high-quality monolayer boron nitride and its thermal expansion. Sci. Adv. 2019, 5, eaav0129. [Google Scholar] [CrossRef] [PubMed]
- Brazhkin, V.V.; Solozhenko, V.L. Myths about new ultrahard phases: Why materials that are significantly superior to diamond in elastic moduli and hardness are impossible. J. Appl. Phys. 2019, 125, 130901. [Google Scholar] [CrossRef]
- Mirkarimi, P.B.; McCarty, K.F.; Medlin, D.L. Review of Advances in Cubic Boron Nitride Film Synthesis. Mater. Sci. Eng. R Rep. 1997, 21, 47–100. [Google Scholar] [CrossRef]
- Boese, R.; Maulitz, A.H.; Stellberg, P. Solid-State Borazine: Does it Deserve to be Entitled “Inorganic Benzene”? Chem. Ber. 1994, 127, 1887–1889. [Google Scholar] [CrossRef]
- Jeon, J.K.; Uchimaru, Y.; Kim, D.P. Synthesis of novel amorphous boron carbonitride ceramics from the borazine derivative copolymer via hydroboration. Inorg. Chem. 2004, 43, 4796–4798. [Google Scholar] [CrossRef]
- Shen, W.; Li, M.; Li, F.; Wang, S. Theoretical study of borazine and its derivatives. Inorg. Chim. Acta 2007, 360, 619–624. [Google Scholar] [CrossRef]
- Islas, R.; Chamorro, E.; Robles, J.; Heine, T.; Santos, J.C.; Merino, G. Borazine: To be or not to be aromatic. Struct. Chem. 2007, 18, 833–839. [Google Scholar] [CrossRef]
- Dong, S.H.; Zheng, Z.M.; Han, W.J.; Zhao, T.; Xu, C.H. Synthesis of new borazines containing crosslinkable groups. Chin. Chem. Lett. 2008, 19, 1398–1400. [Google Scholar] [CrossRef]
- Lei, Y.P.; Wang, Y.D.; Song, Y.C.; Li, Y.H.; Wang, H.; Deng, C.; Xie, Z.F. Facile synthesis of a melt-spinnable polyborazine from asymmetric alkylaminoborazine. Chin. Chem. Lett. 2010, 21, 1079–1082. [Google Scholar] [CrossRef]
- Kervyn, S.; Fenwick, O.; Di Stasio, F.; Shin, Y.S.; Wouters, J.; Accorsi, G.; Osella, S.; Beljonne, D.; Cacialli, F.; Bonifazi, D. Polymorphism, fluorescence, and optoelectronic properties of a borazine derivative. Chem. A Eur. J. 2013, 19, 7771–7779. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, V.; Nagnathappa, M.; Kharat, B.; Chaudhari, A. Theoretical study of borazine and substituted borazines using density functional theory method. J. Mol. Liquids 2014, 193, 13–22. [Google Scholar] [CrossRef]
- Neogi, I.; Szpilman, A.M. Synthesis and Reactions of Borazines. Synthesis 2021, 54, 1877–1907. [Google Scholar] [CrossRef]
- Báez-Grez, R.; Pino-Rios, R. The hidden aromaticity in borazine. RSC Adv. 2022, 12, 7906–7910. [Google Scholar] [CrossRef] [PubMed]
- Pople, A.; Krishnan, R.; Schlegel, H.B.; Binkley, J.S. Electron Correlation Theories and Their Application to the Study of Simple Reaction Potential Surfaces. Int. J. Quantum Chem. 1978, 14, 545–560. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Purvis, G.D., III. Many-body perturbation-theory, coupled-pair many-electron theory, and importance of quadruple excitations for correlation problem. Int. J. Quantum Chem. 1978, 14, 561–581. [Google Scholar] [CrossRef]
- Purvis, G.D., III; Bartlett, R.J. A full coupled-cluster singles and doubles model-the inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Pople, J.A.; Head-Gordon, M.; Krishnan, R. Quadratic configuration interaction-a general technique for determining electron correlation energies. J. Chem. Phys. 1987, 87, 5968–5975. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian-basis sets for molecular calculations. 1. 2nd row atoms, Z=11-18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Raghavachari, K.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 20. Basis set for correlated wave-functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis-sets for anion calculations. 3. The 3-21+G basis set for 1st-row elements, Li-F. J. Comp. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-Consistent Molecular Orbital Methods. 25. Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. (Eds.) Gaussian 09, Revision A.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory. J. Chem. Phys. 2007, 126, 084108. [Google Scholar] [CrossRef]
- Mikhailov, O.V.; Chachkov, D.V. Molecular structures and thermodynamics of stable N4, N6 and N8 neutral poly-nitrogens according to data of QCISD(T)/TZVP method. Chem. Phys. Lett. 2020, 753, 137594. [Google Scholar] [CrossRef]
- Mikhailov, O.V. Molecular and Electronic Structures of Neutral Polynitrogens: Review on the Theory and Experiment in 21st Century. Int. J. Mol. Sci. 2022, 23, 2841. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R.; Glendening, E.D. What is NBO analysis and how is it useful? Int. Rev. Phys. Chem. 2016, 35, 399–440. [Google Scholar] [CrossRef]
- Standard Thermodynamic Properties of Chemical Substances. In Handbook of Chemistry and Physics Online; CRC Press: Taylor & Francis Group: London, UK; Available online: https://hbcp.chemnetbase.com/faces/documents/05_02/05_02_0001.xhtml (accessed on 25 August 2022).
Figure 1.
Structural formula of borazine.
Figure 2.
The possible structures of cyclic B3N3 molecules.
Figure 3.
The images of seven theoretically possible modifications of boron–nitrogen compound having B3N3 composition according to data of quantum-chemical calculation with using CCSD(T)/6-311++G(df,p) method: (I)—B3N3 (I), (II)—B3N3 (II), (III)—B3N3 (III), (IV)—B3N3 (IV), (V)—B3N3 (V), (VI)—B3N3 (VI), (VII)—B3N3 (VII).
Figure 3.
The images of seven theoretically possible modifications of boron–nitrogen compound having B3N3 composition according to data of quantum-chemical calculation with using CCSD(T)/6-311++G(df,p) method: (I)—B3N3 (I), (II)—B3N3 (II), (III)—B3N3 (III), (IV)—B3N3 (IV), (V)—B3N3 (V), (VI)—B3N3 (VI), (VII)—B3N3 (VII).
Table 1.
Geometric parameters of the molecular structure of isomeric B3N3 molecules calculated by using CCSD(T)/6-311++G(df,p) method.
Table 1.
Geometric parameters of the molecular structure of isomeric B3N3 molecules calculated by using CCSD(T)/6-311++G(df,p) method.
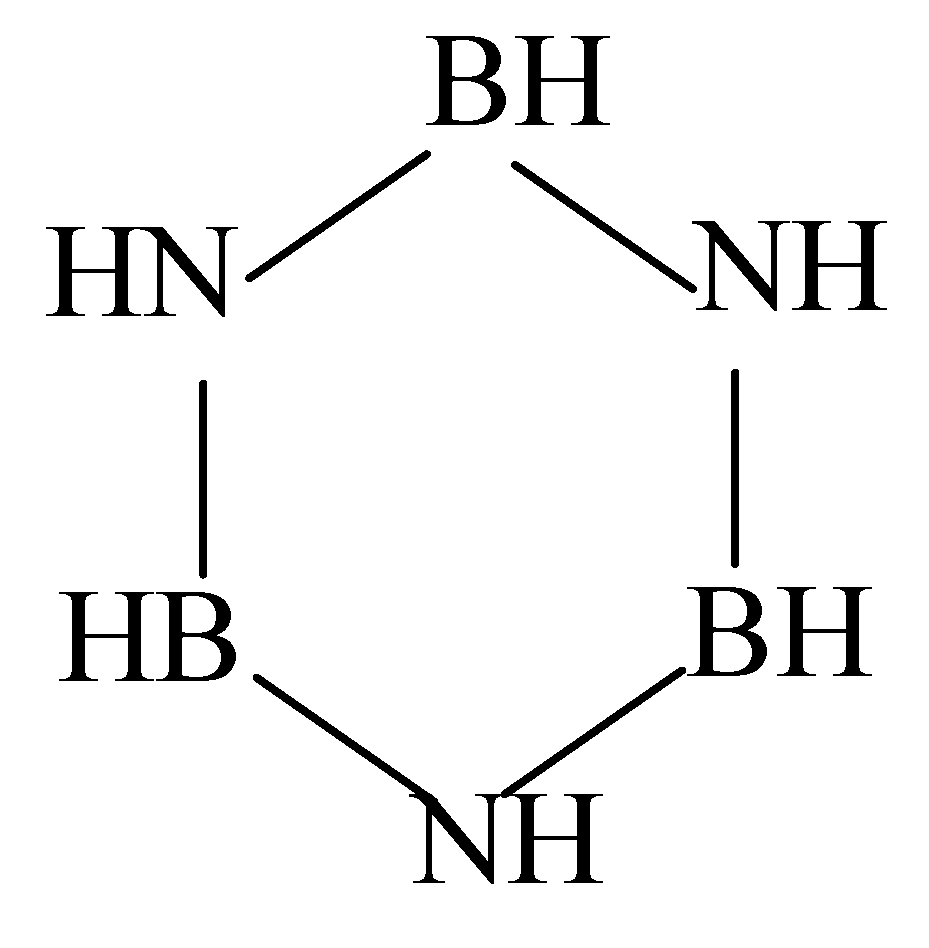
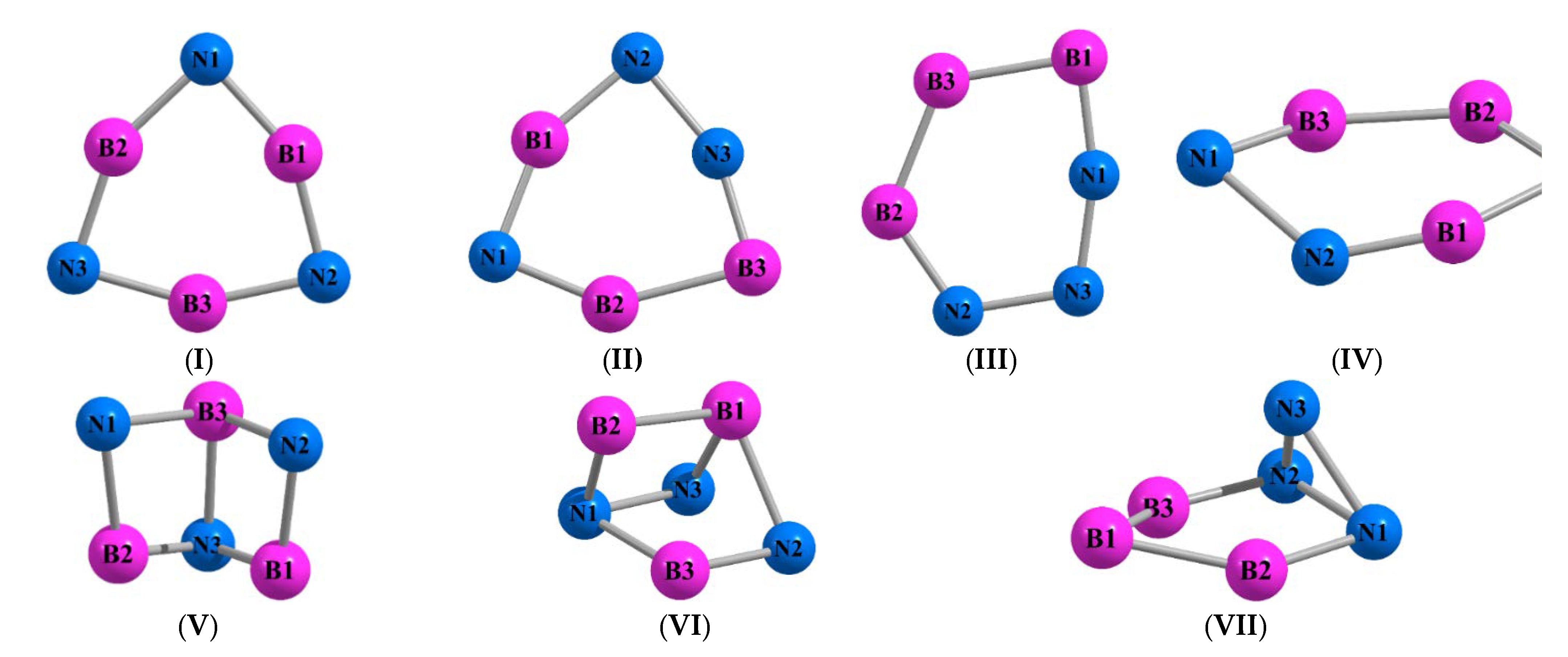
| Molecule B3N3 (I) | |||
|---|---|---|---|
| Bond Lengths, pm | Bond Angles, deg | ||
| (N1B1) | 136.5 | (N1B1N2) | 151.8 |
| (B1N2) | 136.5 | (B1N2B3) | 88.2 |
| (N2B3) | 136.5 | (N2B3N3) | 151.8 |
| (B3N3) | 136.5 | (B3N3B2) | 88.2 |
| (N3B2) | 136.5 | (N3B2N1) | 151.8 |
| (B2N1) | 136.5 | (B2N1B1) | 88.2 |
| Selected torsion (dihedral) angles, deg | |||
| (N1B1N2B3) | −0.4 | (B1N2B3N3) | 0.4 |
| (N1B1B3B2) | 0.0 | (B1N1N3N2) | 0.0 |
| Molecule B3N3 (II) | |||
| Bond lengths, pm | Bond angles, deg | ||
| (N1B1) | 136.3 | (N1B1N2) | 151.3 |
| (B1N2) | 138.1 | (B1N2N3) | 89.6 |
| (N2N3) | 135.4 | (N2N3B3) | 156.8 |
| (N3B3) | 129.5 | (N3B3B2) | 88.0 |
| (B3B2) | 158.7 | (B3B2N1) | 142.8 |
| (B2N1) | 134.6 | (B2N1B1) | 91.5 |
| Selected torsion (dihedral) angles, deg | |||
| (N1B1N3B2) | 0.0 | (N1B1N2B2) | 0.0 |
| (N1B2B3B1) | 0.0 | (B1N2N3N1) | 0.0 |
| Molecule B3N3 (III) | |||
| Bond lengths, pm | Bond angles, deg | ||
| (N1B1) | 131.4 | (N1B1B3) | 87.4 |
| (B1B3) | 154.5 | (B1B3B2) | 121.2 |
| (B3B2) | 157.1 | (B3B2N2) | 123.8 |
| (B2N2) | 133.5 | (B2N2N3) | 115.2 |
| (N2N3) | 134.6 | (N2N3N1) | 107.3 |
| (N3N1) | 130.5 | (N3N1B1) | 164.9 |
| Selected torsion (dihedral) angles, deg | |||
| (N1B1N2B2) | −1.7 | (B1N1N2B2) | −2.3 |
| (N1B1B3B2) | −2.9 | (B1N1N3N2) | −9.7 |
| Molecule B3N3 (IV) | |||
| Bond lengths, pm | Bond angles, deg | ||
| (N1B3) | 134.2 | (N1B3B2) | 150.0 |
| (B3B2) | 163.7 | (B3B2N3) | 128.3 |
| (B2N3) | 132.8 | (B2N3B1) | 80.4 |
| (N3B1) | 142.1 | (N3B1N2) | 154.4 |
| (B1N2) | 132.3 | (B1N2N1) | 126.3 |
| (N2N1) | 154.7 | (N2N1B3) | 75.0 |
| Selected torsion (dihedral) angles, deg | |||
| (N1B3B2N3) | 10.4 | (N2B1N3B2) | 7.3 |
| (N1B3B2B1) | 15.7 | (N1N2B1N3) | −33.0 |
| Molecule B3N3 (V) | |||
| Bond lengths, pm | Bond angles, deg | ||
| (N1B2) | 153.1 | (N1B3N3) | 102.1 |
| (B2N3) | 135.6 | (B3N3B2) | 74.6 |
| (N3B1) | 147.4 | (N3B2N1) | 111.3 |
| (B1N2) | 148.4 | (B2N1B3) | 71.6 |
| (N2B3) | 153.9 | (N2B3N3) | 101.7 |
| (B3N1) | 150.5 | (B3N3B1) | 74.5 |
| (B3N3) | 156.0 | (N3B1N2) | 108.7 |
| (B1N2B3) | 74.9 | ||
| (N1B3N2) | 82.2 | ||
| (B2N3B1) | 73.3 | ||
| Selected torsion (dihedral) angles, deg | |||
| (N1B3N3B2) | −5.2 | (N1N2B1B2) | 1.0 |
| (N2B3N3B1) | 2.7 | (N1N3N2B3) | −54.0 |
| (N3N1B3N2) | −100.4 | (B3B2N3B1) | 78.1 |
| (N1B3N2B1) | 98.1 | (N2N3N1B2) | −95.8 |
| Molecule B3N3 (VI) | |||
| Bond lengths, pm | Bond angles, deg | ||
| (N1B2) | 149.8 | (N1B2B1) | 72.1 |
| (B2B1) | 169.2 | (B2B1N3) | 100.7 |
| (B1N3) | 146.6 | (B1N3N1) | 78.4 |
| (N3N1) | 151.3 | (N3N1B2) | 108.0 |
| (N1B3) | 149.7 | (N1B3N2) | 95.8 |
| (B3B2) | 171.8 | (B3N2N3) | 86.8 |
| (N3N2) | 164.9 | (N2N3N1) | 87.2 |
| (N2B1) | 156.6 | (N3N1B3) | 90.1 |
| (N2B3) | 144.5 | (N2B1B2) | 102.8 |
| (B1B2B3) | 69.7 | ||
| (B2B3N2) | 106.9 | ||
| (B3N2B1) | 80.5 | ||
| (N1B3B2) | 55.0 | ||
| (B3B2N1) | 55.0 | ||
| (B2N1B3) | 70.0 | ||
| (N3B1N2) | 65.8 | ||
| (B1N2N3) | 54.2 | ||
| (N2N3B1) | 60.0 | ||
| Selected torsion (dihedral) angles, deg | |||
| (N1B2B1N3) | 6.1 | (B1N1N2N3) | −70.2 |
| (N1B3N2N3) | −2.3 | (B2N1N2N3) | −118.8 |
| (N2B1B2B3) | −2.8 | (B3N1N2N3) | 176.7 |
| Molecule B3N3 (VII) | |||
| Bond lengths, pm | Bond angles, deg | ||
| (N1N3) | 149.2 | (N1N3N2) | 63.1 |
| (N3N2) | 149.2 | (N3N2B3) | 73.3 |
| (N2B3) | 147.9 | (N2B3B1) | 140.9 |
| (B3B1) | 157.4 | (B3B1B2) | 66.4 |
| (B1B2) | 157.4 | (B1B2N1) | 140.9 |
| (B2N1) | 147.9 | (B2N1N3) | 73.3 |
| Selected torsion (dihedral) angles, deg | |||
| (N2B3B1B2) | −24.3 | (N1N2B3B1) | 20.5 |
| (N1B2B1B3) | 24.3 | (N1N2B3B2) | 0.1 |
| (B1N1N3N2) | −90.8 | (N3B1B2B3) | −52.3 |
| (B2N1N3N2) | −104.6 | (B3N2N3N1) | 104.6 |
Table 2.
Relative total energies of B3N3 molecules in gas phase calculated with using CCSD(T)/6-311++G(df,p) method.
Table 2.
Relative total energies of B3N3 molecules in gas phase calculated with using CCSD(T)/6-311++G(df,p) method.
| Compound | Total Energy, Hartree | Relative Total Energy, kJ∙mole−1 |
|---|---|---|
| B3N3 (I) | −238.347767 | 0.0 |
| B3N3 (II) | −238.192298 | 409.6 |
| B3N3 (III) | −238.062655 | 752.3 |
| B3N3 (IV) | −238.169862 | 470.3 |
| B3N3 (V) | −238.124054 | 588.8 |
| B3N3 (VI) | −238.047742 | 788.7 |
| B3N3 (VII) | −238.005818 | 900.0 |
Table 3.
NBO analysis data of various modifications of B3N3 according to CCSD(T)/6-311++G(df,p) method data.
Table 3.
NBO analysis data of various modifications of B3N3 according to CCSD(T)/6-311++G(df,p) method data.
| Compound | The Charges on the Atoms, in Electron Charge Units (ē) | |||||
|---|---|---|---|---|---|---|
| N1 | N2 | N3 | B1 | B2 | B3 | |
| B3N3 (I) | −1.19049 | −1.19062 | −1.19040 | +1.19069 | +1.19015 | +1.19067 |
| B3N3 (II) | −1.18894 | −0.73637 | −0.44979 | +1.20616 | +0.79351 | +0.37543 |
| B3N3 (III) | −0.45135 | −0.63555 | −0.03730 | +0.48064 | +0.66080 | −0.01723 |
| B3N3 (IV) | −0.53902 | −0.77371 | −1.04131 | +1.05055 | +0.73557 | +0.56792 |
| B3N3 (V) | −0.61776 | −0.61806 | −1.03235 | +0.73432 | +0.73354 | +0.80030 |
| B3N3 (VI) | −0.74180 | −0.75310 | −0.29335 | +0.63671 | +0.35787 | +0.79367 |
| B3N3 (VII) | −0.34059 | −0.34113 | −0.27877 | −0.00824 | +0.48370 | +0.48503 |
Table 4.
Standard thermodynamic parameters of formation of B3N3 molecules in gas phase calculated with using G4 method.
Table 4.
Standard thermodynamic parameters of formation of B3N3 molecules in gas phase calculated with using G4 method.
| Compound | ΔfH0, kJ∙mol−1 | S0, J∙mol−1∙K−1 | ΔfG0, kJ∙mol−1 |
|---|---|---|---|
| B3N3 (I) | 192.1 | 306.8 | 191.0 |
| B3N3 (II) | 597.6 | 314.2 | 594.2 |
| B3N3 (III) | 929.3 | 326.0 | 922.4 |
| B3N3 (IV) | 662.1 | 329.9 | 654.0 |
| B3N3 (V) | 785.1 | 311.0 | 782.6 |
| B3N3 (VI) | 985.7 | 308.6 | 984.0 |
| B3N3 (VII) | 1092.8 | 318.5 | 1088.1 |
Table 5.
Standard thermodynamic parameters of formation of compounds participating in Reaction (1), calculated by G4 method. By italics in brackets () indicate the experimental values [48].
Table 5.
Standard thermodynamic parameters of formation of compounds participating in Reaction (1), calculated by G4 method. By italics in brackets () indicate the experimental values [48].
| Compound | ΔfH0, kJ∙mol−1 | S0, J∙mol−1∙K−1 | ΔfG0, kJ∙mol−1 |
|---|---|---|---|
| B3H6N3 (gas) | −513.7 | 329.1 | −404.8 |
| B3H6N3 (liq) | (−541.0) | (199.6) | (−392.7) |
| O2 (gas) | 2.0 (0) | 222.0 (205.2) | −3.1 (0) |
| B3N3 (I) (gas) | 192.1 | 306.8 | 191.0 |
| H2O (gas) | −239.6 (−241.8) | 197.2 (188.8) | −228.9 (−228.6) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Chachkov, D.V.; Mikhailov, O.V. Cyclic Six-Atomic Boron-Nitrides: Quantum-Chemical Consideration by Ab Initio CCSD(T) Method. Quantum Rep. 2022, 4, 351-361. https://doi.org/10.3390/quantum4030025
AMA Style
Chachkov DV, Mikhailov OV. Cyclic Six-Atomic Boron-Nitrides: Quantum-Chemical Consideration by Ab Initio CCSD(T) Method. Quantum Reports. 2022; 4(3):351-361. https://doi.org/10.3390/quantum4030025
Chicago/Turabian StyleChachkov, Denis V., and Oleg V. Mikhailov. 2022. "Cyclic Six-Atomic Boron-Nitrides: Quantum-Chemical Consideration by Ab Initio CCSD(T) Method" Quantum Reports 4, no. 3: 351-361. https://doi.org/10.3390/quantum4030025
APA StyleChachkov, D. V., & Mikhailov, O. V. (2022). Cyclic Six-Atomic Boron-Nitrides: Quantum-Chemical Consideration by Ab Initio CCSD(T) Method. Quantum Reports, 4(3), 351-361. https://doi.org/10.3390/quantum4030025
