Uncertainty Relation and the Thermal Properties of an Isotropic Harmonic Oscillator (IHO) with the Inverse Quadratic (IQ) Potentials and the Pseudo-Harmonic (PH) with the Inverse Quadratic (IQ) Potentials
Abstract
:1. Introduction
2. Methodology
3. Bound State Solutions
4. Expectation Values
Thermodynamic Properties
- (a)
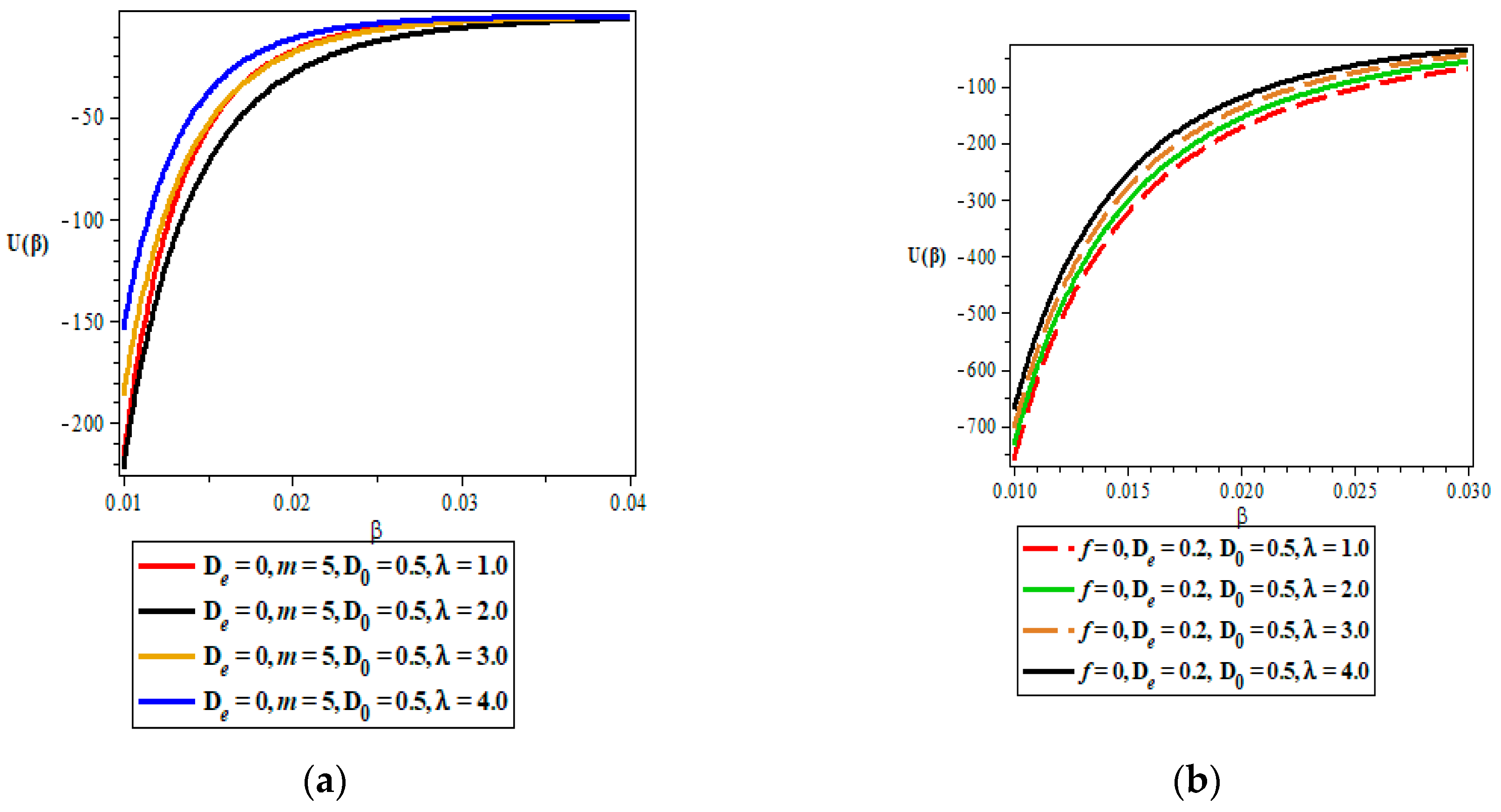
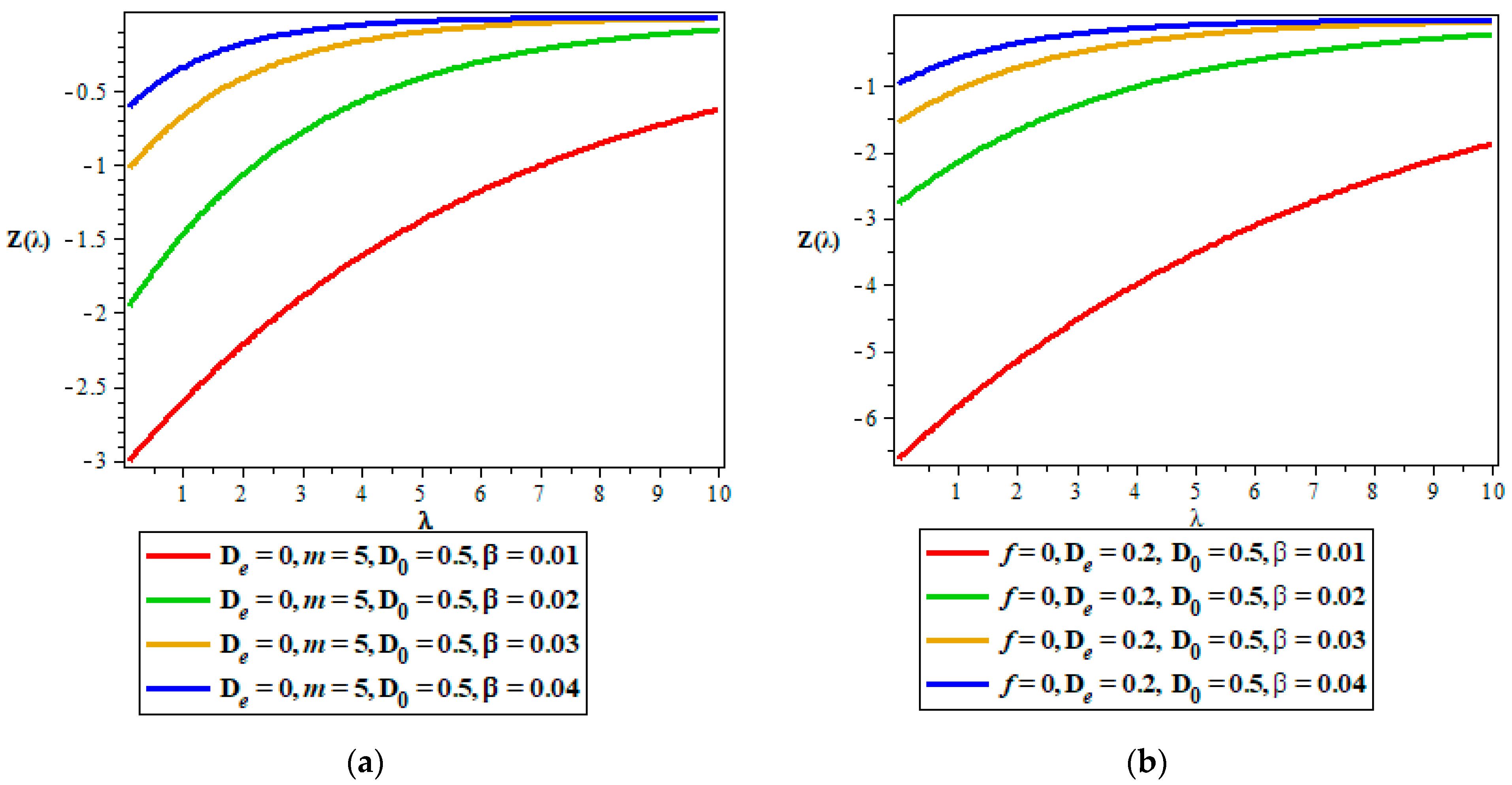
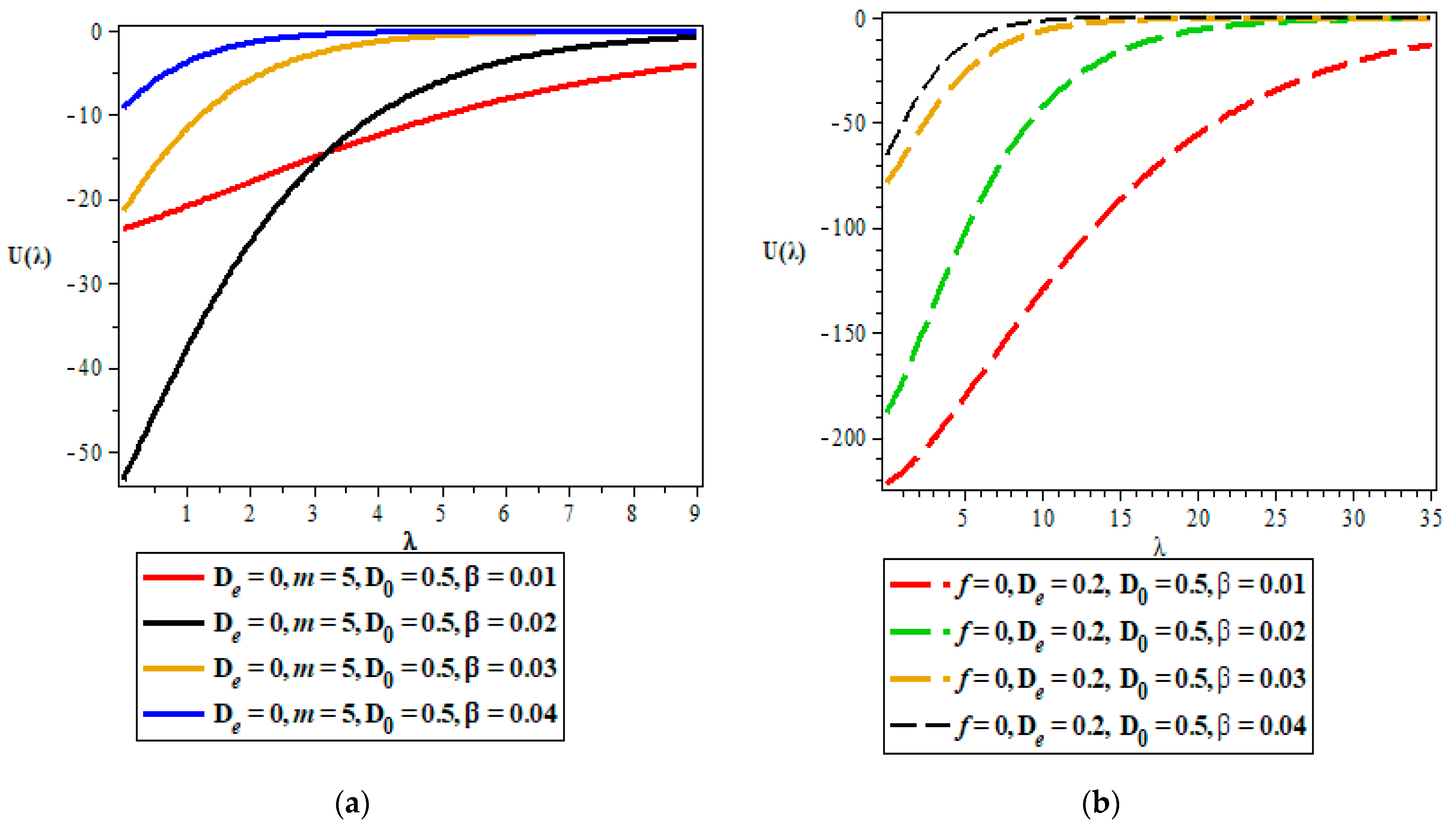
- Vibrational mean energy.
- (b)
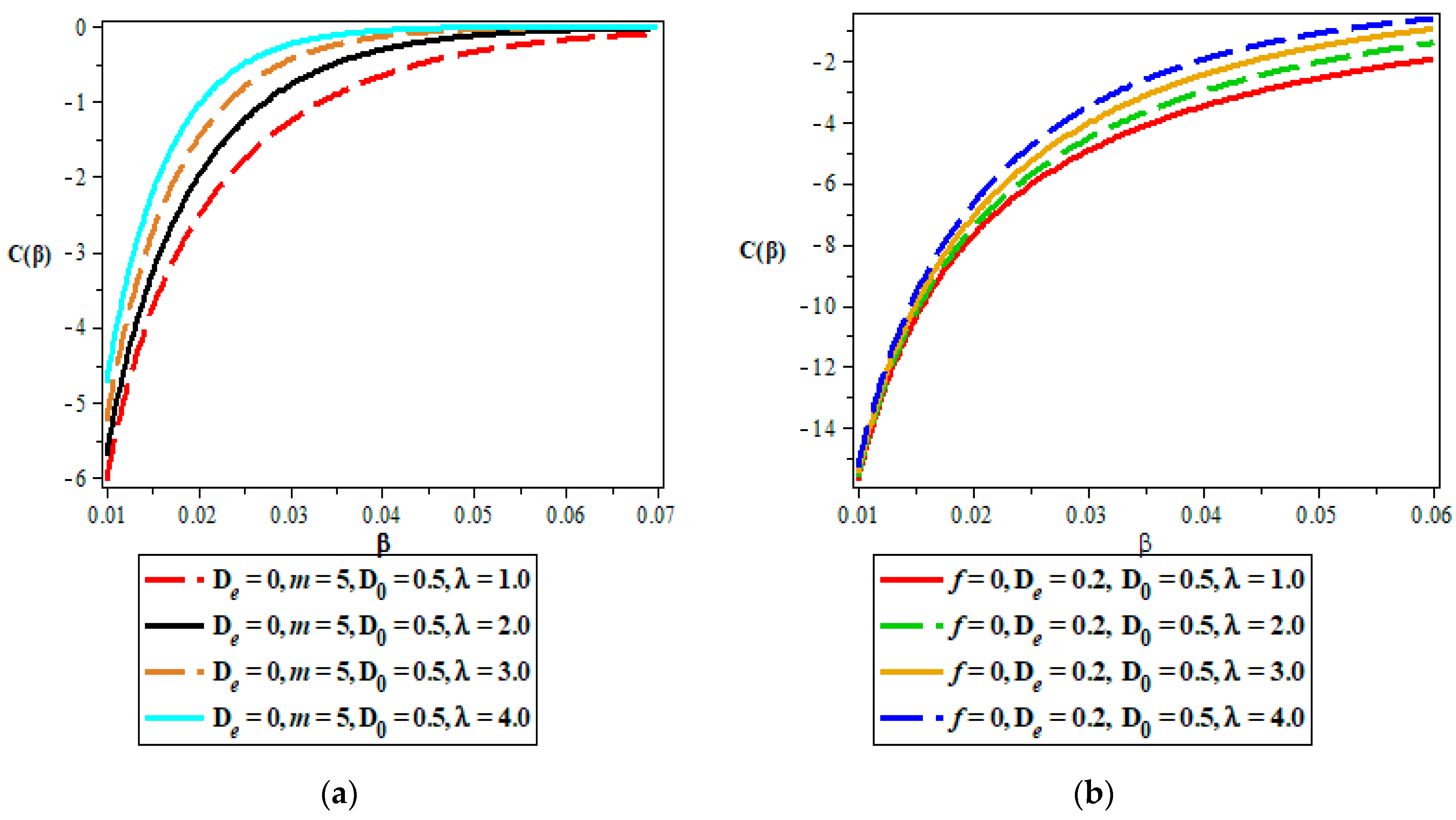
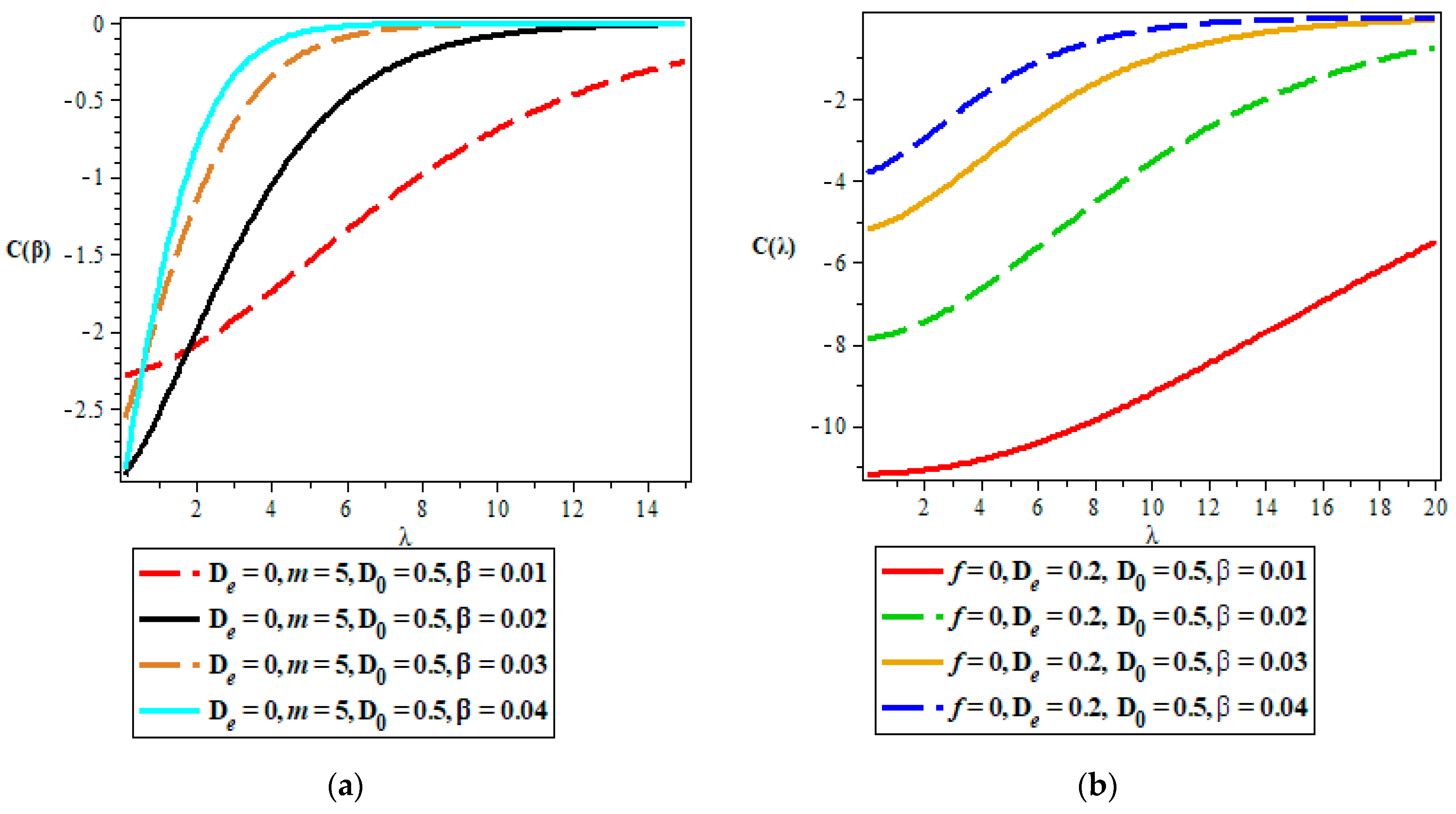
- Vibrational heat capacity.
- (c)
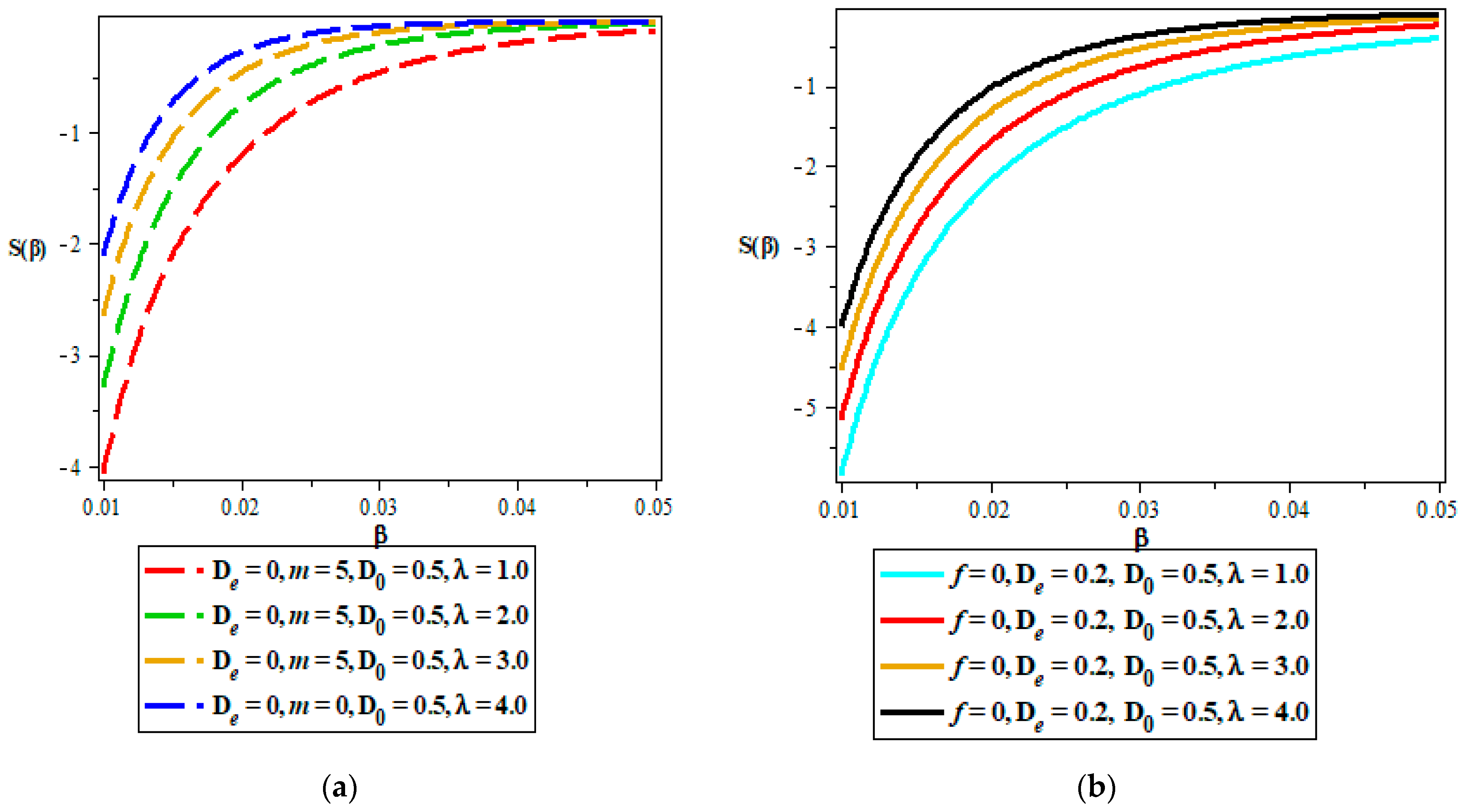
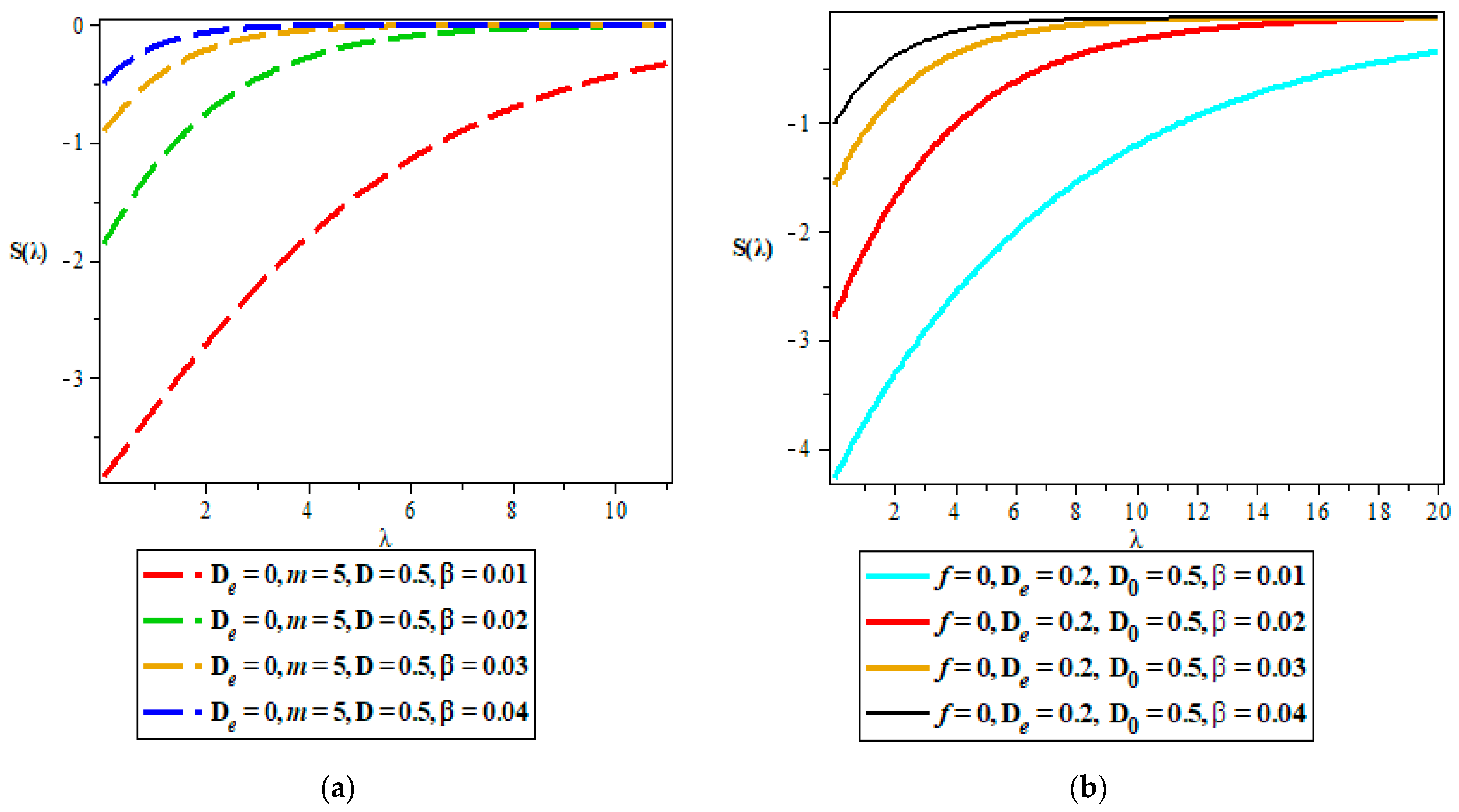
- Vibrational entropy.
- (d)
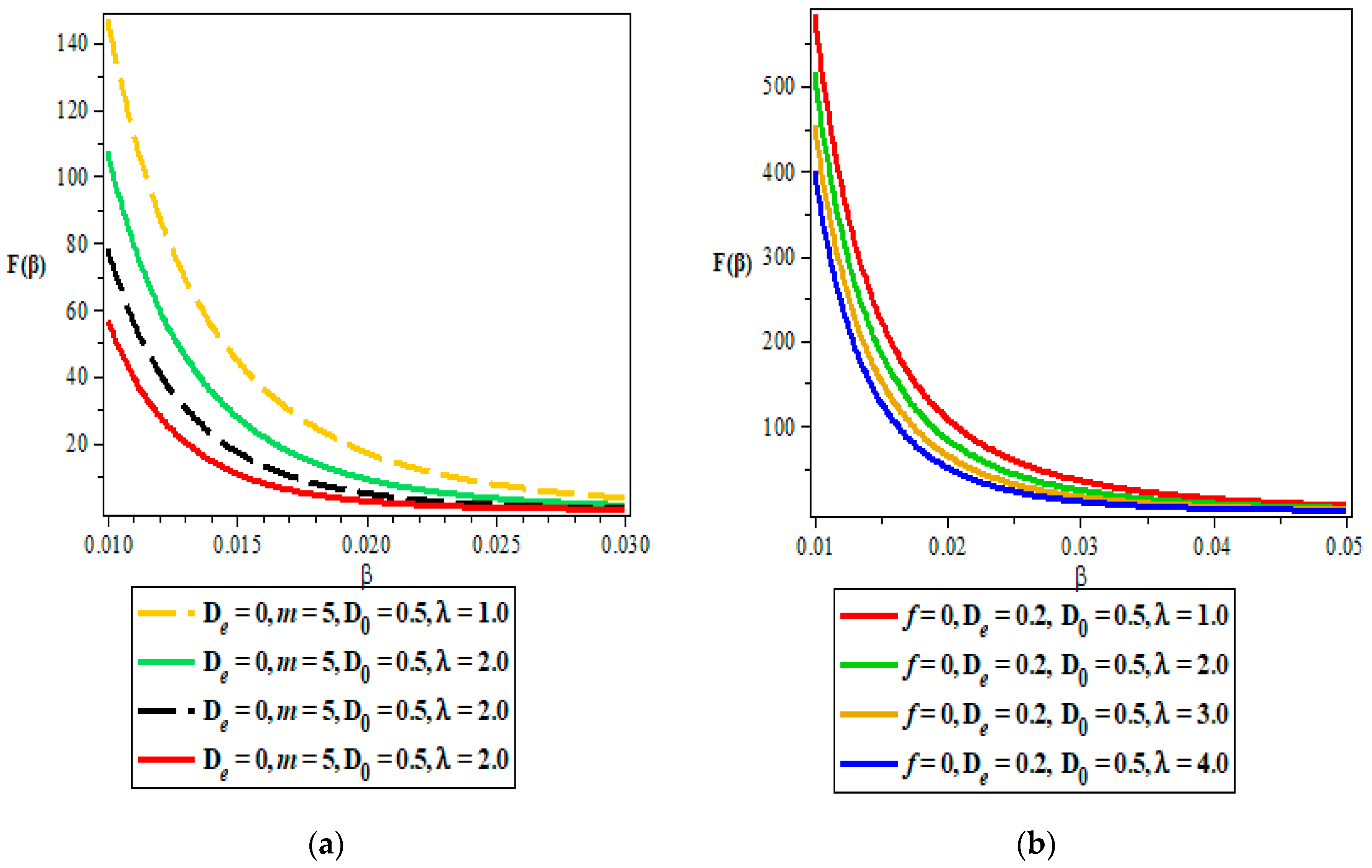
- Vibrational Free energy
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.-C.; An, B. Analytical Solutions of the Manning-Rosen Potential In the Tridiagonal Program. Chin. Phys. Lett. 2010, 27, 110301. [Google Scholar]
- Oyewumi, K.J.; Akosile, C.O. Bound state solutions of the Dirac-Rosen-Morse potential with spin and pseudospin symmetry. Eur. Phys. J. A 2010, 45, 311–318. [Google Scholar] [CrossRef] [Green Version]
- Miraboutalebi, S.; Rajae, L. Solutions of N-dimensional Schrödinger equation with Morse potential via Laplace transforms. J. Math. Chem. 2014, 52, 1119–1128. [Google Scholar] [CrossRef]
- Jia, C.-S.; Zhang, L.-H.; Pen, X.-L. Improved Poschl-Teller potential energy model for diatomic molecules. Int. J. Quantum Chem. 2017, 2017, e25383. [Google Scholar] [CrossRef]
- Antia, A.D.; Ituen, E.E.; Obong, H.P.; Isonguyo, C.N. Analytical solutions of the modified Coulomb potential using the factorization method. Int. J. Recent Adv. Phys. 2015, 4, 55–65. [Google Scholar] [CrossRef]
- Napsuciale, M.; Rodriguez, S. Complete analytical solution to the quantum Yukawa potential. Phys. Lett. B 2021, 816, 136218. [Google Scholar] [CrossRef]
- Onate, C.A.; Onyeaju, M.C.; Ikot, A.N.; Ebomwonyi, O. Eigen solutions and entropic system for Hellmann potential in the presence of the Schrodinger equation. Eur. Phys. J. Plus 2017, 132, 462. [Google Scholar] [CrossRef]
- Antia, A.D.; Eze, C.C.; Akpabio, L.E. Solutions of the Schrödinger equation with the harmonic oscillator potential (HOP) in cylindrical basis. Phys. Astron. Int. J. 2018, 2, 187–191. [Google Scholar] [CrossRef]
- Ghanbari, A.; Khordad, R.; Taghizadeh, F. Influence of Coulomb term on thermal properties of fluorine. Chem. Phys. Lett. 2022, 801, 139725. [Google Scholar] [CrossRef]
- Bayrak, O.; Boztosun, I. Bound state solutions of the Hulthẻn potential by using the asymptotic iteration method. Phys. Scr. 2007, 76, 92–96. [Google Scholar] [CrossRef]
- Falaye, B.J.; Oyewumi, K.J.; Ikhdair, S.M.; Hamzavi, M. Eigensolution techniques, their applications and Fisherʼs information entropy of the Tietz–Wei diatomic molecular model. Phys. Scr. 2014, 89, 115204. [Google Scholar] [CrossRef]
- Wei, G.-F.; Dong, S.-H. Pseudospin symmetry in the relativistic Manning-Rosen potential including a Pekeris-type approximation to the pseudo-centrifugal term. Phys. Lett. B 2010, 686, 288–292. [Google Scholar] [CrossRef] [Green Version]
- Onate, C.A.; Onyeaju, M.C. Fisher information of a vector potential for time-dependent Feinberg–Horodecki equation. Int. J. Quantum Chem. 2020, 2020, e26543. [Google Scholar] [CrossRef]
- Onyeaju, M.C.; Idiodi, J.; Ikot, A.; Solaimani, M.; Hassanabadi, H. Linear and nonlinear optical properties in spherical quantum dots: Generalized Hulthén potential. Few-Body Syst. 2016, 57, 793–805. [Google Scholar] [CrossRef]
- Mustafa, O.; Sever, R. Approach to the shifted 1/N expansion for the Klein-Gordon equation. Phys. Rev. A 1991, 43, 5787. [Google Scholar] [CrossRef]
- Omugbe, E.; Osafile, O.E.; Okon, I.B.; Eyube, E.S.; Inyang, E.P.; Okorie, U.S.; Jahanshir, A.; Onate, C.A. Non-relativistic bound state solutions with α-deformed Kratzer-type potential using the super-symmetric WKB method: Application to theoretic-information measures. Eur. Phys. J. D 2022, 76, 72. [Google Scholar] [CrossRef]
- Gu, X.-Y.; Dong, S.-H.; Ma, Z.-Q. Energy spectra for modified Rosen-Morse potential solved by the exact quantization rule. J. Phys. A Math. Theor. 2009, 42, 035303. [Google Scholar] [CrossRef]
- Falaye, B.J.; Ikhdair, S.M.; Hamzavi, M. Formula method for bound state problems. Few-Body Syst. 2015, 56, 63–78. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.F.; Hafez, M.G.; Hammouch, Z.; Bileanu, D. Periodic and rogue waves for Heisenberg models of ferromagnetic spin chains with fractional beta derivative evolution and obliqueness. Waves Random Complex Media 2021, 31, 2135–2149. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, Z. An effective dissipation-preserving fourth-order difference solver for fractional-in-space nonlinear wave equations. J. Sci. Comput. 2019, 79, 1753–1776. [Google Scholar] [CrossRef]
- Tezcan, C.; Sever, R. A General Approach for the Exact Solution of the Schrödinger equation. Int. J. Theor. Phys. 2009, 48, 337–350. [Google Scholar] [CrossRef]
- Njoku, I.J.; Onyenegecha, C.P.; Okereke, C.J.; Opara, A.I.; Ukewuihe, U.M.; Nwaneho, F.U. Approximate solutions of Schrodinger equation and thermodynamic properties with Hua potential. Results Phys. 2021, 24, 104208. [Google Scholar] [CrossRef]
- Feynman, R.P. Forces in Molecules. Phys. Rev. 1039, 56, 340. [Google Scholar] [CrossRef]
- Barut, A.O.; Inomata, A.; Wilson, R. A new realization of dynamical groups and factorisation method. J. Phys. A Math. Gen. 1987, 20, 4075. [Google Scholar] [CrossRef]
- Oyewumi, K.J.; Sen, K.D. Exact solutions of the Schrödinger equation for the pseudoharmonic potential: An application to some diatomic molecules. J. Math Chem. 2012, 50, 1039–1059. [Google Scholar] [CrossRef]

| 0 | 26.409819 | 28.285714 | 33.4494110 | 41.3654140 |
| 1 | 38.981248 | 40.857143 | 61.7336830 | 69.6496850 |
| 2 | 51.552676 | 53.428571 | 90.0179540 | 97.9339570 |
| 3 | 64.124105 | 66.000000 | 118.302225 | 126.218228 |
| 4 | 76.695533 | 78.571429 | 146.586496 | 154.502499 |
| 5 | 89.266962 | 91.142857 | 174.870768 | 182.786770 |
| 6 | 101.83839 | 103.71429 | 203.155039 | 211.071042 |
| 7 | 114.40982 | 116.28571 | 231.439310 | 239.355313 |
| 8 | 126.98125 | 128.85714 | 259.723581 | 267.639584 |
| 9 | 139.55268 | 141.42857 | 288.007853 | 295.923855 |
| 1 | 9.428571 | 22.00000 | 22.00000 | 34.57143 |
| 2 | 13.33401 | 31.11270 | 31.11270 | 48.89138 |
| 3 | 16.33077 | 38.10512 | 38.10512 | 59.87947 |
| 4 | 18.85714 | 44.00000 | 44.00000 | 69.14286 |
| 5 | 21.08293 | 49.19350 | 49.19350 | 77.30406 |
| 6 | 23.09519 | 53.88877 | 53.88877 | 84.68236 |
| 7 | 24.94566 | 58.20653 | 58.20653 | 91.46740 |
| 8 | 26.66803 | 62.22540 | 62.22540 | 97.78277 |
| 9 | 28.28571 | 66.00000 | 66.00000 | 103.7143 |
| 1 | 1.795918 | 0.715909 | 1.340119 | 0.846114 | 1.285714 | 1.133893 |
| 2 | 3.591837 | 0.357955 | 1.895214 | 0.598293 | 1.285714 | 1.133893 |
| 3 | 5.387755 | 0.238636 | 2.321154 | 0.488504 | 1.285714 | 1.133893 |
| 4 | 7.183673 | 0.178977 | 2.680238 | 0.423057 | 1.285714 | 1.133893 |
| 5 | 8.979592 | 0.143182 | 2.996597 | 0.378394 | 1.285714 | 1.133893 |
| 6 | 10.77551 | 0.119318 | 3.282607 | 0.345425 | 1.285714 | 1.133893 |
| 7 | 12.57143 | 0.102273 | 3.545621 | 0.319801 | 1.285714 | 1.133893 |
| 8 | 14.36735 | 0.089489 | 3.790428 | 0.299147 | 1.285714 | 1.133893 |
| 9 | 16.16327 | 0.079545 | 4.020356 | 0.282038 | 1.285714 | 1.133893 |
| 1 | 1.795918 | 0.715909 | 1.340119 | 0.846114 | 1.285714 | 1.133893 |
| 2 | 2.539812 | 0.506224 | 1.593679 | 0.711494 | 1.285714 | 1.133893 |
| 3 | 3.110622 | 0.413330 | 1.763696 | 0.642908 | 1.285714 | 1.133893 |
| 4 | 3.591837 | 0.357955 | 1.895214 | 0.598293 | 1.285714 | 1.133893 |
| 5 | 4.015796 | 0.320164 | 2.003945 | 0.565831 | 1.285714 | 1.133893 |
| 6 | 4.399084 | 0.292269 | 2.097399 | 0.540619 | 1.285714 | 1.133893 |
| 7 | 4.751553 | 0.270588 | 2.179806 | 0.520181 | 1.285714 | 1.133893 |
| 8 | 5.079624 | 0.253112 | 2.253802 | 0.503102 | 1.285714 | 1.133893 |
| 9 | 5.387755 | 0.238636 | 2.321154 | 0.488504 | 1.285714 | 1.133893 |
| 1 | 63.668581 | 0.318400 | 7.979259 | 0.564269 | 20.272076 | 4.502452 |
| 2 | 90.068553 | 0.225285 | 9.490445 | 0.474642 | 20.291137 | 4.504568 |
| 3 | 110.33413 | 0.184061 | 10.504006 | 0.429024 | 20.308236 | 4.506466 |
| 4 | 127.41968 | 0.159502 | 11.288033 | 0.399378 | 20.323749 | 4.508187 |
| 5 | 142.46878 | 0.142753 | 11.936028 | 0.377827 | 20.337892 | 4.509755 |
| 6 | 156.06754 | 0.130397 | 12.492700 | 0.361106 | 20.350814 | 4.511188 |
| 7 | 168.56396 | 0.120801 | 12.983218 | 0.347564 | 20.362621 | 4.512496 |
| 8 | 180.18462 | 0.113070 | 13.423287 | 0.336258 | 20.373399 | 4.513690 |
| 9 | 191.08683 | 0.106670 | 13.823416 | 0.326604 | 20.383213 | 4.514777 |
| 1 | 142.4688 | 0.142753 | 11.93603 | 0.377827 | 20.337892 | 4.509755 |
| 2 | 70.92286 | 0.288190 | 8.421571 | 0.536833 | 20.439257 | 4.520980 |
| 3 | 46.28354 | 0.438889 | 6.803200 | 0.662487 | 20.313320 | 4.507030 |
| 4 | 33.02793 | 0.597235 | 5.746993 | 0.772810 | 19.725440 | 4.441333 |
| 5 | 24.10503 | 0.765362 | 4.909687 | 0.874850 | 18.449065 | 4.295237 |
| 6 | 17.21077 | 0.945117 | 4.148587 | 0.972171 | 16.266201 | 4.033138 |
| 7 | 11.39367 | 1.138065 | 3.375451 | 1.066802 | 12.966739 | 3.600936 |
| 8 | 6.203733 | 1.345502 | 2.490729 | 1.159958 | 8.3471370 | 2.889141 |
| 9 | 1.408303 | 1.568486 | 1.186719 | 1.252392 | 2.2089030 | 1.486238 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onate, C.A.; Okon, I.B.; Jude, G.O.; Onyeaju, M.C.; Antia, A.D. Uncertainty Relation and the Thermal Properties of an Isotropic Harmonic Oscillator (IHO) with the Inverse Quadratic (IQ) Potentials and the Pseudo-Harmonic (PH) with the Inverse Quadratic (IQ) Potentials. Quantum Rep. 2023, 5, 38-51. https://doi.org/10.3390/quantum5010004
Onate CA, Okon IB, Jude GO, Onyeaju MC, Antia AD. Uncertainty Relation and the Thermal Properties of an Isotropic Harmonic Oscillator (IHO) with the Inverse Quadratic (IQ) Potentials and the Pseudo-Harmonic (PH) with the Inverse Quadratic (IQ) Potentials. Quantum Reports. 2023; 5(1):38-51. https://doi.org/10.3390/quantum5010004
Chicago/Turabian StyleOnate, Clement A., Ituen B. Okon, Gian. O. Jude, Michael C. Onyeaju, and Akaninyene. D. Antia. 2023. "Uncertainty Relation and the Thermal Properties of an Isotropic Harmonic Oscillator (IHO) with the Inverse Quadratic (IQ) Potentials and the Pseudo-Harmonic (PH) with the Inverse Quadratic (IQ) Potentials" Quantum Reports 5, no. 1: 38-51. https://doi.org/10.3390/quantum5010004
APA StyleOnate, C. A., Okon, I. B., Jude, G. O., Onyeaju, M. C., & Antia, A. D. (2023). Uncertainty Relation and the Thermal Properties of an Isotropic Harmonic Oscillator (IHO) with the Inverse Quadratic (IQ) Potentials and the Pseudo-Harmonic (PH) with the Inverse Quadratic (IQ) Potentials. Quantum Reports, 5(1), 38-51. https://doi.org/10.3390/quantum5010004







