Fisher Information for a System Composed of a Combination of Similar Potential Models

Abstract

The solutions to the radial Schrödinger equation for a pseudoharmonic potential and Kratzer potential have been studied separately in the past. Despite different reports on the Kratzer potential, the fundamental theoretical quantities such as Fisher information have not been reported. In this study, we obtain the solution to the radial Schrödinger equation for the combination of the pseudoharmonic and Kratzer potentials in the presence of a constant-dependent potential, utilizing the concepts and formalism of the supersymmetric and shape invariance approach. The position expectation value and momentum expectation value are calculated employing the Hellmann–Feynman Theory. These expectation values are then used to calculate the Fisher information for both position and momentum spaces in both the absence and presence of the constant-dependent potential. The results obtained revealed that the presence of the constant-dependent potential leads to an increase in the energy eigenvalue, as well as in the position and momentum expectation values. Additionally, the constant-dependent potential increases the Fisher information for both position and momentum spaces. Furthermore, the product of the position expectation value and the momentum expectation value, along with the product of the Fisher information, satisfies both Fisher’s inequality and Cramer–Rao’s inequality.

1. Introduction

The utility of potential systems in quantum mechanics spans a wide spectrum, encompassing solutions for both bound states and scattering states, as well as various theoretical quantities such as Fisher information, Shannon entropy, variance, Tsallis entropy, Rényi entropy, and information energy. Diverse physical potential models have been employed to derive energy spectra for different systems, resulting in varying outcomes. For instance, when considering the sodium dimer, the energy predictions from the Yukawa potential differs from those generated through the Woods–Saxon potential. Such discrepancies arise due to the distinct physical natures and parameterization of these potential models. In the realm of quantum systems, atomic interactions are often modeled using potential energy functions, which greatly influence the properties exhibited by different systems. These potential functions, particularly those falling within the class of exponential-type potential models, effectively describe diatomic molecules and provide numerical values that align with observed data. Many of these energy potential functions have been adapted for suitability by Jia et al. [1] and are commonly explored through appropriate approximation schemes. This exploration has piqued the interest of numerous authors and researchers, particularly in nonrelativistic quantum mechanics, where the ro-vibrational spectra of diverse quantum systems have been extensively studied [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. For instance, Njoku et al. [18] studied the Hua potential model under the nonrelativistic system. These authors obtained the bound state solutions of the Schrödinger equation for the Hua potential model. The authors numerically examined the effect of the equilibrium bond length on the energy eigenvalue for different quantum states. They further extended their study to the calculation of thermodynamic properties, investigating the effects of the maximum quantum state and the temperature parameter on the partition function and other thermodynamic properties such as mean energy, specific heat capacity, entropy, and free mean energy. Yașuk et al. [19] studied the Schrödinger equation for a noncentral potential system, employing a combination of radial and angular potential models. Using the method of the separation of variables, these authors calculated the energy equation and the wave function of the system using the Nikiforov–Uvarov method. They obtained special cases of the noncentral potential, such as the Coulomb and Hartmann ring-shaped potentials, and compared the results with those in the existing literature. In ref. [20], Okon et al. studied the solutions of the Schrödinger equation for a combination of the Hulthẻn and an exponential Coulomb-like potential model using the parametric Nikiforov–Uvarov method. They examined the behavior of the energy of the combined potential as well as the subset potential for various quantum states and angular momentum quantum states. The energy of the Hulthẻn potential rises as the quantum state increases. Similarly, the energy rises as the screening parameter increases for the same Hulthẻn potential. Yahya and Issa [21] obtained the solutions of the Schrödinger equation for improved Tietz potential and improved the Rosen–Morse potential model using the methodology of the parametric Nikiforov–Uvarov method. They studied the energy eigenvalue and the wave functions of the two potentials separately. These authors examined the relationship between the energy and the deformed parameter. They also examined the effect of the angular momentum number on the energy of the improved Rosen–Morse potential model at different quantum numbers.

However, there exists another category of potential models tailored toward investigating bound state problems and related quantum systems that are not in the exponential form or Pὂschl–Teller form. Notably, among these models are the pseudoharmonic potential and the Kratzer potential. The pseudoharmonic potential integrates elements of the harmonic potential model, the inverse potential system, and a constant term, and is thereby capable of reproducing solutions from these three distinct potential models. Unlike many other models, the physical nature of the pseudoharmonic potential discourages the application of approximation schemes. Proposed by Davidson [22], the pseudoharmonic potential was specifically devised to elucidate the roto-vibrational states of diatomic molecules. On the other hand, the Kratzer potential serves as a molecular potential used to elucidate molecular structures and atomic interactions. Its widespread application has primarily centered around bound states within the molecular domain. Because of the applications of these potentials, several authors have reported the potentials separately in the field of Physics. Among the reports on the pseudoharmonic potential and the Kratzer potential are the work of Oyewumi and Sen [23], who studied the pure pseudoharmonic potential in the context of bound states and applied their study to diatomic molecules. In ref. [24], Oyewumi et al. studied a D-dimensional system of pseudoharmonic potential and constructed ladder operators. Sever et al. [25] obtained energy spectra for the pseudo-harmonic potential and generated numerical values for some molecules with the first six quantum states. Ikhdair and Sever [26], in their study, calculated the exact polynomial eigensolutions of the Schrödinger equation for the pseudoharmonic potential. In the study, they obtained exact bound-state energy eigenvalues and the corresponding eigenfunctions analytically. The energy states for several diatomic molecular systems were calculated numerically for various principal and angular quantum numbers. Through a proper transformation, the problem was also solved and made very simple using the known eigensolutions of the anharmonic oscillator potential. Das and Arda [27], in one of the articles studied, deduced the exact analytical solution of the N-dimensional radial Schrödinger equation with pseudoharmonic potential using a Laplace transform approach. The authors examined the variation in the spatial dimensions against the energy of the system. Recently, the exact solutions of the κ-dependent Schrödinger equation with quantum pseudo-harmonic oscillator and its applications to the thermodynamic properties in normal and superstatistics were obtained by Okorie et al. [28]. The pseudoharmonic potential is generally used to describe the roto-vibrational states of diatomic molecules, nuclear rotations, and vibrations. The Kratzer potential also received different reports on the nonrelativistic models. Some of the reports on the Kratzer potential include the work of Bayrak et al. [29], who studied the radial Schrödinger equation with the Kratzer potential and obtained the exact analytical solutions to the Kratzer potential using the asymptotic iteration method. They generated numerical values for some molecules using their spectroscopic constants. Despite the extensive reporting on the Kratzer potential, its utilization concerning Fisher information remains underexplored to the best of our understanding. Motivated by the interest in Fisher information for nonexponential-type potentials, the current study aimed to scrutinize the applicability of Fisher information in a scenario involving a combination of the pseudoharmonic potential and the Kratzer potential, alongside a constant-dependent potential. The effects of the constant dependent potential and the potential parameters on the Fisher information will be examined numerically to verify the Cramer–Rao inequality and Fisher inequality. The Fisher information for the combination of these potentials will be obtained using expectation values. The specific form of the potential model under investigation is physically represented as [22]

$$V_1(r)=D_e{\left(\frac{r}{r_e}-\frac{r_e}{r}\right)}^2,$$

(1)

while the Kratzer potential is given as [30]

$$V_2(r)=-D_e\left(\frac{2r_e}{r}-\frac{r_e^2}{r^2}\right),$$

(2)

where $D_e$ is a dissociation energy, $r$ is the internuclear distance, and $r_e$ is an equilibrium bond separation. These two potentials take the form of molecular potential due to their possession of parameters with physical meanings. The combination of Equations (1) and (2) with a constant-dependent potential is given as

$$V(r)=\left[V_1(r)+V_2(r)\right]\left(1+\eta \right).$$

(3)

The parameter $(\eta )$ is known as the constant-dependent potential.

The nonrelativistic solutions for Equation (3) will be obtained using a supersymmetric approach. The pseudoharmonic potential and the Kratzer potential have been reported by different authors for some models.

2. Bound State Solutions

To obtain the solutions of the redial potential system in Equation (3), the radial Schrödinger equation with nonrelativistic energy $E_{n,\mathcal{l}}$, reduced Planck constant $\hslash$, the reduced mass of the molecule $\mu$, and the radial wave function $R_{n,\mathcal{l}}(r)$ is given as

$$-\frac{{\hslash }^2}{2\mu }\frac{d^2{R}_{n,\mathcal{l}}(r)}{d{r}^2}+\left(V(r)+\frac{{\hslash }^2}{2\mu }\frac{1}{r^2}\right)R_{n,\mathcal{l}}(r)=E_{n,\mathcal{l}}{R}_{n,\mathcal{l}}(r).$$

(4)

Substituting the radial potential system in Equation (3) into Equation (4), we obtain a second-order differential equation of the form

$$\frac{d^2{R}_{n,\mathcal{l}}(r)}{d{r}^2}+\left(-\lambda \left(E_{n,\mathcal{l}}-2D_e\left(1+\eta \right)\right)+\frac{\lambda D_e\left(1+\eta \right)r^2}{r_e^2}-\frac{2\lambda D_e{r}_e\left(1+\eta \right)}{r}+\frac{2\lambda D_e{r}_e^2\left(1+\eta \right)+\mathcal{l}(\mathcal{l}+1)}{r^2}\right)R_{n,\mathcal{l}}(r)=0.$$

(5)

where $\lambda =\frac{2\mu }{{\hslash }^2}$. The supersymmetric approach suggests the ground state wave function for the next step. Thus, the ground state wave function is written as

$$R_{0,\mathcal{l}}(r)=exp\left(-{\displaystyle \int W(r)dr}\right),$$

(6)

where $W(r)$ is referred to as a superpotential function in supersymmetry quantum mechanics. The ground state wave function corresponds to the two partner Hamiltonians given as

$$\begin{array}{l}{H}_{+}=\widehat{A}{\widehat{A}}^{†}=-\frac{d^2}{d{r}^2}+V_{+}(r)\\ H_{-}={\widehat{A}}^{†}\widehat{A}=-\frac{d^2}{d{r}^2}-V_{-}(r)\end{array}\},$$

(7)

where

$$\begin{array}{l}\widehat{A}=\frac{d}{dr}-W(r)\\ {\widehat{A}}^{†}=-\frac{d}{dr}-W(r)\end{array}\}.$$

(8)

In substituting the ground state wave function into Equation (5), the resulting solution appears as a differential equation of the form

$$W^2(r)-\frac{dW(r)}{dr}-\lambda \left(E_{0,\mathcal{l}}-2D_e\left(1+\eta \right)\right)+\frac{\lambda D_e\left(1+\eta \right)r^2}{r_e^2}+\frac{2\lambda r_e{D}_e\left(r_e-r\right)\left(1+\eta \right)+\mathcal{l}(\mathcal{l}+1)}{r^2},$$

(9)

where the superpotential $W(r)$ is proposed as follows:

$$W(r)={\theta }_0-{\theta }_1{r}^{-1}.$$

(10)

The two terms ${\theta }_0$ and ${\theta }_1$ in Equation (10) represent constants in the proposed superpotential, which will soon be determined. The superpotential is proposed based on the interacting potential and the nature of the Riccati equation in Equation (9). This will ensure that the property of the left-hand side and the right-hand side of Equation (9) are the same. In substituting Equation (10) into Equation (9) and conducting subsequent mathematical manipulations and simplifications, the values of the superpotential constants in Equation (10) are obtained as follows:

$${\theta }_1=\frac{-1\pm \sqrt{{(1+2)}^2+8\lambda D_e{r}_e^2(1+\eta )}}{2},$$

(11)

$${\theta }_0=\lambda D_e{r}_e(1+\eta ){\theta }_1^{-1},$$

(12)

$${\theta }_0^2=-\lambda \left(E_{n,\mathcal{l}}+2D_e{r}_e(1+\eta )\right)-{\theta }_1\sqrt{{\lambda }^{-1}{D}_e{r}_e^{-2}(1+\eta )}.$$

(13)

With the aid of Equations (7), (8), and (10), the partner potentials in supersymmetry quantum mechanics can be constructed as

$$V_{+}(r)=W^2(r)+\frac{dW(r)}{dr}={\theta }_0^2-\frac{2{\theta }_0{\theta }_1}{r}+\frac{{\theta }_1({\theta }_1-1)}{r^2},$$

(14)

$$V_{-}(r)=W^2(r)-\frac{dW(r)}{dr}={\theta }_0^2-\frac{2{\theta }_0{\theta }_1}{r}+\frac{{\theta }_1({\theta }_1+1)}{r^2}.$$

(15)

Equations (14) and (15) are family potentials and they satisfy the shape invariance condition through the mapping of the form ${\theta }_1\to {\theta }_1+n,$ ${\theta }_1=a_0.$ It is deduced that $a_1=f(a_0)=a_0+1$, where $a_1$ is a new set of parameters uniquely determined from the old set $a_0$, and $R(a_1)$ is a residual term that is independent of the variable $r.$ Since $a_1=a_0+1$ and by recurrence relation, $a_n=a_0+n.$ From the shape invariance approach, we can write [31,32,33]

$$R(a_1)=V_{+}(a_0,r)-V_{-}(a_1,r),$$

(16)

$$R(a_2)=V_{+}(a_1,r)-V_{-}(a_2,r),$$

(17)

$$R(a_3)=V_{+}(a_2,r)-V_{-}(a_3,r),$$

(18)

$$R(a_n)=V_{+}(a_{n-1},r)-V_{-}(a_n,r).$$

(19)

The energy level can be obtained using

$$E_{n,\mathcal{l}}=\sum _{\kappa =1}^{n}R(a_{\kappa })=R(a_1)+R(a_2)+R(a_3)\dots .+R(a_n).$$

(20)

From Equation (20), we obtain the complete energy eigenvalue equation as

$$E_{n,\mathcal{l}}=\frac{2{\mu }^2{D}_e^2{r}_e^2{(1+\eta )}^2}{{\hslash }^2}{\left(n+\frac{1}{2}+\frac{1}{2}\mathrm{\Lambda }\right)}^{-2}+\frac{2\hslash }{\mu }\sqrt{\frac{\mu D_e(1+\eta )}{2r_e^2}}\left(2n+1+\frac{1}{2}\mathrm{\Lambda }\right)-2D_e,$$

(21)

$$\mathrm{\Lambda }=\sqrt{{(1+2)}^2+8\lambda D_e{r}_e^2(1+\eta )}.$$

(22)

3. Calculation of Expectation Values

Here, we calculate the position and momentum expectation values using the Hellmann–Feynman Theorem. The Hellmann–Feynman Theorem relates the derivative of the total energy with respect to a parameter to the expectation value of the derivative of the Hamiltonian with respect to the same parameter [34,35,36,37]. If the spatial distribution of the electrons is determined by the solution of the Schrödinger equation, then the forces in the system can be calculated using classical electrodynamics. If the Hamiltonian $H$ for a particular system is a function of some parameter $v$ with the eigenvalue and eigenfunctions denoted by $E_{n,\mathcal{l}}(v)$ and $R_{n,\mathcal{l}}(v)$, respectively, then we can find the various expectation values provided that the associated normalized eigenfunction $R_{n,\mathcal{l}}(v)$ is continuous with respect to the parameter $v$. Then,

$$\frac{\partial E_{n,\mathcal{l}}(v)}{\partial v}=\langle R_{n,\mathcal{l}}(v)\left|\frac{\partial H(v)}{\partial v}\right|R_{n,\mathcal{l}}(v)\rangle ,$$

(23)

and

$$H=-\frac{{\hslash }^2}{2\mu }\frac{d^2}{d{r}^2}+\frac{{\hslash }^2}{2\mu }\frac{\mathcal{l}(\mathcal{l}+1)}{r^2}+D_e{\left(\frac{r}{r_e}-\frac{r_e}{r}\right)}^2-D_e\left(\frac{2r_e}{r}-\frac{r_e^2}{r}\right).$$

(24)

The various expectation values can now be calculated.

(I): Expectation value $\langle r^2\rangle .$ To obtain the expectation value of $r^2,$ we set $v=D_e,$ and then,

$$\langle r^2\rangle =\frac{2\mu }{\mathrm{\Lambda }}\left(\frac{\hslash {\mathrm{\Lambda }}_2\sqrt{2}}{\mu }-\frac{4{\mu }^2{D}_e^2{r}_e^2{(1+\eta )}^2}{{\hslash }^2{\mathrm{\Lambda }}_0^3}\right).$$

(25)

(II): Expectation value $\langle p^2\rangle .$ Setting $v=\mu ,$ we obtain the following expectation value:

$$\langle p^2\rangle =\frac{4{\mu }^3{D}_e^2{r}_e^2{(1+\eta )}^2}{{\hslash }^2{\mathrm{\Lambda }}_0^2}\left(\frac{1}{{\mu }^2}-\frac{4D_e{r}_e^2(1+\eta )}{\mathrm{\Lambda }{\mathrm{\Lambda }}_0{\hslash }^2}\right)+\frac{\sqrt{2}{D}_e(1+\eta )}{\mu }\left(\frac{{\hslash }^2{\mathrm{\Lambda }}_1}{{\mathrm{\Lambda }}_2{r}_e^2}+\frac{4{\mathrm{\Lambda }}_2{r}_e^2}{\mathrm{\Lambda }\hslash }\right)-\frac{\hslash {\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2\sqrt{2}}{{\mu }^2}.$$

(26)

4. Fisher Information

Fisher information is a concept in information theory that measures the amount of information that is available in a given system. In a quantum system, Fisher information is a probabilistic measure of uncertainty in a system. According to Gibilisco and Isola [38], a family of inequalities, related to the uncertainty principle, has been recently proved [39]. It is known that Heisenberg and Schrödinger uncertainty principles give lower bounds for the product of variances. Gibilisco et al. [40] proved an uncertainty principle in Schrödinger form where the bound for the product of variances depended on the area spanned by the commutators and with respect to an arbitrary quantum version of the Fisher information. According to refs. [41,42], for quantum mechanical systems, the Fisher information-based uncertainty relation has been used as an alternative to the Heisenberg uncertainty relation (HUR). Therefore, for a system with physical parameters $\theta$ and $\rho (r,\theta )$ [41,42],

$${\displaystyle \int dr\rho (r,\theta )=1,}$$

(27)

where $\rho (r,\theta )$ accounts for the details of the probability density. The examination of Fisher information occurs in two distinct parts, namely, Fisher information in the position space and Fisher information in the momentum space. The expressions for Fisher information in both the position and momentum spaces can be written as follows:

$$\begin{array}{l}I(\rho )={\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{\rho (r)}{\left[\frac{d\rho (r)}{dr}\right]}^{2}dr,}\\ I(\gamma )={\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{\gamma (p)}{\left[\frac{d\gamma (p)}{dp}\right]}^{2}dp,}\end{array}\},$$

(28)

where $\rho \left(r\right)$ is the probability density for the position space, and $\rho \left(r\right)$ is the probability density for the momentum space. The implication of Equation (28) is that a concentrated density yields a higher quantity, offering a local change in density where the system can be more effectively described from an information-theoretic perspective. In terms of expectation values, the Fisher information for both the position space and the momentum space can thus be expressed as follows [43,44,45,46]

$$\begin{array}{l}I(\rho )=4\langle p^2\rangle -2\left(2L+1\right)\left|m\right|\langle r^{-2}\rangle ,\\ I(\gamma )=4\langle r^2\rangle -2\left(2L+1\right)\left|m\right|\langle p^{-2}\rangle \end{array}\},$$

(29)

where $L$ is the total angular momentum, and $m$ is the magnetic quantum number. In the absence of the magnetic quantum number $m,$ the terms after the minus sign of Equation (29) vanishes, and then, the Fisher information for the position space and the Fisher information for the momentum space in Equation (29) can be written in the following form:

$$\begin{array}{l}I(\rho )=4\langle p^2\rangle ,\\ I(\gamma )=4\langle r^2\rangle \end{array}\}.$$

(30)

To check the validity of the product of expectation values as a Cramer–Rao inequality, Dehesa et al. [44], gave the following conditions:

$$\begin{array}{l}\langle p^2\rangle \ge {\left(L+\frac{1}{2}\right)}^2\langle r^{-2}\rangle ,\\ \langle r^2\rangle \ge \left(L+\frac{1}{2}\right)\langle p^{-2}\rangle \end{array}\}.$$

(31)

These imply that

$$\begin{array}{l}I(\rho )\ge 4\left(1-\frac{2\left|m\right|}{2L+1}\right)\langle p^2\rangle ,\\ I(\gamma )\ge 4\left(1-\frac{2\left|m\right|}{2L+1}\right)\langle r^2\rangle \end{array}\}.$$

(32)

When $m=0,$ the product of Equation (32) can be written as

$$I(\rho )I(\gamma )\ge 16\langle p^2\rangle \langle r^2\rangle .$$

(33)

The minimum bound for the Fisher product [43] is given by

$$I(\rho )I(\gamma )\ge 36.$$

(34)

In using Equations (21) and (34), the minimum bound of the product of the position and momentum expectation becomes

$$\langle p^2\rangle \langle r^2\rangle \ge \frac{9}{4}.$$

(35)

In substituting Equations (25) and (26) into Equation (30), the Fisher information for the position space and the momentum space, respectively, becomes

$$I\langle \rho \rangle =\frac{16{\mu }^3{D}_e^2{r}_e^2{(1+\eta )}^2}{{\hslash }^2{\mathrm{\Lambda }}_0^2}\left(\frac{1}{{\mu }^2}-\frac{4D_e{r}_e^2(1+\eta )}{\mathrm{\Lambda }{\mathrm{\Lambda }}_0{\hslash }^2}\right)+\frac{4\sqrt{2}{D}_e(1+\eta )}{\mu }\left(\frac{{\hslash }^2{\mathrm{\Lambda }}_1}{{\mathrm{\Lambda }}_2{r}_e^2}+\frac{4{\mathrm{\Lambda }}_2{r}_e^2}{\mathrm{\Lambda }\hslash }\right)-\frac{4\sqrt{2}\hslash {\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2}{{\mu }^2},$$

(36)

$$I\langle \gamma \rangle =\frac{8\mu }{\mathrm{\Lambda }}\left(\frac{\hslash {\mathrm{\Lambda }}_2\sqrt{2}}{\mu }-\frac{4{\mu }^2{D}_e^2{r}_e^2{(1+\eta )}^2}{{\hslash }^2{\mathrm{\Lambda }}_0^3}\right).$$

(37)

5. Discussion

Table 1. Energy eigenvalue for various quantum states and angular momentum with $\mu =\hslash =1$ and $r_e=0.25$ in the absence and presence of constant-dependent potential for two values of the dissociation energy.

$\mathit{n}$	$\mathit{\ell }$	$\mathit{\eta }=0$		$\mathit{\eta }=0.5$
		${\mathit{D}}_{\mathit{e}}=5$	${\mathit{D}}_{\mathit{e}}=10$	${\mathit{D}}_{\mathit{e}}=5$	${\mathit{D}}_{\mathit{e}}=10$
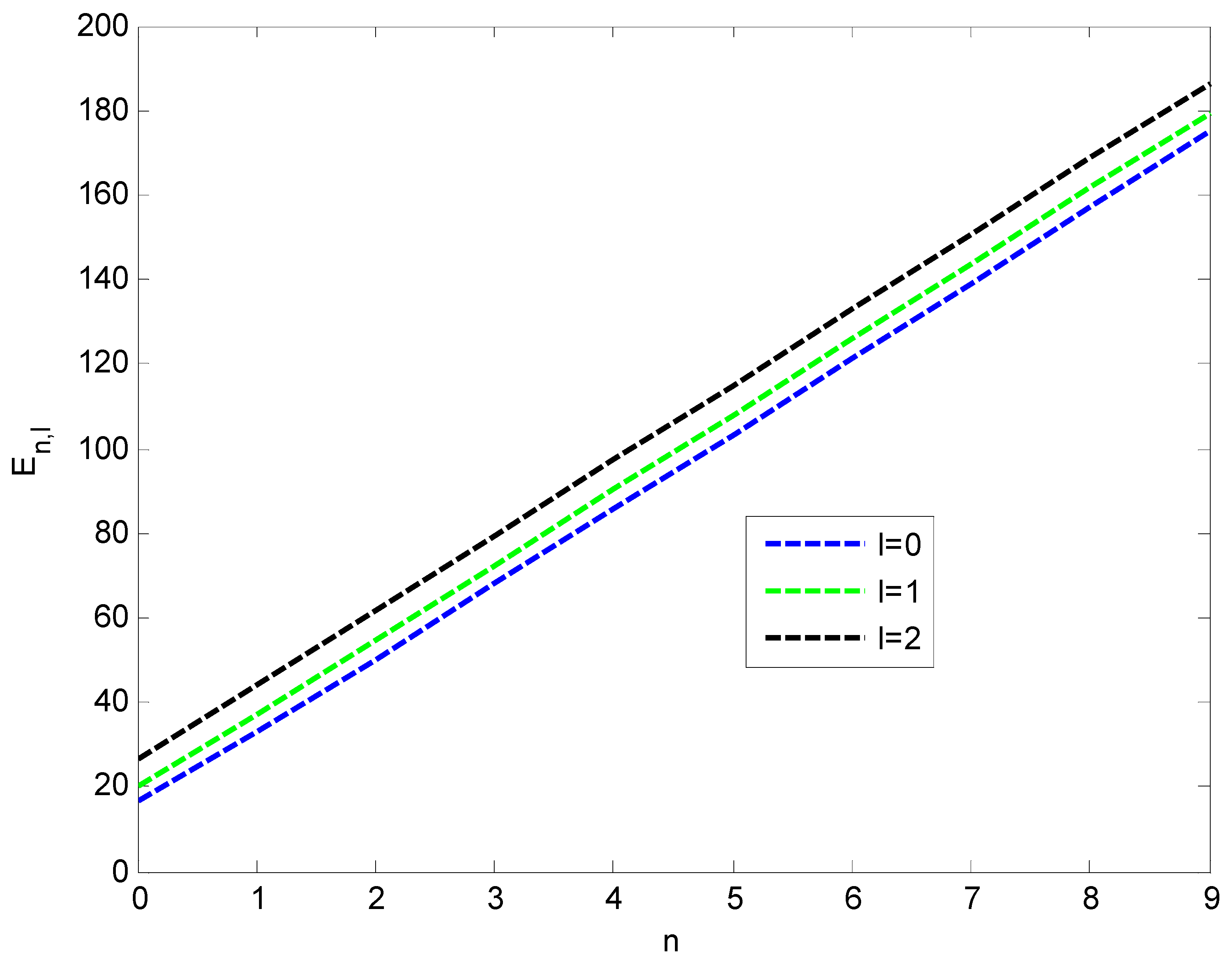
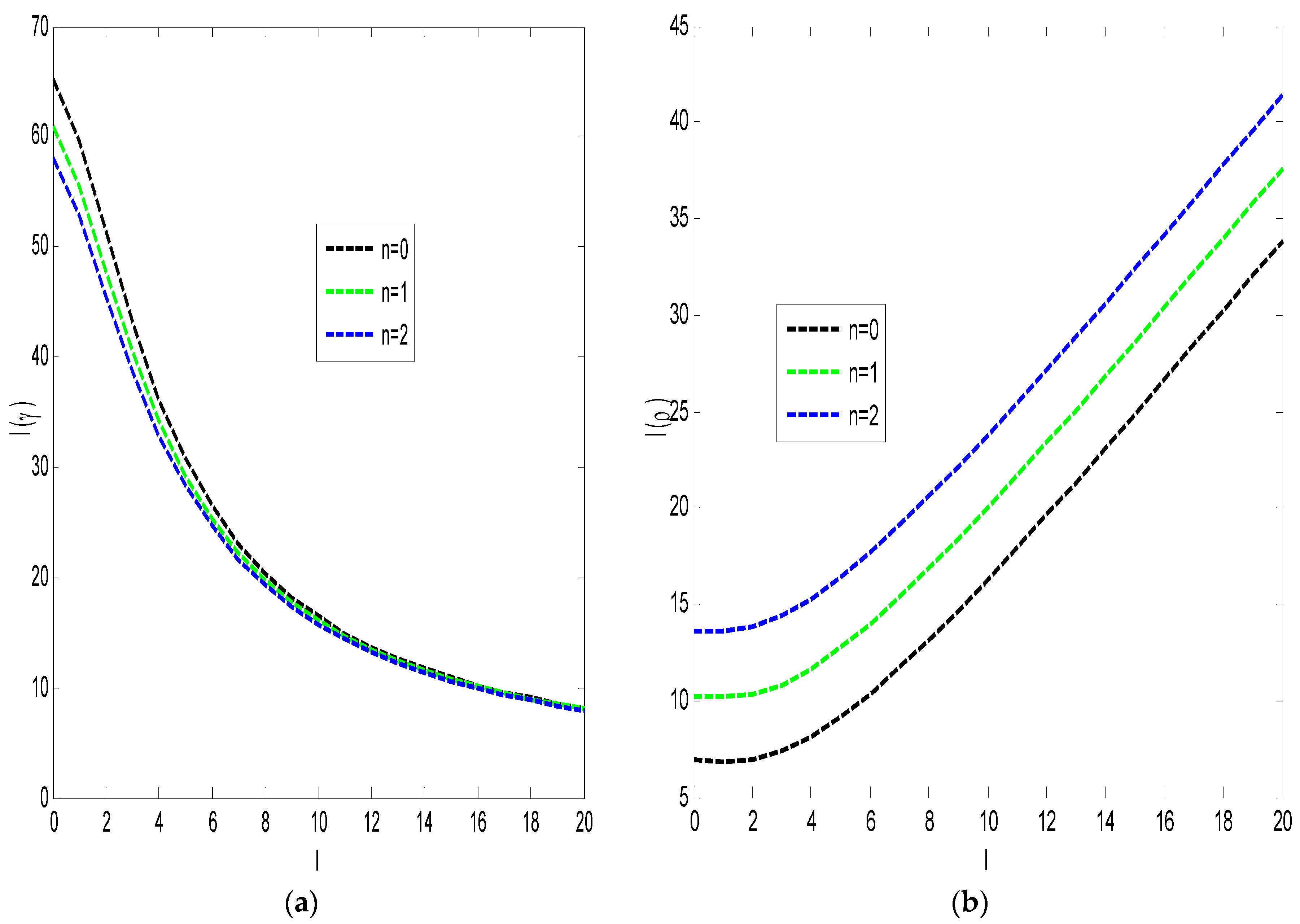
0	0	19.1915543	30.2367130	29.9096370	50.2267069
	1	26.8693976	38.6168018	38.0538010	58.8074820
	2	37.5880690	51.8488919	50.2771052	73.2878939
	3	49.3042587	67.2542617	64.1033929	90.9334004
1	0	43.8601841	64.5835661	59.8627152	91.8404299
	1	51.8866789	73.5761120	68.5040080	101.195400
	2	62.7622893	87.2096164	81.0061110	116.302626
	3	74.5398554	102.806150	94.9538017	134.292068
2	0	68.9627325	99.8304090	90.4917350	134.751205
	1	77.0734494	109.000745	99.2664182	144.358222
	2	88.0004415	122.777346	111.864086	159.703767
	3	99.8033288	138.455898	125.862895	177.845801
3	0	94.1756967	135.354381	121.312779	178.109873
	1	102.316428	144.594507	130.137638	187.822519
	2	113.265083	158.434548	142.776689	203.277995
	3	125.080290	174.154043	156.800703	221.497925

presents the energy eigenvalues of the combination of the pseudoharmonic potential and the Kratzer potential for various quantum numbers and angular momentums in the absence and presence of the constant-dependent potential for two different values of the dissociation energy. The energy of the combined potentials responds positively to an increase in each of the dissociation energy, quantum number, angular momentum, and constant-dependent potential. This implies that an increase in the dissociation energy, quantum number, angular momentum, or constant-dependent potential increases the energy of the interacting potential system. From Table 1, it is noted that as the angular momentum increases, the energy difference between successive angular momenta increases. In

Table 2. Energy eigenvalue for various quantum states and equilibrium bond length with $\mu =\hslash =1$ and $D_e=5$ in the absence and presence of constant-dependent potential for $s-$ wave and $\mathcal{l}-$ wave.

$\mathit{n}$	${\mathit{r}}_{\mathit{e}}$	$\mathit{\eta }=0$		$\mathit{\eta }=0.5$
		$\mathit{\ell }=0$	$\mathit{\ell }=1$	$\mathit{\ell }=0$	$\mathit{\ell }=1$
0	0.5	12.4202881	14.5803237	21.9178843	24.0760055
	1.0	9.39252710	9.91579930	18.2993918	18.8139539
	1.5	8.44361600	8.66857060	17.1549376	17.3764753
	2.0	7.98103440	8.10491030	36.3343188	16.7170015
1	0.5	24.3346767	26.7141787	25.2162768	38.7409248
	1.0	15.1059713	15.6968954	21.6715263	25.7961769
	1.5	12.1681436	12.4202881	19.9405623	21.9178843
	2.0	10.7362083	10.8734364	16.5947227	20.0746906
2	0.5	36.6586629	39.1157627	51.3010558	53.8062866
	1.0	21.0620459	21.6877923	32.4241376	33.0409857
	1.5	16.0437357	16.3126127	26.3605159	26.6233344
	2.0	13.5932412	13.7395803	23.3994205	23.5421470
3	0.5	49.1359643	51.6272352	66.4978821	69.0498216
	1.0	27.1474431	27.7929105	39.8011807	40.4404751
	1.5	20.0143131	20.2940459	31.1657135	31.4398758
	2.0	16.5207835	16.6735512	26.9411554	27.0902716
4	0.5	61.6833974	64.1920084	81.8076698	84.3845319
	1.0	33.3080324	33.9654942	47.2832585	47.9369683
	1.5	24.0475954	24.3346767	36.0520860	36.3343188
	2.0	19.4986801	19.6561126	30.5450424	30.6990056
5	0.5	74.2674019	76.7857329	97.1793420	99.7706981
	1.0	39.5153037	40.1804755	54.8339773	55.4973648
	1.5	28.1239350	28.4161668	40.9968719	41.2850021
	2.0	22.5134945	22.6743939	34.1964520	34.3541585

, the energy of the combination of the pseudoharmonic potential and the Kratzer potential for various quantum numbers and equilibrium bond lengths in the absence and presence of the constant-dependent potential is presented. The numerical values in Table 2 show that the equilibrium bond length varies inversely with the energy of the interacting potential. However, the quantum number and the angular momentum respectively vary directly with the energy of the system. In

Table 3. Energy eigenvalue for various values dissociation energies and constant-dependent potential with $\mu =\hslash =1$ and $r_e=0.25$ at the ground state and first excited state.

${\mathit{D}}_{\mathit{e}}$	$\mathit{\eta }$	$\mathit{n}=0$		$\mathit{n}=1$
		$\mathit{\ell }=0$	$\mathit{\ell }=1$	$\mathit{\ell }=0$	$\mathit{\ell }=1$
1	0	4.18168780	6.0217369	9.72050810	11.6301374
	1	8.50000000	10.5510171	16.2222222	18.4038820
	2	12.5793525	14.7015198	21.9412282	24.2349788
	3	16.5379816	18.6878788	27.2631497	29.6126984
	4	20.4202881	22.5803237	32.3346767	34.7141787
	5	24.2487113	26.4107479	37.2301178	39.6259364
2	0	6.50000000	8.55101710	14.2222222	16.4038820
	1	14.5379816	16.6878788	25.2631497	27.6126984
	2	22.2487113	24.4107479	35.2301178	37.6259364
	3	29.7921099	31.9479971	44.6521671	47.0601538
	4	37.2291330	39.3742236	53.7304216	56.1377674
	5	44.5908154	46.7242693	62.5667333	64.9679851
3	0	8.57935250	10.7015198	17.9412282	20.2349788
	1	20.2487113	22.4107479	33.2301178	35.6259364
	2	31.5215665	33.6722999	47.2265378	49.6351901
	3	42.5908154	44.7242693	60.5667333	62.9679851
	4	53.5303880	55.6472139	73.4925650	75.8806382
	5	64.3780215	66.4800000	86.1265502	88.5000000
4	0	10.5379816	12.6878788	21.2631497	23.6126984
	1	25.7921099	27.9479971	40.6521671	43.0601538
	2	40.5908154	42.7242693	58.5667333	60.9679851
	3	55.1551611	57.2668299	75.7320533	78.1153066
	4	69.5701085	71.6631972	92.4238854	94.7875816
	5	83.8790804	85.9565223	108.781987	111.126964
5	0	12.4202881	14.5803237	24.3346767	26.7141787
	1	31.2291330	33.3742236	47.7304216	50.1377674
	2	49.5303880	51.6472139	69.4925650	71.8806382
	3	67.5701085	69.6631972	90.4238854	92.7875816
	4	85.4430187	87.5169397	110.829779	113.170292
	5	103.197567	105.255816	130.865107	133.184707

, we present the energy eigenvalue of the interacting potential for various dissociation energies and constant-dependent potentials at the ground state and the first excited state. The energy of the combined potential model increases as the dissociation energy and the constant-dependent potential respectively increase. The energy of the system also increases as the quantum number and the angular momentum respectively increase.

The numerical values for the Fisher information in position space and momentum space, as well as their product in the absence and presence of the constant-dependent potential, are presented in

Table 4. Fisher information for position space and momentum space in the absence and presence of constant-dependent potential for various quantum states and the Fisher product with $\mu =\hslash =\mathcal{l}=1,$ $r_e=0.5,$ and $D_e=2.5$.

$\mathit{n}$	$\mathit{\eta }=0$			$\mathit{\eta }=0.5$
	$\mathit{I}\langle \mathit{\rho }\rangle$	$\mathit{I}\langle \mathit{\gamma }\rangle$	$\mathit{I}\langle \mathit{\rho }\rangle \mathit{I}\langle \mathit{\gamma }\rangle$	$\mathit{I}\langle \mathit{\rho }\rangle$	$\mathit{I}\langle \mathit{\gamma }\rangle$	$\mathit{I}\langle \mathit{\rho }\rangle \mathit{I}\langle \mathit{\gamma }\rangle$
0	12.9965839	8.5737778	111.4298232	21.5583462	15.7382452	339.2905400
1	11.8185475	15.2579808	180.3271707	19.6777166	23.7495543	467.3369980
2	11.2615469	22.1905981	249.9004614	18.7115540	32.1266502	601.1395518
3	10.9565616	29.2240214	320.1947901	18.1551929	40.6676667	738.3293339
4	10.7720175	36.3056214	391.0847898	17.8069278	49.2919216	877.7376907
5	10.6520394	43.4130476	462.4374938	17.5749107	57.9626756	1018.688851
6	10.5697147	50.5355353	534.1461897	17.4127458	66.6613706	1160.757499
7	10.5108053	57.6673891	606.1306983	17.2950190	75.3778408	1303.661192
8	10.4672122	64.8053694	678.3315540	17.2068853	84.1061482	1447.204844
8	10.4340553	71.9475241	750.7044447	17.1392093	92.8426388	1591.249420
10	10.4082527	79.0926206	823.2159806	17.0861231	101.584965	1735.693225
11	10.3877810	86.2398494	895.8406674	17.0437192	110.331565	1880.460203
12	10.3712673	93.3886615	968.5587745	17.0093145	119.081364	2025.492369
13	10.3577538	100.538674	1041.354832	16.9810180	127.833606	2170.744768
14	10.3465556	107.689612	1114.216560	16.9574657	136.587746	2316.182020
15	10.3371727	114.841276	1187.134100	16.9376539	145.343382	2461.775909

and

Table 5. Fisher information for position space and momentum space at the ground state for various equilibrium bond separations and the Fisher product in the absence and presence of constant-dependent potential with $\mu =\hslash =\mathcal{l}=1$ and $D_e=2.5$.

${\mathit{r}}_{\mathit{e}}$	$\mathit{\eta }=0$			$\mathit{\eta }=0.5$
	$\mathit{I}\langle \mathit{\rho }\rangle$	$\mathit{I}\langle \mathit{\gamma }\rangle$	$\mathit{I}\langle \mathit{\rho }\rangle \mathit{I}\langle \mathit{\gamma }\rangle$	$\mathit{I}\langle \mathit{\rho }\rangle$	$\mathit{I}\langle \mathit{\gamma }\rangle$	$\mathit{I}\langle \mathit{\rho }\rangle \mathit{I}\langle \mathit{\gamma }\rangle$
1.0	6.3749475	6.7680001	43.1456451	13.9837226	13.7463577	192.2252527
1.5	12.0910640	6.2814977	75.9499903	20.5118296	13.1590415	269.9160160
2.0	14.6231981	6.0423780	88.3588904	23.4211406	12.8653865	301.3220276
2.5	16.0247585	5.8983477	94.5195968	25.0442629	12.6881230	317.7646874
3.0	16.9078176	5.8018537	98.0966833	26.0739294	12.5694080	327.7338557
3.5	17.5129218	5.7326651	100.395716	26.7834340	12.4843480	334.3737107
4.0	17.9525752	5.6806283	101.981906	27.3012806	12.4204164	339.0932721
4.5	18.2860804	5.6400719	103.134809	27.6955632	12.3706163	342.6111838
5.0	18.5475457	5.6075771	104.006792	28.0056349	12.3307320	345.3299783
5.5	18.7579355	5.5809594	104.687276	28.2557876	12.2980723	347.4917179
6.0	18.9308264	5.5587579	105.231880	28.4618122	12.2708384	349.2502995
6.5	19.0753897	5.5399585	105.676868	28.6344110	12.2477829	350.7080500
7.0	19.1980391	5.5238356	106.046812	28.7810910	12.2280132	351.9355594
7.5	19.3033929	5.5098559	106.358913	28.9072717	12.2108738	352.9830473
8.0	19.3948598	5.4976189	106.625548	29.0169624	12.1958730	353.8871873
8.5	19.4750097	5.4868181	106.855836	29.1131925	12.1826340	354.6753683
9.0	19.5458162	5.4772149	107.056635	29.1982930	12.1708638	355.3684483

. In Table 4, the Fisher information in position space and the quantum number vary inversely with each other, but the Fisher information in momentum space varies directly with the quantum number. The Fisher information in both position space and momentum space in the presence of the constant-dependent potential is higher than its counterpart produced in the absence of the constant-dependent potential. The minimum bound for the Fisher product in the absence of constant-dependent potential is 111.4298232, while in the presence of the constant-dependent potential, the minimum bound is 339.29054. These values are above the standard value of 36. Thus, the results in Table 4 satisfy the Fisher inequality given in Equation (34). The variation of the Fisher information shows that a decrease in the Fisher information in position space corresponds to an increase in Fisher information in momentum space. This implies that a diffused density distribution in the configuration space is associated with a localized density distribution in the momentum space. In Table 5, the Fisher information in position space and in momentum space for various values of the equilibrium bond separation is presented in the absence and presence of the constant-dependent potential. In this Table, the Fisher information in position space varies directly with the equilibrium bond separation both in the presence and absence of the constant-dependent potential. However, in the momentum space, the Fisher information varies indirectly with the equilibrium bond separation. The minimum bound for the Fisher product in the absence of constant-dependent potential is 51.4913757, while in the presence of the constant-dependent potential, it is 212.949992. The values of the minimum bound also confirm that the results in Table 5 satisfy the Fisher inequality. The result shows that a diffused density in the configuration space corresponds to the localized density in the momentum space. The variation in the Fisher information against the quantum state in Table 4 is contrary to the variation in Fisher information against the equilibrium bond separation in Table 5 but satisfies the Fisher inequality in both cases. In Table 5, a strongly localized distribution in the momentum space corresponds to a widely delocalized distribution in the position space. The results obtained obey Heisenberg’s uncertainty principle. The position and momentum expectation values and their product for various values of the angular momentum number are presented in

Table 6. Position expectation value and momentum expectation value at the ground state for various angular momentum quantum states and their product in the absence and presence of constant-dependent potential with $\mu =\hslash =1,$ $r_e=0.5,$ and $D_e=2.5$.

$\mathit{\ell }$	$\mathit{\eta }=0$			$\mathit{\eta }=0.5$
	$\langle {\mathit{r}}^2\rangle$	$\langle {\mathit{p}}^2\rangle$	$\langle {\mathit{r}}^2\rangle \langle {\mathit{p}}^2\rangle$	$\langle {\mathit{r}}^2\rangle$	$\langle {\mathit{p}}^2\rangle$	$\langle {\mathit{r}}^2\rangle \langle {\mathit{p}}^2\rangle$
0	2.0753109	4.2441101	8.8078482	3.9027949	6.5411490	25.5287631
1	2.1434445	3.2491460	6.9643639	3.9345613	5.3895866	21.2056588
2	2.4796239	2.3486134	5.8236779	4.2100767	4.1263248	17.3721438
3	3.0345051	1.7624127	5.3480505	4.7530480	3.1895560	15.1601125
4	3.7149293	1.3858907	5.1484858	5.4798280	2.5445494	13.9436929
5	4.4660484	1.1325692	5.0581087	6.3206480	2.0942879	13.2372565
6	5.2591091	0.9534294	5.0141894	7.2328358	1.7693011	12.7970647
7	6.0785638	0.8212049	4.9917465	8.1913537	1.5265679	12.5046576
8	6.9155189	0.7201144	4.9799647	9.1811818	1.3396688	12.2997429
9	7.7645982	0.6405721	4.9737848	10.192968	1.1919700	12.1497115
10	8.6223893	0.5764852	4.9706794	11.220659	1.0726518	12.0358600
11	9.4866342	0.5238228	4.9693156	12.260199	0.9744445	11.9468833
12	10.355785	0.4798244	4.9689582	13.308778	0.8923155	11.8756286
13	11.228746	0.4425416	4.9691872	14.364399	0.8226858	11.8173877
14	12.104725	0.4105633	4.9697553	15.425605	0.7629492	11.7689537
15	12.983131	0.3828440	4.9705140	16.491312	0.7111670	11.7280766

for the absence and presence of the constant-dependent potential. It is noted that as the position space expectation value varies directly with the angular momentum, the momentum space expectation value varies inversely with the angular momentum number. As observed in Table 4, Table 5 and Table 6, the results with the constant-dependent potential are higher than the results without constant-dependent potential. The product of the expectation values for the presence and absence of the constant-dependent potential is greater than the standard value of 2.25. The minimum bounds for the products of the expectation values in the absence and presence of the constant-dependent potential are 3.9027949 and 12.1497115, respectively. These results satisfy Cramer–Rao’s inequality for the product of expectations.

Table 7. Fisher information for both position space and momentum space at the ground state for various angular momentum quantum states and their product with $\mu =\hslash =1,$ $r_e=0.5,$ and $D_e=2.5$ in the absence and presence of the constant-dependent potential.

$\mathit{\ell }$	$\mathit{\eta }=0$			$\mathit{\eta }=0.5$
	$\mathit{I}(\mathit{\rho })$	$\mathit{I}(\mathit{\gamma })$	$\mathit{I}(\mathit{\rho })\mathit{I}(\mathit{\gamma })$	$\mathit{I}(\mathit{\rho })$	$\mathit{I}(\mathit{\gamma })$	$\mathit{I}(\mathit{\rho })\mathit{I}(\mathit{\gamma })$
0	8.30124380	16.976441	140.925571	15.6111797	26.1645959	408.4602096
1	8.57377780	12.996584	111.429823	15.7382452	21.5583462	339.2905400
2	9.91849550	9.3944536	93.1788457	16.8403066	16.5052993	277.9543004
3	12.1380204	7.0496510	85.5688076	19.0121919	12.7582239	242.5618001
4	14.8597170	5.5435626	82.3757720	21.9193120	10.1781975	223.0990871
5	17.8641936	4.5302766	80.9297386	25.2825921	8.37715150	211.7961041
6	21.0364363	3.8137178	80.2270307	28.9313433	7.07720460	204.7530351
7	24.3142550	3.2848197	79.8679439	32.7654146	6.10627160	200.0745216
8	27.6620757	2.8804576	79.6794347	36.7247270	5.35867530	196.7958870
9	31.0583928	2.5622883	79.5805565	40.7718702	4.76788000	194.3953836
10	34.4895572	2.3059406	79.5308712	44.8826362	4.29060710	192.5737593
11	37.9465368	2.0952913	79.5090499	49.0407939	3.89777810	191.1501323
12	41.4231385	1.9192976	79.5033319	53.2351111	3.56926200	190.0100570
13	44.9149846	1.7701664	79.5069946	57.4575959	3.29074340	189.0782028
14	48.4188988	1.6422531	79.5160843	61.7024212	3.05179690	188.3032599
15	51.9325232	1.5313761	79.5282236	65.9652465	2.84466800	187.6492262

presents Fisher information for both position space and momentum space and their product in the absence and presence of the constant-dependent potential for various angular momenta. The Fisher information for the position space in both the absence and presence of constant-dependent potential respectively increases as the angular momentum increases. However, the Fisher information for the momentum space in the absence and presence of constant-dependent potential respectively decreases as the angular momentum increases. The product of the Fisher information satisfies the Cramer–Rao inequality but decreases with an increase in the angular momentum. The variation in energy against the quantum number is shown in Figure 1. The energy of the combined pseudoharmonic potential and Kratzer potential varies linearly with the quantum number. Figure 2 shows the variation in the Fisher information against the dissociation energy for various quantum states. The Fisher information for the momentum space decreases for all the quantum states studied as the dissociation energy increases. At $D_e=5,$ Fisher information for the momentum space at different quantum states intercept each other, as shown in Figure 2a. In Figure 2b, the Fisher information for the position space decreases monotonically as the dissociation energy increases. The variation in the Fisher information for the momentum space decreases monotonically as the angular momentum increases, as shown in Figure 3a. At a higher angular momentum, the Fisher information for the momentum space for various quantum states tends to be equal. In Figure 3b, the Fisher information for the position space increases as the angular momentum increases.

6. Conclusions

The solutions for the combination of the pseudoharmonic potential and Kratzer potential were obtained, and the effects of the constant-dependent potential and the potential parameters on the energy, expectation values, and Fisher information were observed. It was demonstrated that, in the presence of constant-dependent potential, the dissociation energy, quantum number, and angular momentum respectively increase the energy eigenvalue of the system, while the equilibrium bond length reduces the energy. The variation in the quantum number against the Fisher information was found to be contrary to the variation in the equilibrium bond length against the Fisher information. The constant-dependent potential increases the position expectation value but decreases the momentum expectation value. It was discovered that certain parameters increase the Fisher information in position space and decrease Fisher information in momentum space, while some parameters decrease the Fisher information in position space and increase the Fisher information in momentum space. The effect of the potential parameters on the energy and Fisher information in the absence of the constant-dependent potential is the same as in the presence of the constant-dependent potential. The presence of the constant-dependent potential only increases the quantities studied.