Digital Quantum Simulation of Scalar Yukawa Coupling
Abstract
:1. Introduction
2. System and Hamiltonian
2.1. Scalar Yukawa Coupling
2.2. Single-Site Model
3. DQS of Hamiltonian Dynamics and Encoding Fermion/Boson States on Qubits
3.1. Simulating the Dynamics after an Interaction Quench
3.2. Fermion State Encoding
3.3. Boson State Encoding
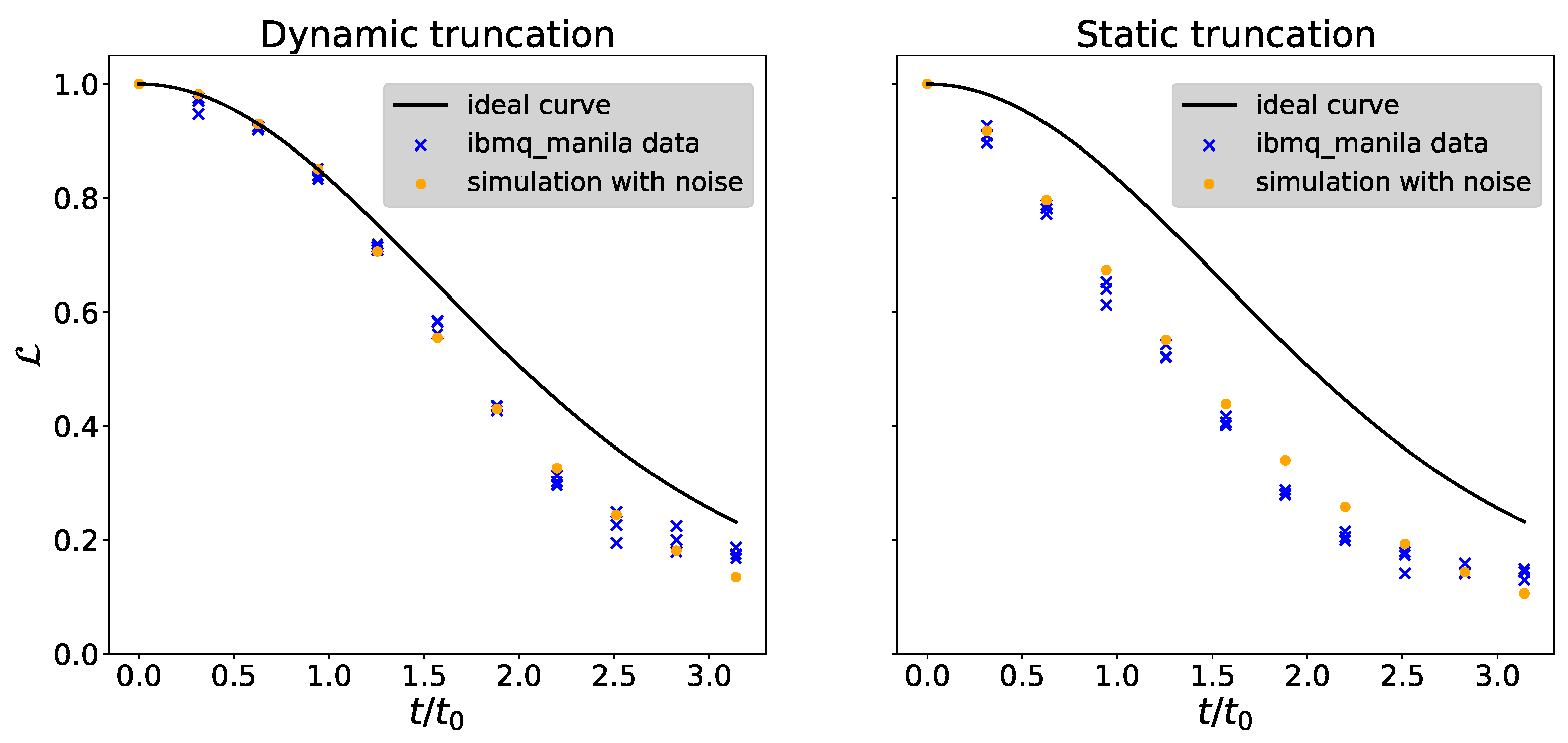
3.4. Truncation of the Boson Hilbert Space
- Define a high-resolution grid of the coupling strength and the time in the regime of interest.
- For each coupling strength, select an initial truncation with qubits ().
- Simulate a Hamiltonian with a truncation using N and qubits on the time grid.
- Compute the fidelity between both simulations for each point on the time grid. This is achieved by extending the lower-dimensional state vector into the higher-dimensional Hilbert space using the zero state .
- If the fidelity falls below a certain threshold at some point in time, the selected truncation is no longer appropriate. Then, increase the qubit number by one , save the qubit number along with the time point, and repeat steps 3, 4, and 5 until the desired fidelity is reached.
4. Circuit Design
4.1. Exchange of up to One Boson (Two-Qubit Circuit)
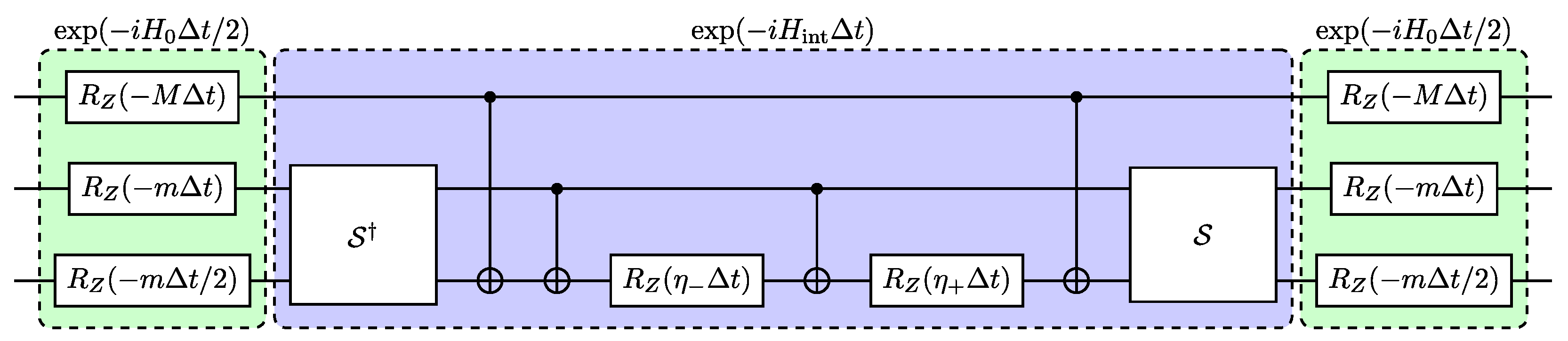
4.2. Exchange of up to Three Bosons (Three-Qubit Circuit)
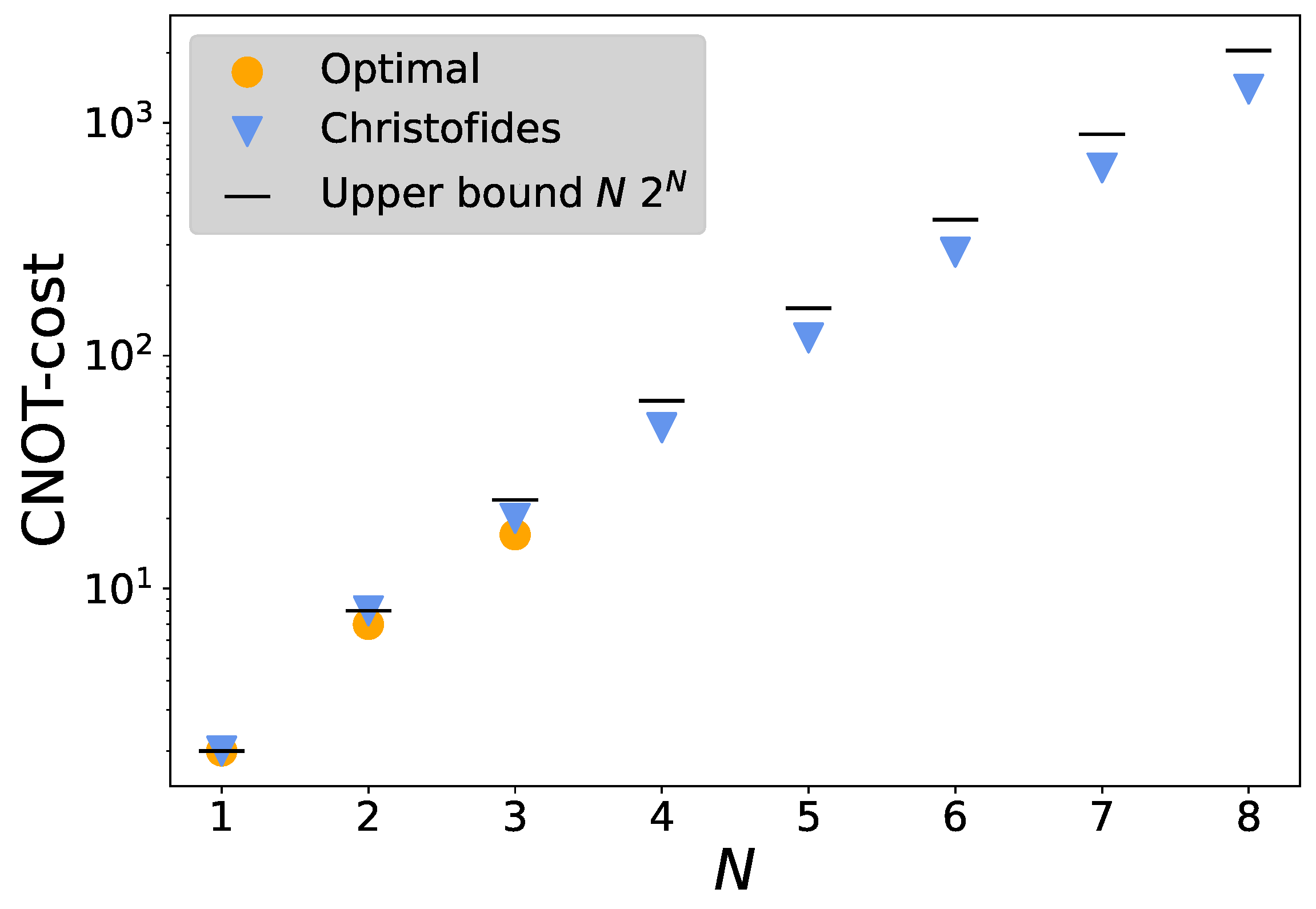
4.3. CNOT Cost Estimation for Higher Boson Number Truncations
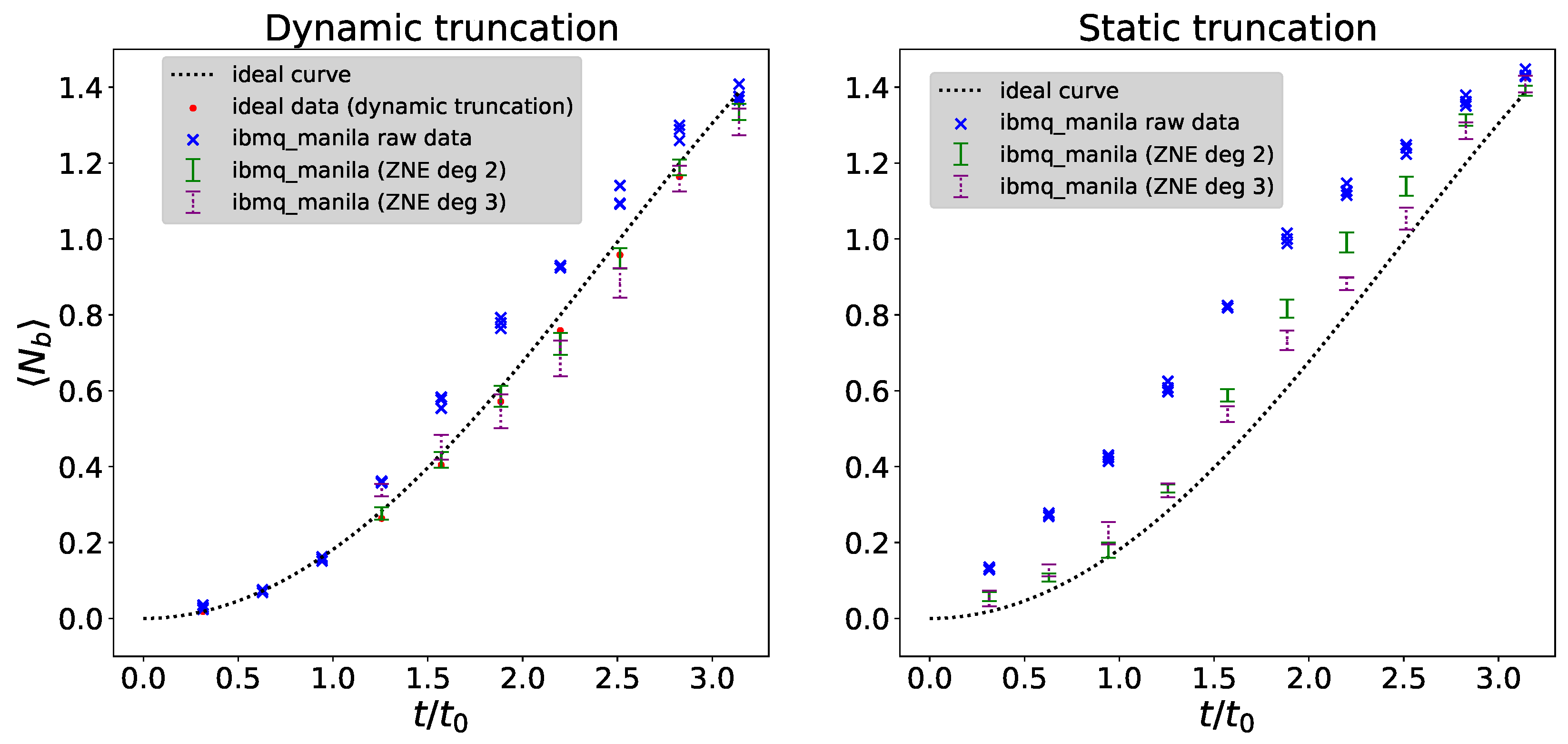
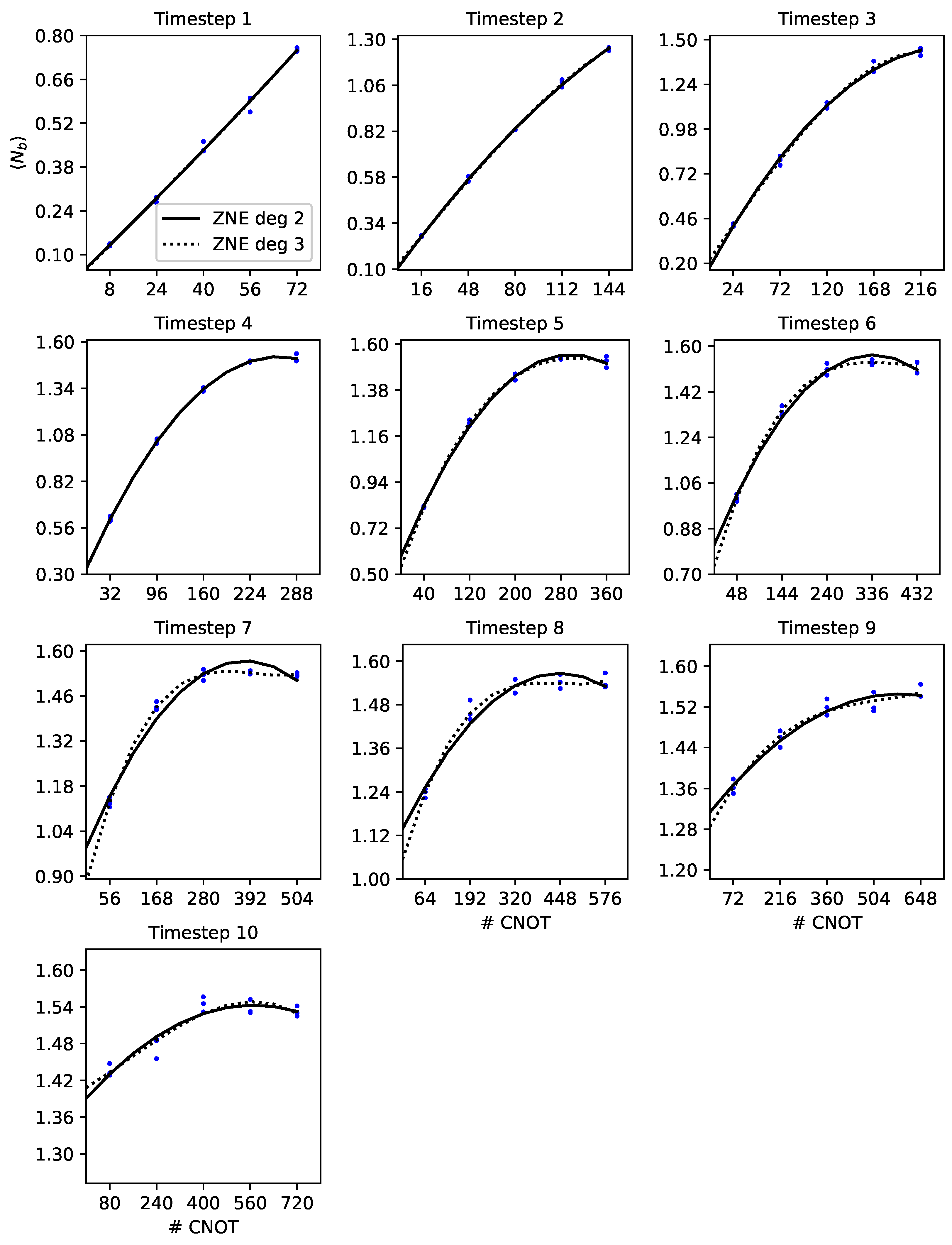
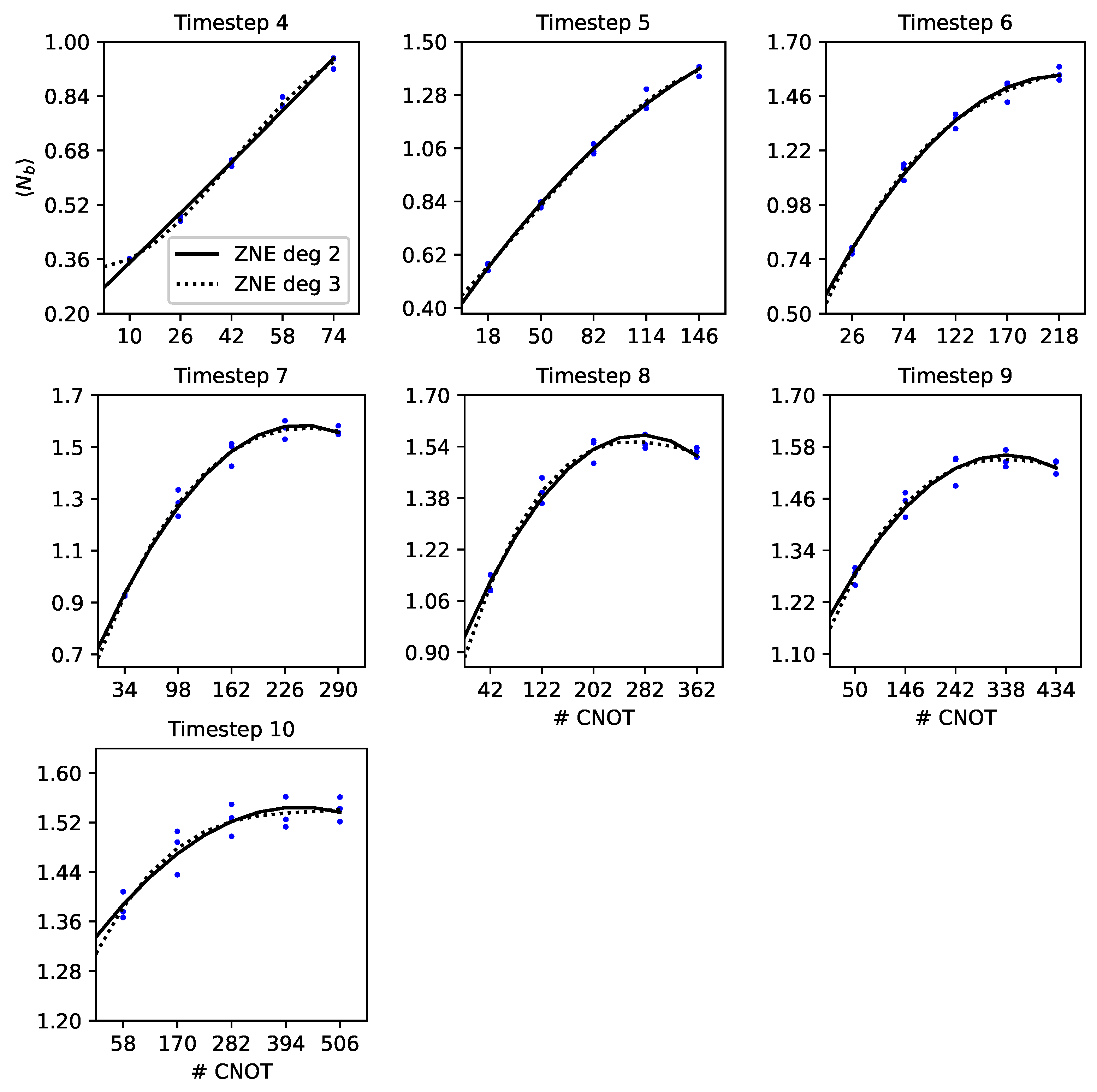
4.4. Error Mitigation by Digital Zero-Noise Extrapolation
5. DQS on IBM Q: Results and Discussion
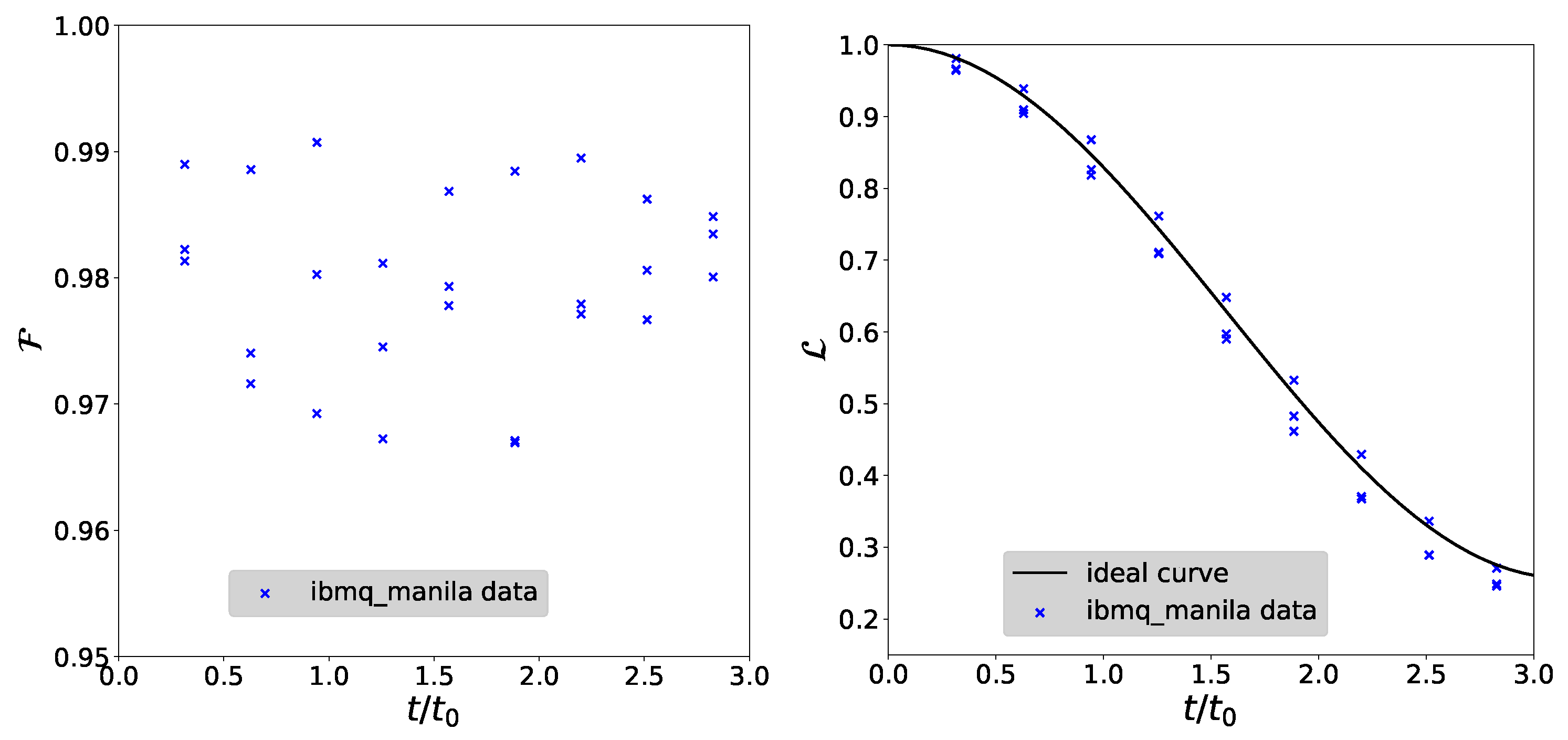
5.1. Loschmidt Echo and State Fidelity
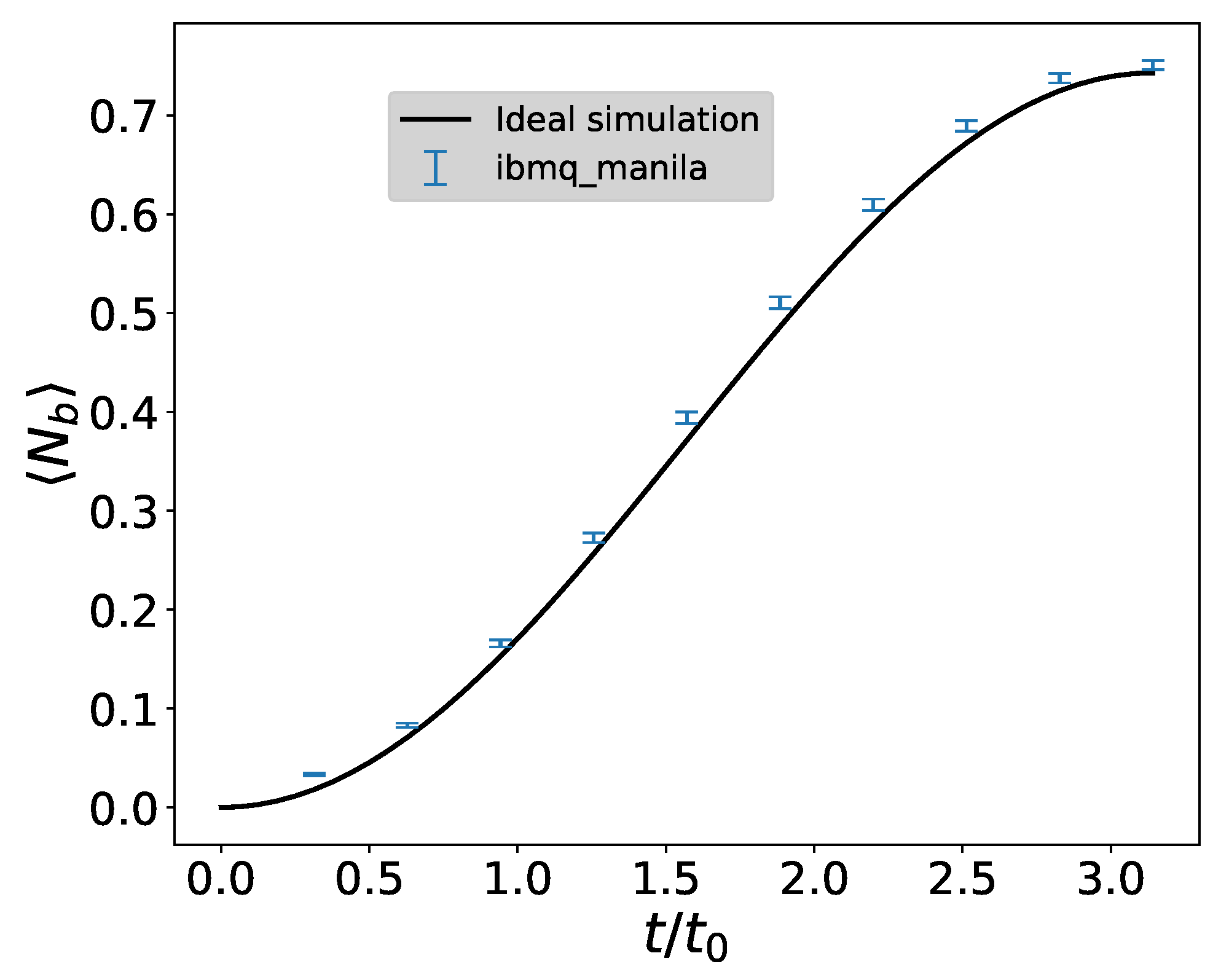
5.2. Boson Occupation Numbers
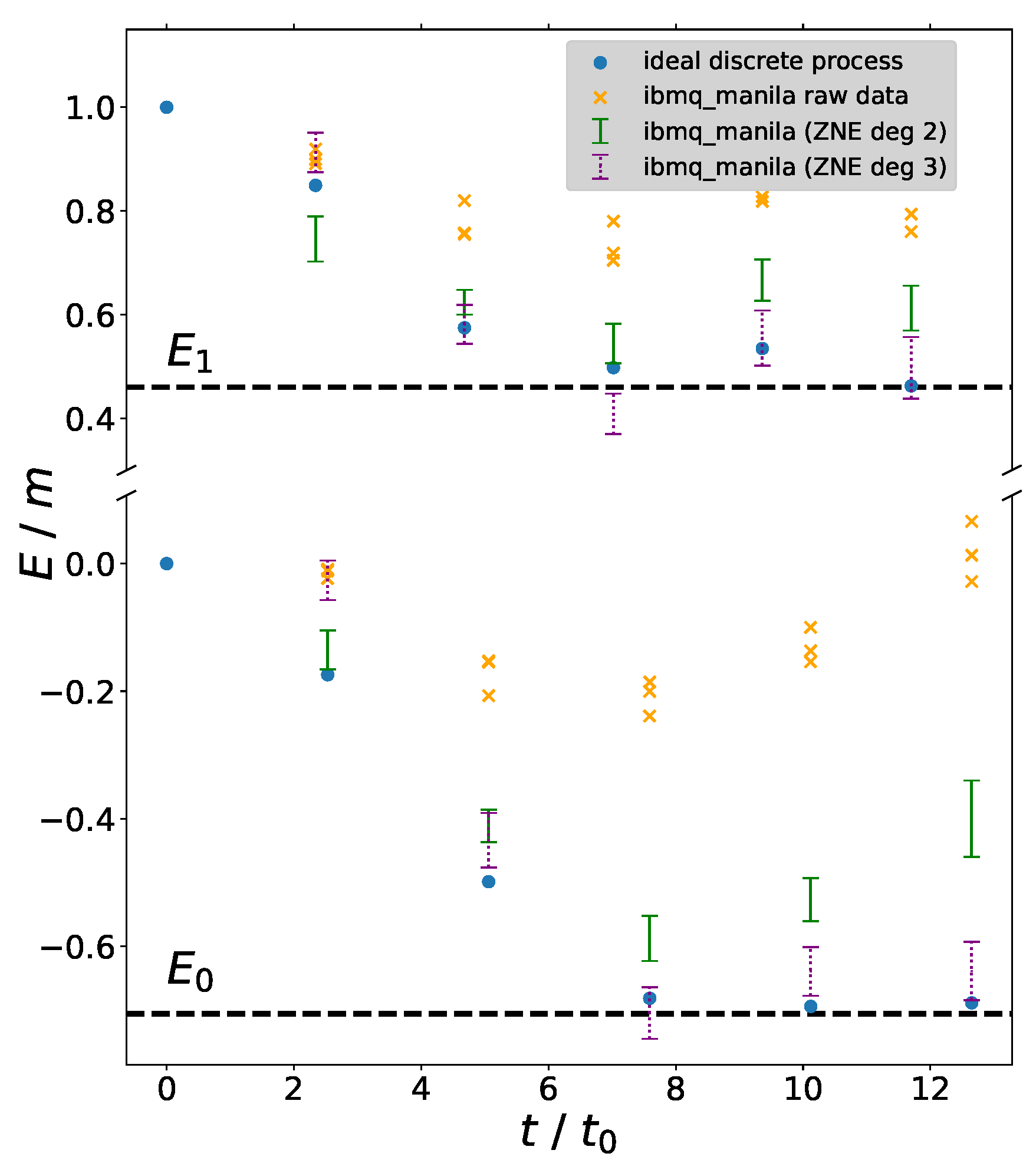
5.3. Adiabatic Preparation of the Ground and First Excited States
6. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Single-Site Hamiltonian
Appendix B. Boson Mapping
Appendix C. Kraus–Cirac Decomposition
Appendix D. The Distance Metric



Appendix E. Generation of Pauli Strings
Appendix F. Upper Bound on the CNOT Cost
References
- Lloyd, S. Universal Quantum Simulators. Science 1996, 273, 1073. [Google Scholar] [CrossRef] [PubMed]
- Zalka, C. Simulating quantum systems on a quantum computer. Proc. R. Soc. Lond. A 1998, 454, 313. [Google Scholar] [CrossRef]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153. [Google Scholar] [CrossRef]
- Wendin, G. Quantum information processing with superconducting circuits: A review. Rep. Prog. Phys. 2017, 10, 142–149. [Google Scholar] [CrossRef] [PubMed]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-Ion Quantum Computing: Progress and Challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Morgado, M.; Whitlock, S. Quantum simulation and computing with Rydberg-interacting qubits. AVS Quantum Sci. 2021, 3, 023501. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467. [Google Scholar] [CrossRef]
- Abrams, D.S.; Lloyd, S. Simulation of Many-Body Fermi Systems on a Universal Quantum Computer. Phys. Rev. Lett. 1997, 79, 2586. [Google Scholar] [CrossRef]
- Somma, R.; Ortiz, G.; Gubernatis, J.E.; Knill, E.; Laflamme, R. Simulating physical phenomena by quantum networks. Phys. Rev. A 2002, 65, 042323. [Google Scholar] [CrossRef]
- Bravyi, S.B.; Kitaev, A.Y. Fermionic quantum computation. Ann. Phys. 2002, 298, 10. [Google Scholar] [CrossRef]
- Whitfield, J.D.; Biamonte, I.; Aspuru-Guzik, A. Simulation of Electronic Structure Hamiltonians Using Quantum Computers. Mol. Phys. 2011, 109, 735. [Google Scholar] [CrossRef]
- Raeisi, S.; Wiebe, N.; Sanders, B.C. Quantum-circuit design for efficient simulations of many-body quantum dynamics. New J. Phys. 2012, 14, 103017. [Google Scholar] [CrossRef]
- Wecker, D.; Hastings, M.B.; Wiebe, N.; Clark, B.K.; Nayak, C.; Troyer, M. Solving strongly correlated electron models on a quantum computer. Phys. Rev. A 2015, 92, 062318. [Google Scholar] [CrossRef]
- Barends, R.; Lamata, L.; Kelly, J.; García-Álvarez, L.; Fowler, A.G.; Megrant, A.; Jeffrey, E.; White, T.C.; Sank, D.; Mutus, J.Y.; et al. Digital quantum simulation of fermionic models with a superconducting circuit. Nat. Commun. 2015, 6, 7654. [Google Scholar] [CrossRef] [PubMed]
- Babbush, R.; Wiebe, N.; McClean, J.; McClain, J.; Neven, H.; Chan, G.K. Low-Depth Quantum Simulation of Materials. Phys. Rev. X 2018, 8, 011044. [Google Scholar] [CrossRef]
- Reiner, J.-M.; Zanker, S.; Schwenk, I.; Leppäkangas, J.; Wilhelm-Mauch, F.; Schön, G.; Marthaler, M. Effects of gate errors in digital quantum simulations of fermionic systems. Quantum Sci. Technol. 2018, 3, 045008. [Google Scholar] [CrossRef]
- Jiang, Z.; Sung, K.J.; Kechedzhi, K.; Smelyanskiy, V.N.; Boixo, S. Quantum Algorithms to Simulate Many-Body Physics of Correlated Fermions. Phys. Rev. Appl. 2018, 9, 044036. [Google Scholar] [CrossRef]
- McArdle, S.; Endo, S.; Aspuru-Guzik, A.; Benjamin, S.C.; Yuan, X. For a recent review of applications in quantum chemistry. Quantum computational chemistry. Rev. Mod. Phys. 2020, 92, 015003. [Google Scholar] [CrossRef]
- Hofer, P.P.; Bruder, C.; Stojanović, V.M. Superfluid drag of two-species Bose-Einstein condensates in optical lattices. Phys. Rev. A 2012, 86, 033627. [Google Scholar] [CrossRef]
- Macridin, A.; Spentzouris, P.; Amundson, J.; Harnik, R. Electron-Phonon Systems on a Universal Quantum Computer. Phys. Rev. Lett. 2018, 121, 110504. [Google Scholar] [CrossRef]
- Macridin, A.; Li, A.C.Y.; Mrenna, S.; Spentzouris, P. Bosonic field digitization for quantum computers. Phys. Rev. A 2022, 105, 052405. [Google Scholar] [CrossRef]
- Miessen, A.; Ollitrault, P.J.; Tavernelli, I. Quantum algorithms for quantum dynamics: A performance study on the spin-boson model. Phys. Rev. Res. 2021, 3, 043212. [Google Scholar] [CrossRef]
- Stojanović, V.M. Entanglement-spectrum characterization of ground-state nonanalyticities in coupled excitation-phonon models. Phys. Rev. B 2020, 101, 134301. [Google Scholar] [CrossRef]
- Stojanović, V.M.; Shi, T.; Bruder, C.; Cirac, J.I. Quantum Simulation of Small-Polaron Formation with Trapped Ions. Phys. Rev. Lett. 2012, 109, 250501. [Google Scholar] [CrossRef] [PubMed]
- Nauth, J.K.; Stojanović, V.M. Spectral features of polaronic excitations in a superconducting analog simulator. Phys. Rev. B 2023, 107, 174306. [Google Scholar] [CrossRef]
- Mei, F.; Stojanović, V.M.; Siddiqi, I.; Tian, L. Analog superconducting quantum simulator for Holstein polarons. Phys. Rev. B 2013, 88, 224502. [Google Scholar] [CrossRef]
- Stojanović, V.M.; Vanević, M.; Demler, E.; Tian, L. Transmon-based simulator of nonlocal electron-phonon coupling: A platform for observing sharp small-polaron transitions. Phys. Rev. B 2014, 89, 144508. [Google Scholar] [CrossRef]
- Stojanović, V.M.; Salom, I. Quantum dynamics of the small-polaron formation in a superconducting analog simulator. Phys. Rev. B 2019, 99, 134308. [Google Scholar] [CrossRef]
- Stojanović, V.M. Bare-Excitation Ground State of a Spinless-Fermion-Boson Model and W-State Engineering in an Array of Superconducting Qubits and Resonators. Phys. Rev. Lett. 2020, 124, 190504. [Google Scholar] [CrossRef]
- Stojanović, V.M. Scalable W-type entanglement resource in neutral-atom arrays with Rydberg-dressed resonant dipole-dipole interaction. Phys. Rev. A 2021, 103, 022410. [Google Scholar] [CrossRef]
- Tong, Y.; Alber, V.V.; McClean, J.R.; Preskill, J.; Su, Y. Provably accurate simulation of gauge theories and bosonic systems. Quantum 2022, 6, 816. [Google Scholar] [CrossRef]
- Heyl, M. Dynamical quantum phase transitions: A review. Rep. Prog. Phys. 2018, 81, 054001. [Google Scholar] [CrossRef] [PubMed]
- Peskin, M.E.; Schroeder, D.V. An Introduction To Quantum Field Theory; Avalon Publishing: Emeryville, CA, USA, 1995. [Google Scholar]
- Martinez, E.A.; Muschik, C.A.; Schindler, P.; Nigg, D.; Erhard, A.; Heyl, M.; Hauke, P.; Dalmonte, M.; Monz, T.; Zoller, P.; et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature 2016, 534, 516. [Google Scholar] [CrossRef] [PubMed]
- Holland, E.T.; Wendt, K.A.; Kravvaris, K.; Wu, X.; Ormand, W.E.; DuBoi, J.L.; Quaglioni, S.; Pederiva, F. Optimal control for the quantum simulation of nuclear dynamics. Phys. Rev. A 2020, 101, 062307. [Google Scholar] [CrossRef]
- Kreshchuk, M.; Kirby, W.M.; Goldstein, G.; Beauchemin, H.; Love, P.J. Quantum simulation of quantum field theory in the light-front formulation. Phys. Rev. A 2022, 105, 032418. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Tran, M.C.; Zhu, Y.; Green, A.M.; Alderete, C.H.; Davoudi, Z.; Linke, N.M. Digital Quantum Simulation of the Schwinger Model and Symmetry Protection with Trapped Ions. PRX Quantum 2022, 3, 020324. [Google Scholar] [CrossRef]
- Kico, N.; Roggero, A.; Savage, M.J. Standard Model Physics and the Digital Quantum Revolution: Thoughts about the Interface. Rep. Prog. Phys. 2022, 85, 064301. [Google Scholar]
- Yukawa, H. On the Interaction of Elementary Particles I. Proc. Phys. Math. Soc. Jpn. (3rd Ser.) 1935, 17, 48. [Google Scholar]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- IBM Quantum. Available online: https://quantum-computing.ibm.com/ (accessed on 25 June 2023).
- Peres, A. Reversible logic and quantum computers. Phys. Rev. A 1985, 32, 3266. [Google Scholar] [CrossRef]
- Born, M.; Fock, V. Beweis des Adiabatensatzes. Z. Physik 1928, 51, 165. [Google Scholar] [CrossRef]
- Albash, T.; Lidar, D.A. Adiabatic quantum computation. Rev. Mod. Phys. 2018, 90, 015002. [Google Scholar] [CrossRef]
- Temme, K.; Bravyi, S.; Gambetta, J.M. Error Mitigation for Short-Depth Quantum Circuits. Phys. Rev. Lett. 2017, 119, 180509. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Benjamin, S.C. Efficient Variational Quantum Simulator Incorporating Active Error Minimization. Phys. Rev. X 2017, 7, 021050. [Google Scholar] [CrossRef]
- Stojanović, V.M.; Nauth, J.K. Interconversion of W- and Greenberger-Horne-Zeilinger states for Ising-coupled qubits with transverse global control. Phys. Rev. A 2022, 106, 052613. [Google Scholar] [CrossRef]
- Stojanović, V.M.; Nauth, J.K. Dicke-state preparation through global transverse control of Ising-coupled qubits. Phys. Rev. A 2023, 108, 012608. [Google Scholar] [CrossRef]
- Kökcü, E.; Camps, D.; Bassman, L.; Freericks, J.K.; de Jong, W.A.; Van Beeumen, R.; Kemper, A.F. Algebraic compression of quantum circuits for Hamiltonian evolution. Phys. Rev. A 2022, 105, 032420. [Google Scholar] [CrossRef]
- Peng, B.; Gulania, S.; Alexeev, Y.; Govind, N. Quantum time dynamics employing the Yang-Baxter equation for circuit compression. Phys. Rev. A 2022, 106, 012412. [Google Scholar] [CrossRef]
- Suzuki, M. Generalized Trotter’s formula and systematic approximants of exponential operators and inner derivations with applications to many-body problem. Commun. Math. Phys. 1976, 51, 183. [Google Scholar] [CrossRef]
- Hatano, N.; Suzuki, M. Finding Exponential Product Formulas of Higher Orders. In Quantum Annealing and Other Optimization Methods; Springer: Berlin/Heidelberg, Germany, 2005; pp. 37–68. [Google Scholar]
- Shende, V.V.; Markov, I.L.; Bullock, S.S. Minimal universal two-qubit controlled-NOT-based circuits. Phys. Rev. A 2004, 69, 062321. [Google Scholar] [CrossRef]
- Stojanović, V.M. Feasibility of single-shot realizations of conditional three-qubit gates in exchange-coupled qubit arrays with local contro. Phys. Rev. A 2019, 99, 012345. [Google Scholar] [CrossRef]
- Skiena, S.S. The Algorithm Design Manual, 2nd ed.; Springer: London, UK, 2012. [Google Scholar]
- Gui, K.; Tomesh, T.; Gokhale, P.; Shi, Y.; Chong, F.T.; Martonosi, M.; Suchara, M. Term Grouping and Travelling Salesperson for Digital Quantum Simulation. arXiv 2020, arXiv:2001.05983. [Google Scholar]
- Bellman, R. Dynamic Programming Treatment of the Traveling Salesman Problem. J. Assoc. Comput. Mach. 1962, 9, 61. [Google Scholar] [CrossRef]
- Held, M.; Karp, R.M. A Dynamic Programming Approach to Sequencing. J. Soc. Indust. Appl. Math. 1962, 10, 196. [Google Scholar] [CrossRef]
- Christofides, N. Worst-Case Analysis of a New Heuristic for the Traveling Salesman Problem; Technical Report; Graduate School of Industrial Administration, Carnegie-Mellon University: Pittsburgh, PA, USA, 1976. [Google Scholar]
- Ranninger, J.; Robin, J.M.; Eschrig, M. Superfluid Precursor Effects in a Model of Hybridized Bosons and Fermions. Phys. Rev. Lett. 1995, 74, 4027. [Google Scholar] [CrossRef] [PubMed]
- Ciavarella, A. Algorithm for quantum computation of particle decays. Phys. Rev. D 2020, 102, 094505. [Google Scholar] [CrossRef]
- Farrell, R.C.; Chernyshev, I.A.; Powell, S.J.M.; Zemlevskiy, N.A.; Illa, M.; Savage, M.J. Preparations for quantum simulations of quantum chromodynamics in 1+1 dimensions. II. Single-baryon -decay in real time. Phys. Rev. D 2023, 107, 054513. [Google Scholar] [CrossRef]
- Trotter, H.F. On the Product of Semi-Groups of Operators. Proc. Am. Math. Soc. 1959, 10, 545. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Abrams, D.S.; Lloyd, S. Nonlinear quantum mechanics implies polynomial-time solution for NP-complete and #P problems. Phys. Rev. Lett. 1998, 81, 3992. [Google Scholar]
- Zheng, C. Universal quantum simulation of single-qubit non-unitary operators using duality quantum algorithm. Sci. Rep. 2021, 11, 3960. [Google Scholar] [CrossRef]
- Jordan, P.; Wigner, E. Ueber das Paulische Aequivalenzverbot. Z. Phys. 1928, 47, 631. [Google Scholar] [CrossRef]
- Seeley, J.T.; Richard, M.J.; Love, P.J. The Bravyi-Kitaev transformation for quantum computation of electronic structure. J. Chem. Phys. 2012, 137, 224109. [Google Scholar] [CrossRef]
- Terhal, B.; DiVincenzo, D.P. Classical simulation of noninteracting-fermion quantum circuits. Phys. Rev. A 2002, 65, 032325. [Google Scholar] [CrossRef]
- Kraus, B.; Cirac, J.I. Optimal creation of entanglement using a two-qubit gate. Phys. Rev. A 2001, 63, 062309. [Google Scholar] [CrossRef]
- Vatan, F.; Williams, C. Optimal quantum circuits for general two-qubit gates. Phys. Rev. A 2004, 69, 032315. [Google Scholar] [CrossRef]
- Available online: https://pypi.org/project/python_tsp (accessed on 17 July 2024).
- Available online: https://pypi.org/project/networkx (accessed on 17 July 2024).
- Kern, O.; Alber, G. Controlling Quantum Systems by Embedded Dynamical Decoupling Schemes. Phys. Rev. Lett. 2005, 95, 250501. [Google Scholar] [CrossRef] [PubMed]
- McArdle, S.; Yuan, X.; Benjamin, S. Error-Mitigated Digital Quantum Simulation. Phys. Rev. Lett. 2019, 122, 180501. [Google Scholar] [CrossRef]
- Czarnik, P.; Arrasmith, A.; Coles, P.J.; Cincio, L. Qubit-efficient exponential suppression of errors. Quantum 2021, 5, 592. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, S. Quantum Error Mitigation via Matrix Product Operators. PRX Quantum 2022, 3, 040313. [Google Scholar] [CrossRef]
- Kern, O.; Alber, G.; Shepelyansky, D.L. Quantum error correction of coherent errors by randomization. Eur. Phys. J. D 2005, 32, 153. [Google Scholar] [CrossRef]
- Giurgica-Tiron, T.; Hindy, Y.; LaRose, R.; Mari, A.; Zeng, W.J. Digital zero noise extrapolation for quantum error mitigation. In Proceedings of the 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), Denver, CO, USA, 12–16 October 2020. [Google Scholar]
- Qiskit Runtime. Available online: https://github.com/Qiskit/qiskit-ibm-runtime/ (accessed on 25 June 2023).
- Smolin, J.A.; Gambetta, J.M.; Smith, G. Efficient Method for Computing the Maximum-Likelihood Quantum State from Measurements with Additive Gaussian Noise. Phys. Rev. Lett. 2012, 108, 070502. [Google Scholar] [CrossRef] [PubMed]
- Gross, D.; Liu, Y.-K.; Flammia, S.T.; Becker, S.; Eisert, J. Quantum State Tomography via Compressed Sensing. Phys. Rev. Lett. 2010, 105, 150401. [Google Scholar] [CrossRef] [PubMed]
- Gross, D. Recovering Low-Rank Matrices From Few Coefficients in Any Basis. IEEE Trans. Inf. Theory 2011, 57, 1548. [Google Scholar] [CrossRef]
- Altepeter, J.B.; James, D.F.; Kwiat, P.G. 4 Qubit Quantum State Tomography. In Quantum State Estimation; Lecture Notes in Physics; Paris, M., Řeháček, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 649, pp. 113–145. [Google Scholar]
- Smith, A.W.R.; Gray, J.; Kim, M.S. Efficient Quantum State Sample Tomography with Basis-Dependent Neural Networks. PRX Quantum 2021, 2, 020348. [Google Scholar] [CrossRef]
- Qiskit Experiments. Available online: https://github.com/Qiskit/qiskit-experiments (accessed on 25 June 2023).
- Uhlmann, A. The “Transition Probability” in the State Space a ∗-algebra. Rep. Math. Phys. 1976, 9, 273–279. [Google Scholar] [CrossRef]
- Quantinuum. System Model H1 Product Data Sheet, Version 5.00; Quantinuum: Cambridge, UK, 2022.
- Huang, X.-Y.; Yu, L.; Lu, X.; Yang, Y.; Li, D.-S.; Wu, C.-W.; Wu, W.; Chen, P.-X. Qubitization of Bosons. arXiv 2021, arXiv:2105.12563. [Google Scholar]




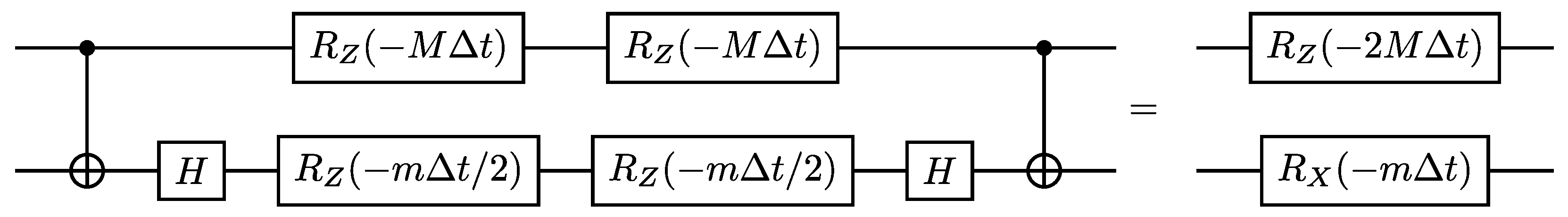
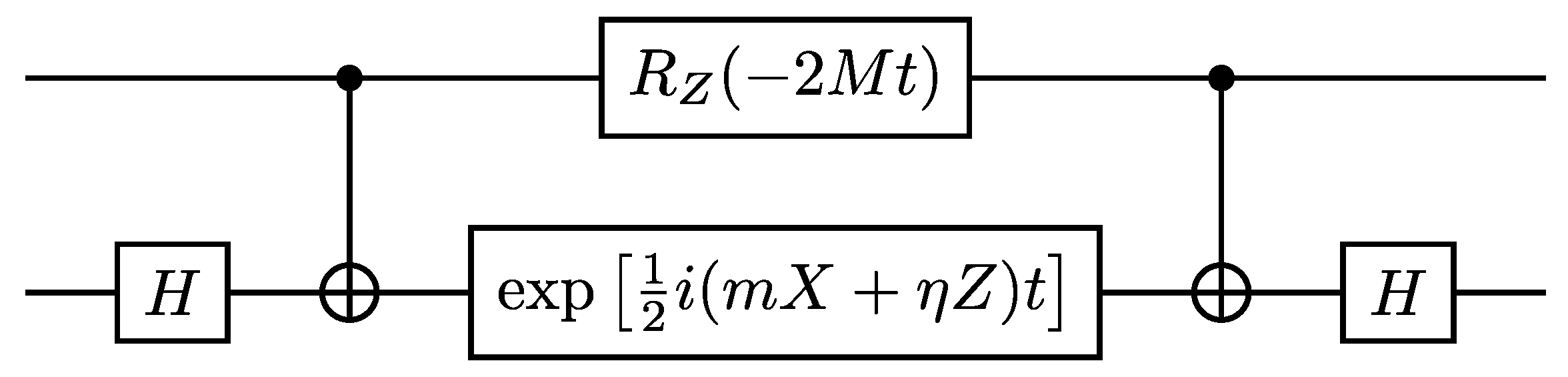









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaldenbach, T.N.; Heller, M.; Alber, G.; Stojanović, V.M. Digital Quantum Simulation of Scalar Yukawa Coupling. Quantum Rep. 2024, 6, 366-400. https://doi.org/10.3390/quantum6030024
Kaldenbach TN, Heller M, Alber G, Stojanović VM. Digital Quantum Simulation of Scalar Yukawa Coupling. Quantum Reports. 2024; 6(3):366-400. https://doi.org/10.3390/quantum6030024
Chicago/Turabian StyleKaldenbach, Thierry N., Matthias Heller, Gernot Alber, and Vladimir M. Stojanović. 2024. "Digital Quantum Simulation of Scalar Yukawa Coupling" Quantum Reports 6, no. 3: 366-400. https://doi.org/10.3390/quantum6030024




