Quantum Computing: Navigating the Future of Computation, Challenges, and Technological Breakthroughs
Abstract
1. Introduction
1.1. Basics of Quantum Computing
1.2. Overview of the Current State of Technology
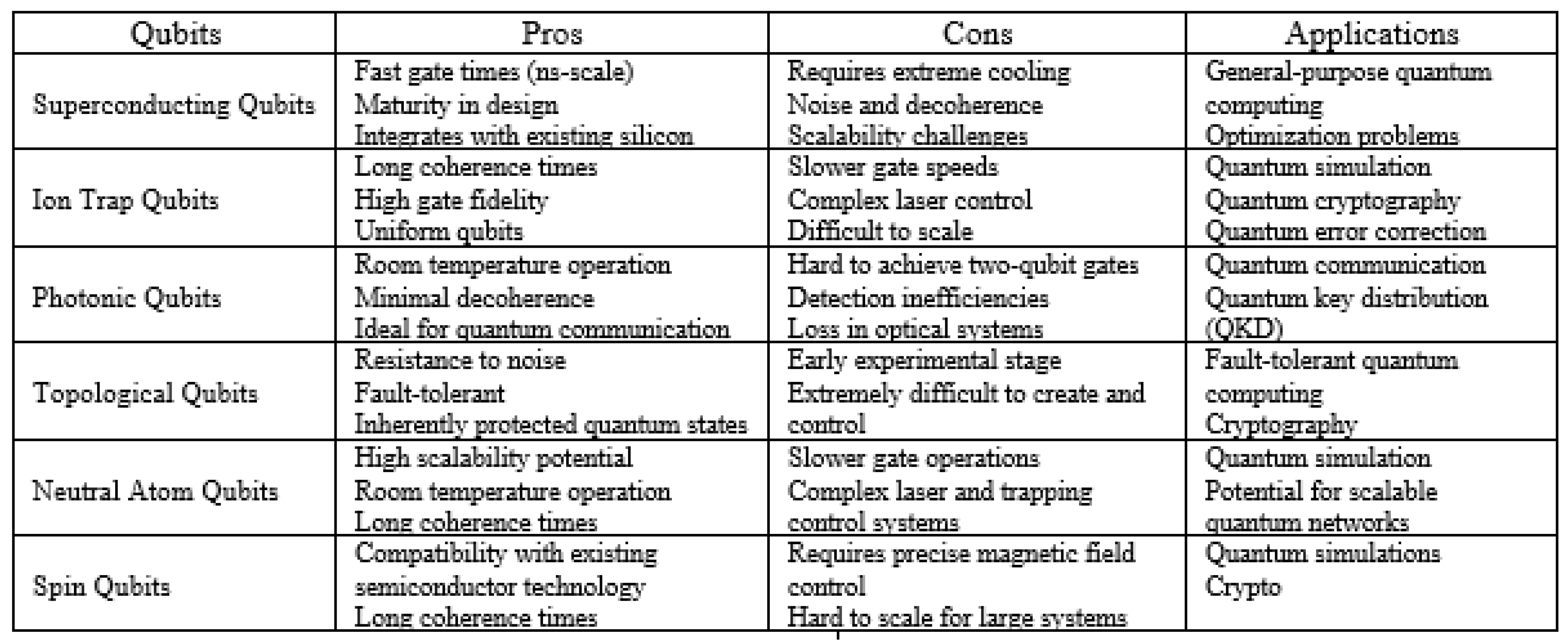
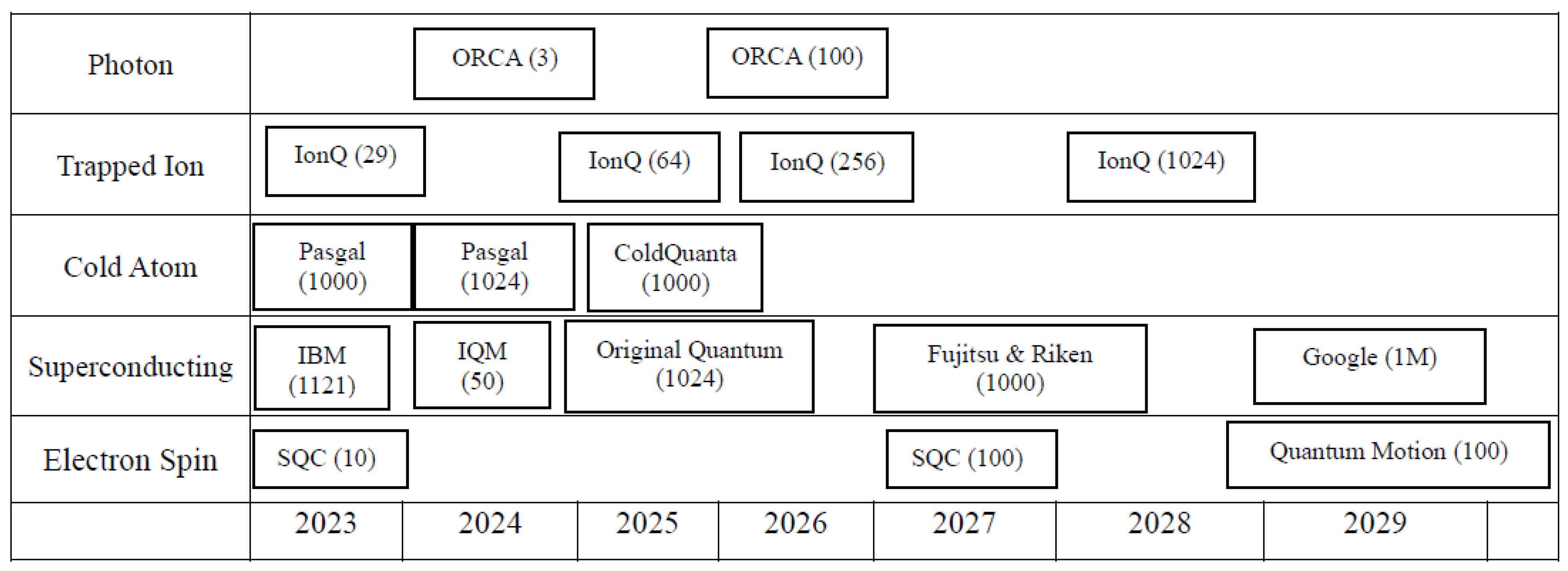
2. Quantum Computing Hardware
- Gate-based quantum computing utilizes discrete gate operations to compute a logical outcome for a quantum algorithm
- Analog quantum computing [50] represents the physical state using continuous variables and continuous transformations. For example, fermionic atoms can be confined within a lattice to mimic electron behavior.
- Measurement-based quantum computing [51] creates a large, entangled state within a photonic lattice. The extraction of photons from this lattice acts as a gate, enabling the execution of quantum algorithms.
- Quantum annealers [52] are specialized for solving specific optimization, and function by seeking the system’s lowest energy state, making them particularly effective for optimization tasks.
3. Technical Challenges and Reliability Issues
3.1. Quantum Algorithms
3.2. Quantum Supremacy and Verification
3.3. Qubit Stability
3.4. Error Handling
3.5. Quantum Decoherence and Its Implications
4. Noise and Error Correction in Quantum Systems
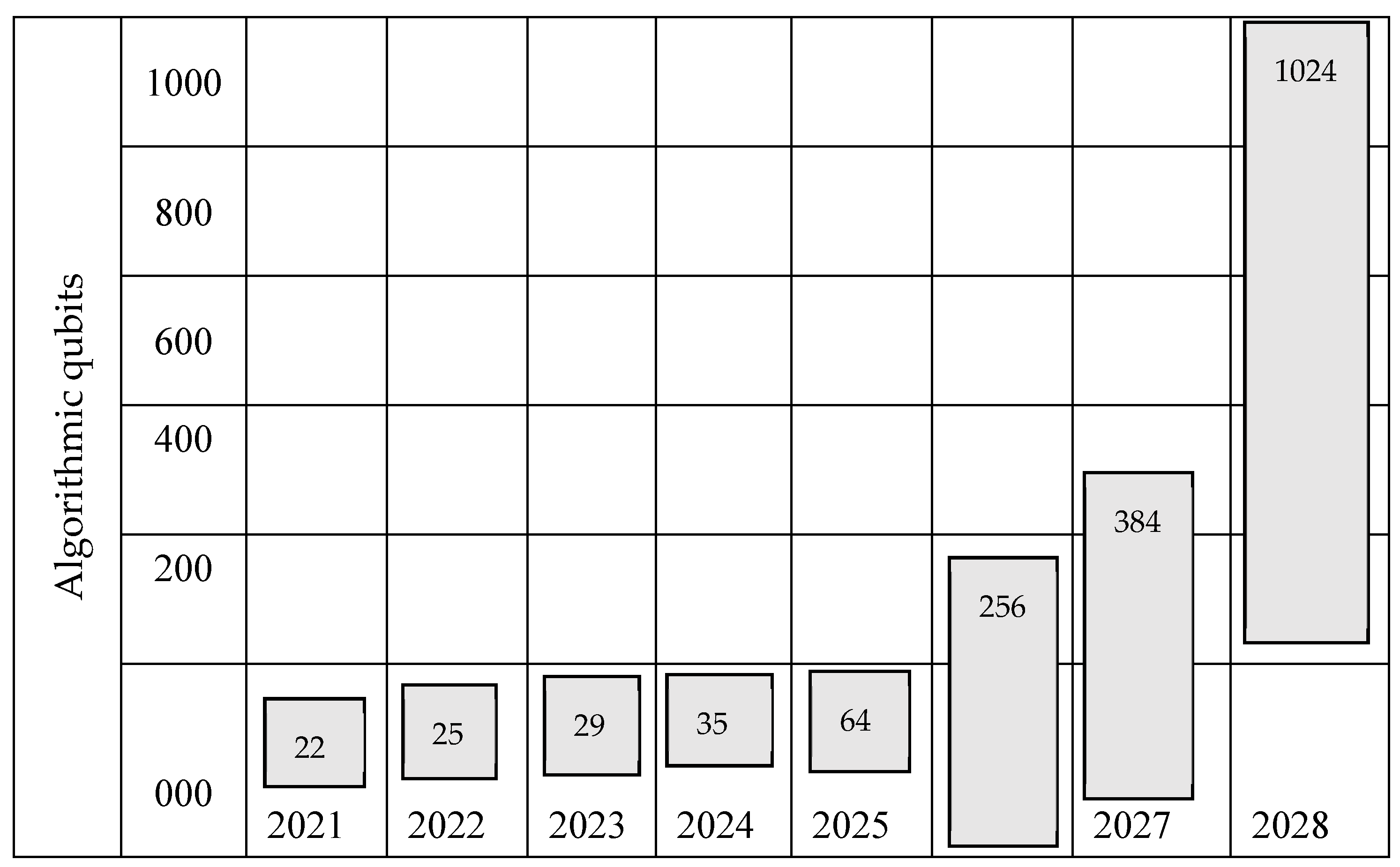
5. Scalability Challenges
5.1. Scaling Quantum Systems
5.2. Hardware Development Challenges
5.3. Multichip Approach
5.4. Circuit Cutting Approach
5.5. Variational Quantum Eigensolver (VQE)
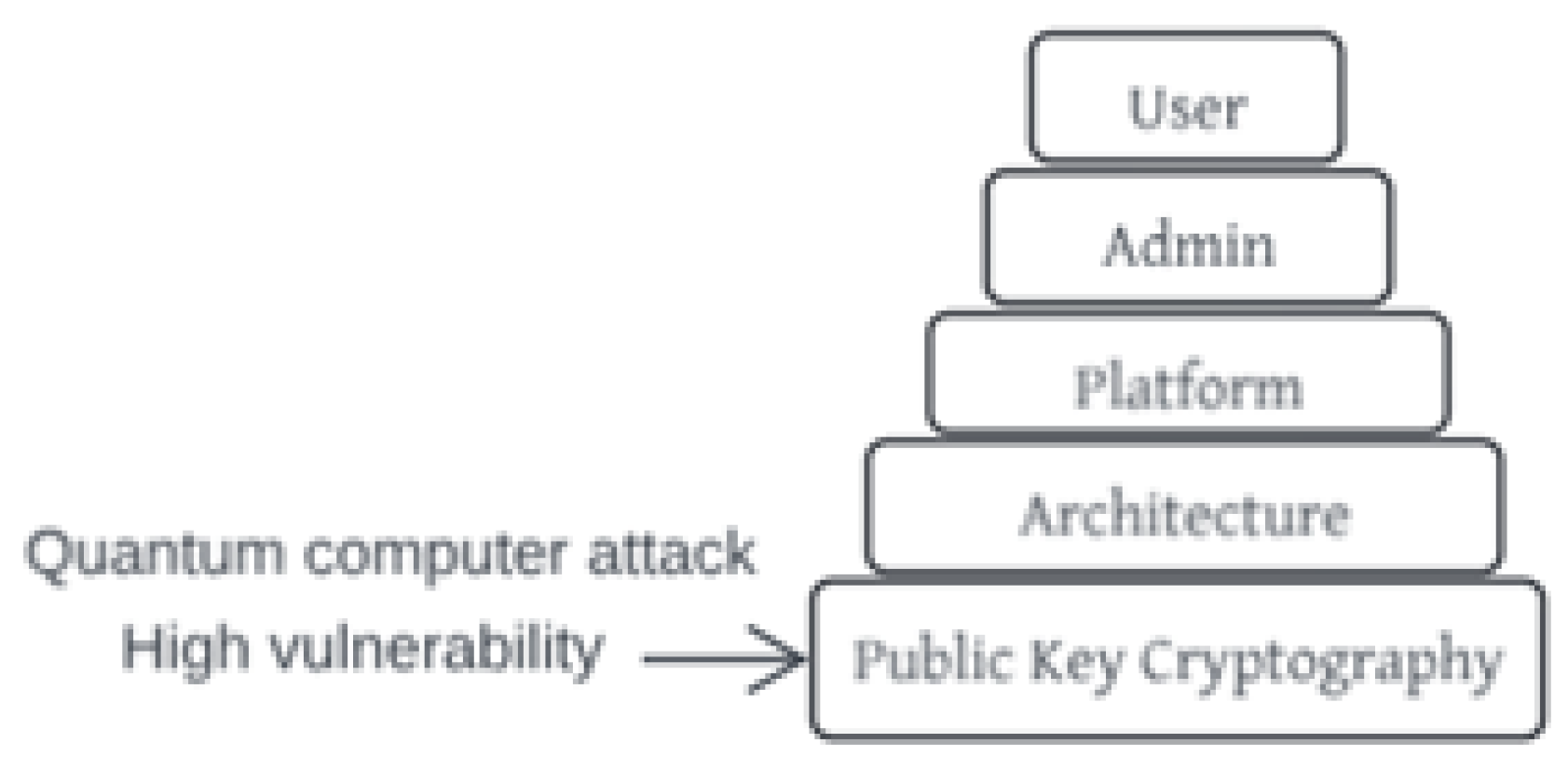
6. Quantum Computing and Cybersecurity
7. Quantum Computing Benchmark Metrics
7.1. Physical Benchmarks
7.2. Aggregated Benchmarks
7.3. Application-Based Benchmarks
8. Environmental and Sustainability Concerns
8.1. Resource Requirements
8.2. Energy Consumption and Ecological Impact
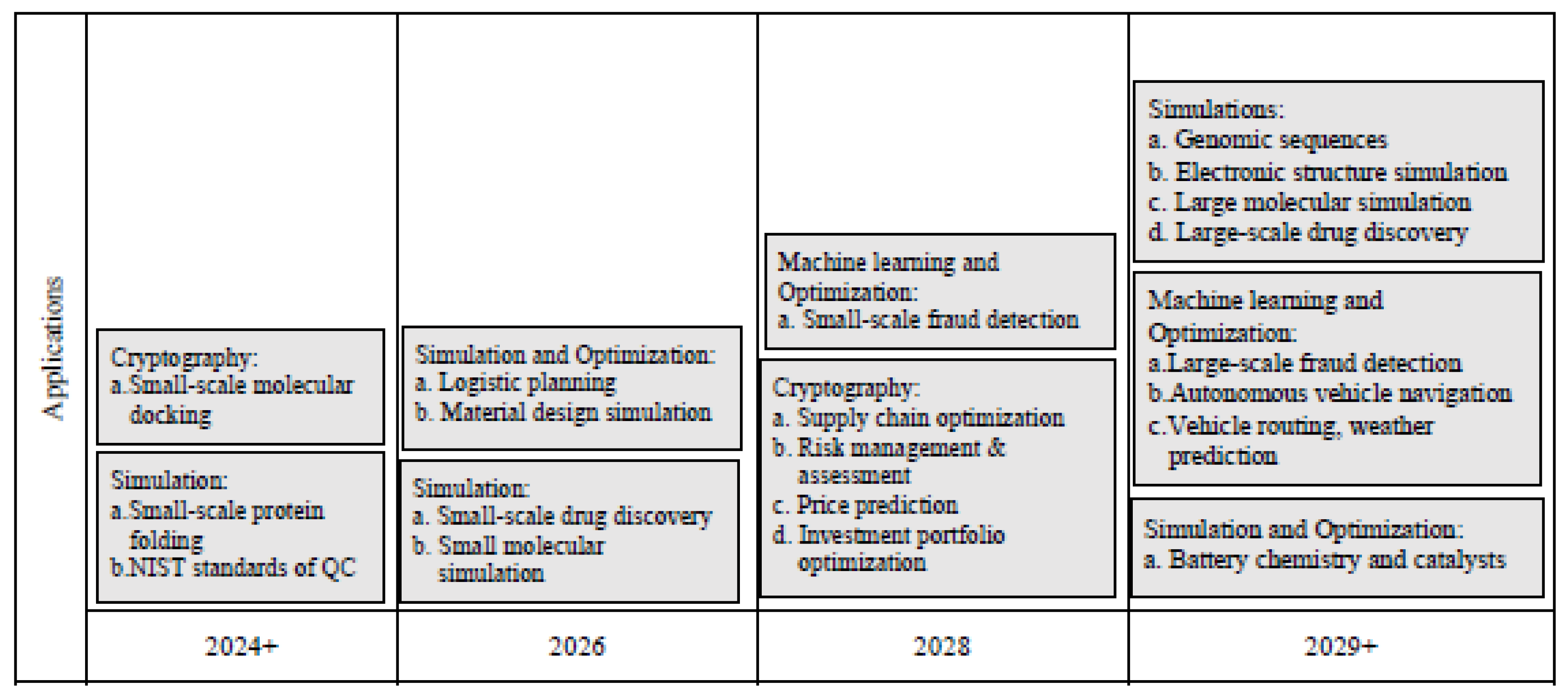
9. Future Prospects and Developments
9.1. Upcoming Technological Breakthroughs
9.2. The Roadmap for Quantum Computing Advancements
9.3. Future Outlook and Recommendations
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feynman, R.P.; Feynman, T.H. Quantum mechanical computers. In Lectures on Computation, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information, 10th ed.; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. The quest for a quantum neural network. Quantum Inf. Process. 2014, 13, 2567–2586. [Google Scholar] [CrossRef]
- Grumbling, E.; Horowitz, M. Quantum Computing: Progress and Prospects; The National Academies Press: Washington, DC, USA, 2019; pp. 1–272. [Google Scholar]
- Haferkamp, J.; Faist, P.; Kothakonda, N.B.T.; Eisert, J.; Halpern, N.Y. Linear growth of quantum circuit complexity. Nat. Phys. 2022, 18, 528–532. [Google Scholar] [CrossRef]
- Sigov, A.; Ratkin, L.; Ivanov, L.A. Quantum Information Technology. J. Ind. Inf. Integr. 2022, 28, 100365. [Google Scholar] [CrossRef]
- Cao, Y.; Romero, J.; Aspuru-Guzik, A. Potential of quantum computing for drug discovery. IBM J. Res. Dev. 2018, 62, 6:1–6:20. [Google Scholar] [CrossRef]
- Joseph, D.; Misoczki, R.; Manzano, M.; Tricot, J.; Pinuaga, F.D.; Lacombe, O.; Leichenauer, S.; Hidary, J.; Venables, P.; Hansen, R. Transitioning organizations to post-quantum cryptography. Nature 2022, 605, 237–243. [Google Scholar] [CrossRef]
- Herman, D.; Googin, C.; Liu, X.; Sun, Y.; Galda, A.; Safro, I.; Pistoia, M.; Alexeev, Y. Quantum computing for finance. Nat. Rev. Phys. 2023, 5, 450–465. [Google Scholar] [CrossRef]
- Weinberg, S.J.; Sanches, F.; Ide, T.; Kamiya, K.; Correll, R. Supply chain logistics with quantum and classical annealing algorithms. Sci. Rep. 2013, 13, 4770. [Google Scholar] [CrossRef]
- Jurczak, C. Investing in the Quantum Future: State of Play and Way Forward for Quantum Venture Capital. arXiv 2023, arXiv:2311.17187. [Google Scholar]
- Kim, Y.; Eddins, A.; Anand, S.; Wei, K.X.; Berg, E.v.D.; Rosenblatt, S.; Nayfeh, H.; Wu, Y.; Zaletel, M.; Temme, K.; et al. Evidence for the utility of quantum computing before fault tolerance. Nature 2023, 618, 500–505. [Google Scholar] [CrossRef]
- Woolnough, A.; Lloyd, C.; Hollenberg, P.; Prowse, T. Quantum computing: A new paradigm for ecology. Trends Ecol. Evol. 2023, 38, 727–735. [Google Scholar] [CrossRef]
- Naz, S.F.; Shah, A.P. Reversible Gates: A Paradigm Shift in Computing. IEEE Open J. Circuits Syst. 2023, 4, 241–257. [Google Scholar] [CrossRef]
- Stroev, N.; Berloff, N. Analog Photonics Computing for Information Processing, Inference, and Optimization. Adv. Quantum Technol. 2023, 6, 2300055. [Google Scholar] [CrossRef]
- Lent, C.S.; Isaksen, B.; Lieberman, M. Molecular Quantum-Dot Cellular Automata. J. Am. Chem. Soc. 2003, 125, 1056–1063. [Google Scholar] [CrossRef] [PubMed]
- Ravichandran, R.; Lim, S.K.; Niemier, M. Automatic cell placement for quantum-dot cellular automata. Integration 2005, 38, 541–548. [Google Scholar] [CrossRef][Green Version]
- Ahmad, F.; Bhat, G.; Ahmad, P. Novel Adder Circuits Based On Quantum-Dot Cellular Automata (QCA). Circuits Syst. 2014, 5, 142–152. [Google Scholar] [CrossRef][Green Version]
- Beigh, M.; Mustafa, M.; Ahmad, F. Performance Evaluation of Efficient XOR Structures in Quantum-Dot Cellular Automata (QCA). Circuits Syst. 2013, 4, 147–156. [Google Scholar] [CrossRef]
- Kurzweil, R. The Singularity Is Near: When Human Transcend Biology; The Viking Press: New York, NY, USA, 2006. [Google Scholar]
- Möller, M.; Vuik, C. On the impact of quantum computing technology on future developments in high-performance scientific computing. Ethics Inf. Technol. 2017, 19, 253–269. [Google Scholar] [CrossRef]
- Yerlanova, G.; Serik, M.; Kopyltsov, A. High performance computers: From parallel computing to quantum computers and biocomputers. J. Phys. Conf. Ser. 2012, 1889, 032032. [Google Scholar] [CrossRef]
- Konig, R.; Maurer, U.; Renner, R. On the power of quantum memory. IEEE Trans. Inf. Theory 2005, 51, 2391–2401. [Google Scholar] [CrossRef]
- Benenti, G.; Casat, G. Quantum computers: Where do we stand? Euro Phys. News 2005, 36, 16–20. [Google Scholar] [CrossRef][Green Version]
- Fouché, W.; Heidema, J.; Jones, G.; Potgieter, P.H. Universality and programmability of quantum computers. Theor. Comput. Sci. 2008, 403, 121–129. [Google Scholar] [CrossRef]
- Calvo, H.; Cuartero, G.; Gómez, F.; González, J.; Mezzini, M.; Pelayo, F. Functional Matrices on Quantum Computing Simulation. Mathematics 2023, 11, 3742. [Google Scholar] [CrossRef]
- Lau, J.W.Z.; Lim, K.H.; Shrotriya, H.; Kwek, L.C. NISQ computing: Where are we and where do we go? AAPPS Bull. 2022, 32, 27. [Google Scholar] [CrossRef]
- Fatsuma, J.; Chiroma, H.; Gital, A.; Almutairi, M.; Abdulhamid, S.; Abawajy, J. Deep learning architectures in emerging cloud computing architectures: Recent development, challenges and next research trend. Appl. Soft Comput. 2020, 96, 06582. [Google Scholar]
- Vadyala, S.; Betgeri, S. General implementation of quantum physics-informed neural networks. Array 2023, 18, 100287. [Google Scholar] [CrossRef]
- National Quantum Initiative. Available online: https://www.quantum.gov/ (accessed on 6 March 2024).
- Martin Gilesarchive. 2019. Available online: https://www.technologyreview.com/2019/09/24/439/quantum-computing-and-quantum-supremacy/ (accessed on 6 March 2024).
- Google, Quantum Supremacy. 2019. Available online: https://www.newsweek.com/quantum-computing-google-scientists-breakthrough-supercomputer-1467256 (accessed on 7 March 2024).
- Google, The Quantum Insider. 2023. Available online: https://thequantuminsider.com/2023/07/04/google-claims-latest-quantum-experiment-would-take-decades-on-classical-computer/ (accessed on 7 March 2024).
- Collins, H.; Nay, C. IBM Unveils. 2022. Available online: https://newsroom.ibm.com/2022-11-09-IBM-Unveils-400-Qubit-Plus-Quantum-Processor-and-Next-Generation-IBM-Quantum-System-Two (accessed on 7 March 2024).
- Porter, J. The Verge. 2021. Available online: https://www.theverge.com/2021/5/19/22443453/google-quantum-computer-2029-decade-commercial-useful-qubits-quantum-transistor (accessed on 8 March 2024).
- Williams, J. T-Systems to Offer Customers Access to IQM Quantum Systems Through the Cloud. 2023. Available online: https://www.telekom.com/en/media/media-information/archive/t-systems-to-offer-customers-access-to-iqm-quantum-systems-through-the-cloud-1043308 (accessed on 8 March 2024).
- Bova, F.; Goldfarb, A.; Melko, R.G. Commercial applications of quantum computing. EPJ Quantum Technol. 2021, 8, 2. [Google Scholar] [CrossRef]
- Bhat, H.A.; Khanday, F.A.; Kaushik, B.K.; Bashir, F.; Shah, K.A. Quantum Computing: Fundamentals, Implementations and Applications. IEEE Open J. Nanotechnol. 2022, 3, 61–77. [Google Scholar] [CrossRef]
- Cooper, L.N. Bound Electron Pairs in a Degenerate Fermi Gas. Phys. Rev. 1956, 104, 1189. [Google Scholar] [CrossRef]
- Friis, N.; Marty, O.; Maier, C.; Hempel, C.; Holzäpfel, M.; Jurcevic, P.; Plenio, M.B.; Huber, M.; Roos, C.; Blatt, R.; et al. Observation of entangled states of a fully controlled 20-qubit system. Phys. Rev. X 2018, 8, 021012. [Google Scholar] [CrossRef]
- Briegel, H.J.; Browne, D.E.; Dür, W.; Raussendorf, R.; Van den Nest, M. Measurement-based quantum computation. Nat. Phys. 2009, 5, 19–26. [Google Scholar] [CrossRef]
- Cong, I.; Levine, H.; Keesling, A.; Bluvstein, D.; Wang, S.-T.; Lukin, M.D. Hardware-efficient, fault-tolerant quantum computation with Rydberg atoms. Phys. Rev. X 2022, 12, 021049. [Google Scholar] [CrossRef]
- QuEra. 2023. Available online: https://www.quera.com/blog-posts/hybrid-quantum-computing-bridging-classical-and-quantum-worlds (accessed on 9 March 2024).
- Sarker, I. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Computer. Sci. 2021, 2, 160. [Google Scholar] [CrossRef] [PubMed]
- Skyrme, T. Quantum Computing 2023–2043. 2023. Available online: https://www.idtechex.com/en/research-report/quantum-computing-2023-2043/912 (accessed on 9 March 2024).
- Pautasso, L.; Pflanzer, A.; Soller, H. McKinsey Digital Blue. 2021. Available online: https://www.mckinsey.com/capabilities/mckinsey-digital/our-insights/tech-forward/the-current-state-of-quantum-computing-between-hype-and-revolution (accessed on 9 March 2024).
- QuTech, Towards Unhackable Quantum Internet. 2019. Available online: https://qutech.h5mag.com/annual_report_2019/towards_unhackable_quantum_internet (accessed on 9 March 2024).
- Dejpasand, M.; Ghamsari, M. Research Trends in Quantum Computers by Focusing on Qubits as Their Building Blocks. Quantum Rep. 2023, 5, 597–608. [Google Scholar] [CrossRef]
- Pfaendler, S.; Konson, K.; Greinert, F. Advancements in Quantum Computing—Viewpoint: Building Adoption and Competency in Industry. Datenbank Spektrum 2024, 24, 5–20. [Google Scholar] [CrossRef]
- Argüello-Luengo, J.; González-Tudela, A.; Shi, T.; Zoller, P.; Cirac, J.I. Analogue quantum chemistry simulation. Nature 2019, 574, 215–218. [Google Scholar] [CrossRef]
- Barz, S. Quantum computing with photons: Introduction to the circuit model, the one-way quantum computer, and the fundamental principles of photonic experiments. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 83001. [Google Scholar] [CrossRef]
- Albertson, D.I.; Rusu, A. Highly reconfigurable oscillator-based Ising Machine through quasiperiodic modulation of coupling strength. Nat. Sci. Rep. 2023, 13, 4005. [Google Scholar] [CrossRef]
- Singh, P.; Dasgupta, R.; Singh, A.; Pandey, H.; Hassija, V.; Chamola, V.; Sikdar, B. A Survey on Available Tools and Technologies Enabling Quantum Computing. IEEE Access 2024, 12, 57974–57991. [Google Scholar] [CrossRef]
- Anferov, A.; Harvey, S.P.; Wan, F.; Simon, J.; Schuster, D.I. Superconducting Qubits above 20 GHz Operating over 200 mK. PRX Quantum 2024, 5, 030347. [Google Scholar] [CrossRef]
- Blümel, R.; Grzesiak, N.; Nguyen, N.H.; Green, A.M.; Li, M.; Maksymov, A.; Linke, N.M.; Nam, Y. Efficient stabilized two-qubit gates on a trapped-ion quantum computer. Phys. Rev. Lett. 2021, 126, 220503. [Google Scholar] [CrossRef]
- Bartolucci, S.; Birchall, P.; Bombín, H.; Cable, H.; Dawson, C.; Gimeno-Segovia, M.; Johnston, E.; Kieling, K.; Nickerson, N.; Pant, M.; et al. Fusion-based quantum computation. Nat. Commun. 2023, 14, 912. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Zalba, M.F. Quantum computing with CMOS technology. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition, Grenoble, France, 1–5 February 2021; p. 761. [Google Scholar]
- Shafique, M.A.; Munir, A.; Latif, I. Quantum Computing: Circuits, Algorithms, and Applications. IEEE Access 2024, 12, 22296–22314. [Google Scholar] [CrossRef]
- De Micheli, G.; Jiang, J.-H.R.; Rand, R.; Smith, K.; Soeken, M. Advances in Quantum Computation and Quantum Technologies: A Design Automation Perspective. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 584–601. [Google Scholar] [CrossRef]
- Ohkura, Y.; Satoh, T.; Van Meter, R. Simultaneous Execution of Quantum Circuits on Current and Near-Future NISQ Systems. IEEE Trans. Quantum Eng. 2022, 3, 2500210. [Google Scholar] [CrossRef]
- Genssler, P.R.; Klemme, F.; Parihar, S.S.; Brandhofer, S.; Pahwa, G.; Polian, I.; Chauhan, Y.S.; Amrouch, H. Cryogenic Embedded System to Support Quantum Computing: From 5-nm FinFET to Full Processor. IEEE Trans. Quantum Eng. 2023, 4, 5500611. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, W.; Wang, L.; Zhao, Y.; Tong, Y.; Rong, X.; Du, J. An FPGA-Based Hardware Platform for the Control of Spin-Based Quantum Systems. IEEE Trans. Instrum. Meas. 2020, 69, 1127–1139. [Google Scholar] [CrossRef]
- Trochatos, T.; Xu, C.; Deshpande, S.; Lu, Y.; Ding, Y.; Szefer, J. A Quantum Computer Trusted Execution Environment. IEEE Comput. Archit. Lett. 2023, 22, 177–180. [Google Scholar] [CrossRef]
- Martiel, S.; Ayral, T.; Allouche, C. Benchmarking Quantum Coprocessors in an Application-Centric, Hardware-Agnostic, and Scalable Way. IEEE Trans. Quantum Eng. 2021, 2, 3102011. [Google Scholar] [CrossRef]
- Lubinski, T.; Johri, S.; Varosy, P.; Coleman, J.; Zhao, L.; Necaise, J.; Baldwin, C.H.; Mayer, K.; Proctor, T. Application-Oriented Performance Benchmarks for Quantum Computing. IEEE Trans. Quantum Eng. 2023, 4, 3100332. [Google Scholar] [CrossRef]
- Gyongyosi, L.; Imre, S. A Survey on quantum computing technology. Comput. Sci. Rev. 2019, 31, 51–71. [Google Scholar] [CrossRef]
- Van Meter, R.; Devitt, S.J. The Path to Scalable Distributed Quantum Computing. IEEE Comput. 2016, 49, 31–42. [Google Scholar] [CrossRef]
- Monroe, C.; Raussendorf, R.; Ruthven, A.; Brown, K.R.; Maunz, P.; Duan, L.-M.; Kim, J. Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 2014, 89, 022317. [Google Scholar] [CrossRef]
- Blakestad, R.; Ospelkaus, C.; VanDevender, A.; Amini, J.; Britton, J.; Leibfried, D.; Wineland, D. High-fidelity transport of trapped-ion qubits through an x-junction trap array. Phys. Rev. Lett. 2009, 102, 153002. [Google Scholar] [CrossRef] [PubMed]
- Barends, R.; Kelly, J.; Megrant, A.; Veitia, A.; Sank, D.; Jeffrey, E.; White, T.C.; Mutus, J.; Fowler, A.G.; Campbell, B.; et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 2014, 508, 500–503. [Google Scholar] [CrossRef]
- DiCarlo, L.; Chow, J.M.; Gambetta, J.M.; Bishop, L.S.; Johnson, B.R.; Schuster, D.I.; Majer, J.; Blais, A.; Frunzio, L.; Girvin, S.M.; et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 2009, 460, 240–244. [Google Scholar] [CrossRef] [PubMed]
- Ofek, N.; Petrenko, A.; Heeres, R.; Reinhold, P.; Leghtas, Z.; Vlastakis, B.; Liu, Y.; Frunzio, L.; Girvin, S.M.; Jiang, L.; et al. Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 2016, 536, 441–445. [Google Scholar] [CrossRef]
- Zhu, X.; Saito, S.; Kemp, A.; Kakuyanagi, K.; Karimoto, S.I.; Nakano, H.; Munro, W.J.; Tokura, Y.; Everitt, M.S.; Nemoto, K.; et al. Coherent coupling of a superconducting flux qubit to an electron spin ensemble in diamond. Nature 2011, 478, 221–224. [Google Scholar] [CrossRef]
- Bernien, H.; Hensen, B.; Pfaff, W.; Koolstra, G.; Blok, M.S.; Robledo, L.; Taminiau, T.H.; Markham, M.; Twitchen, D.J.; Childress, L.; et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 2013, 497, 86–90. [Google Scholar] [CrossRef]
- Dolde, F.; Jakobi, I.; Naydenov, B.; Zhao, N.; Pezzagna, S.; Trautmann, C.; Meijer, J.; Neumann, P.; Jelezko, F.; Wrachtrup, J. Room-temperature entanglement between single defect spins in diamond. Nat. Phys. 2013, 9, 139–143. [Google Scholar] [CrossRef]
- Altaisky, M.V.; Zolnikova, N.N.; Kaputkina, N.E.; Krylov, V.A.; Lozovik, Y.E.; Dattani, N.S. Towards a feasible implementation of quantum neural networks using quantum dots. Appl. Phys. Lett. 2016, 108, 103108. [Google Scholar] [CrossRef]
- Behrman, E.; Niemel, J.; Steck, J.E.; Skinner, S.R. A quantum dot neural network. In Proceedings of the 4th Workshop on Physics of Computation, Boston, MA, USA, 22–24 November 1996; pp. 22–24. [Google Scholar]
- Yao, N.; Jiang, L.; Gorshkov, A.; Maurer, P.; Giedke, G.; Cirac, J.I.; Lukin, M. Scalable architecture for a room temperature solid-state quantum information processor. Nat. Commun. 2012, 3, 800. [Google Scholar] [CrossRef] [PubMed]
- Muhonen, J.T.; Dehollain, J.P.; Laucht, A.; Hudson, F.E.; Kalra, R.; Sekiguchi, T.; Itoh, K.M.; Jamieson, D.N.; McCallum, J.C.; Dzurak, A.S.; et al. Storing quantum information for 30 s in a nanoelectronic device. Nat. Nanotechnol. 2014, 9, 986–991. [Google Scholar] [CrossRef] [PubMed]
- Zwanenburg, F.; Dzurak, A.; Morello, A.; Simmons, M.; Hollenberg, L.; Klimeck, G.; Rogge, S.; Coppersmith, S.; Eriksson, M. Silicon quantum electronics. Rev. Mod. Phys. 2013, 85, 961–1019. [Google Scholar] [CrossRef]
- Mourik, V.; Zuo, K.; Frolov, S.; Plissard, S.; Bakkers, E.; Kouwenhoven, L. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 2012, 336, 1003–1007. [Google Scholar] [CrossRef] [PubMed]
- Giani, A.; Goff-Eldredge, Z. How Quantum Computing Could Solve Our Huge Climate and Energy Challenges. 2022. Available online: https://www.zmescience.com/ecology/climate/how-quantum-computing-can-tackle-climate-and-energy-challenges/ (accessed on 25 March 2024).
- Swayne, M. The Quantum Insider. 2023. Available online: https://thequantuminsider.com/2023/08/03/how-would-room-temperature-superconductors-change-quantum-computing/ (accessed on 9 March 2023).
- Brooks, M. Computing. 2024. Available online: https://www.technologyreview.com/2024/01/04/1084783/quantum-computing-noise-google-ibm-microsoft (accessed on 10 March 2024).
- Pyrkov, A.; Aliper, A.; Bezrukov, D.; Lin, Y.-C.; Polykovskiy, D.; Kamya, P.; Ren, F.; Zhavoronkov, A. Quantum computing for near-term applications in generative chemistry and drug discovery. Drug Discov. Today 2023, 28, 103675. [Google Scholar] [CrossRef]
- Faster Capital, Current Challenges in Quantum Computing. Available online: https://fastercapital.com/startup-topic/Challenges-in-Quantum.html#the-challenges-of-quantum-computing7 (accessed on 25 March 2024).
- Law, M. Cloud Computing. 2023. Available online: https://technologymagazine.com/articles/top-10-quantum-computing-companies (accessed on 10 March 2024).
- Grover, L. A fast quantum mechanical algorithm for database search. In Proceedings of the 28th Annual ACM Symposium on the Theory of Computation, New York, NY, USA, 22–24 May 1996; ACM Press: New York, NY, USA, 1996; pp. 212–219. [Google Scholar]
- Shor, P. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Los Alamitos, CA, USA, 20–22 November 1994; IEEE Press: Piscataway, NJ, USA, 1994; p. 124. [Google Scholar]
- Apolloni, B.; Carvalho, M.; De Falco, D. Quantum stochastic optimization. Stoch. Process Their Appl. 1989, 33, 233–244. [Google Scholar] [CrossRef]
- An, D.; Liu, J.-P.; Lin, L. Linear Combination of Hamiltonian Simulation for Nonunitary Dynamics with Optimal State Preparation Cost. Phys. Rev. Lett. 2023, 131, 6031–6036. [Google Scholar] [CrossRef]
- Dernbach, S.; Mohseni-Kabir, A.; Pal, S.; Gepner, M.; Towsley, D. Quantum walk neural networks with feature dependent coins. Appl. Netw. Sci. 2019, 4, 76. [Google Scholar] [CrossRef]
- François, C.-B.; Belin, E. Fourier-transform quantum phase estimation with quantum phase noise. Signal Process. 2020, 170, 107441. [Google Scholar] [CrossRef]
- Nieman, K.; Durand, H.; Patel, S.; Koch, D.; Alsing, P.M. Investigating amplitude amplification in optimization-based control for a continuous stirred tank reactor. Digit. Chem. Eng. 2024, 13, 100180. [Google Scholar] [CrossRef]
- Long, G.-L. General quantum interference principle and duality computer. Commun. Theor. Phys. 2006, 45, 5. [Google Scholar]
- Zheng, C. Universal quantum simulation of single-qubit nonunitary operators using duality quantum algorithm. Sci. Rep. 2021, 11, 3960. [Google Scholar] [CrossRef] [PubMed]
- Michielsen, K.; Mohseni, M.; Mutus, J.; Naaman, O.; Neeley, M.; Neill, C.; Niu, M.Y.; Ostby, E.; Petukhov, A.; Platt, J.C.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef]
- Mohseni, M.; Read, P.; Neven, H.; Boixo, S.; Denchev, V.; Babbush, R.; Fowler, A.; Smelyanskiy, V.; Martinis, J. Commercialize quantum technologies in five years. Nature 2017, 543, 171–174. [Google Scholar] [CrossRef]
- Villalonga, B.; Lyakh, D.; Boixo, S.; Neven, H.; Humble, T.S.; Biswas, R.; Rieffel, E.G.; Ho, A.; Mandrà, S. Establishing the quantum supremacy frontier with a 281 Pflop/s simulation. Quantum Sci. Technol. 2020, 5, 034003. [Google Scholar] [CrossRef]
- Zlokapa, A.; Villalonga, B.; Boixo, S.; Lidar, D.A. Boundaries of quantum supremacy via random circuit sampling. Npj Quantum Inf. 2023, 9, 36. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Guo, C.; Song, J.; Shi, X.; Gan, L.; Wu, W.; Wu, W.; Fu, H.; Liu, X.; et al. Verifying Quantum Advantage Experiments with Multiple Amplitude Tensor Network Contraction. Phys. Rev. Lett. 2024, 132, 030601. [Google Scholar] [CrossRef] [PubMed]
- Puthussery, E.S.; Poonia, R.C. Quantum Computing’s Path to Supremacy: Progress in the NISQ Epoch. In Innovative Computing and Communications; Lecture Notes in Networks and Systems; Springer: Singapore, 2024; Volume 1021. [Google Scholar]
- AbuGhanem, M.; Eleuch, H. NISQ Computers: A Path to Quantum Supremacy. IEEE Access 2024, 12, 102941–102961. [Google Scholar] [CrossRef]
- Schlör, S.; Lisenfeld, J.; Müller, C.; Bilmes, A.; Schneider, A.; Pappas, D.P.; Ustinov, A.V.; Weides, M. Correlating decoherence in transmon qubits: Low-frequency noise by single fluctuators. Phys. Rev. Lett. 2019, 123, 190502. [Google Scholar] [CrossRef]
- Yeter-Aydeniz, K.; Parks, Z.; Thekkiniyedath, A.N.; Gustafson, E.; Kemper, A.F.; Pooser, R.C.; Meurice, Y.; Dreher, P. Measuring qubit stability in a gate-based NISQ hardware processor. Quantum Inf. Process. 2023, 22, 96. [Google Scholar] [CrossRef]
- Zhou, A.; Sun, Z.; Sun, L. Stable organic radical qubits and their applications in quantum information science. Innov. 2024, 5, 100662. [Google Scholar] [CrossRef] [PubMed]
- Ahsan, M.; Van Meter, R.; Kim, J. Designing a million-qubit quantum computer using a resource performance simulator. ACM J. Emerg. Technol. Comput. Syst. 2015, 12, 1–25. [Google Scholar] [CrossRef]
- Maurer, P.C.; Kucsko, G.; Latta, C.; Jiang, L.; Yao, N.Y.; Bennett, S.D.; Pastawski, F.; Hunger, D.; Chisholm, N.; Markham, M.; et al. Room-temperature quantum bit memory exceeding one second. Science 2012, 336, 1283–1286. [Google Scholar] [CrossRef]
- Van Meter, R.; Devitt, S.J. Local and distributed quantum computation. arXiv 2016, arXiv:1605.06951. [Google Scholar]
- Takeda, K.; Kamioka, J.; Otsuka, T.; Yoneda, J.; Nakajima, T.; Delbecq, M.R.; Amaha, S.; Allison, G.; Kodera, T.; Oda, S.; et al. A fault-tolerant addressable spin qubit in a natural silicon quantum dot. Sci. Adv. 2016, 2, e1600694. [Google Scholar] [CrossRef]
- Steane, A. Error correcting codes in quantum theory. Phys. Rev. Lett. 1996, 77, 793–797. [Google Scholar] [CrossRef]
- Shu, Y.; Truhlar, D. Decoherence and Its Role in Electronically Nonadiabatic Dynamics. J. Chem. Theory Comput. 2023, 19, 380–395. [Google Scholar] [CrossRef]
- Shashank Raghavan, Decoherence: Quantum Computer’s Greatest Obstacle. 2023. Available online: https://www.linkedin.com/pulse/decoherence-quantum-computers-greatest-obstacle-shashank-v-raghavan-j4lcc/ (accessed on 25 March 2024).
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1–57. [Google Scholar] [CrossRef]
- Brandt, H. Qubit devices and the issue of quantum decoherence. Prog. Quantum Electron. 1999, 22, 257–370. [Google Scholar] [CrossRef]
- Crull, E. Exploring Philosophical Implications of Quantum Decoherence. Philos. Compass 2023, 8, 875–885. [Google Scholar] [CrossRef]
- Arzano, M.; D’esposito, V.; Gubitosi, G. Fundamental decoherence from quantum spacetime. Commun. Phys. 2023, 6, 242. [Google Scholar] [CrossRef]
- Martinez, J.E.; Fuentes, P.; Crespo, P.M.; Garcia-Frías, J. Approximating Decoherence Processes for the Design and Simulation of Quantum Error Correction Codes on Classical Computers. IEEE Access 2020, 8, 172623–172643. [Google Scholar] [CrossRef]
- Xiao, S.; Xue, S.; Dong, D.; Zhang, J. Identification of Time-Varying Decoherence Rates for Open Quantum Systems. IEEE Trans. Quantum Eng. 2021, 2, 2102212. [Google Scholar] [CrossRef]
- O′Connell, R.F. Decoherence in quantum systems. IEEE Trans. Nanotechnol. 2005, 4, 77–82. [Google Scholar] [CrossRef]
- Aumentado, J.; Catelani, G.; Serniak, K. Quasiparticle poisoning in superconducting quantum computers. Phys. Today 2023, 76, 34–39. [Google Scholar] [CrossRef]
- Wintersperger, K.; Dommert, F.; Ehmer, T.; Hoursanov, A.; Klepsch, J.; Mauerer, W.; Reuber, G.; Strohm, T.; Yin, M.; Luber, S. Neutral atom quantum computing hardware: Performance and end-user perspective. EPJ Quantum Technol. 2023, 10, 32. [Google Scholar] [CrossRef]
- Guo, Y.; Li, J.; Dou, R.; Ye, H.; Gu, C. Quantum defects in two-dimensional van der Waals materials. In Fundamental Research; KeAi Publishing: Beijing, China, 2024. [Google Scholar] [CrossRef]
- Oh, J.-S.; Zaman, R.; Murthy, A.A.; Bal, M.; Crisa, F.; Zhu, S.; Torres-Castendo, C.G.; Kopas, C.J.; Mutus, J.Y.; Jing, D.; et al. Structure and Formation Mechanisms in Tantalum and Niobium Oxides in Superconducting Quantum Circuits. ACS Nano 2024, 18, 19732–19741. [Google Scholar] [CrossRef]
- Bal, M.; Murthy, A.A.; Zhu, S.; Crisa, F.; You, X.; Huang, Z.; Roy, T.; Lee, J.; Zanten, D.; Pilipenko, R.; et al. Systematic improvements in transmon qubit coherence enabled by niobium surface encapsulation. Npj Quantum Inf. 2024, 10, 43. [Google Scholar] [CrossRef]
- E de Graaf, S.; Un, S.; Shard, A.G.; Lindström, T. Chemical and structural identification of material defects in superconducting quantum circuits. Mater. Quantum Technol. 2022, 2, 032001. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Komura, Y.; Mishima, S.; Tanaka, T.; Niikura, N.; Kosaka, H. Geometric spin echo under zero field. Nat. Commun. 2016, 7, 11668. [Google Scholar] [CrossRef] [PubMed]
- Google Quantum AI. Suppressing quantum errors by scaling a surface code logical qubit. Nature 2023, 614, 676–681. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.; Hann, C.T.; Puri, S.; Girvin, S.M.; Jiang, L. Error Suppression for Arbitrary-Size Black Box Quantum Operations. Phys. Rev. Lett. 2023, 131, 190601. [Google Scholar] [CrossRef]
- Koczor, B. Exponential Error Suppression for Near-Term Quantum Devices. Phys. Rev. X 2021, 11, 031057. [Google Scholar] [CrossRef]
- Giurgica-Tiron, T.; Hindy, Y.; LaRose, R.; Mari, A.; Zeng, W. Digital zero noise extrapolation for quantum error mitigation. In Proceedings of the IEEE International Conference on Quantum Computing and Engineering, Denver, CO, USA, 12–16 October 2020; pp. 306–316. [Google Scholar]
- Shaib, A.; Naim, M.H.; Fouda, M.E.; Kanj, R.; Kurdahi, F. Efficient noise mitigation technique for quantum computing. Sci. Rep. 2023, 13, 3912. [Google Scholar] [CrossRef]
- Hama, Y.; Nishi, H. Quantum error mitigation via quantum-noise-effect circuit groups. Sci. Rep. 2024, 14, 6077. [Google Scholar] [CrossRef] [PubMed]
- Russo, V.; Mari, A.; Shammah, N.; LaRose, R.; Zeng, W.J. Testing Platform-Independent Quantum Error Mitigation on Noisy Quantum Computers. IEEE Trans. Quantum Eng. 2023, 4, 2500318. [Google Scholar] [CrossRef]
- Kim, C.; Park, K.D.; Rhee, J.-K. Quantum Error Mitigation with Artificial Neural Network. IEEE Access 2020, 8, 188853–188860. [Google Scholar] [CrossRef]
- Jose, S.T.; Simeone, O. Error-Mitigation-Aided Optimization of Parameterized Quantum Circuits: Convergence Analysis. IEEE Trans. Quantum Eng. 2022, 3, 3103119. [Google Scholar] [CrossRef]
- Cai, Z.; Babbush, R.; Benjamin, S.; Endo, S.; Huggins, W.; Li, Y.; McClean, J.; O’Brien, T. Quantum error mitigation. Rev. Mod. Phys. 2023, 95, 045005. [Google Scholar] [CrossRef]
- Singh, K.; Bradley, C.E.; Anand, S.; Ramesh, V.; White, R.; Bernien, H. Mid-circuit correction of correlated phase errors using an array of spectator qubits. Science 2023, 380, 1265–1269. [Google Scholar] [CrossRef] [PubMed]
- Ryan-Anderson, C.; Bohnet, J.; Lee, K.; Gresh, D.; Hankin, A.; Gaebler, J.; Francois, D.; Chernoguzov, A.; Lucchetti, D.; Brown, N.; et al. Realization of Real-Time Fault-Tolerant Quantum Error Correction. Phys. Rev. X 2021, 11, 041058. [Google Scholar] [CrossRef]
- Nachman, B.; Urbanek, M.; de Jong, W.A.; Bauer, C.W. Unfolding quantum computer readout noise. Npj Quantum Inf. 2020, 6, 84. [Google Scholar] [CrossRef]
- Cenedese, G.; Benenti, G.; Bondani, M. Correcting Coherent Errors by Random Operation on Actual Quantum Hardware. Entropy 2023, 25, 324. [Google Scholar] [CrossRef]
- Gambetta, J.M.; Chow, J.M.; Steffen, M. Building logical qubits in a superconducting quantum computing system. Npj Quantum Inf. 2017, 3, 2. [Google Scholar] [CrossRef]
- Chapman, P. Scaling IonQ’s Quantum Computers: The Roadmap. 2020. Available online: https://ionq.com/posts/december-09-2020-scaling-quantum-computer-roadmap (accessed on 25 March 2024).
- Ranadive, A.; Fazliji, B.; Gal, G.L.; Cappelli, G.; Butseraen, G.; Bonet, E.; Eyraud, E.; Böhling, S.; Planat, L.; Metelmann, A.; et al. A Traveling Wave Parametric Amplifier Isolator. arXiv 2024, arXiv:2406.19752. [Google Scholar]
- Di Palma, L.; Miano, A.; Mastrovito, P.; Massarotti, D.; Arzeo, M.; Pepe, G.; Tafuri, F.; Mukhanov, O. Discriminating the Phase of a Coherent Tone with a Flux-Switchable Superconducting Circuit. Phys. Rev. Appl. 2023, 19, 064025. [Google Scholar] [CrossRef]
- Bravyi, S.; Cross, A.W.; Gambetta, J.M.; Maslov, D.; Rall, P.; Yoder, T.J. High-threshold and low-overhead fault-tolerant quantum memory. arXiv 2023, arXiv:2308.07915. [Google Scholar] [CrossRef]
- Conner, C.R.; Bienfait, A.; Chang, H.-S.; Chou, M.-H.; Dumur, E.; Grebel, J.; Peairs, G.A.; Povey, R.G.; Yan, H.; Zhong, Y.P.; et al. Cleland, Superconducting qubits in a flip-chip architecture. Appl. Phys. Lett. 2021, 118, 232602. [Google Scholar] [CrossRef]
- Gold, A.; Paquette, J.P.; Stockklauser, A.; Reagor, M.J.; Alam, M.S.; Bestwick, A.; Didier, N.; Nersisyan, A.; Oruc, F.; Razavi, A.; et al. Entanglement across separate silicon dies in a modular superconducting qubit device. NPI Quantum Inf. 2021, 7, 142. [Google Scholar] [CrossRef]
- Zhong, Y.P.; Chang, H.-S.; Satzinger, K.J.; Chou, M.-H.; Bienfait, A.; Conner, C.R.; Dumur, E.; Grebel, J.; Peairs, G.A.; Povey, R.G.; et al. Violating Bell’s inequality with remotely connected superconducting qubits. Nat. Phys. 2019, 15, 741. [Google Scholar] [CrossRef]
- Zhong, Y.; Chang, H.-S.; Bienfait, A.; Dumur, E.; Chou, M.-H.; Conner, C.R.; Grebel, J.; Povey, R.G.; Yan, H.; Schuster, D.I.; et al. Deterministic multi-qubit entanglement in a quantum network. Nature 2021, 590, 571. [Google Scholar] [CrossRef] [PubMed]
- C´orcoles, A.D.; Takita, M.; Inoue, K.; Lekuch, S.; Minev, Z.K.; Chow, J.M.; Gambetta, J.M. Exploiting dynamic quantum circuits in a quantum algorithm with superconducting qubits. Phys. Rev. Lett. 2021, 127, 100501. [Google Scholar] [CrossRef] [PubMed]
- B¨aumer, E.; Tripathi, V.; Wang, D.S.; Rall, P.; Chen, E.H.; Majumder, S.; Seif, A.; Minev, Z.K. Efficient long-range entanglement using dynamic circuits. arXiv 2023, arXiv:2308.13065. [Google Scholar]
- Gyongyosi, L.; Imre, S. Scalable distributed gate-model quantum computers. Sci. Rep. 2021, 11, 5172. [Google Scholar] [CrossRef]
- Alarcón, E.; Abadal, S.; Sebastiano, F.; Babaie, M.; Charbon, E.; Bolívar, P.H.; Palesi, M.; Blokhina, E.; Leipold, D.; Staszewski, B.; et al. Scalable multi-chip quantum architectures enabled by cryogenic hybrid wireless/quantum-coherent network-in-package. In Proceedings of the IEEE International Symposium on Circuits and Systems, Monterey, CA, USA, 21–25 May 2023; pp. 1–5. [Google Scholar]
- Zheng, Y.; Zhai, C.; Liu, D.; Mao, J.; Chen, X.; Dai, T.; Huang, J.; Bao, J.; Fu, Z.; Tong, Y.; et al. Multichip multidimensional quantum networks with entanglement retrievability. Science 2023, 381, 221–226. [Google Scholar] [CrossRef]
- Cho, Z.; Son, Y.; Jeong, H.; Kim, Y.; Paek, S.; Suk, D.; Lee, H. A New Approach to Quantum Computing Multi-Qubit Generation and Development of Quantum Computing Platform with Magnetic Resonance Imaging Techniques. arXiv 2022, arXiv:2206.05932. [Google Scholar]
- Field, M.; Chen, A.; Scharmann, B.; Sete, E.; Oruc, F.; Vu, K.; Kosenko, V.; Mutus, J.; Poletto, S.; Bestwick, A. Modular superconducting-qubit architecture with a multichip tunable coupler. Phys. Rev. Appl. 2024, 21, 054063. [Google Scholar] [CrossRef]
- Qiao, C.; Zhao, Y.; Zhao, G.; Xu, H. Quantum Data Networking for Distributed Quantum Computing: Opportunities and Challenges. In Proceedings of the IEEE Conference on Computer Communications Workshops, New York, NY, USA, 2–5 May 2022; pp. 1–6. [Google Scholar]
- Rodrigo, S.; Abadal, S.; Alarcón, E.; Bandic, M.; Someren, H.V.; Almudéver, C.G. On Double Full-Stack Communication-Enabled Architectures for Multicore Quantum Computers. IEEE Micro 2021, 41, 48–56. [Google Scholar] [CrossRef]
- Mukhanov, O.; Plourde, B.L.T.; Opremcak, A.; Liu, C.-H.; McDermott, R.; Kirichenko, A.; Howington, C.; Walter, J.; Hutchings, M.; Vernik, I.; et al. Scalable Quantum Computing Infrastructure Based on Superconducting Electronics. In Proceedings of the IEEE International Electron Devices Meeting, San Francisco, CA, USA, 7–11 December 2019; pp. 31.2.1–31.2.4. [Google Scholar]
- Cambiucci, W.; Silveira, R.M.; Ruggiero, W.V. Hypergraphic Partitioning of Quantum Circuits for Distributed Quantum Computing. In Proceedings of the IEEE International Conference on Quantum Computing and Engineering, Bellevue, WA, USA, 17–22 September 2023; pp. 268–269. [Google Scholar]
- Perlin, M.A.; Saleem, Z.H.; Suchara, M.; Osborn, J.C. Quantum circuit cutting with maximum-likelihood tomography. Npj Quantum Inf. 2021, 7, 64. [Google Scholar] [CrossRef]
- Baheri, B.; Guan, Q.; Xu, S.; Chaudhary, V. SQCC: Smart Quantum Circuit Cutting. In Proceedings of the IEEE International Parallel and Distributed Processing Symposium Workshops, Lyon, France, 30 May–3 June 2022; pp. 614–615. [Google Scholar]
- Lowe, A.; Medvidović, M.; Hayes, A.; O’Riordan, L.J.; Bromley, T.R.; Arrazola, J.M.; Killoran, N. Fast quantum circuit cutting with randomized measurements. Quantum 2023, 7, 934. [Google Scholar] [CrossRef]
- Smith, K.; Perlin, M.; Gokhale, P.; Frederick, P.; Owusu-Antwi, D.; Rines, R.; Omole, V.; Chong, F. Clifford-based Circuit Cutting for Quantum Simulation. In Proceedings of the 50th Annual International Symposium on Computer Architecture, Orlando, FL, USA, 17–21 June 2023; pp. 1–13. [Google Scholar]
- Tomesh, T.; Saleem, Z.H.; Perlin, M.A.; Gokhale, P.; Suchara, M.; Martonosi, M. Divide and Conquer for Combinatorial Optimization and Distributed Quantum Computation. In Proceedings of the IEEE International Conference on Quantum Computing and Engineering, Bellevue, WA, USA, 17–22 September 2023; pp. 1–12. [Google Scholar]
- Andrés, E.; Cuéllar, M.P.; Navarro, G. Efficient Dimensionality Reduction Strategies for Quantum Reinforcement Learning. IEEE Access 2023, 11, 104534–104553. [Google Scholar] [CrossRef]
- El-Araby, E.; Mahmud, N.; Jeng, M.J.; MacGillivray, A.; Chaudhary, M.; Nobel, A.I.; Islam, S.I.U.; Levy, D.; Kneidel, D.; Watson, M.R.; et al. Towards Complete and Scalable Emulation of Quantum Algorithms on High-Performance Reconfigurable Computers. IEEE Trans. Comput. 2023, 72, 2350–2364. [Google Scholar] [CrossRef]
- Sun, R.-Y.; Shirakawa, T.; Yunoki, S. Scalable Quantum Simulation for Topological Phases on NISQ Devices. In Proceedings of the IEEE International Conference on Quantum Computing and Engineering, Bellevue, WA, USA, 17–22 September 2023; pp. 244–245. [Google Scholar]
- Ferrari, D.; Carretta, S.; Amoretti, M. A Modular Quantum Compilation Framework for Distributed Quantum Computing. IEEE Trans. Quantum Eng. 2023, 4, 2500213. [Google Scholar] [CrossRef]
- Farrell, R.C.; Illa, M.; Ciavarella, A.; Savage, M. Scalable Circuits for Preparing Ground States on Digital Quantum Computers: The Schwinger Model Vacuum on 100 Qubits. PRX Quantum 2024, 5, 020315. [Google Scholar] [CrossRef]
- Clary, J.M.; Jones, E.B.; Vigil-Fowler, D.; Chang, C.; Graf, P. Exploring the scaling limitations of the variational quantum eigensolver with the bond dissociation of hydride diatomic molecules. Proc. Int. J. Quantum Chem. 2023, 123, e27097. [Google Scholar] [CrossRef]
- Quantum Xchange. Available online: https://quantumxc.com/blog/quantum-computing-impact-on-cybersecurity/ (accessed on 1 March 2024).
- Emerging India Analytics. 2024. Available online: https://medium.com/@analyticsemergingindia/quantum-computing-and-cybersecurity-implications-for-encryption-and-data-protection-03f8cd4d959a (accessed on 10 March 2024).
- Buchanan, W.; Woodward, A. Will Quantum Computers Be the End of Public Key Encryption? J. Cyber Secur. Technol. 2017, 1, 1–22. [Google Scholar] [CrossRef]
- O’Neil, P. MIT Technology Review. 2021. Available online: https://www.technologyreview.com/2021/11/03/1039171/hackers-quantum-computers-us-homeland-security-cryptography/ (accessed on 11 March 2024).
- Kumar, M. Post-quantum cryptography Algorithm’s standardization and performance analysis. Array 2022, 15, 100242. [Google Scholar] [CrossRef]
- García, C.; Rommel, S.; Takarabt, S.; Olmos, J.; Guilley, S.; Nguyen, P.; Monroy, I. Quantum-resistant Transport Layer Security. Comput. Commun. 2024, 213, 345–358. [Google Scholar] [CrossRef]
- Nurhadi, A.I.; Syambas, N.R. Quantum Key Distribution (QKD) Protocols: A Survey. In Proceedings of the 4th International Conference on Wireless and Telematics, Bali, Indonesia, 12–13 July 2018; pp. 1–5. [Google Scholar]
- Li, S.; Chen, Y.; Chen, L.; Liao, J.; Kuang, C.; Li, K.; Liang, W.; Xiong, N. Post-Quantum Security: Opportunities and Challenges. Sensors 2023, 23, 8744. [Google Scholar] [CrossRef]
- Wang, J.; Guo, G.; Shan, Z. SoK: Benchmarking the Performance of a Quantum Computer. Entropy 2022, 24, 1467. [Google Scholar] [CrossRef] [PubMed]
- Evered, S.J.; Bluvstein, D.; Kalinowski, M.; Ebadi, S.; Manovitz, T.; Zhou, H.; Li, S.H.; Geim, A.A.; Wang, T.T.; Maskara, N.; et al. High-fidelity parallel entangling gates on a neutral-atom quantum computer. Nature 2023, 622, 268–272. [Google Scholar] [CrossRef] [PubMed]
- Mesman, K.; Al-Ars; Möller, M. QPack: Quantum Approximate Optimization Algorithms as universal benchmark for quantum computers. arXiv 2022, arXiv:2103.17193. [Google Scholar]
- Dong, Y.; Lin, L. Random circuit block-encoded matrix and a proposal of quantum LINPACK benchmark. Phys. Rev. A 2020, 103, 062412. [Google Scholar] [CrossRef]
- Giani, A.; Goff-Eldredge, Z. Eos. 2022. Available online: https://eos.org/features/how-quantum-computing-can-tackle-climate-and-energy-challenges (accessed on 11 March 2024).
- Krinner, S.; Storz, S.; Kurpiers, P.; Magnard, P.; Heinsoo, J.; Keller, R.; Lütolf, J.; Eichler, C.; Wallraff, A. Engineering cryogenic setups for 100-qubit scale superconducting circuit systems. EPJ Quantum Technol. 2019, 6, 2. [Google Scholar] [CrossRef]
- Golestan, S.; Habibi, M.; Mousavi, S.M.; Guerrero, J.; Vasquez, J. Quantum computation in power systems: An overview of recent advances. Energy Rep. 2023, 9, 584–596. [Google Scholar] [CrossRef]
- Broholm, C.; Fisher, I.; Moore, J.; Murnane, M.; Moreo, A.; Tranquada, J.; Basov, D.; Freericks, J.; Aronson, M.; MacDonald, A.; et al. Basic Research Needs Workshop on Quantum Materials for Energy Relevant Technology. 2016. Available online: https://www.osti.gov/servlets/purl/1616509 (accessed on 11 March 2024).
- Hatami, H. Quantum Computing Just Might Save the Planet. 2022. Available online: https://www.mckinsey.com/capabilities/mckinsey-digital/our-insights/quantum-computing-just-might-save-the-planet (accessed on 12 March 2024).
- Abalansa, S.; El Mahrad, B.; Icely, J.; Newton, A. Electronic Waste, an Environmental Problem Exported to Developing Countries: The GOOD, the BAD and the UGLY. Sustainability 2021, 13, 5302. [Google Scholar] [CrossRef]
- Dawton, E. The Environmental Impact of Quantum Computing. 2023. Available online: https://medium.com/@eldawton/the-environmental-impact-of-quantum-computing-3fa1b6ed22cf (accessed on 12 March 2024).
- Celsi, M.; Celsi, L. Quantum Computing as a Game Changer on the Path towards a Net-Zero Economy: A Review of the Main Challenges in the Energy Domain. Energies 2024, 17, 1039. [Google Scholar] [CrossRef]
- Butterfield, K.; Sarkar, A.; Quantum Computing Governance Principles. World Economic Forum. 2022. Available online: https://www.weforum.org/publications/quantum-computing-governance-principles/ (accessed on 13 March 2024).
- Ganga, P. Quantum Technology Challenge: What Role for the Government? 2024. Available online: https://www.businessofgovernment.org/blog/quantum-technology-challenge-what-role-government (accessed on 13 March 2024).
- Nofer, M.; Bauer, K.; Hinz, O.; van der Aalst, W.; Weinhardt, C. Quantum Computing. Bus. Inf. Syst. Eng. 2023, 65, 361–367. [Google Scholar] [CrossRef]
- Anderson, C.; Awschalom, D. Embracing imperfection for quantum technologies. Phys. Today 2023, 76, 26–33. [Google Scholar] [CrossRef]
- Technology.org, Quantum Computing. 2024. Available online: https://www.technology.org/2024/02/01/quantum-computing-unraveling-the-future-of-information-processing-and-technological-advancement/ (accessed on 13 March 2024).
- Boger, Y. Quantum Computing Has Entered the Logical Qubit Era. 2024. Available online: https://builtin.com/articles/quantum-computing-logical-qubit-era (accessed on 13 March 2024).
- Keesling, A. The Future Of Computing Is Hybrid. 2023. Available online: https://www.forbes.com/sites/forbestechcouncil/2023/11/10/the-future-of-computing-is-hybrid-why-quantum-computers-will-work-alongside-classical-systems/?sh=12267d058c28 (accessed on 1 March 2024).
- Tripathi, A. Observer Research Foundation. 2023. Available online: https://www.orfonline.org/expert-speak/global-initiatives-in-quantum-computing (accessed on 1 March 2024).
- Meige, A.; Könnecke, L.; Ezratty, O.; Babinet, S.; Bourdoncle, F. Unleashing the Business Potential of Quantum Computing. 2022. Available online: https://www.adlittle.com/en/insights/report/unleashing-business-potential-quantum-computing (accessed on 4 March 2024).
- Cheng, B.; Deng, X.-H.; Gu, X.; He, Y.; Hu, G.; Huang, P.; Li, J.; Lin, B.-C.; Lu, D.; Lu, Y.; et al. Noisy intermediate-scale quantum computers. Front. Phys. 2023, 18, 21308. [Google Scholar]
- Goh, K.E.J.; A Krivitsky, L.; Polla, D.L. Quantum Technologies for Engineering: The materials challenge. Mater. Quantum Technol. 2022, 2, 013002. [Google Scholar] [CrossRef]
- Kietzmann, J.; Demetis, D.; Eriksson, T.; Dabirian, A. Hello Quantum! How Quantum Computing Will Change the World. In IT Professional; IEEE: Piscataway, NJ, USA, 2021; Volume 23, pp. 106–111. [Google Scholar]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memon, Q.A.; Al Ahmad, M.; Pecht, M. Quantum Computing: Navigating the Future of Computation, Challenges, and Technological Breakthroughs. Quantum Rep. 2024, 6, 627-663. https://doi.org/10.3390/quantum6040039
Memon QA, Al Ahmad M, Pecht M. Quantum Computing: Navigating the Future of Computation, Challenges, and Technological Breakthroughs. Quantum Reports. 2024; 6(4):627-663. https://doi.org/10.3390/quantum6040039
Chicago/Turabian StyleMemon, Qurban A., Mahmoud Al Ahmad, and Michael Pecht. 2024. "Quantum Computing: Navigating the Future of Computation, Challenges, and Technological Breakthroughs" Quantum Reports 6, no. 4: 627-663. https://doi.org/10.3390/quantum6040039
APA StyleMemon, Q. A., Al Ahmad, M., & Pecht, M. (2024). Quantum Computing: Navigating the Future of Computation, Challenges, and Technological Breakthroughs. Quantum Reports, 6(4), 627-663. https://doi.org/10.3390/quantum6040039






