Diffusion in a Comb-Structured Media: Non-Local Terms and Stochastic Resetting
Abstract
:1. Introduction
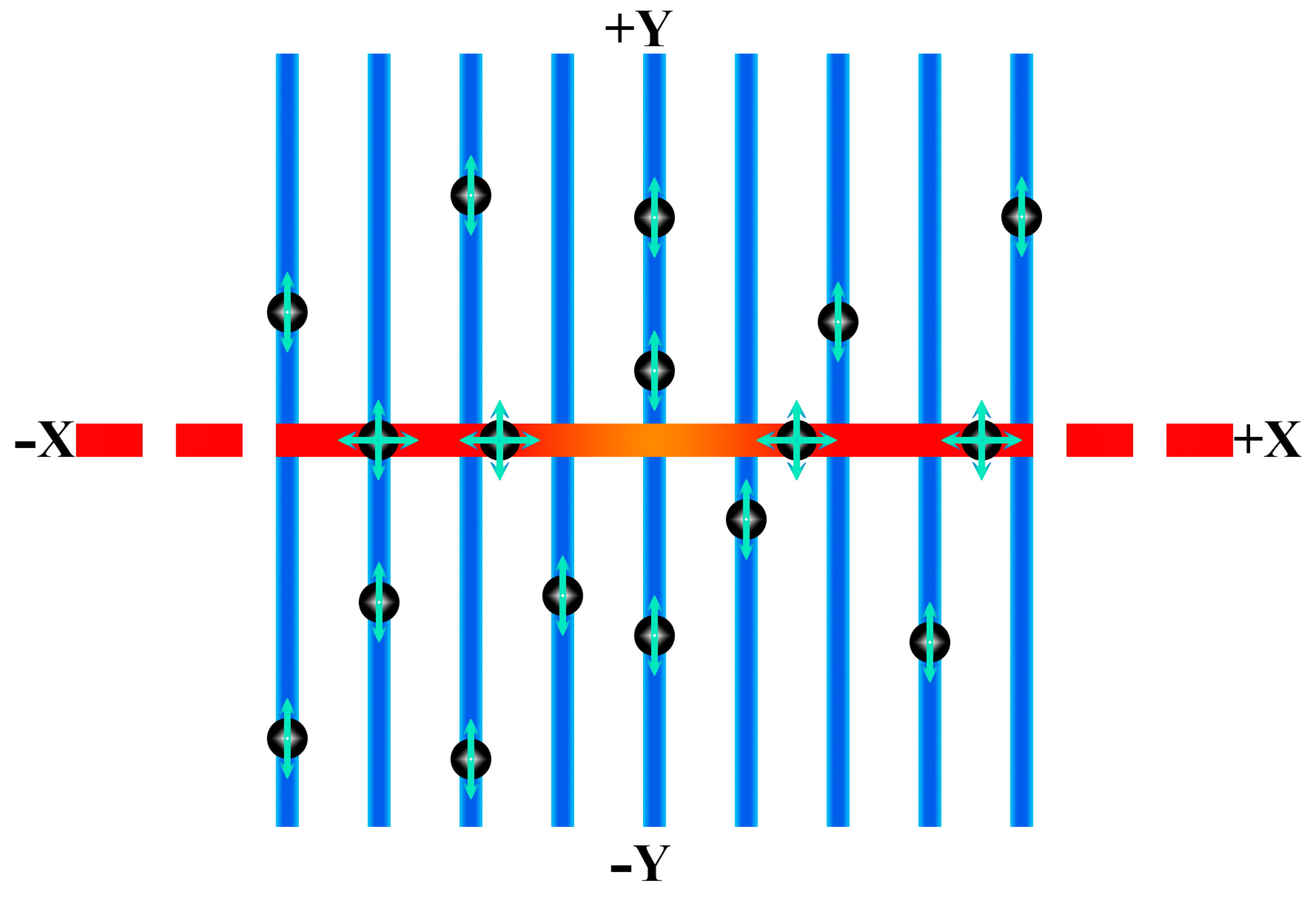
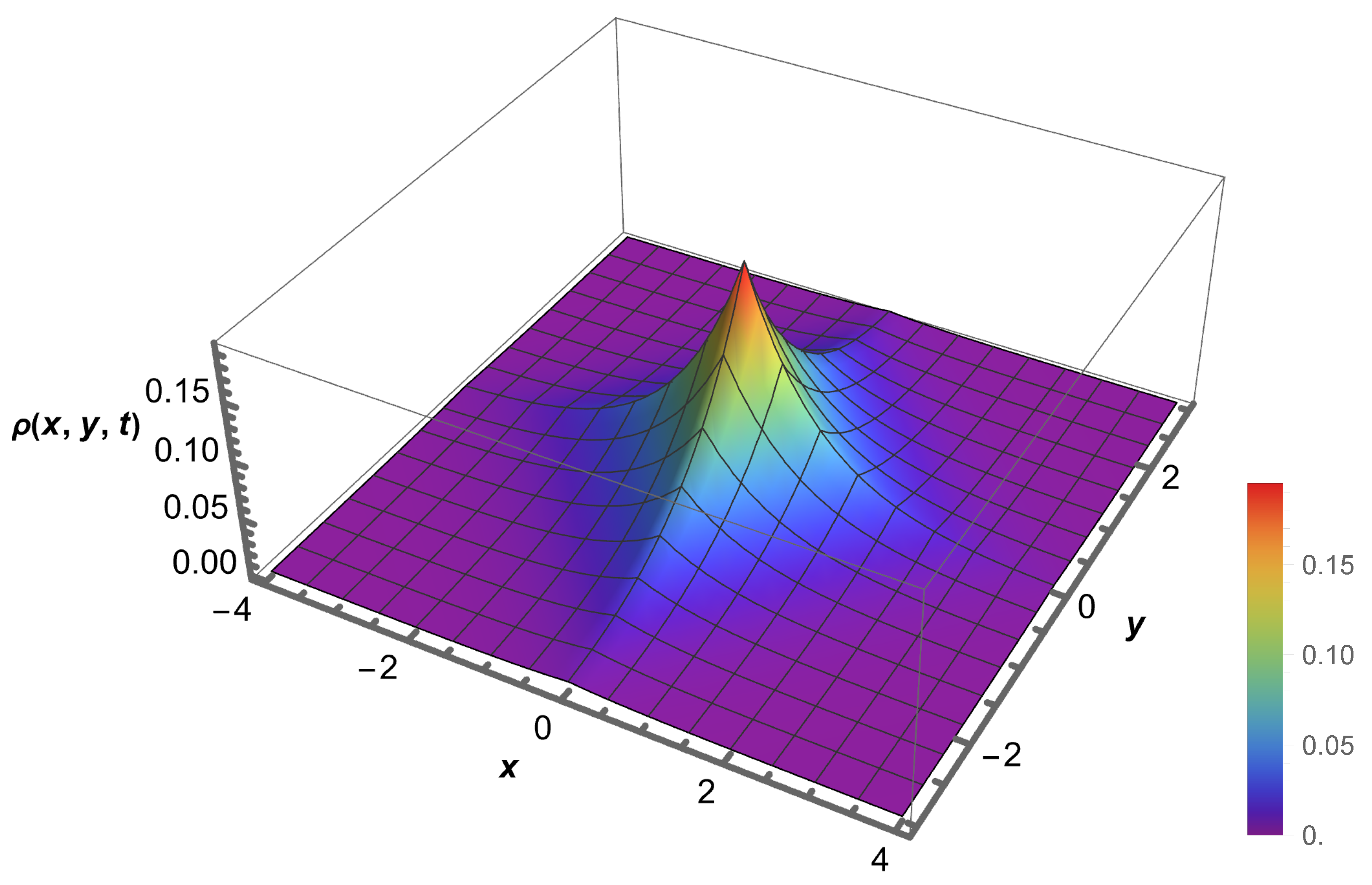
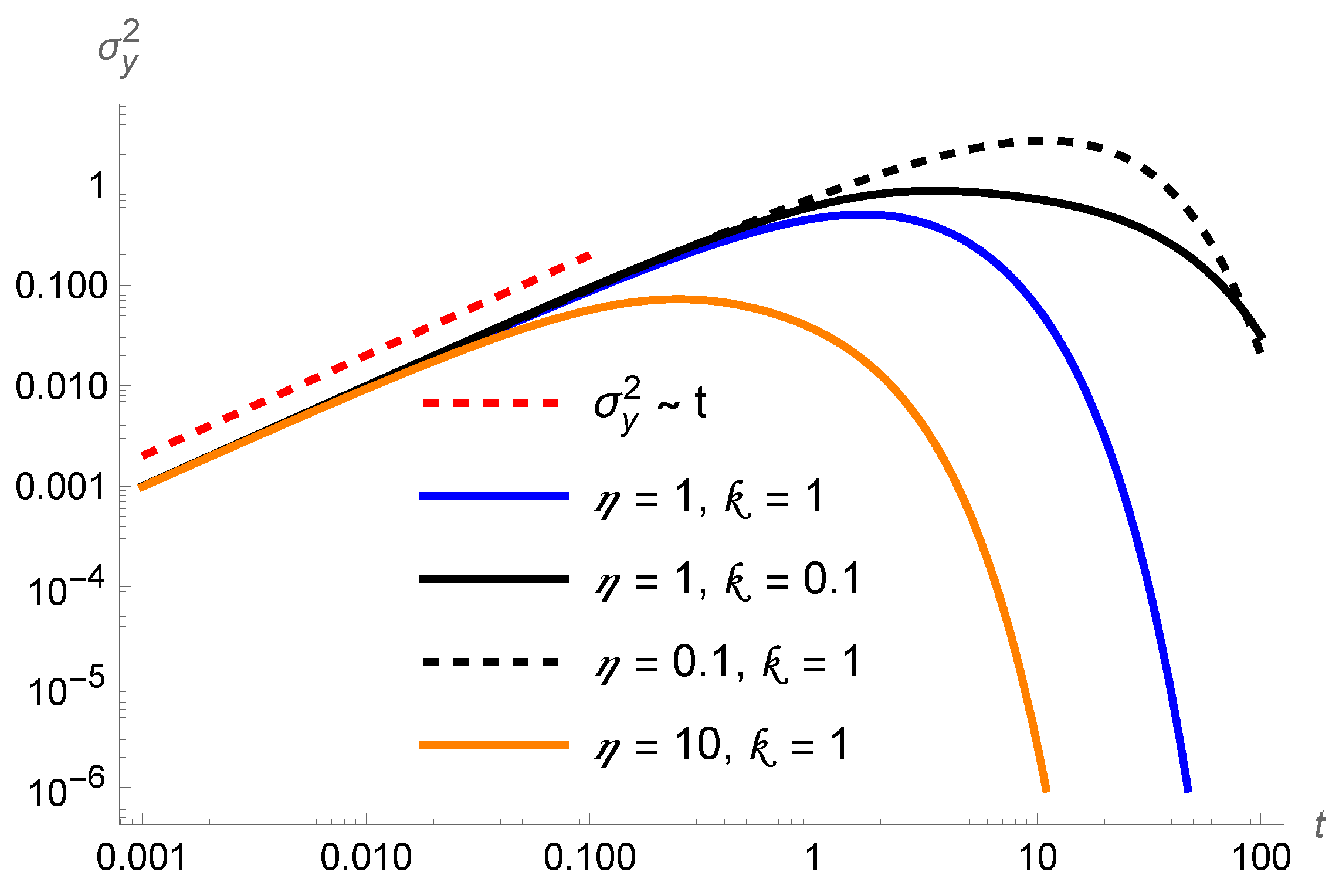
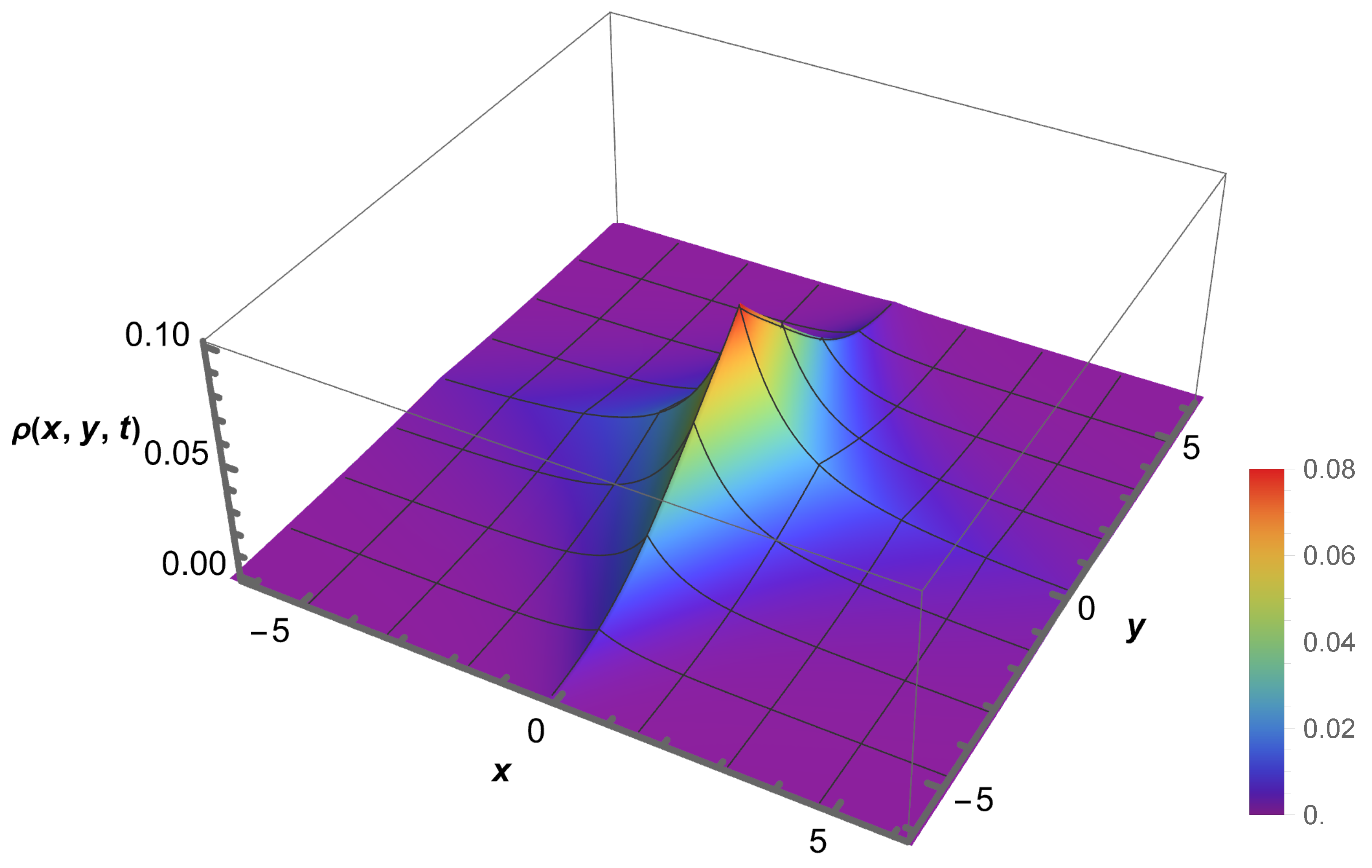
2. The Problem: Formal Investigation
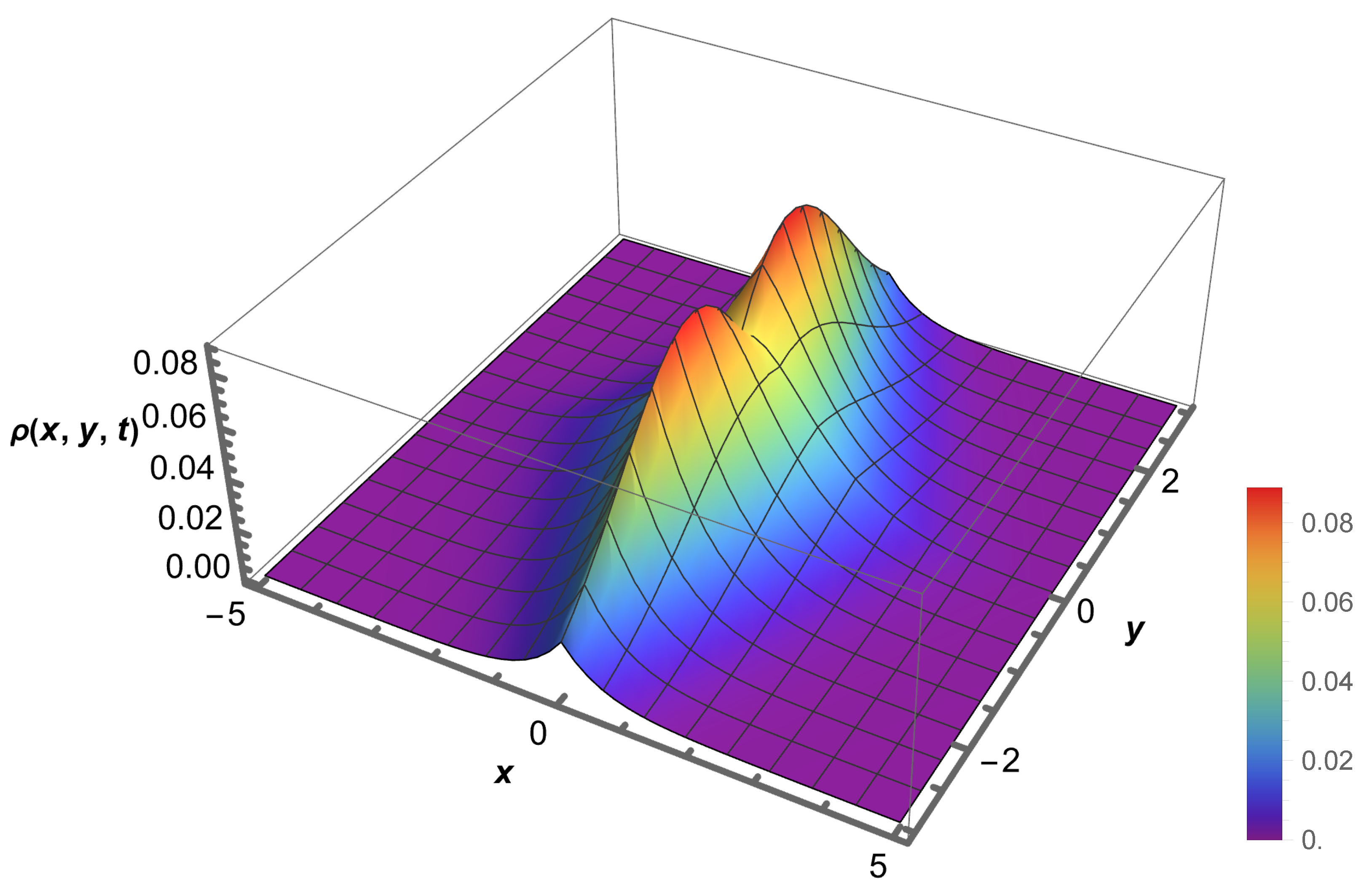
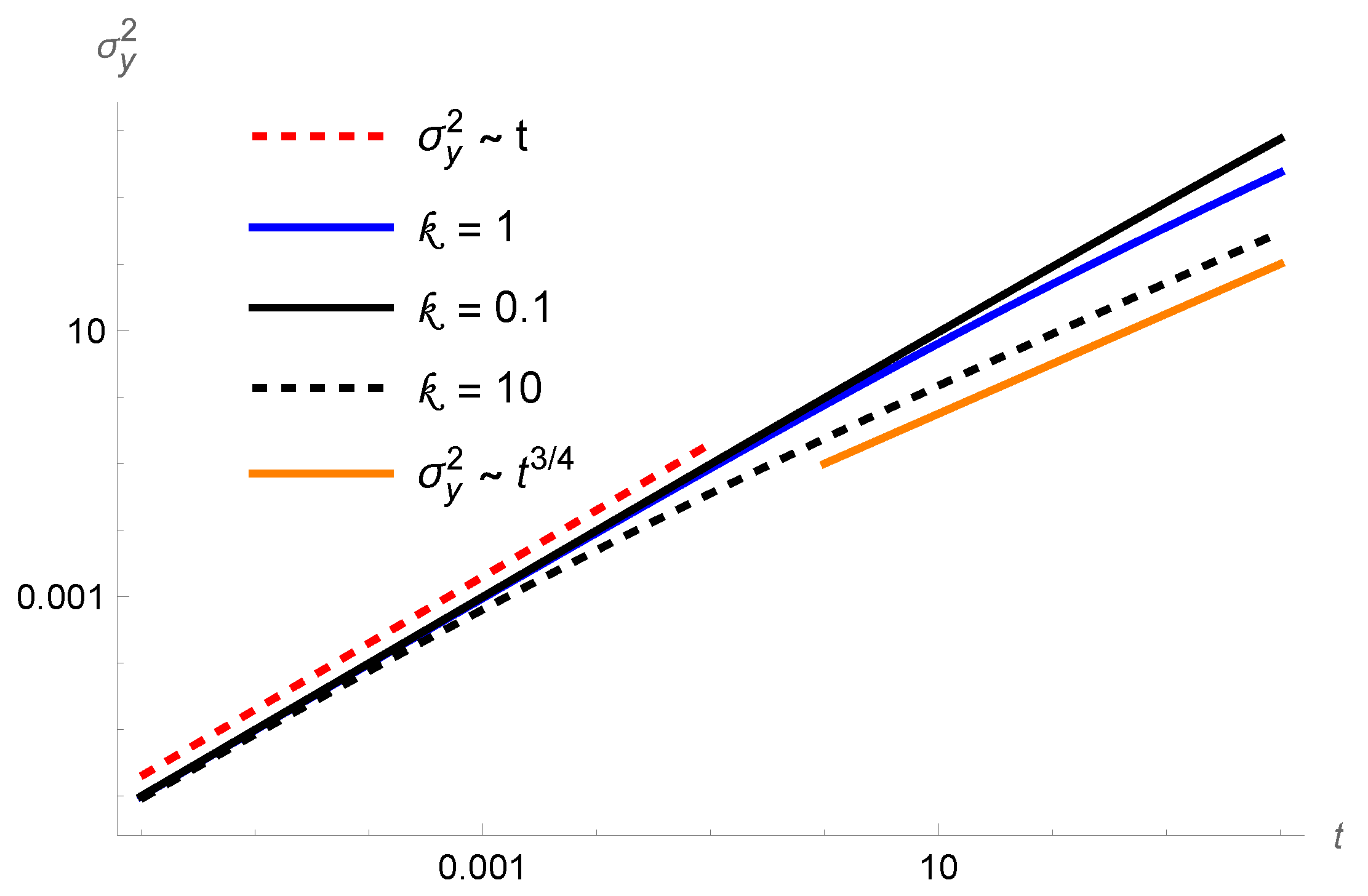
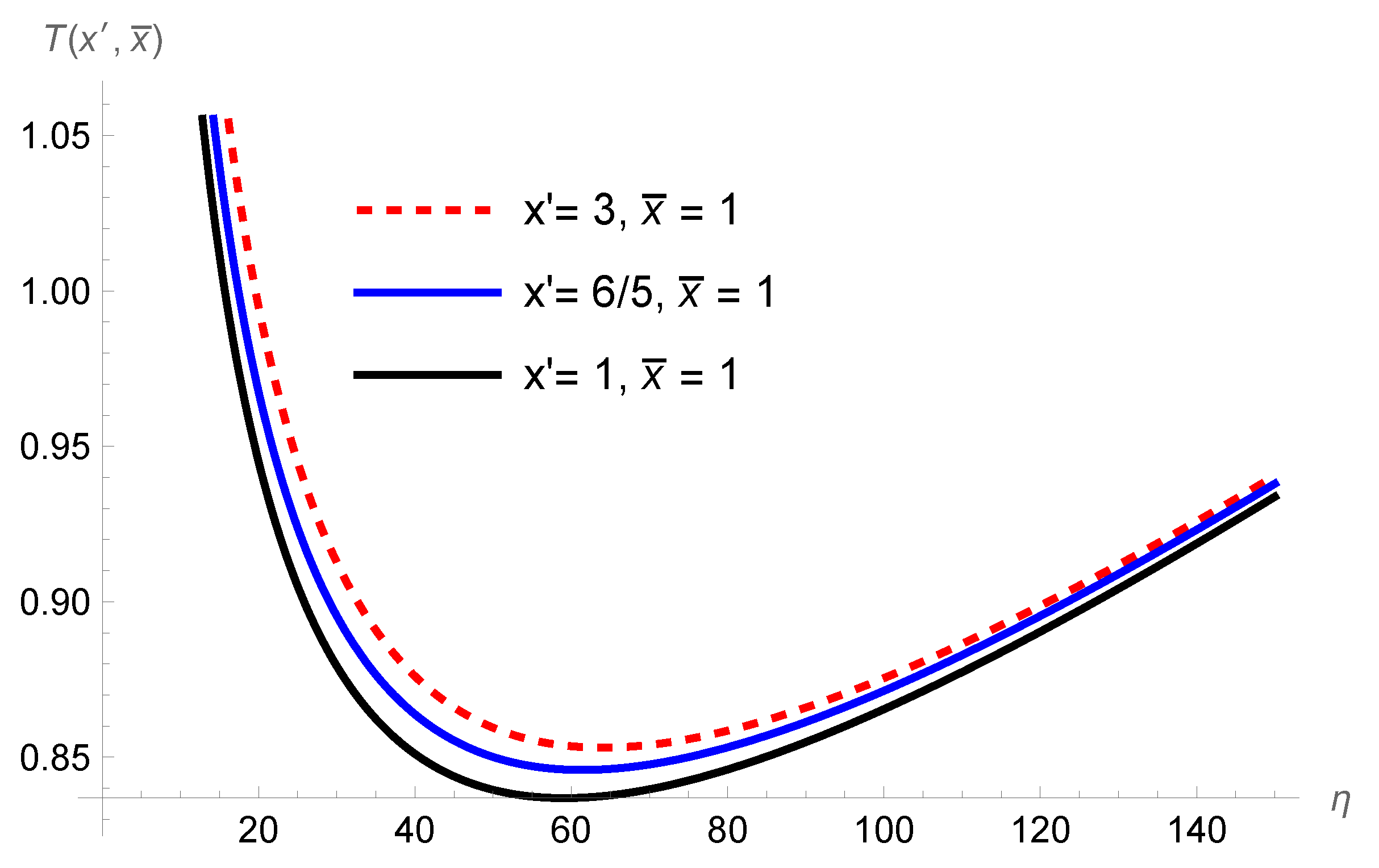
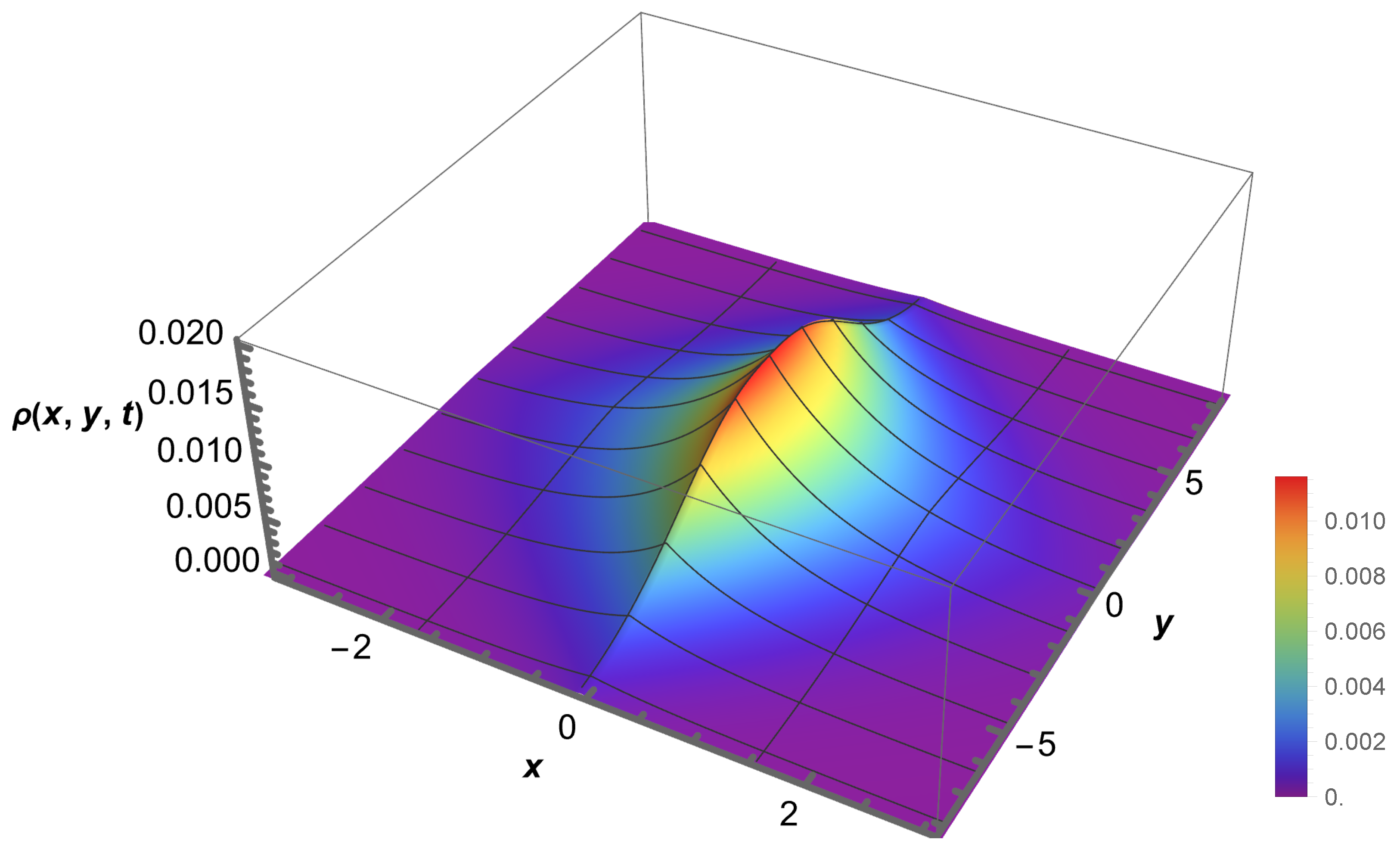
3. The Problem: Numerical Investigation
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Numerical Discretizations Procedure
References
- Rajyaguru, A.; Metzler, R.; Dror, I.; Grolimund, D.; Berkowitz, B. Diffusion in Porous Rock Is Anomalous. Environ. Sci. Technol. 2024, 58, 8946–8954. [Google Scholar] [CrossRef] [PubMed]
- Kumar, G.; Ardekani, A.M. Concentration-Dependent Diffusion of Monoclonal Antibodies: Underlying Mechanisms of Anomalous Diffusion. Mol. Pharm. 2024, 21, 2212–2222. [Google Scholar] [CrossRef] [PubMed]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Leben, R.; Rausch, S.; Elomaa, L.; Hauser, A.E.; Weinhart, M.; Fischer, S.C.; Stark, H.; Hartmann, S.; Niesner, R. Anomalous diffusion analysis reveals cooperative locomotion of adult parasitic nematodes in sex-mixed groups. bioRxiv 2024. [Google Scholar] [CrossRef]
- Lee, Y.; Cho, J.; Kim, J.; Lee, W.B.; Jho, Y. Anomalous diffusion of lithium-anion clusters in ionic liquids. Eur. Phys. J. E 2023, 46, 105. [Google Scholar] [CrossRef]
- Abelenda-Núñez, I.; Ortega, F.; Rubio, R.G.; Guzmán, E. Anomalous Colloidal Motion under Strong Confinement. Small 2023, 19, 2302115. [Google Scholar] [CrossRef]
- Strzelewicz, A.; Krasowska, M.; Cieśla, M. Lévy flights diffusion with drift in heterogeneous membranes. Membranes 2023, 13, 417. [Google Scholar] [CrossRef]
- Umarov, S.; Hahn, M.; Kobayashi, K. Beyond the Triangle: Brownian Motion, Itô Calculus, and Fokker-Planck Equation-Fractional Generalizations; World Scientific: Singapore, 2018. [Google Scholar]
- Shen, G.; Zhang, T.; Song, J.; Wu, J.L. On a Class of Distribution Dependent Stochastic Differential Equations Driven by Time-Changed Brownian Motions. Appl. Math. Optim. 2023, 88, 33. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. An Introduction to Anomalous Diffusion and Relaxation; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Liang, Y.; Wang, S.; Chen, W.; Zhou, Z.; Magin, R.L. A survey of models of ultraslow diffusion in heterogeneous materials. Appl. Mech. Rev. 2019, 71, 040802. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Scheffler, H.P. Stochastic model for ultraslow diffusion. Stoch. Process. Their Appl. 2006, 116, 1215–1235. [Google Scholar] [CrossRef]
- Sandev, T.; Iomin, A.; Kantz, H.; Metzler, R.; Chechkin, A. Comb model with slow and ultraslow diffusion. Math. Model. Nat. Phenom. 2016, 11, 18–33. [Google Scholar] [CrossRef]
- Siegle, P.; Goychuk, I.; Hänggi, P. Origin of Hyperdiffusion in Generalized Brownian Motion. Phys. Rev. Lett. 2010, 105, 100602. [Google Scholar] [CrossRef] [PubMed]
- Albers, J.; Deutch, J.M.; Oppenheim, I. Generalized Langevin Equations. J. Chem. Phys. 1971, 54, 3541–3546. [Google Scholar] [CrossRef]
- Lee, M.H. Derivation of the generalized Langevin equation by a method of recurrence relations. J. Math. Phys. 1983, 24, 2512–2514. [Google Scholar] [CrossRef]
- Kenkre, V.M.; Montroll, E.W.; Shlesinger, M.F. Generalized master equations for continuous-time random walks. J. Stat. Phys. 1973, 9, 45–50. [Google Scholar] [CrossRef]
- Swenson, R.J. Derivation of generalized master equations. J. Math. Phys. 1962, 3, 1017–1022. [Google Scholar] [CrossRef]
- Eliazar, I. Power Brownian motion. J. Phys. A Math. Theor. 2023, 57, 03LT01. [Google Scholar] [CrossRef]
- Eliazar, I. Power Levy motion. I. Diffusion. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35. [Google Scholar] [CrossRef]
- Eliazar, I. Power Levy motion. II. Evolution. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35. [Google Scholar] [CrossRef]
- Hughes, B.D. Random Walks and Random Environments; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Shlesinger, M.F. Asymptotic solutions of continuous-time random walks. J. Stat. Phys. 1974, 10, 421–434. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Somer, A.; Zola, R.S.; da Silva, L.R.; Lenzi, M.K. A Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids 2023, 8, 34. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, W.; Zhou, H.; Metzler, R.; Chechkin, A. Time-fractional Caputo derivative versus other integrodifferential operators in generalized Fokker-Planck and generalized Langevin equations. Phys. Rev. E 2023, 108, 024125. [Google Scholar] [CrossRef] [PubMed]
- Darve, E.; Solomon, J.; Kia, A. Computing generalized Langevin equations and generalized Fokker–Planck equations. Proc. Natl. Acad. Sci. USA 2009, 106, 10884–10889. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, L.; Chen, Y. Macroscopic and microscopic anomalous diffusion in comb model with fractional dual-phase-lag model. Appl. Math. Model. 2018, 62, 629–637. [Google Scholar] [CrossRef]
- Arkhincheev, V.; Baskin, E. Anomalous diffusion and drift in a comb model of percolation clusters. Sov. Phys. JETP 1991, 73, 161–300. [Google Scholar]
- Arkhincheev, V. Diffusion on random comb structure: Effective medium approximation. Phys. A Stat. Mech. Its Appl. 2002, 307, 131–141. [Google Scholar] [CrossRef]
- Kapetanoski, O.; Petreska, I. Geometrically constrained quantum dynamics: Numerical solution of the Schrödinger equation on a comb. Phys. Scr. 2025, 100, 025254. [Google Scholar] [CrossRef]
- Iomin, A. Non-Markovian quantum mechanics on comb. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 093135. [Google Scholar] [CrossRef]
- Méndez, V.; Iomin, A. Comb-like models for transport along spiny dendrites. Chaos Solitons Fractals 2013, 53, 46–51. [Google Scholar] [CrossRef]
- Iomin, A.; Méndez, V.; Horsthemke, W. Fractional Dynamics in Comb-Like Structures; World Scientific: Singapore, 2018. [Google Scholar]
- Iomin, A.; Méndez, V.; Horsthemke, W. Comb model: Non-markovian versus markovian. Fractal Fract. 2019, 3, 54. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Tateishi, A.A.; Lenzi, E.K.; Magin, R.L.; Perc, M. Interplay between particle trapping and heterogeneity in anomalous diffusion. Commun. Phys. 2023, 6, 244. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, L.; Chen, Y.; Liu, F. Anomalous diffusion in comb model with fractional dual-phase-lag constitutive relation. Comput. Math. Appl. 2018, 76, 245–256. [Google Scholar] [CrossRef]
- Trajanovski, P.; Jolakoski, P.; Zelenkovski, K.; Iomin, A.; Kocarev, L.; Sandev, T. Ornstein-Uhlenbeck process and generalizations: Particle dynamics under comb constraints and stochastic resetting. Phys. Rev. E 2023, 107, 054129. [Google Scholar] [CrossRef] [PubMed]
- Domazetoski, V.; Masó-Puigdellosas, A.; Sandev, T.; Méndez, V.; Iomin, A.; Kocarev, L. Stochastic resetting on comblike structures. Phys. Rev. Res. 2020, 2, 033027. [Google Scholar] [CrossRef]
- Jolakoski, P.; Trajanovski, P.; Iomin, A.; Kocarev, L.; Sandev, T. Mean first-passage time of heterogeneous telegrapher’s process under stochastic resetting. Europhys. Lett. 2025. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, P.; Wang, E. Modeling multiple anomalous diffusion behaviors on comb-like structures. Chaos Solitons Fractals 2021, 148, 111009. [Google Scholar] [CrossRef]
- Iomin, A.; Méndez, V. Reaction-subdiffusion front propagation in a comblike model of spiny dendrites. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2013, 88, 012706. [Google Scholar] [CrossRef]
- Liang, Y.; Sandev, T.; Lenzi, E.K. Reaction and ultraslow diffusion on comb structures. Phys. Rev. E 2020, 101, 042119. [Google Scholar] [CrossRef]
- Sandev, T.; Iomin, A.; Méndez, V. Lévy processes on a generalized fractal comb. J. Phys. A Math. Theor. 2016, 49, 355001. [Google Scholar] [CrossRef]
- Arkhincheev, V. Random walks on the comb model and its generalizations. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 043102. [Google Scholar] [CrossRef]
- Iomin, A. Anomalous diffusion in umbrella comb. Chaos Solitons Fractals 2021, 142, 110488. [Google Scholar] [CrossRef]
- Sandev, T.; Iomin, A.; Kantz, H. Fractional diffusion on a fractal grid comb. Phys. Rev. E 2015, 91, 032108. [Google Scholar] [CrossRef] [PubMed]
- Evans, M.R.; Majumdar, S.N.; Schehr, G. Stochastic resetting and applications. J. Phys. A Math. Theor. 2020, 53, 193001. [Google Scholar] [CrossRef]
- Gupta, S.; Jayannavar, A.M. Stochastic resetting: A (very) brief review. Front. Phys. 2022, 10, 789097. [Google Scholar] [CrossRef]
- Nagar, A.; Gupta, S. Stochastic resetting in interacting particle systems: A review. J. Phys. A Math. Theor. 2023, 56, 283001. [Google Scholar] [CrossRef]
- Santamaria, E.; Wils, S.; De Schutter, E.; Augustine, G. Anomalous diffusion in spiny dendrites: A modeling study. J. Neurosci. 2006, 26, 8181–8193. [Google Scholar]
- Santamaria-Holek, C.; García, H. Memory effects and anomalous diffusion in dendritic spine dynamics. Phys. A Stat. Mech. Its Appl. 2019, 523, 722–730. [Google Scholar]
- Dentz, M.; Scher, H.; Berkowitz, B. Transport behavior of a passive solute in continuous time random walks and multirate mass transfer models. Water Resour. Res. 2004, 40, W04212. [Google Scholar]
- Bauer, M.; Metzler, R. Generalized facilitated diffusion model for DNA-binding proteins with search and recognition states. Biophys. J. 2012, 102, 2321–2330. [Google Scholar] [CrossRef]
- Kepten, E.; Bronshtein, I.; Garini, Y. Ergodicity convergence test suggests telomere motion obeys fractional dynamics. Phys. Rev. E 2012, 85, 031918. [Google Scholar] [CrossRef]
- Baleanu, D.; Fernandez, A. On fractional operators and their classifications. Mathematics 2019, 7, 830. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763. [Google Scholar] [CrossRef]
- Tomovski, Ž.; Hilfer, R.; Srivastava, H.M. Fractional and operational calculus with generalized fractional derivative operators and Mittag–Leffler type functions. Integral Transform. Spec. Funct. 2010, 21, 797–814. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N. Diffusion with Stochastic Resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef]




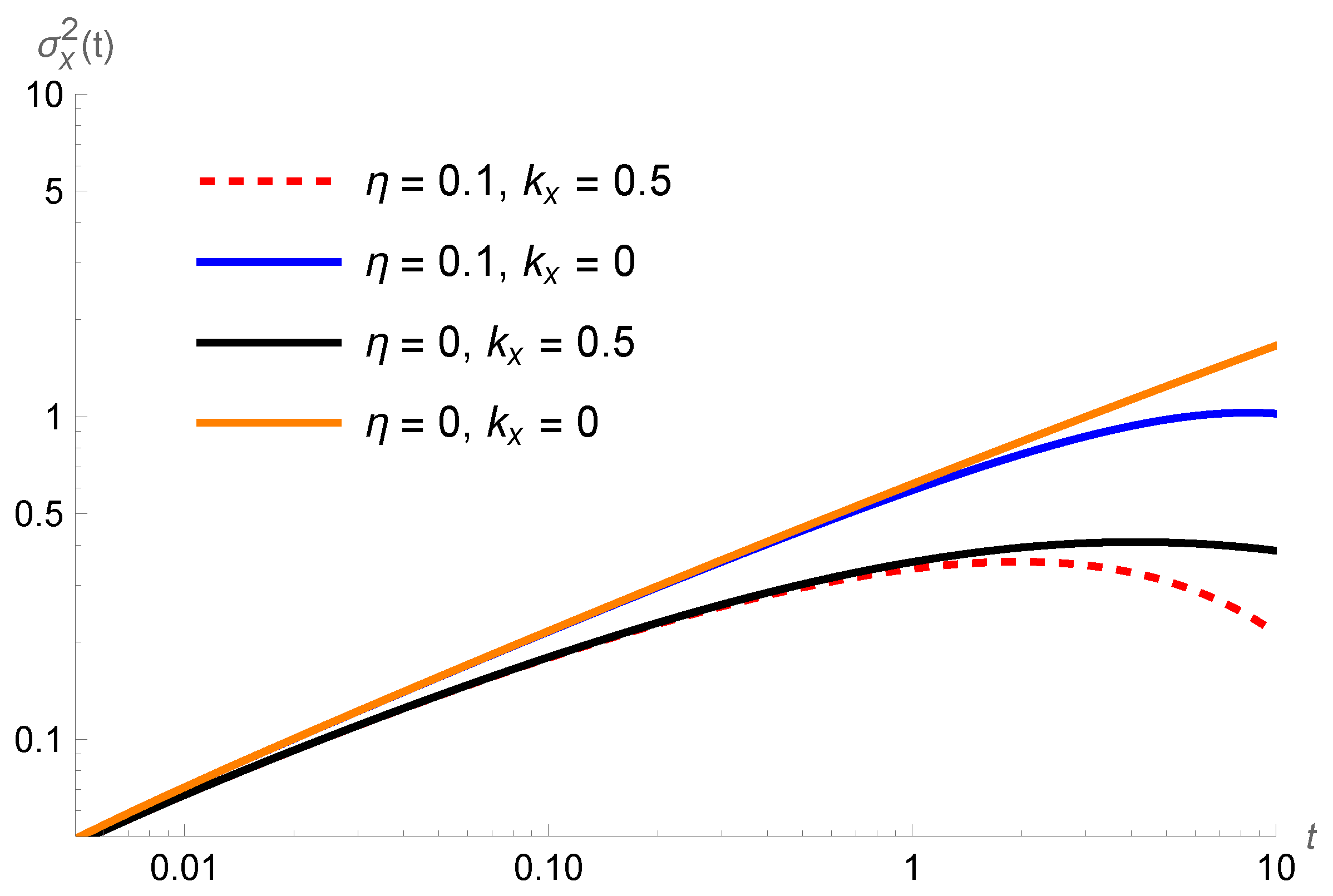
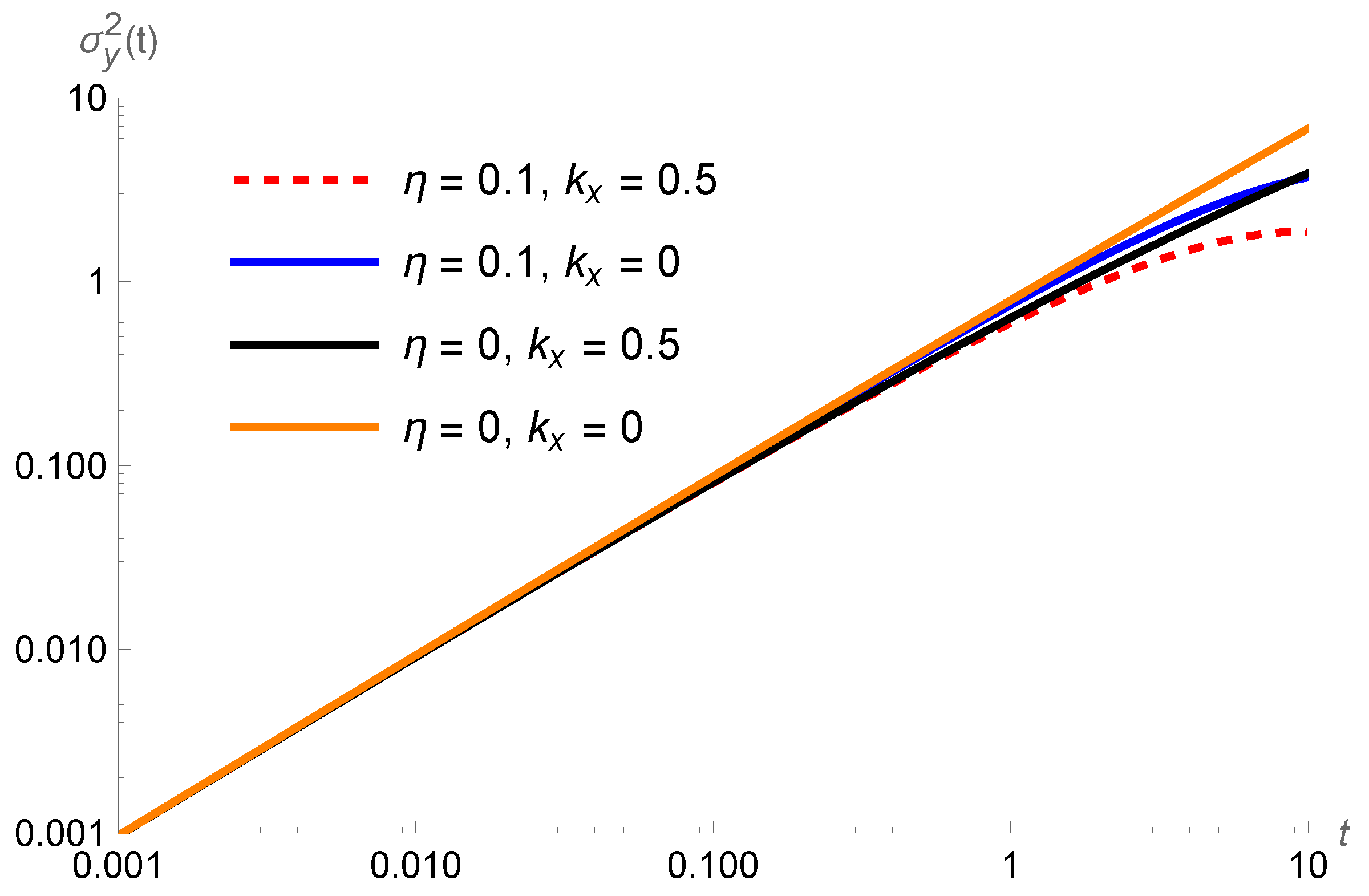


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenzi, E.K.; Gryczak, D.W.; da Silva, L.R.; Ribeiro, H.V.; Zola, R.S. Diffusion in a Comb-Structured Media: Non-Local Terms and Stochastic Resetting. Quantum Rep. 2025, 7, 20. https://doi.org/10.3390/quantum7020020
Lenzi EK, Gryczak DW, da Silva LR, Ribeiro HV, Zola RS. Diffusion in a Comb-Structured Media: Non-Local Terms and Stochastic Resetting. Quantum Reports. 2025; 7(2):20. https://doi.org/10.3390/quantum7020020
Chicago/Turabian StyleLenzi, Ervin Kaminski, Derik William Gryczak, Luciano Rodrigues da Silva, Haroldo Valentin Ribeiro, and Rafael Soares Zola. 2025. "Diffusion in a Comb-Structured Media: Non-Local Terms and Stochastic Resetting" Quantum Reports 7, no. 2: 20. https://doi.org/10.3390/quantum7020020
APA StyleLenzi, E. K., Gryczak, D. W., da Silva, L. R., Ribeiro, H. V., & Zola, R. S. (2025). Diffusion in a Comb-Structured Media: Non-Local Terms and Stochastic Resetting. Quantum Reports, 7(2), 20. https://doi.org/10.3390/quantum7020020










