Probability Representation of Quantum States: Tomographic Representation in Standard Potentials and Peres–Horodecki Criterion for Probabilities
Abstract
:1. Introduction
Brief Review of Lebedev Institute–Mexico Collaboration
2. Tomographic Representation of Common Quantum-Mechanical Wave Functions
2.1. Free Motion
Free Evolution of a Wave Packet
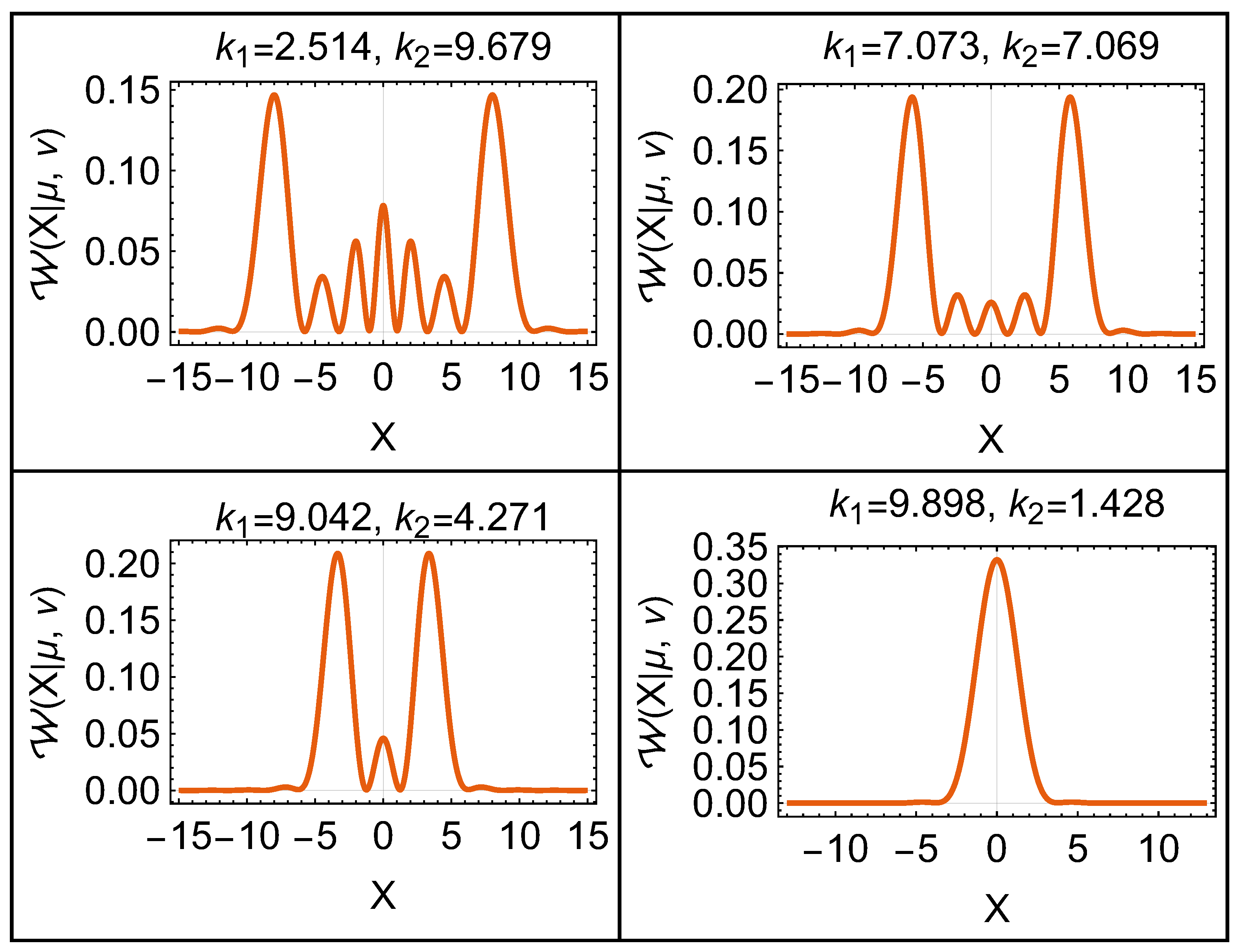
2.2. Finite Potential Well
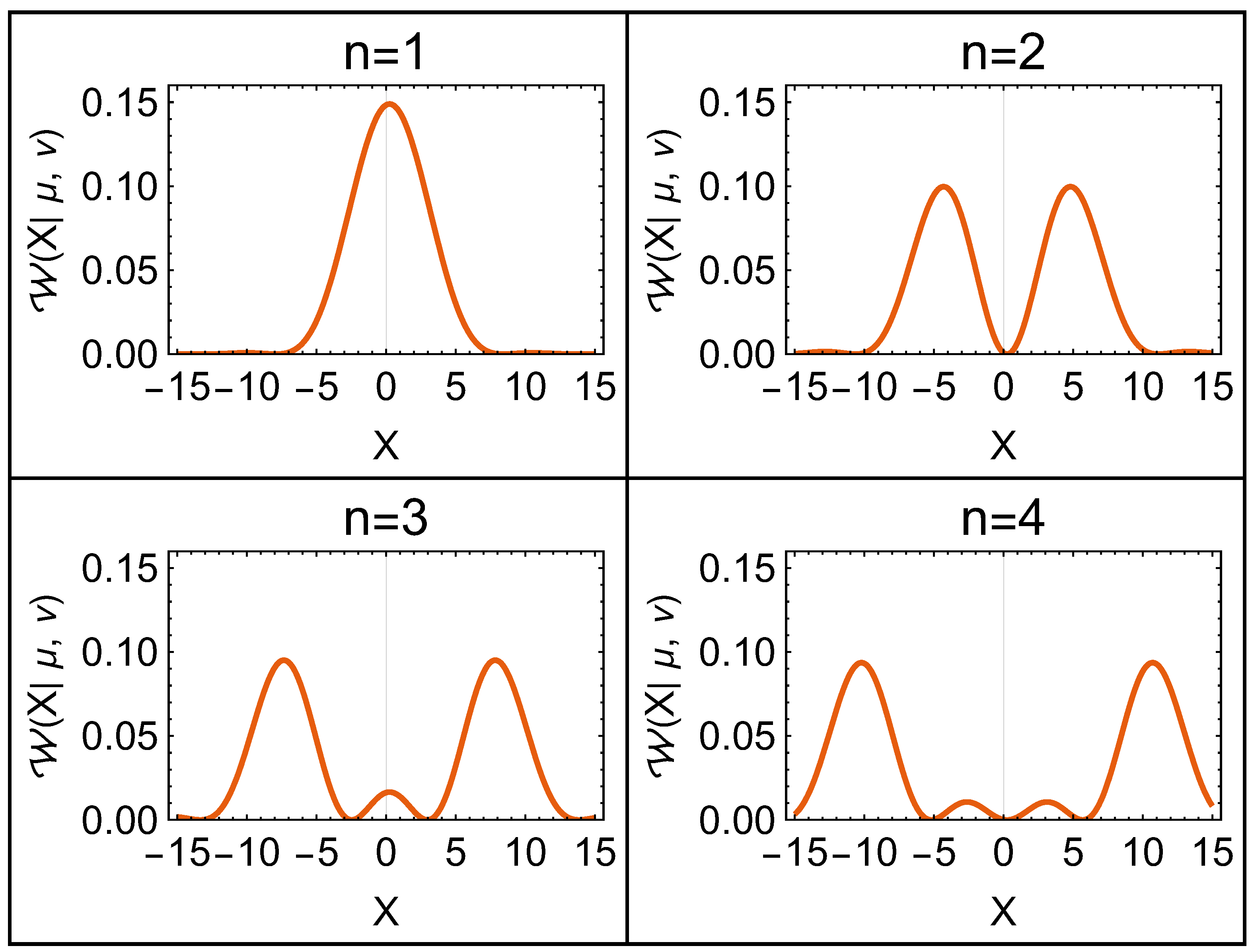
2.3. Infinite Potential Well
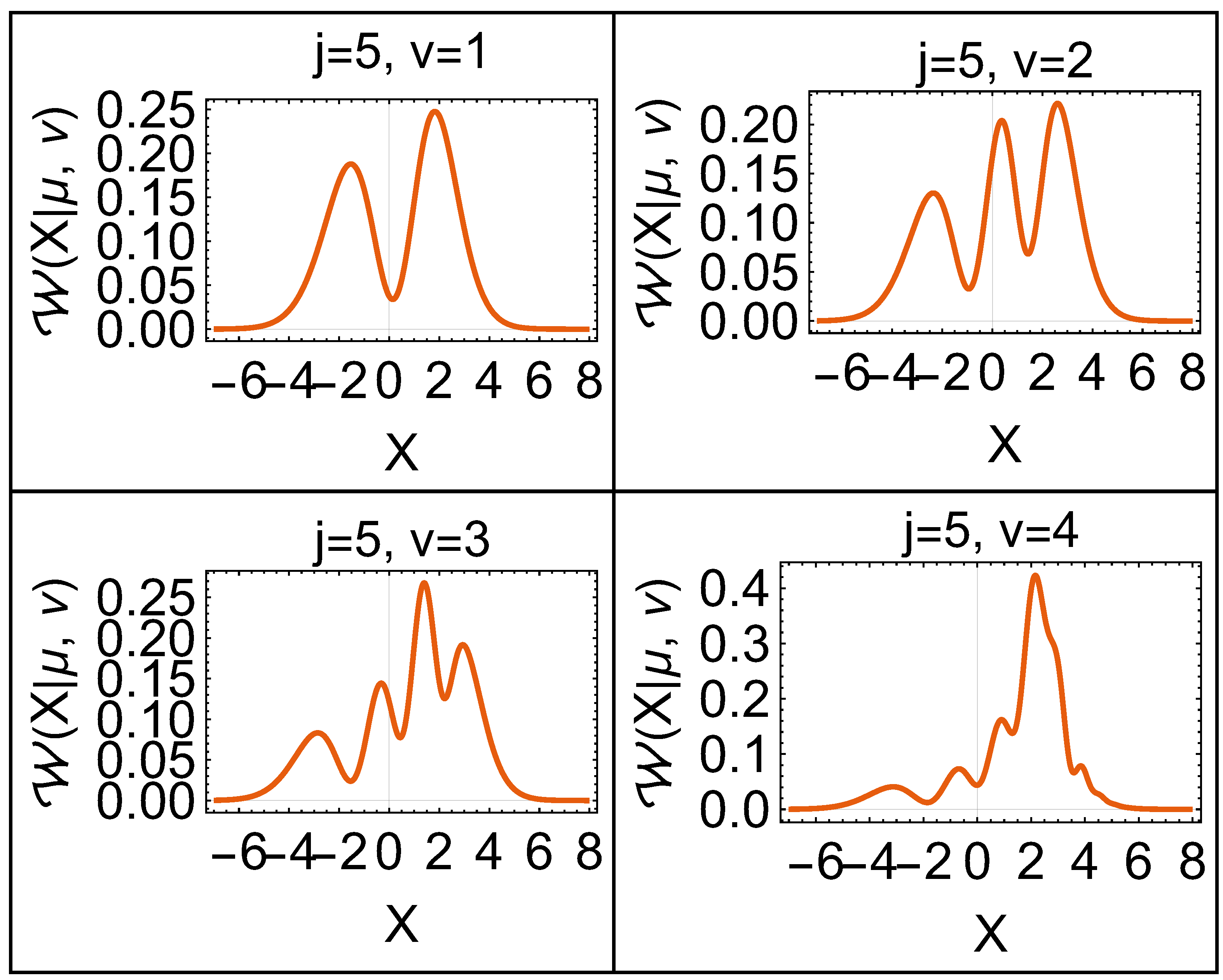
2.4. Morse Potential
3. Separability Criteria for Asymmetric Real States
Example
4. Summaryand Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Feder, T. 2025 is the International Year of Quantum Science and Technology. Phys. Today 2025, 78, 7. [Google Scholar] [CrossRef]
- Castaños, O.; López-Peña, R.; Man’ko, V.I. Schrödinger cat states of a non-stationary generalized oscillator. J. Phys. A Math. Gen. 1996, 29, 2091. [Google Scholar] [CrossRef]
- Castaños, O.; López-Peña, R.; Man’ko, V.I. Crystallized Schrödinger cat states. Russ. Laser Res. 1995, 16, 477. [Google Scholar] [CrossRef]
- Castaños, O.; López-Peña, R. Quantum-Like Models and Coherent Effects; Fedele, R., Shukla, P.K., Eds.; World Scientific Publishing: Singapore, 1995; pp. 3–17. [Google Scholar] [CrossRef]
- Castaños, O.; López-Peña, R.; Man’ko, V.I. Variational formulation of linear time-dependent invariants. Europhys. Lett. 1996, 33, 497. [Google Scholar] [CrossRef]
- Castaños, O.; Jáuregui, R.; López-Peña, R.; Recamier, J.; Man’ko, V.I. Schrödinger-cat states in Paul traps. Phys. Rev. A 1997, 55, 1208. [Google Scholar] [CrossRef]
- Castaños, O.; Hacyan, S.; López-Peña, R.; Man’ko, V.I. Schrödinger cat states in a Penning trap. J. Phys. A Math. Gen. 1998, 31, 1227. [Google Scholar] [CrossRef]
- Man’ko, O.V.; Man’ko, V.I. Quantum states in probability representation and tomography. J. Russ. Laser Res. 1997, 18, 407. [Google Scholar] [CrossRef]
- Castaños, O.; Hacyan, S.; López-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Kernel of star-product for spin tomograms. J. Phys. A Math. Gen. 2003, 36, 4677. [Google Scholar] [CrossRef]
- Castaños, O.; López-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Nonstationary linear spin systems in the probability representation. J. Opt. B Quantum Semiclass. Opt. 2003, 5, 227. [Google Scholar] [CrossRef]
- Castaños, O.; López-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Squeeze tomography of quantum states. J. Phys. A Math. Gen. 2004, 37, 8529. [Google Scholar] [CrossRef]
- López-Saldívar, J.A.; Figueroa, A.; Castaños, O.; López-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Discretization of the Density Matrix as a Nonlinear Positive Map and Entanglement. J. Russ. Laser Res. 2016, 37, 313. [Google Scholar] [CrossRef]
- López-Saldívar, J.A.; Figueroa, A.; Castaños, O.; López-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Evolution and Entanglement of Gaussian States in the Parametric Amplifier. J. Russ. Laser Res. 2016, 37, 23. [Google Scholar] [CrossRef]
- Figueroa, A.; López-Saldívar, J.A.; Castaños, O.; López-Peña, R. Extremal Density Matrices for Qudit States. arXiv 2016, arXiv:1609.09835. [Google Scholar]
- Castaños, O.; Figueroa, A.; López, J.; López-Peña, R. Extremal density matrices for the expectation value of a qudit hamiltonian. J. Phys. Conf. Ser. 2017, 839, 012012. [Google Scholar] [CrossRef]
- Figueroa, A.; López-Saldívar, J.; Castaños, O.; López-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Entropy–energy inequalities for qudit states. J. Phys. A Math. Theor. 2015, 48, 065301. [Google Scholar] [CrossRef]
- López-Saldívar, J.; Castaños, O.; Man’ko, M.A.; Man’ko, V.I. Entropic bounds between two thermal equilibrium states. Phys. Rev. E. 2018, 97, 022128. [Google Scholar] [CrossRef] [PubMed]
- López-Saldívar, J.A.; Castaños, O.; Man’ko, M.A.; Man’ko, V.I. New entropic inequalities for qubit and unimodal Gaussian states. Phys. A 2018, 491, 64. [Google Scholar] [CrossRef]
- López-Saldívar, J.; Castaños, O.; Nahmad-Achar, E.; López-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Geometry and entanglement of two-qubit states in the quantum probabilistic representation. Entropy 2018, 20, 630. [Google Scholar] [CrossRef]
- López-Saldívar, J.A.; Castaños, O.; Man’ko, M.A.; Man’ko, V.I. A new mechanism of open system evolution and its entropy using unitary transformations in noncomposite qudit systems. Entropy 2019, 21, 736. [Google Scholar] [CrossRef]
- López-Saldívar, J.A.; Castaños, O.; Man’ko, M.A.; Man’ko, V.I. Qubit representation of qudit states: Correlations and state reconstruction. Quantum Inf. Process. 2019, 18, 210. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem (Erste Mitteilung). Ann. Phys. 1926, 384, 361–376. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem (Zweite Mitteilung). Ann. Phys. 1926, 384, 489–527. [Google Scholar] [CrossRef]
- Landau, L. Das Dämpfungsproblem in der Wellenmechanik. Z. Phys. 1927, 45, 430–441. [Google Scholar] [CrossRef]
- Von Neumann, J. Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. 1927. Volume 1927, pp. 245–272. Available online: http://eudml.org/doc/59230 (accessed on 7 January 2025).
- Mancini, S.; Man’ko, V.I.; Tombesi, P. Symplectic tomography as classical approach to quantum systems. Phys. Lett. A 1996, 213, 1–6. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Mendes, R.V. Non-commutative time-frequency tomography. Phys. Lett. A 1999, 263, 53–61. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I.; Mendes, R.V. A probabilistic operator symbol framework for quantum information. J. Russ. Laser Res. 2006, 27, 507–532. [Google Scholar] [CrossRef]
- Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Husimi, K. Some formal properties of the density matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264–314. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, V.I. Positive distribution description for spin states. Phys. Lett. A 1997, 229, 335–339. [Google Scholar] [CrossRef]
- Landau, L.D. The damping problem in wave mechanics. In Collected Papers of L.D. Landau; Pergamon: Berlin, Germany, 1965; pp. 8–18. [Google Scholar] [CrossRef]
- Sakurai, J.J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2021; p. 118. [Google Scholar] [CrossRef]
- Zee, A. Quantum Field Theory in a Nutshell; Princeton University Press: Princeton, NJ, USA, 2010; p. 523. [Google Scholar]
- Morse, P.M. Diatomic molecules according to the wave mechanics. II. Vibrational levels. Phys. Rev. 1929, 34, 357. [Google Scholar] [CrossRef]
- Lemus, R.; Arias, J.M.; Gómez-Camacho, J. An su(1, 1) dynamical algebra for the Morse potential. J. Phys. A Math. Gen. 2004, 37, 1805. [Google Scholar] [CrossRef]
- Peres, A. Separability criterion for density matrices. Phys. Rev. Lett. 1996, 77, 1413. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Saldívar, J.A.; Man’ko, M.A.; Man’ko, V.I. Probability Representation of Quantum States: Tomographic Representation in Standard Potentials and Peres–Horodecki Criterion for Probabilities. Quantum Rep. 2025, 7, 22. https://doi.org/10.3390/quantum7020022
López-Saldívar JA, Man’ko MA, Man’ko VI. Probability Representation of Quantum States: Tomographic Representation in Standard Potentials and Peres–Horodecki Criterion for Probabilities. Quantum Reports. 2025; 7(2):22. https://doi.org/10.3390/quantum7020022
Chicago/Turabian StyleLópez-Saldívar, Julio A., Margarita A. Man’ko, and Vladimir I. Man’ko. 2025. "Probability Representation of Quantum States: Tomographic Representation in Standard Potentials and Peres–Horodecki Criterion for Probabilities" Quantum Reports 7, no. 2: 22. https://doi.org/10.3390/quantum7020022
APA StyleLópez-Saldívar, J. A., Man’ko, M. A., & Man’ko, V. I. (2025). Probability Representation of Quantum States: Tomographic Representation in Standard Potentials and Peres–Horodecki Criterion for Probabilities. Quantum Reports, 7(2), 22. https://doi.org/10.3390/quantum7020022






