Energy Efficiency Analysis of a Deformable Wave Energy Converter Using Fully Coupled Dynamic Simulations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Computational Modelling
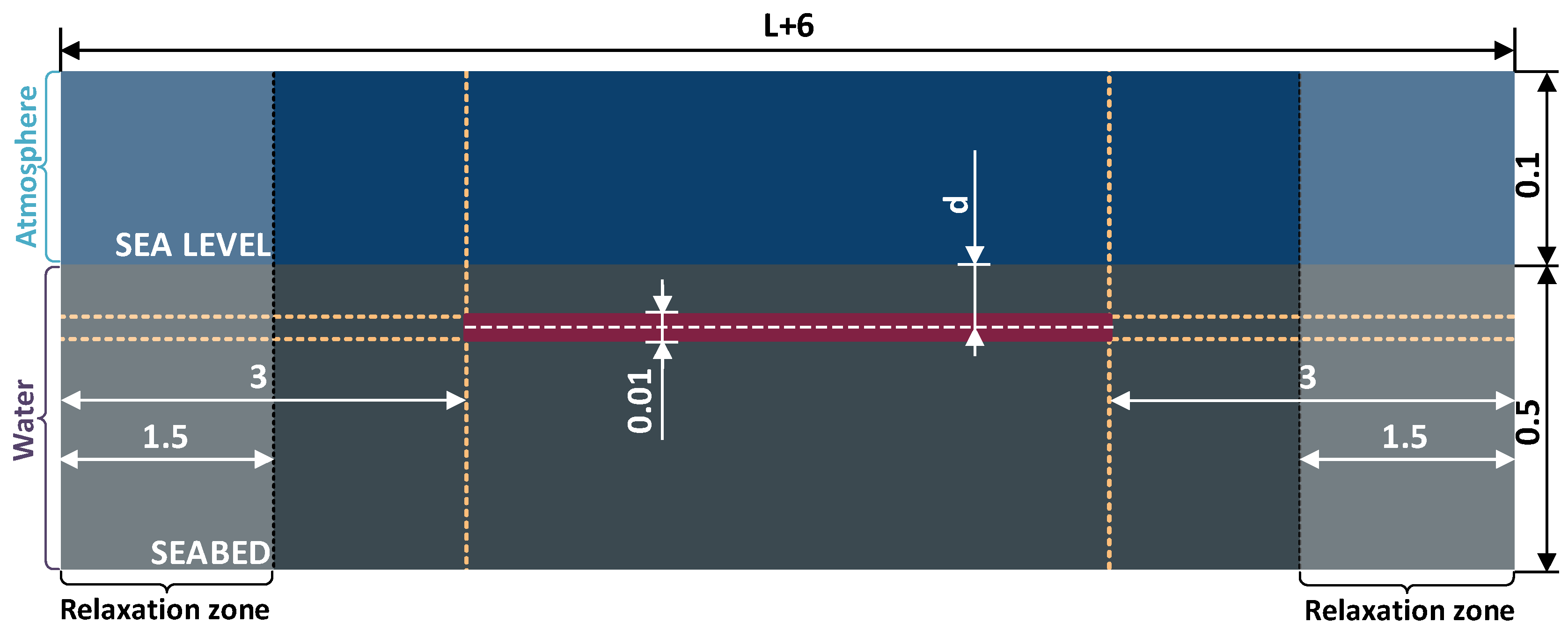
2.1.1. Computational Domain and Boundary Conditions
2.1.2. Computational Method
2.1.3. Fluid Solution
2.1.4. Structural Solution
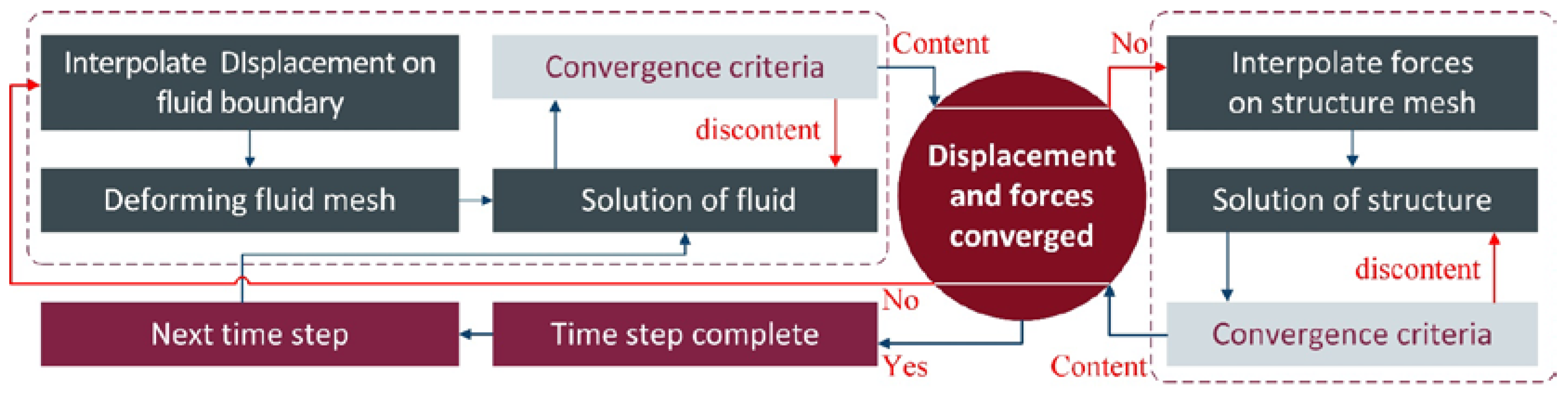
2.1.5. Fluid-Structure Interaction
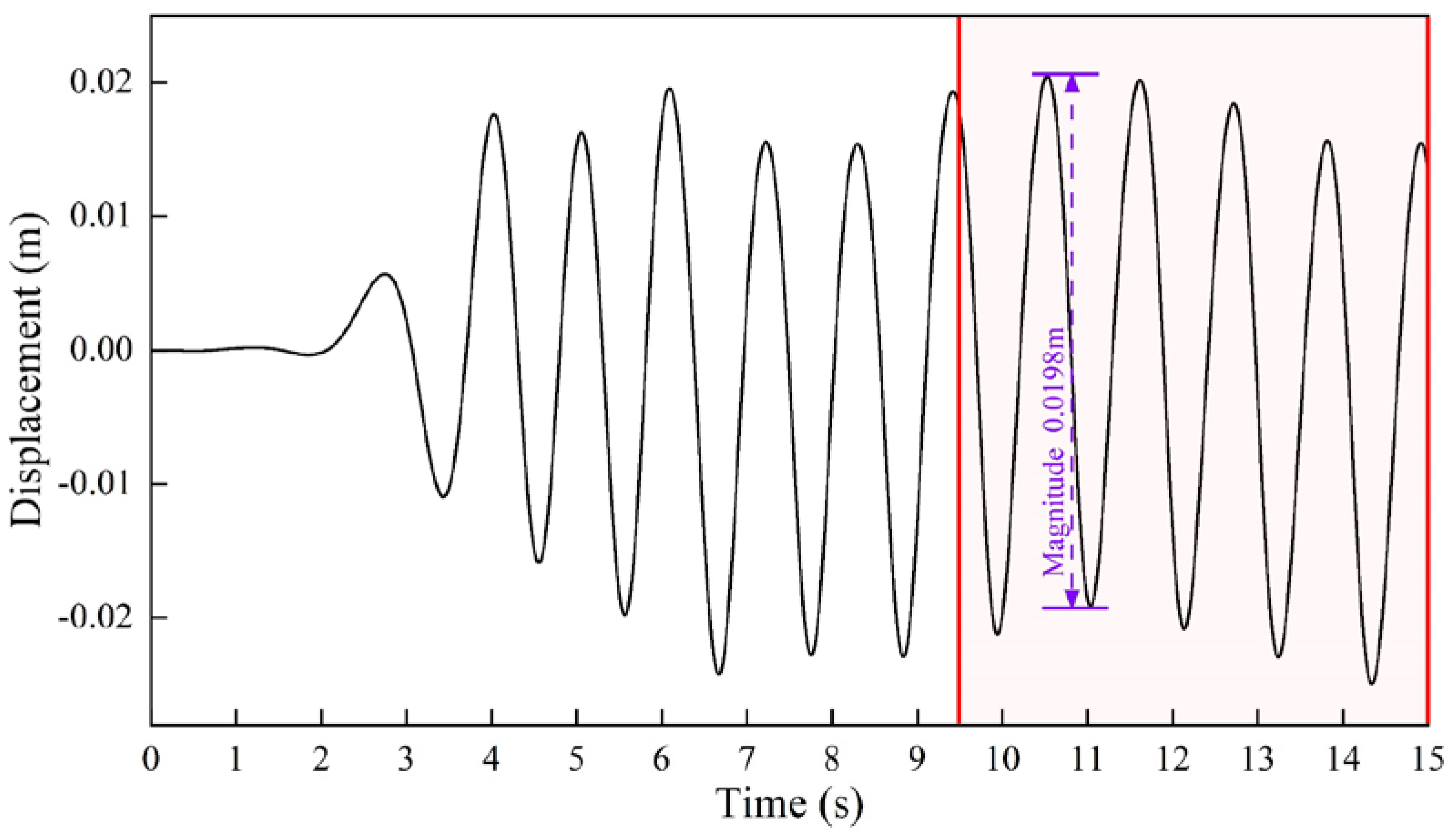
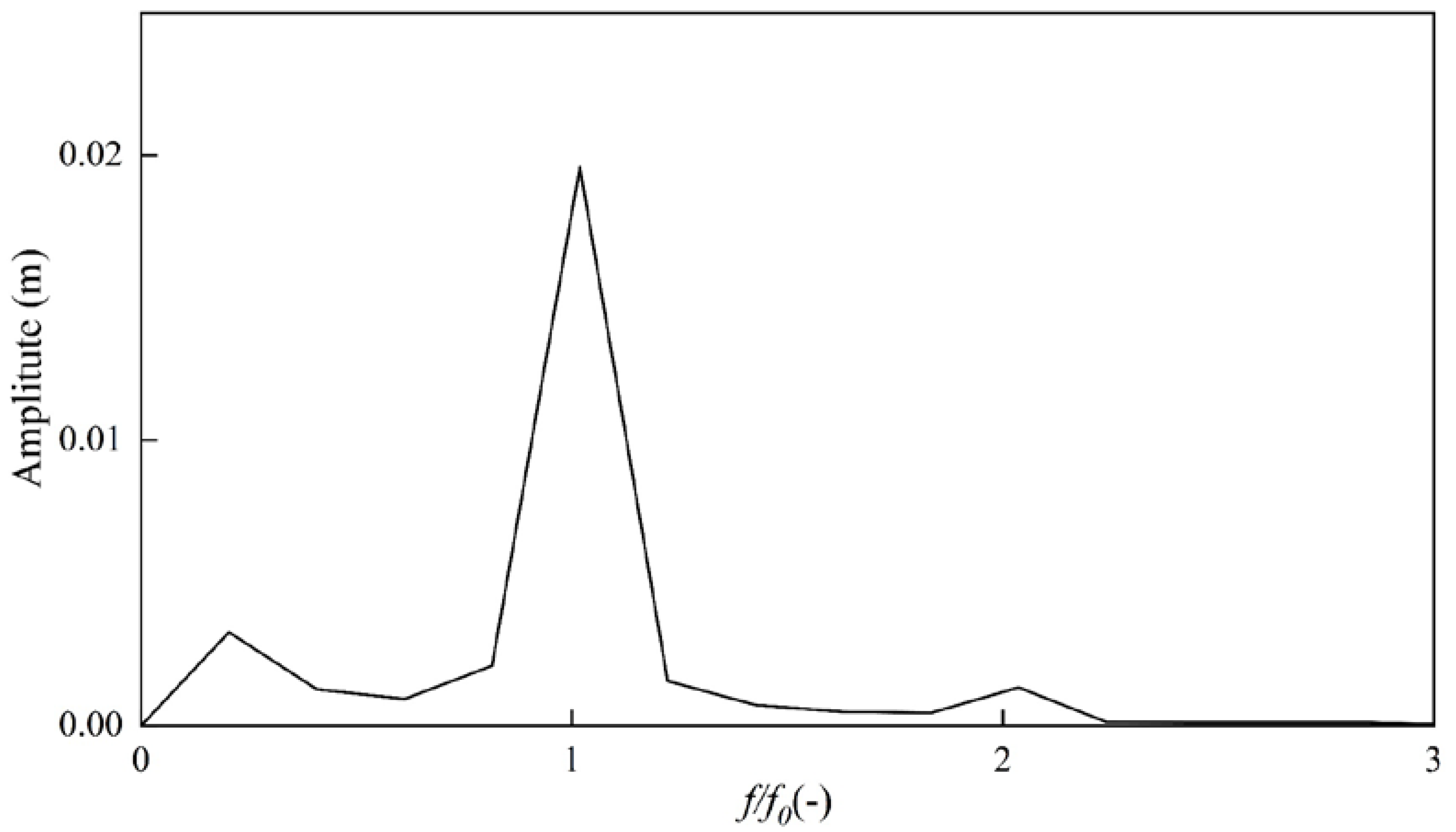
2.1.6. Data Acquisition and Processing
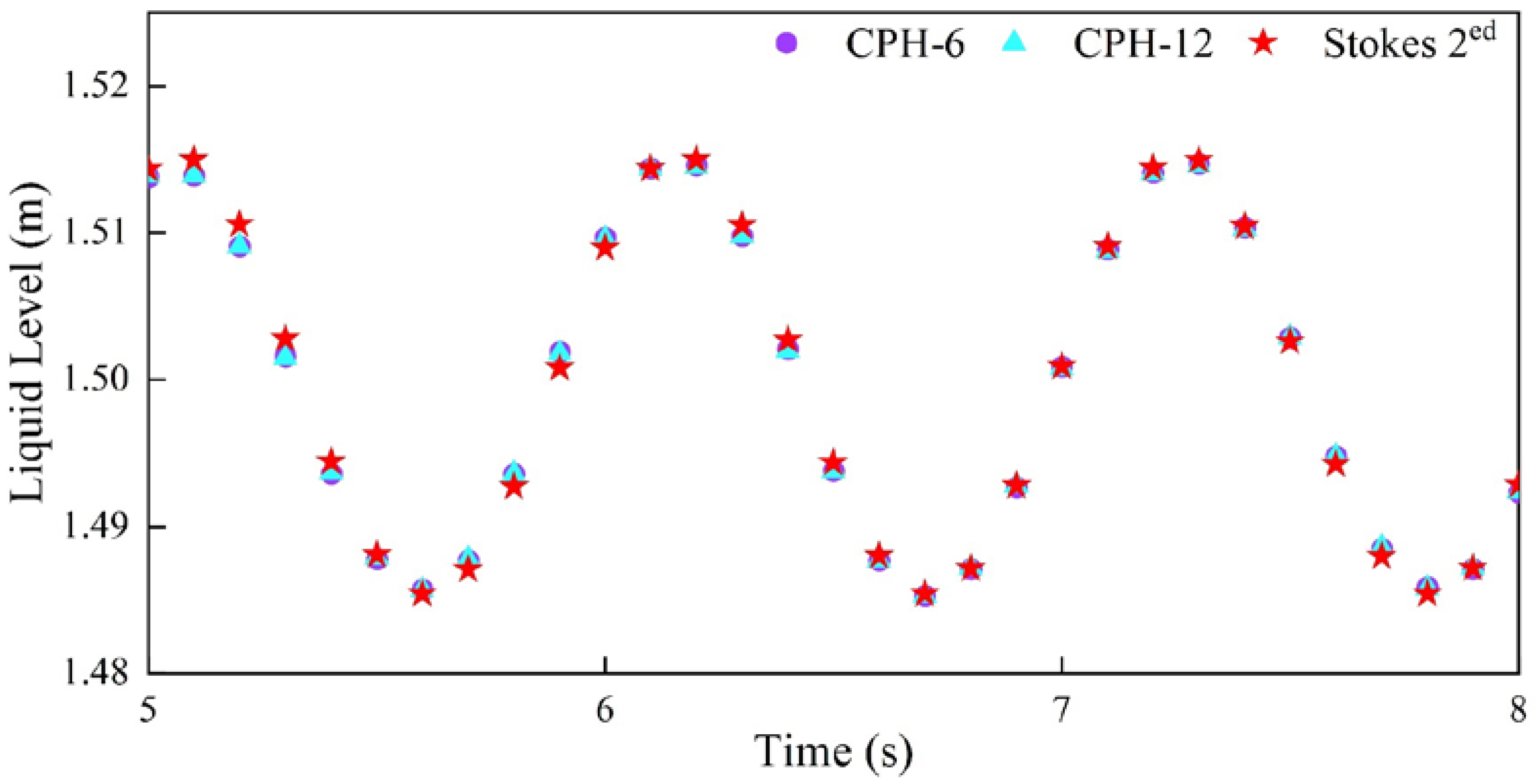
2.2. Verifications
2.2.1. Fluid and Structural Parameters
2.2.2. Laminar Flow
2.2.3. Mesh Convergence Study for Wave Modelling
2.2.4. Mesh Convergence Study for Structural Modelling
3. Results and Discussion
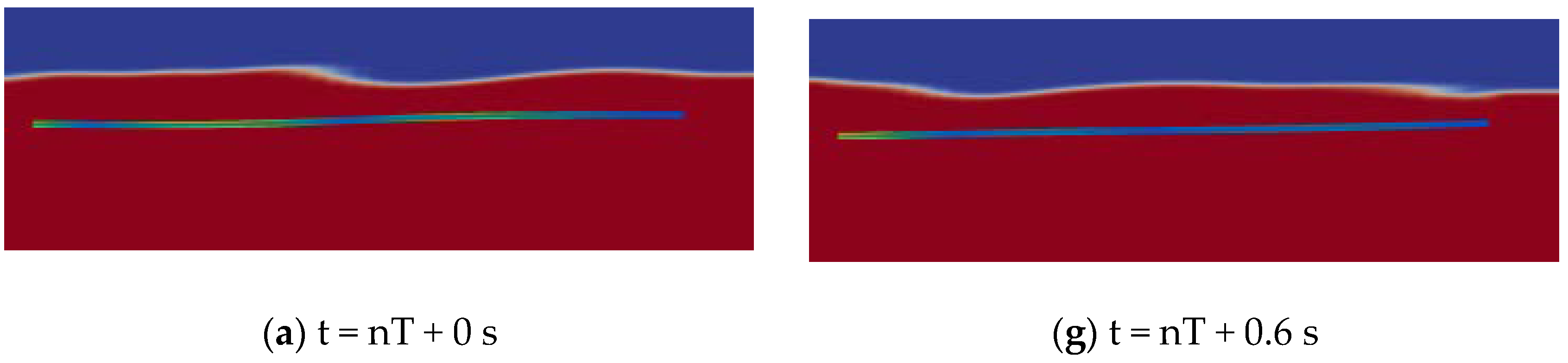
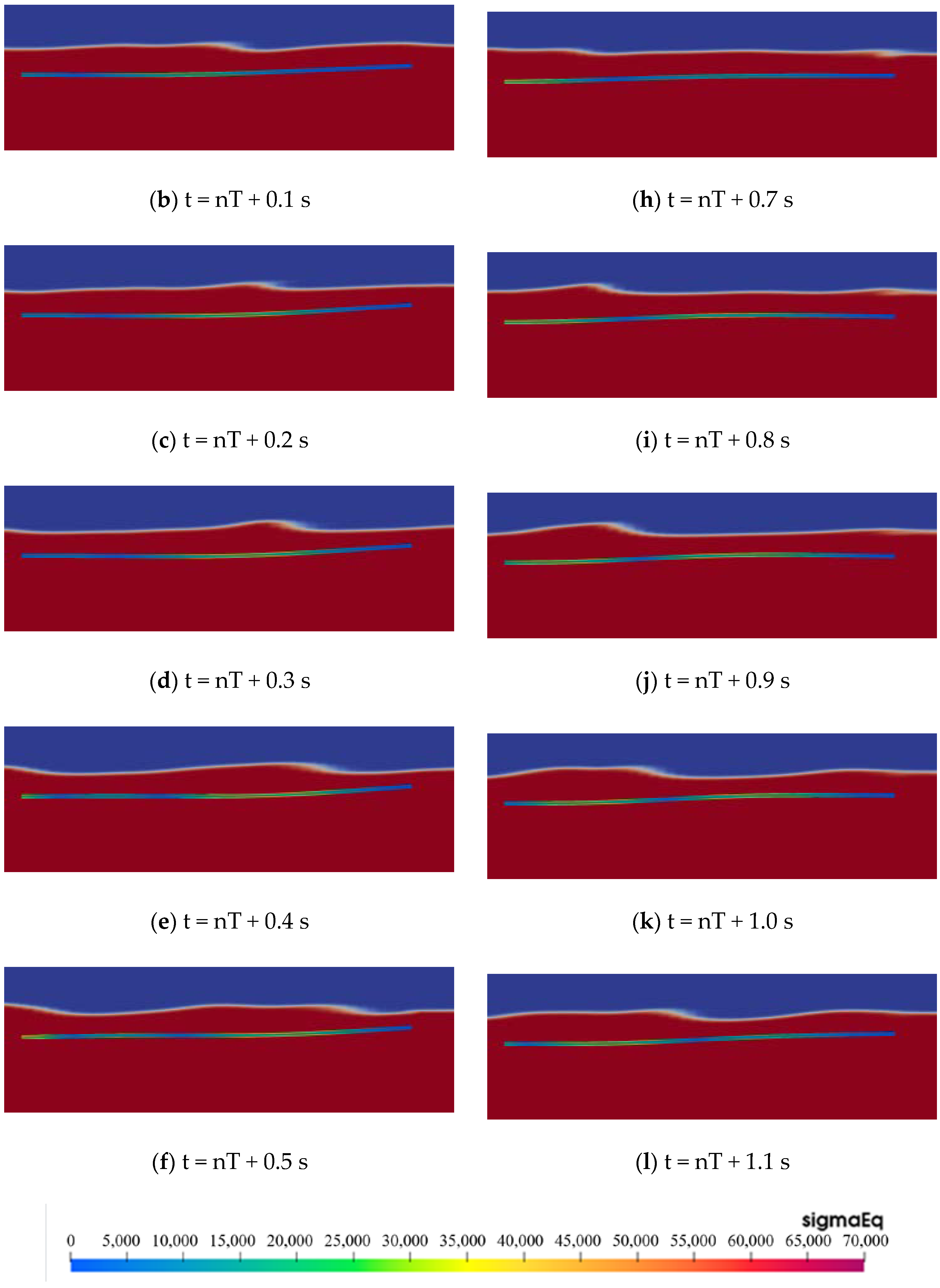
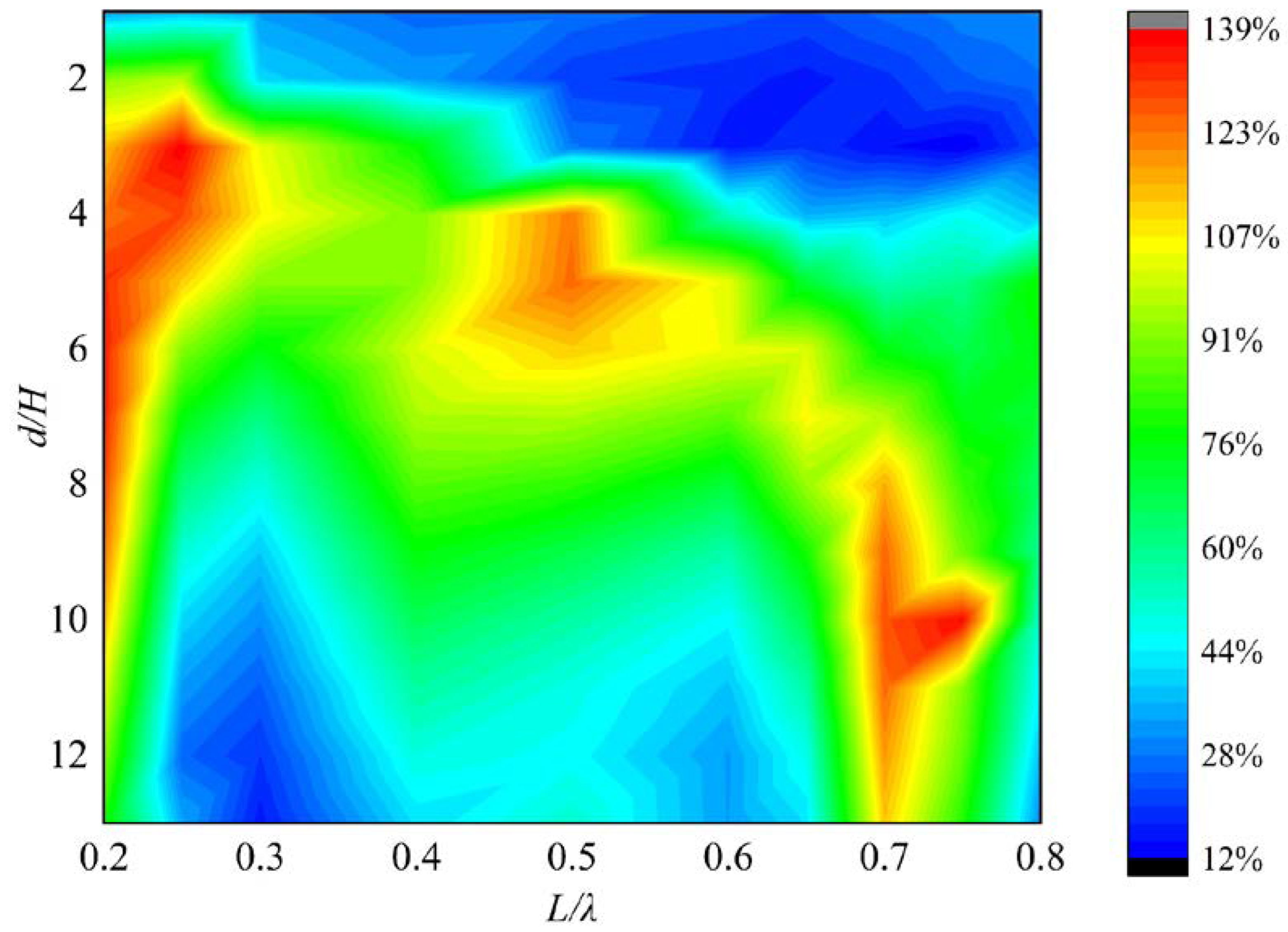
3.1. Effect of Deployment Depth and Length of Flexible Structure on Energy Conversion Efficiency
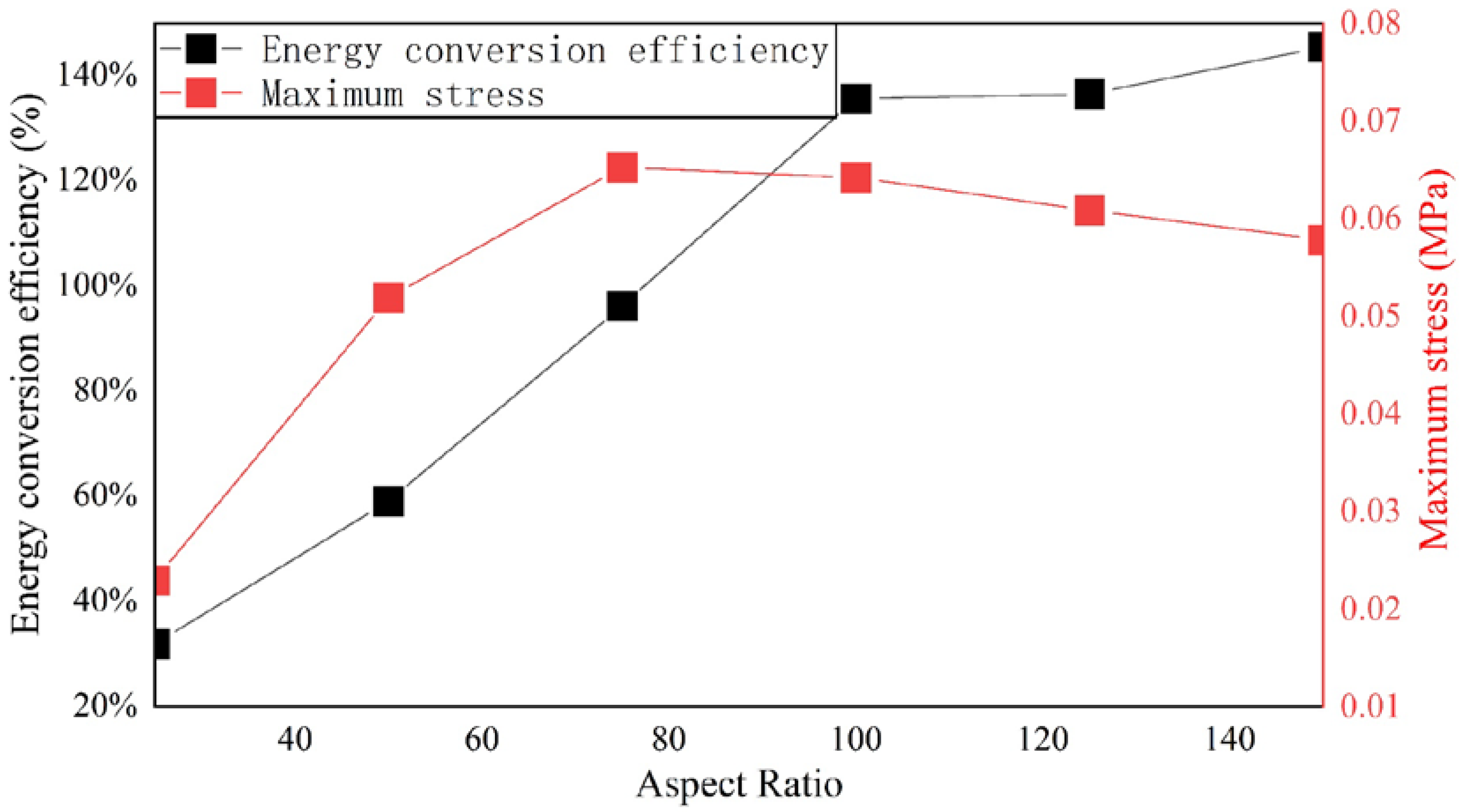
3.2. Relationship between AR and Energy Conversion Efficiency of Flexible Structure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A Global Wave Power Resource and Its Seasonal, Interannual and Long-Term Variability. Appl. Energy 2015, 148, 366–380. [Google Scholar] [CrossRef]
- Mwasilu, F.; Jung, J. Potential for Power Generation from Ocean Wave Renewable Energy Source: A Comprehensive Review on State-of-the-art Technology and Future Prospects. IET Renew. Power Gener. 2019, 13, 363–375. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Ringwood, J.V. Numerical Analysis of the Hydrodynamic Scaling Effects for the Wavestar Wave Energy Converter. J. Fluids Struct. 2021, 105, 103328. [Google Scholar] [CrossRef]
- Renzi, E.; Michele, S.; Zheng, S.; Jin, S.; Greaves, D. Niche Applications and Flexible Devices for Wave Energy Conversion: A Review. Energies 2021, 14, 6537. [Google Scholar] [CrossRef]
- Collins, I.; Hossain, M.; Dettmer, W.; Masters, I. Flexible Membrane Structures for Wave Energy Harvesting: A Review of the Developments, Materials and Computational Modelling Approaches. Renew. Sustain. Energy Rev. 2021, 151, 111478. [Google Scholar] [CrossRef]
- Farley, F.J.M.; Rainey, R.C.T.; Chaplin, J.R. Rubber Tubes in the Sea. Phil. Trans. R. Soc. A 2012, 370, 381–402. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.-R. A Flexible Seafloor Carpet for High-Performance Wave Energy Extraction. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; Volume 4: Offshore Geotechnics; Ronald W. Yeung Honoring Symposium on Offshore and Ship Hydrodynamics. American Society of Mechanical Engineers: New York, NY, USA; pp. 839–846. [Google Scholar]
- Lehmann, M.; Elandt, R.; Pham, H.; Ghorbani, R.; Shakeri, M.; Alam, M.-R. An Artificial Seabed Carpet for Multidirectional and Broadband Wave Energy Extraction: Theory and Experiment. In Proceedings of the 10th European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013. [Google Scholar]
- Rosati Papini, G.P.; Moretti, G.; Vertechy, R.; Fontana, M. Control of an Oscillating Water Column Wave Energy Converter Based on Dielectric Elastomer Generator. Nonlinear. Dyn. 2018, 92, 181–202. [Google Scholar] [CrossRef]
- Moretti, G.; Rosati Papini, G.P.; Daniele, L.; Forehand, D.; Ingram, D.; Vertechy, R.; Fontana, M. Modelling and Testing of a Wave Energy Converter Based on Dielectric Elastomer Generators. Proc. R. Soc. A 2019, 475, 20180566. [Google Scholar] [CrossRef] [PubMed]
- Tarrant, K.; Meskell, C. Investigation on Parametrically Excited Motions of Point Absorbers in Regular Waves. Ocean Eng. 2016, 111, 67–81. [Google Scholar] [CrossRef]
- Kornbluh, R.D.; Pelrine, R.; Prahlad, H.; Wong-Foy, A.; McCoy, B.; Kim, S.; Eckerle, J.; Low, T. From Boots to Buoys: Promises and Challenges of Dielectric Elastomer Energy Harvesting; Bar-Cohen, Y., Carpi, F., Eds.; Springer: San Diego, CA, USA, 2011; p. 797605. [Google Scholar]
- Zheng, S.; Michele, S.; Liang, H.; Meylan, M.H.; Greaves, D. Wave Power Extraction from a Floating Elastic Disk-Shaped Wave Energy Converter. J. Fluid Mech. 2022, 948, A38. [Google Scholar] [CrossRef]
- Michele, S.; Zheng, S.; Buriani, F.; Borthwick, A.G.L.; Greaves, D.M. Floating Hydroelastic Circular Plate in Regular and Irregular Waves. Eur. J. Mech. B/Fluids 2023, 99, 148–162. [Google Scholar] [CrossRef]
- Zheng, S.; Phillips, J.W.; Hann, M.; Greaves, D. Mathematical Modelling of a Floating Clam-Type Wave Energy Converter. Renew. Energy 2023, 210, 280–294. [Google Scholar] [CrossRef]
- Benites-Munoz, D.; Huang, L.; Anderlini, E.; Marín-Lopez, J.R.; Thomas, G. Hydrodynamic Modelling of An Oscillating Wave Surge Converter Including Power Take-Off. JMSE 2020, 8, 771. [Google Scholar] [CrossRef]
- Cheng, Y.; Ji, C.; Zhai, G. Fully Nonlinear Analysis Incorporating Viscous Effects for Hydrodynamics of an Oscillating Wave Surge Converter with Nonlinear Power Take-off System. Energy 2019, 179, 1067–1081. [Google Scholar] [CrossRef]
- López, M.; Taveira-Pinto, F.; Rosa-Santos, P. Numerical Modelling of the CECO Wave Energy Converter. Renew. Energy 2017, 113, 202–210. [Google Scholar] [CrossRef]
- Penalba, M.; Kelly, T.; Ringwood, J.V. Using NEMOH for Modelling Wave Energy Converters: A Comparative Study with WAMIT. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC), Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Tan, M.; Cen, Y.; Yang, Y.; Liu, X.; Si, Y.; Qian, P.; Zhang, D. Power Absorption Modelling and Analysis of a Multi-axis Wave Energy Converter. IET Renew. Power Gen 2021, 15, 3368–3384. [Google Scholar] [CrossRef]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Mathematical Modelling of Wave Energy Converters: A Review of Nonlinear Approaches. Renew. Sustain. Energy Rev. 2017, 78, 1188–1207. [Google Scholar] [CrossRef]
- Finnegan, W.; Rosa-Santos, P.; Taveira-Pinto, F.; Goggins, J. Development of a Numerical Model of the CECO Wave Energy Converter Using Computational Fluid Dynamics. Ocean. Eng. 2021, 219, 108416. [Google Scholar] [CrossRef]
- Chen, W.; Dolguntseva, I.; Savin, A.; Zhang, Y.; Li, W.; Svensson, O.; Leijon, M. Numerical Modelling of a Point-Absorbing Wave Energy Converter in Irregular and Extreme Waves. Appl. Ocean. Res. 2017, 63, 90–105. [Google Scholar] [CrossRef]
- Yeylaghi, S.; Moa, B.; Oshkai, P.; Buckham, B.; Crawford, C. ISPH Modelling of an Oscillating Wave Surge Converter Using an OpenMP-Based Parallel Approach. J. Ocean Eng. Mar. Energy 2016, 2, 301–312. [Google Scholar] [CrossRef]
- Huang, L.; Ren, K.; Li, M.; Tuković, Ž.; Cardiff, P.; Thomas, G. Fluid-Structure Interaction of a Large Ice Sheet in Waves. Ocean Eng. 2019, 182, 102–111. [Google Scholar] [CrossRef]
- Huang, L.; Li, Y. Design of the Submerged Horizontal Plate Breakwater Using a Fully Coupled Hydroelastic Approach. Comput. Aided Civ. Eng. 2022, 37, 915–932. [Google Scholar] [CrossRef]
- Hu, Z.; Huang, L.; Li, Y. Fully-Coupled Hydroelastic Modeling of a Deformable Wall in Waves. Coast. Eng. 2023, 179, 104245. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ Library for Complex Physics Simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics IUC, Dubrovnik, Croatia, 19–21 September 2007. [Google Scholar]
- Cardiff, P.; Karač, A.; De Jaeger, P.; Jasak, H.; Nagy, J.; Ivanković, A.; Tuković, Ž. An Open-Source Finite Volume Toolbox for Solid Mechanics and Fluid-Solid Interaction Simulations. arXiv 2018, arXiv:1808.10736. [Google Scholar]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A Wave Generation Toolbox for the Open-Source CFD Library: OpenFoam®: WAVE GENERATION TOOLBOX. Int. J. Numer. Meth. Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Windt, C. High-Fidelity Numerical Modelling of Ocean Wave Energy Systems_ A Review of Computational Fluid Dynamics-Based Numerical Wave Tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef]
- Huang, L.; Li, Y.; Benites, D.; Windt, C.; Feichtner, A.; Tavakoli, S.; Davidson, J.; Paredes, R.; Quintuna, T.; Ransley, E.; et al. A review on the modelling of wave-structure interactions based on OpenFOAM. OpenFOAM J. 2022, 2, 116–142. [Google Scholar]
- Tuković, Ž.; Karač, A.; Cardiff, P.; Jasak, H.; Ivanković, A. OpenFOAM Finite Volume Solver for Fluid-Solid Interaction. Trans. FAMENA 2018, 42, 1–31. [Google Scholar] [CrossRef]
- Benra, F.-K.; Dohmen, H.J.; Pei, J.; Schuster, S.; Wan, B. A Comparison of One-Way and Two-Way Coupling Methods for Numerical Analysis of Fluid-Structure Interactions. J. Appl. Math. 2011, 2011, 1–16. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Hydrodynamics around Cylindrical Strucures; World Scientific: Singapore, 2006; Volume 26. [Google Scholar]
- Connell, K.O.; Cashman, A. Development of a Numerical Wave Tank with Reduced Discretization Error. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; IEEE: Chennai, India, 2016; pp. 3008–3012. [Google Scholar]
- Huang, L.; Hu, Z.; Li, Y.; Thomas, G. Fully-Coupled CFD+CSM Analysis on an Elastic Floating/Submerged Plate for Wave Energy Harvest. In Proceedings of the 9th International Conference on Hydroelasticity in Marine Technology, Rome, Italy, 10–13 July 2022. [Google Scholar]
- Cerik, B.C.; Choung, J. Fracture Prediction of Steel-Plated Structures under Low-Velocity Impact. JMSE 2023, 11, 699. [Google Scholar] [CrossRef]
- Ringsberg, J. Life Prediction of Rolling Contact Fatigue Crack Initiation. Int. J. Fatigue 2001, 23, 575–586. [Google Scholar] [CrossRef]
- Ringsberg, J. Prediction of Fatigue Crack Initiation for Rolling Contact Fatigue. Int. J. Fatigue 2000, 22, 205–215. [Google Scholar] [CrossRef]
- Benites-Munoz, D.; Huang, L.; Thomas, G. Optimal Array Arrangement of Oscillating Wave Surge Converters: An Analysis Based on Three Devices. Renew. Energy 2024, 222, 119825. [Google Scholar] [CrossRef]
- Zheng, S.; Michele, S.; Liang, H.; Iglesias, G.; Greaves, D. Wave Power Extraction from a Wave Farm of Tubular Structure Integrated Oscillating Water Columns. Renew. Energy 2024, 225, 120263. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, C.; Chen, W.; Huang, L. Array analysis on a seawall-type of deformable wave energy converters. Renew. Energy 2024, 225, 120344. [Google Scholar] [CrossRef]
- Anderlini, E. Control of wave energy converters using machine learning strategies. PhD Thesis, University of Edinburgh, Edinburgh, UK, 2017. [Google Scholar]
- Edwards, E.C.; Yue, D.K.P. Optimisation of the geometry of axisymmetric point-absorber wave energy converters. J. Fluid Mech. 2022, 933, A1. [Google Scholar] [CrossRef]
- Wei, Y.; Yu, S.; Jin, P.; Huang, L.; Elsherbiny, K.; Tezdogan, T. Coupled analysis between catenary mooring and VLFS with structural hydroelasticity in waves. Mar. Struct. 2024, 93, 103516. [Google Scholar] [CrossRef]



| Wave Type | Wave Period [s] | Height [m] | Wave Depth [m] | Wave Length [m] |
|---|---|---|---|---|
| Stokes Second | 1.1 | 0.03 [m] | 1.5 | 1.889 |
| Transport Model | Simulation Type | Density [kg/m3] | Kinematic Viscosity [m2/s] |
|---|---|---|---|
| Newtonian | Laminar | 1000 | 1 × 10−6 |
| Flexible Material Type | Density [kg/m3] | Young’s Modulus [Pa] | Poisson’s Ratio [-] |
|---|---|---|---|
| St. Venant–Kirchhoff Elastic | 1000 | 5 × 107 | 0.3 |
| CPH | 3 | 6 | 9 | 12 |
|---|---|---|---|---|
| RMSE | 7.12 × 10−7 | 7.26 × 10−7 | 6.97 × 10−7 | 7.14 × 10−7 |
| Number of Cells | 114 | 190 | 380 | 608 |
|---|---|---|---|---|
| Energy conversion efficiency | 137.93% | 138.49% | 137.77% | 138.52% |
| L/λ = 0.2 | L/λ = 0.25 | L/λ = 0.3 | L/λ = 0.4 | L/λ = 0.5 | L/λ = 0.6 | L/λ = 0.65 | L/λ = 0.7 | L/λ = 0.75 | L/λ = 0.8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| d/H = 01 | C020 | C020.5 | C021 | C022 | C023 | C024 | C024.5 | C025 | C025.5 | C026 |
| L = 0.3778 d = 0.03 | L = 0.4723 d = 0.03 | L = 0.5667 d = 0.03 | L = 0.7556 d = 0.03 | L = 0.9445 d = 0.03 | L = 1.1334 d = 0.03 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.03 | L = 1.4168 d = 0.03 | L = 1.5112 d = 0.03 | |
| d/H = 02 | C030 | C030.5 | C031 | C032 | C033 | C034 | C034.5 | C035 | C035.5 | C036 |
| L = 0.3778 d = 0.06 | L = 0.4723 d = 0.06 | L = 0.5667 d = 0.06 | L = 0.7556 d = 0.06 | L = 0.9445 d = 0.06 | L = 1.1334 d = 0.06 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.06 | L = 1.4168 d = 0.06 | L = 1.5112 d = 0.06 | |
| d/H = 03 | C040 | C040.5 | C041 | C042 | C043 | C044 | C044.5 | C045 | C045.5 | C046 |
| L = 0.3778 d = 0.09 | L = 0.4723 d = 0.09 | L = 0.5667 d = 0.09 | L = 0.7556 d = 0.09 | L = 0.9445 d = 0.09 | L = 1.1334 d = 0.09 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.09 | L = 1.4168 d = 0.09 | L = 1.5112 d = 0.09 | |
| d/H = 04 | C050 | C050.5 | C051 | C052 | C053 | C054 | C054.5 | C055 | C055.5 | C056 |
| L = 0.3778 d = 0.12 | L = 0.4723 d = 0.12 | L = 0.5667 d = 0.12 | L = 0.7556 d = 0.12 | L = 0.9445 d = 0.12 | L = 1.1334 d = 0.12 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.12 | L = 1.4168 d = 0.12 | L = 1.5112 d = 0.12 | |
| d/H = 05 | C060 | C060.5 | C061 | C062 | C063 | C064 | C064.5 | C065 | C065.5 | C066 |
| L = 0.3778 d = 0.15 | L = 0.4723 d = 0.15 | L = 0.5667 d = 0.15 | L = 0.7556 d = 0.15 | L = 0.9445 d = 0.15 | L = 1.1334 d = 0.15 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.15 | L = 1.4168 d = 0.15 | L = 1.5112 d = 0.15 | |
| d/H = 06 | C070 | C070.5 | C071 | C072 | C073 | C074 | C074.5 | C075 | C075.5 | C076 |
| L = 0.3778 d = 0.18 | L = 0.4723 d = 0.18 | L = 0.5667 d = 0.18 | L = 0.7556 d = 0.18 | L = 0.9445 d = 0.18 | L = 1.1334 d = 0.18 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.18 | L = 1.4168 d = 0.18 | L = 1.5112 d = 0.18 | |
| d/H = 07 | C080 | C080.5 | C081 | C082 | C083 | C084 | C084.5 | C085 | C085.5 | C086 |
| L = 0.3778 d = 0.21 | L = 0.4723 d = 0.21 | L = 0.5667 d = 0.21 | L = 0.7556 d = 0.21 | L = 0.9445 d = 0.21 | L = 1.1334 d = 0.21 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.21 | L = 1.4168 d = 0.21 | L = 1.5112 d = 0.21 | |
| d/H = 08 | C090 | C090.5 | C091 | C092 | C093 | C094 | C094.5 | C095 | C095.5 | C096 |
| L = 0.3778 d = 0.24 | L = 0.4723 d = 0.24 | L = 0.5667 d = 0.24 | L = 0.7556 d = 0.24 | L = 0.9445 d = 0.24 | L = 1.1334 d = 0.24 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.24 | L = 1.4168 d = 0.24 | L = 1.5112 d = 0.24 | |
| d/H = 09 | C100 | C100.5 | C101 | C102 | C103 | C104 | C104.5 | C105 | C105.5 | C106 |
| L = 0.3778 d = 0.27 | L = 0.4723 d = 0.27 | L = 0.5667 d = 0.27 | L = 0.7556 d = 0.27 | L = 0.9445 d = 0.27 | L = 1.1334 d = 0.27 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.27 | L = 1.4168 d = 0.27 | L = 1.5112 d = 0.27 | |
| d/H = 10 | C110 | C110.5 | C111 | C112 | C113 | C114 | C114.5 | C115 | C115.5 | C116 |
| L = 0.3778 d = 0.30 | L = 0.4723 d = 0.30 | L = 0.5667 d = 0.30 | L = 0.7556 d = 0.30 | L = 0.9445 d = 0.30 | L = 1.1334 d = 0.30 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.30 | L = 1.4168 d = 0.30 | L = 1.5112 d = 0.30 | |
| d/H = 11 | C120 | C120.5 | C121 | C122 | C123 | C124 | C124.5 | C125 | C125.5 | C126 |
| L = 0.3778 d = 0.33 | L = 0.4723 d = 0.33 | L = 0.5667 d = 0.33 | L = 0.7556 d = 0.33 | L = 0.9445 d = 0.33 | L = 1.1334 d = 0.33 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.33 | L = 1.4168 d = 0.33 | L = 1.5112 d = 0.33 | |
| d/H = 12 | C130 | C130.5 | C131 | C132 | C133 | C134 | C134.5 | C135 | C135.5 | C136 |
| L = 0.3778 d = 0.36 | L = 0.4723 d = 0.36 | L = 0.5667 d = 0.36 | L = 0.7556 d = 0.36 | L = 0.9445 d = 0.36 | L = 1.1334 d = 0.36 | L = 1.228 d = 0.03 | L = 1.3223 d = 0.36 | L = 1.4168 d = 0.36 | L = 1.5112 d = 0.36 | |
| d/H = 13 | C140 | C140.5 | C141 | C142 | C143 | C144 | C144.5 | C145 | C145.5 | C146 |
| L = 0.3778 d = 0.39 | L = 0.4723 d = 0.39 | L = 0.5667 d = 0.39 | L = 0.7556 d = 0.39 | L = 0.9445 d = 0.39 | L = 1.1334 d = 0.39 | L = 1.228 d = 0.09 | L = 1.3223 d = 0.39 | L = 1.4168 d = 0.39 | L = 1.5112 d = 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Huang, L. Energy Efficiency Analysis of a Deformable Wave Energy Converter Using Fully Coupled Dynamic Simulations. Oceans 2024, 5, 227-243. https://doi.org/10.3390/oceans5020014
Luo C, Huang L. Energy Efficiency Analysis of a Deformable Wave Energy Converter Using Fully Coupled Dynamic Simulations. Oceans. 2024; 5(2):227-243. https://doi.org/10.3390/oceans5020014
Chicago/Turabian StyleLuo, Chen, and Luofeng Huang. 2024. "Energy Efficiency Analysis of a Deformable Wave Energy Converter Using Fully Coupled Dynamic Simulations" Oceans 5, no. 2: 227-243. https://doi.org/10.3390/oceans5020014
APA StyleLuo, C., & Huang, L. (2024). Energy Efficiency Analysis of a Deformable Wave Energy Converter Using Fully Coupled Dynamic Simulations. Oceans, 5(2), 227-243. https://doi.org/10.3390/oceans5020014








