Prediction of Tensile Strain Capacity for X52 Steel Pipeline Materials Using the Extended Finite Element Method
Abstract
:1. Introduction
2. Full-Scale Test Experiment
3. Problem Formulation and the XFEM Model
4. Results and Discussion
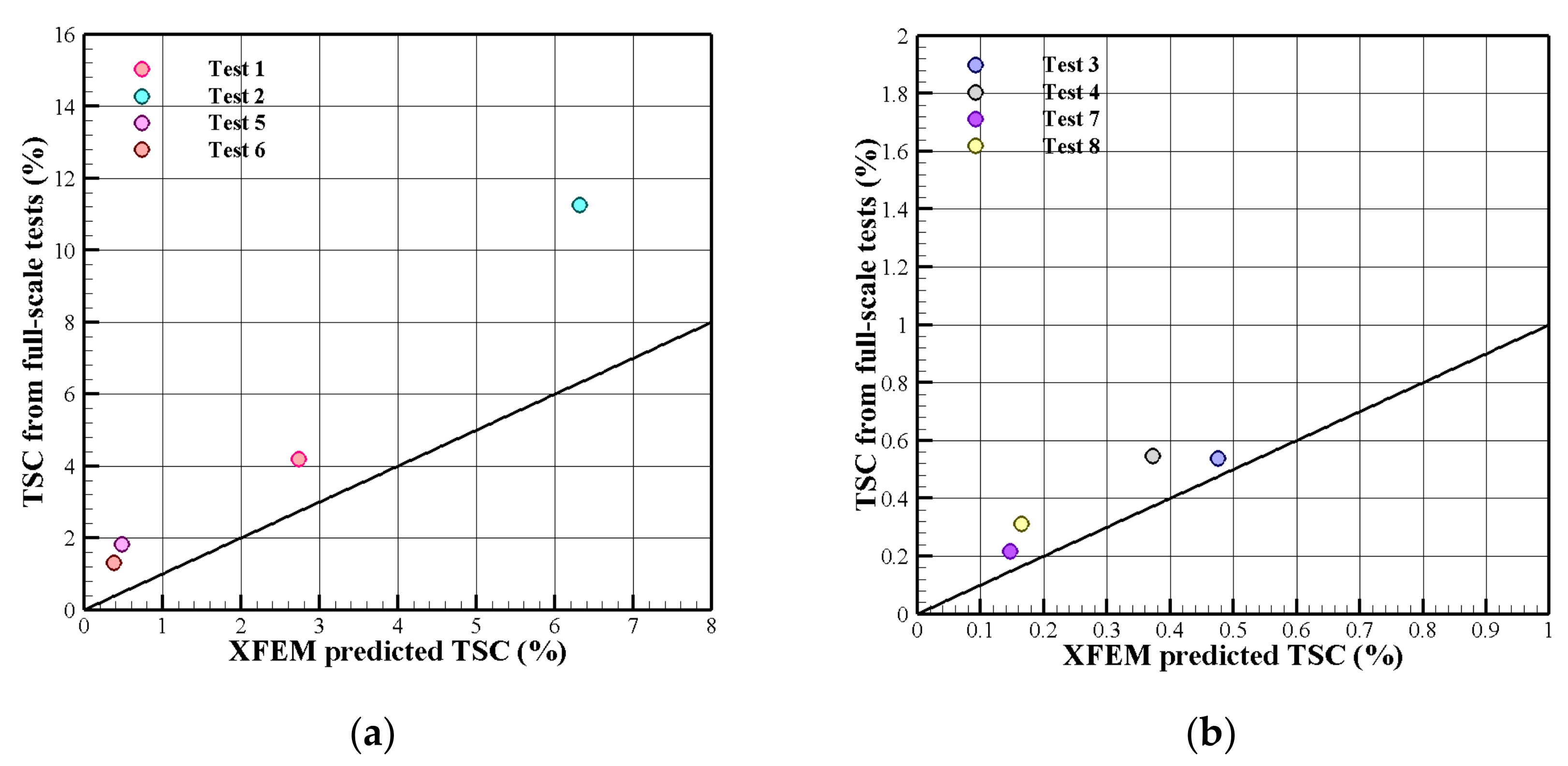
4.1. Tensile Strain Capacity Comparison with Experiments
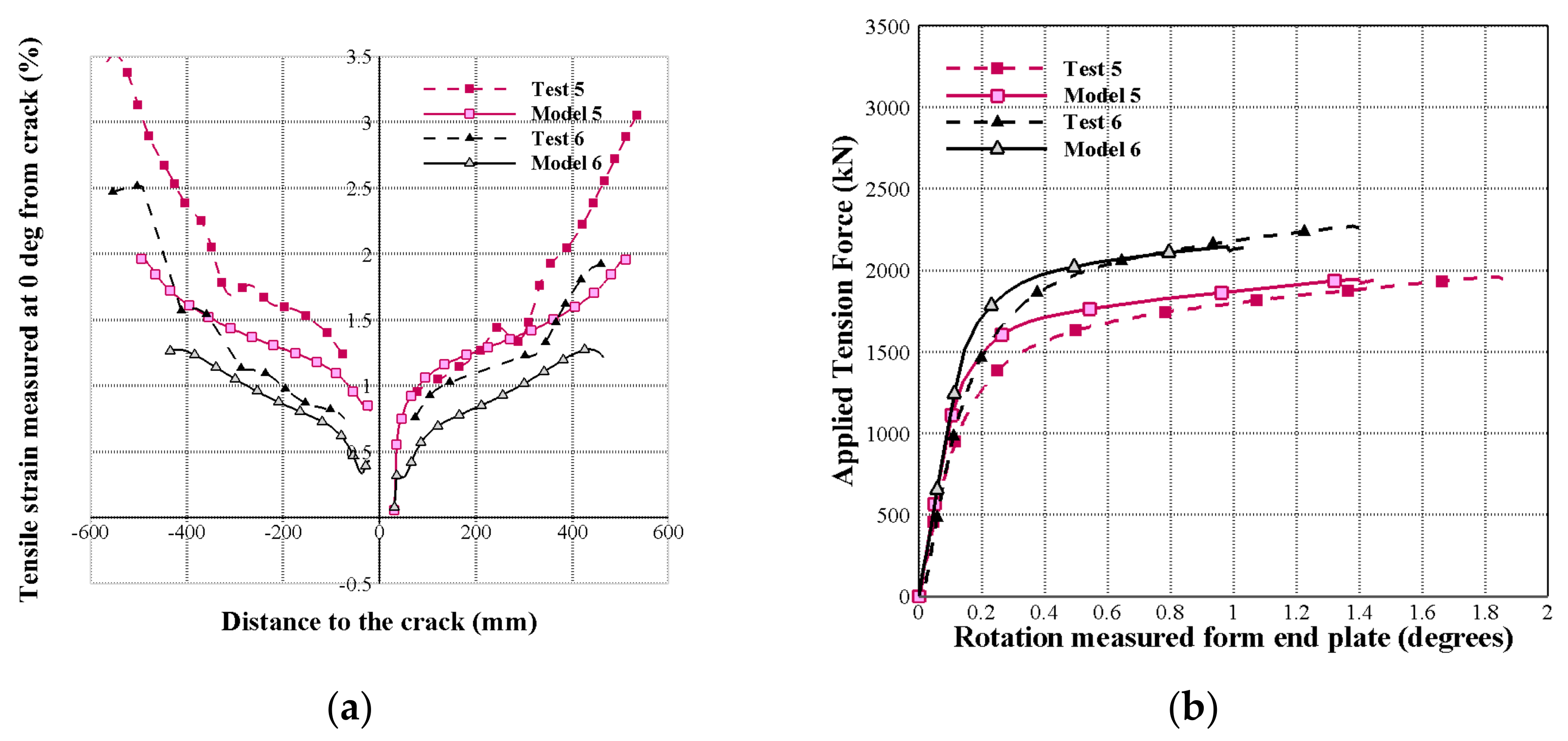
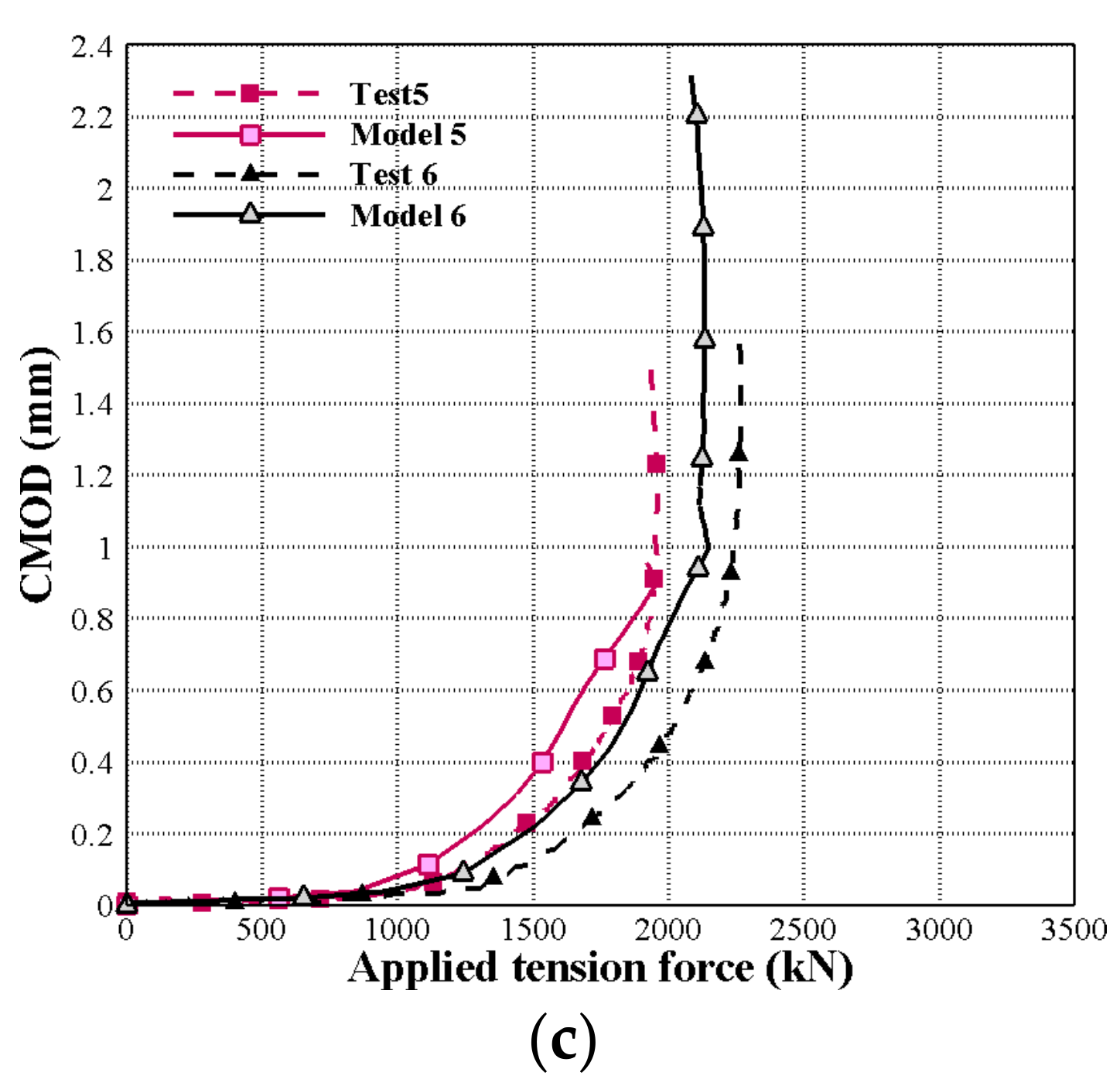
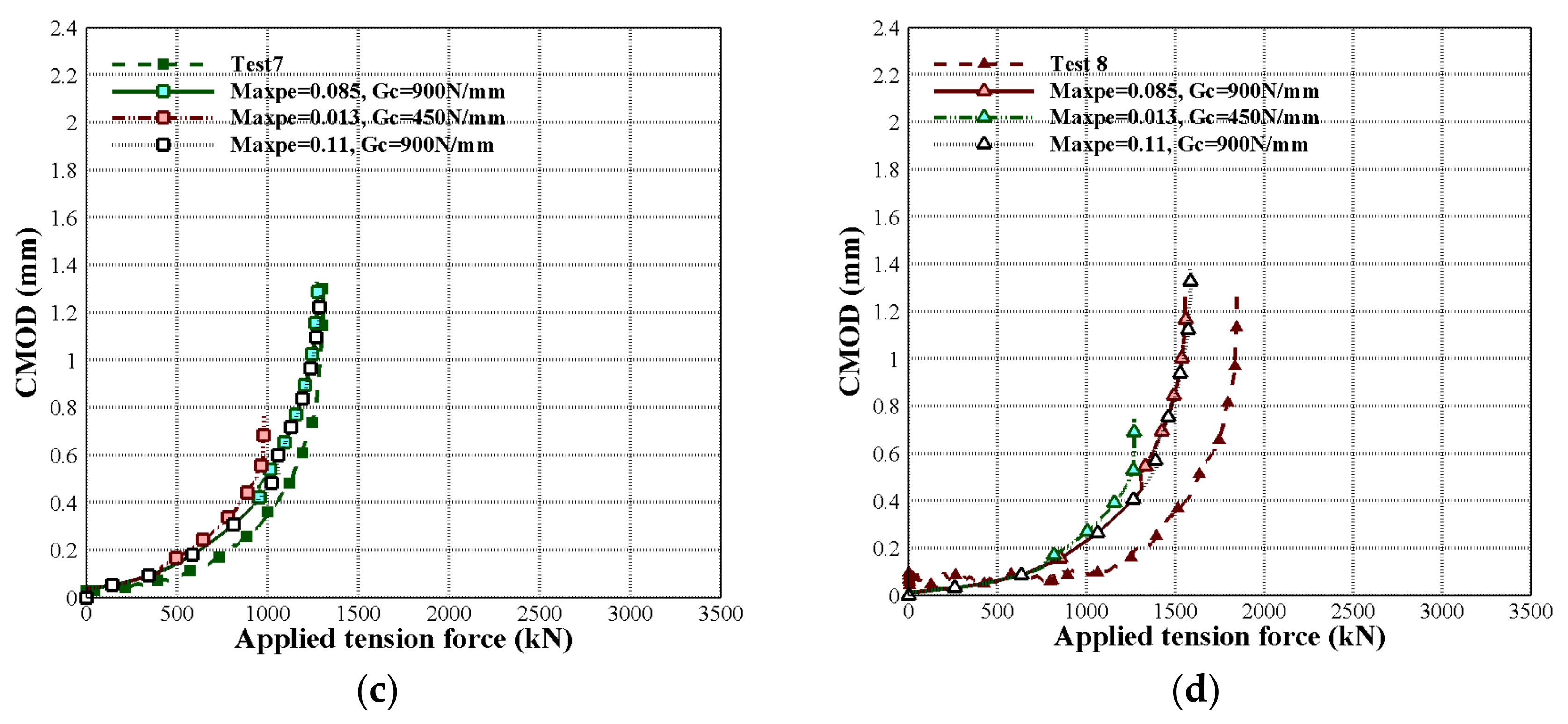
4.2. CMOD, Applied Tension Force, and Endplate Rotation
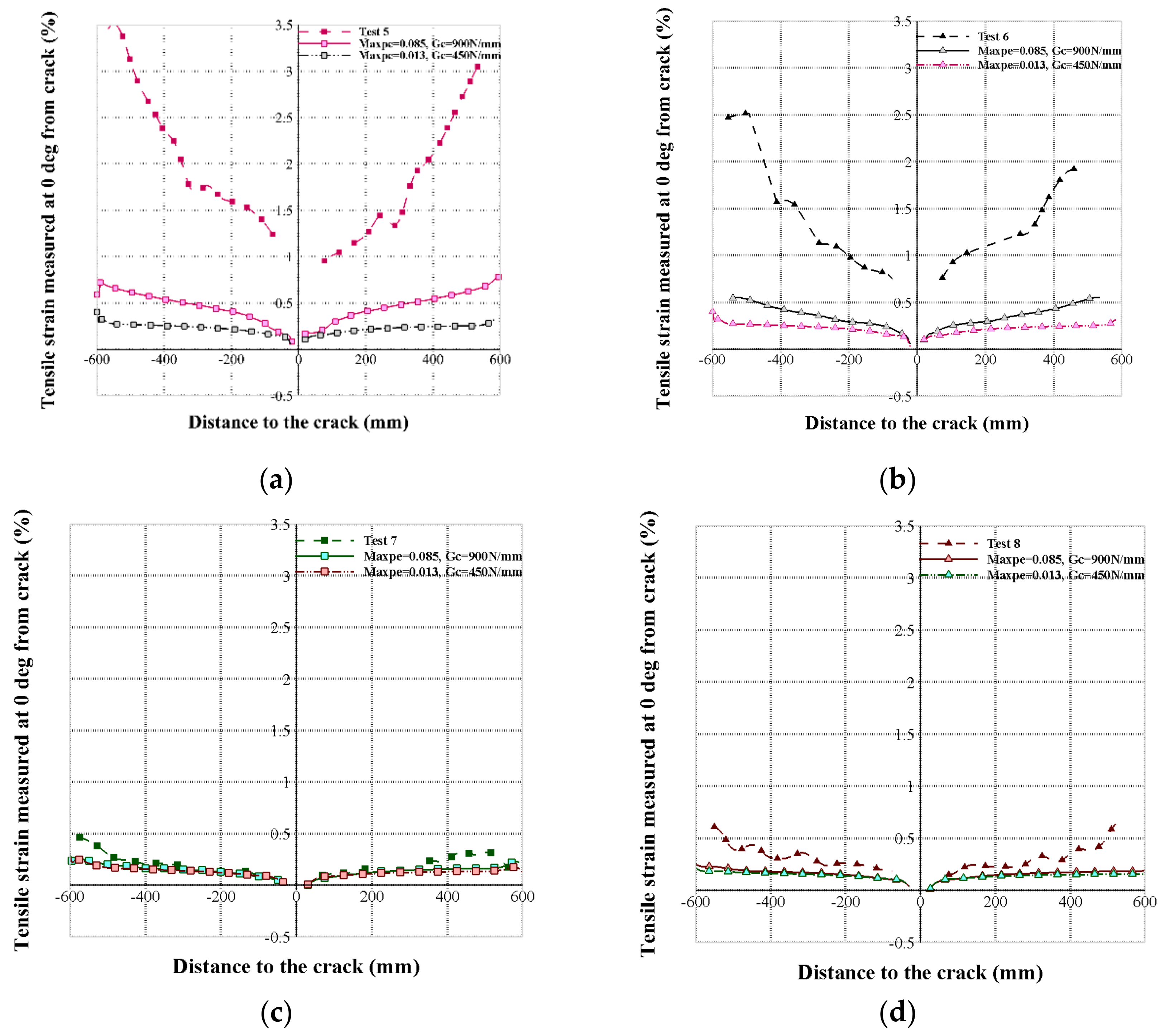
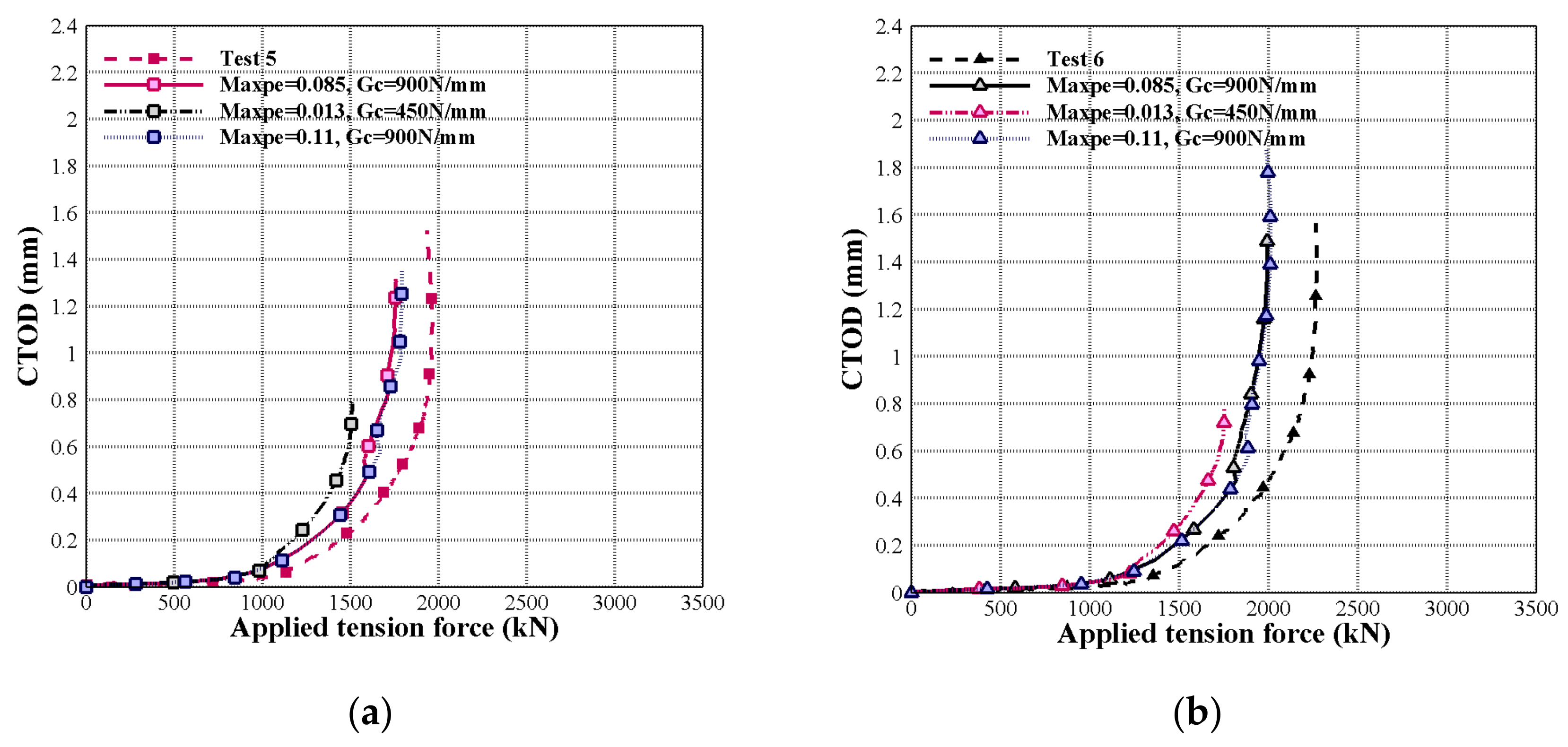
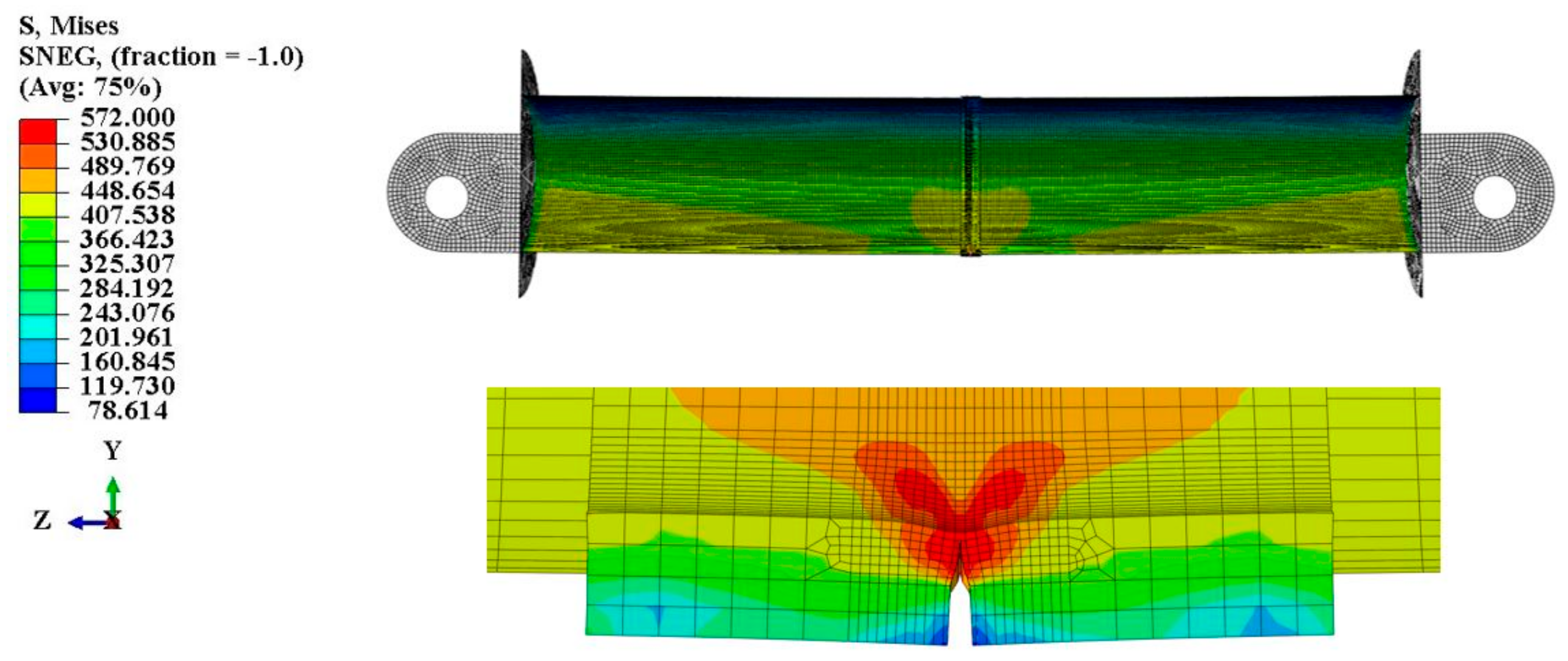
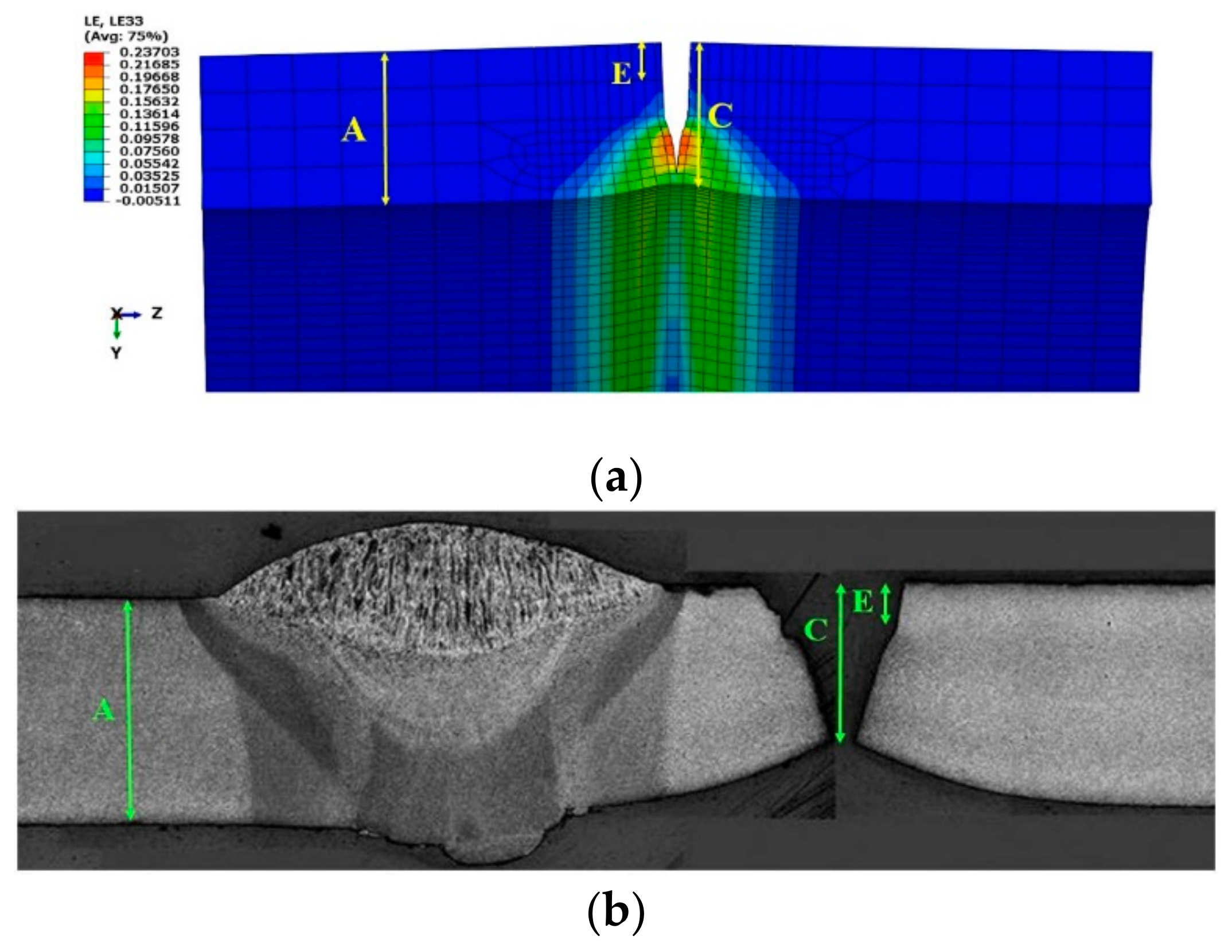
4.3. Geometry of Cracked Pipe in the Vicinity of the Flaw
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, B.; Liu, X.J.; Zhang, H. Strain-Based Design Criteria of Pipelines. J. Loss Prev. Process. Ind. 2009, 22, 884–888. [Google Scholar] [CrossRef]
- Pan, J.H. Several Concernment Task under Development of High Strength Pipeline Steel. Welded Pipe Tube 2005, 28, 1–2. [Google Scholar]
- Macia, M.L.; Kibey, S.A.; Arslan, H.; Bardi, F.; Ford, S.J.; Kan, W.C.; Cook, M.F.; Newbury, B. Approaches to Qualify Strain-Based Designed Pipelines. In Biennial International Pipeline Conference; American Society of Mechanical Engineers: Calgary, AB, Canada, 2010; Volume 4, pp. 365–374. [Google Scholar]
- Agbo, S.; Lin, M.; Ameli, I.; Imanpour, A.; Duan, D.-M.; Cheng, J.J.R.; Adeeb, S. Experimental Evaluation of the Effect of the Internal Pressure and Flaw Size on the Tensile Strain Capacity of Welded X42 Vintage Pipelines. Int. J. Press. Vessel. Pip. 2019, 173, 55–67. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Rudland, D.; Denys, R.; Horsley, D. A Preliminary Strain-Based Design Criterion for Pipeline Girth Welds. In International Pipeline Conference; American Society of Mechanical Engineers: Calgary, AB, Canada, 2002; Volume A, pp. 415–427. [Google Scholar]
- Wang, Y.Y.; Cheng, W.; Horsley, D. Tensile Strain Limits of Buried Defects in Pipeline Girth Welds. In Biennial International Pipeline Conference; American Society of Mechanical Engineers: Calgary, AB, Canada, 2004; Volume 2, pp. 1607–1614. [Google Scholar]
- Wang, Y.Y.; Horsley, D.; Cheng, W.; Glover, A.; McLamb, M.; Zhou, J.; Denys, R. Tensile Strain Limits of Girth Welds with Surface-Breaking Defects Part II Experimental Correlation and Validation. In Proceedings of the 4th International Conference Pipeline Technology, Calgary, AB, Canada, 30 September–3 October 2002; pp. 251–266. [Google Scholar]
- Kibey, S.; Wang, X.; Minnaar, K.; Macia, M.L.; Fairchild, D.P.; Kan, W.C.; Ford, S.J.; Newbury, B. Tensile Strain Capacity Equations for Strain-Based Design of Welded Pipelines. In Proceedings of the 2010 8th International Pipeline Conference, Calgary, AB, Canada, 27 September–1 October 2010; Volume 4, pp. 355–363. [Google Scholar]
- Fairchild, D.P.; Kibey, S.A.; Tang, H.; Krishnan, V.R.; Wang, X.; Macia, M.L.; Cheng, W. Continued Advancements Regarding Capacity Prediction of Strain-Based Pipelines. In International Pipeline Conference; American Society of Mechanical Engineers: Calgary, AB, Canada, 2012; Volume 4, pp. 297–305. [Google Scholar]
- Tang, H.; Fairchild, D.; Panico, M.; Crapps, J.; Cheng, W. Strain Capacity Prediction of Strain-Based Pipelines. In Proceedings of the 2014 10th International Pipeline Conference, Calgary, AB, Canada, 29 September 2014; p. V004T11A025. [Google Scholar]
- Wang, Y.-Y.; Liu, M.; Song, Y.; Stephens, M.; Petersen, R.; Gordon, R. Second Generation Models for Strain-Based Design; Pipeline Research Council International: Houston, TX, USA, 2011. [Google Scholar]
- Agbo, S.; Lin, M.; Ameli, I.; Imanpour, A.; Duan, D.M.; Cheng, J.J.R.; Adeeb, S. Evaluation of the Effect of Internal Pressure and Flaw Size on the Tensile Strain Capacity of X42 Vintage Pipeline Using Damage Plasticity Model in Extended Finite Element Method. In Proceedings of the American Society of Mechanical Engineers, Pressure Vessels and Piping Division (Publication) PVP, San Antonio, TX, USA, 14–19 July 2019; American Society of Mechanical Engineers (ASME): San Antonio, TX, USA, 2019; Volume 5, p. PVP2019-94005. [Google Scholar]
- Lin, M.; Agbo, S.; Duan, D.-M.; Cheng, J.J.R.; Adeeb, S. Simulation of Crack Propagation in API 5L X52 Pressurized Pipes Using XFEM-Based Cohesive Segment Approach. J. Pipeline Syst. Eng. Pract. 2020, 11, 04020009. [Google Scholar] [CrossRef]
- Rashid, F.M.; Banerjee, A. Simulation of Fracture in a Low Ductility Aluminum Alloy Using a Triaxiality Dependent Cohesive Model. Eng. Fract. Mech. 2017, 179, 1–12. [Google Scholar] [CrossRef]
- Oh, C.-S.; Kim, N.-H.; Kim, Y.-J.; Baek, J.-H.; Kim, Y.-P.; Kim, W.-S. A Finite Element Ductile Failure Simulation Method Using Stress-Modified Fracture Strain Model. Eng. Fract. Mech. 2011, 78, 124–137. [Google Scholar] [CrossRef]
- Ameli, I.; Asgarian, B.; Lin, M.; Agbo, S.; Cheng, R.; Duan, D.M.; Adeeb, S. Estimation of the CTOD-Crack Growth Curves in SENT Specimens Using the EXtended Finite Element Method. Int. J. Press. Vessel. Pip. 2019, 169, 16–25. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Han, Y.; Xia, M.; Ji, Y. Numerical and Experimental Study on Critical Crack Tip Opening Displacement of X80 Pipeline Steel. Mechanika 2017, 23, 204–208. [Google Scholar] [CrossRef] [Green Version]
- Okodi, A.; Li, Y.; Cheng, R.; Kainat, M.; Yoosef-Ghodsi, N.; Adeeb, S. Crack Propagation and Burst Pressure of Pipeline with Restrained and Unrestrained Concentric Dent-Crack Defects Using Extended Finite Element Method. Appl. Sci. 2020, 10, 7554. [Google Scholar] [CrossRef]
- Okodi, A.; Lin, M.; Yoosef-Ghodsi, N.; Kainat, M.; Hassanien, S.; Adeeb, S. Crack Propagation and Burst Pressure of Longitudinally Cracked Pipelines Using Extended Finite Element Method. Int. J. Press. Vessel. Pip. 2020, 184, 104115. [Google Scholar] [CrossRef]
- Agbo, S.; Imanpour, A.; Li, Y.; Kainat, M.; Yoosef-Ghodsi, N.; Cheng, J.J.R.; Adeeb, S. Development of a Tensile Strain Capacity Predictive Model for American Petroleum Institute 5L X42 Welded Vintage Pipelines. J. Press. Vessel Technol. 2020, 142. [Google Scholar] [CrossRef]
- Abdulhameed, D.; Cakiroglu, C.; Lin, M.; Cheng, R.; Nychka, J.; Sen, M.; Adeeb, S. The Effect of Internal Pressure on the Tensile Strain Capacity of X52 Pipelines With Circumferential Flaws. J. Press. Vessel Technol. 2016, 138, 61701. [Google Scholar] [CrossRef]
- Dassault Systemes. Abaqus 6.17 Documentation; Dassault Systemes: Vélizy-Villacoublay, France, 2017. [Google Scholar]
- Lin, M. Characterization of Tensile and Fracture Properties of X52 Steel Pipes and Their Girth Weld. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2015. [Google Scholar]
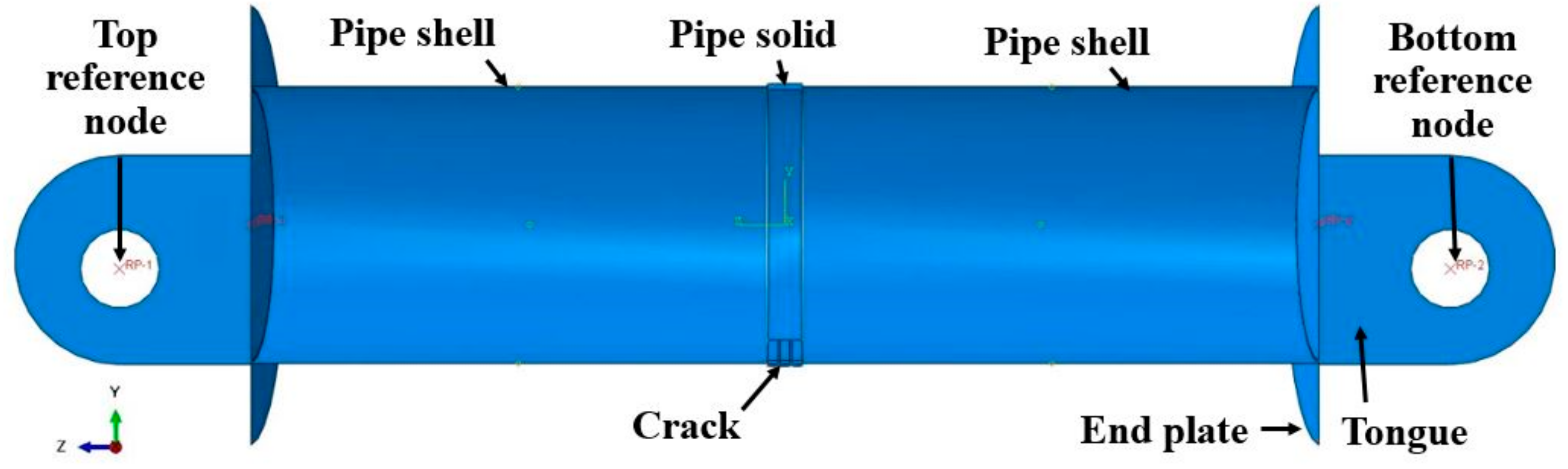
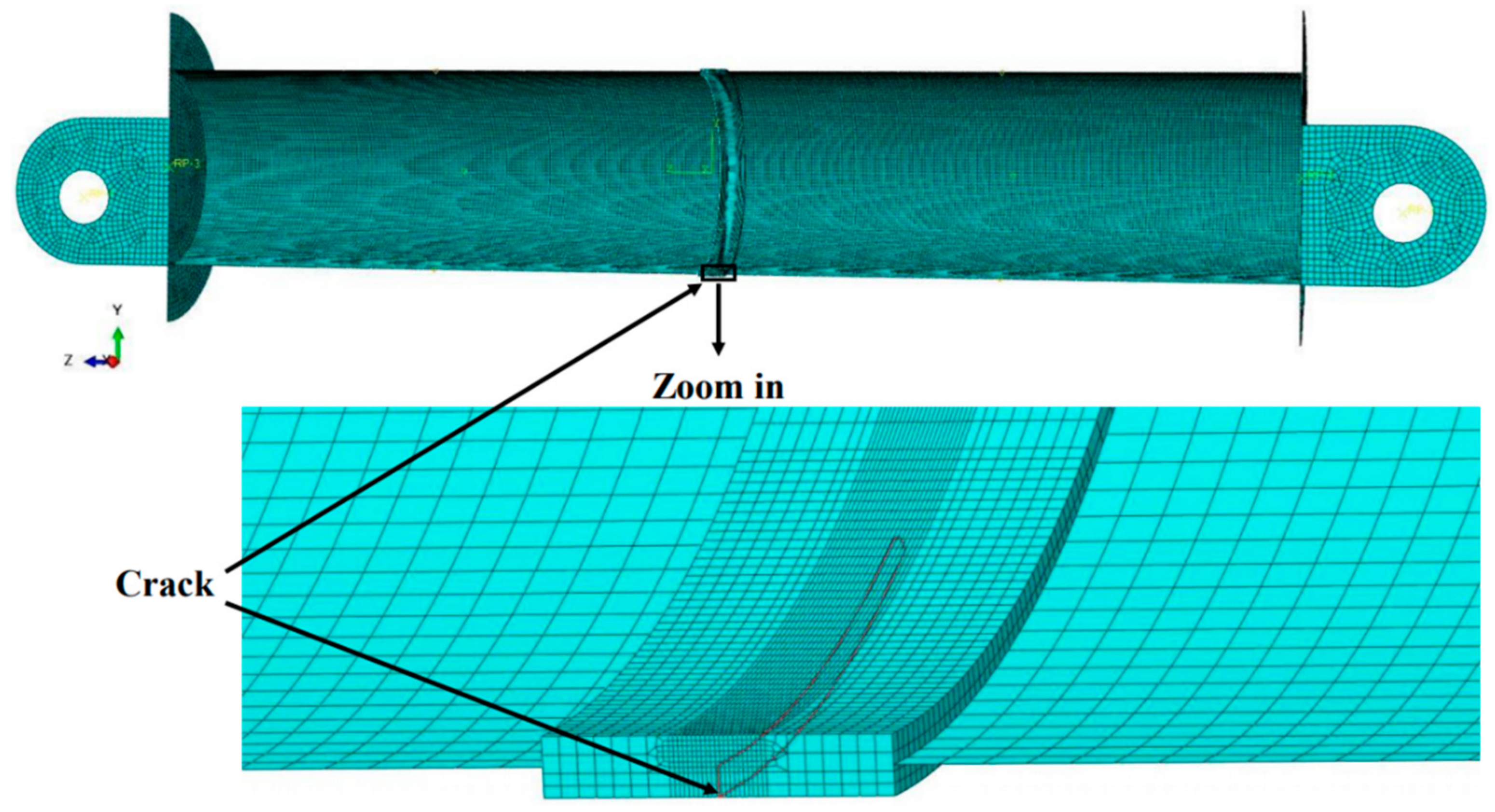




| Test /Model | Pipe Specimen Dimensions | Crack Dimensions | Internal Pressure Level | ||||
|---|---|---|---|---|---|---|---|
| Outer Diameter (mm) | Pipe Length (mm) | Wall Thickness (mm) | Crack Depth (mm) | Crack Length (mm) | Internal Pressure (MPa) | Hoop Stress/SMYS (%) | |
| Test 1 | 324 | 1828.8 | 6.95 | 1.7 | 50 | 11.65 | 75 |
| Model 1 | 324 | 1828.8 | 6.8 | 1.7 | 50 | 11.65 | 77 |
| Test 2 | 324 | 1828.8 | 6.8 | 1.5 | 50 | 3.50 | 23 |
| Model 2 | 324 | 1828.8 | 6.8 | 1.5 | 50 | 3.50 | 23 |
| Test 3 | 324 | 1828.8 | 6.8 | 3.1 | 50 | 11.67 | 77 |
| Model 3 | 324 | 1828.8 | 6.8 | 3.1 | 50 | 11.65 | 77 |
| Test 4 | 324 | 1828.8 | 6.8 | 3.3 | 50 | 4.70 | 31 |
| Model 4 | 324 | 1828.8 | 6.8 | 3.3 | 50 | 4.65 | 31 |
| Test 5 | 324 | 1219.2 | 6.8 | 1.4 | 150 | 11.65 | 77 |
| Model 5 | 324 | 1219.2 | 6.8 | 1.4 | 150 | 11.65 | 77 |
| Test 6 | 324 | 1219.2 | 6.8 | 1.8 | 150 | 4.60 | 31 |
| Model 6 | 324 | 1219.2 | 6.8 | 1.8 | 150 | 4.65 | 31 |
| Test 7 | 324 | 1219.2 | 6.8 | 3.5 | 150 | 11.65 | 77 |
| Model 7 | 324 | 1219.2 | 6.8 | 3.3 | 150 | 11.65 | 77 |
| Test 8 | 324 | 1219.2 | 6.8 | 2.7 | 150 | 4.65 | 31 |
| Model 8 | 324 | 1219.2 | 6.8 | 2.7 | 150 | 4.65 | 31 |
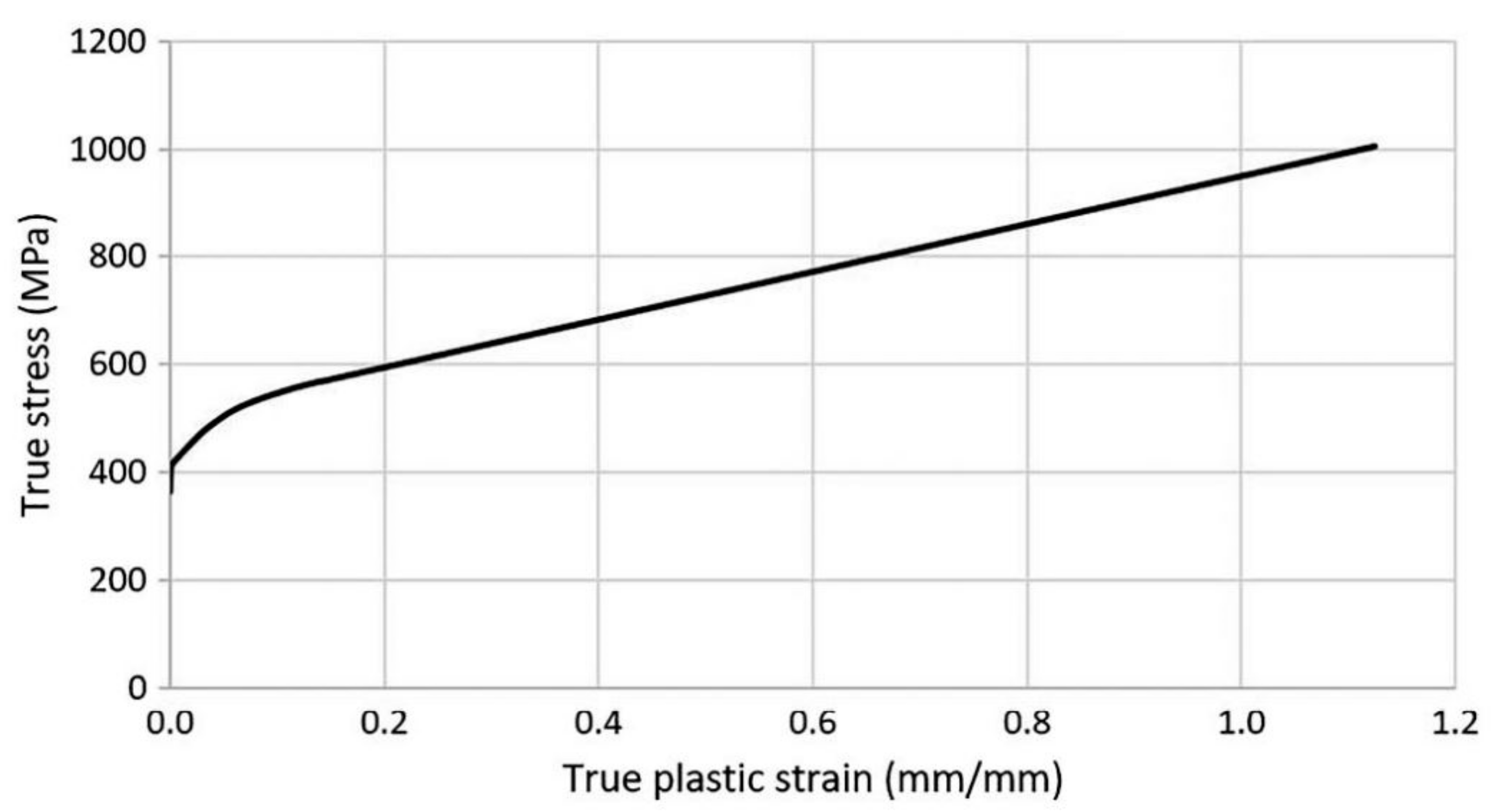
| Young’s Modulus (GPa) | Poisson’s Ratio | 0.2% Offset Yield Strength (MPa) | Ultimate True Plastic Strain |
|---|---|---|---|
| 199 | 0.3 | 411 | 0.147 |
| Model/Test | Test TSC (%) | XFEM TSC Maxpe = 0.085 Gc = 900N/mm (%) | Difference (%) | Ratio (Test/Model) | XFEM TSC Maxpe = 0.11 Gc = 900N/mm (%) | Difference (%) | Ratio (Test/Model) |
|---|---|---|---|---|---|---|---|
| 1 | 4.187 | 2.730 | 34.798 | 1.534 | 3.0680 | 26.726 | 1.365 |
| 2 | 11.25 | 6.310 | 43.911 | 1.783 | 7.0750 | 37.100 | 1.590 |
| 3 | 0.537 | 0.476 | 11.359 | 1.128 | 0.600 | −11.732 | 0.895 |
| 4 | 0.546 | 0.372 | 31.868 | 1.468 | 0.415 | 23.992 | 1.316 |
| 5 | 1.829 | 0.478 | 73.865 | 3.826 | 0.628 | 65.660 | 2.912 |
| 6 | 0.726 | 0.373 | 48.622 | 1.946 | 0.432 | 40.495 | 1.681 |
| 7 | 0.217 | 0.146 | 32.719 | 1.486 | 0.151 | 30.414 | 1.437 |
| 8 | 0.312 | 0.165 | 47.115 | 1.890 | 0.170 | 45.510 | 1.835 |
| Mean (Ratios) | - | - | - | 1.883 | - | 1.629 | |
| COV (%) | - | - | - | 44.038 | - | 36.228 |
| Model/Test | Max Load (kN) | Rotation at Endplate (Degrees) | CMODfailure (mm) | CMODcritical (mm) | Reduction in Pipe Wall Thickness (%) |
|---|---|---|---|---|---|
| Test 1 | 2299 | 5.080 | 2.110 | 1.190 | 32.400 |
| Model 1 | 2360 | 5.135 | 1.910 | 1.508 | 16.050 |
| Difference (%) | 2.661 | 1.093 | −9.455 | 26.723 | −50.462 |
| Ratio | 0.974 | 0.989 | 1.105 | 0.789 | 2.019 |
| Test 2 | 3100 | 6.820 | 2.160 | 1.090 | 27.900 |
| Model 2 | 3112 | 5.634 | 2.060 | 1.367 | 14.253 |
| Difference (%) | 0.415 | −17.391 | −4.611 | 25.413 | −48.914 |
| Ratio | 0.996 | 1.211 | 1.049 | 0.797 | 1.957 |
| Test 3 | 1623 | 0.980 | 2.370 | 1.180 | 19.100 |
| Model 3 | 1773 | 0.847 | 1.631 | 1.304 | 10.032 |
| Difference (%) | 9.259 | −13.578 | −31.169 | 10.508 | −47.476 |
| Ratio | 0.9153 | 1.157 | 1.453 | 0.905 | 1.904 |
| Test 4 | 2061 | 1.040 | 2.050 | 1.160 | 20.600 |
| Model 4 | 1996 | 0.663 | 1.373 | 0.943 | 8.107 |
| Difference (%) | −3.145 | −36.242 | −33.035 | −18.707 | −60.64 |
| Ratio | 1.032 | 1.569 | 1.493 | 1.230 | 2.541 |
| Test 5 | 1934 | 1.860 | 1.520 | 0.770 | 26.500 |
| Model 5 | 1755 | 0.621 | 1.693 | 0.761 | 16.850 |
| Difference (%) | −9.218 | −66.588 | 11.395 | −1.169 | −36.415 |
| Ratio | 1.102 | 2.995 | 0.898 | 1.0119 | 1.572 |
| Test 6 | 2261 | 1.400 | 1.560 | 0.900 | 27.900 |
| Model 6 | 1990 | 0.506 | 1.745 | 0.878 | 15.325 |
| Difference (%) | −11.981 | −63.820 | 11.829 | −2.444 | −45.072 |
| Ratio | 1.136 | 2.767 | 0.894 | 1.025 | 1.821 |
| Test 7 | 1304 | 0.260 | 1.300 | 0.900 | 19.100 |
| Model 7 | 1275 | 0.204 | 1.273 | 0.998 | 8.295 |
| Difference (%) | −2.254 | −21.664 | −2.061 | 10.888 | −56.571 |
| Ratio | 1.023 | 1.275 | 1.021 | 0.902 | 2.303 |
| Test 8 | 1831 | 0.420 | 1.270 | 0.850 | 20.600 |
| Model 8 | 1556 | 0.221 | 1.152 | 0.898 | 7.295 |
| Difference (%) | −15.018 | −47.314 | −9.274 | 5.647 | −63.146 |
| Ratio | 1.177 | 1.900 | 1.102 | 0.947 | 2.824 |
| Mean (Ratios) | 1.044 | 1.733 | 1.127 | 0.951 | 2.118 |
| COV (%) | 8.390 | 44.086 | 20.281 | 14.950 | 19.377 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elyasi, N.; Shahzamanian, M.; Lin, M.; Westover, L.; Li, Y.; Kainat, M.; Yoosef-Ghodsi, N.; Adeeb, S. Prediction of Tensile Strain Capacity for X52 Steel Pipeline Materials Using the Extended Finite Element Method. Appl. Mech. 2021, 2, 209-225. https://doi.org/10.3390/applmech2020013
Elyasi N, Shahzamanian M, Lin M, Westover L, Li Y, Kainat M, Yoosef-Ghodsi N, Adeeb S. Prediction of Tensile Strain Capacity for X52 Steel Pipeline Materials Using the Extended Finite Element Method. Applied Mechanics. 2021; 2(2):209-225. https://doi.org/10.3390/applmech2020013
Chicago/Turabian StyleElyasi, Nahid, Mohammadmehdi Shahzamanian, Meng Lin, Lindsey Westover, Yong Li, Muntaseer Kainat, Nader Yoosef-Ghodsi, and Samer Adeeb. 2021. "Prediction of Tensile Strain Capacity for X52 Steel Pipeline Materials Using the Extended Finite Element Method" Applied Mechanics 2, no. 2: 209-225. https://doi.org/10.3390/applmech2020013
APA StyleElyasi, N., Shahzamanian, M., Lin, M., Westover, L., Li, Y., Kainat, M., Yoosef-Ghodsi, N., & Adeeb, S. (2021). Prediction of Tensile Strain Capacity for X52 Steel Pipeline Materials Using the Extended Finite Element Method. Applied Mechanics, 2(2), 209-225. https://doi.org/10.3390/applmech2020013







