Numerical and Experimental Studies of Free-Fall Drop Impact Tests Using Strain Gauge, Piezoceramic, and Fiber Optic Sensors
Abstract
:1. Introduction
2. Experimental Set-Up and Numerical Simulations
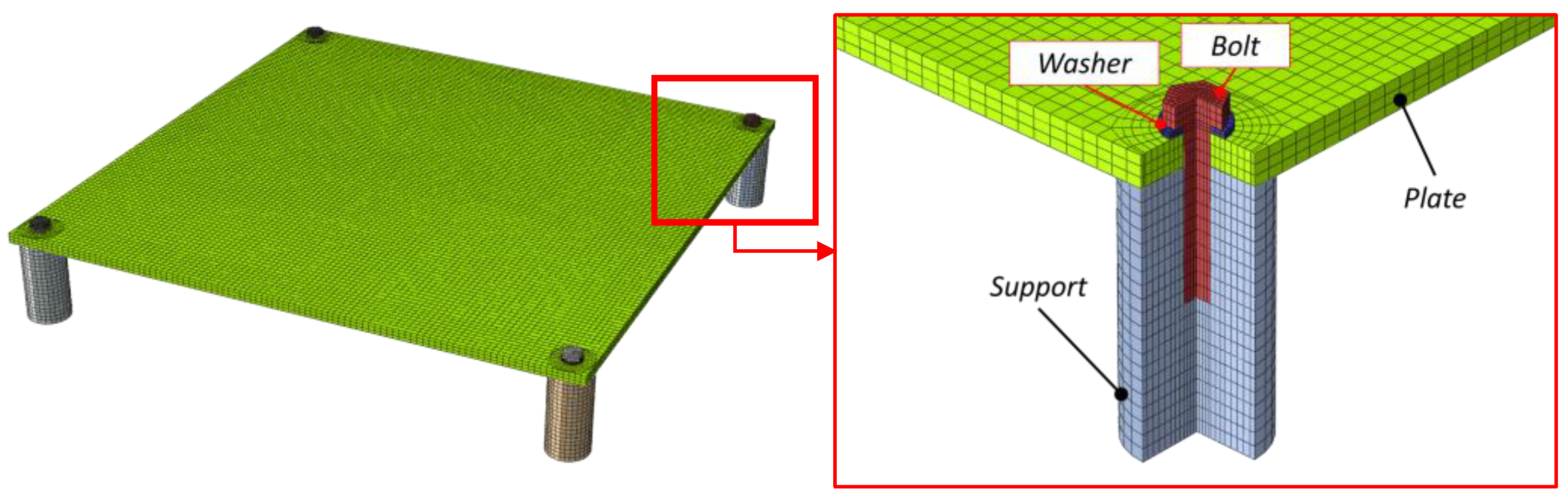
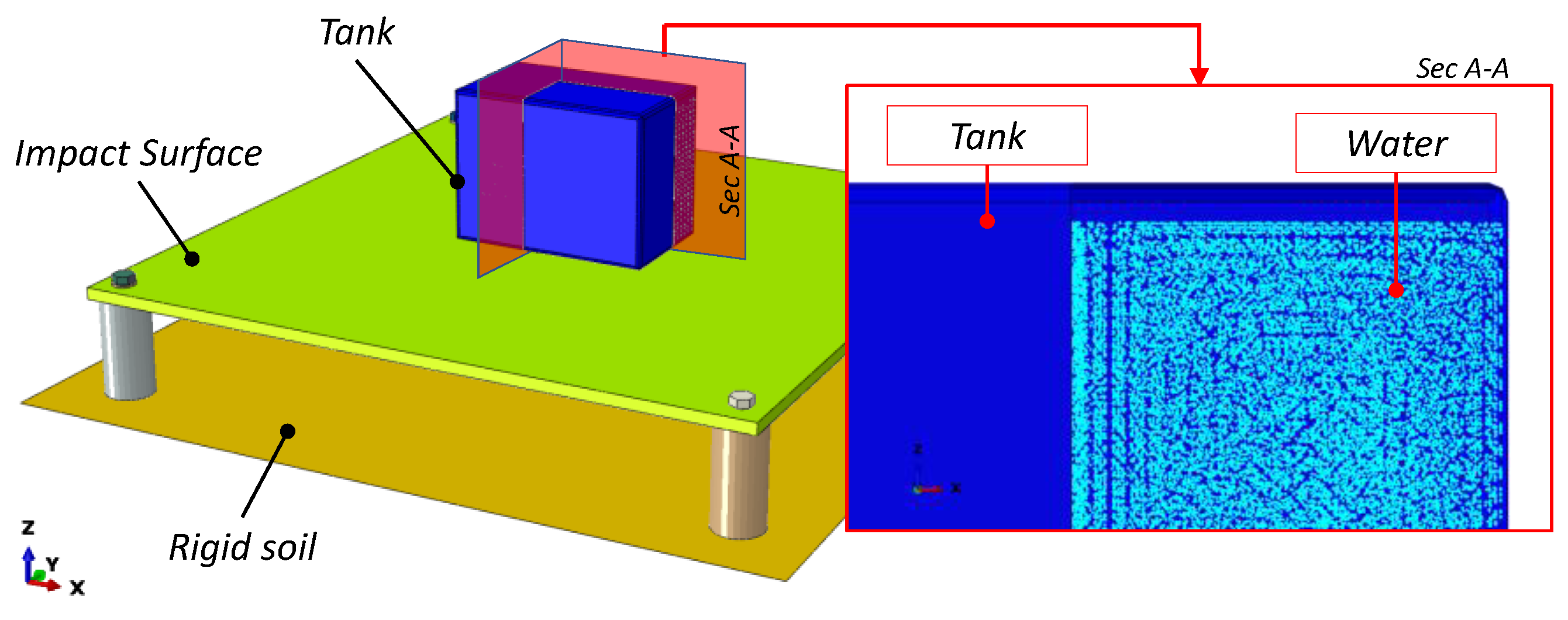
2.1. FE Model
2.1.1. Water Modelling
- h is the smoothing length
- mi and ρi are the mass and density of the particle
- xi and xj are the position of the particles
- W is the kernel interpolation.
2.1.2. Water Material Model
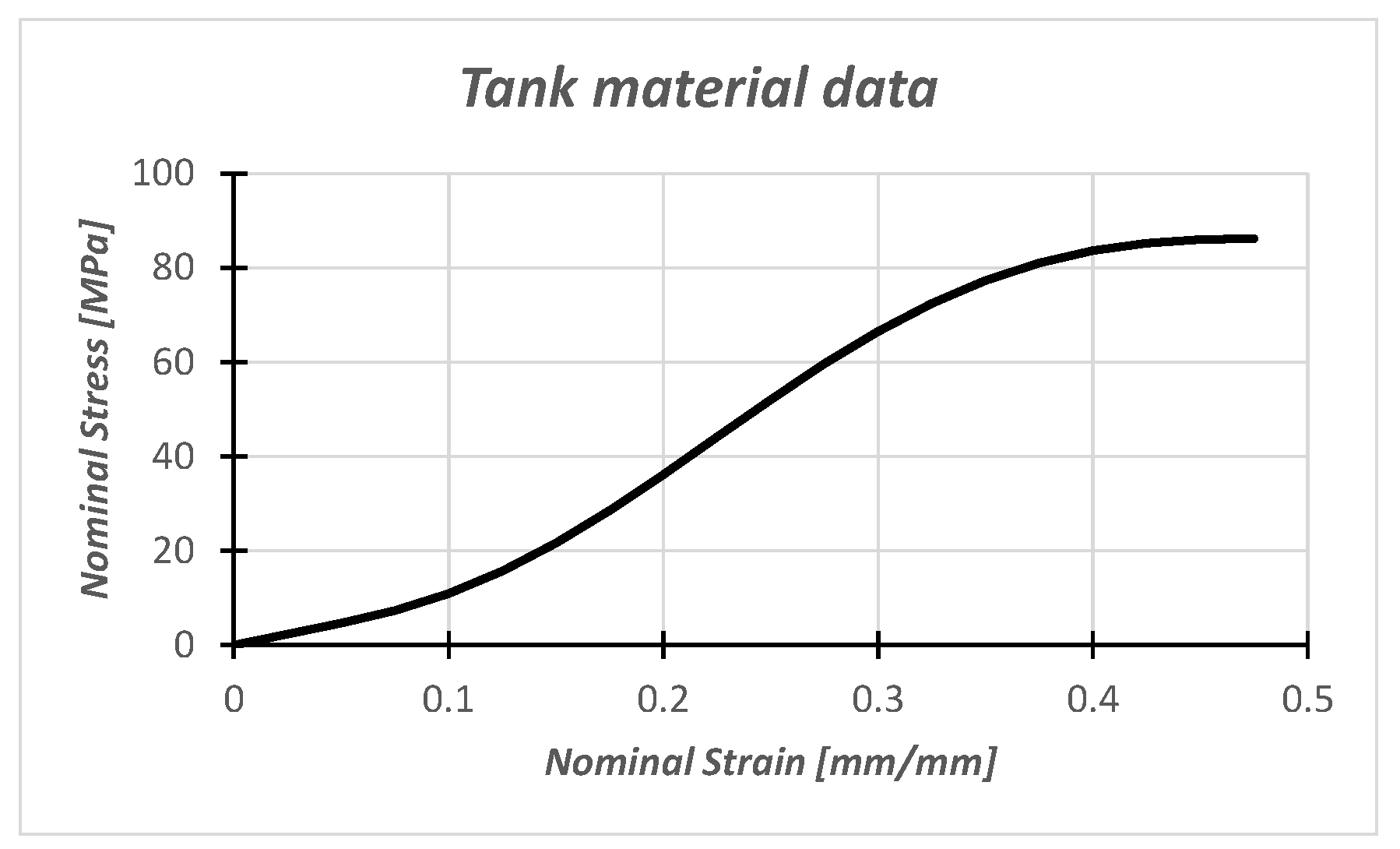
2.1.3. Tank Material Model
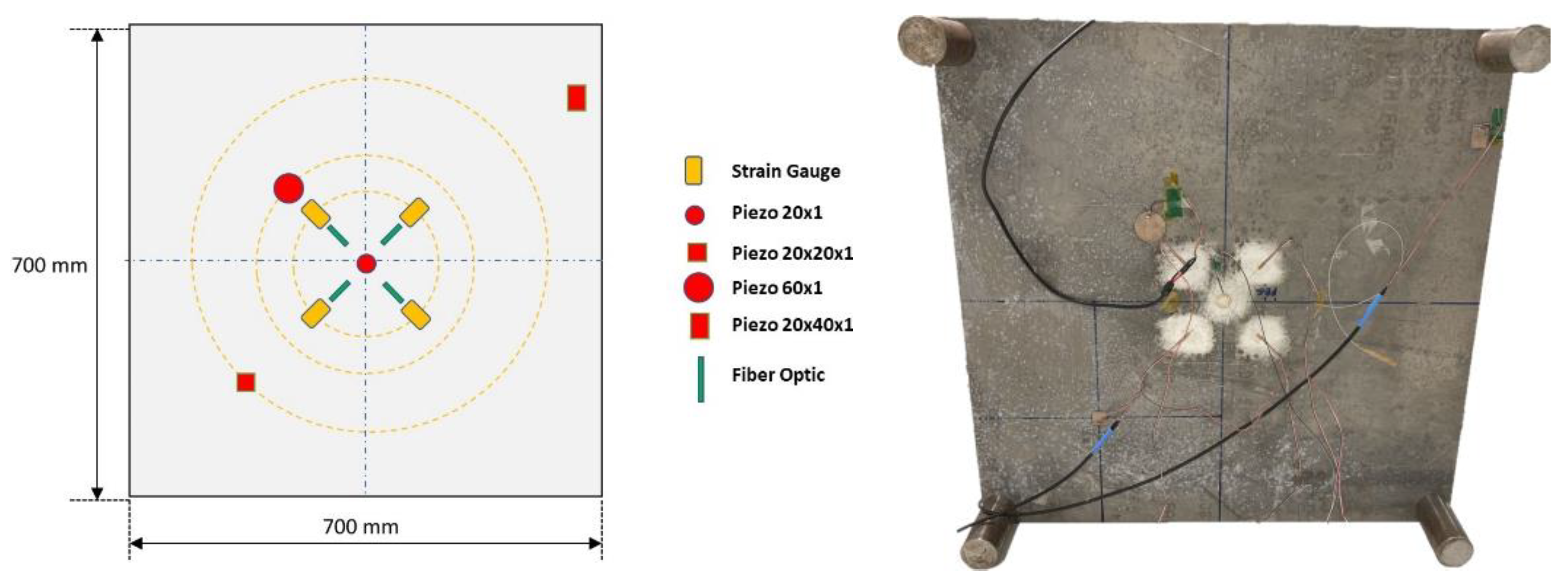
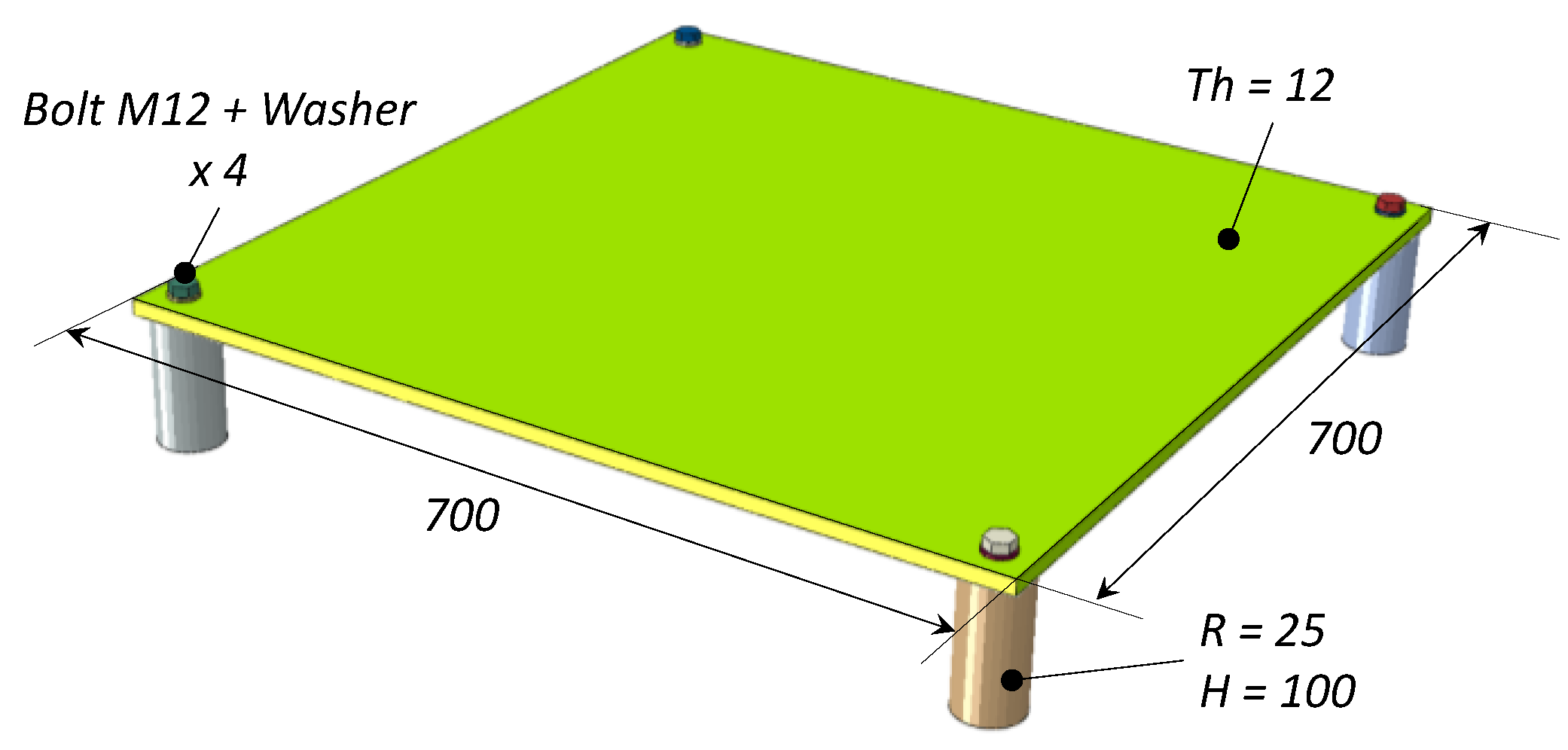
2.2. Instrumented Plate
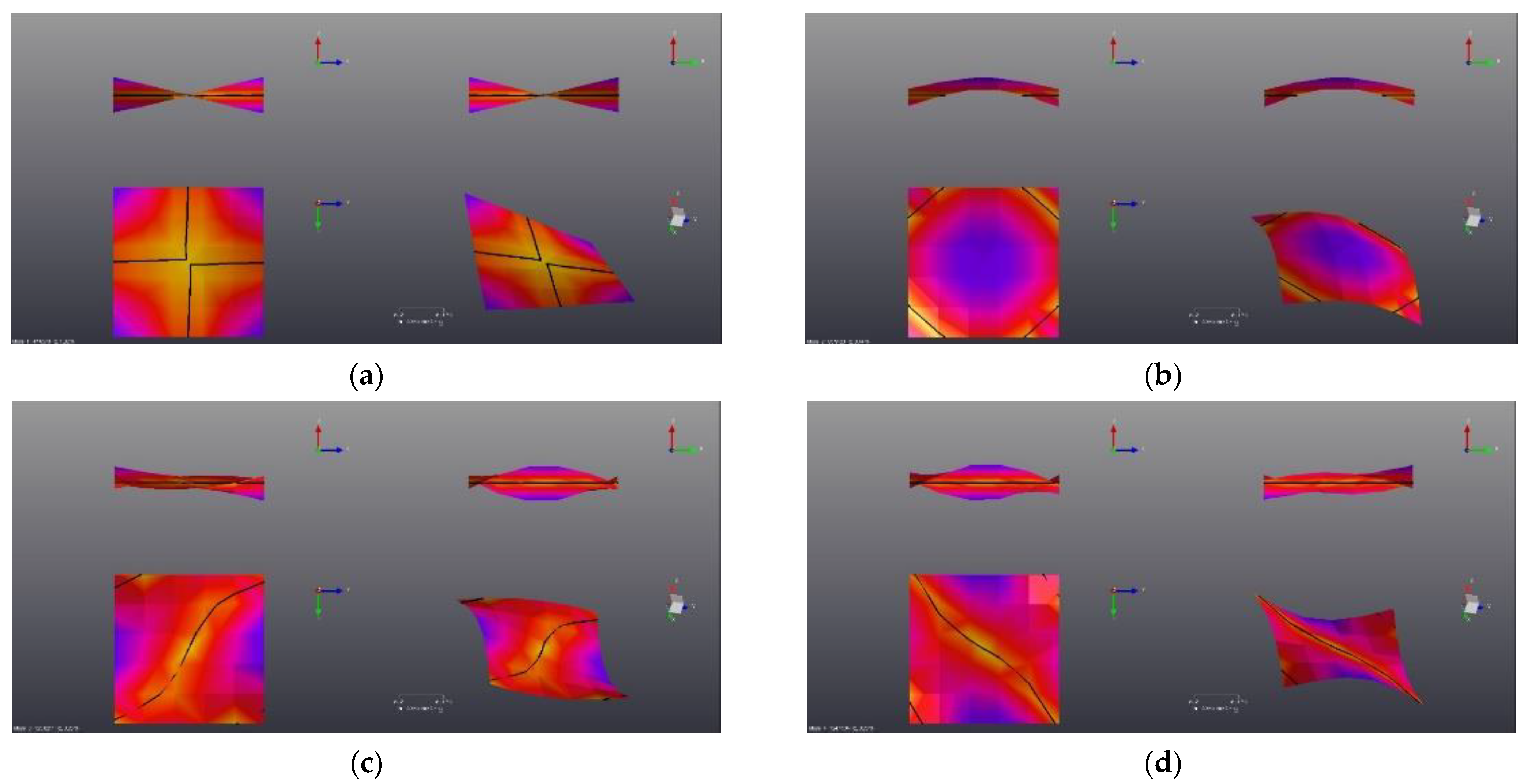
Numerical Modal Analysis
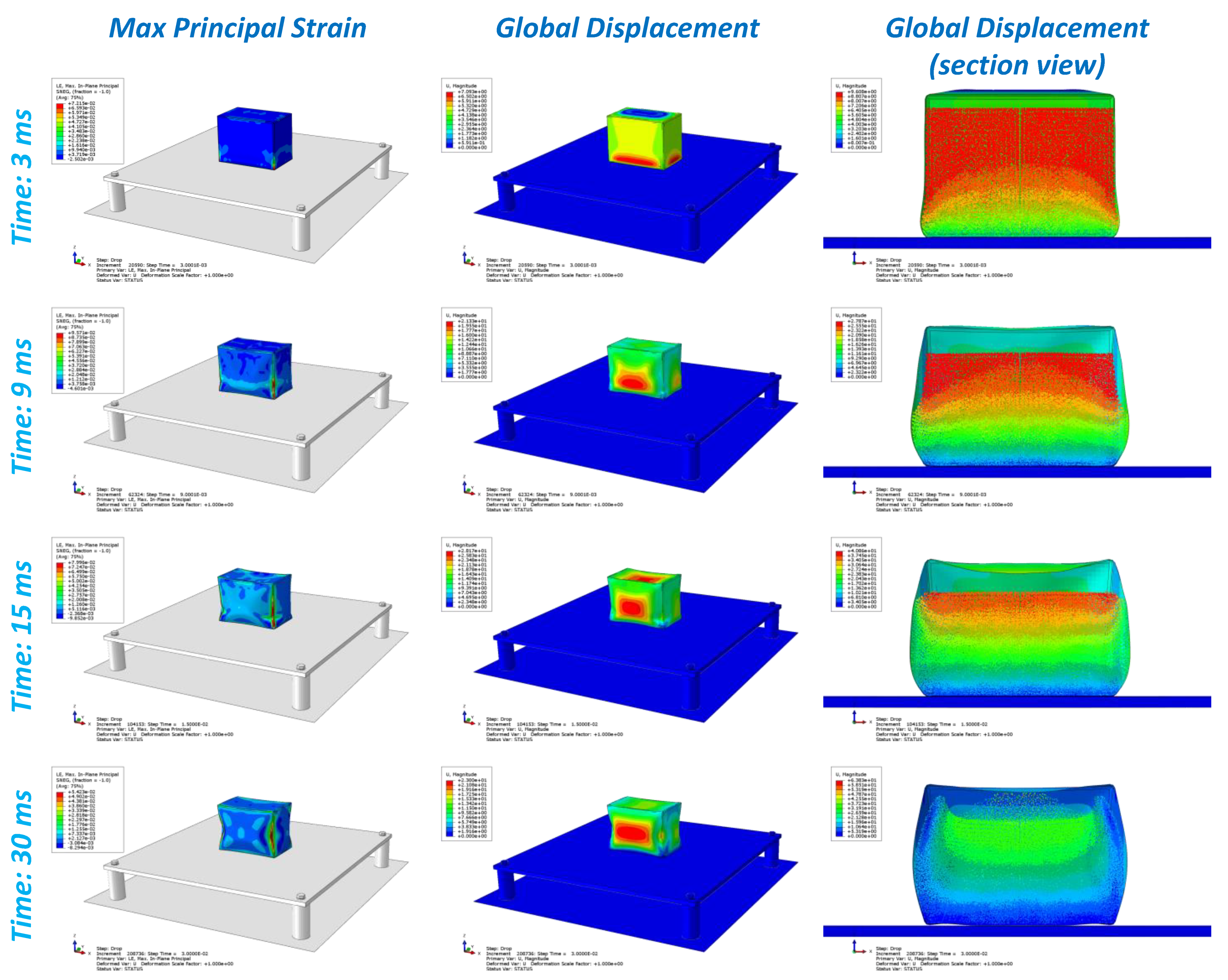
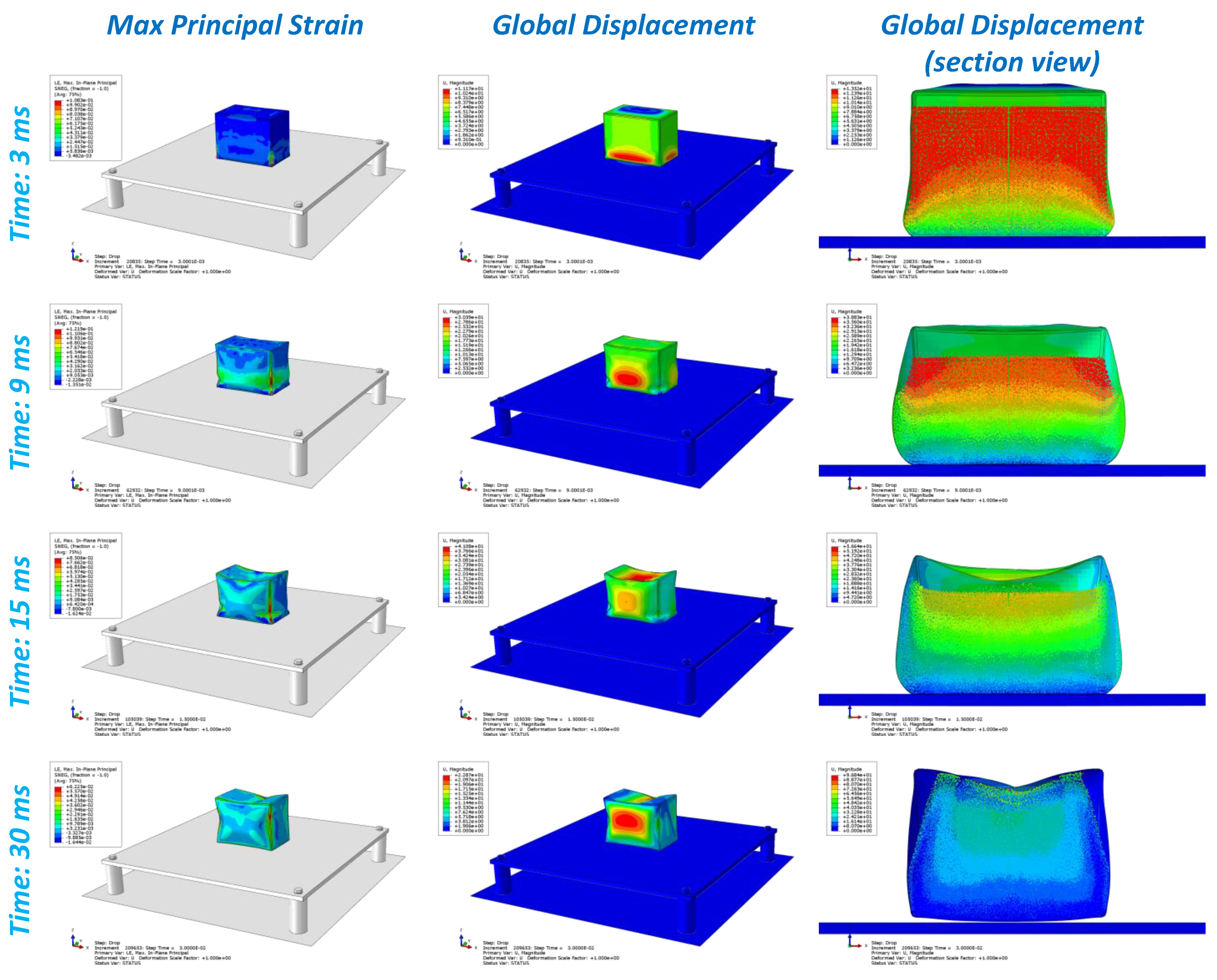
2.3. Drop Test Simulations
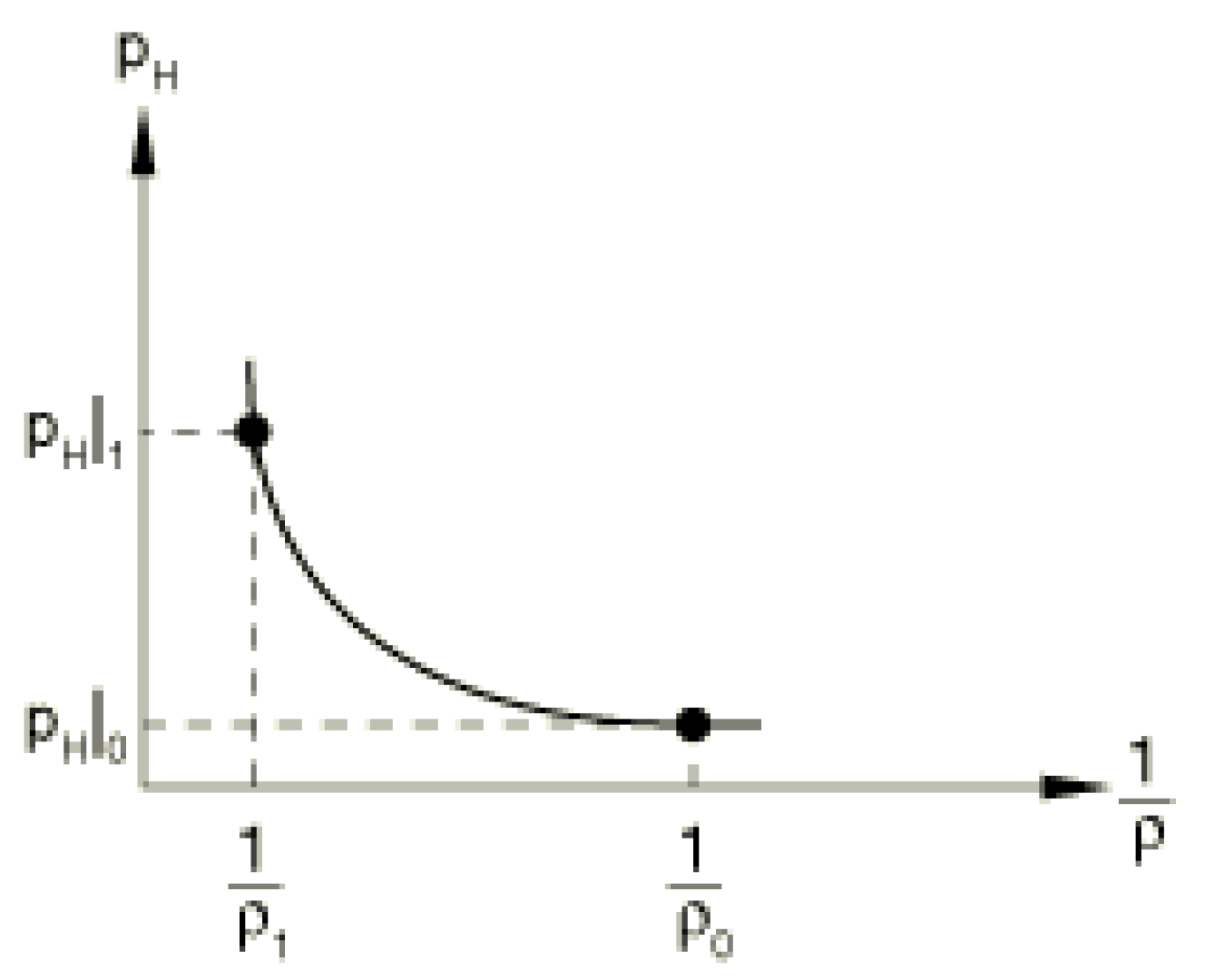
3. Signal Deconvolution
4. Experimental Results
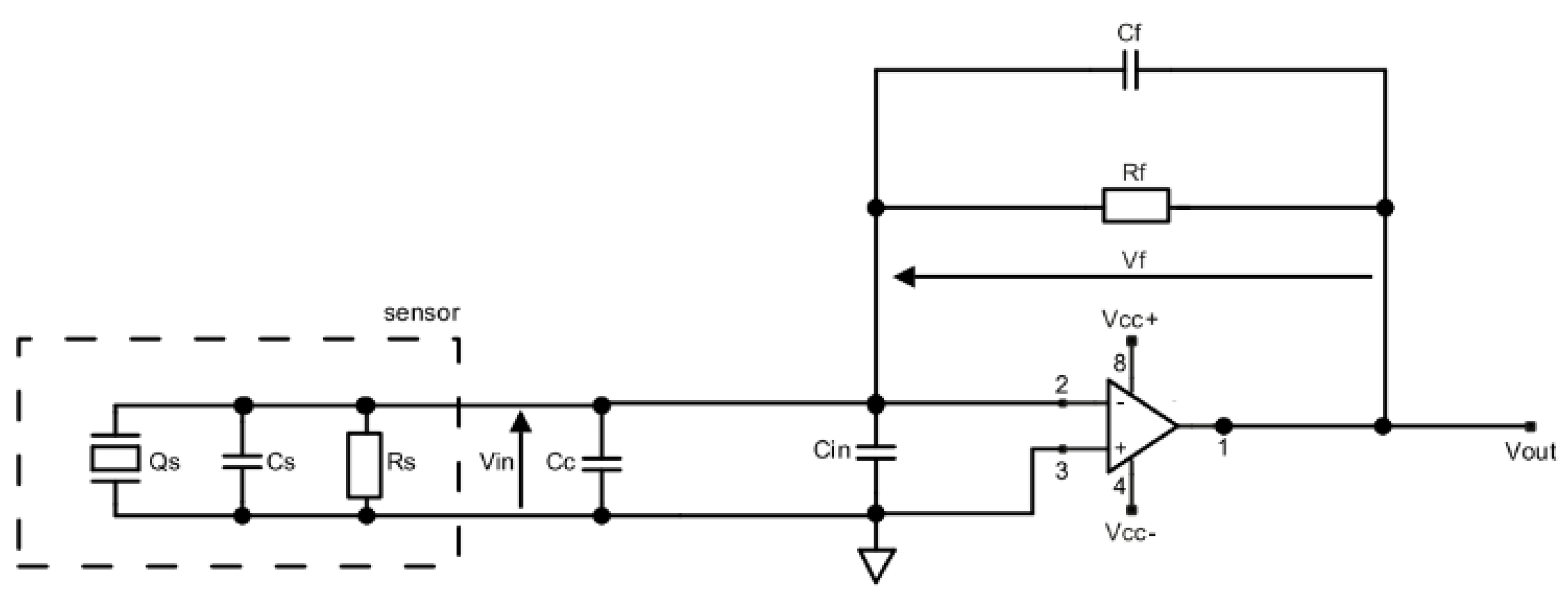
4.1. Electronic Circuit for Impact Measurements with PZT Sensors
- −
- piezoelectric coefficient d31 = 280 × 10–12 C/N
- −
- static capacitance (Cs) = 9 nF.
- Qs is the input charge
- Cs and Rs are the characteristic parameters of piezoelectric
- Cc is the cable capacitance
- Cin is the amplifier input capacitance
- Cf is the feedback capacitance
- Rf is the feedback resistance
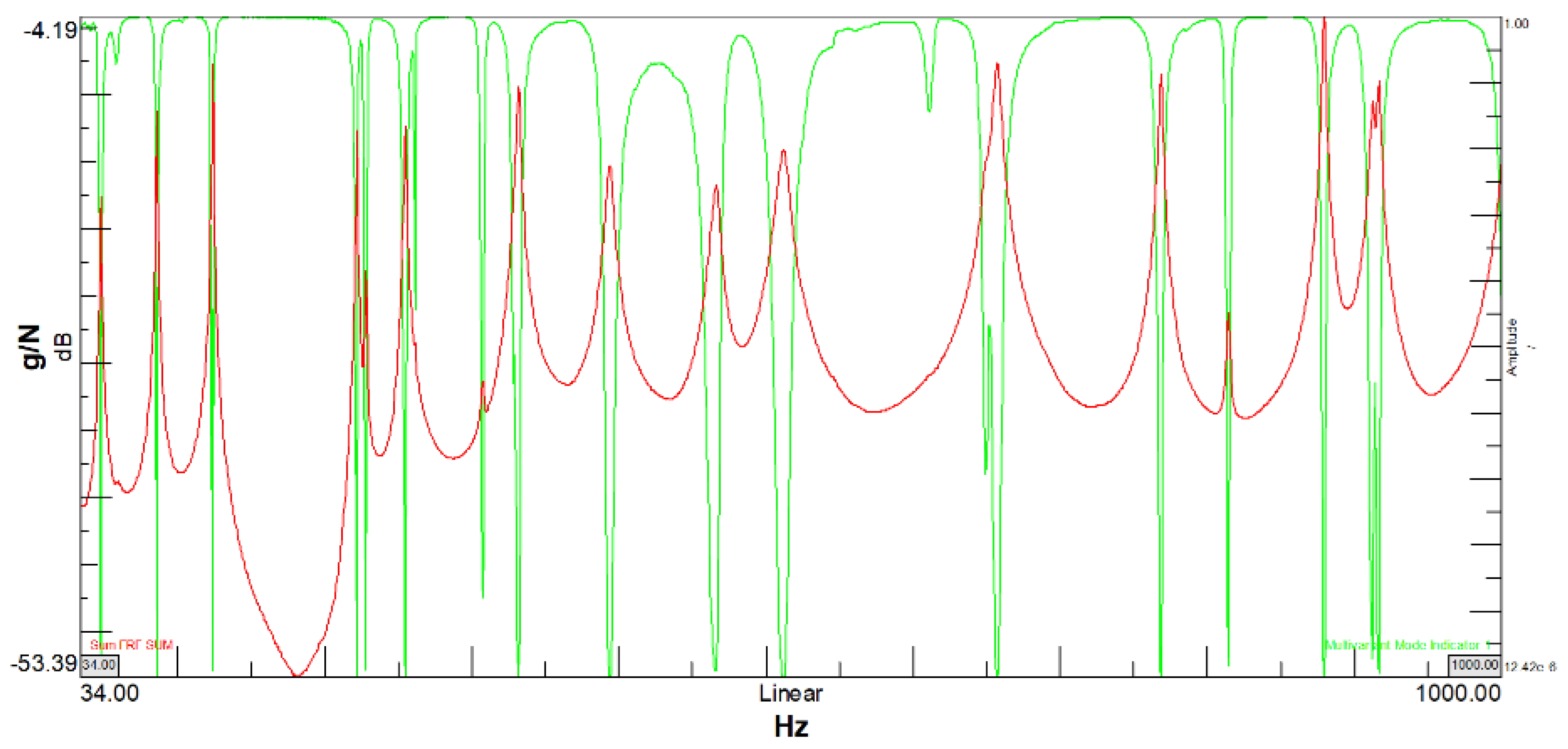
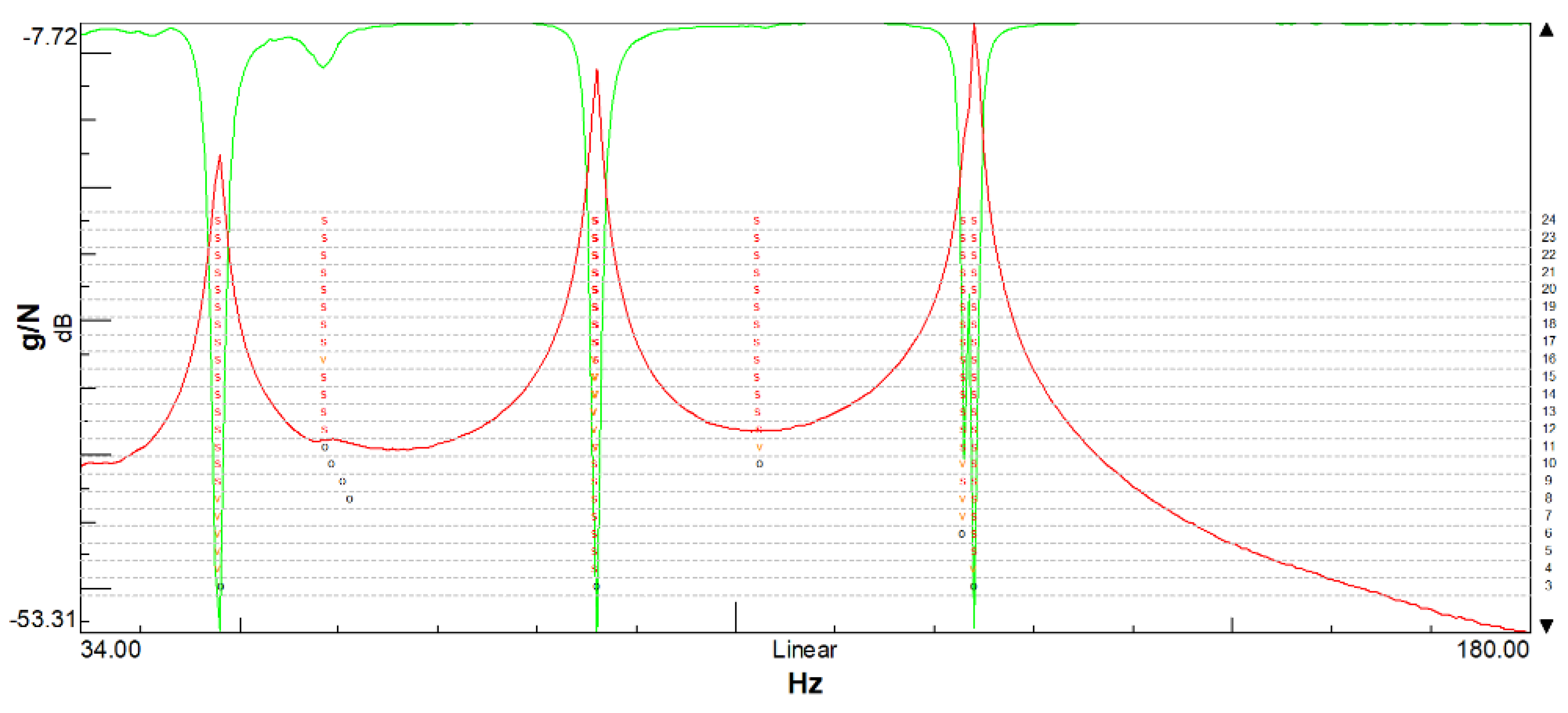
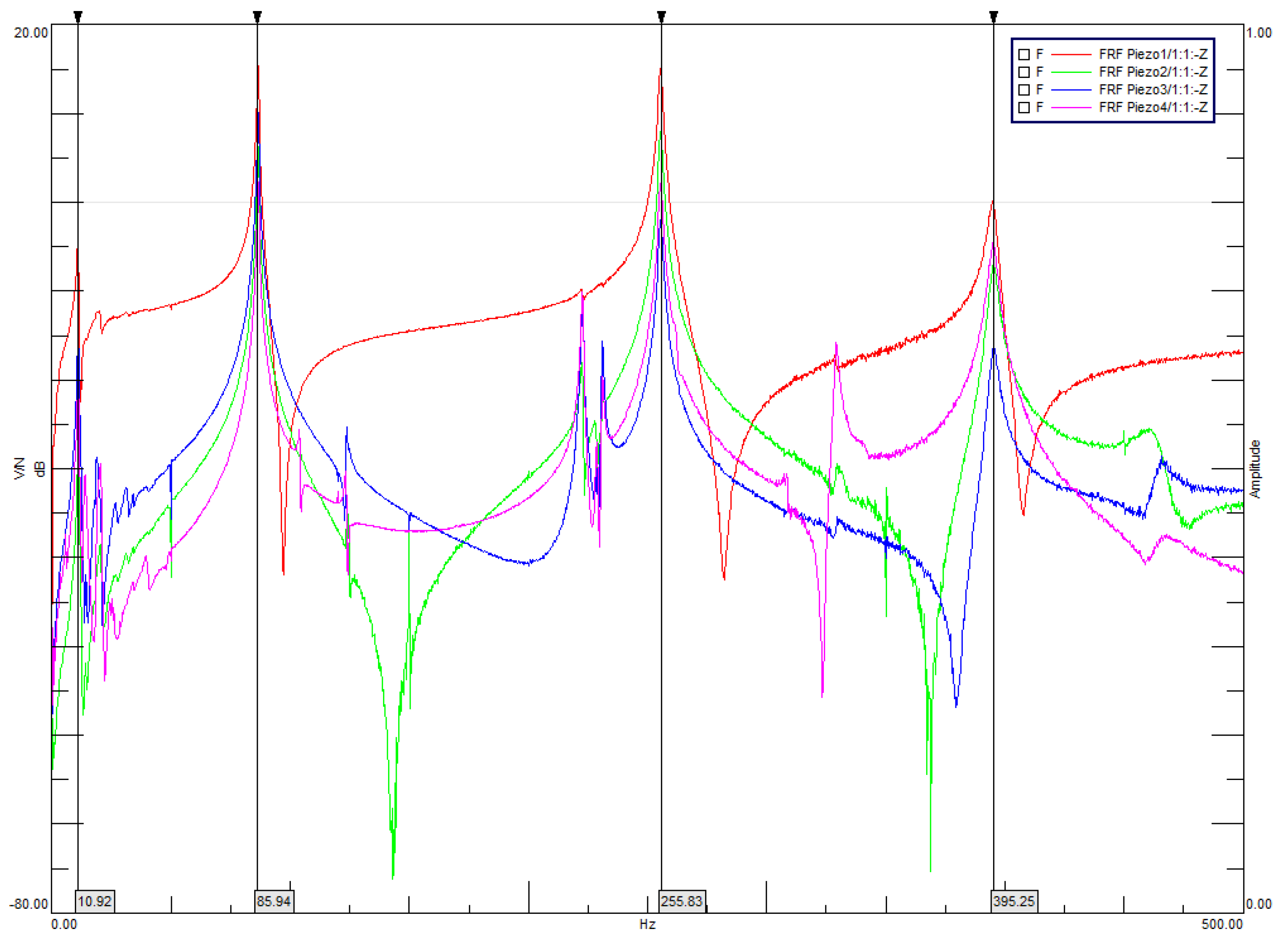
4.2. Experimental Modal Analysis
Numerical—Experimental Modal Correlation
4.3. Reconstruction of Impact Force Profiles
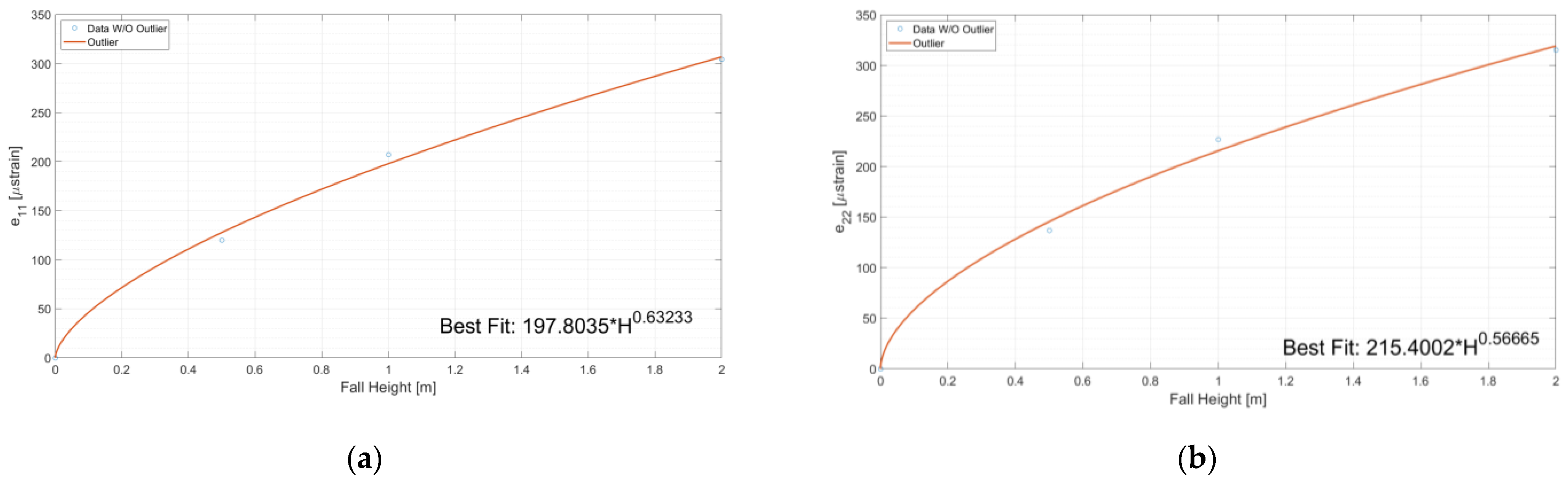
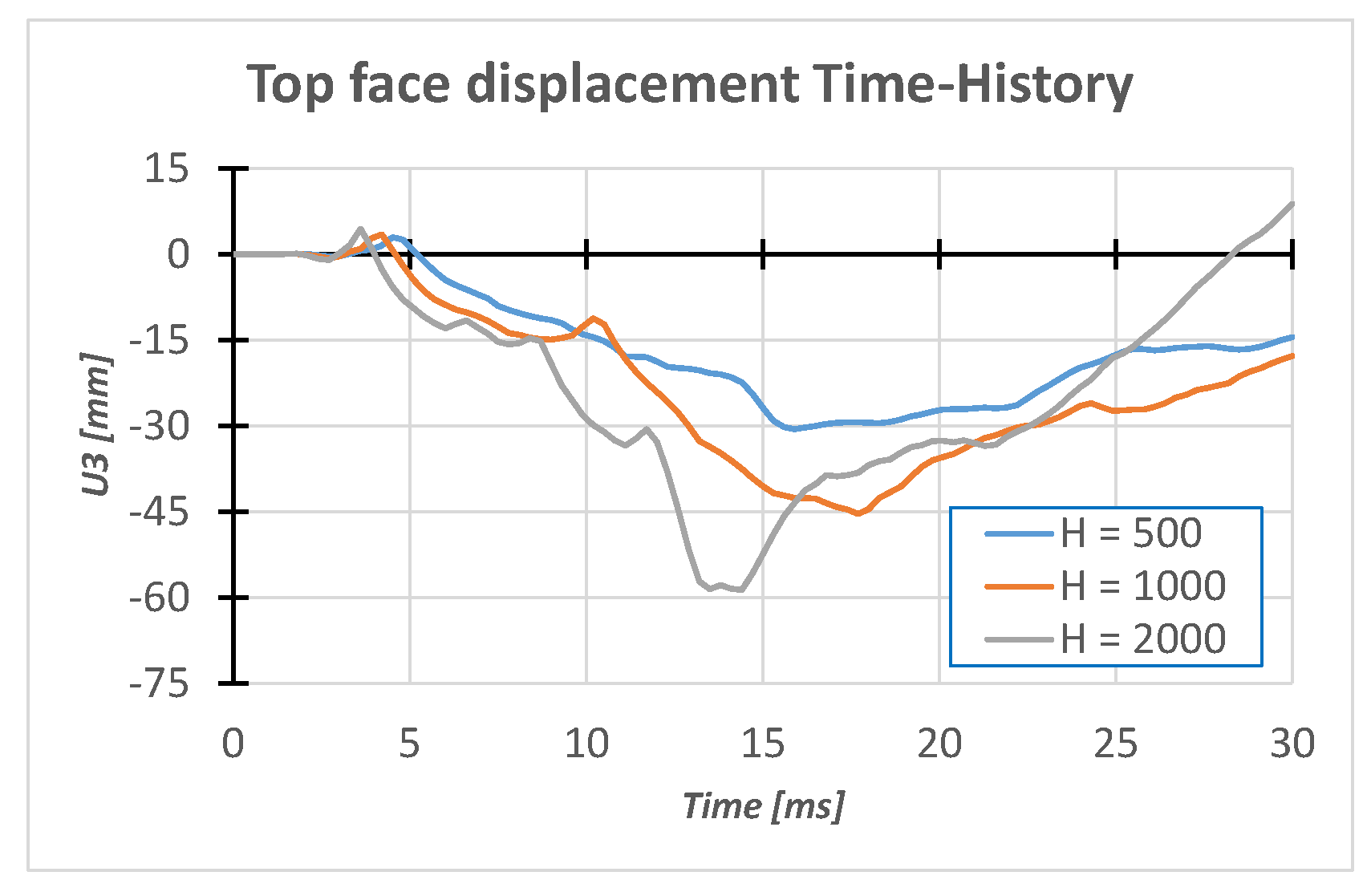
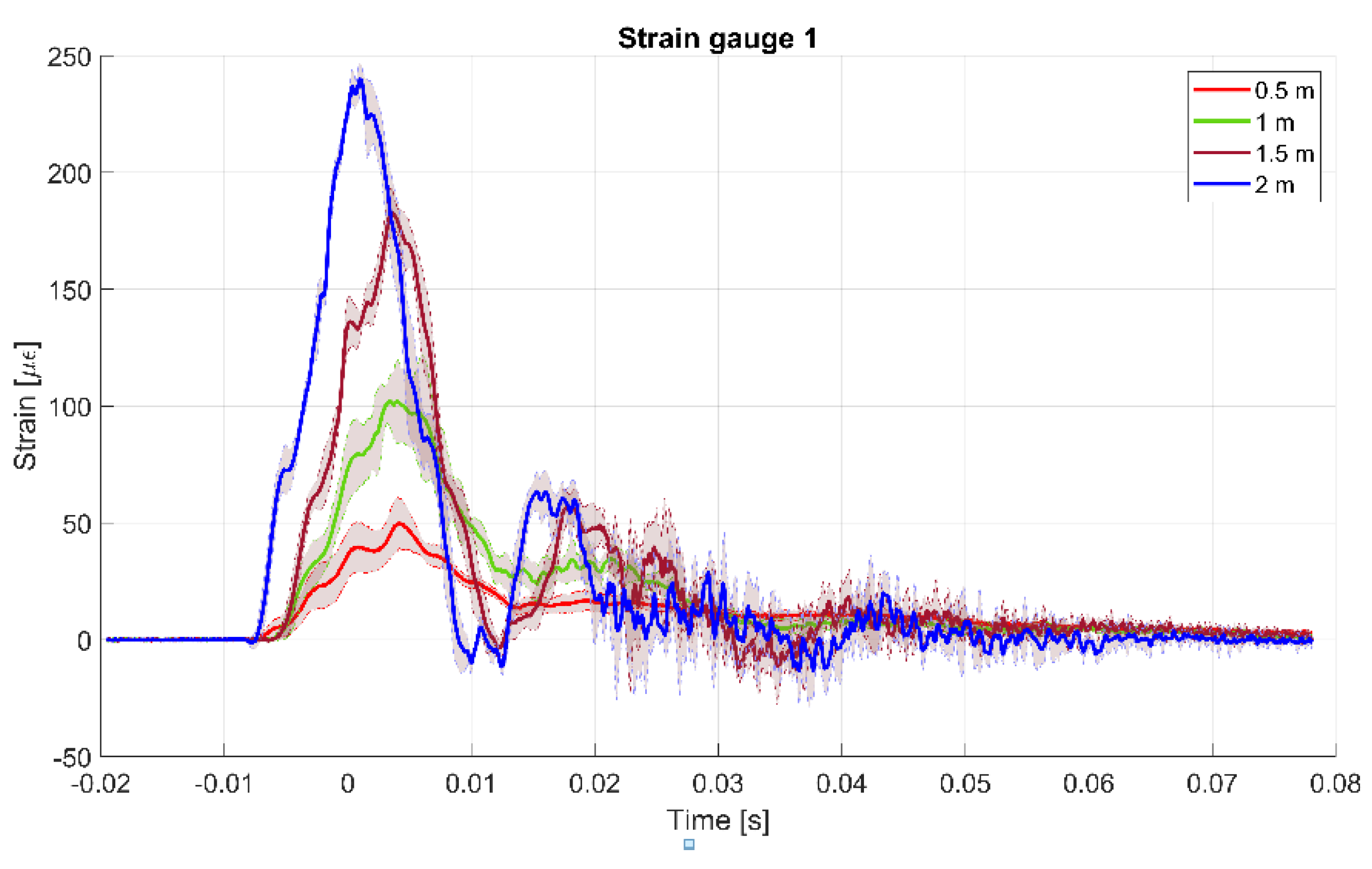
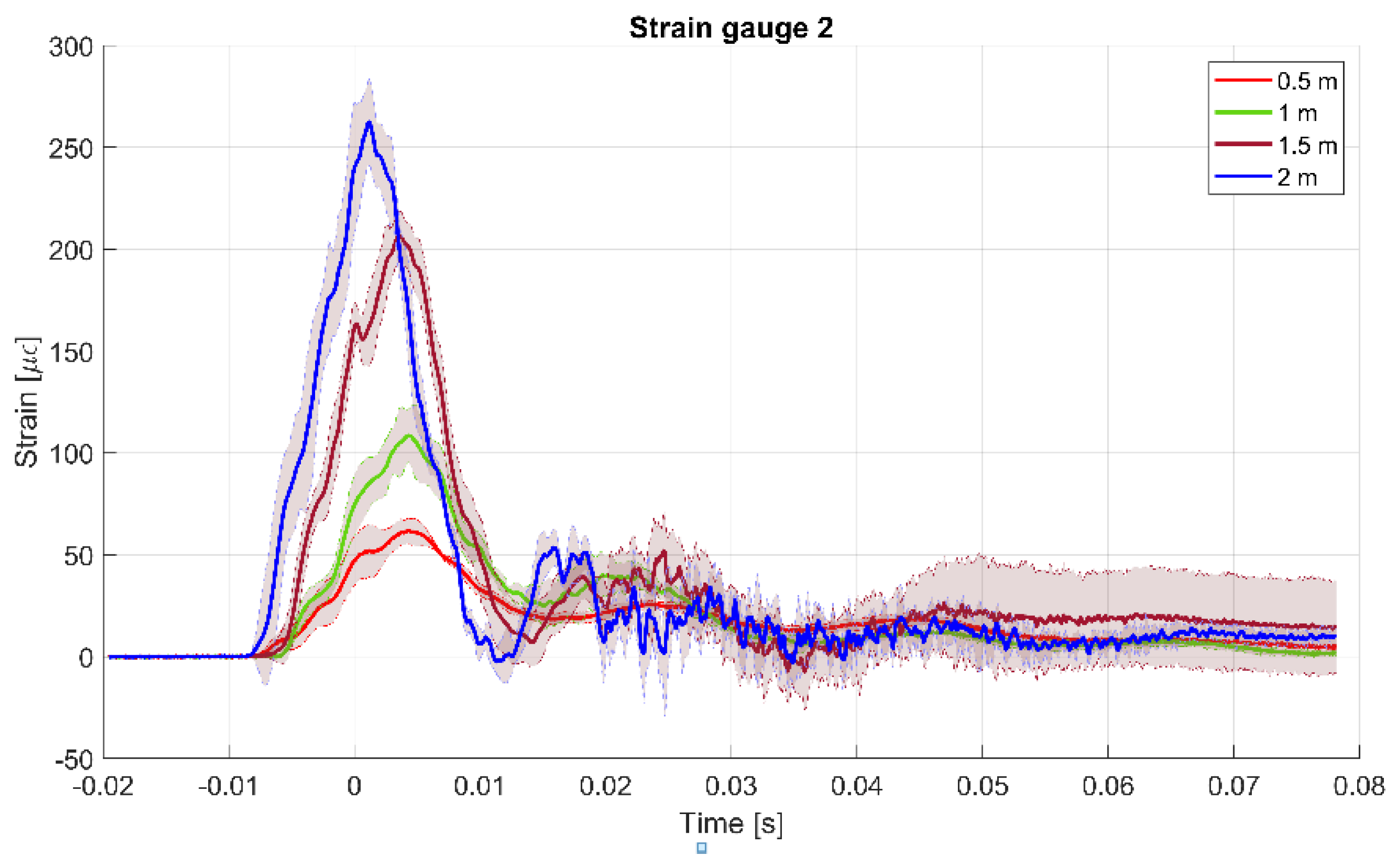
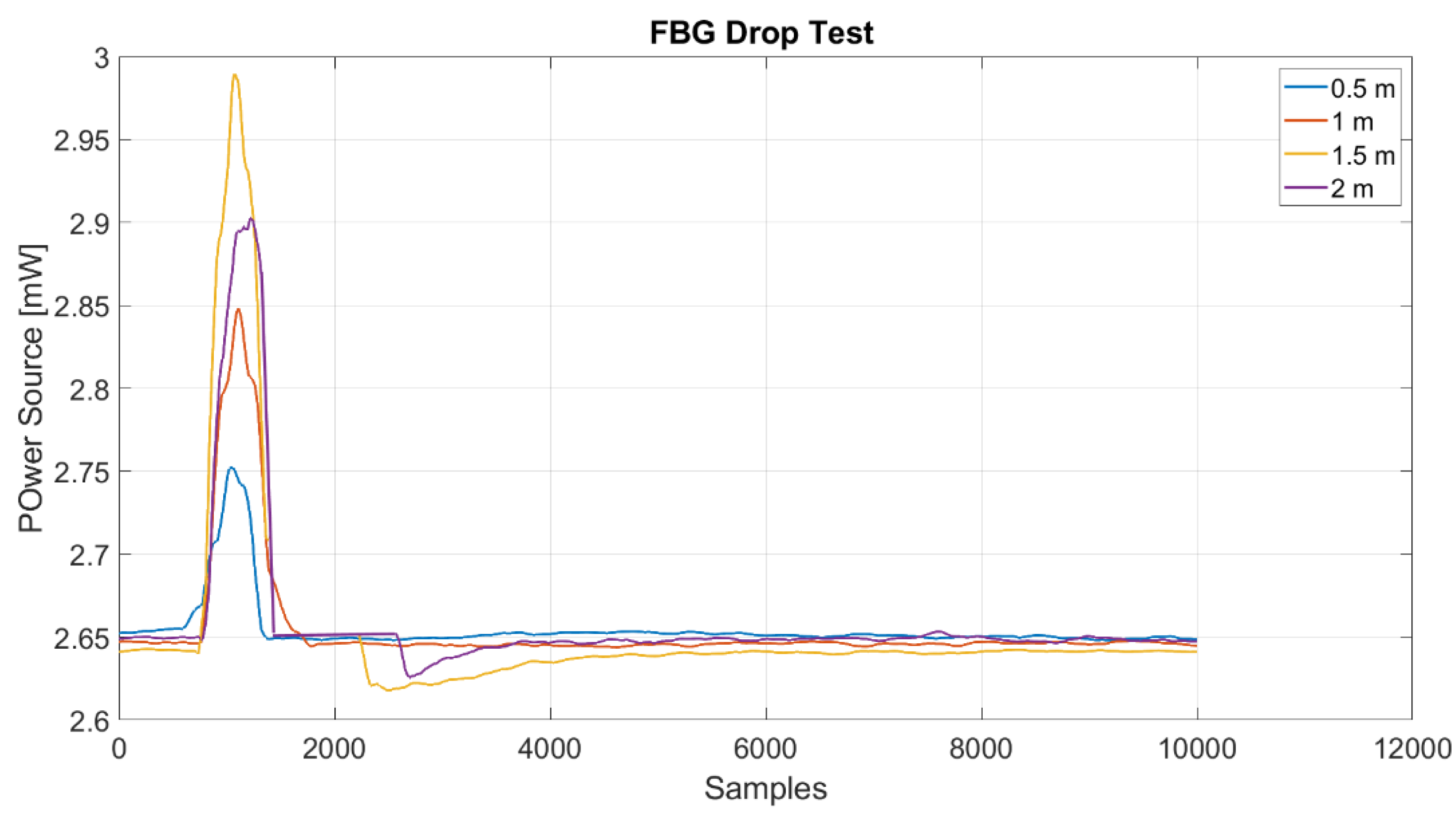
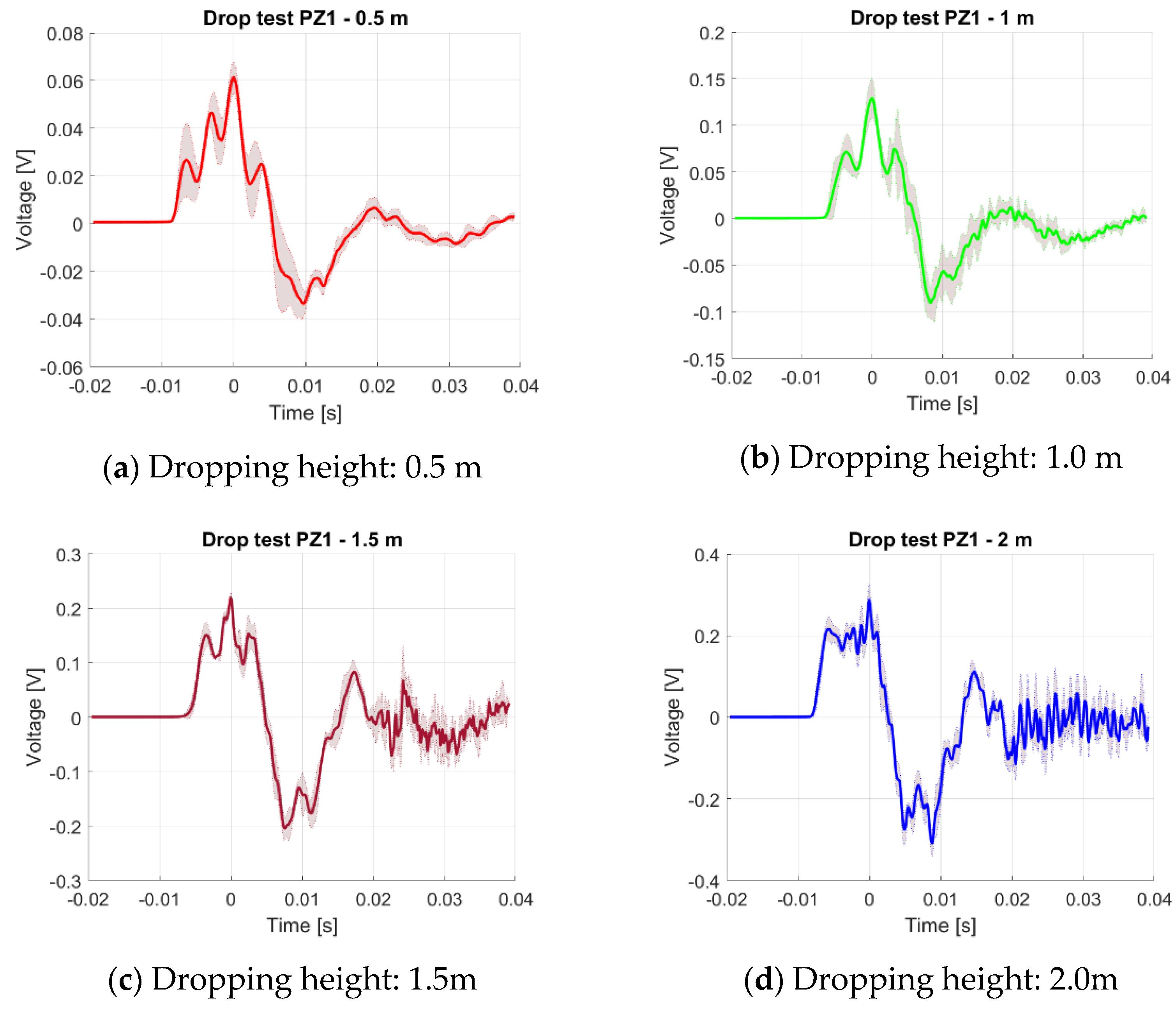
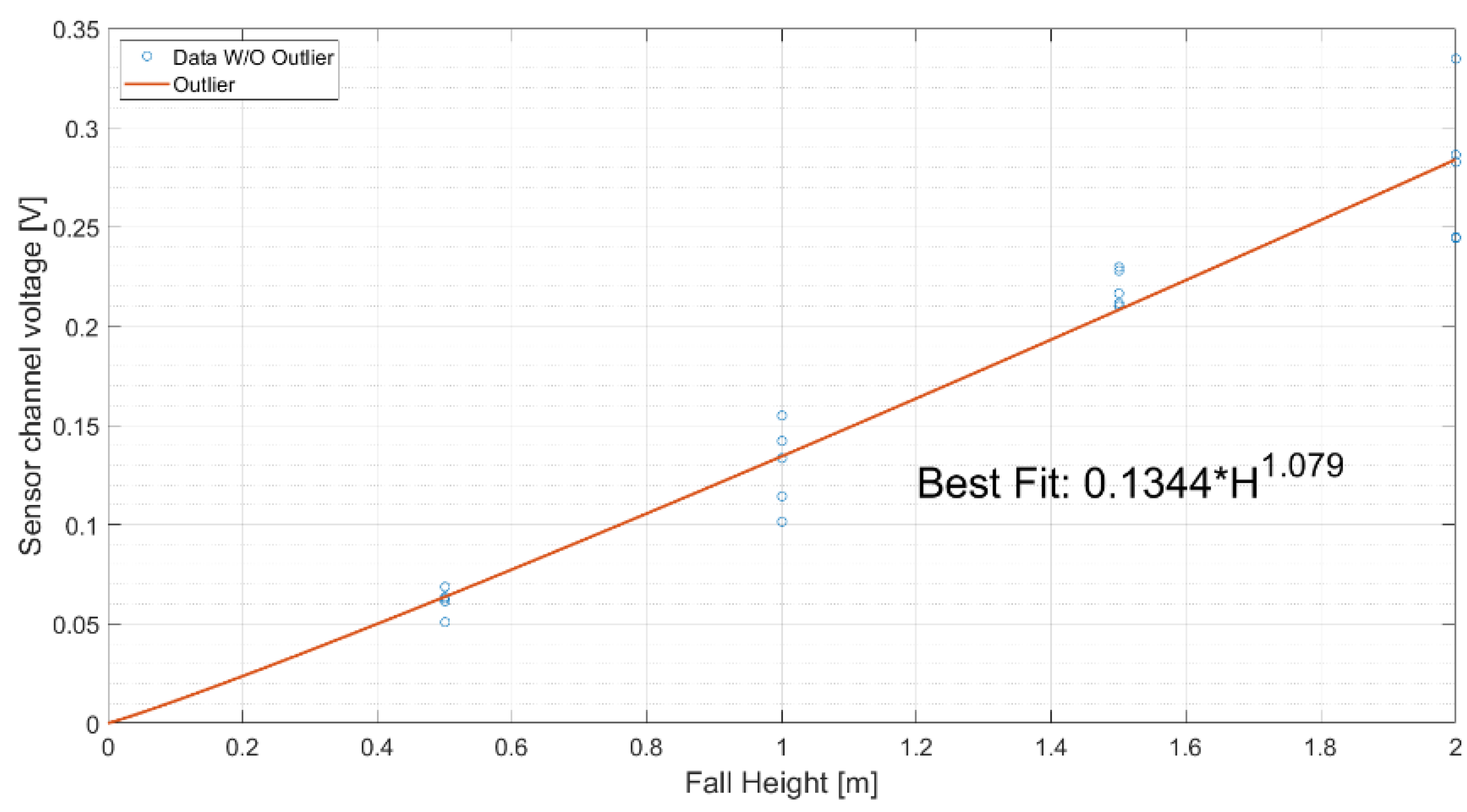
4.4. Drop Tests Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CS2 | Clean Sky 2 |
| NGCTR | Next Generation Civil Tiltrotor |
| TRL | Technology Readiness Level |
| BVID | Barely visible impact damage |
| SPH | Smoothed Particle Hydrodynamics |
| Op Amp | Operational Amplifier |
| FRF | Frequency Response Function |
| MIF | Modal Indicator Factor |
References
- Jackson, K.; Boitnott, R.; Fasanella, E.L.; Jones, L.E.; Lyle, K. A History of Full-Scale Aircraft and Rotorcraft Crash Testing and Simulation at NASA Langley Research Center; BiblioGov: Columbus, OH, USA, 2013. [Google Scholar]
- Robertson, S.H.; Johnson, N.B.; Hall, D.S.; Rimson, I.J. A Study of Helicopter Crash-Resistant Fuel Systems; Research Report no. DOT/FAA/AR-01/76; Federal Aviation Administration, U.S. Department of Transportation: Washington, DC, USA, 2002.
- Paciello, C.S.; Pezzella, C.; Belardo, M.; Magistro, S.; Di Caprio, F.; Musella, V.; Lamanna, G.; Di Palma, L. Crashworthiness of a Composite Bladder Fuel Tank for a Tilt Rotor Aircraft. J. Compos. Sci. 2021, 5, 285. [Google Scholar] [CrossRef]
- Luo, C.; Liu, H.R.; Yang, J.; Liu, K. Simulation and Analysis of Crashworthiness of Fuel Tank for Helicopters. Chin. J. Aeronaut. 2007, 20, 230–235. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Zhang, Z.; Yang, J.; Sun, Y. Fluid–structure interaction analysis of the drop impact test for helicopter fuel tank. SpringerPlus 2016, 5, 1573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, H.-G.; Kim, S. Numerical simulation of crash impact test for fuel cell group of rotorcraft. Int. J. Crashworthiness 2014, 19, 639–652. [Google Scholar] [CrossRef]
- Lu, G.Y.; Han, Z.J.; Lei, J.P.; Zhang, S.Y. A study on the impact response of liquid-filled cylindrical shells. Thin-Walled Struct. 2009, 47, 1557–1566. [Google Scholar] [CrossRef]
- Fast Rotorcraft, Clean Sky. Available online: https://www.cleansky.eu/fast-rotorcraft-iadp (accessed on 4 February 2022).
- Ciminello, M.; De Fenza, A.; Dimino, I.; Pecora, R. Skin-Spar Failure Detection of a Composite Winglet Using FBG Sensors. Arch. Mech. Eng. 2017, 64, 287–300. [Google Scholar] [CrossRef] [Green Version]
- Abaqus Analysis Guide, version 2020. Available online: http://130.149.89.49:2080/v6.11/books/usb/default.htm (accessed on 1 February 2022).
- Liu, M.B.; Liu, G.R. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to nonspherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monoghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Lattanzio, J.C. A refined particle method for astrophysical problems. Astron. Astrophys. 1985, 149, 135–143. [Google Scholar]
- Inoue, H.; Watanabe, R.; Shibuya, T.; Koizumi, T. Measurement of impact force by the deconvolution method (part-a). J. Jpn. Soc. Non-Destr. Insp. 1988, 34, 337–342. [Google Scholar]
- Inoue, H.; Watanabe, R.; Koizumi, T.; Fukuchi, J. Measurement of impact force applied to a plate by the deconvolution method (part-b). J. Jpn. Soc. Non-Destr. Insp. 1988, 37, 874–878. [Google Scholar]
- Wu, E.; Yeh, J.C.; Yen, C.S. Identification of impact forces at multiple locations on laminated plates. AIAA J. 1994, 32, 2433–2439. [Google Scholar] [CrossRef]
- Hu, N.; Fukunaga, H.; Yan, B. An efficient approach for identifying impact force using embedded piezoelectric sensors and Chebyshev polynomial. Proc. SPIE—Int. Soc. Opt. Eng. 2005, 6041, 60412Z. [Google Scholar] [CrossRef]
- Seno, A.H.; Ferri Aliabadi, M.H. A novel method for impact force estimation in composite plates under simulated environmental and operational conditions. Smart Mater. Struct. 2020, 29, 115029. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, L.; Wang, Y.; Cai, Y. Impact energy identification on a composite plate using basis vectors. Smart Mater. Struct. 2015, 24, 095007. [Google Scholar] [CrossRef]
- Jang, B.W.; Kim, C.G. Real-time detection of low-velocity impact-induced delamination onset in composite laminates for efficient management of structural health Composites. Smart Mater. Struct. 2017, 123, 124–135. [Google Scholar] [CrossRef]
- Dung, C.V.; Sasaki, E. Experimental study on impact force identification using output response of polyvinylidene fluoride sensor. Sens. Mater. 2018, 30, 7–21. [Google Scholar]
- Kalhori, H.; Ye, L.; Mustapha, S.; Li, J.; Li, B. Reconstruction and analysis of impact forces on a steel-beam-reinforced concrete deck. Exp. Mech. 2016, 56, 1547–1558. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Y.; Cai, Y.; Wu, Z.; Peng, W. Determination of impact events on a plate-like composite structure. Aeronaut. J. 2016, 120, 984–1004. [Google Scholar] [CrossRef]
- Gunawan, F.E. Levenberg—Marquardt iterative regularization for the pulse-type impact-force reconstruction. J. Sound Vib. 2012, 331, 5424–5434. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Egusquiza, M.; Bossio, M. Accurate Determination of the Frequency Response Function of Submerged and Confined Structures by Using PZT-Patches. Sensors 2017, 17, 660. [Google Scholar] [CrossRef] [PubMed] [Green Version]


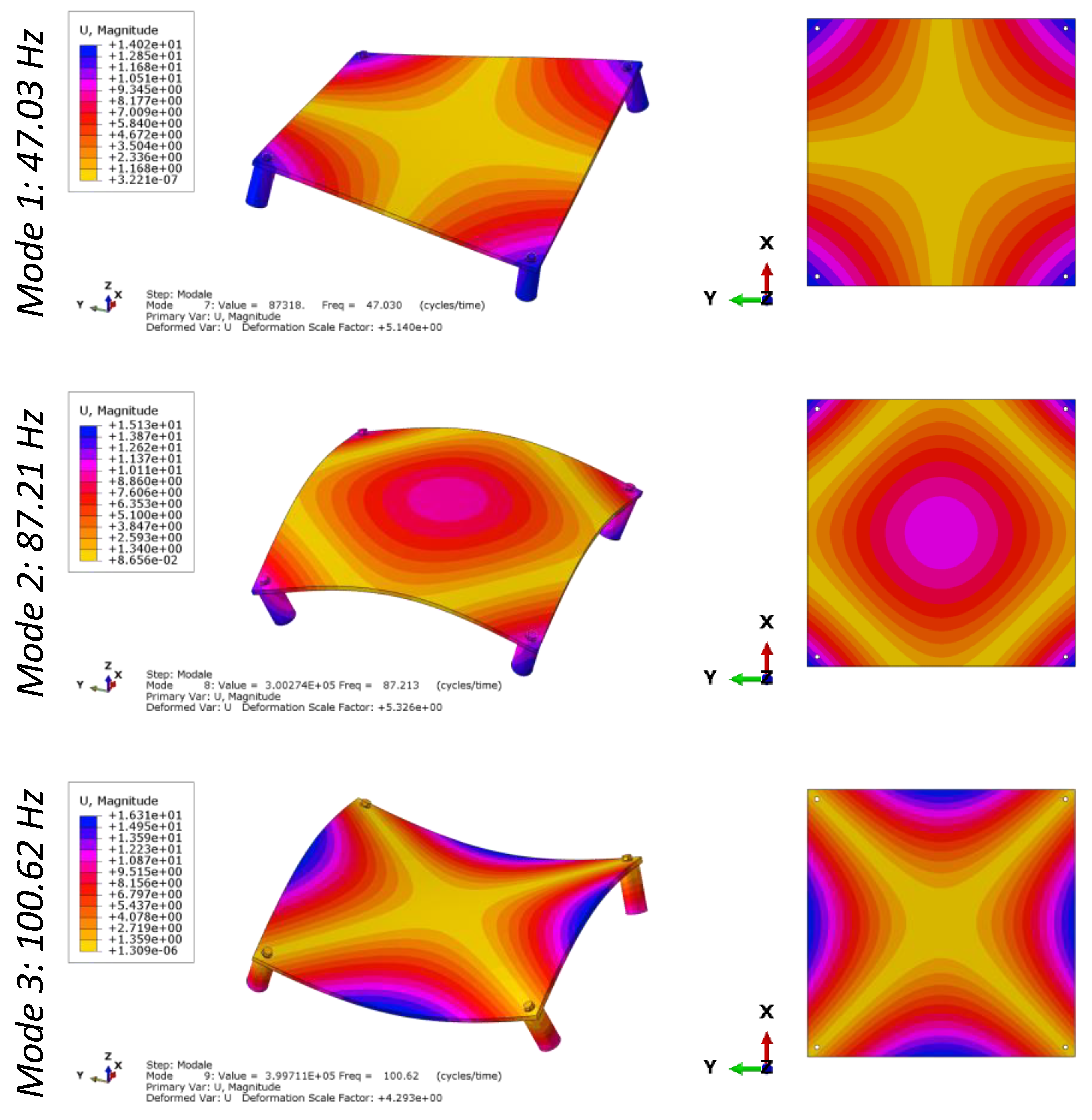








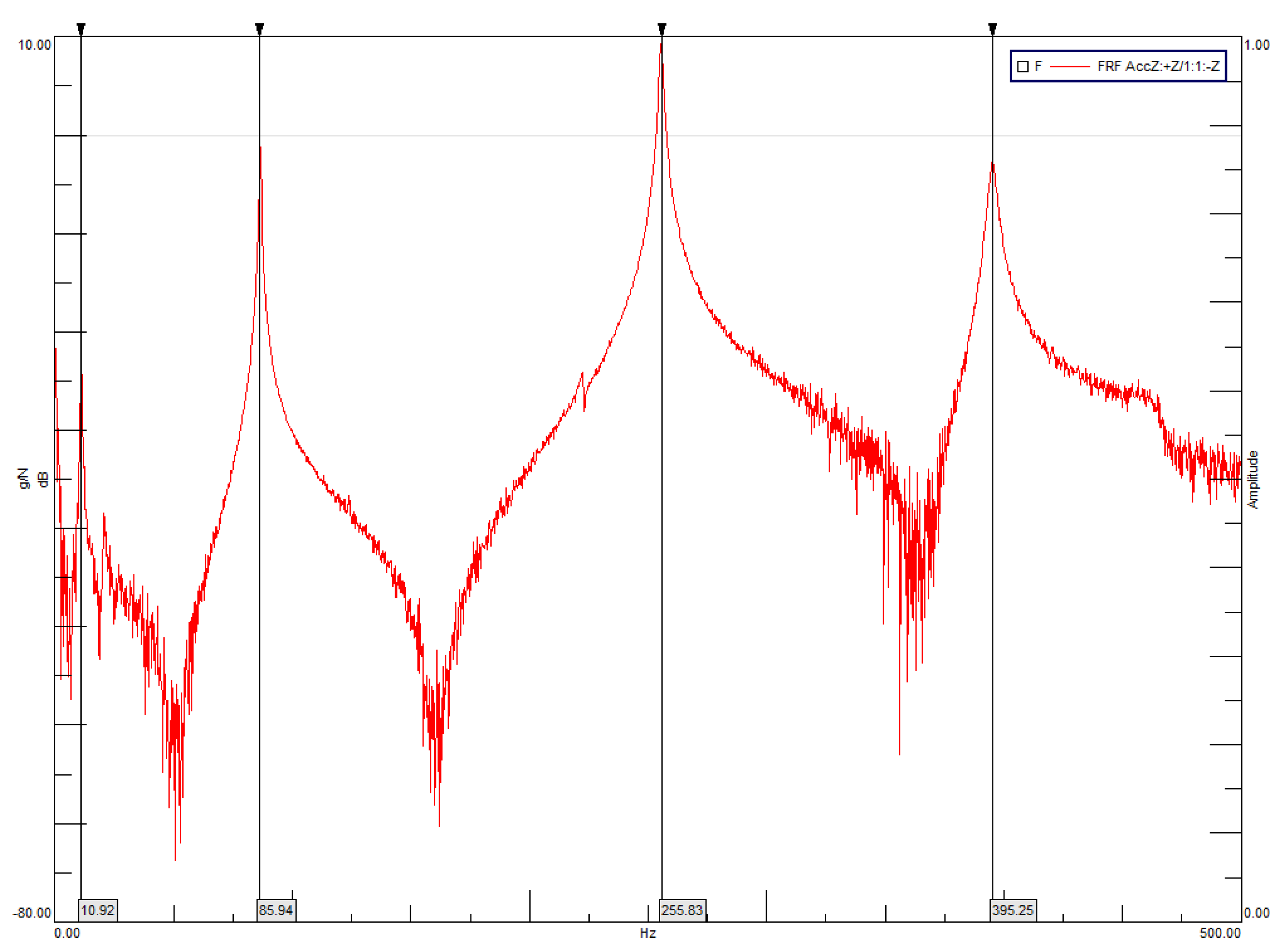

| Mode Number | Free–Free Condition (Hz) |
|---|---|
| Mode 1 | 47.03 |
| Mode 2 | 87.21 |
| Mode 3 | 100.62 |
| Mode 4 | 127.71 |
| Mode 5 | 127.71 |
| Mode Number | Numerical (Hz) | Experimental (Hz) | Error (%) |
|---|---|---|---|
| Mode 1 | 47.03 | 47.84 | −1.7% |
| Mode 2 | 87.21 | 85.90 | 1.5% |
| Mode 3 | 100.62 | - | N.A. |
| Mode 4 | 127.71 | 123.01 | 3.8% |
| Mode 5 | 127.71 | 124.10 | 2.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimino, I.; Diodati, G.; Di Caprio, F.; Ciminello, M.; Menichino, A.; Inverno, M.; Belardo, M.; Di Palma, L. Numerical and Experimental Studies of Free-Fall Drop Impact Tests Using Strain Gauge, Piezoceramic, and Fiber Optic Sensors. Appl. Mech. 2022, 3, 313-338. https://doi.org/10.3390/applmech3010020
Dimino I, Diodati G, Di Caprio F, Ciminello M, Menichino A, Inverno M, Belardo M, Di Palma L. Numerical and Experimental Studies of Free-Fall Drop Impact Tests Using Strain Gauge, Piezoceramic, and Fiber Optic Sensors. Applied Mechanics. 2022; 3(1):313-338. https://doi.org/10.3390/applmech3010020
Chicago/Turabian StyleDimino, Ignazio, Gianluca Diodati, Francesco Di Caprio, Monica Ciminello, Aniello Menichino, Michele Inverno, Marika Belardo, and Luigi Di Palma. 2022. "Numerical and Experimental Studies of Free-Fall Drop Impact Tests Using Strain Gauge, Piezoceramic, and Fiber Optic Sensors" Applied Mechanics 3, no. 1: 313-338. https://doi.org/10.3390/applmech3010020
APA StyleDimino, I., Diodati, G., Di Caprio, F., Ciminello, M., Menichino, A., Inverno, M., Belardo, M., & Di Palma, L. (2022). Numerical and Experimental Studies of Free-Fall Drop Impact Tests Using Strain Gauge, Piezoceramic, and Fiber Optic Sensors. Applied Mechanics, 3(1), 313-338. https://doi.org/10.3390/applmech3010020










