Impact Testing on the Pristine and Repaired Composite Materials for Aerostructures
Abstract
:1. Introduction
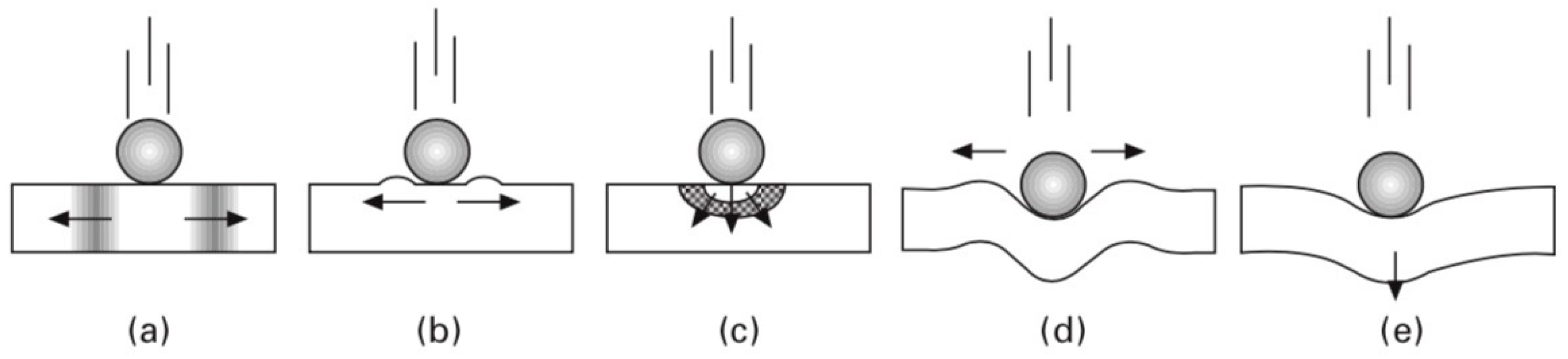
2. Response of Pristine Composites under Impact Loading
2.1. Hard Impact
2.1.1. Low Velocity
2.1.2. Intermediate Velocity
2.2. Soft Impact
3. Performance of Repaired Composites Subjected to Impact Loading
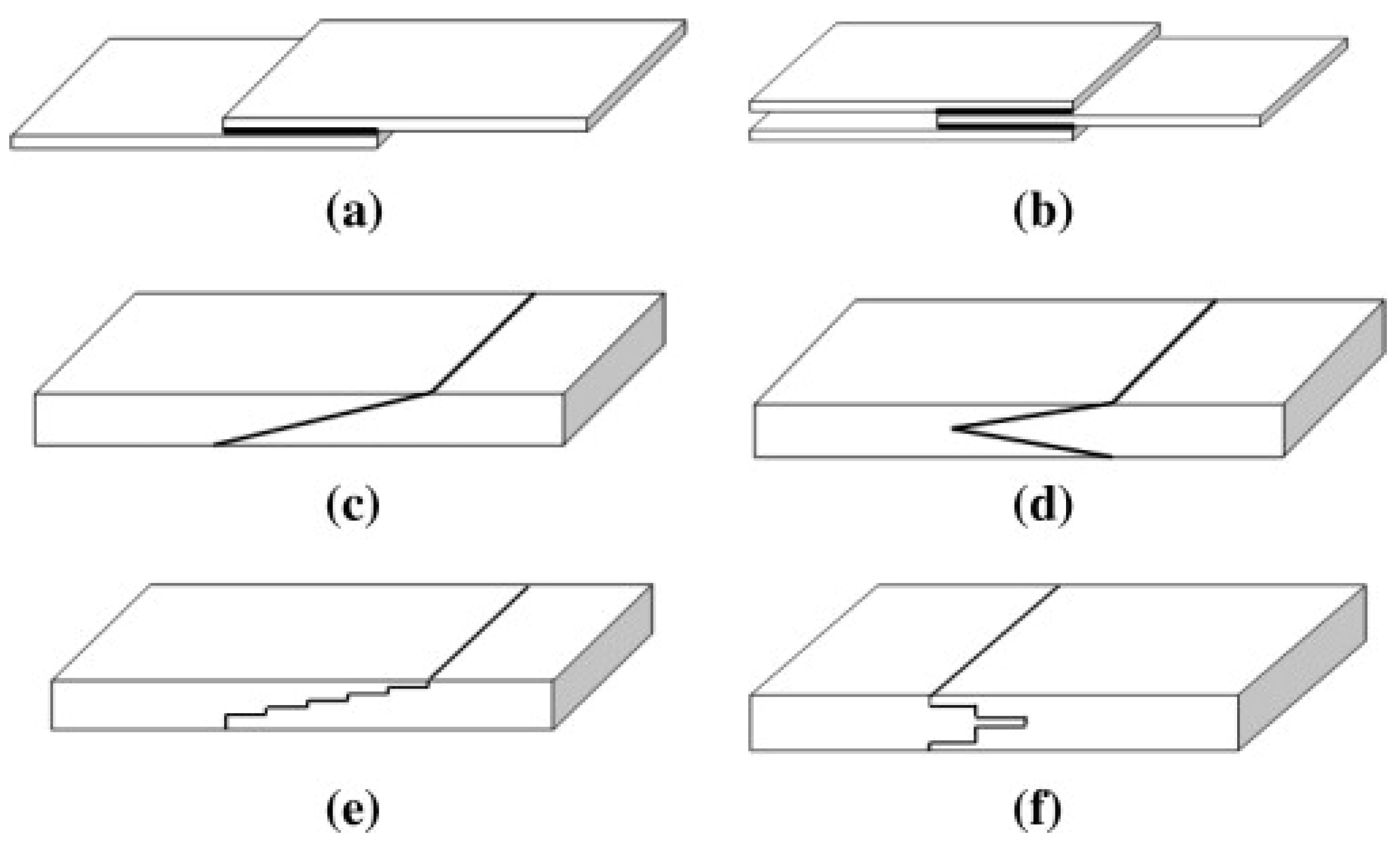
3.1. Adhesively Bonded Repair
3.2. Tensile Testing
3.3. Impact Testing
3.3.1. Scarf Repairs under Low-Velocity Impacts
3.3.2. Patch Repairs under Low-Velocity Impacts
3.3.3. High-Velocity Impacts
4. Numerical Simulation
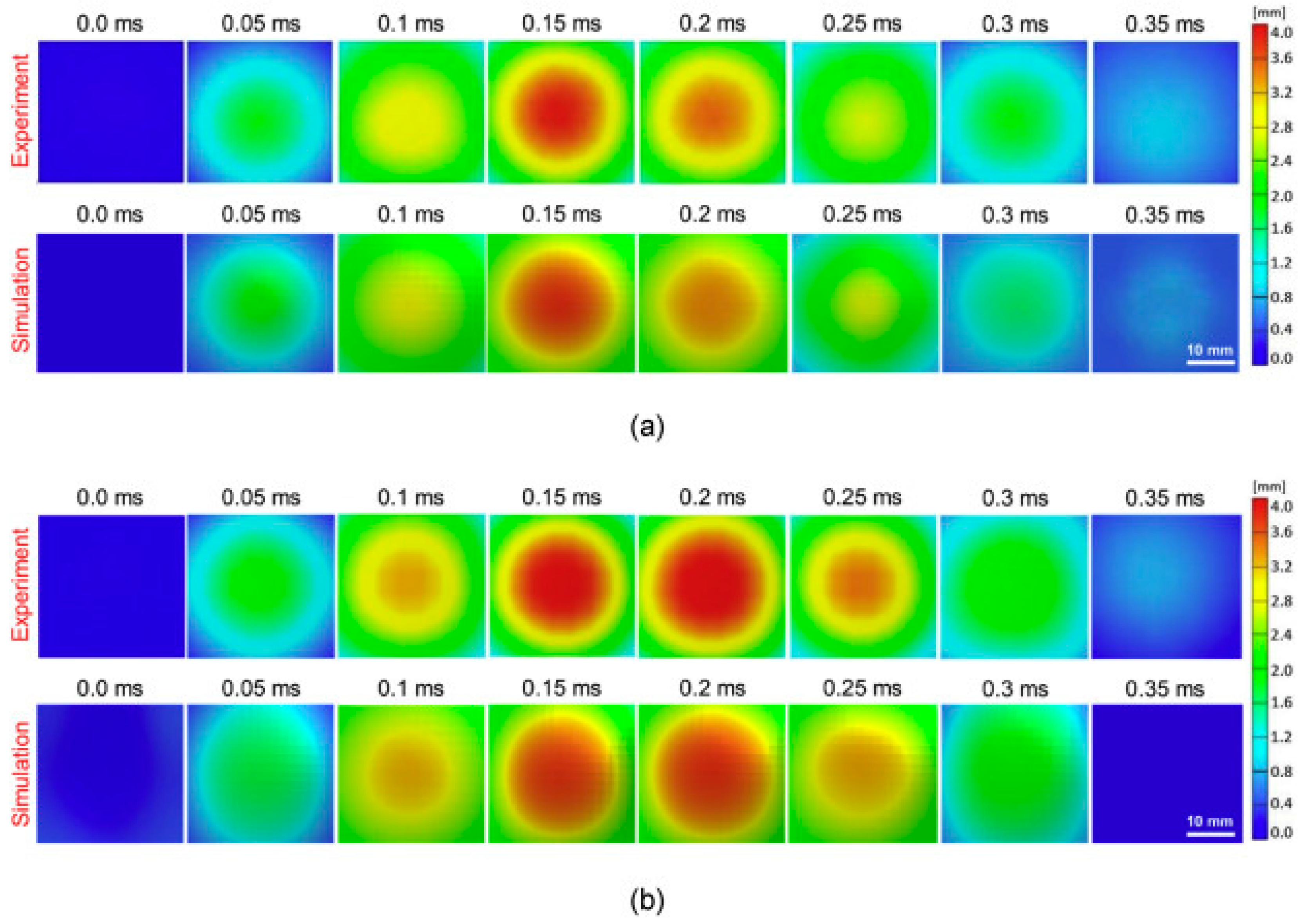
4.1. Modelling Impact of Pristine Composites
4.1.1. Hard Impact
4.1.2. Soft Impact
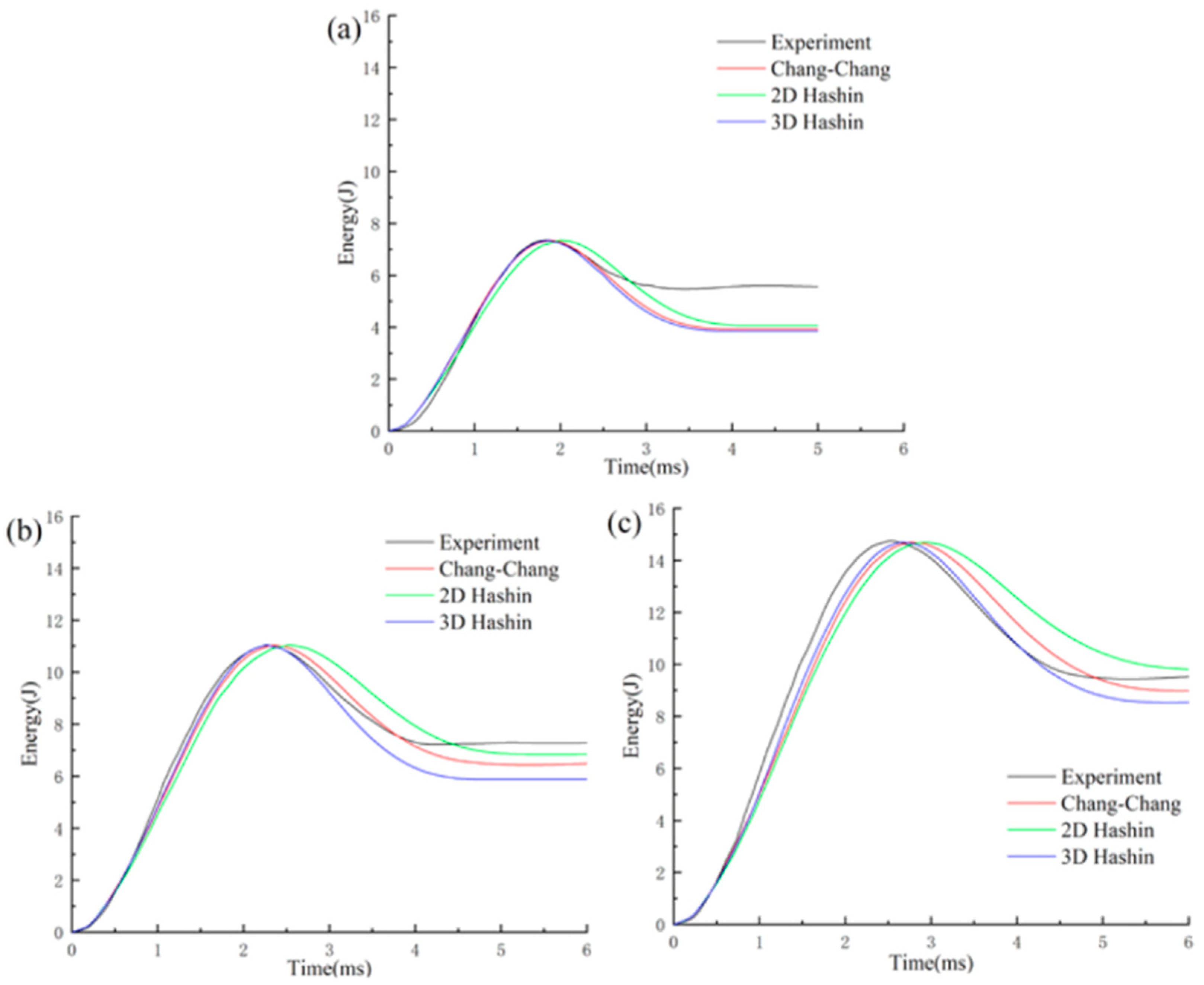
4.2. Impact Simulation of Repaired Composites
4.2.1. Mechanical Testing
4.2.2. Low Velocity
4.2.3. High Velocity
4.3. Modelling Summary
5. Discussions
5.1. Hard Impact on Pristine Samples
5.2. Soft Impact on Pristine Samples
5.3. Repaired Composites
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Minh, P.; Nguyen, D.T.; Doan, L.T.; Nguyen, D.V.; Duong, T.V. Numerical investigation on static bending and free vibration responses of two-layer variable thickness plates with shear connectors. Iran J. Sci. Technol. Trans. Mech. Eng. 2022, 46, 1047–1065. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Van Minh, P.; Hoang, C.P.; Tam, T.D.; Nhung, N.T.C.; Nguyen, T.D. Bending of symmetric sandwich FGM beams with shear connectors. Math Probl. Eng. 2021, 2021, 7596300. [Google Scholar] [CrossRef]
- Nguyen, T.C.; Van Thom, D.; Pham, C.H.; Zenkour, A.M.; Doan, D.H.; Van Minh, P. Finite element modelling of the bending and vibration behaviour of three-layer composite plates with a crack in the core layer. Compos. Struct. 2023, 305, 116529. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Van Minh, P.; Hoang, M.H.; Dao, M.T. The third-order shear deformation theory for modelling the static bending and dynamic responses of piezoelectric bidirectional functionally graded plates. Adv. Mater Sci. Eng. 2021, 2021, 5520240. [Google Scholar] [CrossRef]
- Nam, V.H.; Nguyen, N.H.; Pham, V.V.; Khoa, D.N.; Van Thom, D.; Van Minh, P. A new efficient modified first-order shear model for static bending and vibration behaviours of two-layer composite plate. Adv. Civ. Eng. 2019, 2019, 2385106. [Google Scholar] [CrossRef]
- Liu, H.; Falzon, B.G.; Tan, W. Experimental and numerical studies on the impact response of damage-tolerant hybrid unidirectional/woven carbon-fibre reinforced composite laminates. Compos. Part B 2018, 136, 101–118. [Google Scholar] [CrossRef] [Green Version]
- Sjogren, A.; Krasnikovs, A.; Varna, J. Experimental determination of elastic properties of impact damage in carbon fibre/epoxy laminates. Compos. Part A 2001, 32, 1237–1242. [Google Scholar] [CrossRef]
- Clark, G.; Van Blaricum, T.J. Load spectrum modification effects on fatigue of impact-damaged carbon fibre composite coupons. Composites 1987, 18, 243–251. [Google Scholar] [CrossRef]
- Topac, O.T.; Gozluklu, B.; Gurses, E.; Coker, D. Experimental and computational study of the damage process in CFRP composite beams under low-velocity impact. Compos. Part A 2017, 92, 167–182. [Google Scholar] [CrossRef]
- Ullah, H.; Harland, A.R.; Silberschmidt, V.V. Damage and fracture in carbon fabric reinforced composites under impact bending. Compos. Struct. 2013, 101, 144–156. [Google Scholar] [CrossRef]
- Olsson, R. Low-and medium-velocity impact as a cause of failure in polymer matrix composites. In Failure Mechanisms in Polymer Matrix Composites; Woodhead Publishing: Sawston, UK, 2012; pp. 53–78. [Google Scholar] [CrossRef]
- Hou, J.P.; Ruiz, C. Soft body impact on laminated composite materials. Compos. Part A 2007, 38, 505–515. [Google Scholar] [CrossRef]
- Pernas-Sanchez, J.; Artero-Guerrero, J.A.; Varas, D.; Lopez-Puente, J. Experimental analysis of ice sphere impacts on unidirectional carbon/epoxy laminates. Int. J. Impact Eng. 2016, 96, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Kimiaeifar, A.; Toft, H.; Lund, E.; Thomsen, O.T.; Sorensen, J.D. Reliability analysis of adhesive bonded scarf joints. Eng. Struct. 2012, 35, 281–287. [Google Scholar] [CrossRef]
- Pinto, A.M.; Campilho, R.D.; de Moura, M.F.; Mendes, I.R. Numerical evaluation of three-dimensional scarf repairs in carbon-epoxy structures. Int. J. Adhes. Adhes. 2010, 30, 329–337. [Google Scholar] [CrossRef] [Green Version]
- Katnam, K.B.; Da Silva, L.F.; Young, T.M. Bonded repair of composite aircraft structures: A review of scientific challenges and opportunities. Prog. Aerosp. Sci. 2013, 61, 26–42. [Google Scholar] [CrossRef]
- Demiral, M.; Abbassi, F.; Saracyakupoglu, T.; Habibi, M. Damage analysis of a CFRP cross-ply laminate subjected to abrasive water jet cutting. Alex. Eng. J. 2022, 61, 7669–7684. [Google Scholar] [CrossRef]
- Preau, M.; Hubert, P. Processing of co-bonded scarf repairs: Void reduction strategies and influence on strength recovery. Compos. Part A 2016, 84, 236–245. [Google Scholar] [CrossRef]
- Charalambides, M.N.; Hardouin, R.; Kinloch, A.J.; Matthews, F.L. Adhesively-bonded repairs to fibre-composite materials I: Experimental. Compos. Part A 1998, 29, 1371–1381. [Google Scholar] [CrossRef]
- Kumar, S.B.; Sridhar, I.; Sivashanker, S.; Osiyemi, S.O.; Bag, A. Tensile failure of adhesively bonded CFRP composite scarf joints. Mater. Sci. Eng. B 2006, 132, 113–120. [Google Scholar] [CrossRef]
- Li, J.; Yan, Y.; Zhang, T.; Liang, Z. Experimental study of adhesively bonded CFRP joints subjected to tensile loads. Int. J. Adhes. Adhes. 2015, 57, 95–104. [Google Scholar] [CrossRef]
- Slattery, P.G.; McCarthy, C.T.; O’Higgins, R.M. Assessment of residual strength of repaired solid laminate composite materials through mechanical testing. Compos. Struct. 2016, 84, 236–245. [Google Scholar] [CrossRef]
- Liu, B.; Xu, F.; Qin, J.; Lu, Z. Study on impact damage mechanisms and TAI capacity for the composite scarf repair of the primary load-bearing level. Compos. Struct. 2017, 181, 183–193. [Google Scholar] [CrossRef]
- Liu, B.; Han, Q.; Zhong, X.; Lu, Z. The impact damage and residual load capacity of composite stepped bonding repairs and joints. Compos. Part B 2019, 158, 339–351. [Google Scholar] [CrossRef]
- Atas, C.; Akgun, Y.; Dagdelen, O.; Icten, B.M.; Sarikanat, M. An experimental investigation on low velocity impact response of composite plates repaired by VARIM and hand lay-up process. Compos. Struct. 2011, 93, 1178–1186. [Google Scholar] [CrossRef]
- Li, H.C.H.; Mitrevski, T.; Herszberg, I. Impact on bonded repairs to CFRP laminates under load. In Proceedings of the 25th International Congress of the Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006. [Google Scholar]
- Herszberg, I.; Feih, S.; Gunnion, A.J.; Li, H.C.H. Impact damage tolerance of tension loaded bonded scarf repairs to CFRP laminates. In Proceedings of the 16th International Conference on Composite Materials, Kyoto, Japan, 8–13 July 2007. [Google Scholar]
- Liu, S.F.; Cheng, X.Q.; Xu, Y.Y.; Bao, J.W.; Guo, X. Study on impact performances of scarf-repaired carbon fibre reinforced polymer laminates. J. Reinf. Plast. Compos. 2015, 34, 60–71. [Google Scholar] [CrossRef]
- Tie, Y.; Hou, Y.; Li, C.; Zhou, X.; Sapanathan, T.; Rachik, M. An insight into the low-velocity impact behaviour of patch repaired CFRP laminates using numerical and experimental approaches. Compos. Struct. 2018, 190, 179–188. [Google Scholar] [CrossRef]
- Coelho, S.R.M.; Reis, P.N.B.; Ferreira, J.A.M.; Pereira, A.M. Effects of external patch configuration on repaired composite laminates subjected to multi-impacts. Compos. Struct. 2017, 168, 259–265. [Google Scholar] [CrossRef]
- Hou, Y.; Tie, Y.; Li, C.; Sapanathan, T.; Rachik, M. Low-velocity impact behaviours of repaired CFRP laminates: Effect of impact location and external patch configurations. Compos. Part B 2019, 163, 669–680. [Google Scholar] [CrossRef]
- Kim, M.K.; Elder, D.J.; Wang, C.H.; Feih, S. Interaction of laminate damage and adhesive disbonding in composite scarf joints subjected to combined in-plane loading and impact. Compos. Struct. 2012, 94, 945–953. [Google Scholar] [CrossRef] [Green Version]
- Balaganesan, G.; Khan, V.C. Energy absorption of repaired composite laminates subjected to impact loading. Compos. Part B 2016, 98, 39–48. [Google Scholar] [CrossRef]
- Clark, G. Modelling of impact damage in composite laminates. Composites 1989, 20, 209–214. [Google Scholar] [CrossRef]
- Bouvet, C.; Rivallant, S.; Barrau, J.J. Low velocity impact modelling in composite laminates capturing permanent indentation. Compos. Sci. Technol. 2012, 72, 1977–1988. [Google Scholar] [CrossRef] [Green Version]
- Iannucci, L. Progressive failure modelling of woven carbon composite under impact. Int. J. Impact Eng. 2006, 32, 1013–1043. [Google Scholar] [CrossRef]
- Iannucci, L.; Willows, M.L. An energy based damage mechanics approach to modelling impact onto woven composite materials: Part, I. Numerical models. Compos. Part A 2007, 37, 2041–2056. [Google Scholar] [CrossRef]
- Iannucci, L.; Willows, M.L. An energy based damage mechanics approach to modelling impact onto woven composite materials: Part II. Experimental and numerical results. Compos. Part A 2007, 38, 540–554. [Google Scholar] [CrossRef]
- Xin, S.H.; Wen, H.M. A progressive damage model for fibre reinforced plastic composites subjected to impact loading. Int. J. Impact. Eng. 2015, 75, 40–52. [Google Scholar] [CrossRef]
- Ansari, M.M.; Chakrabarti, A. Impact behaviour of FRP composite plate under low to hyper velocity impact. Compos. Part B 2016, 95, 462–474. [Google Scholar] [CrossRef]
- Pham, D.C.; Lua, J.; Sun, H.; Zhang, D. A three-dimensional progressive damage model for drop-weight impact and compression after impact. J. Compos. Mater. 2018, 54, 449–462. [Google Scholar] [CrossRef]
- Johnson, A.F.; Holzapfel, M. Modelling soft body impact on composite structures. Compos. Struct. 2003, 61, 103–113. [Google Scholar] [CrossRef]
- Johnson, A.F.; Holzapfel, M. Numerical prediction of damage in composite structures from soft body impacts. J. Mater. Sci. 2006, 41, 6622–6630. [Google Scholar] [CrossRef]
- Nishikawa, M.; Hemmi, K.; Takeda, N. Finite-element simulation for modelling composite plates subjected to soft-body, high-velocity impact for application to bird-strike problem of composite fan blades. Compos. Struct. 2011, 93, 1416–1423. [Google Scholar] [CrossRef]
- Li, C.F.; Hu, N.; Cheng, J.G.; Fukunaga, H.; Sekine, H. Low-velocity impact-induced damage of continuous fiber-reinforced composite laminates. Part II. Verification and numerical investigation. Compos. Part A 2002, 33, 1063–1072. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Kaboglu, C.; Chai, H.; Kong, X.; Blackman, B.R.K.; Kinloch, A.J.; Dear, J.P. Experimental and numerical studies on the behaviour of fibre-reinforced composites subjected to soft impact loading. In Proceedings of the 3rd International Conference on Structural Integrity, Madeira, Portugal, 2–5 September 2019; pp. 992–1001. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Kaboglu, C.; Zhou, J.; Kong, X.; Blackman, B.R.K.; Kinloch, A.J.; Dear, J.P. The behaviour of fibre-reinforced composites subjected to a soft impact-loading: An experimental and numerical study. Eng. Fract. Anal. 2020, 111, 104448. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Ding, Y.; Zheng, J.; Luo, L.; Kong, X.; Zhou, J.; Blackman, B.R.K.; Kinloch, A.J.; Dear, J.P. Modelling the effect of projectile hardness on the impact response of a woven carbon-fibre reinforced thermoplastic-matrix composite. Int. J. Lightweight Mater. Manuf. 2020, 3, 403–415. [Google Scholar] [CrossRef]
- Charalambides, M.N.; Kinloch, A.J.; Matthews, F.L. Adhesively-bonded repairs to fibre-composite materials II: Finite element modelling. Compos. Part A 1998, 29, 1383–1396. [Google Scholar] [CrossRef]
- Dan, H.; Sawa, T.; Iwamoto, T.; Hirayama, Y. Stress analysis and strength evaluation of scarf adhesive joints subjected to static tensile loadings. Int. J. Adhes. Adhes. 2010, 30, 387–392. [Google Scholar] [CrossRef] [Green Version]
- Gunnion, A.J.; Herszberg, I. Parametric study of scarf joints in composite structures. Compos. Struct. 2006, 75, 364–376. [Google Scholar] [CrossRef]
- Cheng, X.; Du, X.; Zhang, J.; Zhang, J.; Guo, X.; Bao, J. Effects of stacking sequence and rotation angle of patch on low velocity impact performance of scarf repaired laminates. Compos. Part B 2018, 133, 78–85. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, J.; Bao, J.; Zeng, B.; Cheng, Y.; Hu, R. Low-velocity impact performance and effect factor analysis of scarf-repaired composite laminates. Int. J. Impact Eng. 2018, 111, 85–93. [Google Scholar] [CrossRef]
- Jiang, H.; Ren, Y.; Zhang, S.; Liu, Z.; Yu, G.; Xiang, J. Damage and perforation resistance behaviours induced by projectile impact load on bonding-patch repaired and scarf-patch repaired composite laminates. Int. J. Damage Mech. 2019, 28, 502–537. [Google Scholar] [CrossRef]
- Heimbs, S.; Bergmann, T. High-velocity impact behaviour of prestressed composite plates under bird strike loading. Int. J. Aerosp. Eng. 2012, 2012, 372167. [Google Scholar] [CrossRef] [Green Version]
- Shao, J.R.; Liu, N.; Zheng, Z.J. Numerical comparison between Hashin and Chang-Chang failure criteria in terms of inter-laminar damage behaviour of laminated composites. Mater. Res. Express 2021, 8, 085602. [Google Scholar] [CrossRef]

| Model | Composite Panel | Adhesive | Soft Impactor | Agreement | |
|---|---|---|---|---|---|
| Intralaminar | Interlaminar | ||||
| Pristine panels—hard impact | |||||
| Clark [34] | Predicts blocked damage in line with fibre direction of bottom ply at each interface | - | - | Predicts directions accurately but not delamination shapes | |
| Topac et al. [9] | LaRC04 failure criterion | Cohesive zone model | - | - | Predicts the correct type of failure but otherwise does not match with experimental results |
| Ullah et al. [10] | Cohesive zone model implemented for both inter- and intralaminar damage | - | - | Predicts force time traces relatively well but too high for peak force value | |
| Bouvet et al. [35] | Modified 2D Hashin criteria | Cohesive zone model | - | - | Predicts delamination shapes and areas well |
| Iannucci et al. [36,37] | Unconventional thermodynamic maximum energy dissipation approach | - | - | Predicts rear fibre breakage well but not as accurate for the force time traces | |
| Xin et al. [39] | Quadratic stress-based failure criteria | Cohesive zone model with fracture energy approach | - | - | Predicts rear fibre breakage and force displacement traces relatively well but peak load too high |
| Ansari et al. [40] | Modified 3D Hashin criteria | - | - | Predicts residual velocity relatively well | |
| Pham et al. [41] | General 3D maximum stress failure criterion | Cohesive zone model | - | - | Predicts damage orientation and initial stress–strain relationship well |
| Li et al. [45] | Modified Chang-Chang failure criteria | Griffith criterion | - | - | Predicts delamination size and shape, force time, and displacement time traces well |
| Pristine panels—soft impact | |||||
| Johnson et al. [42,43] | Elastic or elastic-plastic damage mechanics model | Elastic damaging interface stress-displacement model | - | SPH method | Predicts the pressure in the soft projectile over time and damage relatively well |
| Nishikawa et al. [44] | Modified Chang-Chang failure criteria | - | Lagrange multiplier method | Predicts the force time traces well | |
| Liu et al. [46,47,48] | 2D Hashin criteria | Cohesive zone model | - | SPH method | Predicts displacement and rear face damage well |
| Repaired panels—general mechanical testing | |||||
| Charalambides et al. [49] | Modelling as one block vs. individual plies, thermal and hygrothermal expansion coefficients added to FEA model | Linear elastic vs. linear elastic- plastic | - | Predicts crack location well, modelling individual plies gave more accurate results and both adhesive models gave similar outputs | |
| Dan et al. [50] | 2D and 3D finite element method, with material treated as elastic | Bi-linear material model | - | Predicts strain through adhesive well | |
| Pinto et al. [15] | Interlaminar and intralaminar failure near the scarf not considered | Trapezoidal cohesive zone model | - | No experimental work to verify, but agrees well with literature | |
| Gunnion et al. [51] | Parametric FEA model | Linearity assumed | - | No experimental work to verify, but agrees well with literature | |
| Repaired panels—low-velocity impact | |||||
| Liu et al. [24] | 3D Hashin criteria | Yeh delamination failure criterion | Bi-linear cohesive zone model | - | Predicts adhesive damage and delamination area relatively well |
| Cheng et al. [52,53] | 3D Hashin criteria | Cohesive zone model | Ductile damage criterion | - | Relative error of 8.2% in delamination area between model and experiments |
| Tie et al. [29] | 3D Hashin criteria | Cohesive zone model | Quadratic separation law | - | Predicts load time traces well, not as accurate in predicting damage area |
| Repaired panels—high-velocity impact | |||||
| Kim et al. [32] | Intralaminar damage not considered | Cohesive zone model | Bi-linear traction separation law | - | Predicts load time traces well, not as accurate in predicting damage area |
| Jiang et al. [54] | Modified 3D Hashin criteria | Exponential softening law | Triangle traction separation law | - | Predicts rear face damage well |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hall, Z.E.C.; Liu, J.; Brooks, R.A.; Liu, H.; Dear, J.P. Impact Testing on the Pristine and Repaired Composite Materials for Aerostructures. Appl. Mech. 2023, 4, 421-444. https://doi.org/10.3390/applmech4020024
Hall ZEC, Liu J, Brooks RA, Liu H, Dear JP. Impact Testing on the Pristine and Repaired Composite Materials for Aerostructures. Applied Mechanics. 2023; 4(2):421-444. https://doi.org/10.3390/applmech4020024
Chicago/Turabian StyleHall, Zoe E. C., Jun Liu, Richard A. Brooks, Haibao Liu, and John P. Dear. 2023. "Impact Testing on the Pristine and Repaired Composite Materials for Aerostructures" Applied Mechanics 4, no. 2: 421-444. https://doi.org/10.3390/applmech4020024
APA StyleHall, Z. E. C., Liu, J., Brooks, R. A., Liu, H., & Dear, J. P. (2023). Impact Testing on the Pristine and Repaired Composite Materials for Aerostructures. Applied Mechanics, 4(2), 421-444. https://doi.org/10.3390/applmech4020024





