A Surrogate Model of Heat Transfer Mechanism in a Domestic Gas Oven: A Numerical Simulation Approach for Premixed Flames
Abstract
:1. Introduction
2. Materials and Methods
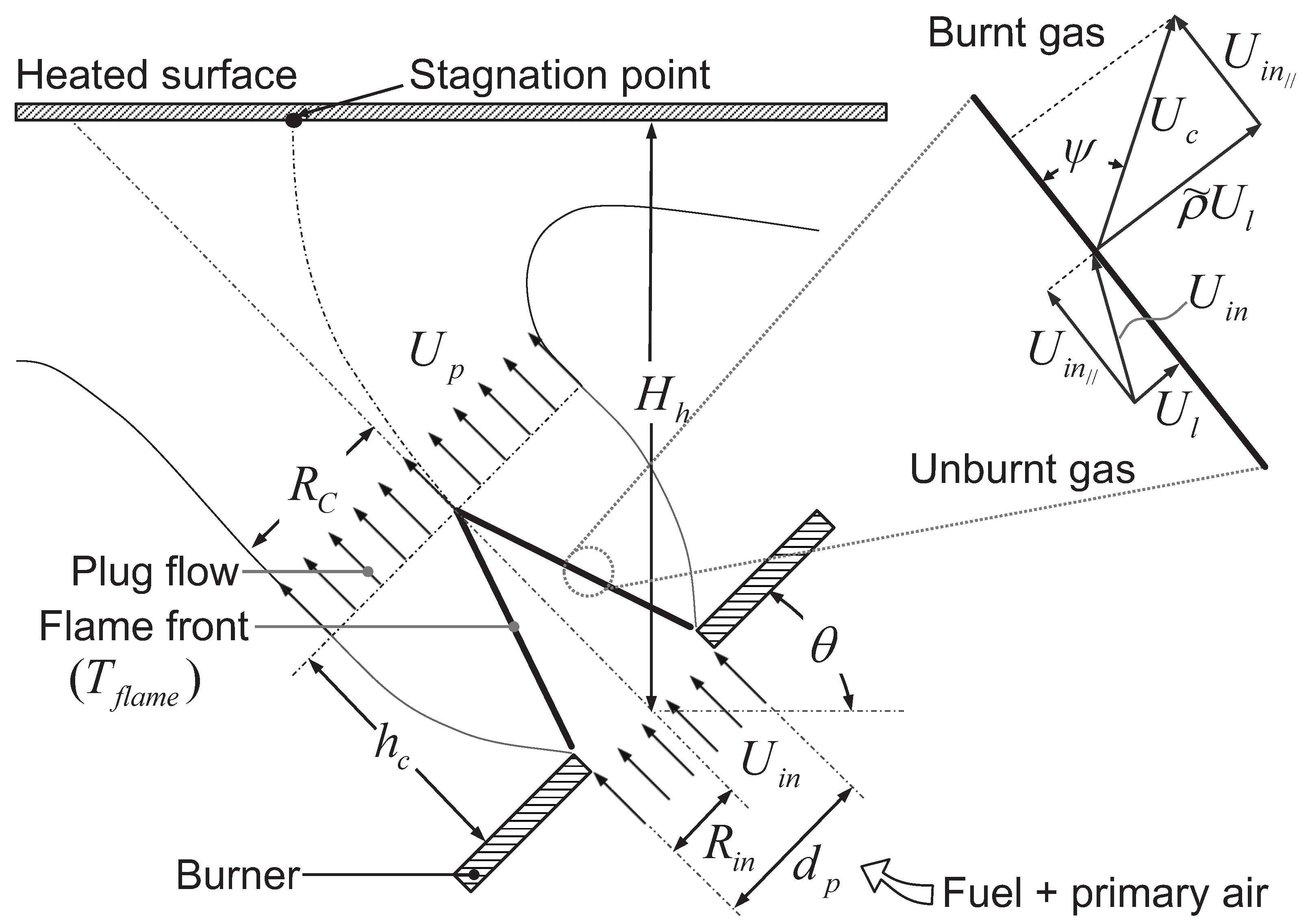
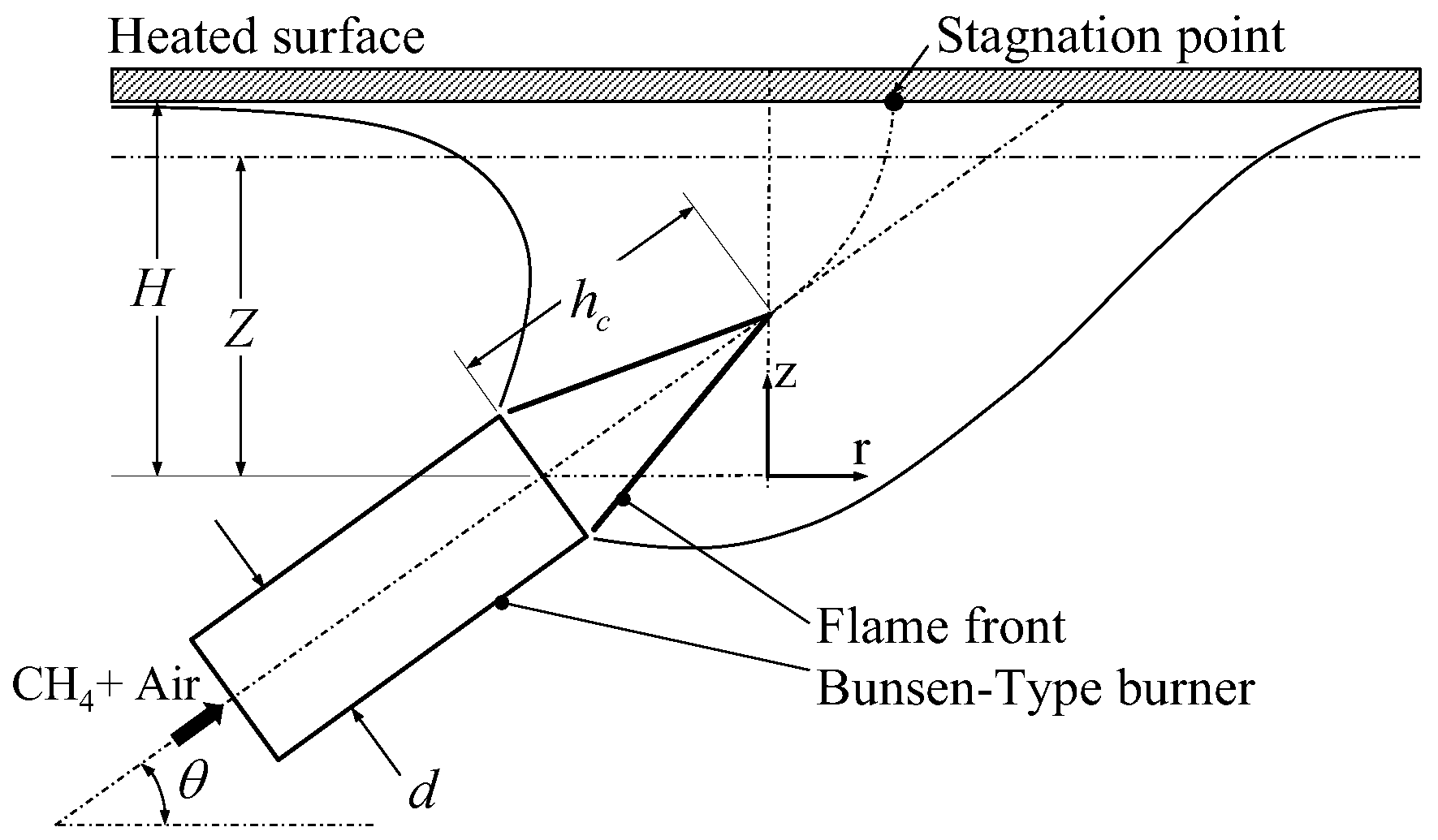
2.1. Analytical Modeling of Heat Transfer Mechanisms in Premix Gas Oven Burners
2.2. Numerical Model (CFD)
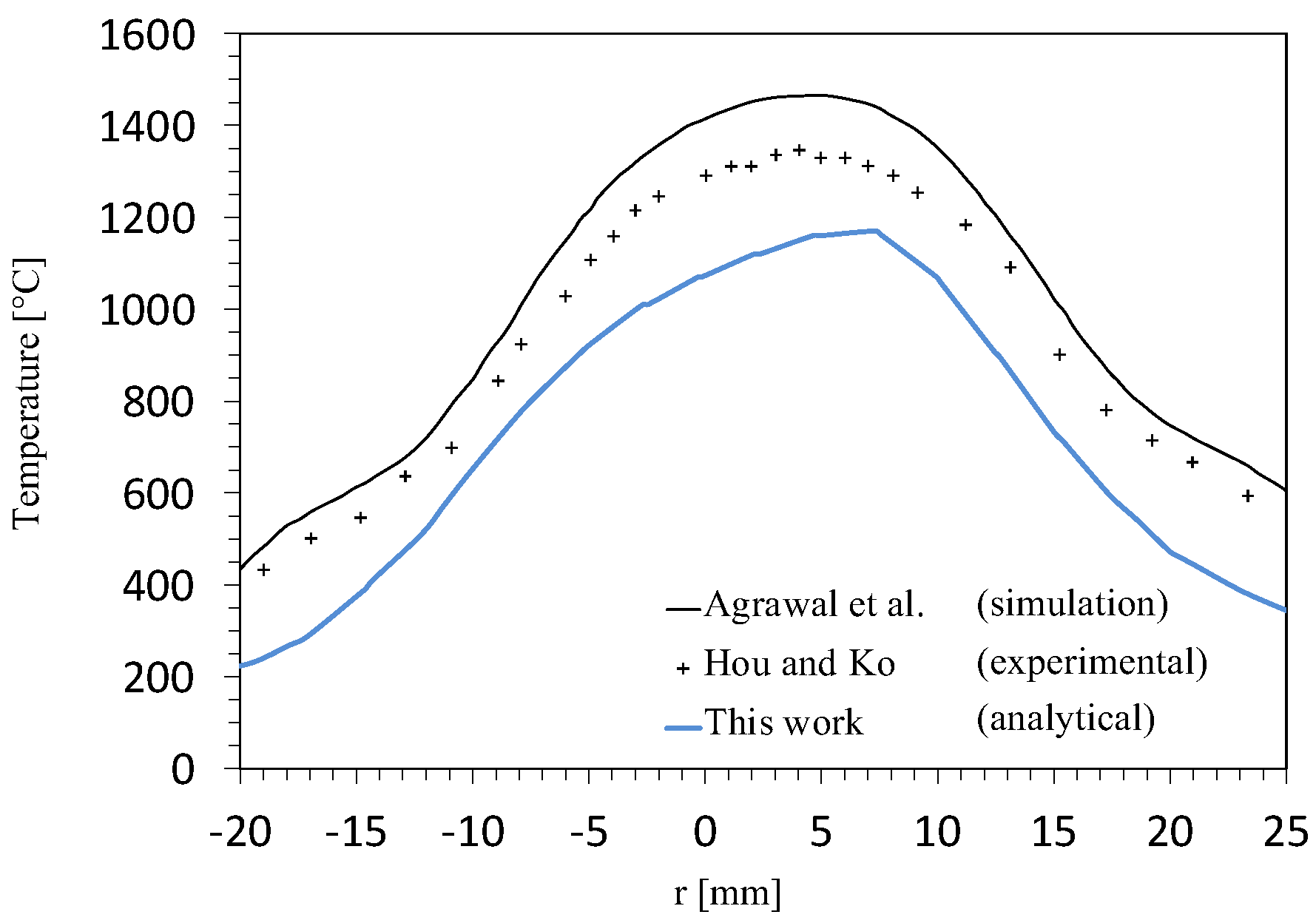
3. Validation of the Analytical Model
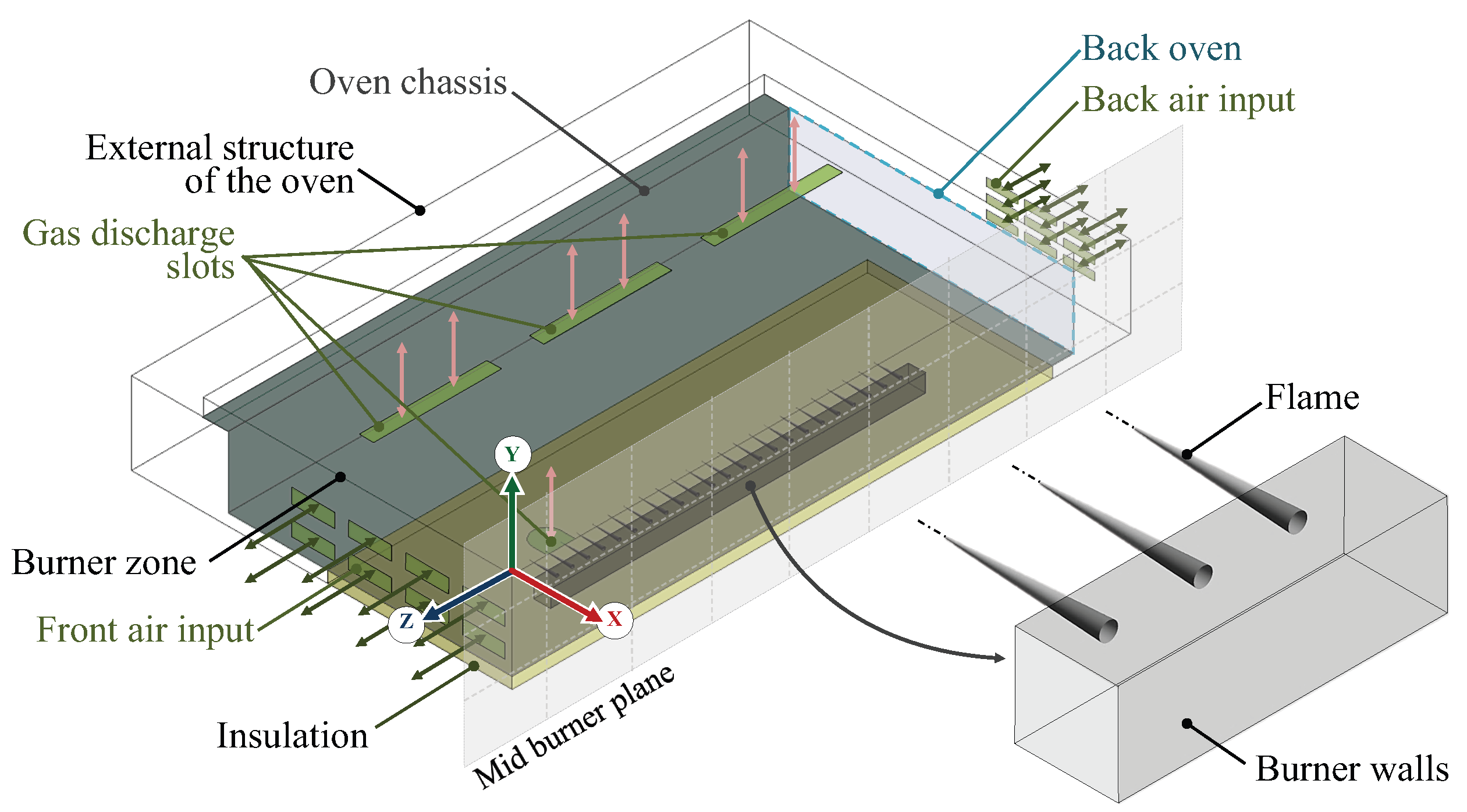
4. Numerical Setup
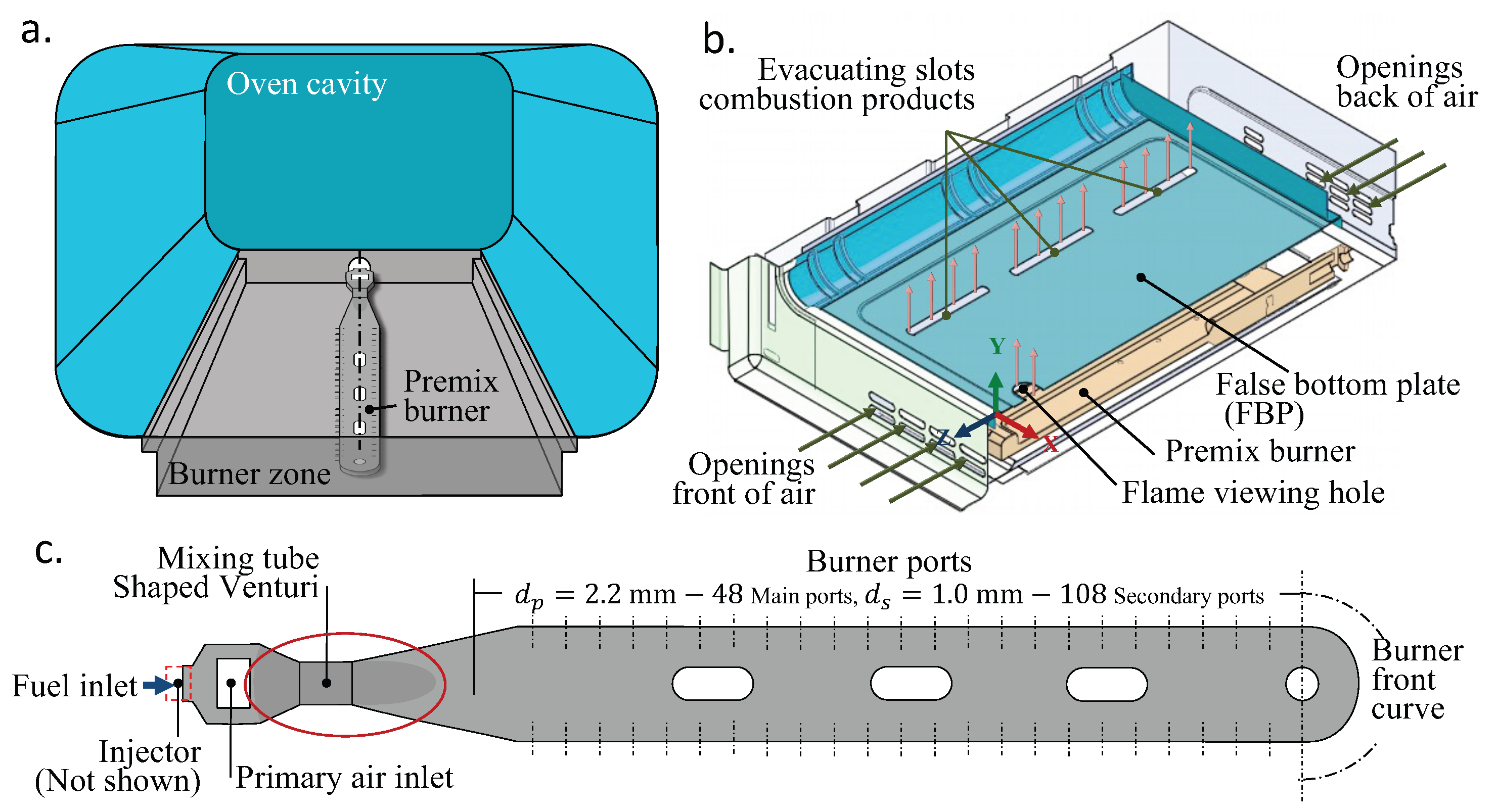
4.1. Burner Zone Description
4.2. Boundary Conditions
- Front air input, back input, and gas discharge slots: These are treated as opening boundaries with a relative pressure of 0 Pa and a temperature of 300 K.
- Flame: Modeled as a cone with the adiabatic flame temperature, , and the combustion products velocity, , in cylindrical coordinates relative to its axis of rotation. These values remain constant across the entire surface of the cone, as determined by the analytical model outlined in Section 2.
- Burner walls: Subjected to a non-slip condition on the burner surface and treated as adiabatic surfaces.
- Mid burner plane: This is a symmetry plane. Given the shape and location of the thermal energy source within the oven, only the left half of the domain was simulated.
- Oven chassis and back oven: Defined as fluid-solid and fluid-fluid interfaces, respectively. Non-slip conditions apply to the interface surfaces, with the conservation of heat flux ensured at these boundaries.
4.3. Mesh and Grid Independence Study
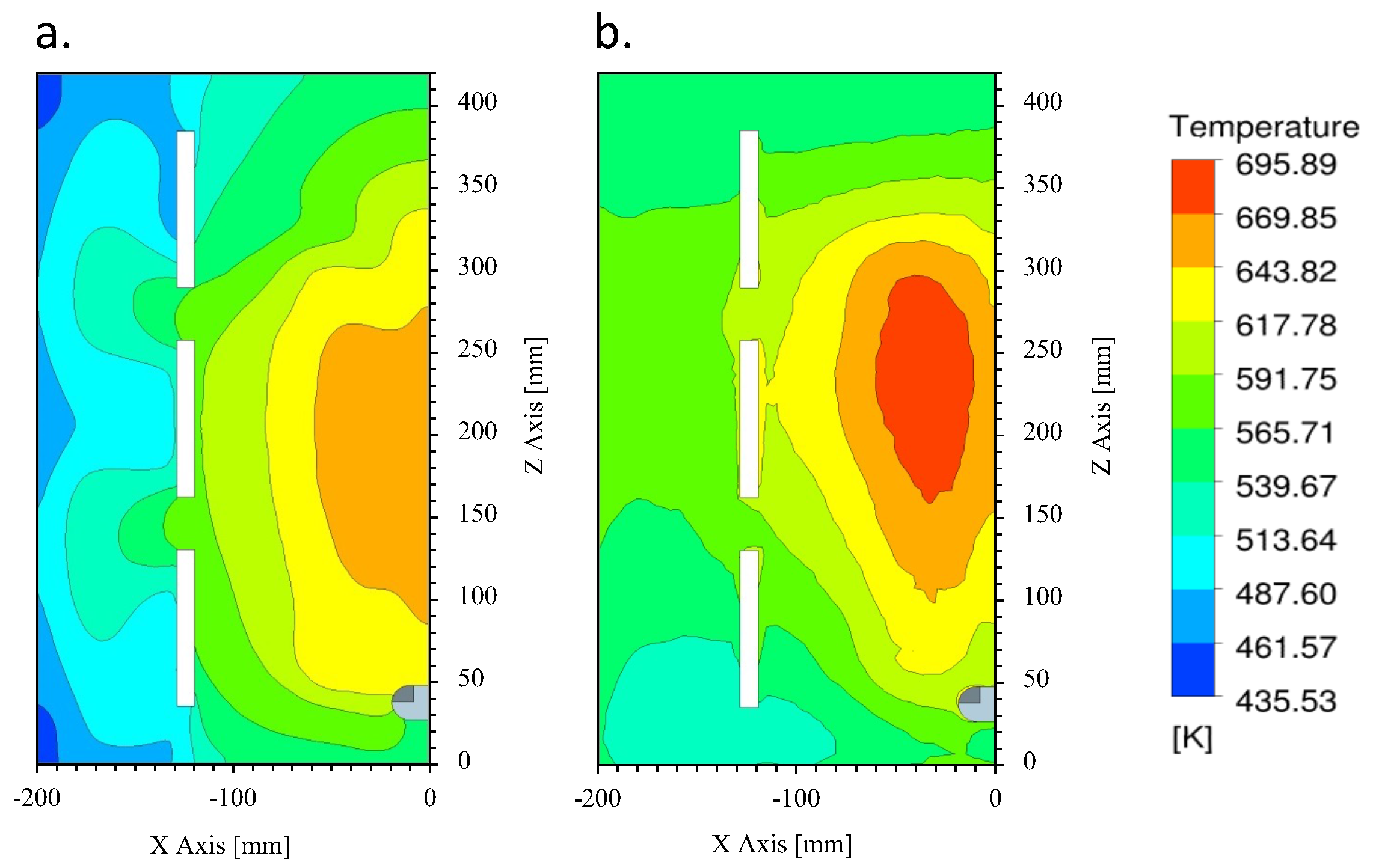
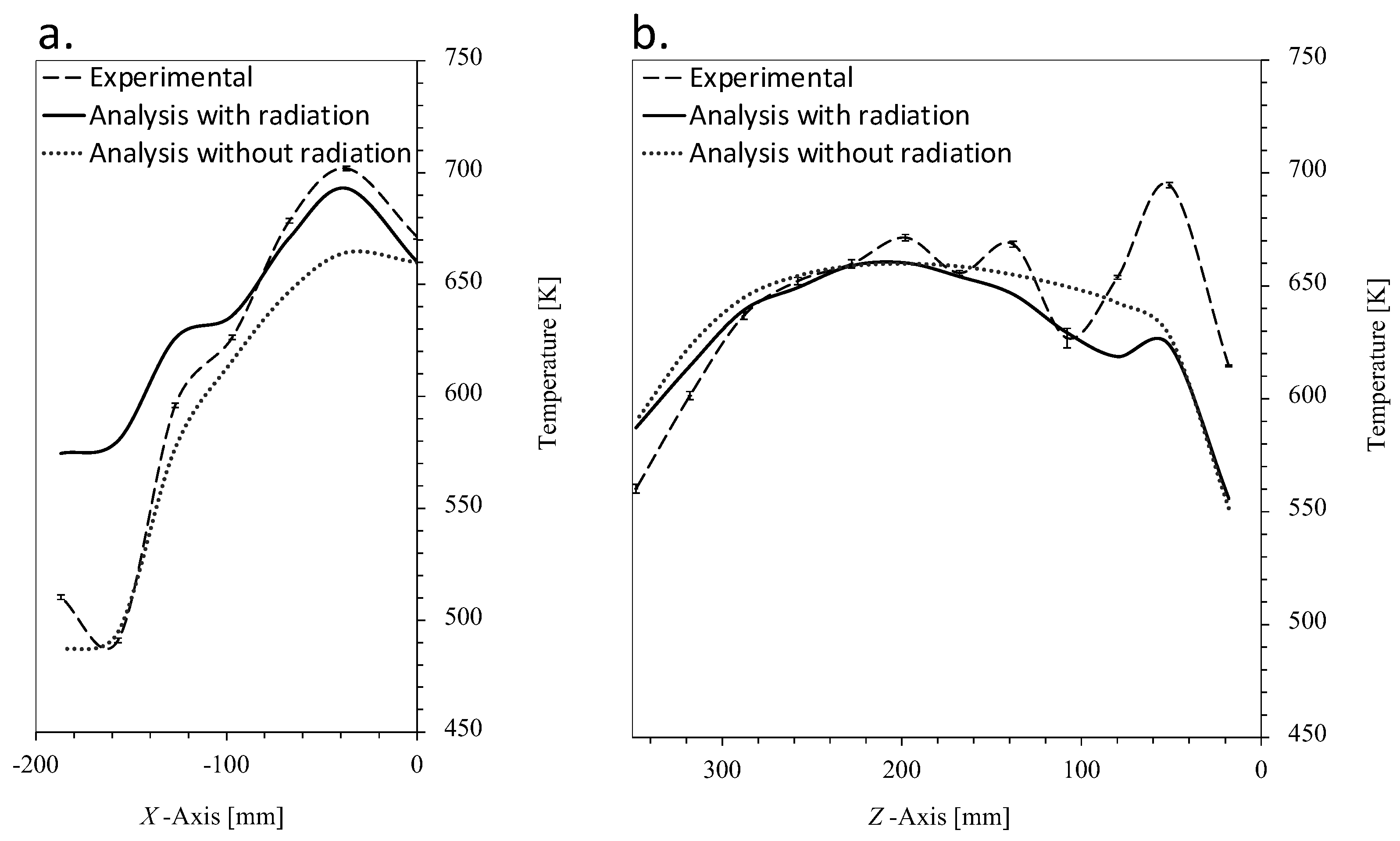
5. Results and Discussion
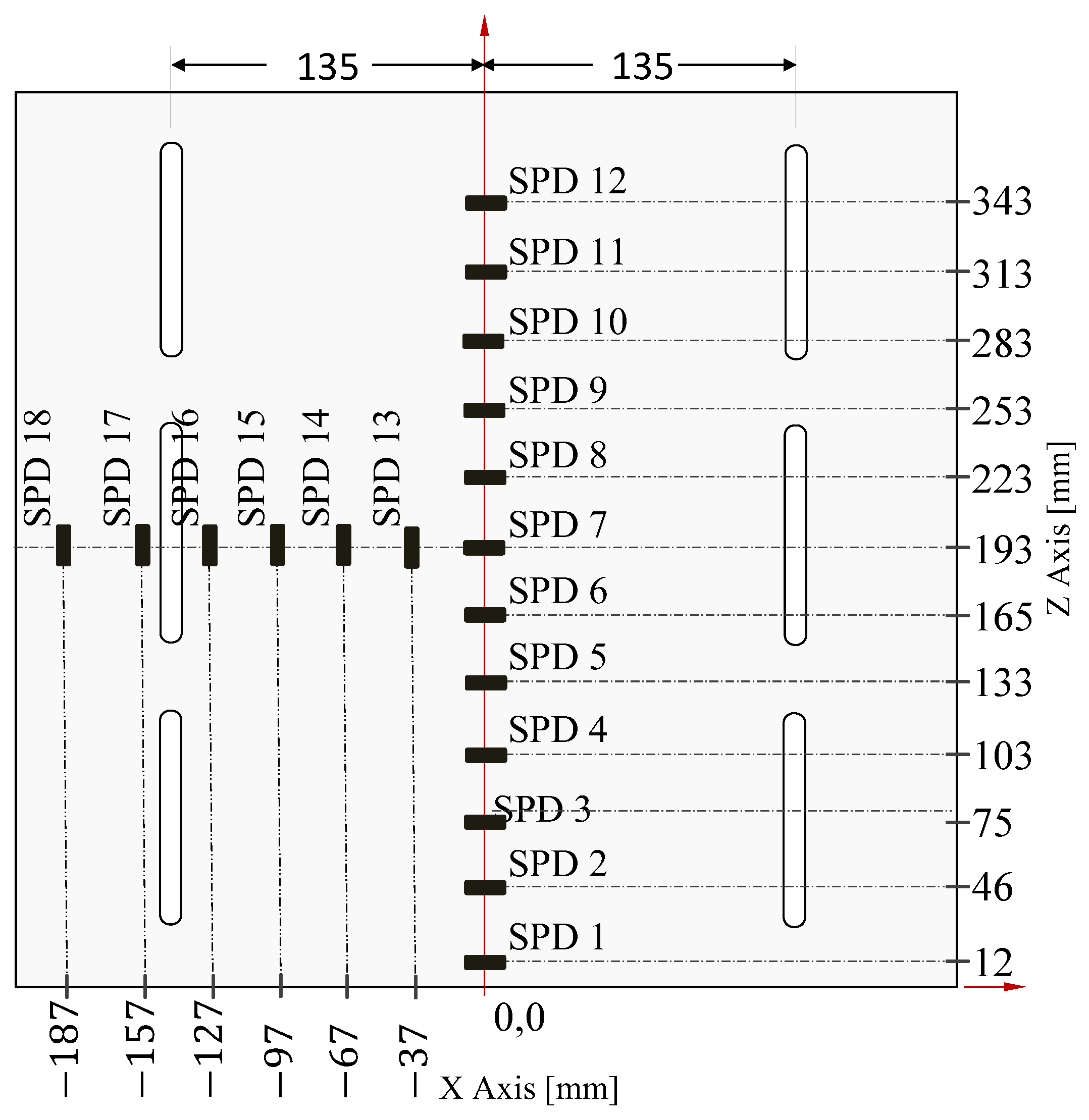
Experimental Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| specific heat at constant pressure, kJ/kg K | |
| main port diameter, mm | |
| secondary port diameter, mm | |
| g | gravitational acceleration, m/s |
| heating height, m | |
| cone height, m | |
| thermal conductivity, W/m K | |
| k | turbulence kinetic energy, J/kg |
| LVH | low heating value of the methane, kJ/ |
| P | pressure, Pa |
| pressure on site, atm | |
| atmospheric pressure, 1 atm | |
| T | temperature, K |
| fluctuating temperature, K | |
| adiabatic flame temperature, K | |
| U | velocity vector, m/s |
| fluctuating velocity, m/s | |
| velocity of the fuel/air mixture, m/s | |
| burning velocity for the methane, m/s | |
| burning velocity corrected for the methane, m/s | |
| velocity burnt gases, m/s | |
| plug flow velocity, m/s | |
| reynolds stress, / | |
| turbulent heat flux, m K/s | |
| non-dimensional wall distance | |
| mass fraction | |
| Greek symbols | |
| equivalence ratio | |
| flame angle | |
| velocity burnt gases angle on blue cone | |
| fluid density, kg/ | |
| unburnt gases density, kg/ | |
| burnt gases density, kg/ | |
| density ratio | |
| fluid viscosity, kg/m s | |
| specific dissipation rate, 1/s | |
References
- Ryu, J.; Kwon, J.; Kim, R.; Kim, M.; Kim, Y.; Jeon, C.; Song, J. Surface ignition behaviors of methane–air mixture in a gas oven burner. Appl. Therm. Eng. 2014, 65, 262–272. [Google Scholar] [CrossRef]
- Gotoda, H.; Maeda, K.; Ueda, T.; Cheng, R.K. Periodic motion of a Bunsen flame tip with burner rotation. Combust. Flame 2003, 134, 67–79. [Google Scholar] [CrossRef]
- Makmool, U.; Jugjai, S.; Tia, S.; Vallikul, P.; Fungtammasan, B. Performance and analysis by particle image velocimetry (PIV) of cooker-top burners in Thailand. Energy 2007, 32, 1986–1995. [Google Scholar] [CrossRef]
- Wu, C.Y.; Chen, K.H.; Yang, S.Y. Experimental study of porous metal burners for domestic stove applications. Energy Convers. Manag. 2014, 77, 380–388. [Google Scholar] [CrossRef]
- Bidi, M.; Hosseini, R.; Nobari, M. Numerical analysis of methane–air combustion considering radiation effect. Energy Convers. Manag. 2008, 49, 3634–3647. [Google Scholar] [CrossRef]
- Özdemir, İ.B. Simulation of turbulent combustion in a self-aerated domestic gas oven. Appl. Therm. Eng. 2017, 113, 160–169. [Google Scholar] [CrossRef]
- Medapati, S.; Monde, A.D. Discretized low-order model of an electric oven: Transient thermal analysis of door sub-system. Int. Commun. Heat Mass Transf. 2023, 142, 106619. [Google Scholar] [CrossRef]
- Monde, A.D.; Cannistraro, M. Design and control intended low-order model for transient investigation of an electric oven: Static mode. Int. J. Heat Mass Transf. 2024, 221, 125061. [Google Scholar] [CrossRef]
- Mulemane, A.; Hurst, L.; Fraser, A.; Sinclair, J. A Reduced Order Model for Simulating Heat Transfer Processes in Automotive Paint Shop Ovens; Technical Report 2015-01-0030, SAE Technical Paper; SAE: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Ahanj, M.D.; Rahimi, M.; Alsairafi, A.A. CFD modeling of a radiant tube heater. Int. Commun. Heat Mass Transf. 2012, 39, 432–438. [Google Scholar] [CrossRef]
- Cadavid, F.; Herrera, B.; Amell, A. Numerical simulation of the flow streams behavior in a self-regenerative crucible furnace. Appl. Therm. Eng. 2010, 30, 826–832. [Google Scholar] [CrossRef]
- Karzar Jeddi, M.; Kazemzadeh Hannani, S.; Farhanieh, B. Study of Mixed-Convection Heat Transfer from an Impinging Jet to a Solid Wall Using a Finite-Element Method—Application to Cooktop Modeling. Numer. Heat Transf. Part B Fundam. 2004, 46, 387–397. [Google Scholar] [CrossRef]
- Wong, S.Y.; Zhou, W.; Hua, J. CFD modeling of an industrial continuous bread-baking process involving U-movement. J. Food Eng. 2007, 78, 888–896. [Google Scholar] [CrossRef]
- Mistry, H.; Ganapathisubbu, S.; Dey, S.; Bishnoi, P.; Castillo, J.L. A methodology to model flow-thermals inside a domestic gas oven. Appl. Therm. Eng. 2011, 31, 103–111. [Google Scholar] [CrossRef]
- Hou, S.S.; Ko, Y.C. Influence of oblique angle and heating height on flame structure, temperature field and efficiency of an impinging laminar jet flame. Energy Convers. Manag. 2005, 46, 941–958. [Google Scholar] [CrossRef]
- Agrawal, G.; Chakraborty, S.; Som, S. Heat transfer characteristics of premixed flame impinging upwards to plane surfaces inclined with the flame jet axis. Int. J. Heat Mass Transf. 2010, 53, 1899–1907. [Google Scholar] [CrossRef]
- Chander, S.; Ray, A. Flame impingement heat transfer: A review. Energy Convers. Manag. 2005, 46, 2803–2837. [Google Scholar] [CrossRef]
- Zuckerman, N.; Lior, N. Jet impingement heat transfer: Physics, correlations, and numerical modeling. Adv. Heat Transf. 2006, 39, 565–631. [Google Scholar]
- Morley, C. GASEQ A Chemical Equilibrium Program for Windows Ver. 0.79. 2005. Available online: http://www.gaseq.co.uk (accessed on 30 September 2014).
- El-Sherif, A. Effects of natural gas composition on the nitrogen oxide, flame structure and burning velocity under laminar premixed flame conditions. Fuel 1998, 77, 1539–1547. [Google Scholar] [CrossRef]
- Uberoi, M.; Kuethe, A.; Menkes, H. Flow field of a Bunsen flame. Phys. Fluids 1958, 1, 150–158. [Google Scholar] [CrossRef]
- Remie, M.; Cremers, M.; Schreel, K.; De Goey, L. Flame jet properties of Bunsen-type flames. Combust. Flame 2006, 147, 163–170. [Google Scholar] [CrossRef]
- Kleijn, C.R. Heat transfer from laminar impinging methane/air flames. Am. Soc. Mech. Eng. Press. Vessel. Pip. Div. Publ. ASME 2001, 424, 259–270. [Google Scholar]
- Cremers, M.; Remie, M.; Schreel, K.; de Goey, L. Thermochemical heat release of laminar stagnation flames of fuel and oxygen. Int. J. Heat Mass Transf. 2010, 53, 952–961. [Google Scholar] [CrossRef]
- Viskanta, R. Heat transfer to impinging isothermal gas and flame jets. Exp. Therm. Fluid Sci. 1993, 6, 111–134. [Google Scholar] [CrossRef]
- Higuera, F. Aerodynamics of a slender axisymmetric Bunsen flame with large gas expansion. Combust. Flame 2009, 156, 1063–1067. [Google Scholar] [CrossRef]
- Hung, K.S.; Cheng, C.H. Pressure effects on natural convection for non-Boussinesq fluid in a rectangular enclosure. Numer. Heat Transf. Part A Appl. 2002, 41, 515–528. [Google Scholar] [CrossRef]
- Ting, D. Thermofluids: From Nature to Engineering; Academic Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Ji, Y. CFD modelling of natural convection in air cavities. CFD Lett. 2014, 6, 15–31. [Google Scholar]
- Aounallah, M.; Addad, Y.; Benhamadouche, S.; Imine, O.; Adjlout, L.; Laurence, D. Numerical investigation of turbulent natural convection in an inclined square cavity with a hot wavy wall. Int. J. Heat Mass Transf. 2007, 50, 1683–1693. [Google Scholar] [CrossRef]
- Zhong, Z.; Yang, K.; Lloyd, J. Variable property effects in laminar natural convection in a square enclosure. J. Heat Transf. 1985, 107, 133–138. [Google Scholar] [CrossRef]
- Incropera, F.P. Introduction to Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- GASURE. Medición de la tasa de aireación primaria y distribución de la temperatura de llama de un quemador atmosférico de industrias HACEB. Technical Report. Universidad de Antioquia: Medellín, Colombia, 2014. [Google Scholar]
- Abraham, J.P.; Sparrow, E.M. A simple model and validating experiments for predicting the heat transfer to a load situated in an electrically heated oven. J. Food Eng. 2004, 62, 409–415. [Google Scholar] [CrossRef]
- CEM. Procedimiento TH-001 Para la Calibración de Termómetros Digitales, 1st ed.; Centro Español de Metrología, Ministerio de Industria, Turismo y Comercio: CEM, Madrid, Spain, 2003. [Google Scholar]
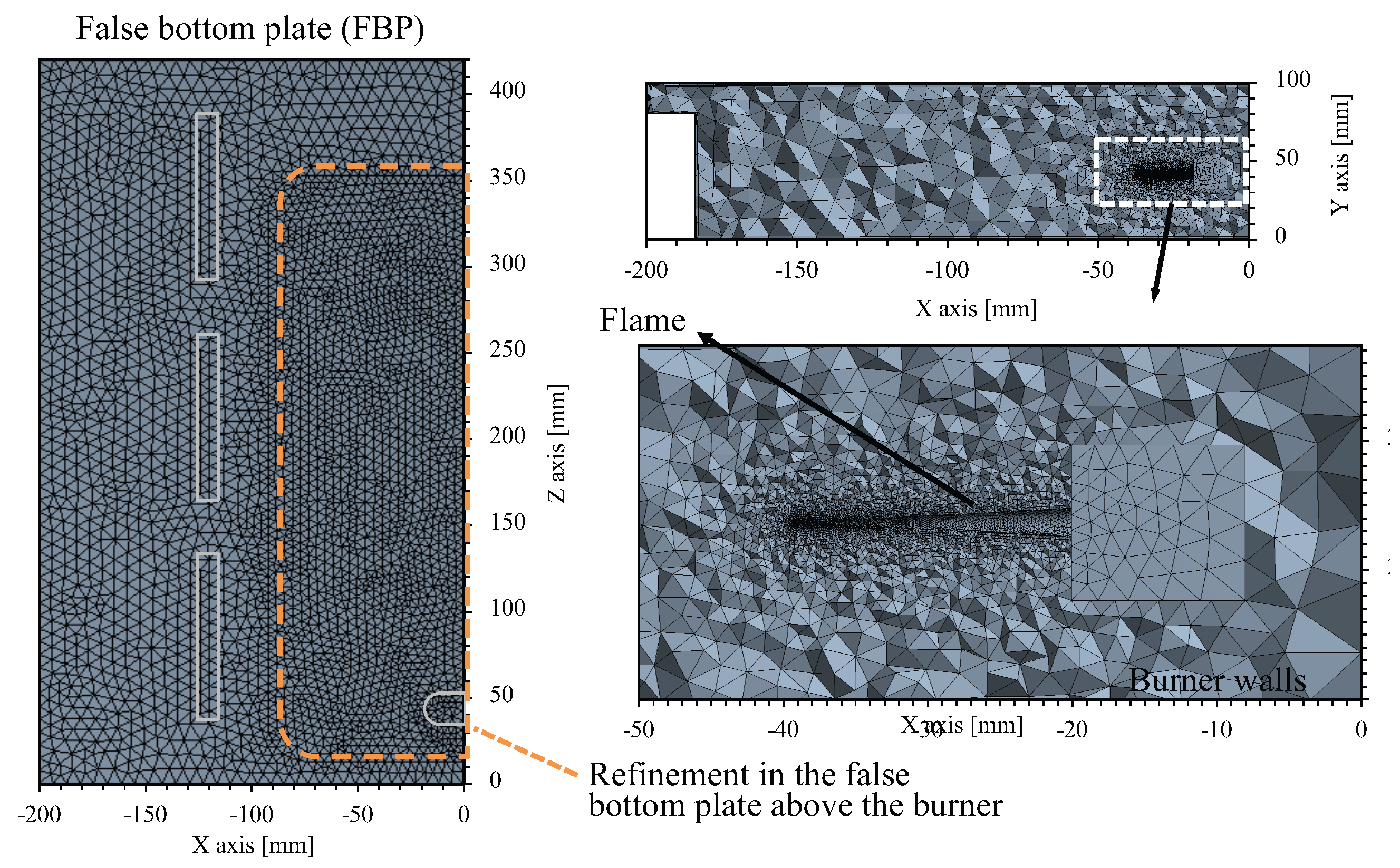

| Mesh | Elements | Nodes Plate | (K) | (K) | time (h:m:s) | |
|---|---|---|---|---|---|---|
| 1 | 3,598,576 | 757,098 | 0.492 | 589.063 | 677.349 | 07:10:36 |
| 2 | 4,111,743 | 763,278 | 1.09 | 595.62 | 695.89 | 12:20:11 |
| 3 | 5,437,027 | 1,066,570 | 0.494 | 598.305 | 697.5 | 18:51:20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hincapié, F.F.; García, M.J. A Surrogate Model of Heat Transfer Mechanism in a Domestic Gas Oven: A Numerical Simulation Approach for Premixed Flames. Appl. Mech. 2024, 5, 391-404. https://doi.org/10.3390/applmech5020023
Hincapié FF, García MJ. A Surrogate Model of Heat Transfer Mechanism in a Domestic Gas Oven: A Numerical Simulation Approach for Premixed Flames. Applied Mechanics. 2024; 5(2):391-404. https://doi.org/10.3390/applmech5020023
Chicago/Turabian StyleHincapié, Fredy F., and Manuel J. García. 2024. "A Surrogate Model of Heat Transfer Mechanism in a Domestic Gas Oven: A Numerical Simulation Approach for Premixed Flames" Applied Mechanics 5, no. 2: 391-404. https://doi.org/10.3390/applmech5020023
APA StyleHincapié, F. F., & García, M. J. (2024). A Surrogate Model of Heat Transfer Mechanism in a Domestic Gas Oven: A Numerical Simulation Approach for Premixed Flames. Applied Mechanics, 5(2), 391-404. https://doi.org/10.3390/applmech5020023




