Influence of the 3D Printing Fabrication Parameters on the Tensile Properties of Carbon-Based Composite Filament
Abstract
1. Introduction
2. Materials and Methods
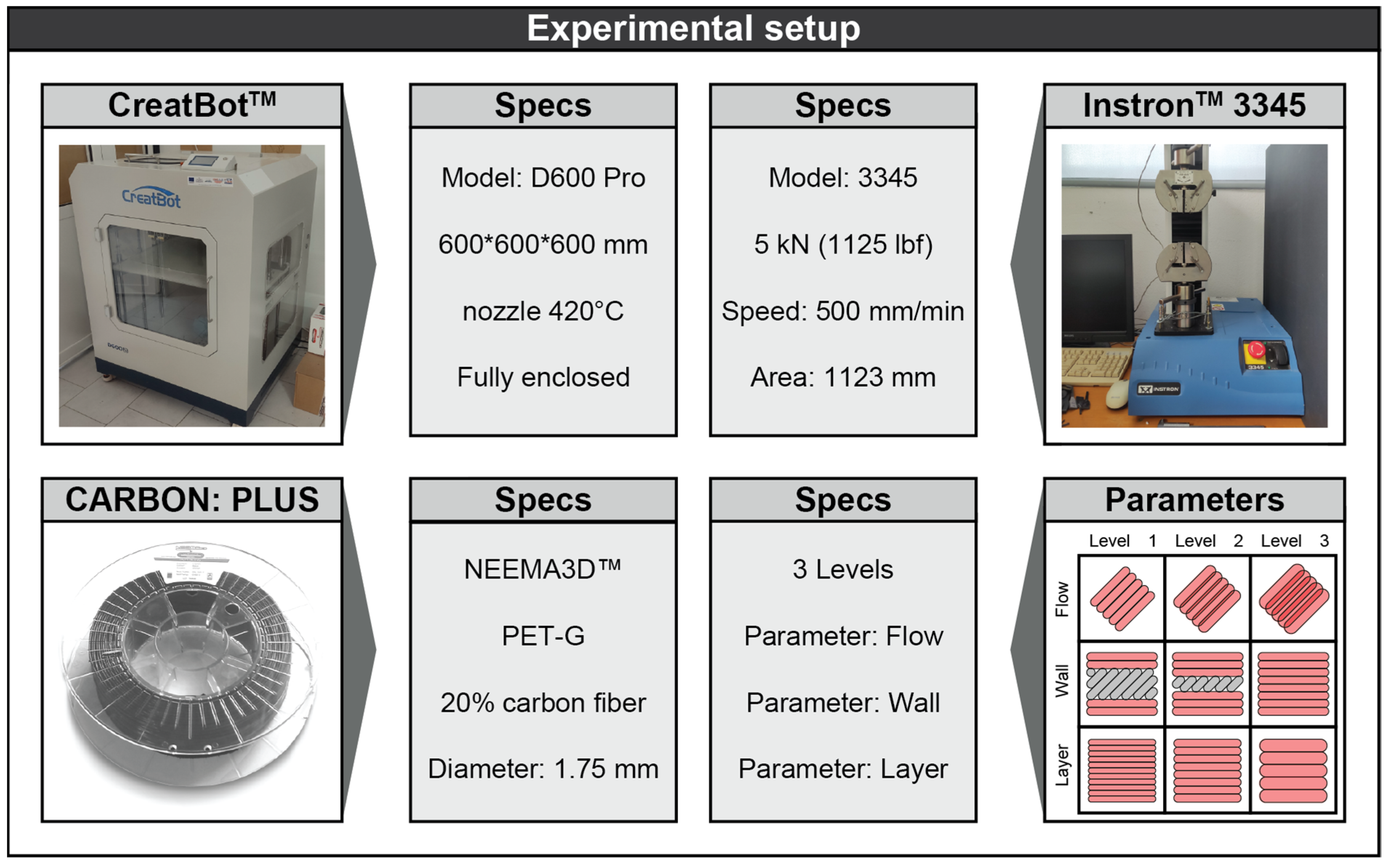
Experimental Setup
- The flow variable is the flow rate and determines the amount of material that passes through the 3D printer nozzle. The flow is expressed as a percentage. The percentage at its original value is equal to 100%. For each increase or decrease in the percentage, the amount of material that passes through the nozzle increases or decreases accordingly.
- The wall is the wall thickness around the geometry. The walls are expressed by the number of parallel passes of the nozzle, for example, if walls = 2, then the thickness of the printed geometry would be (wall = 2 × 0.6 mm = 1.2 mm) for a nozzle = 0.6 mm.
- The layer is the last variable to be parameterized. The layer defines the thickness of the layers with which the geometry is to be fabricated. The measurement unit of the layer is millimeters (mm).
3. Results
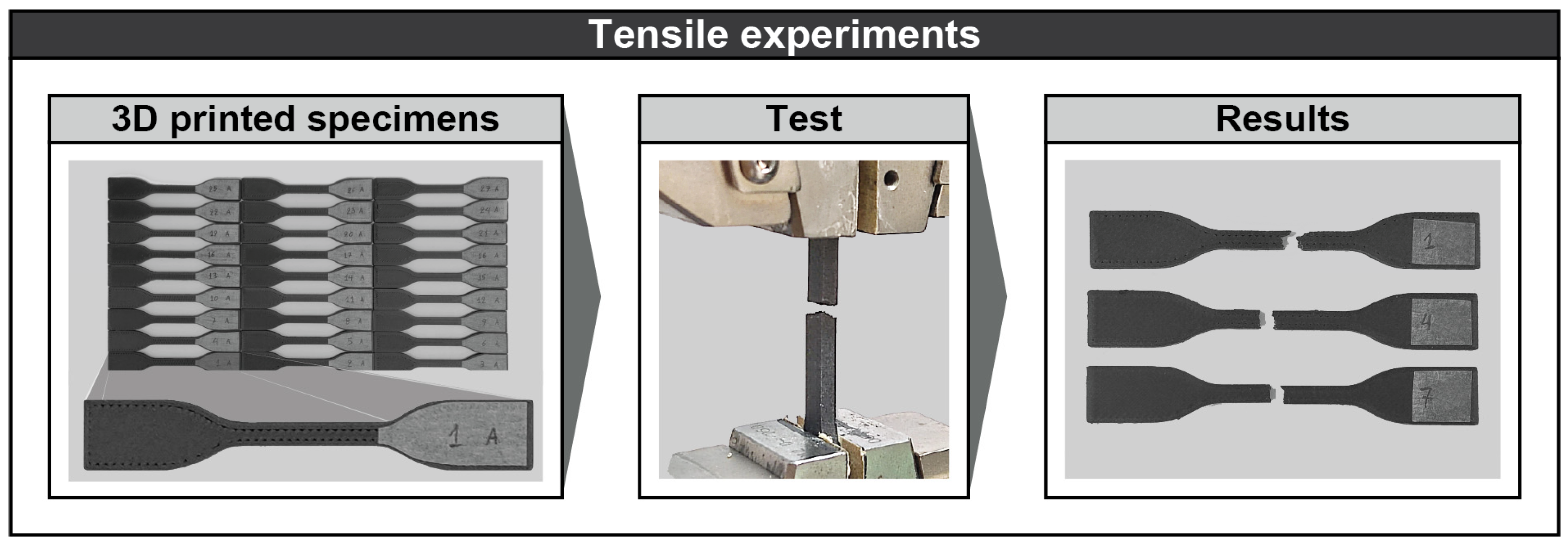
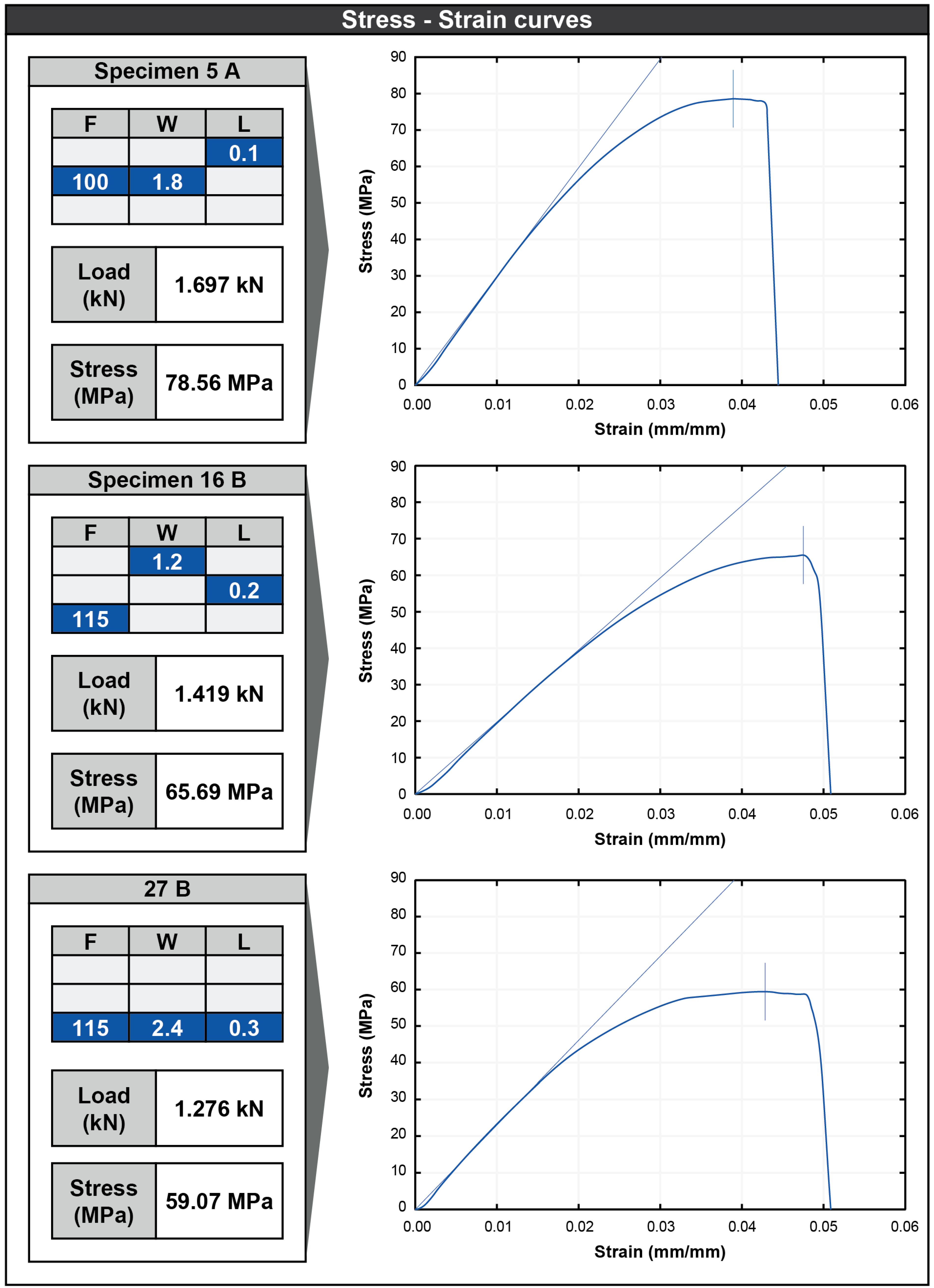
3.1. 3D Printing and Tensile Strength Measurement
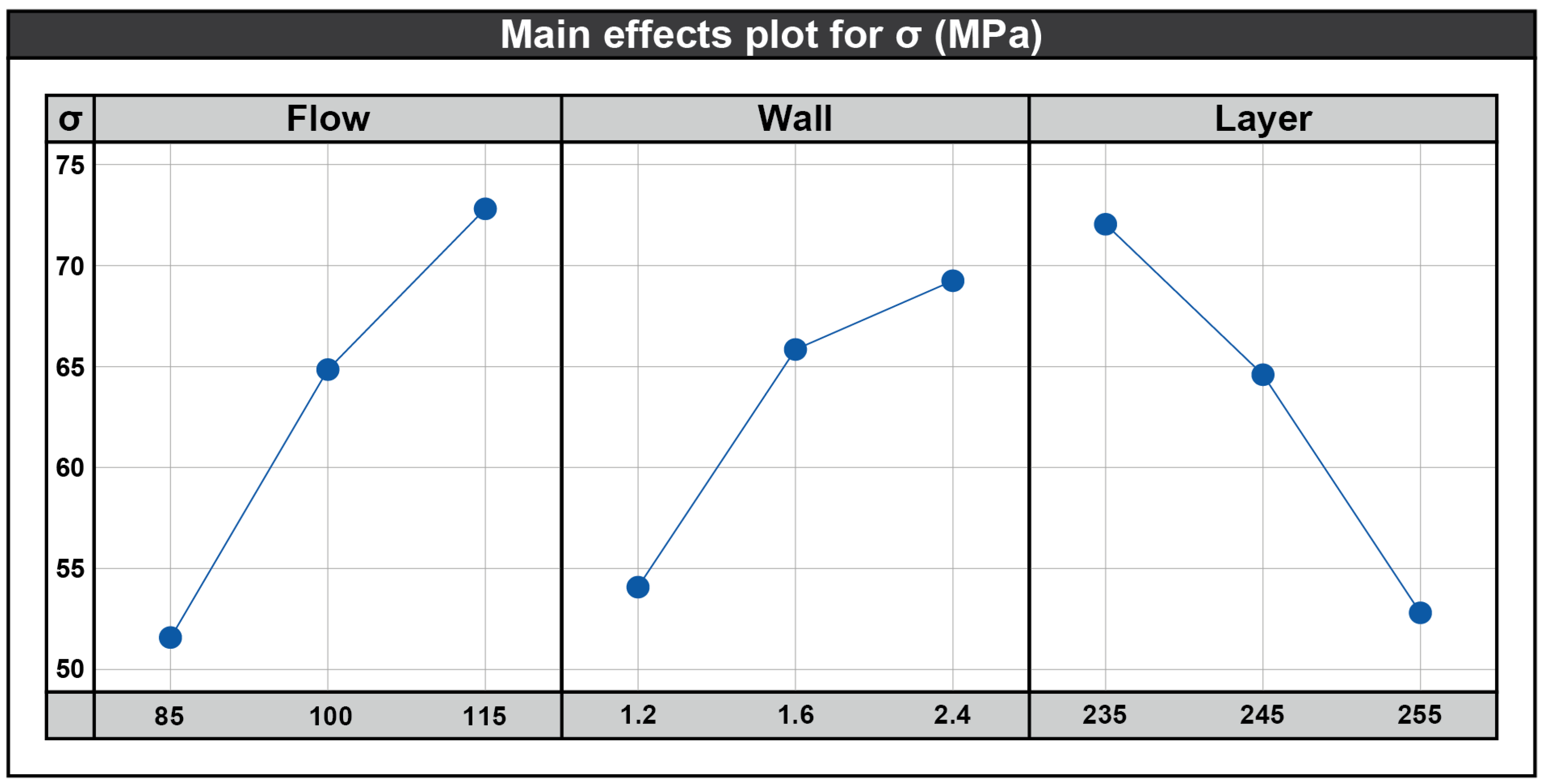
3.2. Main Effects Plot Diagrams
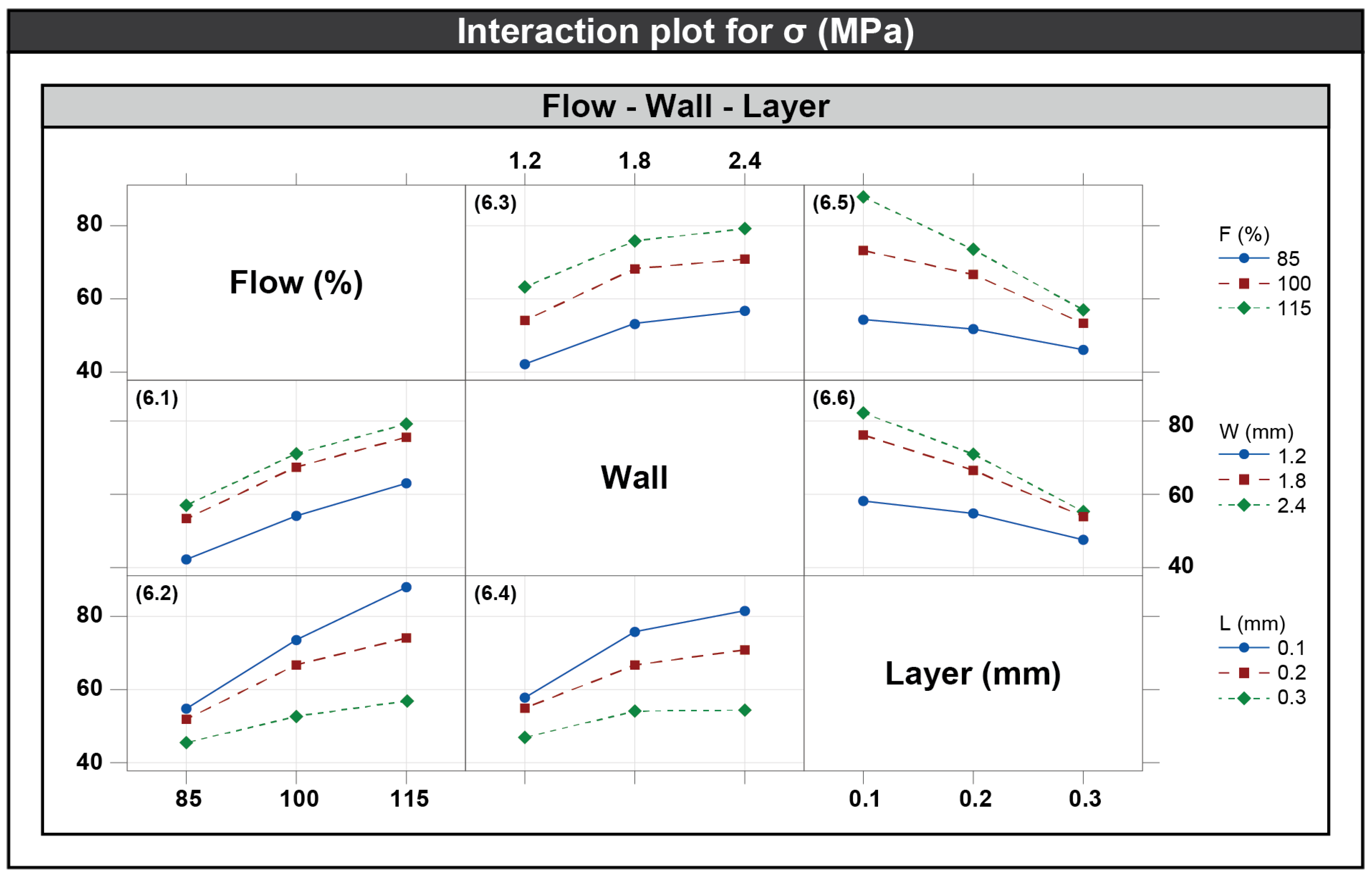
3.3. Interaction Plot Diagrams
- The flow affected the strength of the specimens with similar results to those of the wall parameter. In diagrams (6.1) and (6.2), we can see the lines and their slopes. More specifically, the increase in the flow in all cases increased the strength of the samples accordingly. The changes in the wall values did not affect the lines, as shown in diagram (6.1). However, the layer also, in this case, seemed to affect the slopes of the lines in diagram (6.2).
- The wall parameter with a value of 2.4 mm increased the trend against values of 1.8 mm and 2.4 mm, respectively. The increase in stress does not follow a linear pattern, as seen in diagrams (6.3) and (6.4). The slope of the lines decreased between values of 1.2–1.8 mm and 1.8–2.4 mm.
- The layer is a parameter that affects the tensile strength of the 3D-printed structure. More specifically, the height of 0.1 mm presented a higher resistance in tension compared to 0.2 mm and 0.3 mm, respectively. In diagrams (6.5) and (6.6), it is evident that the changes in the values of the wall and flow affect the slope rate of the curves separately for each value of the layer. For example, in diagram (6.5), the difference in stress between 0.1 mm and 0.3 mm with constant flow = 115% is equal to 30.22 MPa, while the difference in stress between 0.1 mm and 0.3 mm with constant flow = 85% is equal to 8.23 MPa. The difference between the two stresses is also visible, as there is a large difference in the slope of the lines. A similar trend is depicted in diagram (6.4) with a smaller difference in the influence of the stress. Therefore, the layer directly affects the strength of the printed structure, with the lowest value contributing the most. At the same time, any increase in the flow and wall affects the stress increasingly and, therefore, makes the stress differences more distinct.
- Diagram (6.1) illustrates the flow vs. wall interaction on the generated stress. It is observed that as the flow rate increases, so does the stress at a steady rate per wall level. Similarly, when the wall is increasing, the stress rises as well. However, it is noticed that when shifting from wall = 1.8 mm to wall = 2.4 mm, the increase is much lower compared to shifting between 1.2 mm and 1.8 mm.
- Diagram (6.2) shows the flow vs. layer interaction. The stress rises as the flow rate increases per layer height level. Moreover, it is noted that lower values of layer height act increasingly. The largest increase is observed when shifting from an 85% flow rate to 115% at 0.1 mm layer height.
- Diagram (6.3), which visualizes the interaction between the wall and flow, presents a similar pattern to diagram (6.1).
- Diagram (6.4) shows the wall vs. layer interaction. The diagram suggests that increasing the wall thickness affects stress increasingly, regardless of the layer height. The increase, however, is more significant when shifting the wall value from 1.2 mm to 1.8 mm compared to the increase generated when changing the wall value from 1.8 mm to 2.4 mm. Moreover, it is evident that smaller layer height contributes to higher values of strength for each level of the wall.
- Diagram (6.5) presents the layer vs. flow interaction, indicating that increasing the wall thickness acts decreasingly on the generated stress, regardless of the flow rate level. Contrarily, shifting the flow rate upwards increases the stress. In addition, this increase is more evident at a layer height equal to 0.1 mm.
- Finally, diagram (6.6) shows the interaction between the layer and wall, with an effect pattern similar to the one in diagram (6.5). The exception here is that a 0.3 mm layer height combined with either a wall thickness of 1.8 mm or 2.4 mm produces the same levels of stress.
3.4. Definition of the Regression Equation
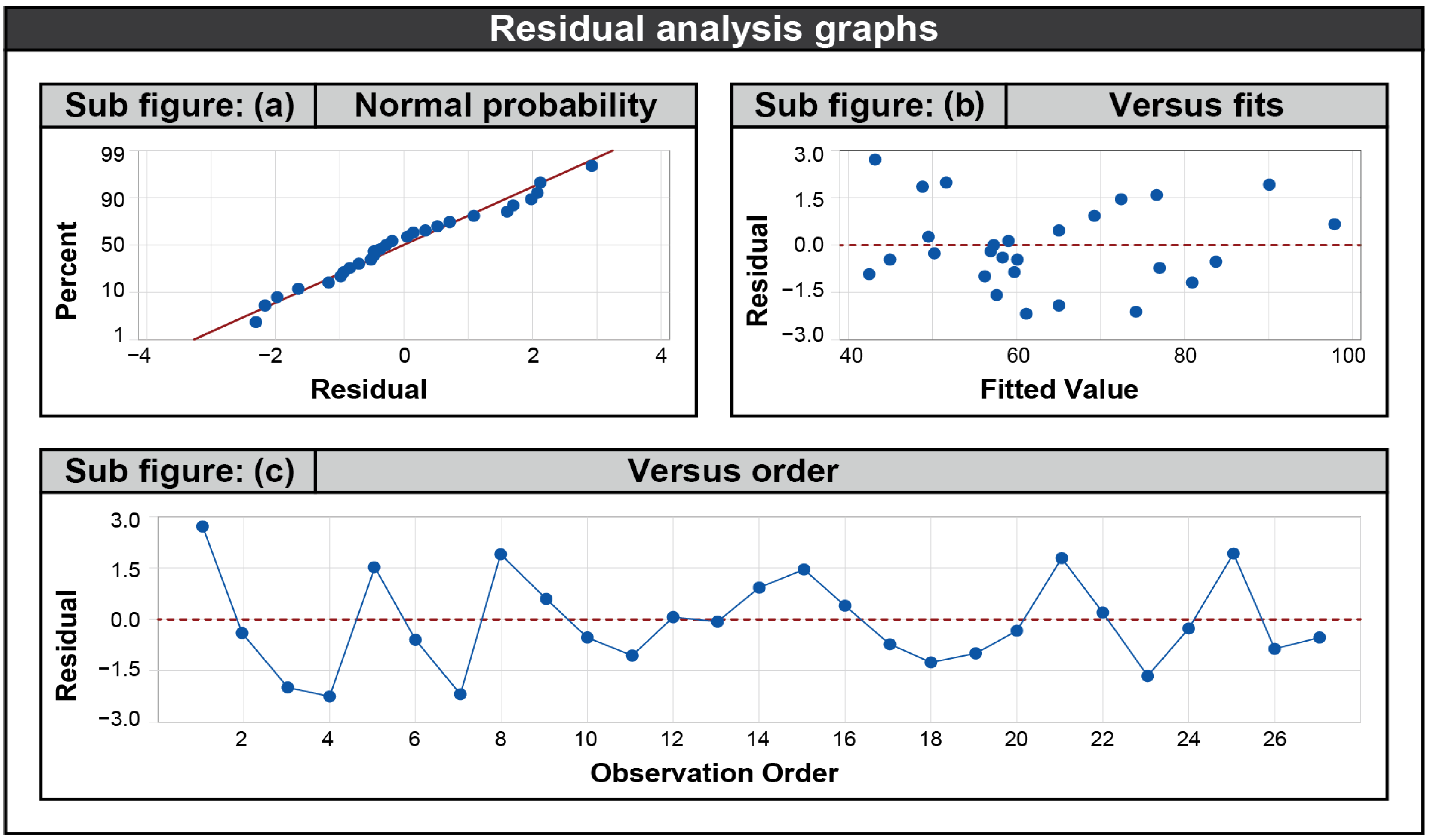
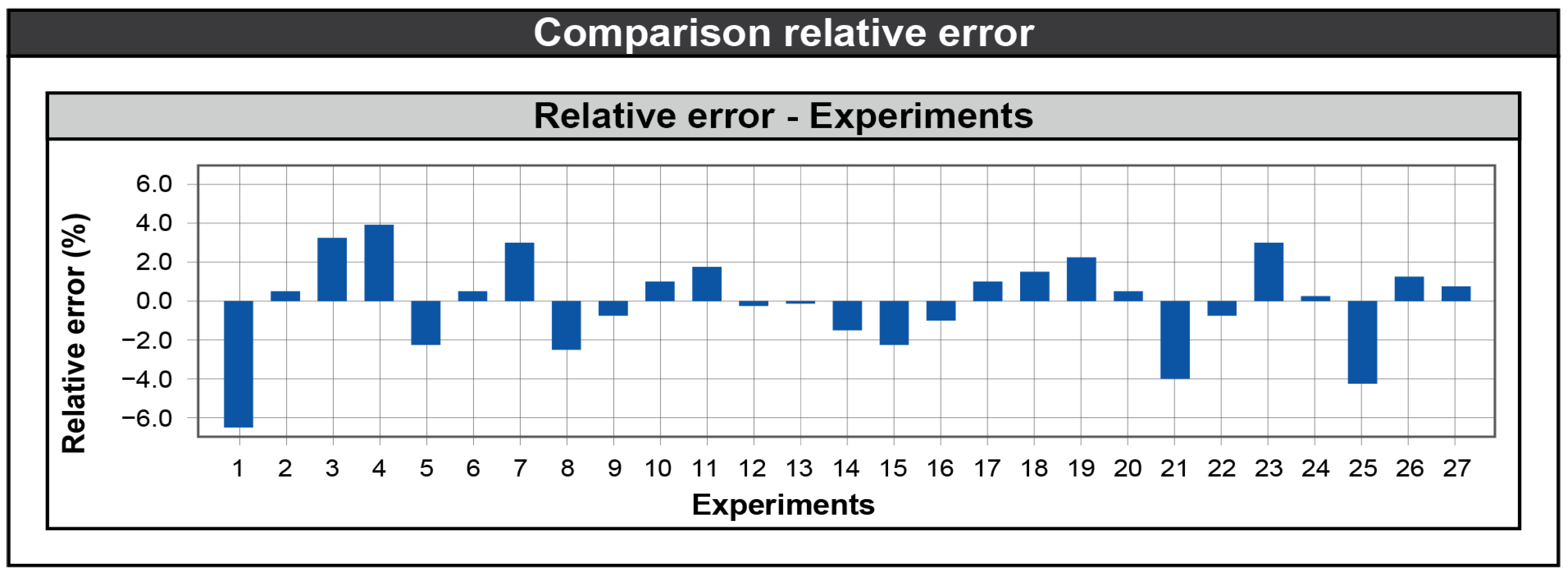
3.5. Residual Analysis Graphs and Relative Error
3.6. 3D Surface Plots
3.7. Prediction and Validation
4. Conclusions
- Decreasing the layer parameter significantly increases the strength of the 3D-printed sample. Also, changes to the values of the wall and flow affect the slope rate of the curves separately for each value of the layer.
- The increase in the wall parameter increased the tensile strength of the structures at a corresponding rate. The increase in tensile stress did not show a linear rate. At the same time, the flow did not seem to affect the rate of stress increase, as the slopes of the lines in the diagram (6.3) in Figure 6 show a uniform increase at all three values of the flow.
- The smaller the number of the layer, the more incremental the rate of increase was in tensile strength.
- The flow parameter affected the strength of the specimens with similar results to those of the wall. Increasing the flow in all cases increased the strength of the specimens accordingly. Changes in wall values did not affect the slope of the lines. However, the layer also in this case seemed to affect the gradients of the lines.
- The flow and layer are two important parameters, as they affect either directly or indirectly in any case the tendency of the essays. This fact can be seen in Figure 6, where the combinations of the flow and layer diagrams (6.2) and (6.5) show the maximum slopes of the lines.
- The maximum tensile strength was equal to σ = 98.48 MPa and was found in test series 9 (layer = 0.1 mm, wall = 2.4 mm, flow = 115%).
- The minimum tensile strength was equal to σ = 41.26 MPa and was found in test series 19 (layer = 0.3 mm, wall = 1.2 mm, flow = 85%).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, S.S.; Jin, F.L.; Rhee, K.Y.; Hui, D.; Park, S.J. Recent Advances in Carbon-Fiber-Reinforced Thermoplastic Composites: A Review. Compos. B Eng. 2018, 142, 241–250. [Google Scholar] [CrossRef]
- Grünewald, J.; Parlevliet, P.; Altstädt, V. Manufacturing of Thermoplastic Composite Sandwich Structures: A Review of Literature. J. Thermoplast. Compos. Mater. 2017, 30, 437–464. [Google Scholar] [CrossRef]
- Blok, L.G.; Longana, M.L.; Yu, H.; Woods, B.K.S. An Investigation into 3D Printing of Fibre Reinforced Thermoplastic Composites. Addit. Manuf. 2018, 22, 176–186. [Google Scholar] [CrossRef]
- Bahari, S.A.; Krause, A. Utilizing Malaysian Bamboo for Use in Thermoplastic Composites. J. Clean Prod. 2016, 110, 16–24. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, H.; Li, Z.; Li, P.; Shi, S.Q. Development and Application of Wood Flour-Filled Polylactic Acid Composite Filament for 3d Printing. Materials 2017, 10, 339. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Zaoutsos, S.P.; Chaidas, D.; Vidakis, N. Multi-Parameter Optimization of PLA/Coconut Wood Compound for Fused Filament Fabrication Using Robust Design. Int. J. Adv. Manuf. Technol. 2022, 119, 4317–4328. [Google Scholar] [CrossRef]
- Mohammadizadeh, M.; Lu, H.; Fidan, I.; Tantawi, K.; Gupta, A.; Hasanov, S.; Zhang, Z.; Alifui-Segbaya, F.; Rennie, A. Mechanical and Thermal Analyses of Metal-PLA Components Fabricated by Metal Material Extrusion. Inventions 2020, 5, 1–11. [Google Scholar] [CrossRef]
- Elessawy, N.A.; El Shakhs, A.; Fahmy El-Saka, M.; Youssef, M.E.; Youssef, B.A.B.; Malek Ali, M.A. Sustainable and Eco-Friendly 3D Printing Filament Fabricated from Different Recycled Solid Wastes and Evaluate Its Impact on Interior and Furniture Design. Results Eng. 2024, 23, 102428. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. FDM-Based 3D Printing of Polymer and Associated Composite: A Review on Mechanical Properties, Defects and Treatments. Polymers 2020, 12, 1–42. [Google Scholar] [CrossRef]
- Baechle-Clayton, M.; Loos, E.; Taheri, M.; Taheri, H. Failures and Flaws in Fused Deposition Modeling (FDM) Additively Manufactured Polymers and Composites. J. Compos. Sci. 2022, 6, 202. [Google Scholar] [CrossRef]
- Fetecau, C.; Dobrea, D.V.; Postolache, I. Overmolding injection molding simulation of tensile test specimen. Int. J. Mod. Manuf. Technol. 2010, 2, 45. [Google Scholar]
- Takemura, K.; Minekage, Y. Effect of Molding Condition on Tensile Properties of Hemp Fiber Reinforced Composite. Adv. Compos. Mater. Off. J. Jpn. Soc. Compos. Mater. 2007, 16, 385–394. [Google Scholar] [CrossRef]
- Pothan, L.A.; Mai, Y.W.; Thomas, S.; Li, R.K.Y. Tensile and Flexural Behavior of Sisal Fabric/Polyester Textile Composites Prepared by Resin Transfer Molding Technique. J. Reinf. Plast. Compos. 2008, 27, 1847–1866. [Google Scholar] [CrossRef]
- Sanford, L.T.; Jaafar, I.H.; Seibi, A.; Gohn, A. The Effect of Infill Angle, Build Orientation, and Void Fraction on the Tensile Strength and Fracture of 3D Printed ASA via Fused Filament Fabrication. Manuf. Lett. 2022, 33, 569–573. [Google Scholar] [CrossRef]
- Tzotzis, A.; Manavis, A.; Efkolidis, N.; García-Hernández, C.; Kyratsis, P. Analysis of the Influence of Structural Characteristics on the Tensile Properties of Fused Filament Fabricated ABS Polymer Using Central Composite Design. Appl. Mech. 2024, 5, 20–35. [Google Scholar] [CrossRef]
- Samykano, M.; Selvamani, S.K.; Kadirgama, K.; Ngui, W.K.; Kanagaraj, G.; Sudhakar, K. Mechanical Property of FDM Printed ABS: Influence of Printing Parameters. Int. J. Adv. Manuf. Technol. 2019, 102, 2779–2796. [Google Scholar] [CrossRef]
- Torrado Perez, A.R.; Roberson, D.A.; Wicker, R.B. Fracture Surface Analysis of 3D-Printed Tensile Specimens of Novel ABS-Based Materials. J. Fail. Anal. Prev. 2014, 14, 343–353. [Google Scholar] [CrossRef]
- Lobov, E.; Vindokurov, I.; Tashkinov, M. Mechanical Properties and Performance of 3D-Printed Acrylonitrile Butadiene Styrene Reinforced with Carbon, Glass and Basalt Short Fibers. Polymers 2024, 16, 1106. [Google Scholar] [CrossRef]
- Abid, S.; Messadi, R.; Hassine, T.; Ben Daly, H.; Soulestin, J.; Lacrampe, M.F. Optimization of Mechanical Properties of Printed Acrylonitrile Butadiene Styrene Using RSM Design. Int. J. Adv. Manuf. Technol. 2019, 100, 1363–1372. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Wang, K.; Yao, S.; Peng, Y.; Rao, Y.; Ahzi, S. Progressive collapse behaviors and mechanisms of 3D printed thin-walled composite structures under multi-conditional loading. Thin-Walled Struct. 2022, 171, 108810. [Google Scholar] [CrossRef]
- Forcellese, A.; Simoncini, M.; Vita, A.; Di Pompeo, V. 3D printing and testing of composite isogrid structures. Int. J. Adv. Manuf. Technol. 2020, 109, 1881–1893. [Google Scholar] [CrossRef]
- Fisher, T.; Almeida, J.H.S., Jr.; Falzon, B.G.; Kazancı, Z. Tension and compression properties of 3D-printed composites: Print orientation and strain rate effects. Polymers 2023, 15, 1708. [Google Scholar] [CrossRef]
- Bragaglia, M.; Paleari, L.; Passaro, J.; Russo, P.; Fabbrocino, F.; Luciano, R.; Nanni, F. 3D printing of biodegradable and self-monitoring SWCNT-loaded biobased resin. Compos. Sci. Technol. 2023, 243, 110253. [Google Scholar] [CrossRef]
- Hanon, M.M.; Ghaly, A.; Zsidai, L.; Szakál, Z.; Szabó, I.; Kátai, L. Investigations of the mechanical properties of DLP 3D printed graphene/resin composites. Acta Polytech. Hung 2021, 18, 143–161. [Google Scholar] [CrossRef]
- ASTM D638-22; Standard Test Method for Tensile Properties of Plastics. American Society for Testing and Materials: West Conshohocken, PA, USA, 2022. Available online: https://www.astm.org/d0638-22.html (accessed on 1 July 2024).
- Rismalia, M.; Hidajat, S.C.; Permana, I.G.R.; Hadisujoto, B.; Muslimin, M.; Triawan, F. Infill Pattern and Density Effects on the Tensile Properties of 3D Printed PLA Material. J. Phys. Conf. Ser. 2019, 1402, 044041. [Google Scholar]
- Atakok, G.; Kam, M.; Koc, H.B. Tensile, Three-Point Bending and Impact Strength of 3D Printed Parts Using PLA and Recycled PLA Filaments: A Statistical Investigation. J. Mater. Res. Technol. 2022, 18, 1542–1554. [Google Scholar] [CrossRef]
- Anderson, I. Mechanical Properties of Specimens 3D Printed with Virgin and Recycled Polylactic Acid. 3D Print Addit. Manuf. 2017, 4, 110–115. [Google Scholar] [CrossRef]
- Breški, T.; Hentschel, L.; Godec, D.; Đuretek, I. Suitability of Recycled PLA Filament Application in Fused Filament Fabrication Process. Teh. Glas. 2021, 15, 491–497. [Google Scholar] [CrossRef]
- Ghabezi, P.; Sam-Daliri, O.; Flanagan, T.; Walls, M.; Harrison, N.M. Circular economy innovation: A deep investigation on 3D printing of industrial waste polypropylene and carbon fibre composites. Resour. Conserv. Recycl. 2024, 206, 107667. [Google Scholar] [CrossRef]
- Khabia, S.; Jain, K.K. Comparison of Mechanical Properties of Components 3D Printed from Different Brand ABS Filament on Different FDM Printers. Mater. Today Proc. 2019, 26, 2907–2914. [Google Scholar] [CrossRef]
- Marșavina, L.; Vălean, C.; Mărghitaș, M.; Linul, E.; Razavi, N.; Berto, F.; Brighenti, R. Effect of the Manufacturing Parameters on the Tensile and Fracture Properties of FDM 3D-Printed PLA Specimens. Eng. Fract. Mech. 2022, 274, 108766. [Google Scholar] [CrossRef]
- Tzotzis, A.; Antoniadis, A.; Kyratsis, P. Multivariate Modelling of AA6082-T6 Drilling Performance Using RSM, ANN and Response Optimization. Int. J. Lightweight Mater. Manuf. 2024, 7, 531–545. [Google Scholar] [CrossRef]
- Tzotzis, A.; García-Hernández, C.; Huertas-Talón, J.L.; Kyratsis, P. Influence of the Nose Radius on the Machining Forces Induced during AISI-4140 Hard Turning: A CAD-Based and 3D FEM Approach. Micromachines 2020, 11, 798. [Google Scholar] [CrossRef] [PubMed]
- Tzotzis, A.; Garciá-Hernández, C.; Huertas-Talón, J.L.; Kyratsis, P. 3D FE Modelling of Machining Forces during AISI 4140 Hard Turning. Stroj. Vestn./J. Mech. Eng. 2020, 66, 467–478. [Google Scholar] [CrossRef]
- NEEMA3D™ CARBON: PLUS. Available online: http://www.neema3d.com/neema3dt-plus-sign-materials/carbon-plus (accessed on 1 July 2024).
- Blaj, M.I.; Zaharia, S.M.; Pop, M.A.; Oancea, G.H.E.O.R.G.H.E. Tensile properties and manufacturing defectives of short carbon fiber specimens made with the FDM process. Mater. Plast. 2022, 59, 33–43. [Google Scholar] [CrossRef]
- Muhamedagic, K.; Berus, L.; Potočnik, D.; Cekic, A.; Begic-Hajdarevic, D.; Cohodar Husic, M.; Ficko, M. Effect of process parameters on tensile strength of FDM printed carbon fiber reinforced polyamide parts. Appl. Sci. 2022, 12, 6028. [Google Scholar] [CrossRef]
- Cao, M.; Cui, T.; Yue, Y.; Li, C.; Guo, X.; Jia, X.; Wang, B. Investigation of carbon fiber on the tensile property of FDM-produced PLA specimen. Polymers 2022, 14, 5230. [Google Scholar] [CrossRef]
- Kamaal, M.; Anas, M.; Rastogi, H.; Bhardwaj, N.; Rahaman, A. Effect of FDM process parameters on mechanical properties of 3D-printed carbon fibre–PLA composite. Prog. Addit. Manuf. 2021, 6, 63–69. [Google Scholar] [CrossRef]
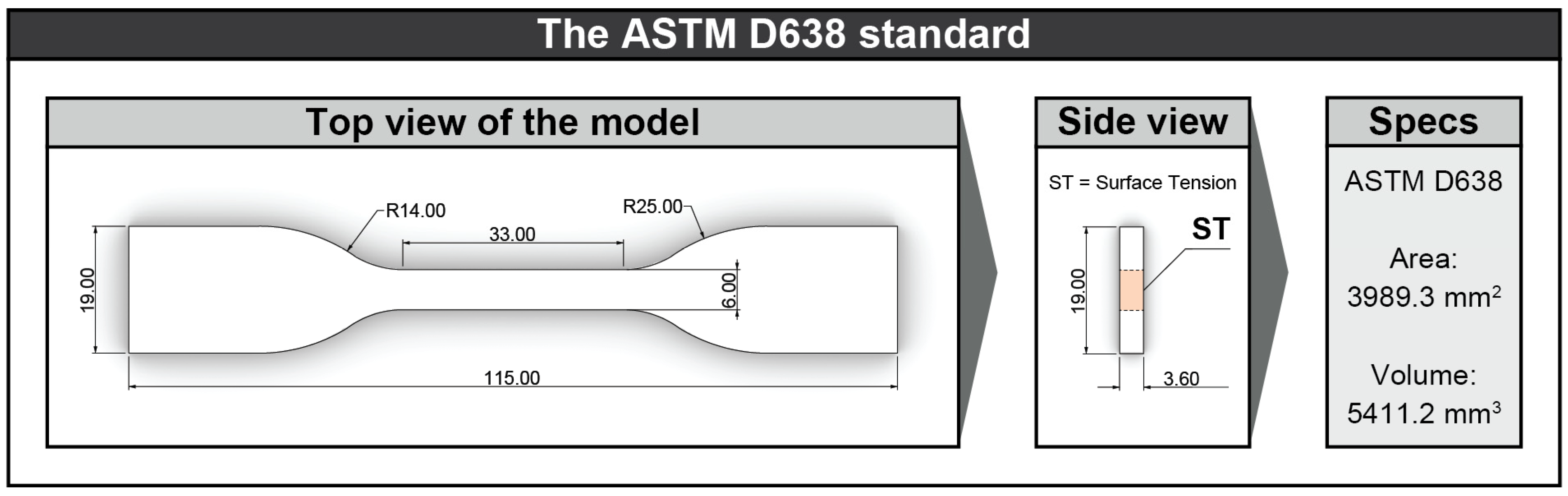

| Description | Typical Value |
|---|---|
| Specific gravity | 1.19 g/cc |
| E-modulus 1 mm/min | 3800 MPa |
| Yield stress 50 mm/min | 52.5 MPa |
| Yield strain 50 mm/min | 4.2% |
| Strain at break 50 min/min | 8% |
| Impact strength izod notched 23 °C | 3.8 kJ/m2 |
| Heat distortion | 80 °C |
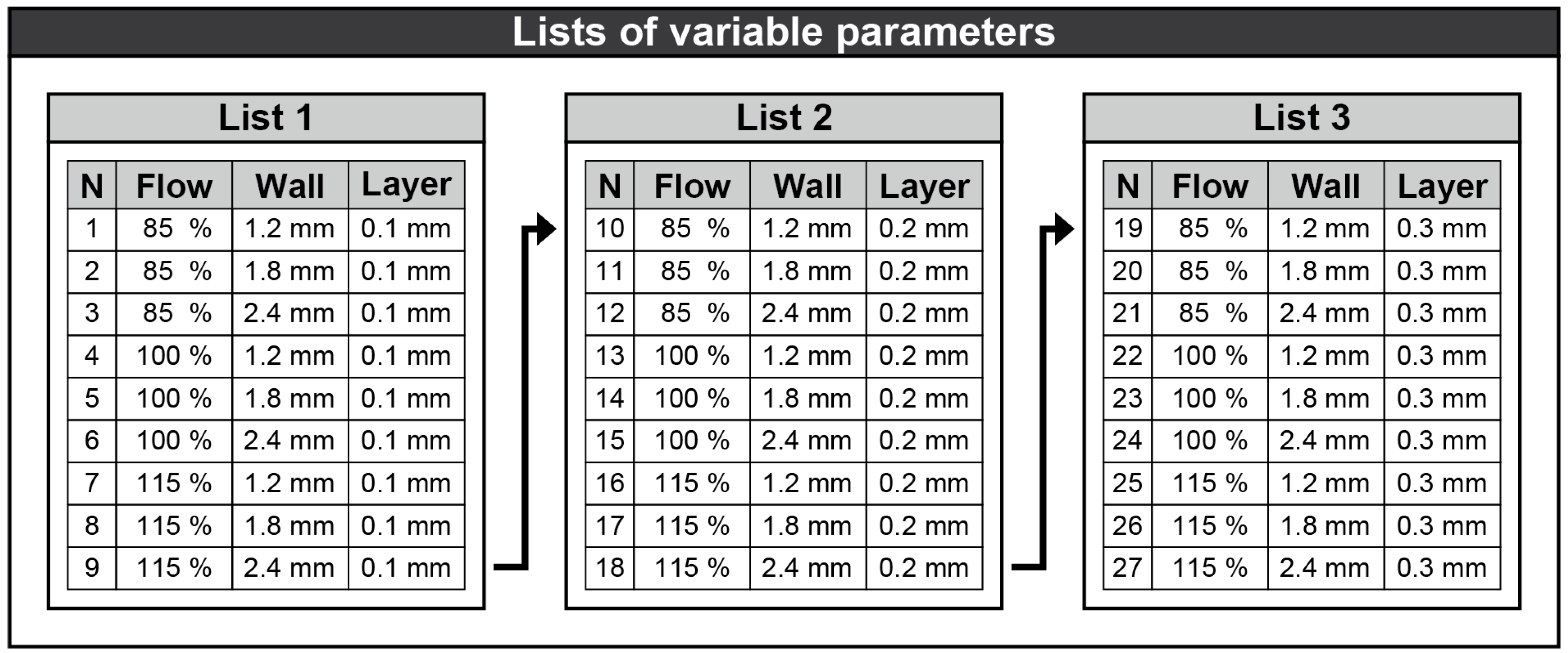
| Level | Flow (%) | Wall (mm) | Layer (mm) |
| −1 | 85 | 1.2 (2 walls) | 0.1 |
| 0 | 100 | 1.8 (3 walls) | 0.2 |
| +1 | 115 | 2.4 (4 walls) | 0.3 |
| Operation Parameter | Value |
|---|---|
| Nozzle Temperature | 245 °C |
| Bed Temperature | 60 °C |
| Infill | 100% |
| Filament Diameter | 1.75 mm |
| Nozzle Diameter | 0.6 mm |
| Printing Speed | 40 mm/s |
| Perimeter Speed | 50% |
| Cooling Fan | 100% |
| Test | Flow (%) | Wall (mm) | Layer (mm) | Flow Level | Wall Level | Layer Level | Average Max Load (kN) | σ (MPa) |
|---|---|---|---|---|---|---|---|---|
| 1 | 85 | 1.2 | 0.1 | −1 | −1 | −1 | 0.985 | 45.606 |
| 2 | 85 | 1.8 | 0.1 | −1 | 0 | −1 | 1.247 | 57.733 |
| 3 | 85 | 2.4 | 0.1 | −1 | 1 | −1 | 1.357 | 62.829 |
| 4 | 100 | 1.2 | 0.1 | 0 | −1 | −1 | 1.266 | 58.633 |
| 5 | 100 | 1.8 | 0.1 | 0 | 0 | −1 | 1.693 | 78.373 |
| 6 | 100 | 2.4 | 0.1 | 0 | 1 | −1 | 1.800 | 83.320 |
| 7 | 115 | 1.2 | 0.1 | 1 | −1 | −1 | 1.551 | 71.825 |
| 8 | 115 | 1.8 | 0.1 | 1 | 0 | −1 | 1.993 | 92.286 |
| 9 | 115 | 2.4 | 0.1 | 1 | 1 | −1 | 2.127 | 98.483 |
| 10 | 85 | 1.2 | 0.2 | −1 | −1 | 0 | 0.953 | 44.097 |
| 11 | 85 | 1.8 | 0.2 | −1 | 0 | 0 | 1.189 | 55.040 |
| 12 | 85 | 2.4 | 0.2 | −1 | 1 | 0 | 1.275 | 59.029 |
| 13 | 100 | 1.2 | 0.2 | 0 | −1 | 0 | 1.237 | 57.290 |
| 14 | 100 | 1.8 | 0.2 | 0 | 0 | 0 | 1.517 | 70.216 |
| 15 | 100 | 2.4 | 0.2 | 0 | 1 | 0 | 1.599 | 74.014 |
| 16 | 115 | 1.2 | 0.2 | 1 | −1 | 0 | 1.412 | 65.381 |
| 17 | 115 | 1.8 | 0.2 | 1 | 0 | 0 | 1.652 | 76.465 |
| 18 | 115 | 2.4 | 0.2 | 1 | 1 | 0 | 1.720 | 79.635 |
| 19 | 85 | 1.2 | 0.3 | −1 | −1 | 1 | 0.891 | 41.260 |
| 20 | 85 | 1.8 | 0.3 | −1 | 0 | 1 | 1.070 | 49.514 |
| 21 | 85 | 2.4 | 0.3 | −1 | 1 | 1 | 1.095 | 50.707 |
| 22 | 100 | 1.2 | 0.3 | 0 | −1 | 1 | 1.074 | 49.724 |
| 23 | 100 | 1.8 | 0.3 | 0 | 0 | 1 | 1.204 | 55.751 |
| 24 | 100 | 2.4 | 0.3 | 0 | 1 | 1 | 1.222 | 56.554 |
| 25 | 115 | 1.2 | 0.3 | 1 | −1 | 1 | 1.159 | 53.644 |
| 26 | 115 | 1.8 | 0.3 | 1 | 0 | 1 | 1.276 | 59.083 |
| 27 | 115 | 2.4 | 0.3 | 1 | 1 | 1 | 1.279 | 59.219 |
| Info | PET 15% carbon | PA6/66 10% carbon | PLA 30% carbon | PLA 5.5% carbon |
| Max stress (MPa) | 58.0 MPa | 91.53 MPa | 49.41 MPa | 46.26 MPa |
| Authors | Madalina et al. | Muhamedagic et al. | Cao et al. | Kamaal et al. |
| Reference | [37] | [38] | [39] | [40] |
| Source | Degree of Freedom | Sum of Squares | Mean Square | f-Value | p-Value | Contribution% |
|---|---|---|---|---|---|---|
| Regression | 9 | 5440.98 | 604.553 | 202.72 | 0.000 | |
| Error | 17 | 50.70 | 2.982 | |||
| Total | 26 | 5491.68 | ||||
| R-sq = 99.08% R-sq (adj) = 98.59% R-sq (pred) = 97.05% | ||||||
| Term | ||||||
| F (%) | 1 | 96.00 | 96.004 | 32.19 | 0.000 | 7.5 |
| W | 1 | 147.14 | 147.140 | 49.34 | 0.000 | 11.5 |
| L (mm) | 1 | 308.84 | 308.841 | 103.56 | 0.000 | 24.2 |
| F2 | 1 | 39.04 | 39.039 | 13.09 | 0.002 | 3.1 |
| W2 | 1 | 111.72 | 111.720 | 37.46 | 0.000 | 8.8 |
| L2 | 1 | 26.45 | 26.446 | 8.87 | 0.008 | 2.1 |
| F × W | 1 | 1.99 | 1.989 | 0.67 | 0.425 | 0.2 |
| F × L | 1 | 362.60 | 362.598 | 121.59 | 0.000 | 28.4 |
| W × L | 1 | 181.86 | 181.860 | 60.98 | 0.000 | 14.3 |
| Validation Test | Flow (%) | Wall (mm) | Layer (mm) | Max Load (kN) | Average Max Load (kN) | σ (MPa) | Regression (MPa) | Relative Error (%) |
|---|---|---|---|---|---|---|---|---|
| V1.1 | 110 | 1.2 | 0.15 | 1.430 | 1.434 | 66.410 | 67.044 | 0.95 |
| V1.2 | 110 | 1.2 | 0.15 | 1.438 | ||||
| V2.1 | 90 | 1.8 | 0.25 | 1.251 | 1.258 | 58.240 | 57.439 | −1.37 |
| V2.2 | 90 | 1.8 | 0.25 | 1.264 | ||||
| V3.1 | 95 | 2.4 | 0.20 | 1.436 | 1.425 | 65.995 | 68.444 | 3.72 |
| V3.2 | 95 | 2.4 | 0.20 | 1.414 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minaoglou, P.; Tzotzis, A.; Efkolidis, N.; Kyratsis, P. Influence of the 3D Printing Fabrication Parameters on the Tensile Properties of Carbon-Based Composite Filament. Appl. Mech. 2024, 5, 745-761. https://doi.org/10.3390/applmech5040041
Minaoglou P, Tzotzis A, Efkolidis N, Kyratsis P. Influence of the 3D Printing Fabrication Parameters on the Tensile Properties of Carbon-Based Composite Filament. Applied Mechanics. 2024; 5(4):745-761. https://doi.org/10.3390/applmech5040041
Chicago/Turabian StyleMinaoglou, Prodromos, Anastasios Tzotzis, Nikolaos Efkolidis, and Panagiotis Kyratsis. 2024. "Influence of the 3D Printing Fabrication Parameters on the Tensile Properties of Carbon-Based Composite Filament" Applied Mechanics 5, no. 4: 745-761. https://doi.org/10.3390/applmech5040041
APA StyleMinaoglou, P., Tzotzis, A., Efkolidis, N., & Kyratsis, P. (2024). Influence of the 3D Printing Fabrication Parameters on the Tensile Properties of Carbon-Based Composite Filament. Applied Mechanics, 5(4), 745-761. https://doi.org/10.3390/applmech5040041






