Analysis of Damage Value of Aluminum Alloys—Application of a Continuum Damage Mechanics Model
Abstract
:1. Introduction
2. Material
3. Methodology
4. Results and Discussions
4.1. Result Analysis of All Materials
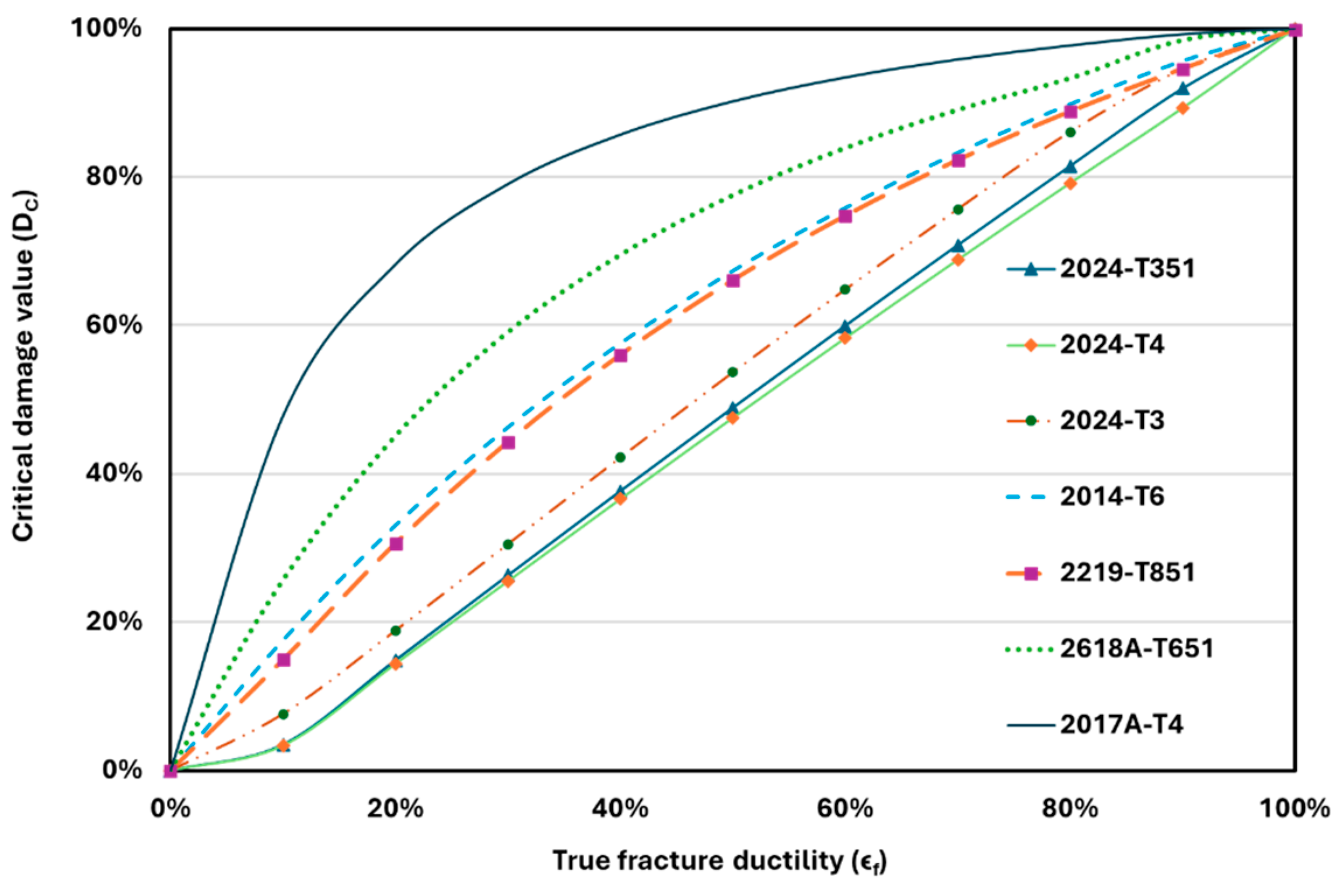
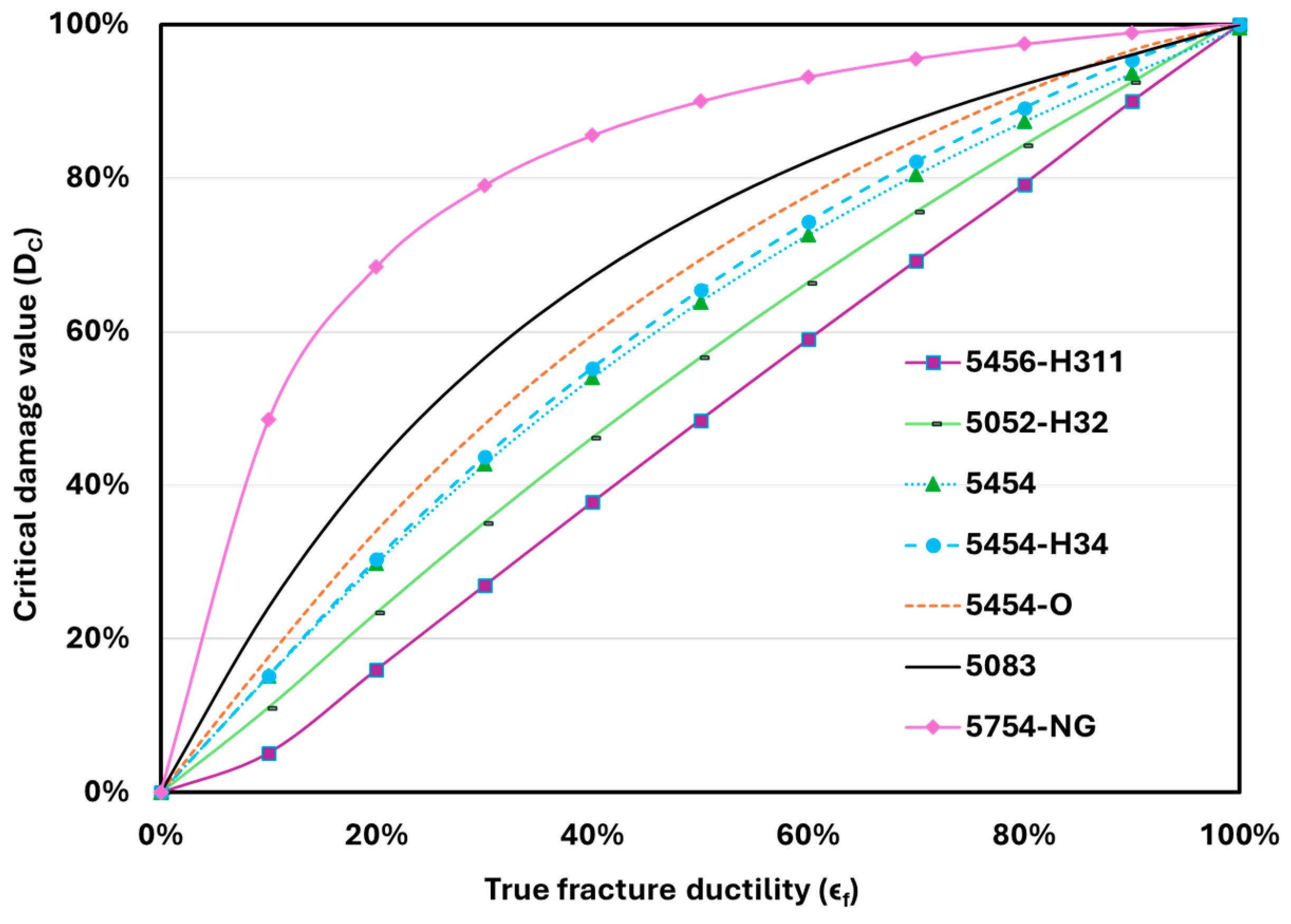
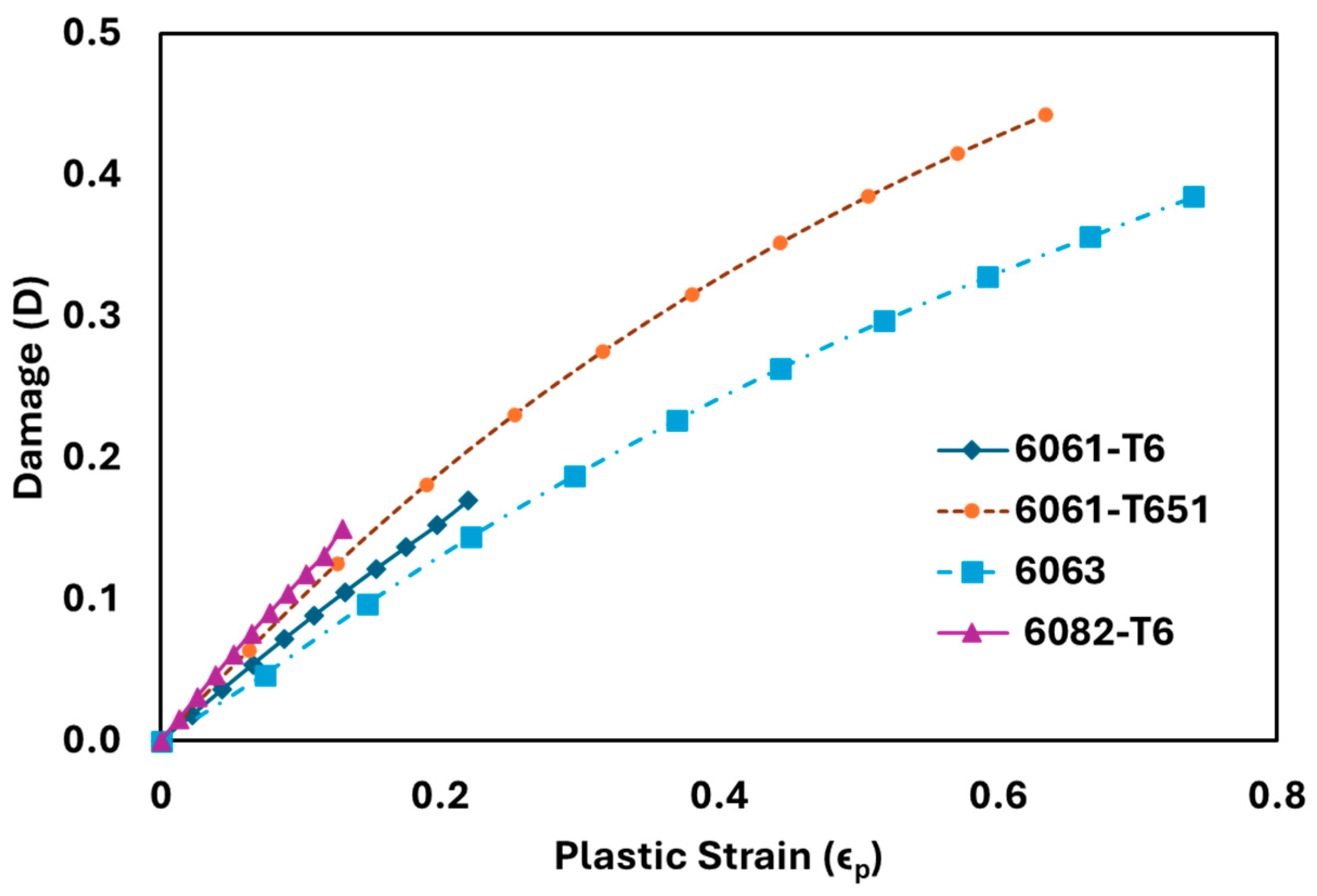
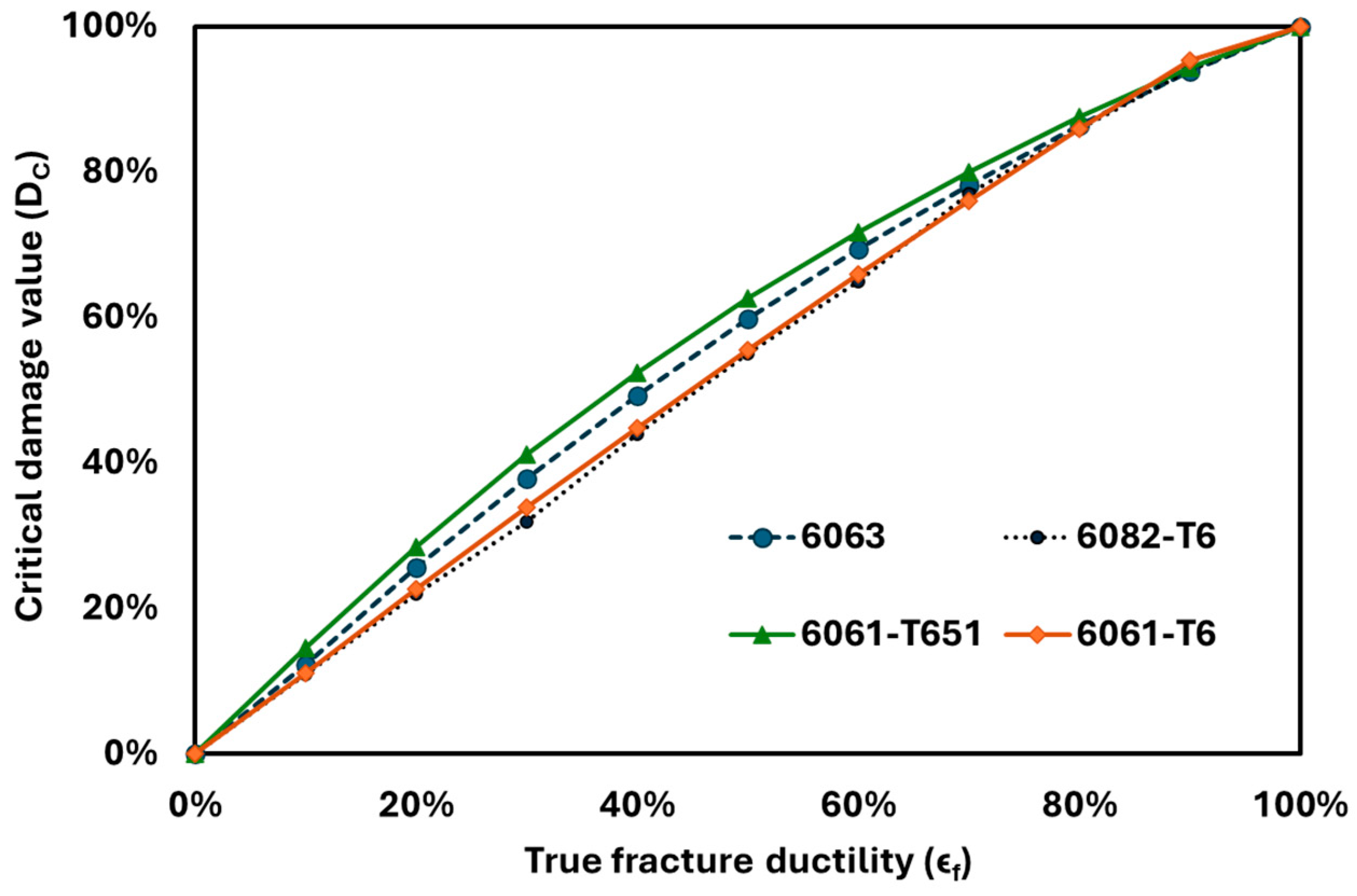
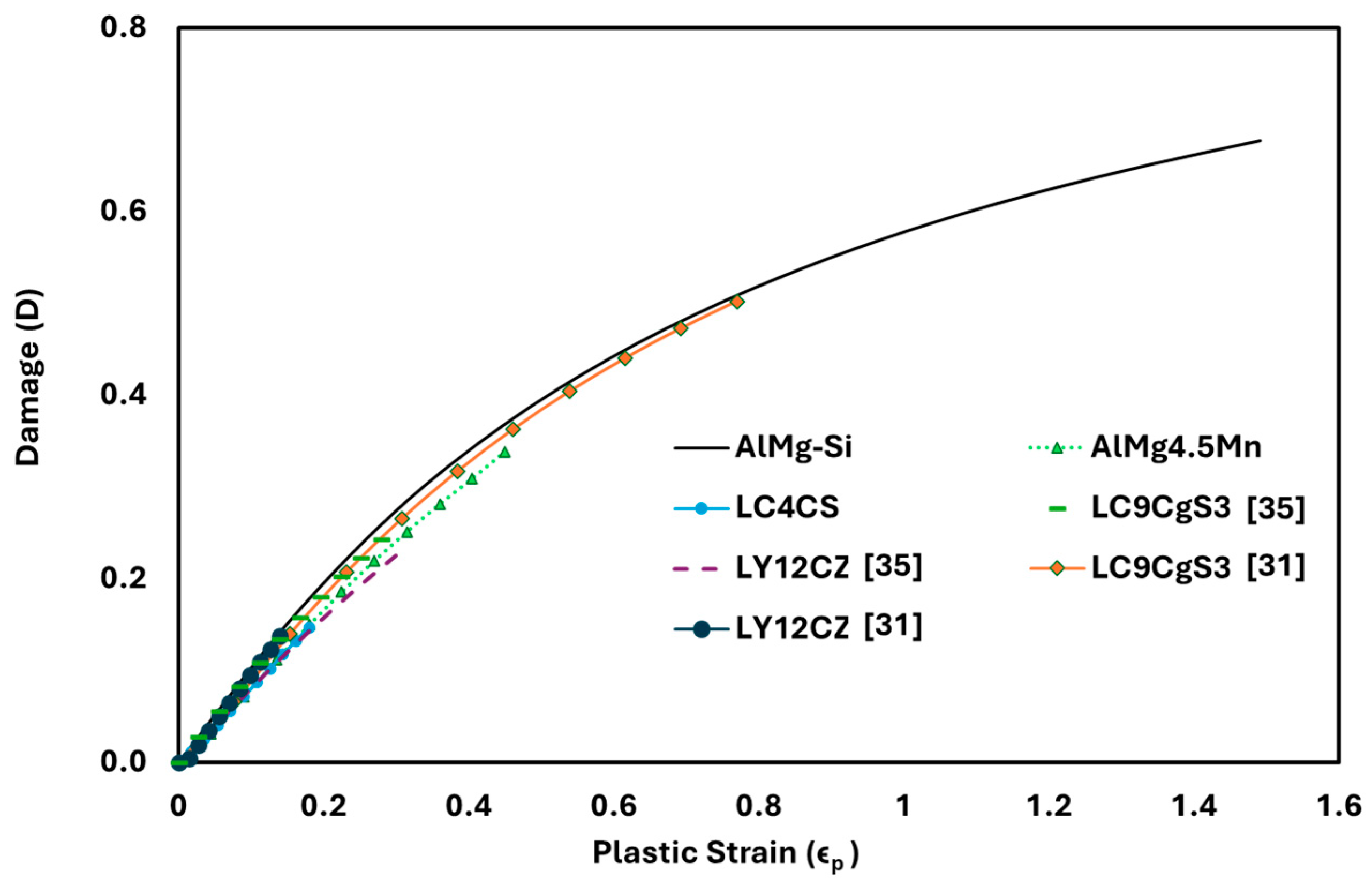
4.2. Result Analysis of Various Material Series
4.3. Summary
5. Conclusions
- As this study provides results for critical damage values from 0.1 to 0.9, the damage behavior of almost any material is covered because the range for critical damage is 0 to 1. Therefore, this study acts as a ready reckoner of data for a wide range of materials.
- Variation in damage against strain could be either linear or non-linear, depending upon the influence of monotonic properties like true fracture strength, strength coefficient, the strain hardening exponent, and plastic strain. All materials of the 2xxx, 5xxx, and other series shown both linear and non-linear variation in damage with strain. But the 6xxx series materials exhibited linear variation, and the 7xxx series materials exhibited non-linear variation.
- By analyzing the variation in damage against strain, it was found that 2017A-T4, 5754-NG, 6061-T651, 7075-T7351, and AlMg-Si offer the highest resistance to crack initiation under the respective series. Among the 32 Al alloys considered in this study, the 7075-T7351 alloy offers the maximum resistance to crack initiation at any value of strain loading.
- Determining the critical damage value of a wide range of aluminum alloys helps select a specific material when the focus is on damage criteria like crack initiation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lemaitre, J.; Desmorat, R. Engineering Damage Mechanics: Ductile, Creep, Fatigue and Brittle Failures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Bai, P.; Shang, C.; Zhu, D.; Zhao, H.; Liu, Y.; Kuang, J.; Li, F.; Ji, J.; Wang, S.; Wu, G.; et al. The interpretable descriptors for fatigue performance of wrought aluminum alloys. J. Mater. Res. Technol. 2024, 32, 3423–3431. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Ellingwood, B. A new CDM-based approach to structural deterioration. Int. J. Solids Struct. 1999, 36, 1757–1779. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Kraisnik, M.; Vilotic, D.; Siðanin, L.; Stefanovic, M. Various approaches to defining the criteria of ductile crack in cold bulk forming processes. Ann. Fac. Eng. Hunedoara-Int. J. Eng. 2015, 13, 213–218. [Google Scholar]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields∗. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Oyane, M. Criteria of ductile fracture strain. Bull. JSME 1972, 15, 1507–1513. [Google Scholar] [CrossRef]
- Ma, H.; Xu, W.; Jin, B.C.; Shan, D.; Nutt, S.R. Damage evaluation in tube spinnability test with ductile fracture criteria. Int. J. Mech. Sci. 2015, 100, 99–111. [Google Scholar] [CrossRef]
- Niemsakul, S.; Sae-Eawa, N.; Aue-U-Lan, Y. Determination and analysis of critical damage criteria for predicting fracture in forming process by uniaxial tensile test. Mater. Today Proc. 2018, 5, 9642–9650. [Google Scholar] [CrossRef]
- Freudenthal, A.M. The Inelastic Behavior in Solids, 1st ed.; Wiley: New York, NY, USA, 1950. [Google Scholar]
- Cockcroft, M.G. Ductility and workability of metals. J. Met. 1968, 96, 2444. [Google Scholar]
- Mashayekhi, M.; Taghipour, A.; Askari, A.; Farzin, M. Continuum damage mechanics application in low-cycle thermal fatigue. Int. J. Damage Mech. 2013, 22, 285–300. [Google Scholar] [CrossRef]
- Fan, Z.C.; Chen, X.D.; Chen, L.; Jiang, J.L. A CDM-based study of fatigue–creep interaction behavior. Int. J. Press. Vessel. Pip. 2009, 86, 628–632. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Ellingwood, B. Continuum damage mechanics analysis of fatigue crack initiation. Int. J. Fatigue 1998, 20, 631–639. [Google Scholar] [CrossRef]
- Gautam, A.; Yadav, R.K.; Ajit, K.P.; Rajak, V.K. A review on CDM-based ductile models and its application. Trans. Indian Inst. Met. 2023, 76, 1141–1154. [Google Scholar] [CrossRef]
- Aluminum or Aluminium Alloys-List. [Online]. Available online: https://www.thoughtco.com/aluminum-or-aluminium-alloys-603707 (accessed on 4 December 2023).
- Bintoro, S.R.; Putri, E.D.; Suhartono, A.; Muhayat, N.; Badaruddin, M.; Fauzun, F.; Triyono, T. Effect of welding environment on fatigue crack growth rate of aluminium alloy 1100. J. Achiev. Mater. Manuf. Eng. 2024, 122, 49–60. [Google Scholar] [CrossRef]
- Gates, N.R.; Fatemi, A. On the consideration of normal and shear stress interaction in multiaxial fatigue damage analysis. Int. J. Fatigue 2017, 100, 322–336. [Google Scholar] [CrossRef]
- Gautam, A.; Ajit, K.P.; Sarkar, P.K. A nonlinear CDM based damage growth law for ductile materials. Mater. Res. Express 2018, 5, 026518. [Google Scholar] [CrossRef]
- Xue, F.; Li, F. Characterization of damage and toughness of 5052 aluminum alloy based on continuum damage mechanics. IOP Conf. Ser. Mater. Sci. Eng. 2018, 452, 022046. [Google Scholar] [CrossRef]
- Amer, M.; Shazly, M.; Mohamed, M.; Hegazy, A.A. Ductile damage prediction of AA 5754 sheet during cold forming condition. J. Mech. Sci. Technol. 2020, 34, 4219–4228. [Google Scholar] [CrossRef]
- Sun, Y. The use of aluminum alloys in structures: Review and outlook. Structures 2023, 57, 105290. [Google Scholar] [CrossRef]
- Kamath, T.R.; Upadhyaya, Y.S.; Kaushik, D. Fatigue life prediction of aluminum alloy 6061-T6 using continuum damage mechanics. Adv. Sci. Lett. 2017, 23, 1914–1916. [Google Scholar] [CrossRef]
- Won, J.Y.; Kim, C.; Hong, S.; Yoon, H.S.; Park, J.K.; Lee, M.G. Evaluation of crush performance of extruded aluminum alloy tubes based on finite element analysis with ductile fracture modeling. Thin-Walled Struct. 2024, 200, 111937. [Google Scholar] [CrossRef]
- Li, J.; Qiu, Y. A path-dependent multiaxial fatigue life estimation criterion for metals under various loading conditions. Int. J. Fatigue 2021, 149, 106300. [Google Scholar] [CrossRef]
- Jones, R.; Krishnapillai, K.; Pitt, S. Crack patching: Predicting fatigue crack growth. Theor. Appl. Fract. Mech. 2006, 45, 79–91. [Google Scholar] [CrossRef]
- Zhao, T.; Jiang, Y. Fatigue of 7075-T651 aluminum alloy. Int. J. Fatigue 2008, 30, 834–849. [Google Scholar] [CrossRef]
- François, H.; Gilbert, H.; Damien, H.; Gueguen, M.; Thomas, B. CDM approach applied to fatigue crack propagation on airframe structural alloys. Procedia Eng. 2010, 2, 1403–1412. [Google Scholar] [CrossRef]
- Metal Fatigue Laboratory, University of Waterloo. Tested Data for Steels [Internet]. Available online: http://fde.uwaterloo.ca (accessed on 10 December 2023).
- Kvackaj, T. (Ed.) Aluminium Alloys, Theory and Applications; Intechopen: Rijeka, Croatia, 2011. [Google Scholar]
- Science and Technology Committee of Aeronautic Engineering Department. Handbook of Strain Fatigue Analysis; Science Publishing House: Beijing, China, 1987. [Google Scholar]
- Wong, W.A. Monotonic and cyclic fatigue properties of automotive aluminum alloys. SAE Trans. 1984, 93, 720–727. [Google Scholar]
- Fatemi, A.; Plaseied, A.; Khosrovaneh, A.K.; Tanner, D. Application of bi-linear log–log S–N model to strain-controlled fatigue data of aluminum alloys and its effect on life predictions. Int. J. Fatigue 2005, 27, 1040–1050. [Google Scholar] [CrossRef]
- Georgantzia, E.; Kashani, M.M. Monotonic and cyclic behaviour of 6082-T6 aluminium alloy. ce/papers 2023, 6, 2220–2225. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, Q.; Li, C.; Zhao, W. Theoretical calculation of the strain-hardening exponent and the strength coefficient of metallic materials. J. Mater. Eng. Perform. 2006, 15, 19–22. [Google Scholar] [CrossRef]
- Chow, C.L.; Wei, Y. A damage mechanics model of fatigue crack initiation in notched plates. Theor. Appl. Fract. Mech. 1991, 16, 123–133. [Google Scholar] [CrossRef]
- Bannantine, J.A.; Comer, J.J.; Handrock, J.L. Fundamentals of Metal Fatigue Analysis, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1990. [Google Scholar]
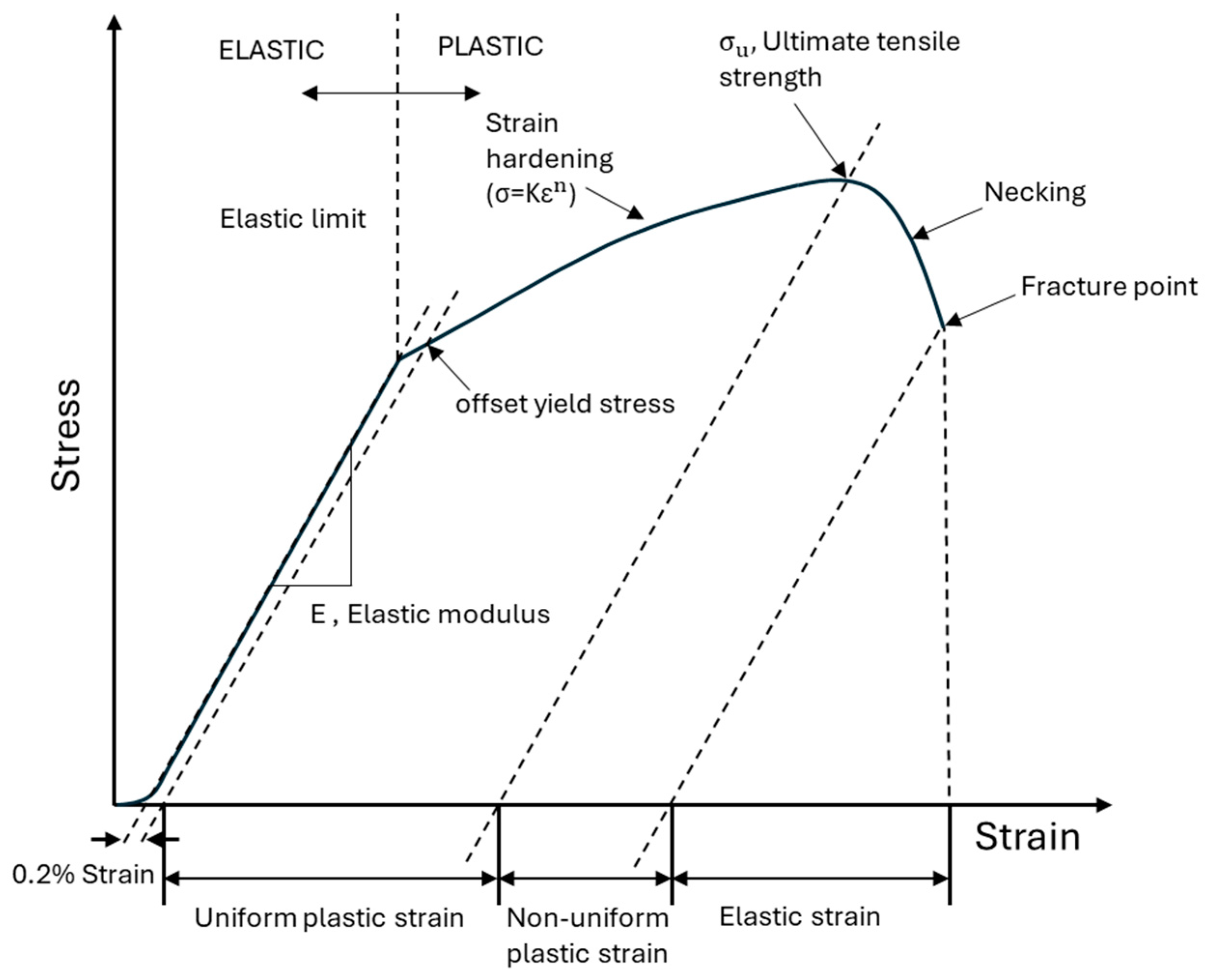


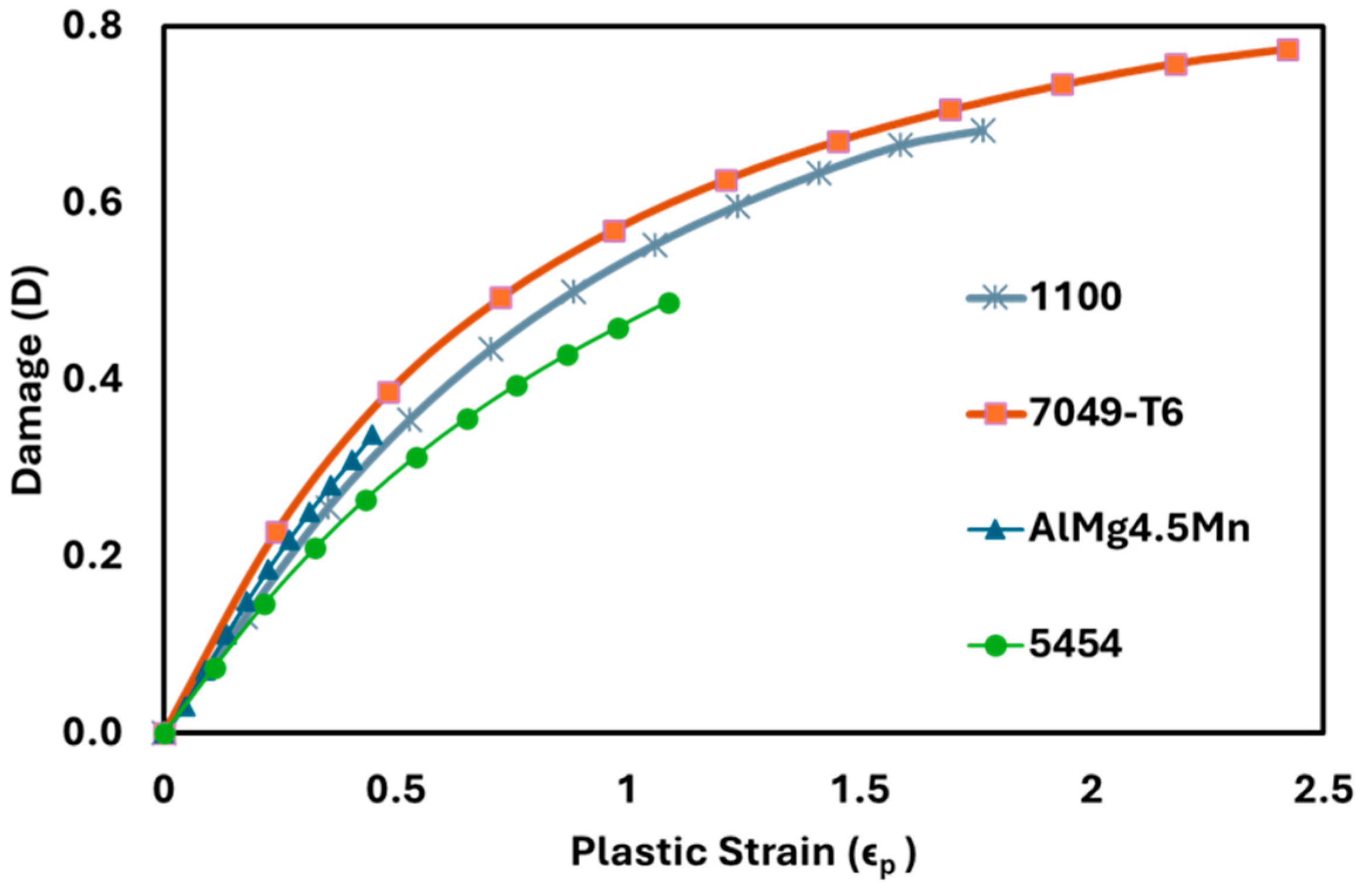
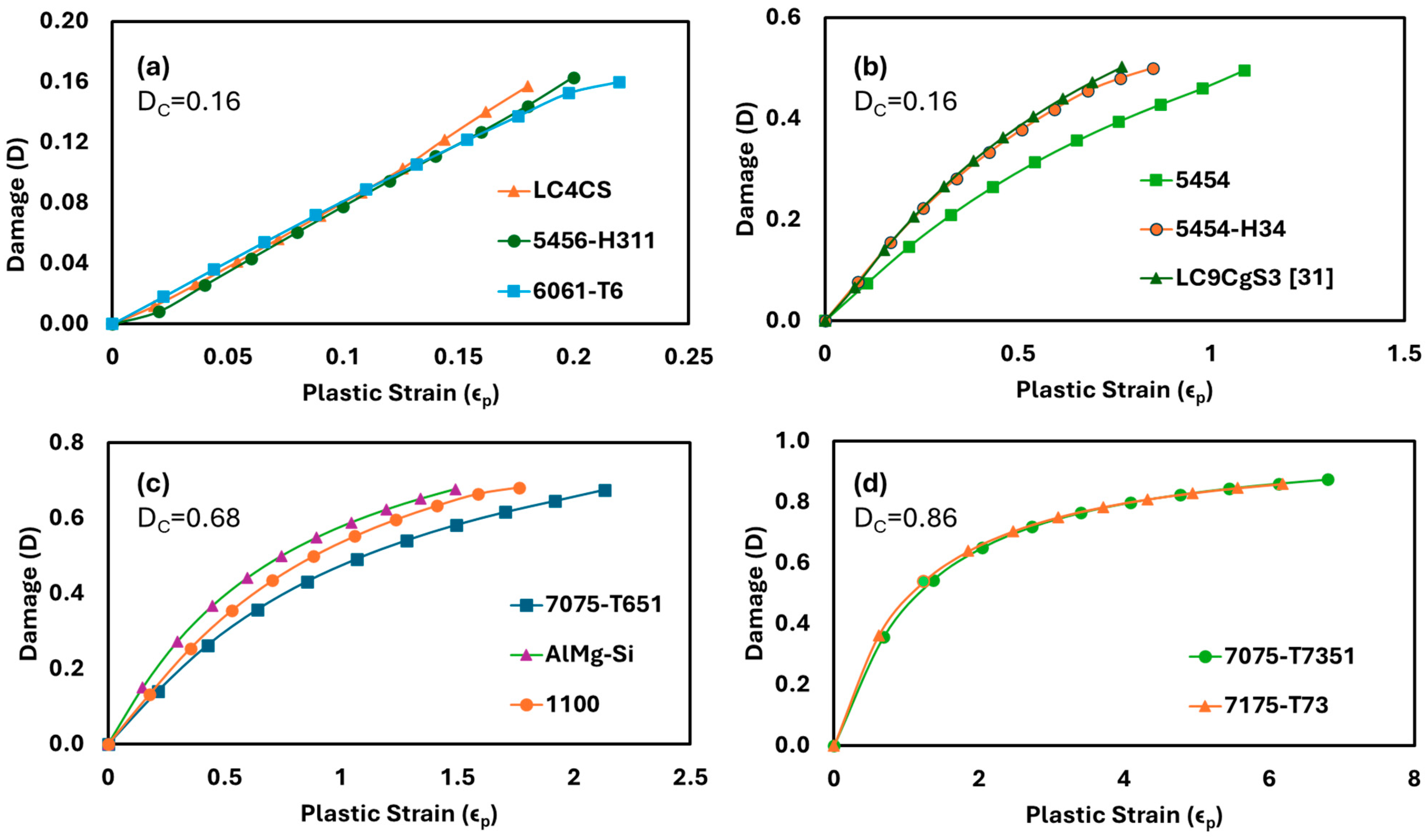
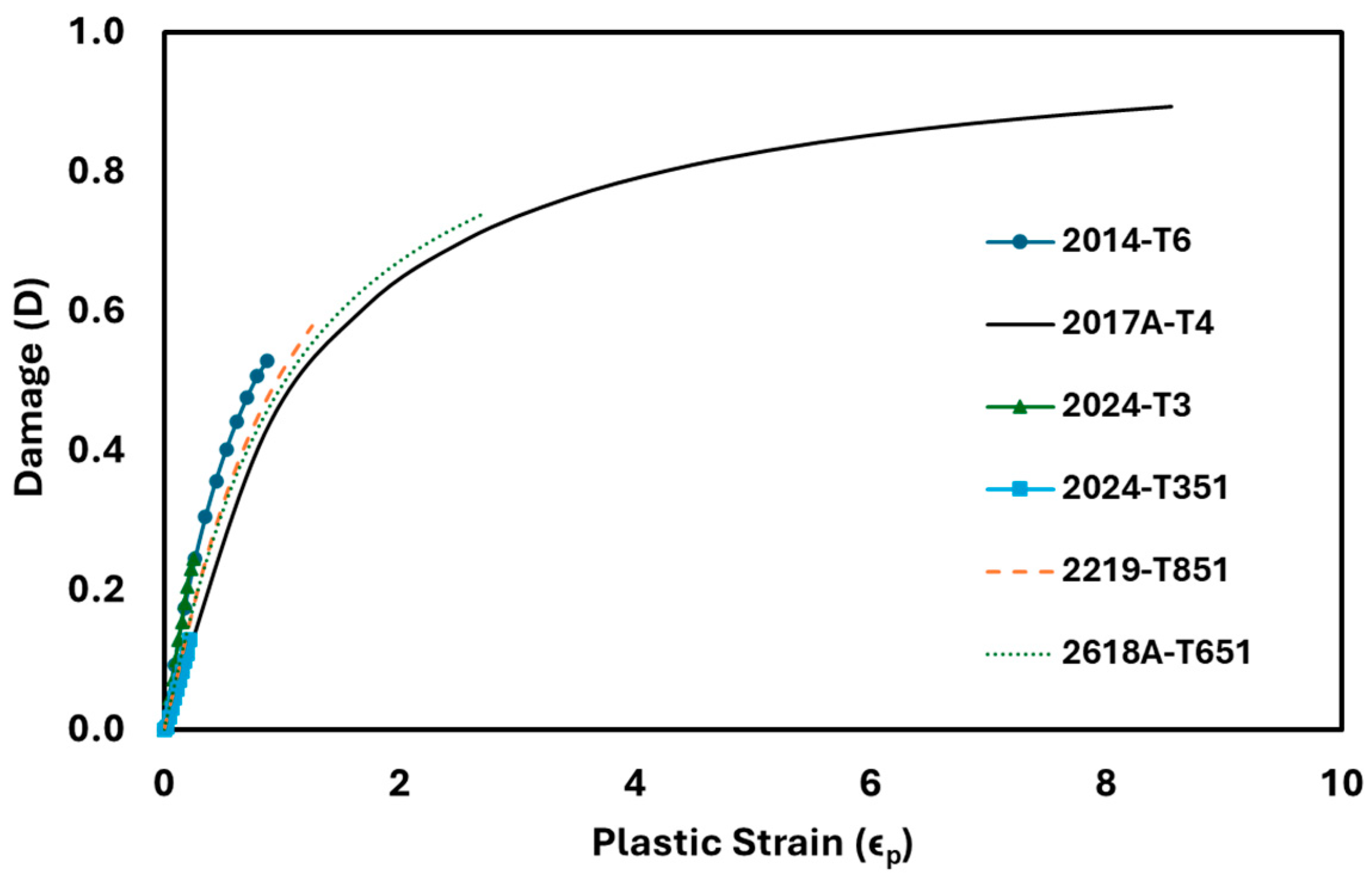




| Sl. No. | Material | (MPa) | (MPa) | E (GPa) | (MPa) | K | n | Ref. | |
|---|---|---|---|---|---|---|---|---|---|
| 1xxx series | |||||||||
| 1 | 1100 | 97 | 117 | 72.0 | 166 | 169 | 0.168 | 1.77 | [29] |
| 2xxx series | |||||||||
| 2 | 2014-T6 | 451 | 483 | 70.8 | 585 | 605 | 0.049 | 0.88 | [30] |
| 3 | 2017A-T4 | 305 | 441 | 72.4 | 876 | 611 | 0.053 | 8.55 | [29] |
| 4 | 2024-T3 | 275 | 415 | 74.5 | 435 | 680 | 0.180 | 0.21 | [30] |
| 5 | 2024-T351 | 379 | 469 | 73.1 | 1103 | 655 | 0.065 | 0.22 | [31] |
| 6 | 2024-T4 | 303 | 476 | 70.0 | 1014 | 756 | 0.080 | 0.21 | [32] |
| 7 | 2219-T851 | 361 | 470 | 74.5 | 832 | 752 | 0.131 | 1.25 | [29] |
| 8 | 2618A-T651 | 437 | 487 | 70.4 | 811 | 640 | 0.070 | 2.70 | [29] |
| 5xxx series | |||||||||
| 9 | 5052-H32 | 167 | 231 | 69.6 | 361 | 286 | 0.044 | 0.42 | [29] |
| 10 | 5083 | 305 | 414 | 73.2 | 616 | 592 | 0.077 | 2.00 | [30] |
| 11 | 5454 | 294 | 334 | 69.8 | 530 | 363 | 0.046 | 1.09 | [29] |
| 12 | 5454-H34 | 257 | 301 | 72.7 | 436 | 447 | 0.075 | 0.85 | [29] |
| 13 | 5454-O | 116 | 248 | 69.6 | 462 | 420 | 0.082 | 1.26 | [29] |
| 14 | 5456-H311 | 235 | 400 | 69.1 | 702 | 636 | 0.084 | 0.20 | [33] |
| 15 | 5754-NG | 107 | 253 | 73.4 | 455 | 294 | 0.032 | 9.19 | [33] |
| 6xxx series | |||||||||
| 16 | 6061-T6 | 324 | 340 | 72.7 | 547 | 416 | 0.042 | 0.22 | [30] |
| 17 | 6061-T651 | - | - | 68.9 | 394 | 404 | 0.062 | 0.63 | [32] |
| 18 | 6063 | 239 | 263 | 73.4 | 556 | 384 | 0.067 | 0.74 | [33] |
| 19 | 6082-T6 | 264 | 296 | 66.6 | 314 | 335 | 0.031 | 0.13 | [34] |
| 7xxx series | |||||||||
| 20 | 7049-T6 | 616 | 649 | 71.3 | 820 | 900 | 0.058 | 2.42 | [29] |
| 21 | 7050-T7351 | 451 | 518 | 69.6 | 712 | 705 | 0.070 | 2.38 | [29] |
| 22 | 7075-T6 | 469 | 579 | 71.0 | 880 | 897 | 0.083 | 0.47 | [31] |
| 23 | 7075-T651 | 501 | 561 | 71.0 | 1103 | 807 | 0.068 | 2.13 | [29] |
| 24 | 7075-T7351 | 382 | 462 | 65.7 | 989 | 695 | 0.094 | 6.81 | [33] |
| 25 | 7175-T73 | 434 | 524 | 71.0 | 728 | 529 | 0.033 | 6.18 | [30] |
| Other aluminum alloys | |||||||||
| 26 | LY12CZ | 400 | 545 | 73.2 | 724 | 870 | 0.097 | 0.14 | [31] |
| 27 | LC4CS | 571 | 614 | - | 711 | 775 | 0.158 | 0.18 | [31] |
| 28 | LC9CgS3 | 518 | 560 | - | 748 | 725 | 0.053 | 0.28 | [35] |
| 29 | LY12CZ | 332 | 476 | - | 618 | 545 | 0.089 | 0.30 | [35] |
| 30 | AlMg4.5Mn | 298 | 363 | 71.5 | 654 | 693 | 0.125 | 0.45 | [33] |
| 31 | LC9CgS3 | 518 | 560 | 72.2 | 808 | 906 | 0.101 | 0.77 | [31] |
| 32 | AlMg-Si | 219 | 305 | 69.0 | 394 | 431 | 0.060 | 1.49 | [29] |
| Sl. No. | Material | DC | |
|---|---|---|---|
| 1 | 2024-T351 | 0.220 | 0.12 |
| 2 | LY12CZ [31] | 0.140 | 0.14 |
| 3 | 2024-T3 | 0.210 | 0.14 |
| 4 | 6082-T6 | 0.132 | 0.15 |
| 5 | LC4CS | 0.180 | 0.16 |
| 6 | 5456-H311 | 0.200 | 0.16 |
| 7 | 6061-T6 | 0.220 | 0.16 |
| 8 | 2024-T3 | 0.250 | 0.24 |
| 9 | LC9CgS3 [35] | 0.280 | 0.24 |
| 10 | LY12CZ [35] | 0.300 | 0.24 |
| 11 | 5052-H32 | 0.424 | 0.29 |
| 12 | AlMg4.5Mn | 0.450 | 0.34 |
| 13 | 7075-T6 | 0.466 | 0.34 |
| 14 | 6063 | 0.740 | 0.38 |
| 15 | 6061-T651 | 0.634 | 0.44 |
| 16 | LC9CgS3 [31] | 0.770 | 0.50 |
| 17 | 5454-H34 | 0.850 | 0.50 |
| 18 | 5454 | 1.087 | 0.50 |
| 19 | 2014-T6 | 0.880 | 0.53 |
| 20 | 2219-T851 | 1.254 | 0.58 |
| 21 | 5454-O | 1.258 | 0.58 |
| 22 | AlMg-Si | 1.492 | 0.68 |
| 23 | 1100 | 1.765 | 0.68 |
| 24 | 7075-T651 | 2.133 | 0.68 |
| 25 | 5083 | 2.000 | 0.72 |
| 26 | 2618A-T651 | 2.703 | 0.74 |
| 27 | 7050-T7351 | 2.376 | 0.77 |
| 28 | 7049-T6 | 2.421 | 0.77 |
| 29 | 7175-T73 | 6.180 | 0.86 |
| 30 | 7075-T7351 | 6.810 | 0.86 |
| 31 | 2017A-T4 | 8.549 | 0.89 |
| 32 | 5754-NG | 9.190 | 0.89 |
| Sl. No. | Materials | DC | |
|---|---|---|---|
| 1 | 2024-T351 | 0.22 | 0.12 |
| 2 | 2024-T4 | 0.21 | 0.14 |
| 3 | 2024-T3 | 0.25 | 0.24 |
| 4 | 2014-T6 | 0.88 | 0.53 |
| 5 | 2219-T851 | 1.25 | 0.58 |
| 6 | 2618A-T651 | 2.70 | 0.74 |
| 7 | 2017A-T4 | 8.55 | 0.89 |
| Sl. No. | Material | DC | |
|---|---|---|---|
| 1 | 5456-H311 | 0.20 | 0.16 |
| 2 | 5052-H32 | 0.42 | 0.29 |
| 3 | 5454 | 1.09 | 0.50 |
| 4 | 5454-H34 | 0.85 | 0.50 |
| 5 | 5454-O | 1.26 | 0.58 |
| 6 | 5083 | 2.00 | 0.72 |
| 7 | 5754-NG | 9.19 | 0.89 |
| Sl. No. | Material | DC | |
|---|---|---|---|
| 1 | 6082-T6 | 0.13 | 0.15 |
| 2 | 6061-T6 | 0.22 | 0.16 |
| 3 | 6063 | 0.74 | 0.38 |
| 4 | 6061-T651 | 0.63 | 0.44 |
| 4 | 6082-T6 | 0.70 | 0.44 |
| Sl. No. | Material | DC | |
|---|---|---|---|
| 1 | 7075-T6 | 0.47 | 0.34 |
| 2 | 7075-T651 | 2.13 | 0.68 |
| 3 | 7050-T7351 | 2.38 | 0.77 |
| 4 | 7049-T6 | 2.42 | 0.77 |
| 5 | 7175-T73 | 6.18 | 0.86 |
| 6 | 7075-T7351 | 6.81 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanwar, V.; Managuli, V.; Upadhyaya, Y.S. Analysis of Damage Value of Aluminum Alloys—Application of a Continuum Damage Mechanics Model. Appl. Mech. 2024, 5, 908-923. https://doi.org/10.3390/applmech5040050
Kanwar V, Managuli V, Upadhyaya YS. Analysis of Damage Value of Aluminum Alloys—Application of a Continuum Damage Mechanics Model. Applied Mechanics. 2024; 5(4):908-923. https://doi.org/10.3390/applmech5040050
Chicago/Turabian StyleKanwar, Vishavbandhu, Vishwanath Managuli, and Y. S. Upadhyaya. 2024. "Analysis of Damage Value of Aluminum Alloys—Application of a Continuum Damage Mechanics Model" Applied Mechanics 5, no. 4: 908-923. https://doi.org/10.3390/applmech5040050
APA StyleKanwar, V., Managuli, V., & Upadhyaya, Y. S. (2024). Analysis of Damage Value of Aluminum Alloys—Application of a Continuum Damage Mechanics Model. Applied Mechanics, 5(4), 908-923. https://doi.org/10.3390/applmech5040050





