A Reduction-Based Approach to Improving the Estimation Consistency of Partial Path Contributions in Operational Transfer-Path Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Operational Transfer-Path Analysis
2.2. Reduction-Based Approach Within OTPA
2.2.1. Interface-Deformation Modes
2.2.2. Physical Modes
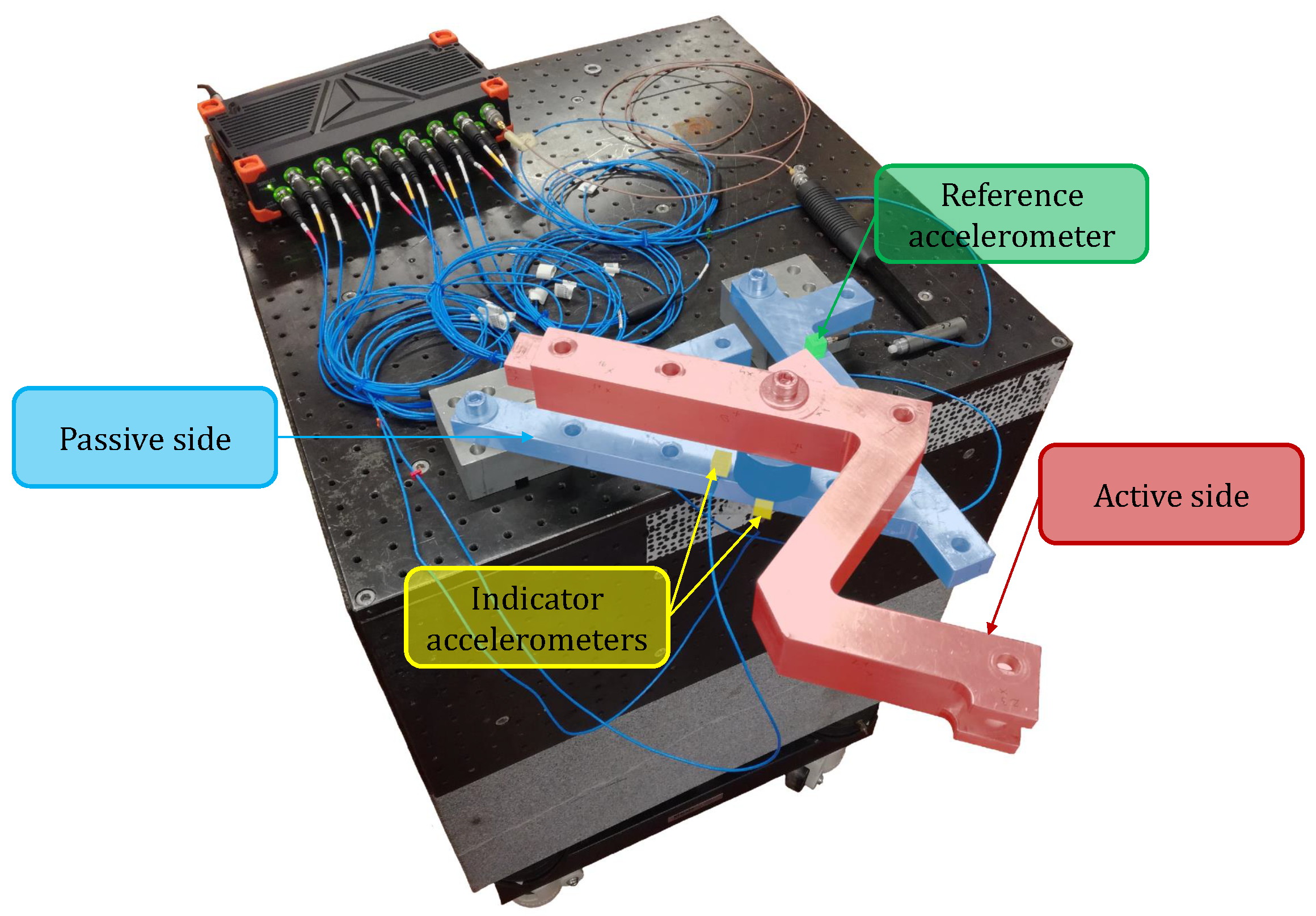
3. Experimental Case Studies
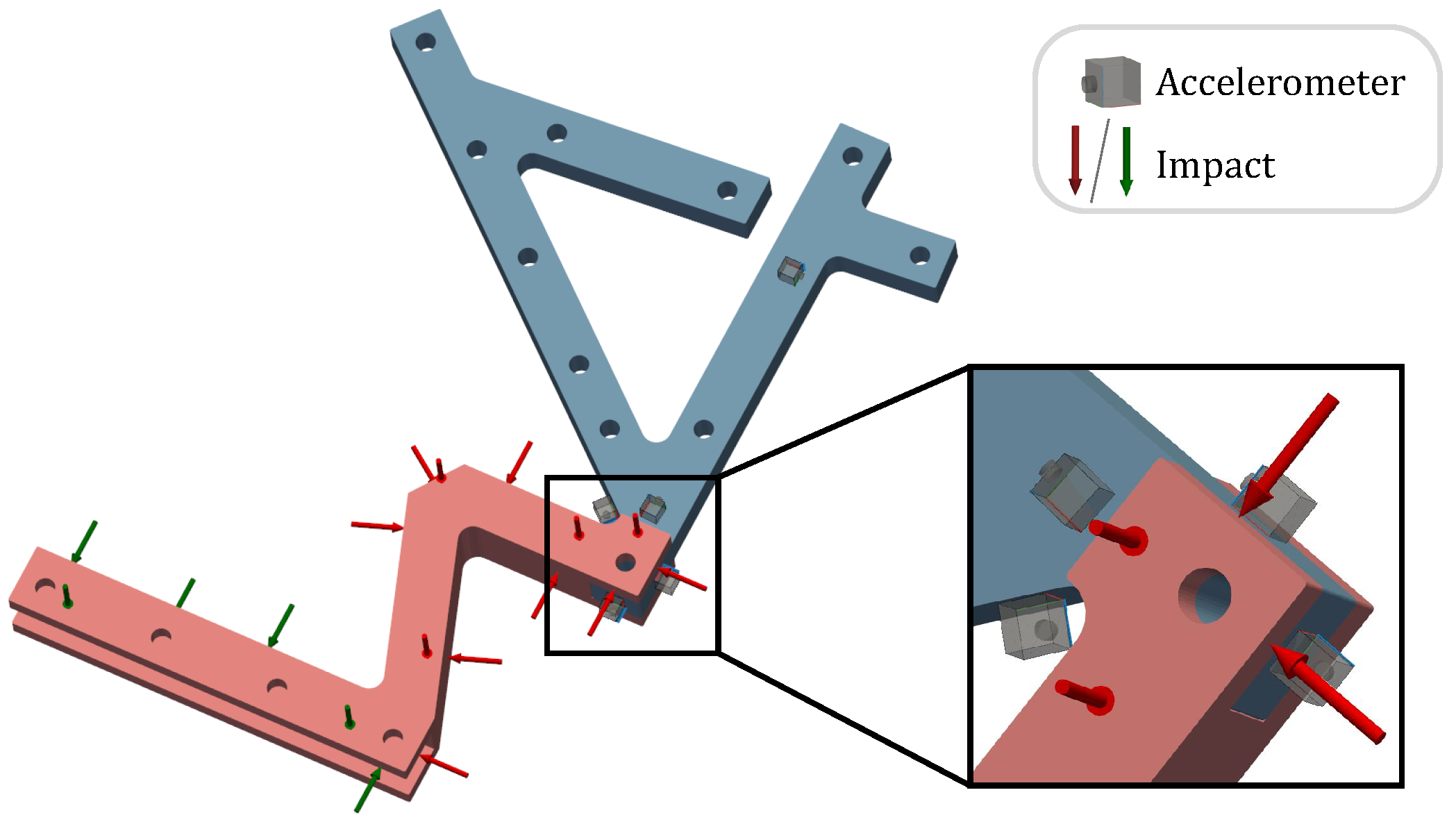
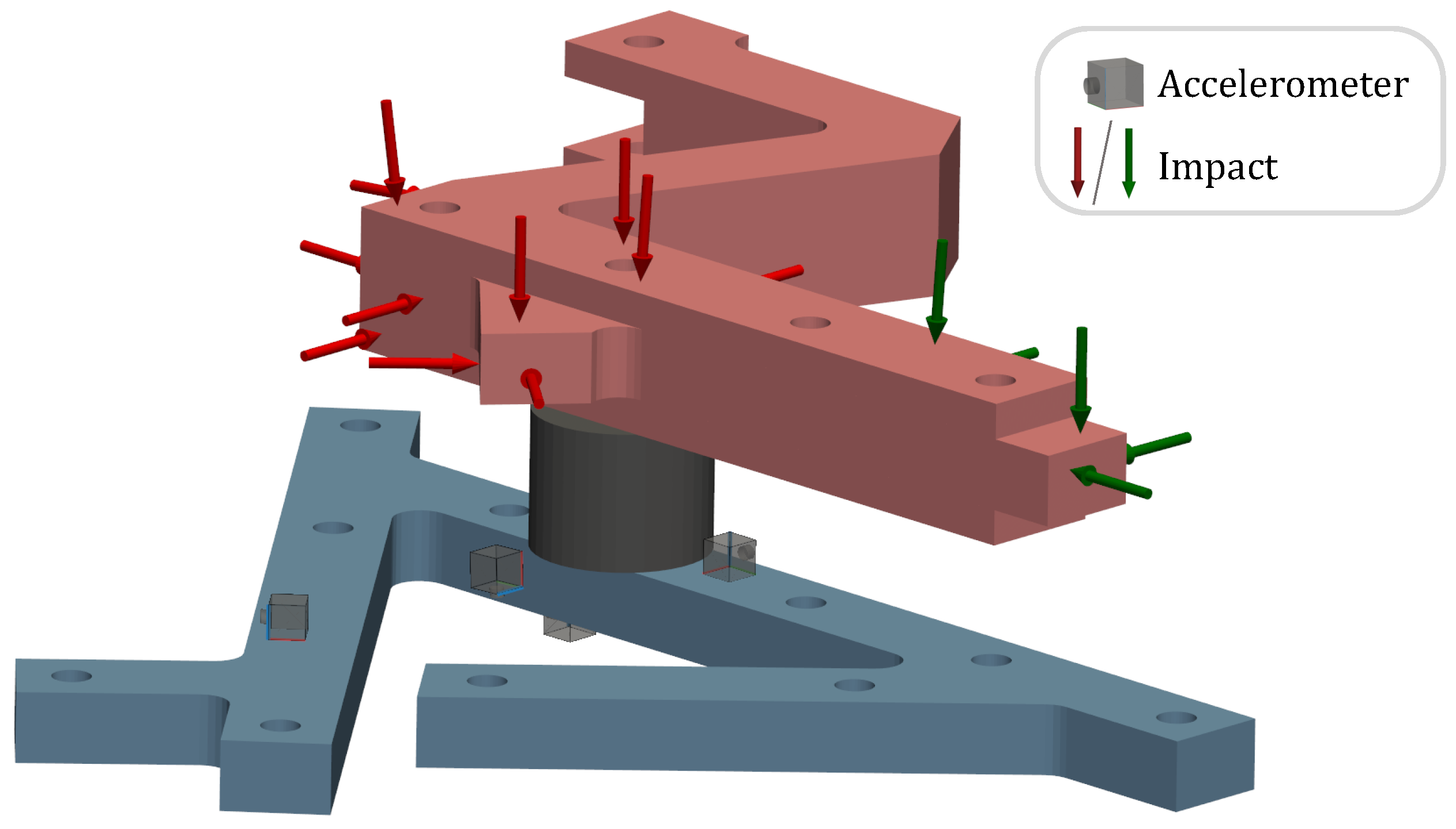
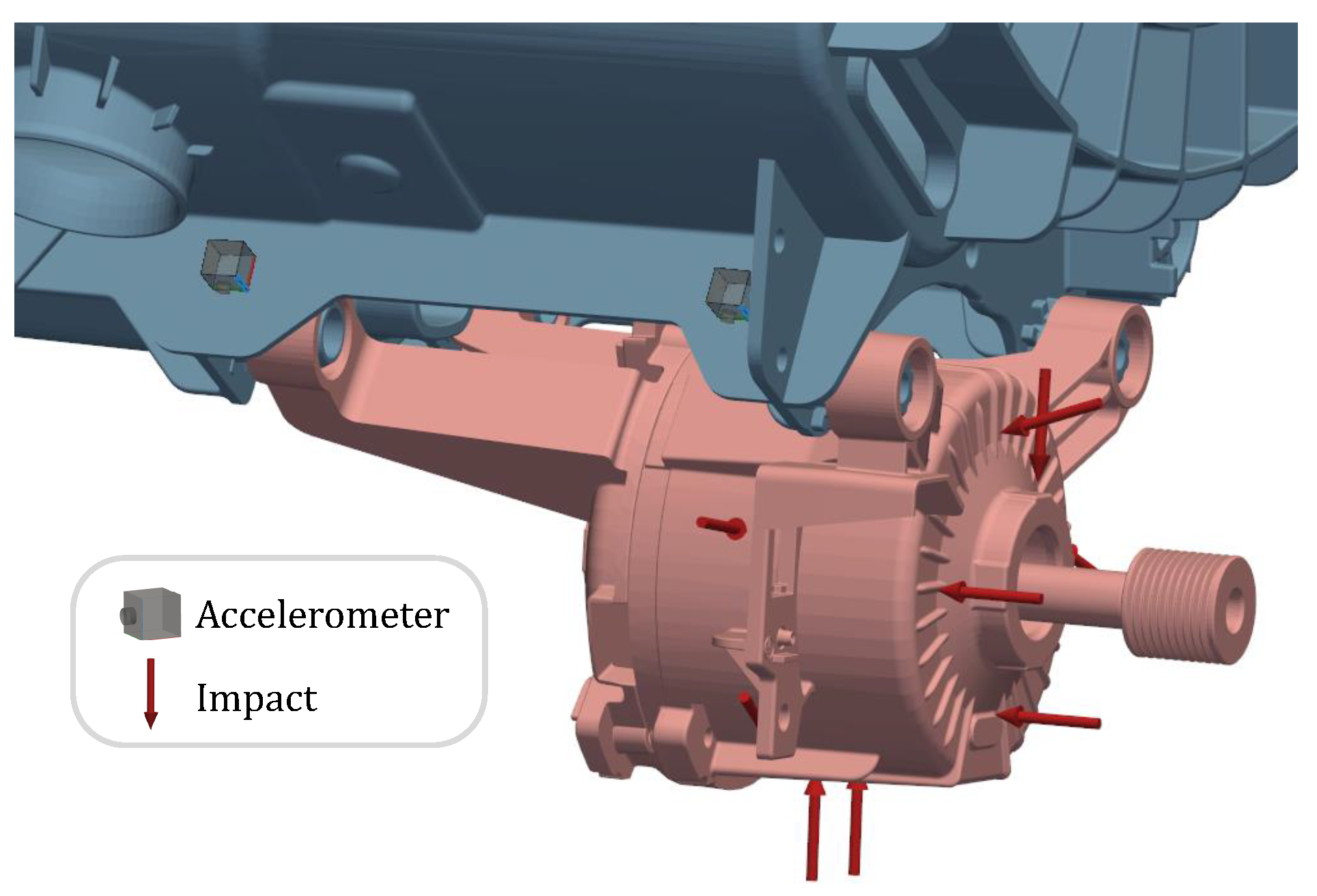
3.1. Bolted Connection
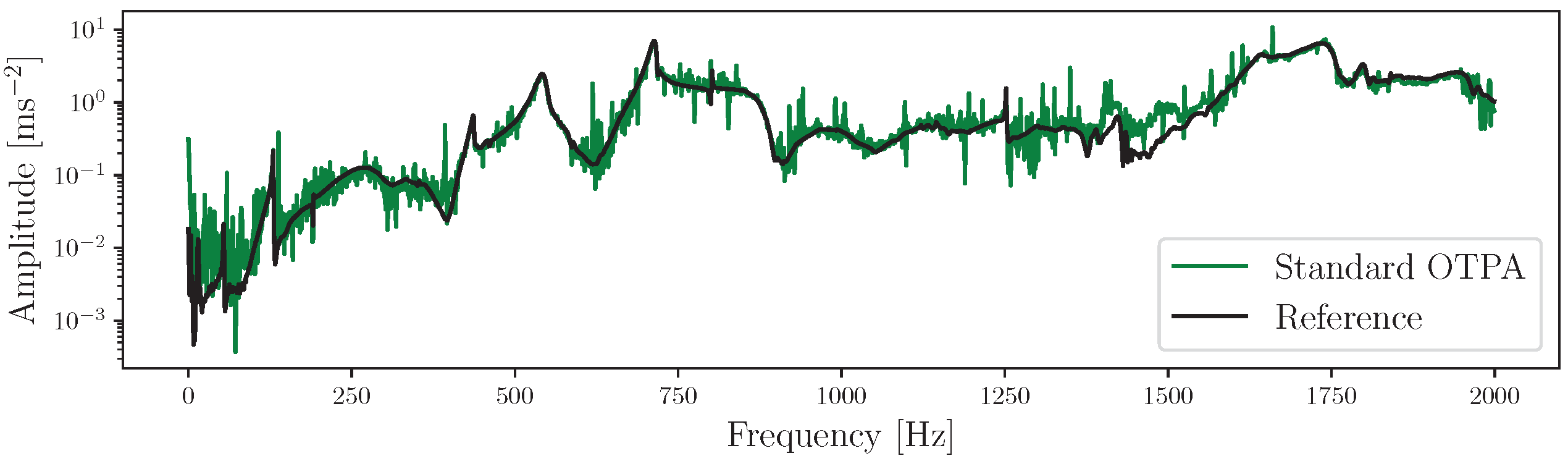
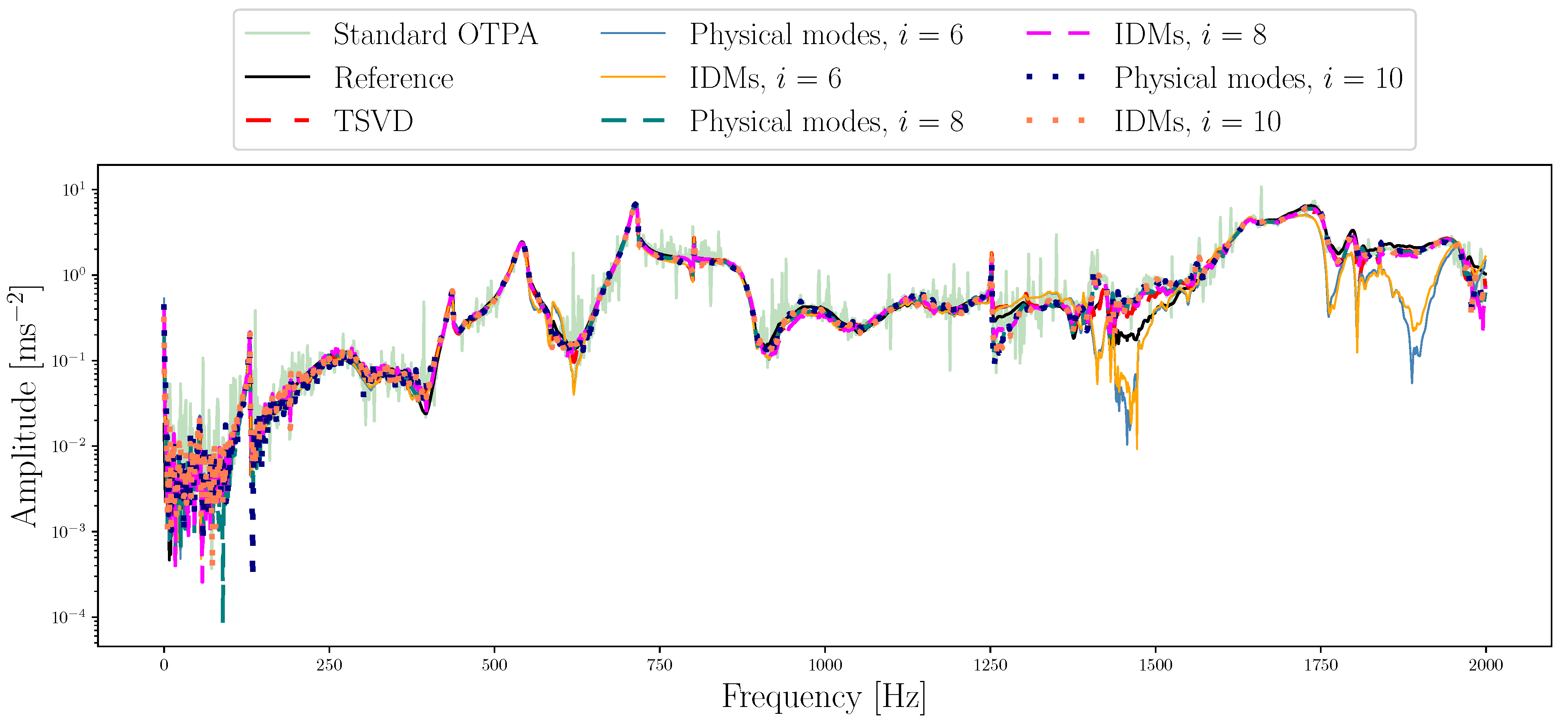
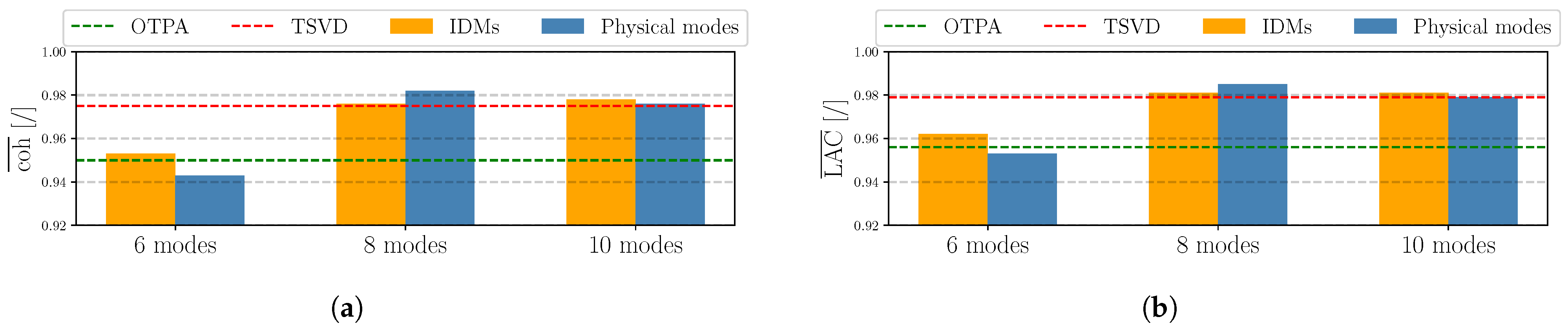
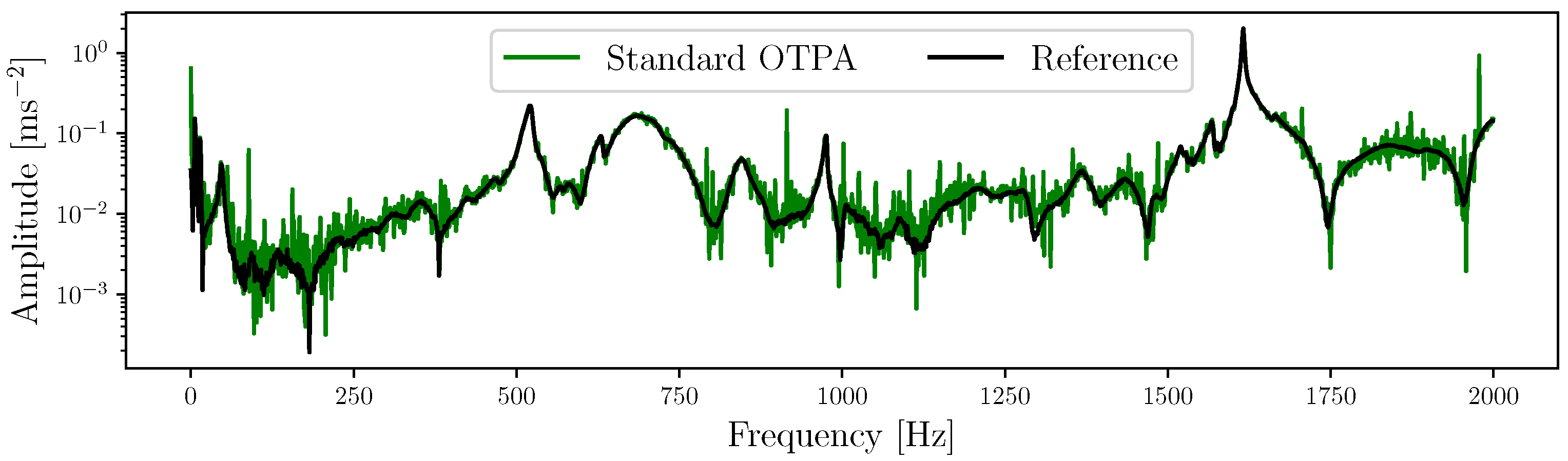
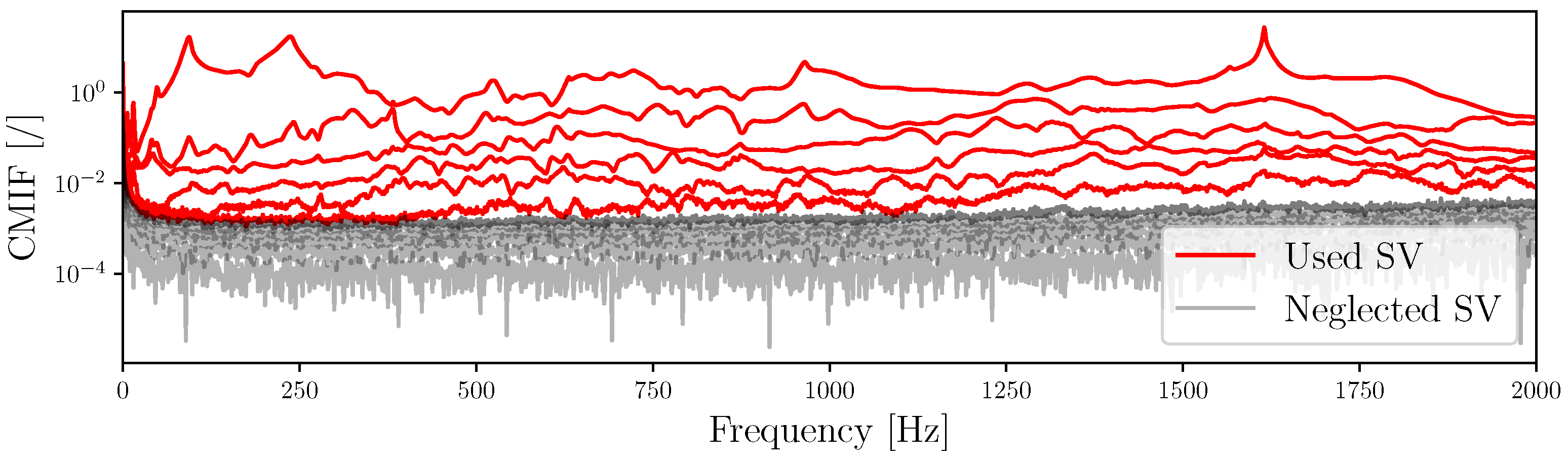
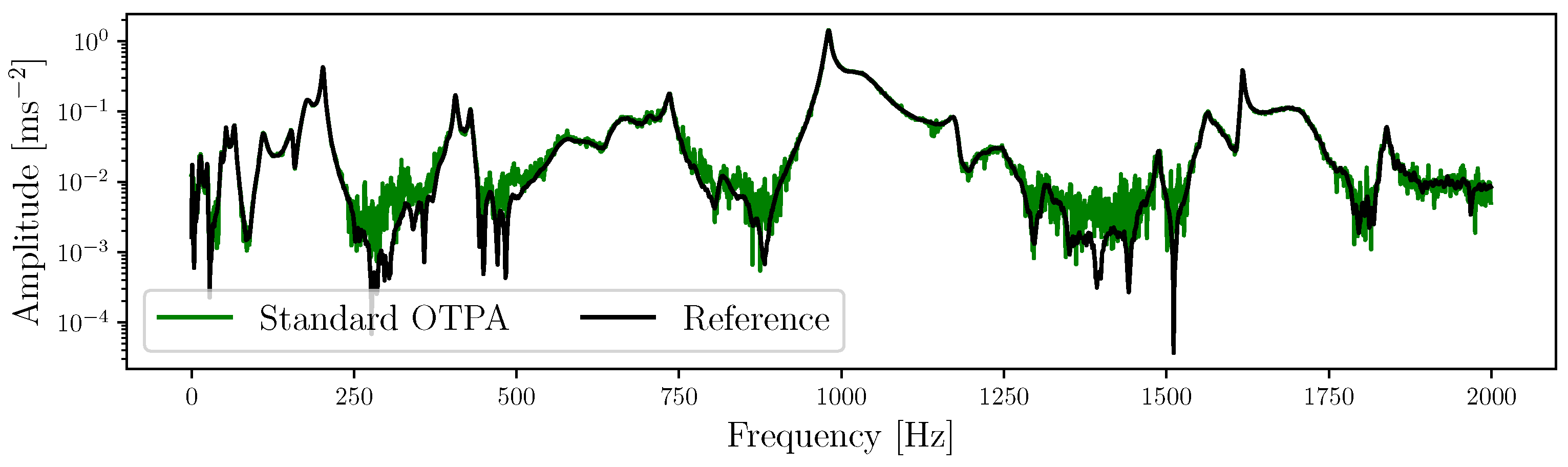
Results
3.2. Rubber Connection
Results
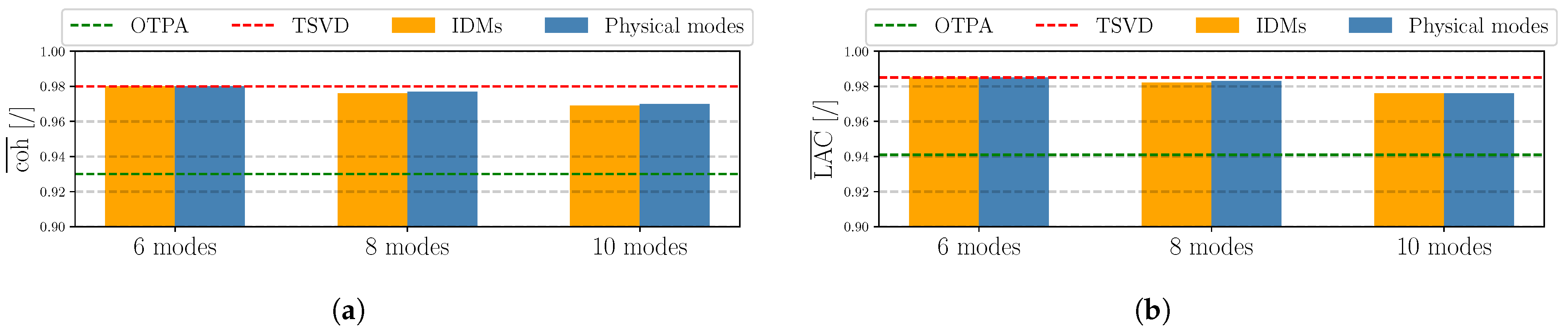
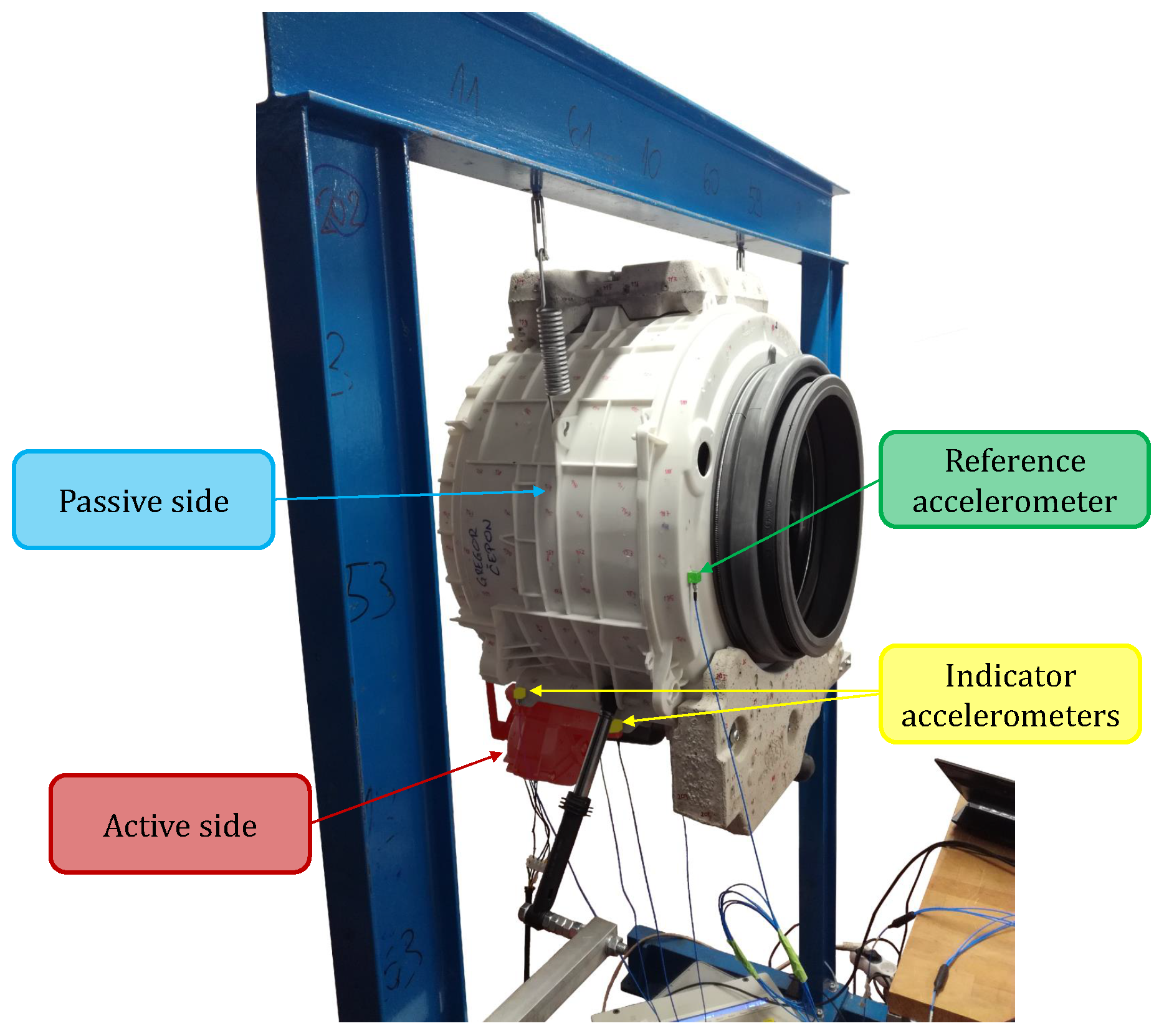
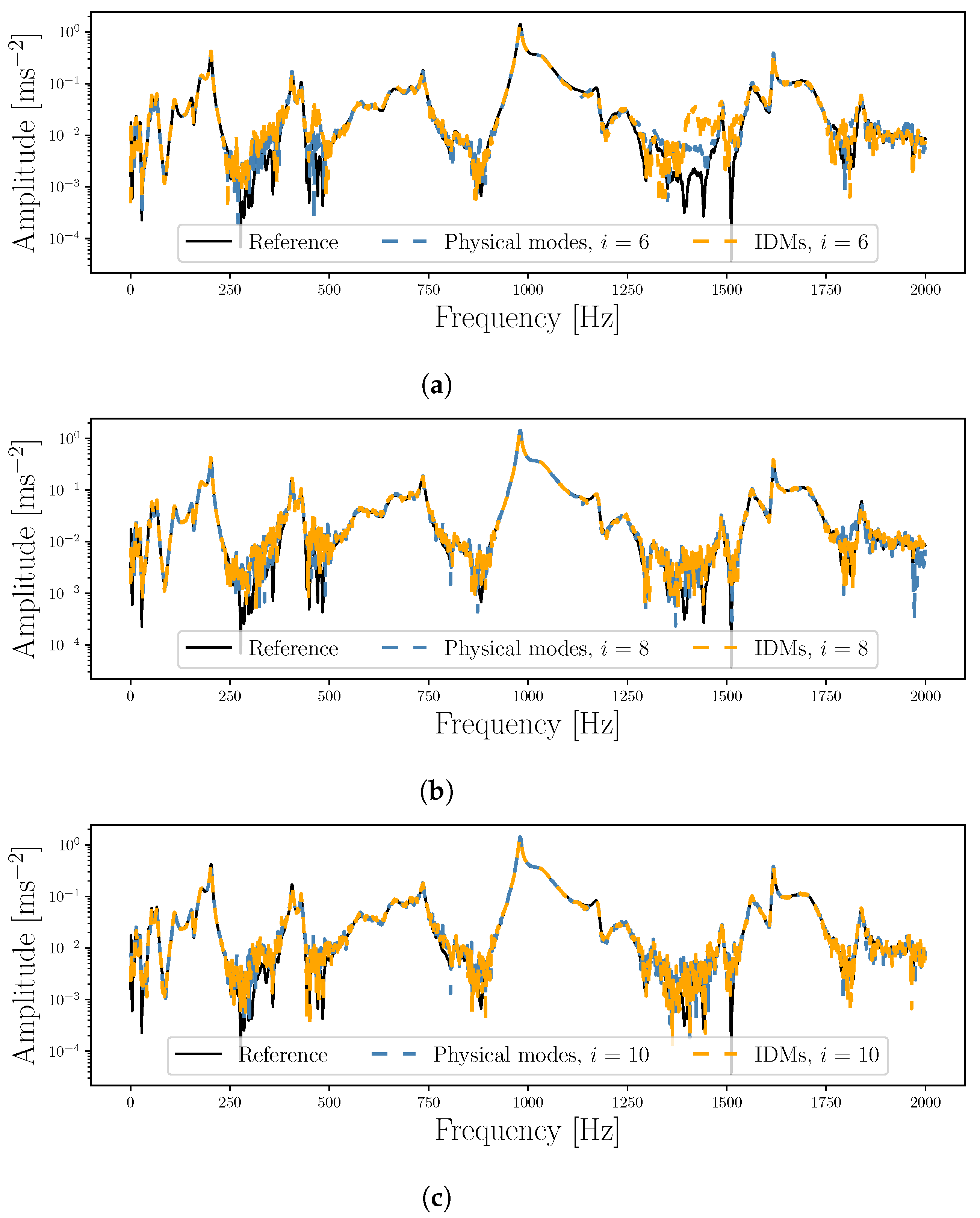
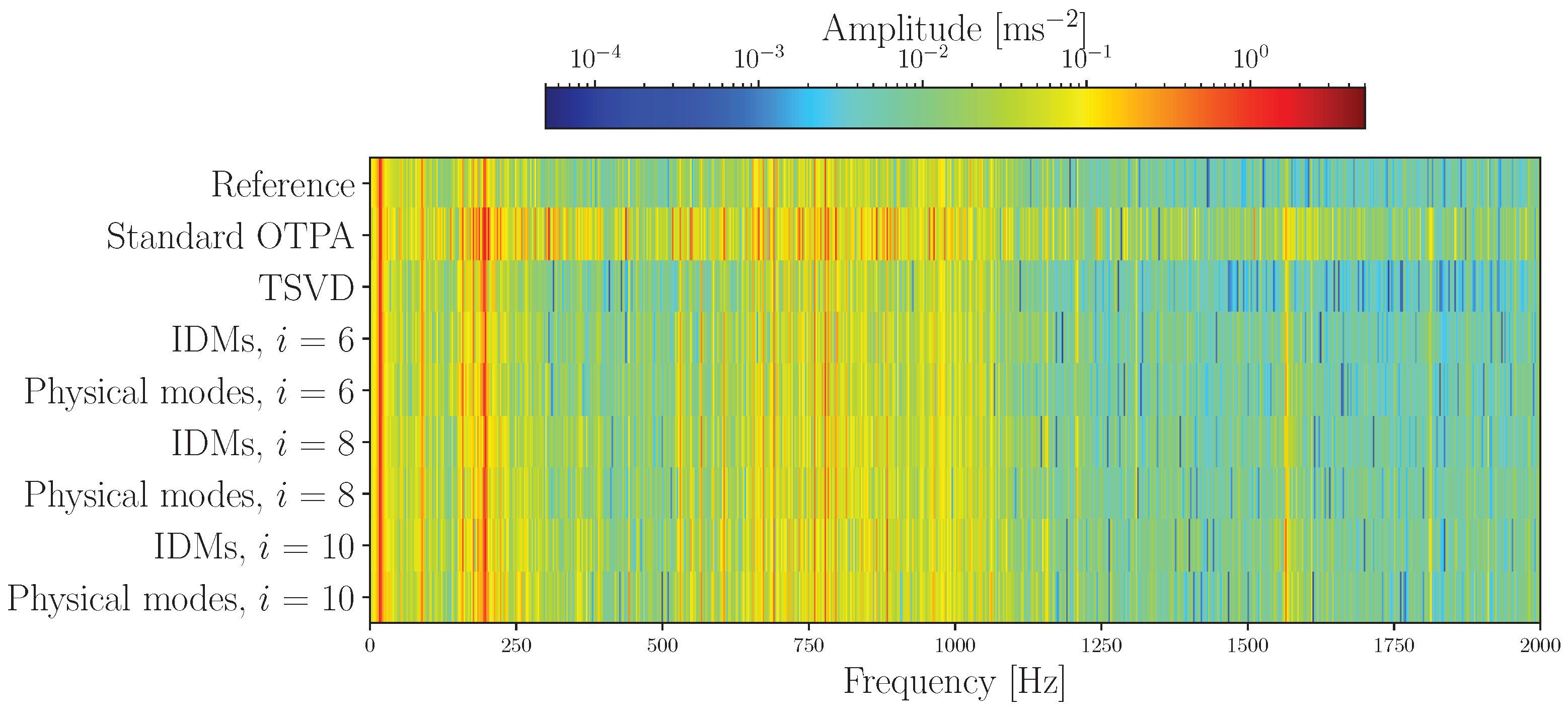
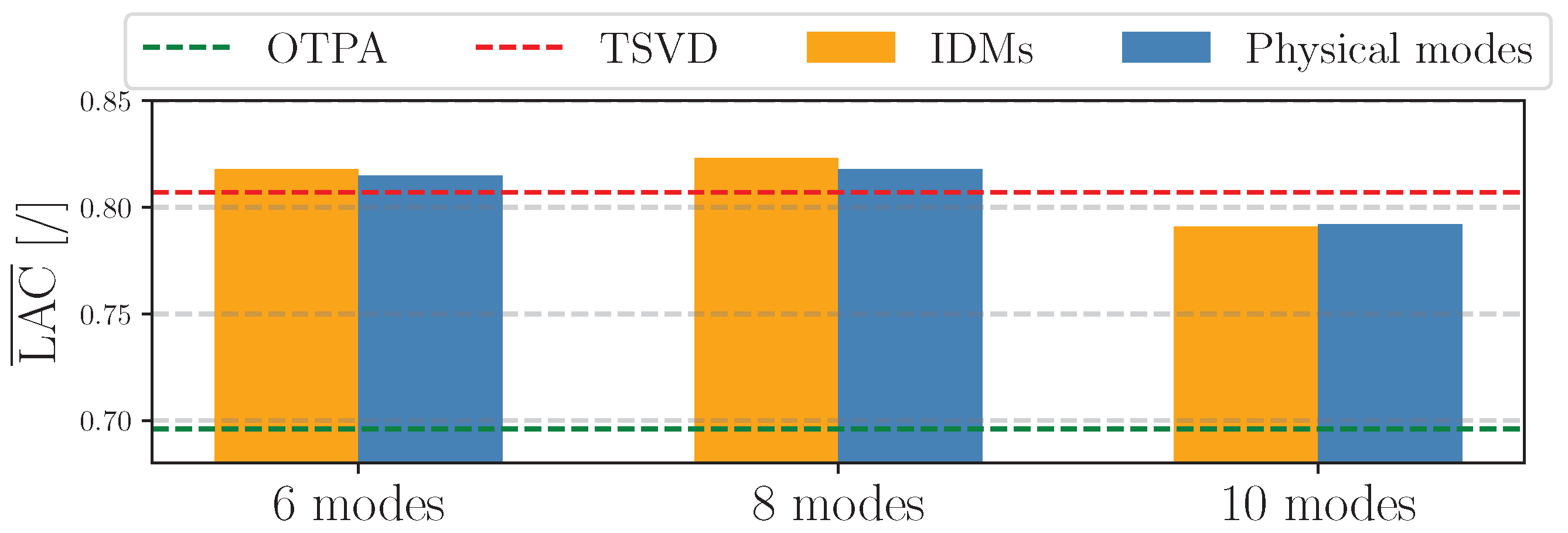
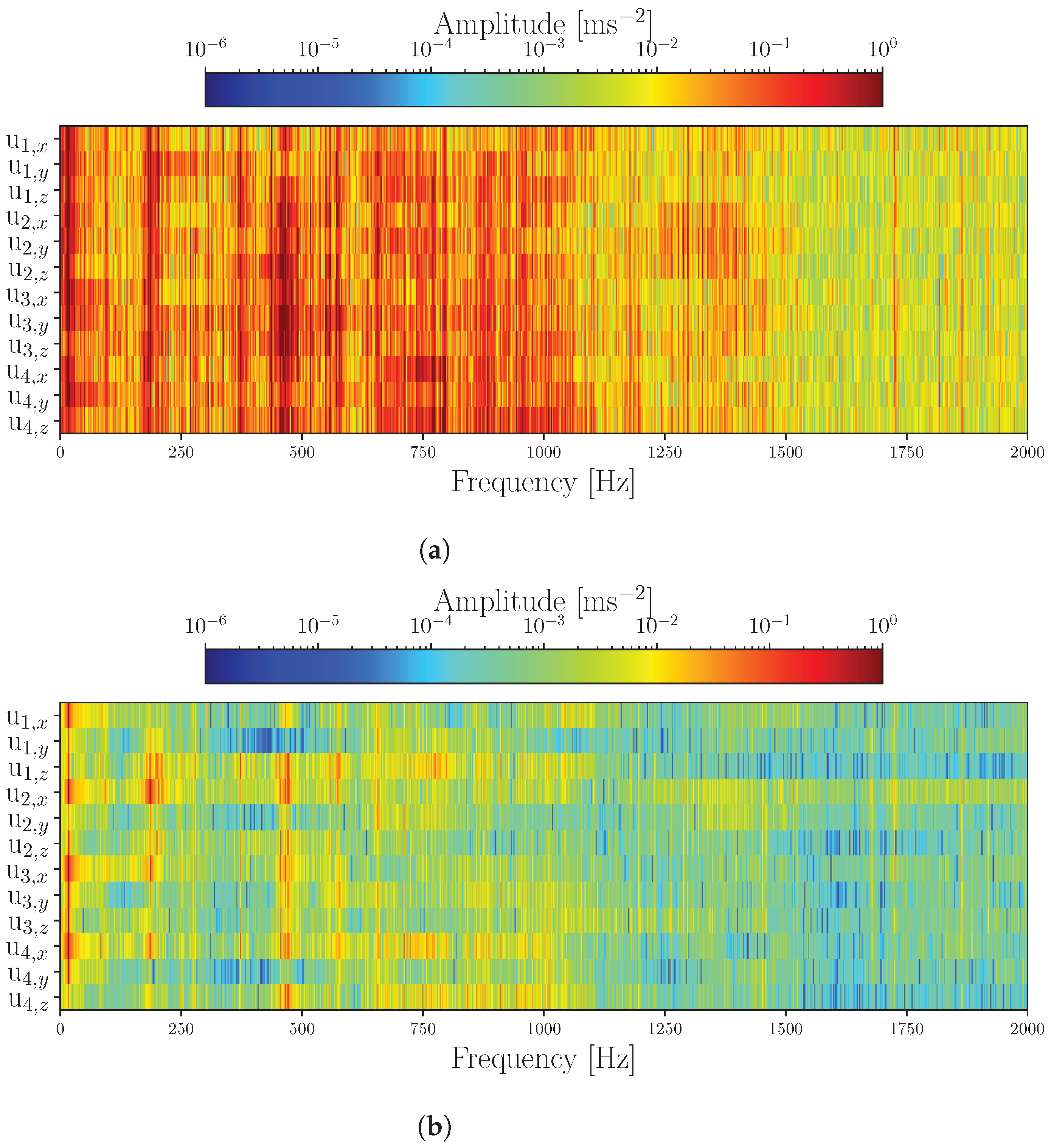
3.3. Washing Machine Drum Setup
Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DoFs | Degrees of freedom |
| IDMs | Interface-deformation modes |
| OTPA | Operational transfer-path analysis |
| RPM | Revolutions per minute |
| SVD | Singular value decomposition |
| TPA | Transfer-path analysis |
| TSVD | Truncated singular-value decomposition |
References
- Verheij, J.W. Multi-Path Sound Transfer from Resiliently Mounted Shipboard Machinery: Experimental Methods for Analyzing and Improving Noise Control. Ph.D. Thesis, TU Delft, Delft University of Technology, Delft, The Netherlands, 1982. [Google Scholar]
- Kong, L.; Zhao, X.; Yuan, X.; Yu, Q.; Shi, P.; Zhou, C.; Zhang, D. A novel vibration transfer path analysis for electric vehicle driving motor controllers under strong signal crosstalk. Mech. Syst. Signal Process. 2025, 223, 111919. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, Z.; Zhou, Q.; Hao, Z.; Qiu, Y. A study on the hybrid FE-experimental analysis method for dash panel response excited by the brake booster based on BF-TPA. Measurement 2021, 172, 108854. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, D.; Gao, Y.; Yang, J. Numerical and experimental-aided framework based on TPA for acoustic contributions of individual transfer paths on a vehicle door in the slamming event. Appl. Acoust. 2023, 203, 109220. [Google Scholar] [CrossRef]
- Hou, L.; Cao, S.; Gao, T.; Wang, S. Vibration signal model of an aero-engine rotor-casing system with a transfer path effect and rubbing. Measurement 2019, 141, 429–441. [Google Scholar] [CrossRef]
- El Khatiri, W.; Cherif, R.; El Bikri, K.; Atalla, N. Experimental study of component-based transfer path analysis hybrid methods applied to a helicopter. Appl. Acoust. 2023, 210, 109431. [Google Scholar] [CrossRef]
- Prenant, S.; Padois, T.; Rolland, V.; Etchessahar, M.; Dupont, T.; Doutres, O. Effects of mobility matrices completeness on component-based transfer path analysis methods with and without substructuring applied to aircraft-like components. J. Sound Vib. 2023, 547, 117541. [Google Scholar] [CrossRef]
- Li, C.; Lu, P.; Chen, G. VNCCD: A gearbox fault diagnosis technique under nonstationary conditions via virtual decoupled transfer path. Mech. Syst. Signal Process. 2024, 221, 111741. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y.H.; Zhang, X.Z.; Zhang, Y.B.; Chen, L.Q. Source contribution analysis of vehicle pass-by noise using a moving multi-band model based OPAX method. Measurement 2023, 218, 113170. [Google Scholar] [CrossRef]
- van der Seijs, M.V.; de Klerk, D.; Rixen, D.J. General framework for transfer path analysis: History, theory and classification of techniques. Mech. Syst. Signal Process. 2016, 68–69, 217–244. [Google Scholar] [CrossRef]
- Mondot, J.; Petersson, B. Characterization of structure-borne sound sources: The source descriptor and the coupling function. J. Sound Vib. 1987, 114, 507–518. [Google Scholar] [CrossRef]
- de Klerk, D.; Rixen, D. Component transfer path analysis method with compensation for test bench dynamics. Mech. Syst. Signal Process. 2010, 24, 1693–1710. [Google Scholar] [CrossRef]
- Elliott, A.; Moorhouse, A.; Huntley, T.; Tate, S. In-situ source path contribution analysis of structure borne road noise. J. Sound Vib. 2013, 332, 6276–6295. [Google Scholar] [CrossRef]
- de Klerk, D.; Ossipov, A. Operational transfer path analysis: Theory, guidelines and tire noise application. Mech. Syst. Signal Process. 2010, 24, 1950–1962. [Google Scholar] [CrossRef]
- Gajdatsy, P.; Janssens, K.; Desmet, W.; Van der Auweraer, H. Application of the transmissibility concept in transfer path analysis. Mech. Syst. Signal Process. 2010, 24, 1963–1976. [Google Scholar] [CrossRef]
- Janssens, K.; Gajdatsy, P.; Gielen, L.; Mas, P.; Britte, L.; Desmet, W.; Van der Auweraer, H. OPAX: A new transfer path analysis method based on parametric load models. Mech. Syst. Signal Process. 2011, 25, 1321–1338. [Google Scholar] [CrossRef]
- van der Seijs, M.V. Experimental Dynamic Substructuring: Analysis and Design Strategies for Vehicle Development. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Aragonès, À.; Poblet-Puig, J.; Arcas, K.; Rodríguez, P.V.; Magrans, F.X.; Rodríguez-Ferran, A. Experimental and numerical study of Advanced Transfer Path Analysis applied to a box prototype. Mech. Syst. Signal Process. 2019, 114, 448–466. [Google Scholar] [CrossRef]
- Gajdatsy, P.; Janssens, K.; Gielen, L.; Mas, P. Critical assessment of operational path analysis: Effect of coupling between path inputs. J. Acoust. Soc. Am. 2008, 123, 5821–5826. [Google Scholar] [CrossRef]
- Roozen, N.; Leclère, Q. On the use of artificial excitation in operational transfer path analysis. Appl. Acoust. 2013, 74, 1167–1174. [Google Scholar] [CrossRef]
- Cheng, W.; Chu, Y.; Chen, X.; Zhou, G.; Blamaud, D.; Lu, J. Operational transfer path analysis with crosstalk cancellation using independent component analysis. J. Sound Vib. 2020, 473, 115224. [Google Scholar] [CrossRef]
- Cheng, W.; Chu, Y.; Lu, J.; Song, C.; Chen, X.; Zhang, L.; Wajid, B.A.; Gao, L. A customized scheme of crosstalk cancellation for operational transfer path analysis and experimental validation. J. Sound Vib. 2021, 515, 116506. [Google Scholar] [CrossRef]
- Cheng, W.; Lu, Y.; Zhang, Z. Tikhonov regularization-based operational transfer path analysis. Mech. Syst. Signal Process. 2016, 75, 494–514. [Google Scholar] [CrossRef]
- Tang, Z.; Zan, M.; Zhang, Z.; Xu, Z.; Xu, E. Operational transfer path analysis with regularized total least-squares method. J. Sound Vib. 2022, 535, 117130. [Google Scholar] [CrossRef]
- Choi, H.G.; Thite, A.N.; Thompson, D.J. Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination. J. Sound Vib. 2007, 304, 894–917. [Google Scholar] [CrossRef]
- van der Seijs, M.V.; van den Bosch, D.D.; Rixen, D.J.; de Klerk, D. An improved methodology for the virtual point transformation of measured frequency response functions in dynamic substructuring. In Proceedings of the 4th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Kos Island, Greece, 12–14 June 2013; Volume 4. [Google Scholar]
- Allen, M.S.; Mayes, R.L.; Bergman, E.J. Experimental modal substructuring to couple and uncouple substructures with flexible fixtures and multi-point connections. J. Sound Vib. 2010, 329, 4891–4906. [Google Scholar] [CrossRef]
- Wernsen, M.; Van der Seijs, M.; Klerk, D. An indicator sensor criterion for in-situ characterisation of source vibrations. In Proceedings of the IMAC XXXV: 35th International Modal Anaylsis Conference, Los Angeles, CA, USA, 30 January–2 February 2017. [Google Scholar]
- Allen, M.S.; Rixen, D.; Van der Seijs, M.; Tiso, P.; Abrahamsson, T.; Mayes, R.L. Substructuring in Engineering Dynamics: Emerging Numerical and Experimental Techniques; Springer: Cham, Switzerland, 2019; Volume 594. [Google Scholar]
- Ocepek, D.; Trainotti, F.; Čepon, G.; Rixen, D.J.; Boltežar, M. On the experimental coupling with continuous interfaces using frequency based substructuring. Mech. Syst. Signal Process. 2024, 217, 111517. [Google Scholar] [CrossRef]
- Häußler, M.; Rixen, D.J. Optimal Transformation of Frequency Response Functions on Interface Deformation Modes. In Dynamics of Coupled Structures, Volume 4; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Pasma, E.; Seijs, M.v.d.; Klaassen, S.; Kooij, M.v.d. Frequency based substructuring with the virtual point transformation, flexible interface modes and a transmission simulator. In Dynamics of Coupled Structures, Volume 4: Proceedings of the 36th IMAC, A Conference and Exposition on Structural Dynamics 2018; Springer: Cham, Switzerland, 2018; pp. 205–213. [Google Scholar]
- Almirón, J.O.; Bianciardi, F.; Desmet, W. Flexible interface models for force/displacement field reconstruction applications. J. Sound Vib. 2022, 534, 117001. [Google Scholar] [CrossRef]
- Bregar, T.; Mahmoudi, A.E.; Kodrič, M.; Ocepek, D.; Trainotti, F.; Pogačar, M.; Göldeli, M.; Čepon, G.; Boltežar, M.; Rixen, D.J. pyFBS: A Python package for Frequency Based Substructuring. J. Open Source Softw. 2022, 7, 3399. [Google Scholar] [CrossRef]
- Zang, C.; Grafe, H.; Imregun, M. Frequency–domain criteria for correlating and updating dynamic finite element models. Mech. Syst. Signal Process. 2001, 15, 139–155. [Google Scholar] [CrossRef]






| Young’s Modulus | Density | |
|---|---|---|
| PPCaCo3 | 2800 MPa | |
| Structural steel | 200 GPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senčič, J.; Pogačar, M.; Ocepek, D.; Čepon, G. A Reduction-Based Approach to Improving the Estimation Consistency of Partial Path Contributions in Operational Transfer-Path Analysis. Appl. Mech. 2025, 6, 13. https://doi.org/10.3390/applmech6010013
Senčič J, Pogačar M, Ocepek D, Čepon G. A Reduction-Based Approach to Improving the Estimation Consistency of Partial Path Contributions in Operational Transfer-Path Analysis. Applied Mechanics. 2025; 6(1):13. https://doi.org/10.3390/applmech6010013
Chicago/Turabian StyleSenčič, Jan, Miha Pogačar, Domen Ocepek, and Gregor Čepon. 2025. "A Reduction-Based Approach to Improving the Estimation Consistency of Partial Path Contributions in Operational Transfer-Path Analysis" Applied Mechanics 6, no. 1: 13. https://doi.org/10.3390/applmech6010013
APA StyleSenčič, J., Pogačar, M., Ocepek, D., & Čepon, G. (2025). A Reduction-Based Approach to Improving the Estimation Consistency of Partial Path Contributions in Operational Transfer-Path Analysis. Applied Mechanics, 6(1), 13. https://doi.org/10.3390/applmech6010013





