Experimental Validation of Exact Burst Pressure Solutions for Thick-Walled Cylindrical Pressure Vessels
Abstract
1. Introduction
2. Burst Prediction Models for Cylindrical Pressure Vessels
2.1. Burst Pressure Models for Thin-Walled Cylinders
2.1.1. Strength Models for Thin-Walled Cylinders
- Tresca strength solution:
- von Mises strength solution:
- Zhu–Leis strength solution:
- Flow stress-based failure solution:
2.1.2. Flow Models for Thin-Walled Cylinders
2.2. Burst Pressure Models for Thick-Walled Cylinders
2.2.1. Strength Models for Thick-Walled Cylinders
- Tresca strength solution:
- von Mises strength solution:
- Svensson approximate solution:
2.2.2. Flow Models for Thick-Walled Cylinders
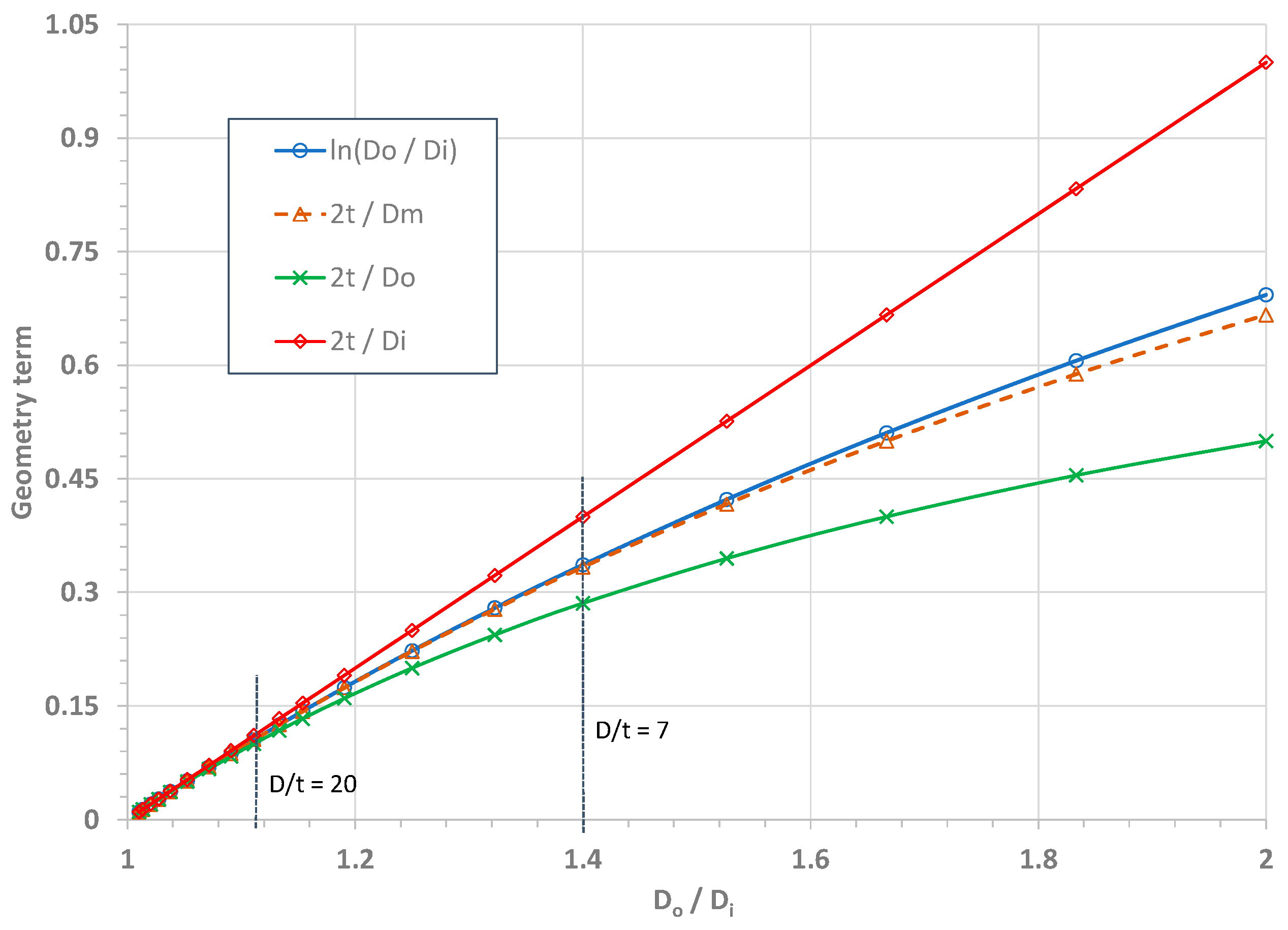
2.3. Comparison of Thin and Thick-Wall Burst Pressure Models
3. Experimental Validation
3.1. Grade B Carbon Steel Pipes
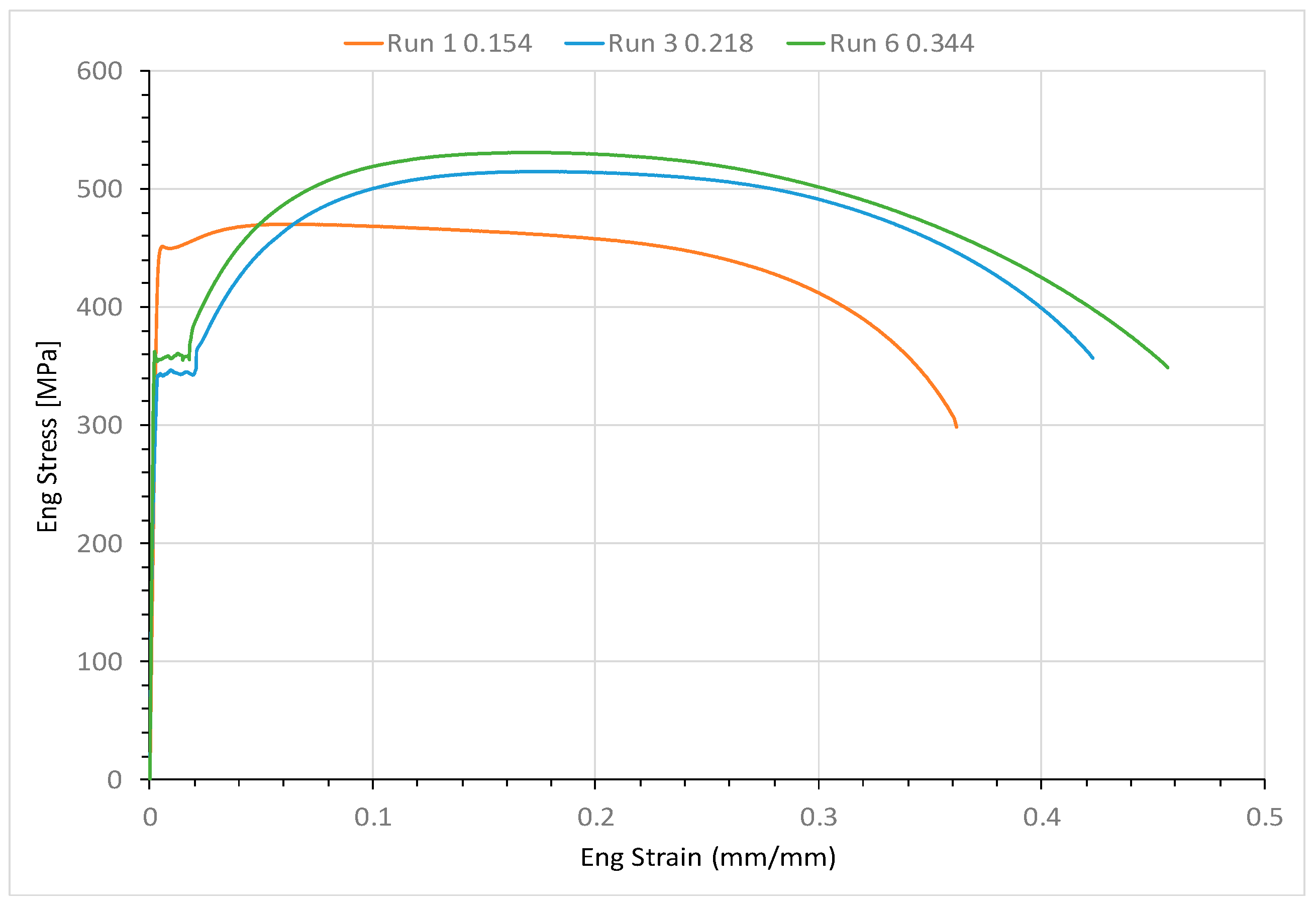
3.2. Tensile Tests
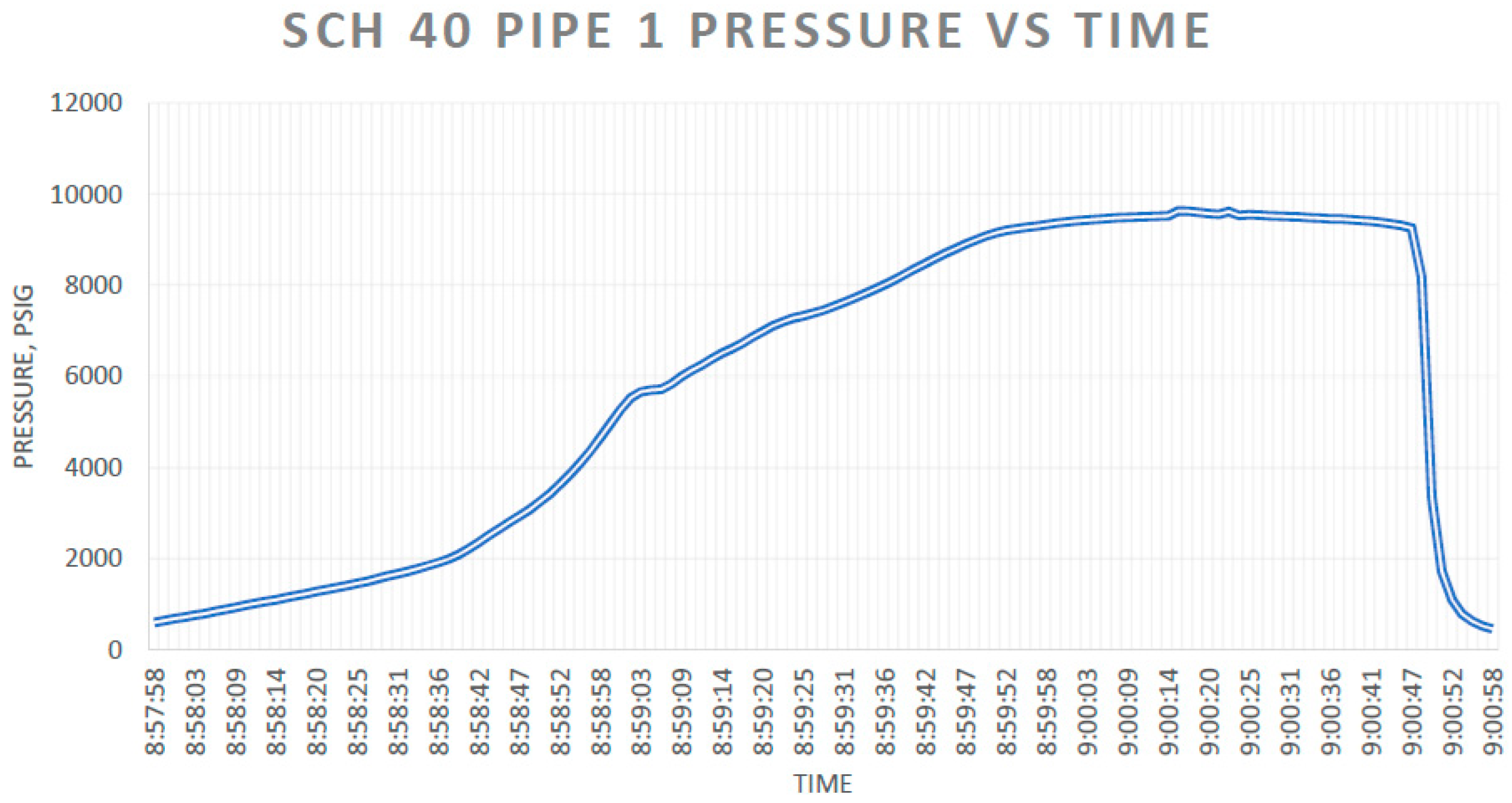
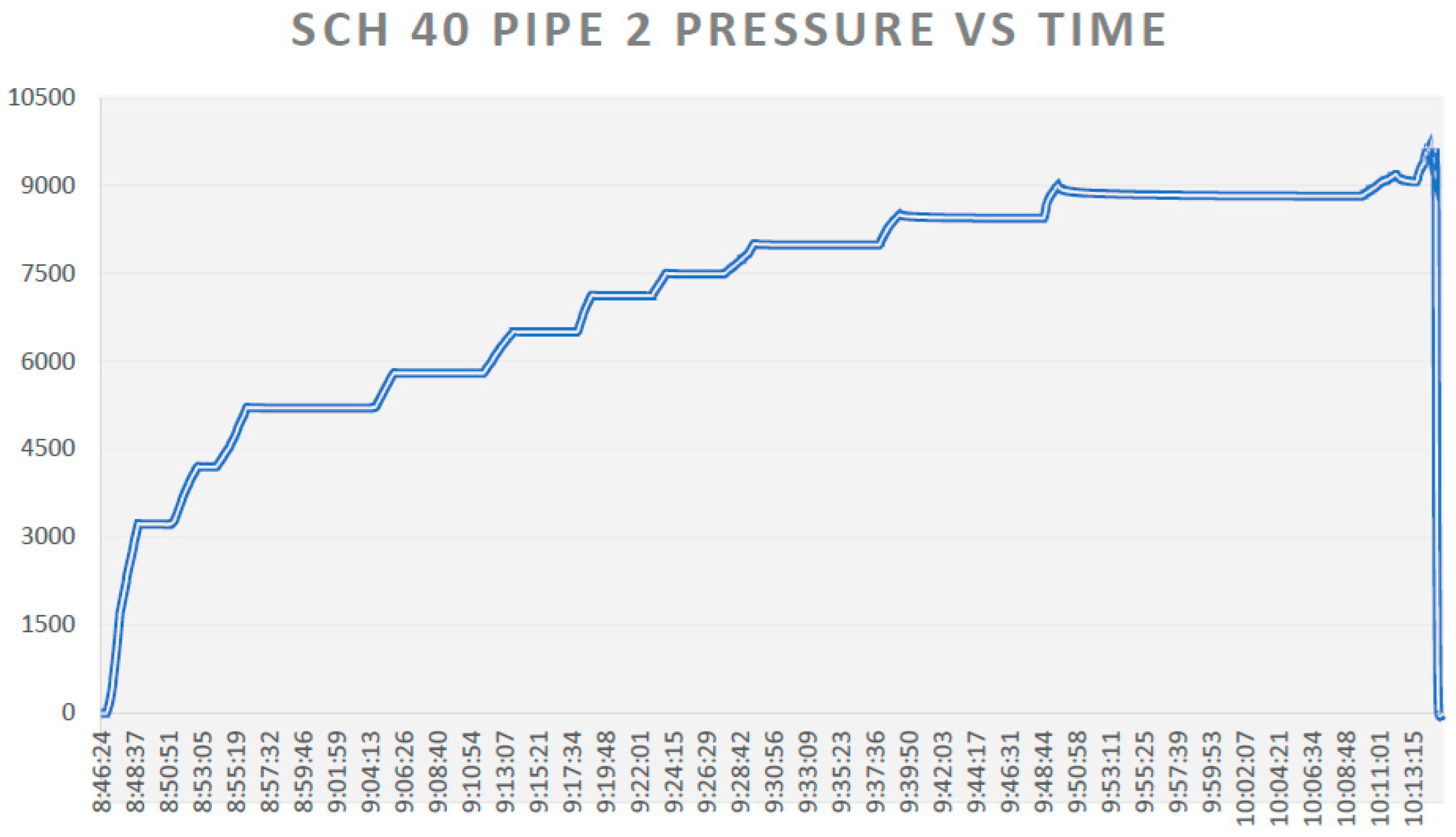
3.3. Pressure Burst Tests and Results
- For SCH-40 Pipe 1, bursting occurred in the pipe body close to the middle of the pipe, and burst pressure was achieved at 9646.4 psig (66.5 MPa). The pipe failure was ideally located in the pipe body for this burst test.
- For SCH-40 Pipe 2, likewise, bursting occurred in the pipe body, near the middle of the pipe, and burst pressure was measured as 9634.95 psig (66.4 MPa). The pipe failure was also ideally located in the pipe body for this burst test.
- For SCH-80 Pipe 1, bursting occurred in the pipe body close to one end of the pipe, and burst pressure was measured as 14,369.81 psig (99.1 MPa). The pipe failure was located in the pipe body but close to the pipe end for this burst test.
- For SCH-80 Pipe 2, the test result was questionable. The pipe failure occurred in the seam weld of the test pipe. After the seam weld ruptured, the crack propagated into the end weld. The failure pressure was achieved at 14,110 psig (97.3 MPa). This seam weld failure pressure may be less than that for the pipe body failure.
- For SCH-160 Pipe 1, the failure was present around the high-pressure fitting weld, and pressurization was not possible due to leaking. Thus, no burst datum was recorded.
- For SCH-160 Pipe 2, the failure occurred at the end cap weld. This demonstrated that the end cap welds used in this work may be inappropriate and not have the sufficient strength required for thick-walled pipes. Accordingly, stronger end cap welds are needed. The weld failure occurred at 24,887 psig (171.6 MPa). This weld failure pressure may be less than that for the pipe body failure.
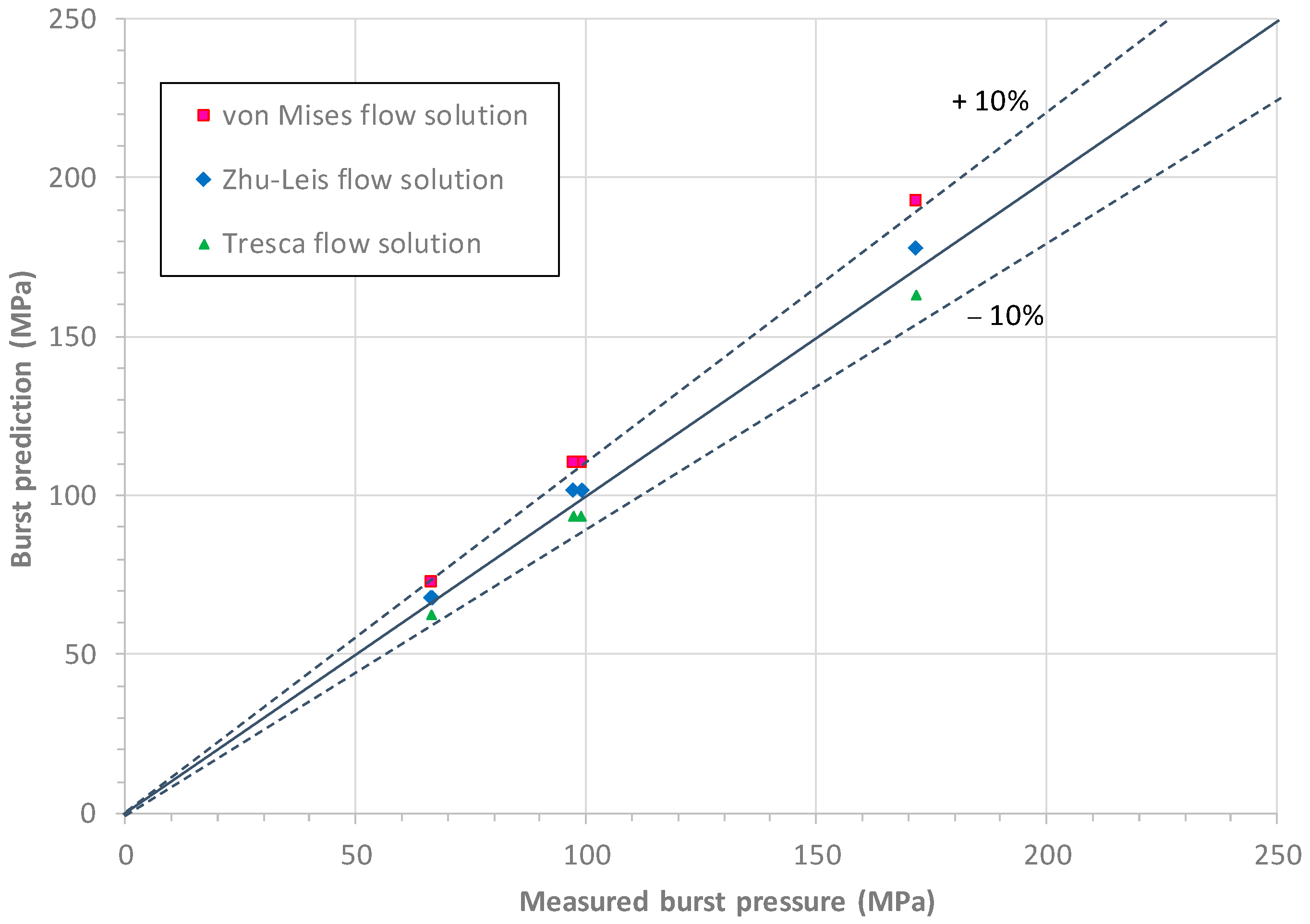
3.4. Comparison of Measured and Predicted Burst Pressures
4. Additional Experimental Validations
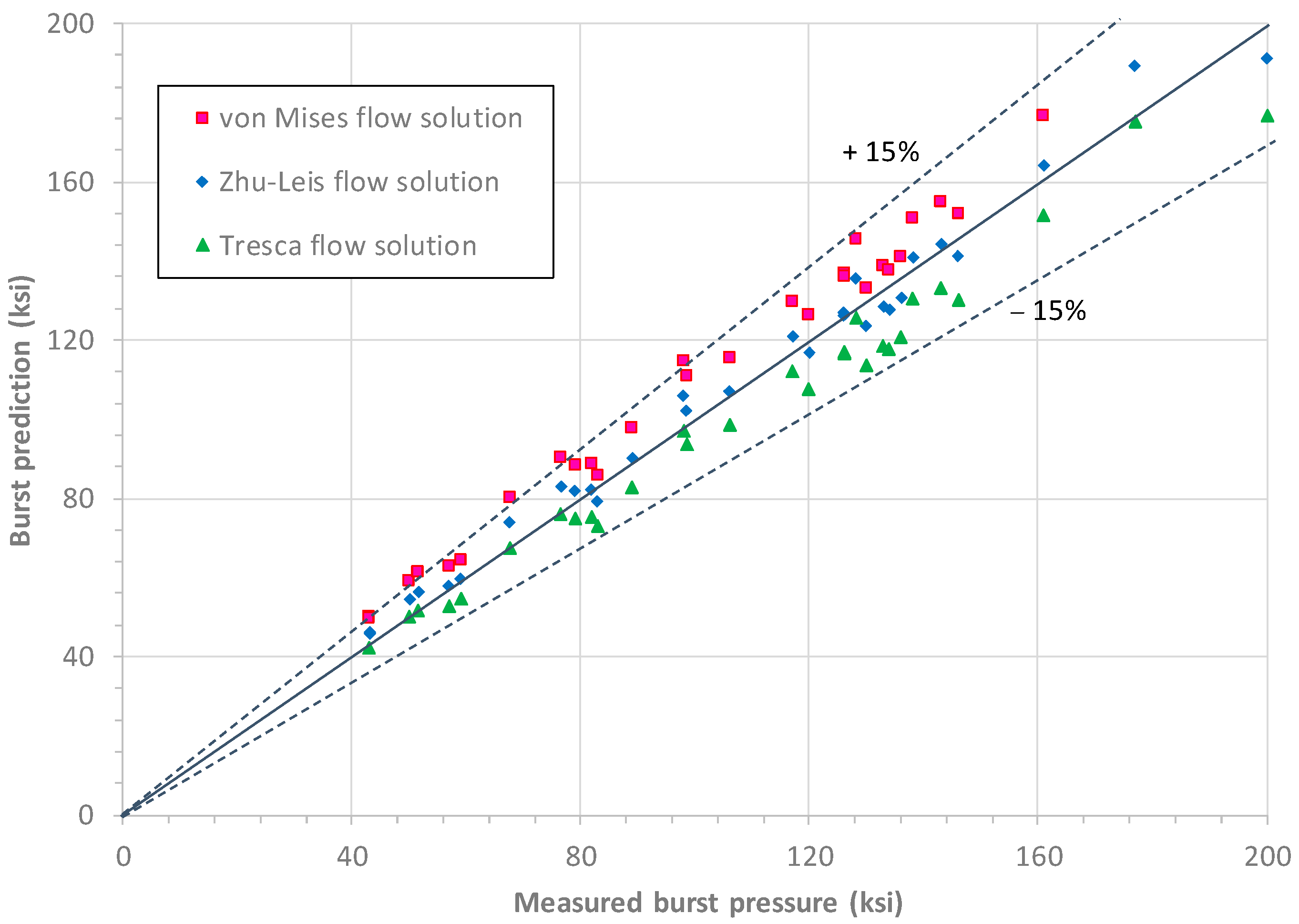
4.1. Validation for Thin-Walled Line Pipes
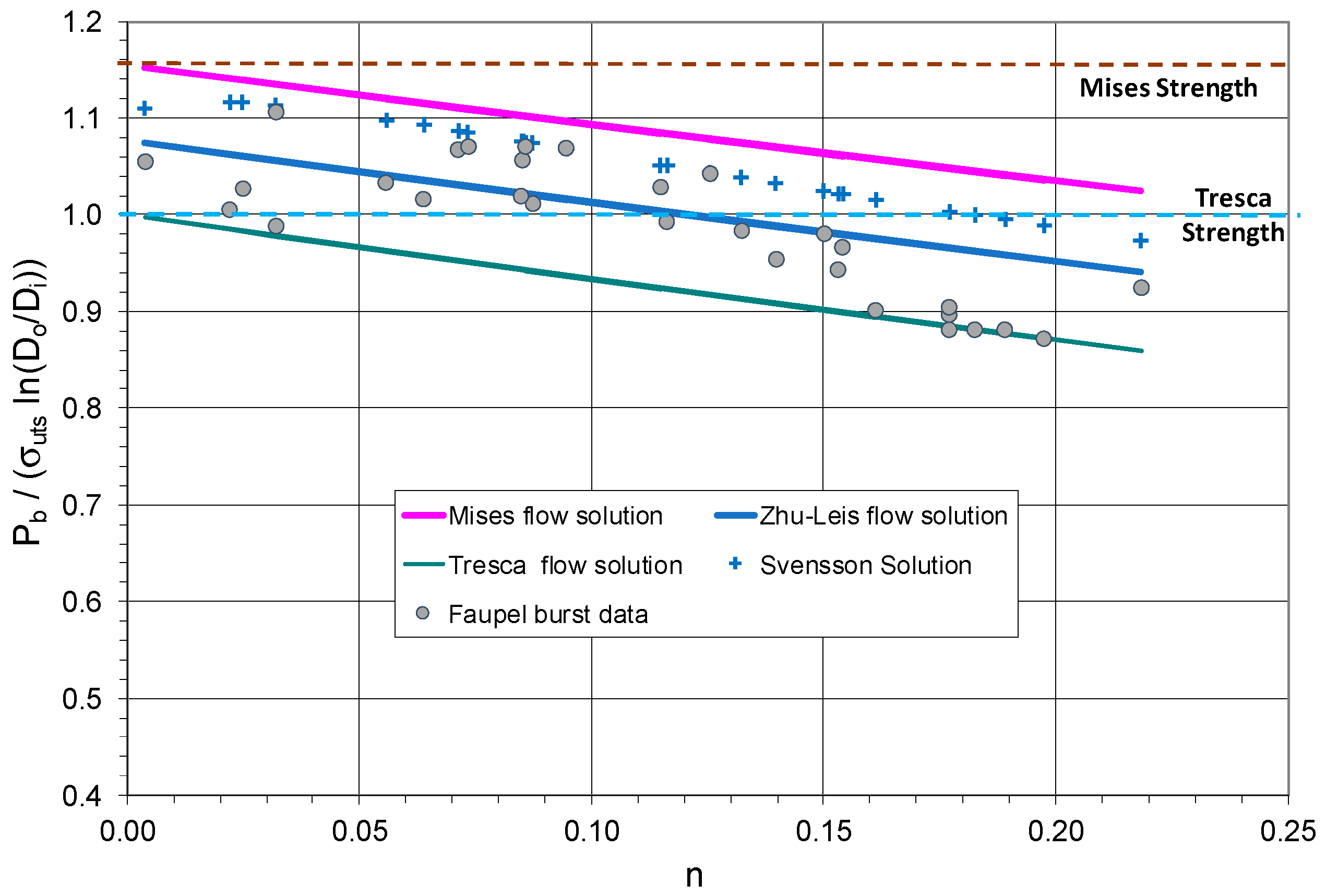
4.2. Validation for Thick-Walled Tubes
5. Conclusions
- (1)
- Three exact flow solutions of burst pressure based on the Tresca, von Mises and Zhu–Leis yield criteria are functions of UTS, n, and ln(Do/Di) for thick-walled pipes. Among them, the Tresca flow solution is a lower bound prediction of burst data, the von Mise flow solution is an upper bound prediction, and the Zhu–Leis flow solution is an averaged prediction.
- (2)
- For three Grade B carbon steel pipes, the materials’ mechanical properties were measured from the uniaxial tensile tests. The measured stress–strain curves were similar for the two thicker pipes (i.e., SCH-80 and SCH-160), but differed for the thinner one (i.e., SCH-40). The reason for the differences between the same purchased pipes is unknown. The possible factors may include (1) these same labeled Grade B steels were manufactured by different manufacturing processes, and (2) small variations in the chemical compositions were possible for these steels.
- (3)
- The “air-over-water” pressurization process was successfully utilized in all the pressure burst tests at SRNL. Both monotonical loading and multi-step loading approaches were applied to the pipe pressure burst tests. The slow multi-step loading approach showed up as a more reasonable procedure for a pressure burst test.
- (4)
- The outside circular welding process used to join the end plate caps for the pressure test pipe specimens worked well for the thinner walls of the pipes (SCH-40 and SCH-80) but was inappropriate for thick walls (SCH-160). In the latter case, circular welds failed first due to insufficient weld strength. Accordingly, the single V-groove welding process is suggested for joining the end plate caps onto the pipe specimen to avoid a circumferential crack forming inside of the pipe at each end plate cap.
- (5)
- The burst pressure test data measured at SRNL and obtained from the literature all validated that the Zhu–Leis flow solution is the best burst prediction model for both thin and thick-walled pipes, whereas the von Mises flow solution predicts an upper bound result, and the Tresca flow solution predicts a lower bond result for both thin and thick-walled pipes.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Exact Burst Pressure Solutions for Thick-Walled Cylindrical Shells

Appendix B. Burst Testing Pipe Specimen Design Drawing
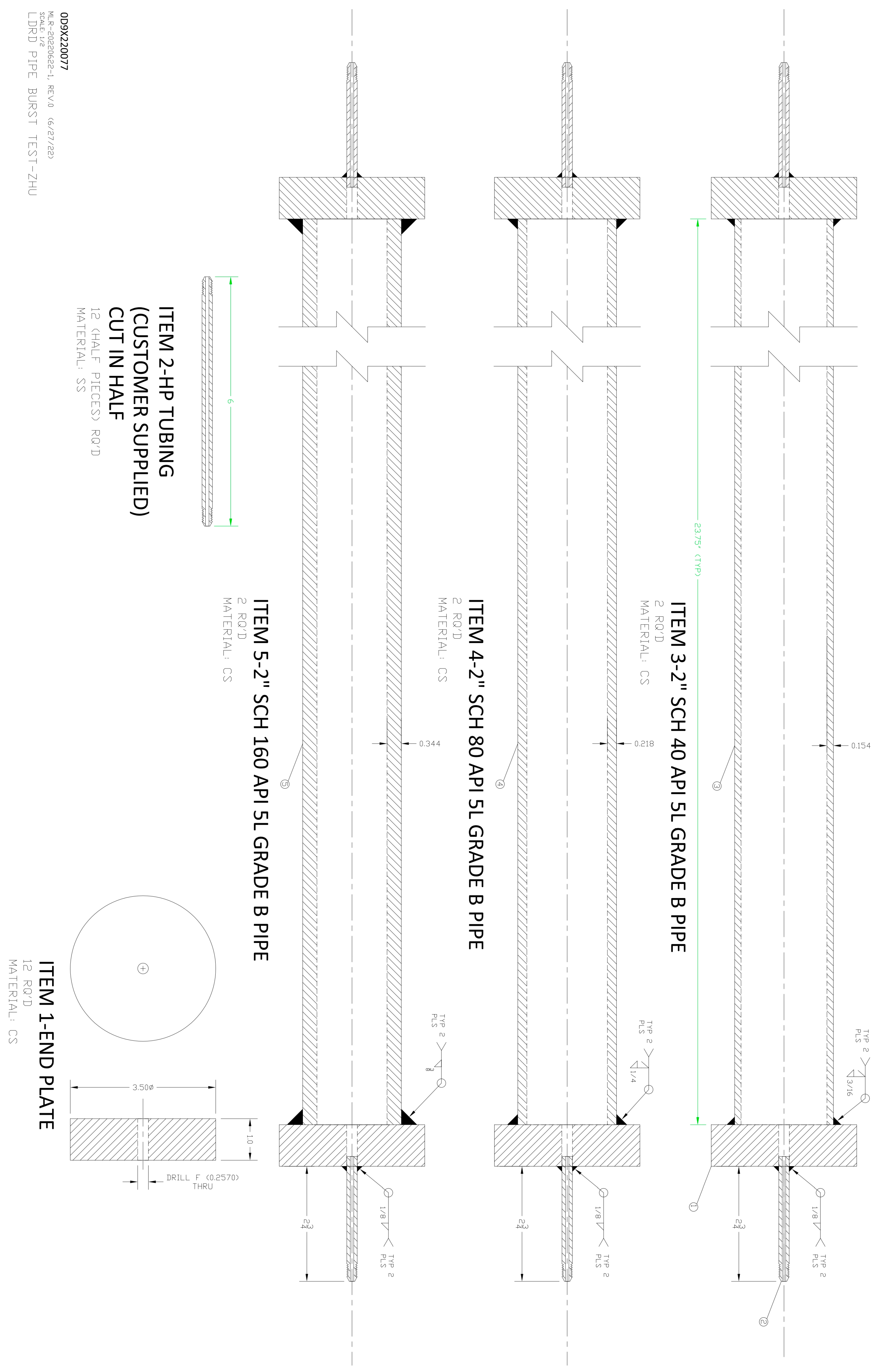
Appendix C. Failure Appearance of Pressure Burst Test Pipes





References
- Zhu, X.K. Strength criteria versus plastic flow criteria used in pressure vessel design and analysis. J. Press. Vessel. Technol. 2016, 138, 041402. [Google Scholar] [CrossRef]
- Hamgung, I.; Giang, N.H. Investigation of burst pressures in PWR primary pressure boundary components. Nucl. Eng. Technol. 2016, 48, 236–245. [Google Scholar] [CrossRef]
- Lyons, C.J.; Race, J.M.; Change, E.; Cosham, A.; Wetenhall, B.; Barnett, J. Validation of the NG-18 equations for thick-walled pipelines. Eng. Fail. Anal. 2020, 112, 104494. [Google Scholar] [CrossRef]
- Kadam, M.; Balamurugan, G.; Bujurke, A.A.; Joshi, K.M. Finite element prediction of static burst pressure in closed thick-walled unflawed cylinders of different diameter ratios. Procedia Eng. 2017, 173, 577–594. [Google Scholar] [CrossRef]
- Hamada, M.; Yokoyama, R.; Kitagawa, H. An estimation of maximum pressure for a thick-walled tube subjected to internal pressure. Int. J. Press. Vessel. Pip. 1986, 22, 311–323. [Google Scholar] [CrossRef]
- Christopher, T.; Rama Sarma, B.S.; Govinda Potti, P.K.; Rao, B.N. A comparative study on failure pressure estimation of unflawed cylindrical vessels. Int. J. Press. Vessel. Pip. 2002, 79, 53–66. [Google Scholar] [CrossRef]
- Krishnaveni, A.; Christopher, T.; Jeyakumar, K.; Jebakani, D. Probabilistic failure prediction of high strength steel rocket motor cases. J. Fail. Anal. Prev. 2014, 14, 478–490. [Google Scholar] [CrossRef]
- Law, M.; Bowie, G. Prediction of failure strain and burst pressure in high yield to-tensile strength ratio linepipe. Int. J. Press. Vessel. Pip. 2007, 84, 487–492. [Google Scholar] [CrossRef]
- Zhu, X.K.; Leis, B.N. Evaluation of burst pressure prediction models for line pipes. Int. J. Press. Vessel. Pip. 2012, 89, 85–97. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, T.; Sang, Z.; Krakauer, B.W. Burst pressures of thin-walled cylinders constructed of steel exhibiting a yield plateau. Int. J. Press. Vessel. Pip. 2021, 193, 104483. [Google Scholar] [CrossRef]
- Sun, M.; Chen, Y.; Zhao, H.; Li, X. Analysis of the impact factor of burst capacity models for defect-free pipelines. Int. J. Press. Vessel. Pip. 2022, 200, 104805. [Google Scholar] [CrossRef]
- Stewart, G.; Klever, F.J. An analytical model to predict the burst capacity of pipelines. In Proceedings of the International Conference of Offshore Mechanics and Arctic Engineering, Houston, TX, USA, 27 February–3 March 1994; American Society of Mechanical Engineers: New York, NY, USA, 1994; Volume V: Pipeline Technology, pp. 177–188. [Google Scholar]
- Cooper, W.E. The significance of the tensile test to pressure vessel design. Weld. J.-Weld. Res. Suppl. 1957, 36, 49s–56s. [Google Scholar]
- Svensson, N.L. The bursting pressure of cylindrical and spherical vessels. J. Appl. Mech. 1958, 25, 89–96. [Google Scholar] [CrossRef]
- Zhu, X.K.; Leis, B.N. Average shear stress yield criterion and its application to plastic collapse analysis of pipelines. Int. J. Press. Vessel. Pip. 2006, 83, 663–671. [Google Scholar] [CrossRef]
- Zimmermann, S.; Hohler, S.; Marewski, U. Modeling ultimate limit states on burst pressure and yielding of flawless pipes. In Proceedings of the 16th Biennial Pipeline Research Joint Technical Meeting, Canberra, Australia, 16–19 April 2007. Paper 13. [Google Scholar]
- Knoop, F.M.; Flaxa, V.; Zimmermann, S.; Grob-Weege, J. Mechanical properties and component behavior of x80 helical seam welded large diameter pipes. In Proceedings of the 8th International Pipeline Conference, Calgary, AB, Canada, 27 September–1 October 2010. [Google Scholar]
- Bony, M.; Alamilla, J.L.; Vai, R.; Flores, E. Failure pressure in corroded pipelines based on equivalent solutions for undamaged pipe. J. Press. Vessel. Technol. 2010, 132, 051001. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G. Model error assessment of burst capacity models for defect-free pipes. In Proceedings of the 9th International Pipeline Conference, Calgary, AB, Canada, 24–28 September 2012. [Google Scholar]
- Seghier, M.E.A.B.; Keshtegar, B.; Elahmoune, B. Reliability analysis of low, mid and high-grade strength corroded pipes based on plastic flow theory using adaptive nonlinear conjugate map. Eng. Fail. Anal. 2018, 90, 245–261. [Google Scholar] [CrossRef]
- Zhu, X.K.; Wiersma, B.; Johnson, W.R.; Sindelar, R. Burst pressure solutions of thin and thick-walled cylindrical vessels. J. Press. Vessel. Technol. 2023, 145, 044202. [Google Scholar] [CrossRef]
- Zhu, X.K. Exact solution of burst pressure for thick-walled pipes using the flow theory of plasticity. Int. J. Mech. Sci. 2023, 259, 108582. [Google Scholar] [CrossRef]
- Zhu, X.K.; Wiersma, B.; Johnson, W.R.; Sindelar, R. Exact solutions of burst pressure for thick-walled cylinders in power-law strain hardening steels. Int. J. Press. Vessel. Pip. 2023, 206, 105053. [Google Scholar] [CrossRef]
- Zhu, X.K. Recent advances in corrosion assessment models for buried transmission pipelines. CilvilEng 2023, 4, 391–425. [Google Scholar] [CrossRef]
- Bhardwaj, U.; Teixeira, A.P.; Soares, C.G. Burst strength assessment of X100 to X120 ultra-high strength corroded pipes. Ocean Eng. 2021, 241, 110004. [Google Scholar] [CrossRef]
- Amaya-Gomez, R.; Sanchez-Silva, M.; Bastidas-Arteaga, E.; Schoefs, F.; Munoz, F. Reliability assessments of corroded pipelines based on internal pressure—A review. Eng. Fail. Anal. 2019, 98, 190–214. [Google Scholar] [CrossRef]
- Bhardwaj, U.; Teixeira, A.P.; Soares, C.G. Uncertainty quantification of burst pressure models of corroded pipelines. Int. J. Press. Vessel. Pip. 2020, 188, 104208. [Google Scholar] [CrossRef]
- Faupel, J.H. Yield and bursting characteristics of heavy-wall cylinders, Transaction of ASME. J. Fluid Eng. 1956, 78, 1031–1064. [Google Scholar]
- Faupel, J.H.; Furbeck, A.R. Influence of residual stress on behavior of thick-wall closed-end cylinders. Trans. ASME J. Fluid Eng. 1953, 75, 345–354. [Google Scholar] [CrossRef]
- API 5L; Specification for Line Pipe. American Petroleum Institute: Washington, DC, USA, 2013.
- Baggett, H.W.; Restivo, M.L. Summary Report of LDRD Burst Pipe Testing; Savannah River National Laboratory: Aiken, SC, USA, 2022.
- ASTM E8/E8M-21; Standard Test Methods for Tension Testing of Metallic Materials. American Society for Testing and Materials International: West Conshohocken, PA, USA, 2021.
- API 579-1/ASME FFS-1 2021 Edition; Fitness-For-Service. The American Petroleum Institute and The American Society of Mechanical Engineers: Washington, DC, USA, 2021.
- Deng, K.; Peng, Y.; Liu, B.; Lin, Y.; Wang, J. Through-wall yield ductile burst pressure of high-grade steel tube and casing with and without corroded defect. Mar. Struct. 2021, 76, 102902. [Google Scholar]
- Shi, J.; Zhang, Q.; Lian, Z.; Ding, L.; Wan, Z. A calculation method for ultimate and allowable loads in high-pressure thick-walled worn casing. Ocean Eng. 2024, 313, 119448. [Google Scholar] [CrossRef]




| SCH | YS (MPa) | YS (ksi) | UTS (MPa) | UTS (ksi) | n | Elon |
|---|---|---|---|---|---|---|
| SCH-40 | 450 | 65.3 | 470 | 68.2 | 0.062 | 37% |
| SCH-80 | 342 | 49.6 | 515 | 74.7 | 0.161 | 43% |
| SCH-160 | 356 | 51.6 | 531 | 77.0 | 0.156 | 46% |
| Pipe # | Failure Type | Measured Burst Pb, Psi (MPa) | Zhu–Leis Bust Pb, Psi (MPa) | Relative Error (%) |
|---|---|---|---|---|
| SCH-40, Pipe 1 | Body burst | 9646.4 (66.5) | 9817 (67.7) | 1.76 |
| SCH-40, Pipe 2 | Body burst | 9634.95 (66.4) | 9817 (67.7) | 1.89 |
| SCH-80, Pipe 1 | Body burst | 14,369.81 (99.1) | 14,774 (101.9) | 2.81 |
| SCH-80, Pipe 2 | Seam failure | 14,110.03 (97.3) | 14,774 (101.9) | 4.71 |
| SCH-160, Ppe 1 | fitting leaks | N/A | 25,768 (177.7) | N/A |
| SCH-160, Pipe 2 | Weld failure | 24,886.65 (171.6) | 25,768 (177.7) | 3.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.-K. Experimental Validation of Exact Burst Pressure Solutions for Thick-Walled Cylindrical Pressure Vessels. Appl. Mech. 2025, 6, 20. https://doi.org/10.3390/applmech6010020
Zhu X-K. Experimental Validation of Exact Burst Pressure Solutions for Thick-Walled Cylindrical Pressure Vessels. Applied Mechanics. 2025; 6(1):20. https://doi.org/10.3390/applmech6010020
Chicago/Turabian StyleZhu, Xian-Kui. 2025. "Experimental Validation of Exact Burst Pressure Solutions for Thick-Walled Cylindrical Pressure Vessels" Applied Mechanics 6, no. 1: 20. https://doi.org/10.3390/applmech6010020
APA StyleZhu, X.-K. (2025). Experimental Validation of Exact Burst Pressure Solutions for Thick-Walled Cylindrical Pressure Vessels. Applied Mechanics, 6(1), 20. https://doi.org/10.3390/applmech6010020




