An Analytical Approximation of the Stress Function for Conical Flywheels
Abstract
:1. Introduction
Background
2. Methodology
- is the outer radius of the flywheel;
- is the inner radius of the flywheel;
- r is the radial distance at which the stress is to be computed;
- is the Poisson ratio of the flywheel material;
- is the density of the flywheel material;
- is the angular velocity of the flywheel.
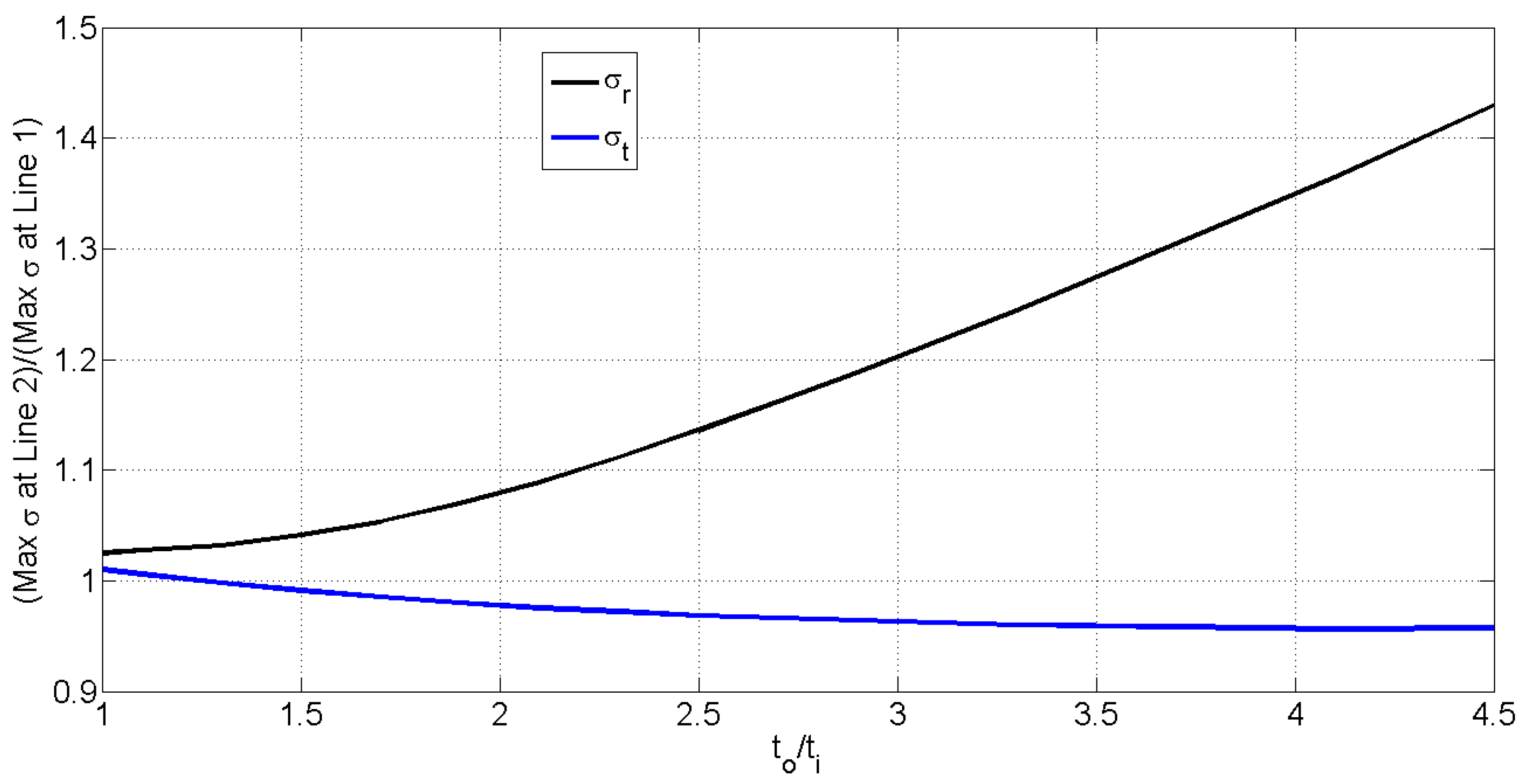
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FESS | Flywheel energy storage system |
| FEM | Finite element method |
| FEA | Finite element analysis |
| MAPE | Mean absolute percentage error |
| RMSE | Root mean squared error |
| NRMSE | Normalized RMSE |
References
- Zenkour, A.; Mashat, D. Stress Function of a Rotating Variable-Thickness Annular Disk Using Exact and Numerical Methods. Engineering 2011, 3, 422–430. [Google Scholar] [CrossRef]
- Xu, K.; Guo, Y.; Lei, G.; Zhu, J. A Review of Flywheel Energy Storage System Technologies. Energies 2023, 16, 6462. [Google Scholar] [CrossRef]
- Semsri, A. Experimental Design of Flywheel Rotor with a Flywheel Energy Storage System for Residential uses. Int. Energy J. 2023, 23, 105. [Google Scholar]
- Acarnley, P.P.; Mecrow, B.C.; Burdess, J.S.; Fawcett, J.N.; Kelly, J.G.; Dickinson, P.G. Design Principles for a Flywheel Energy Storage for Road Vehicles. IEEE Trans. Ind. Appl. 1996, 32, 1402–1408. [Google Scholar] [CrossRef]
- Kailasan, A.; Dimond, T.; Allaire, P.; Sheffler, D. Design and Analysis of a Unique Energy Storage Flywheel System—An Integrated Flywheel, Motor/Generator, and Magnetic Bearing Configuration. J. Eng. Gas Turbines Power 2015, 137, 042505. [Google Scholar] [CrossRef]
- Motaman, S.; Eltaweel, M.; Herfatmanesh, M.R.; Knichel, T.; Deakin, A. Numerical analysis of a flywheel energy storage system for low carbon powertrain applications. J. Energy Storage 2023, 61, 106808. [Google Scholar] [CrossRef]
- Kale, V.; Aage, N.; Secanell, M. Stress Constrained Topology Optimization of Energy Storage Flywheels Using a Specific Energy Formulation. J. Energy Storage 2023, 61, 106733. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, W.; Ma, G.J.; Wu, C.W. Shape Optimization of Energy Storage Flywheel Rotor. Struct. Multidiscip. Optim. 2016, 55, 739–750. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, C.W. Topology Optimization of Energy Storage Flywheel. Struct. Multidiscip. Optim. 2016, 55, 1917–1925. [Google Scholar] [CrossRef]
- Sondhi, L.; Kumar Thawait, A.; Sanyal, S.; Bhowmick, S. Stress and deformation analysis of functionally graded varying thickness profile orthotropic rotating disk. Mater. Today Proc. 2020, 33, 5455–5460. [Google Scholar] [CrossRef]
- Hassan, S.U.; He, B.; Khayyam, U. Design and Analysis of Flywheel for Small Scale Energy Storage System Using Different Structures and their Comparison. In Proceedings of the 2019 4th International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 21–23 September 2019; pp. 295–299. [Google Scholar] [CrossRef]
- Bankston, S.; Mo, C. Geometry Modification of Flywheels and its Effect on Energy Storage. Energy Res. J. 2015, 6, 54–63. [Google Scholar] [CrossRef]
- Kale, V.; Thomas, M.; Secanell, M. On determining the optimal shape, speed, and size of metal flywheel rotors with maximum kinetic energy. Struct. Multidiscip. Optim. 2021, 64, 1481–1499. [Google Scholar] [CrossRef]
- Wen, S. Analysis of Maximum Radial Stress Location of Composite Energy Storage Flywheel Rotor. Arch. Appl. Mech. 2014, 84, 1007–1013. [Google Scholar] [CrossRef]
- Ugural, A.C.; Fenster, S.K. Advanced Mechanics of Materials and Applied Elasticity; Pearson: London, UK, 2020. [Google Scholar]
- Timoshenko, S.; Goodier, J. Theory of Elasticity; McGraw-Hill: New York City, NY, USA, 1951. [Google Scholar]
- Berman, J.J. Data Simplification. Taming Information with Open Source Tools; Morgan Kaufmann: Burlington, MA, USA, 1951. [Google Scholar]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
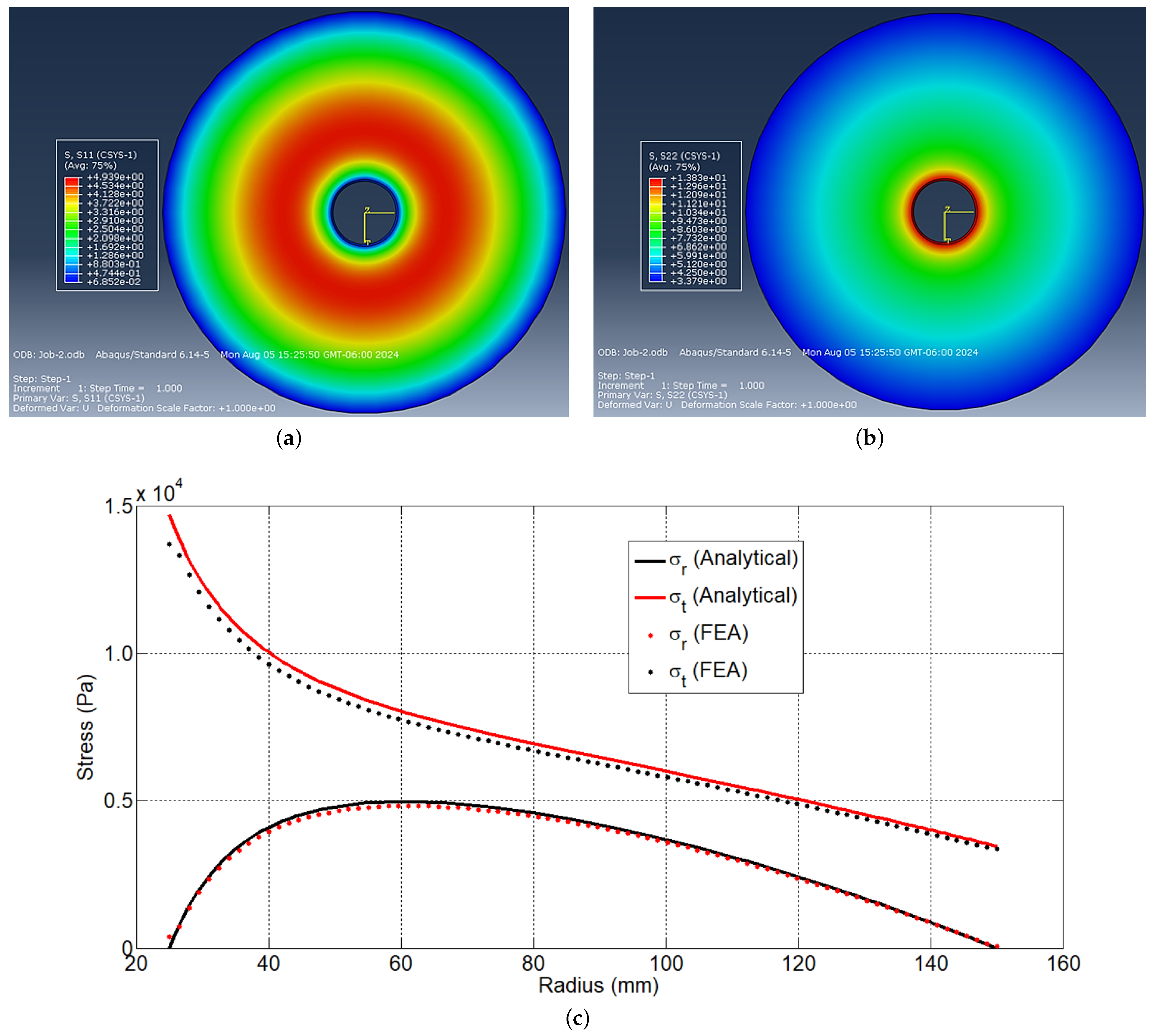
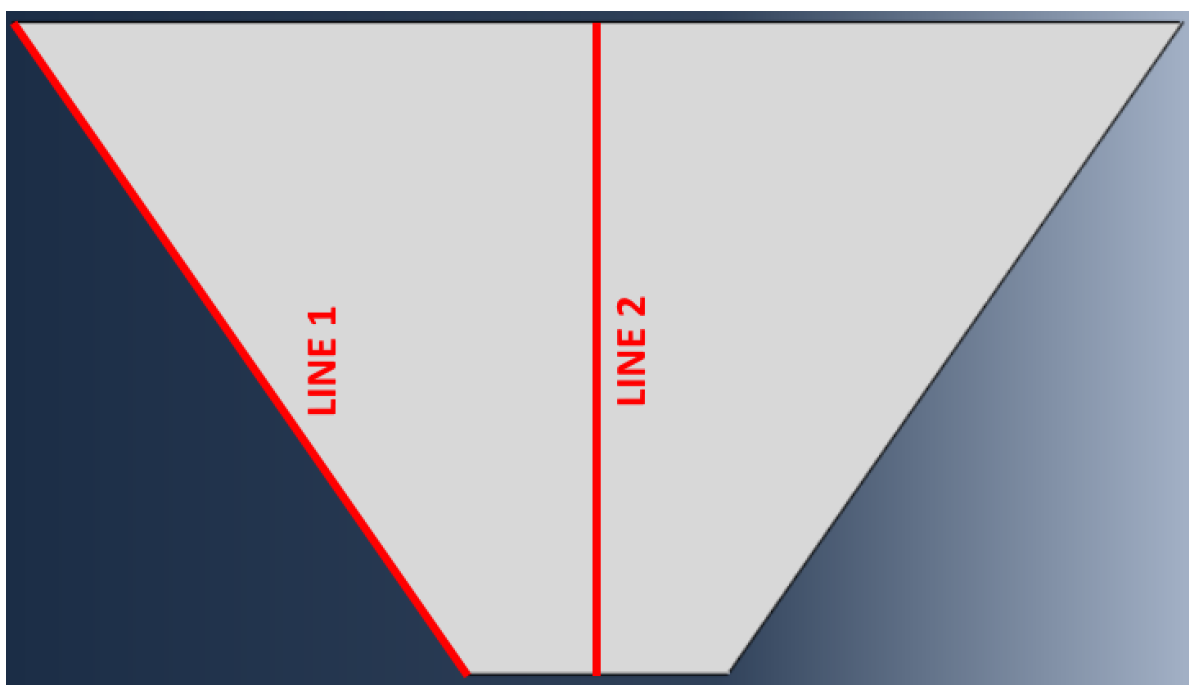
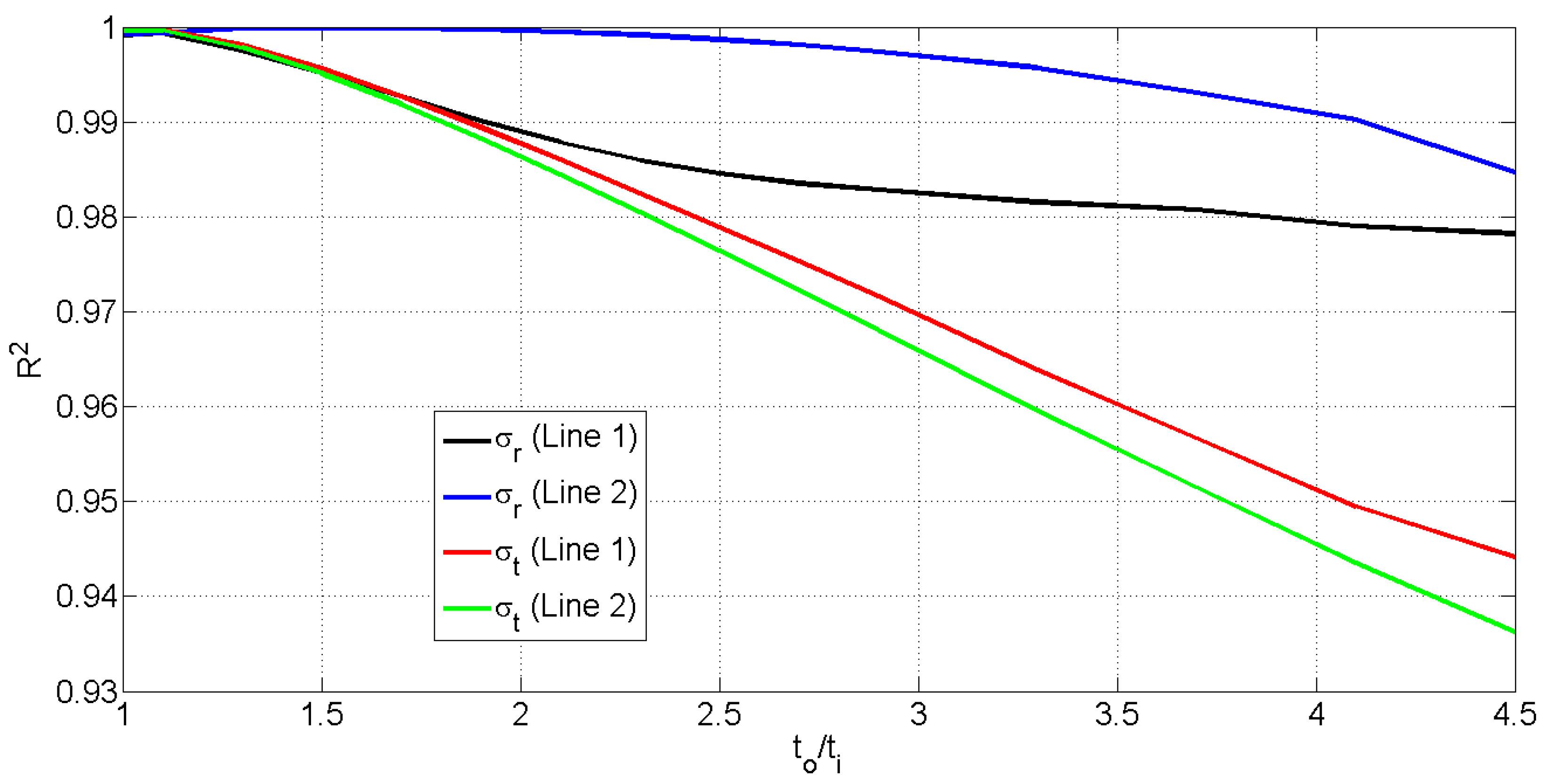
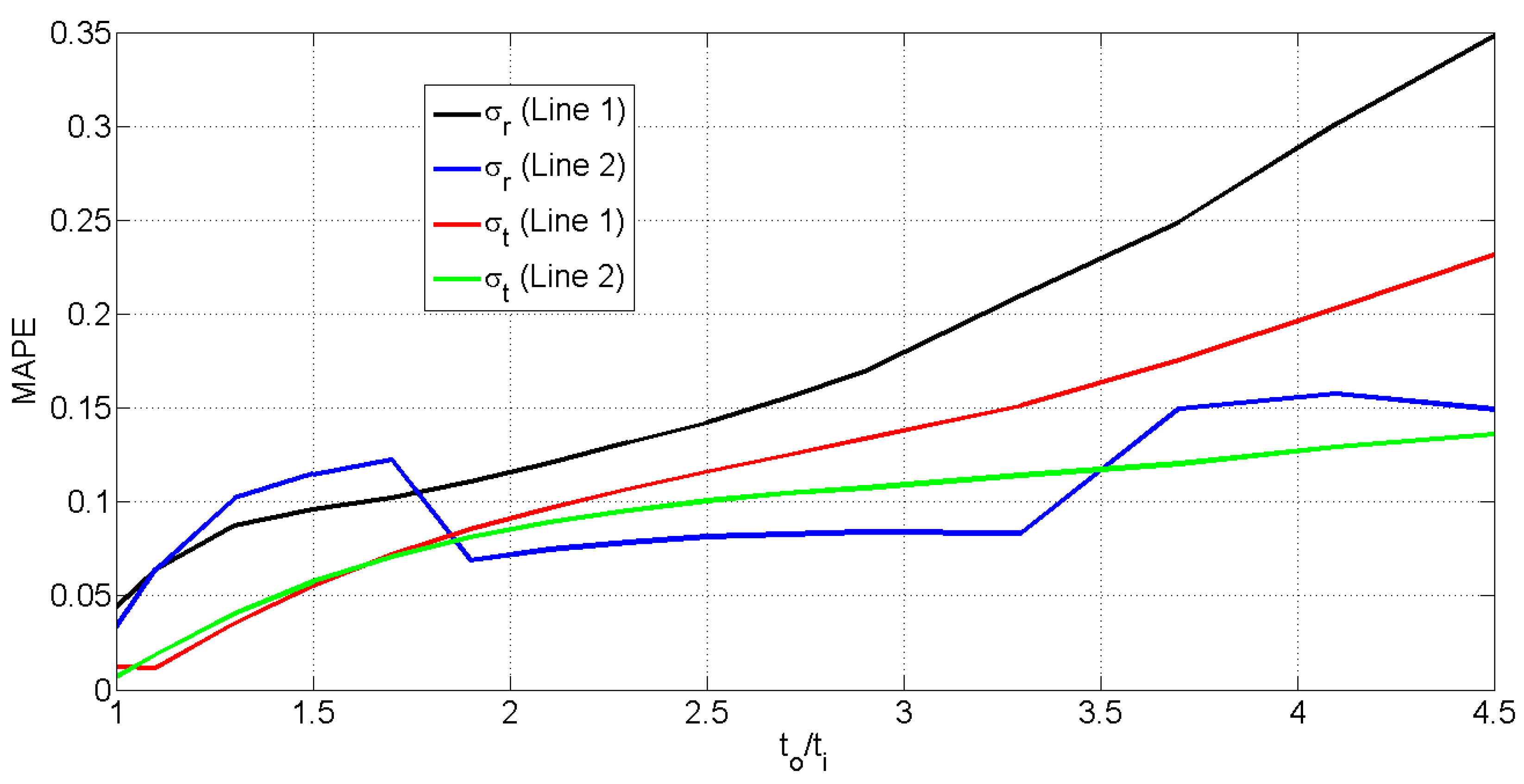
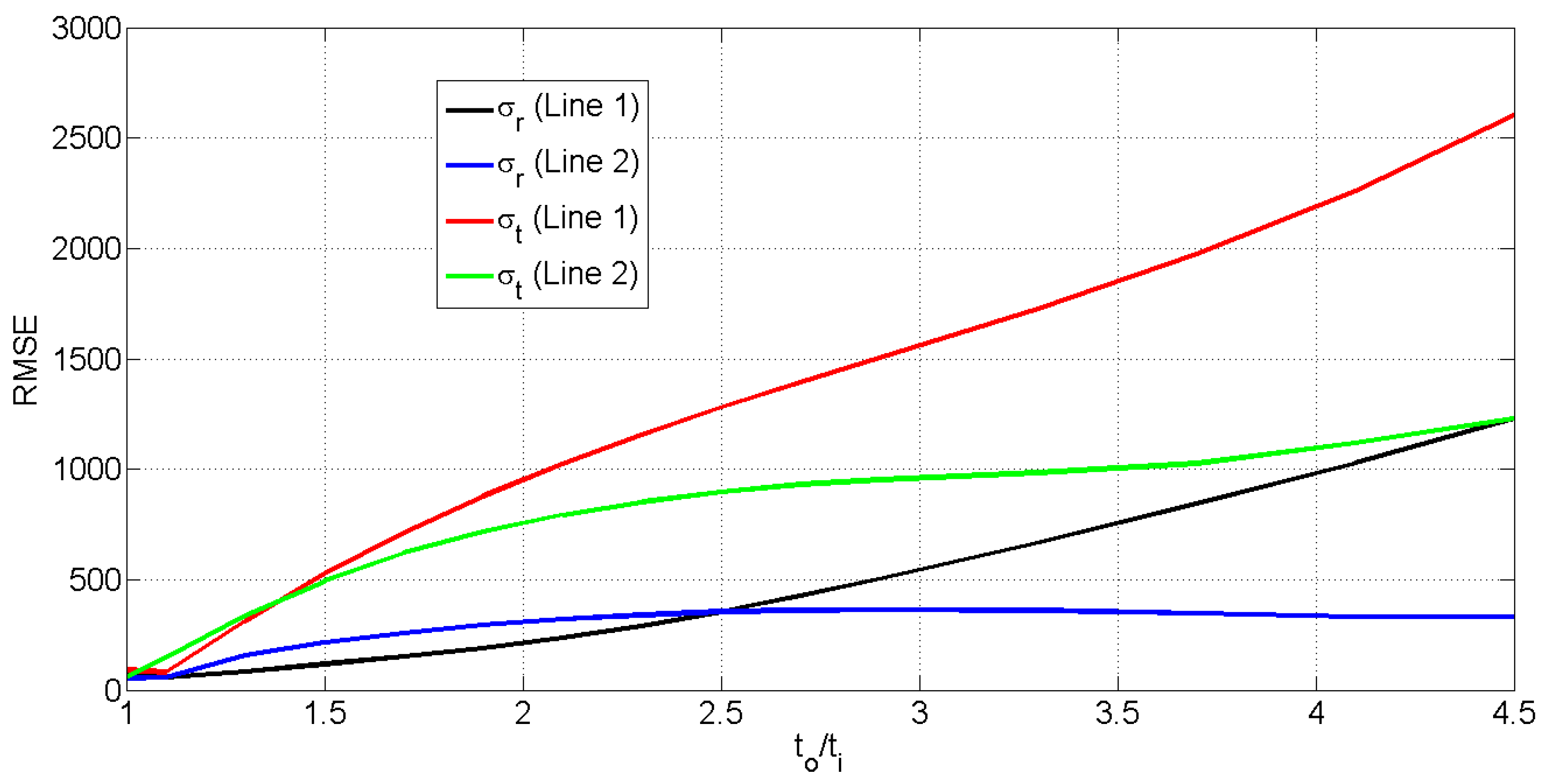
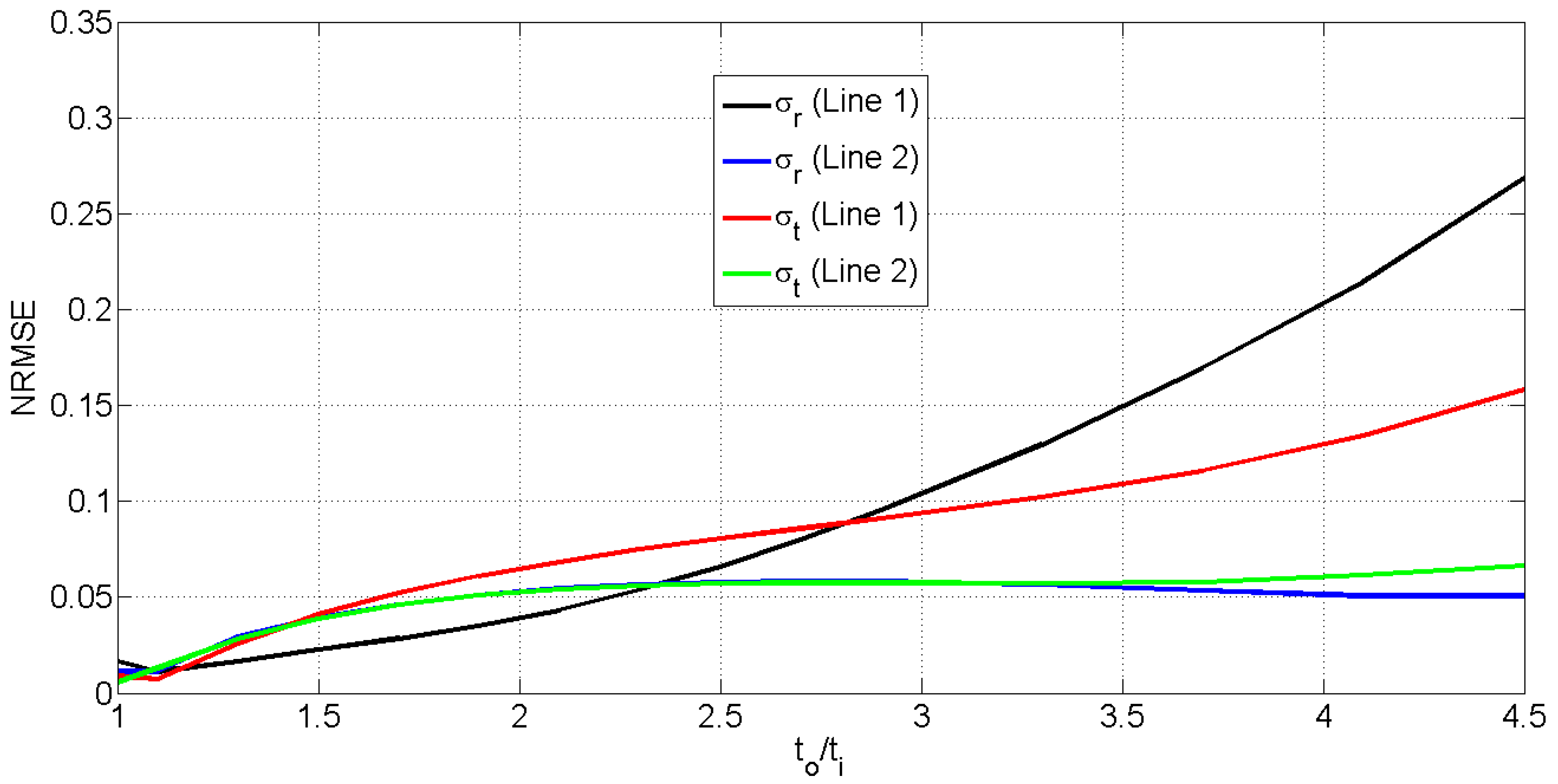
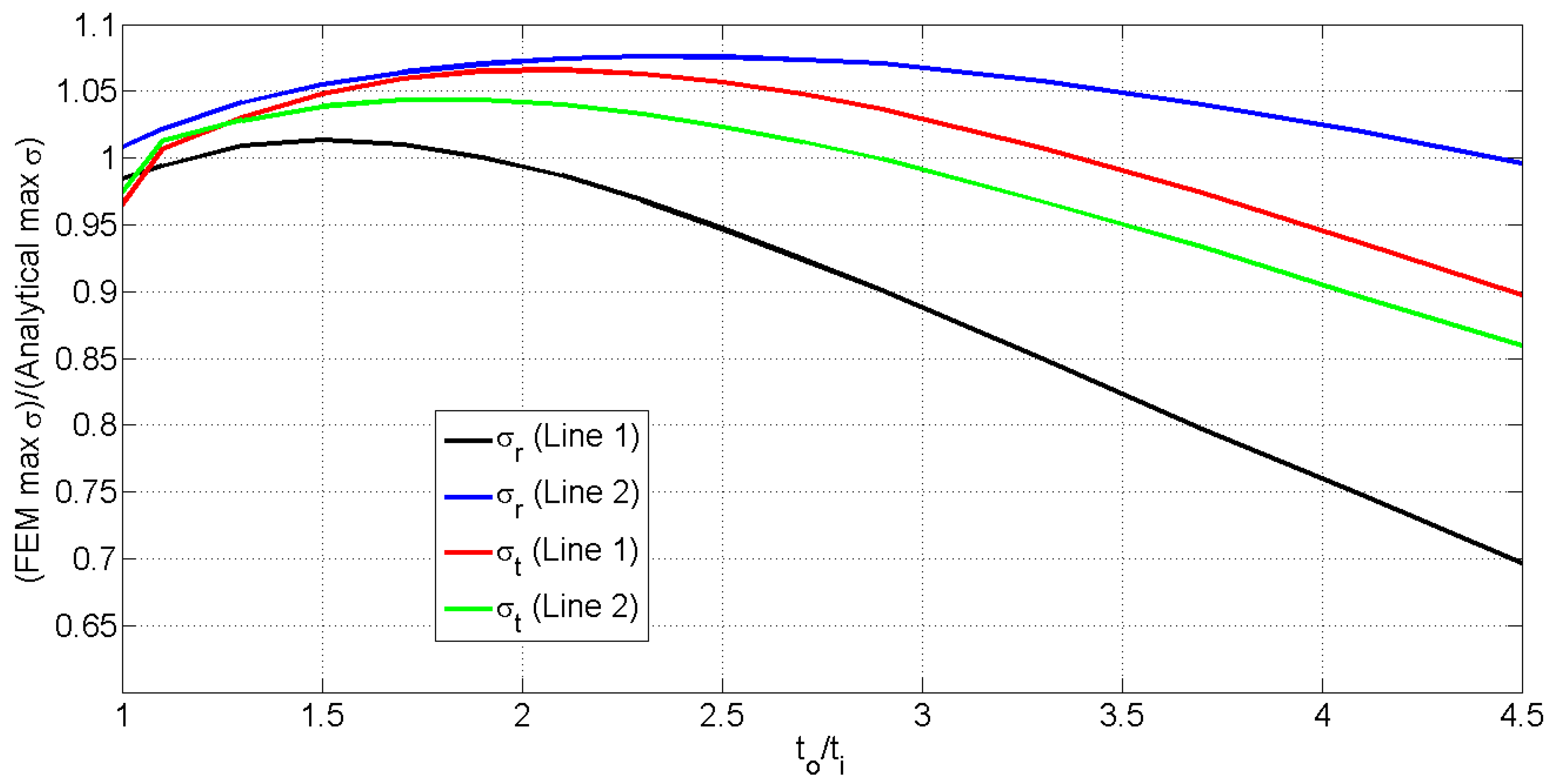
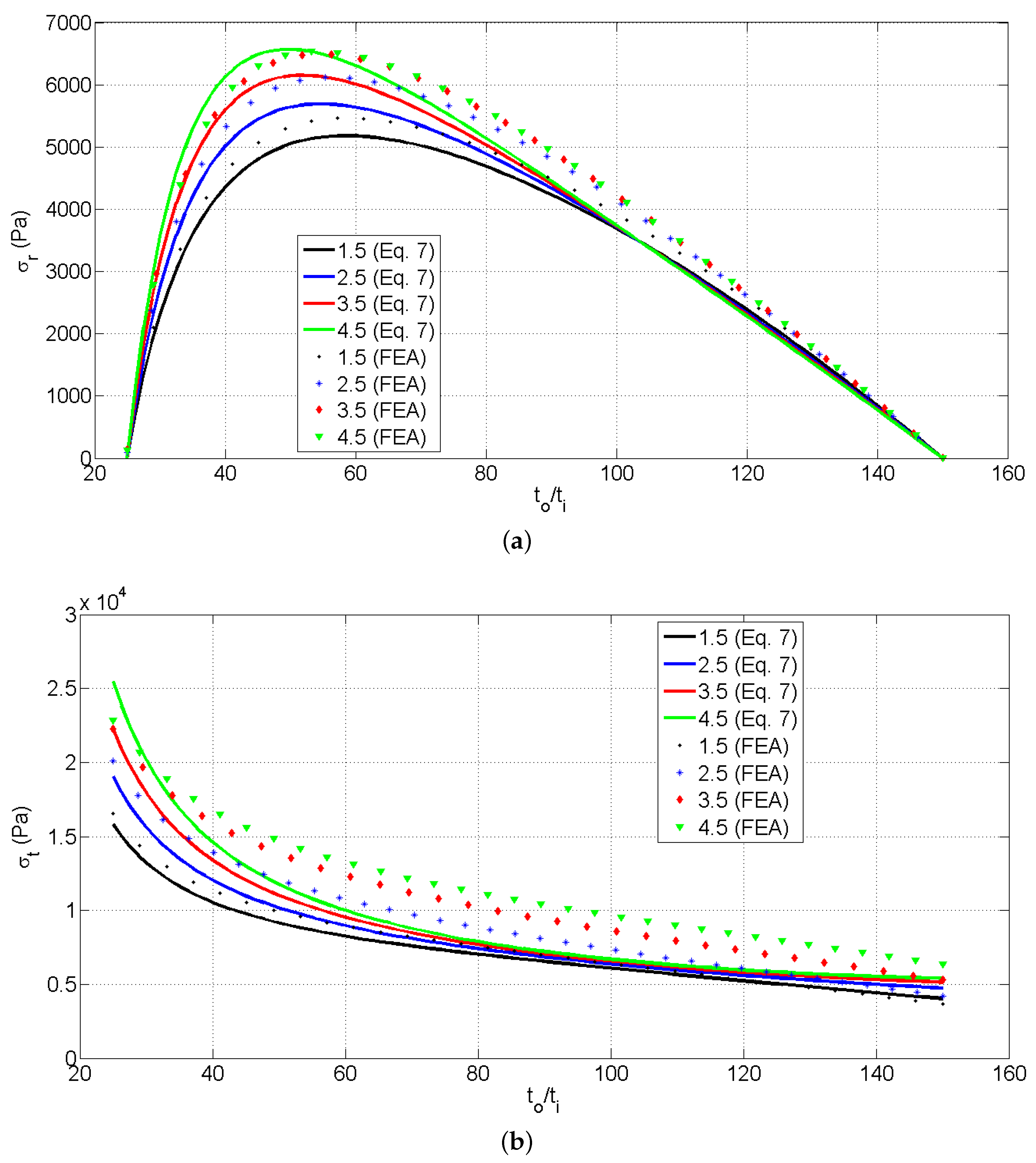
| Parameter | Numerical Value |
|---|---|
| 25 mm | |
| 150 mm | |
| 0.3 | |
| 7850 kg/m3 | |
| 9.84 rad/s |
| Parameter | Numerical Value |
|---|---|
| 25 mm | |
| 150 mm | |
| 0.3 | |
| 50 mm | |
| 55 mm | |
| 7850 kg/m3 | |
| 9.84 rad/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia, M.; Orozco-López, O.; Uribe-Chavira, J.; Blanco-Ortega, A. An Analytical Approximation of the Stress Function for Conical Flywheels. Appl. Mech. 2025, 6, 30. https://doi.org/10.3390/applmech6020030
Garcia M, Orozco-López O, Uribe-Chavira J, Blanco-Ortega A. An Analytical Approximation of the Stress Function for Conical Flywheels. Applied Mechanics. 2025; 6(2):30. https://doi.org/10.3390/applmech6020030
Chicago/Turabian StyleGarcia, Miguel, Onofre Orozco-López, Jesús Uribe-Chavira, and Andrés Blanco-Ortega. 2025. "An Analytical Approximation of the Stress Function for Conical Flywheels" Applied Mechanics 6, no. 2: 30. https://doi.org/10.3390/applmech6020030
APA StyleGarcia, M., Orozco-López, O., Uribe-Chavira, J., & Blanco-Ortega, A. (2025). An Analytical Approximation of the Stress Function for Conical Flywheels. Applied Mechanics, 6(2), 30. https://doi.org/10.3390/applmech6020030