Coupled Electrochemical-Thermal Simulations and Validation of Minichannel Cold-Plate Water-Cooled Prismatic 20 Ah LiFePO4 Battery
Abstract
:1. Introduction and Literature
2. Experimental Test Bench for Battery with Cold-Plates
3. Mathematical and Numerical Modelling
3.1. Li-ion (P2D) Battery Model
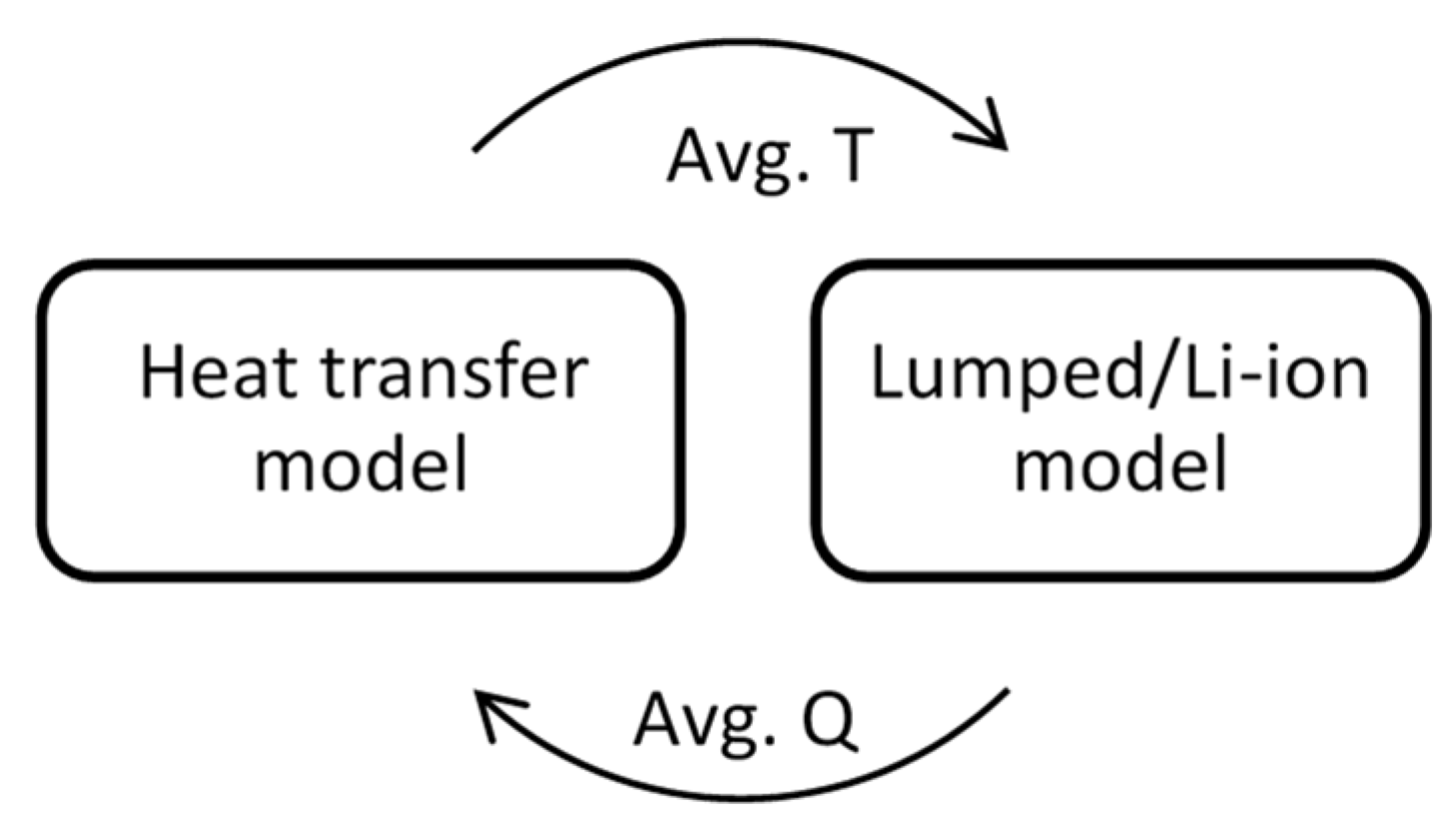
3.2. Conjugate Heat Transfer Model
- -
- Mass conservation equation:
- -
- Momentum conservation equation:where is velocity vector, is pressure, and are density and viscosity of coolant, respectively.
- -
- Energy conservation equation:where is thermal conductivity, is specific heat, is volumetric heat generation rate in the battery, and is battery volume.
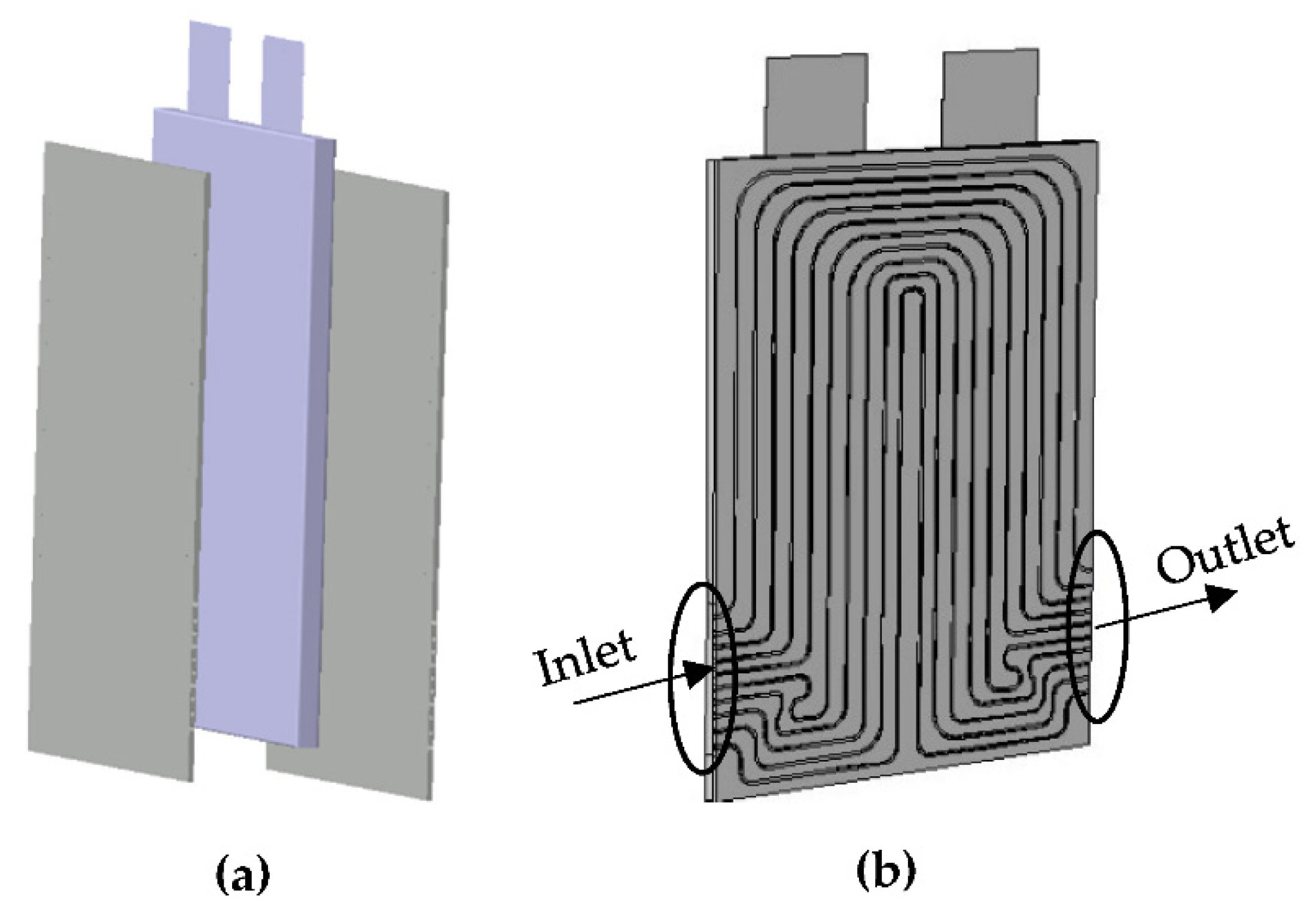
3.3. Geometry and Mesh
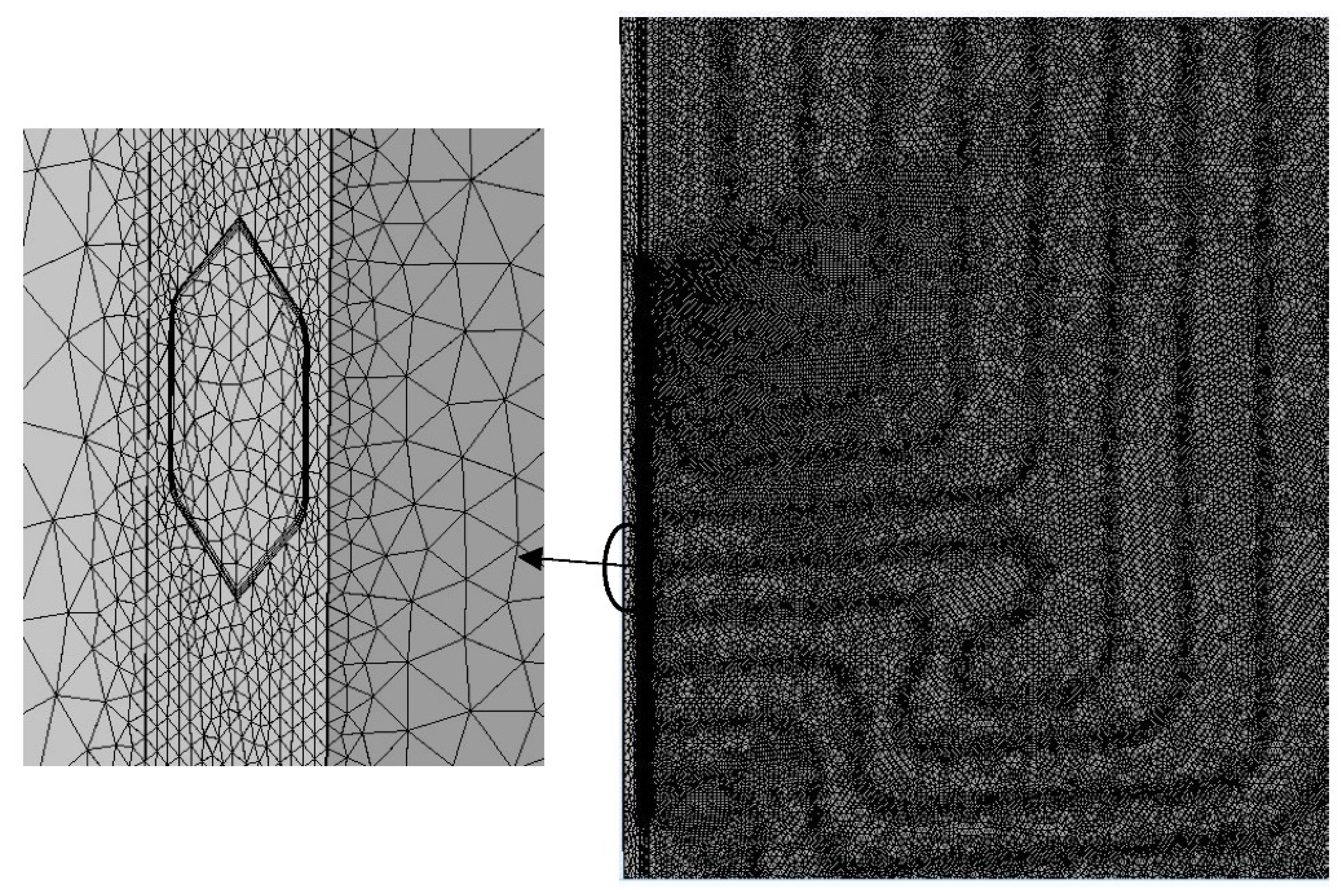
3.4. Grid Independence Study
4. Results and Discussion
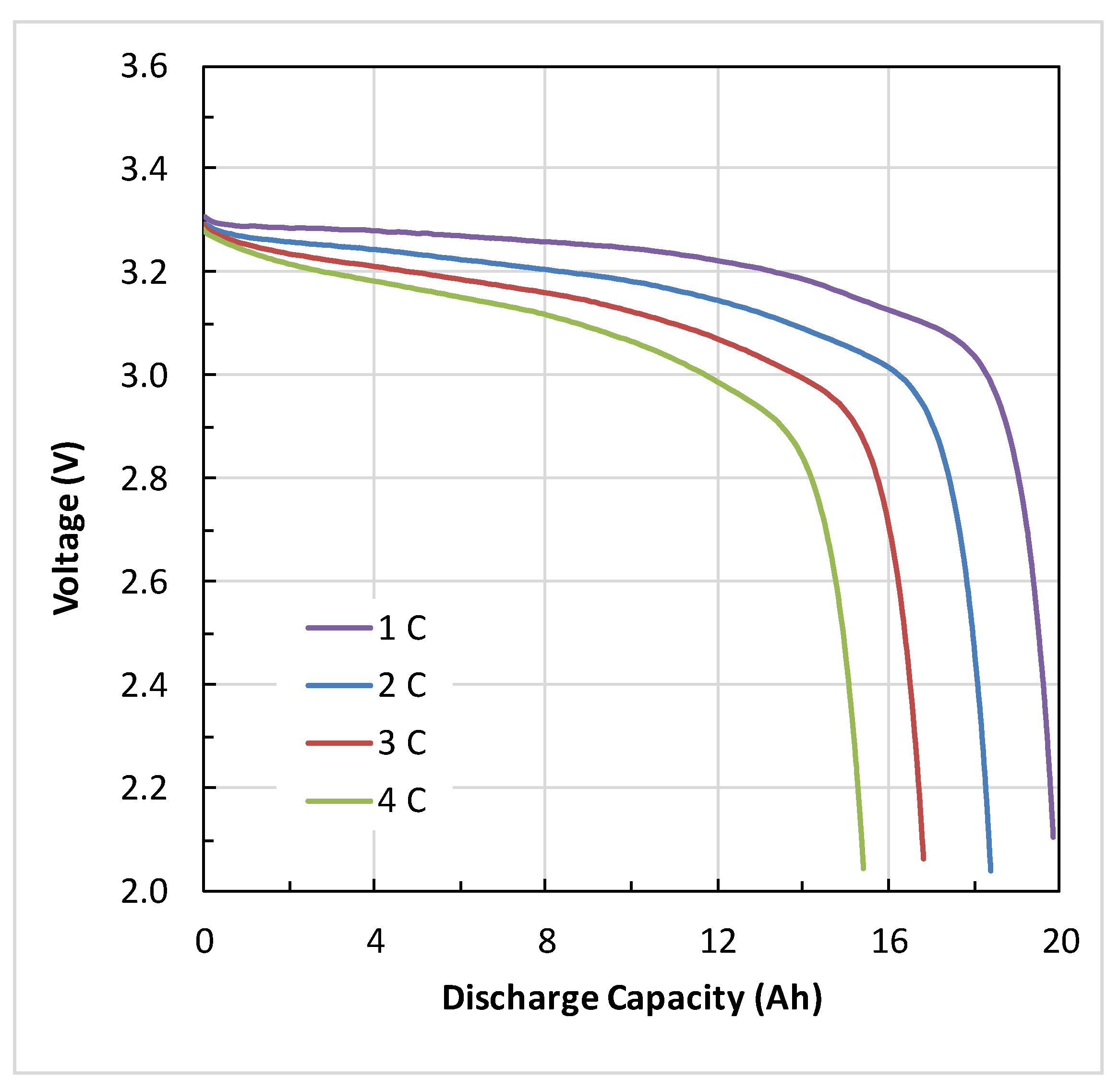
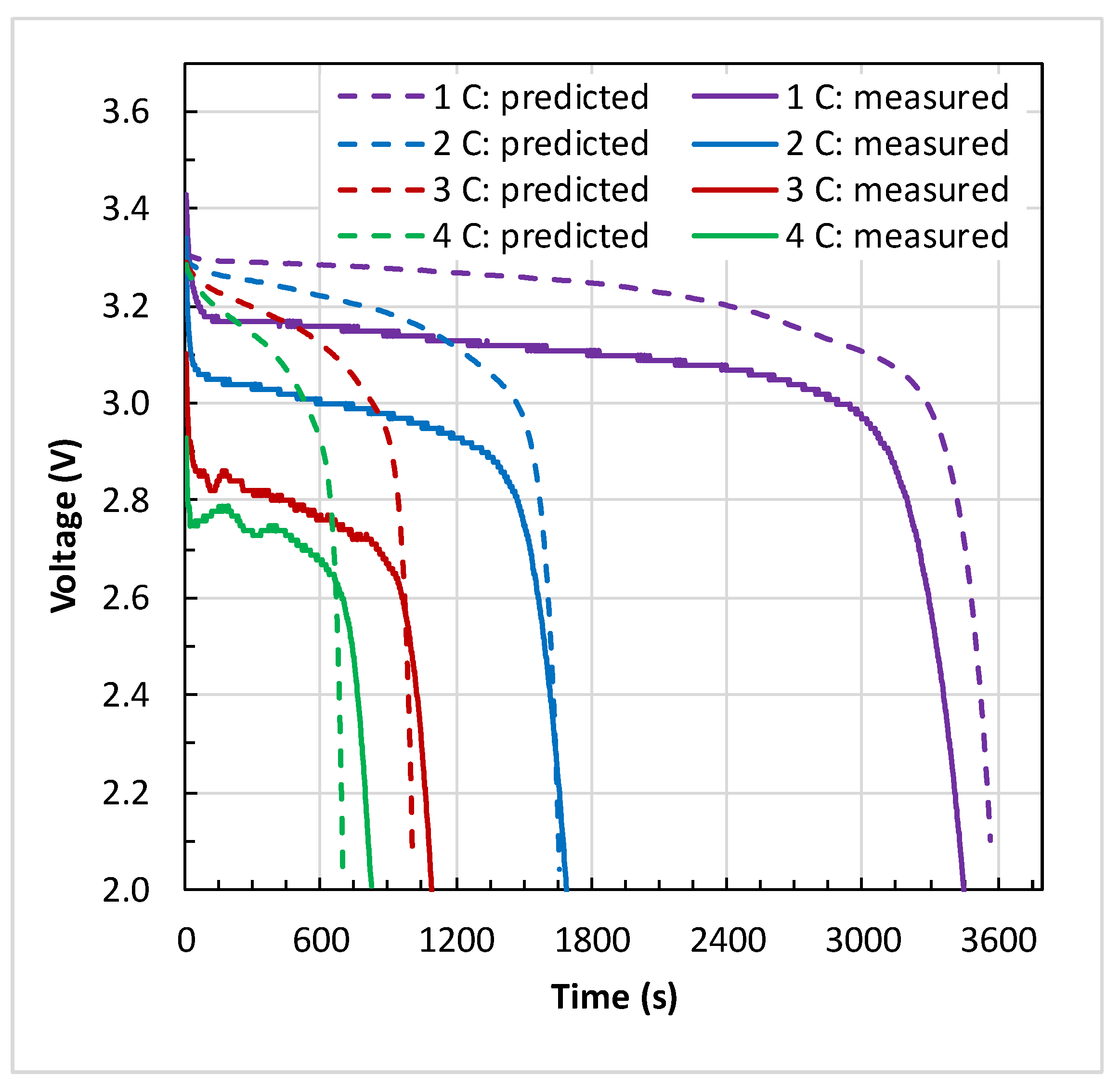
4.1. Battery Electrical Response
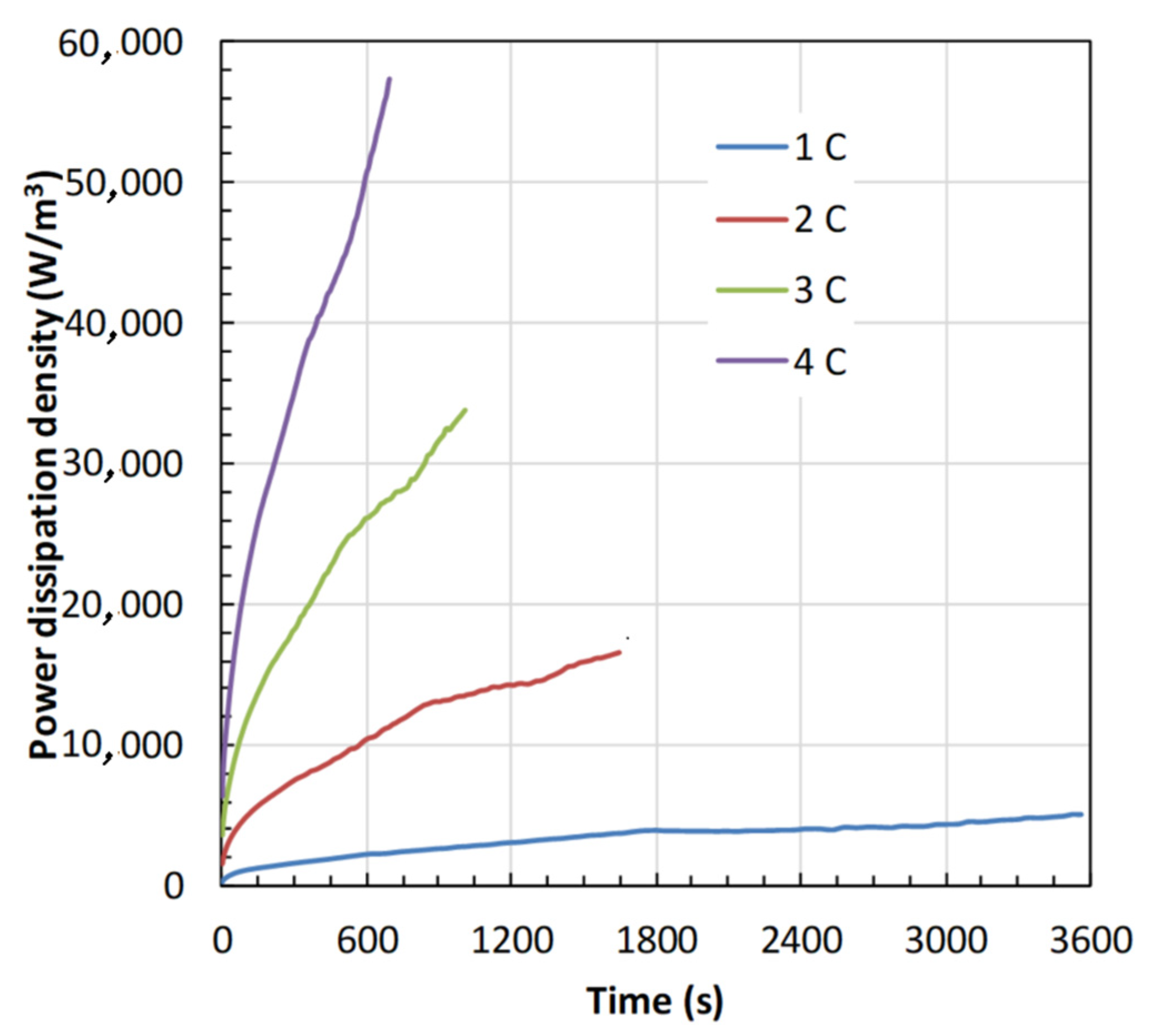
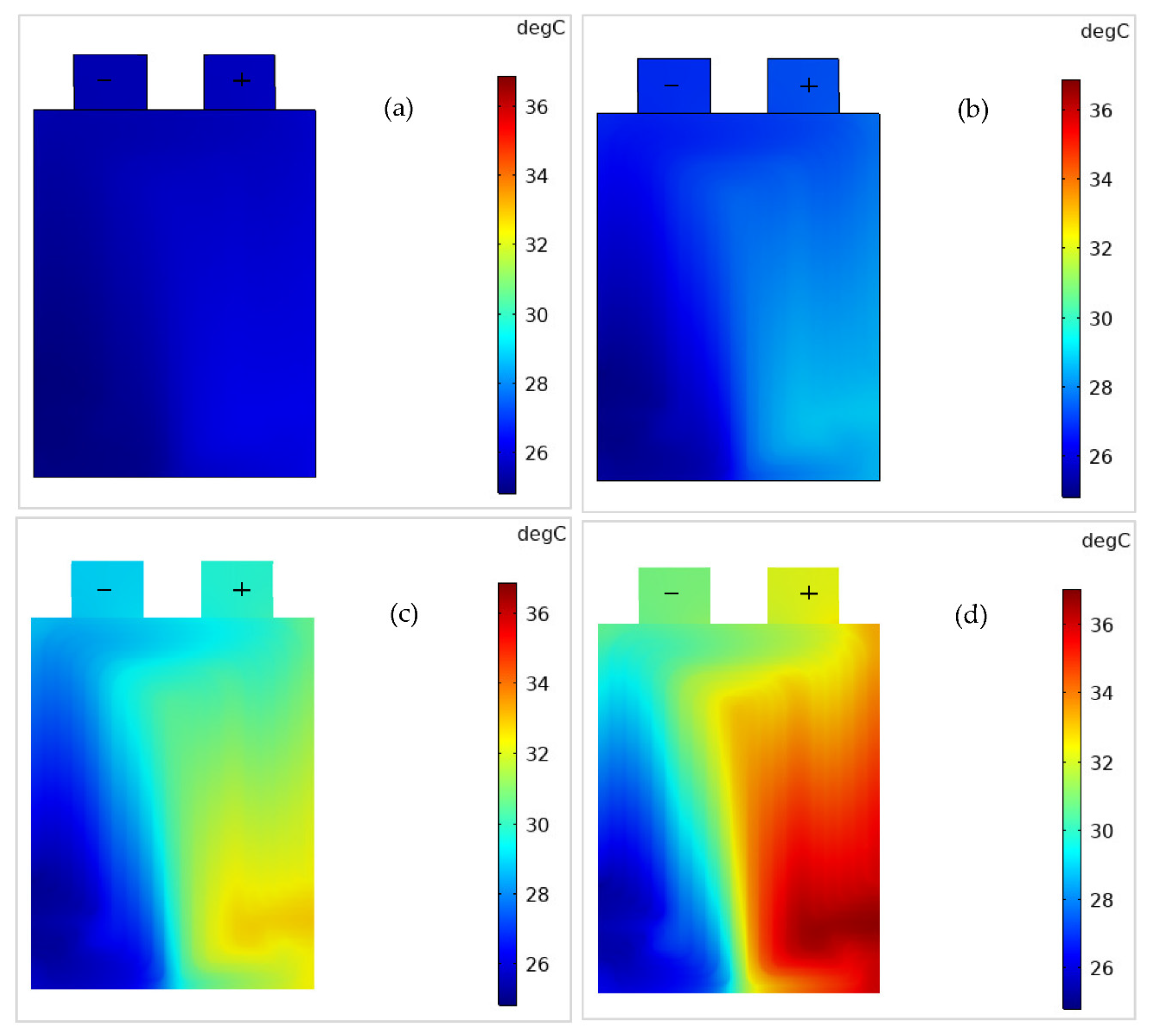
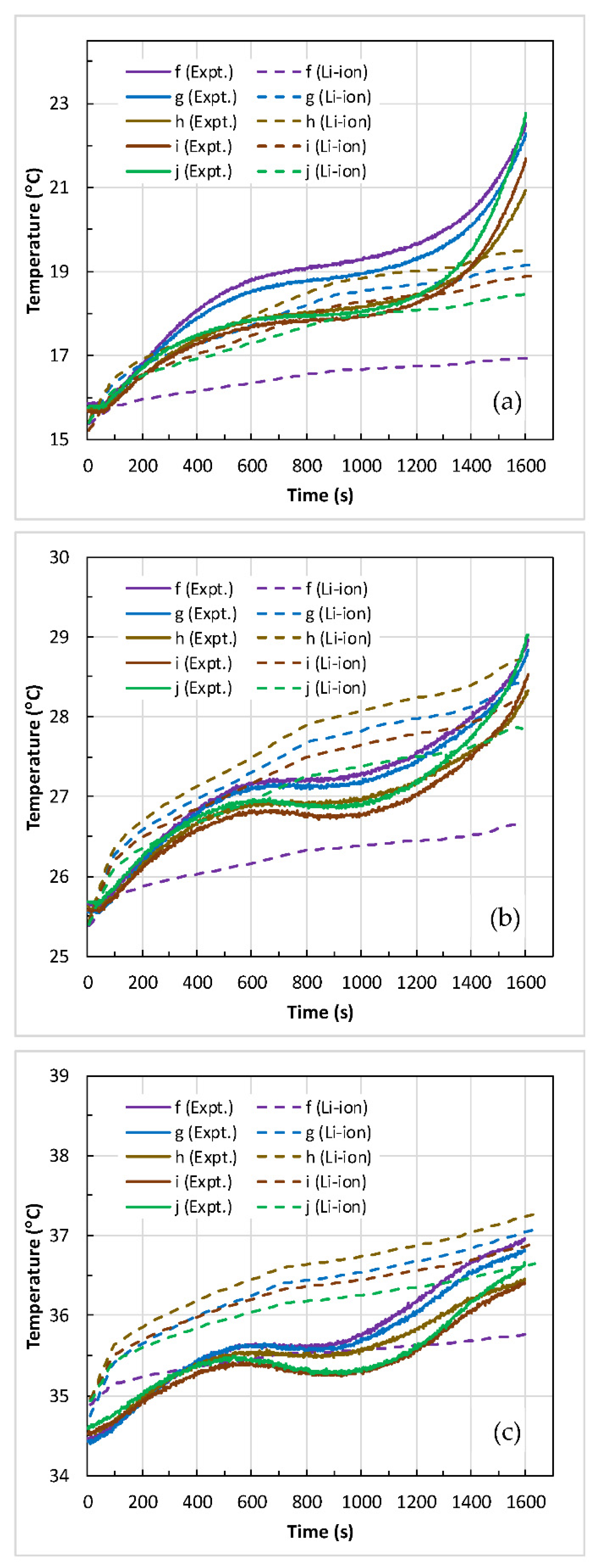
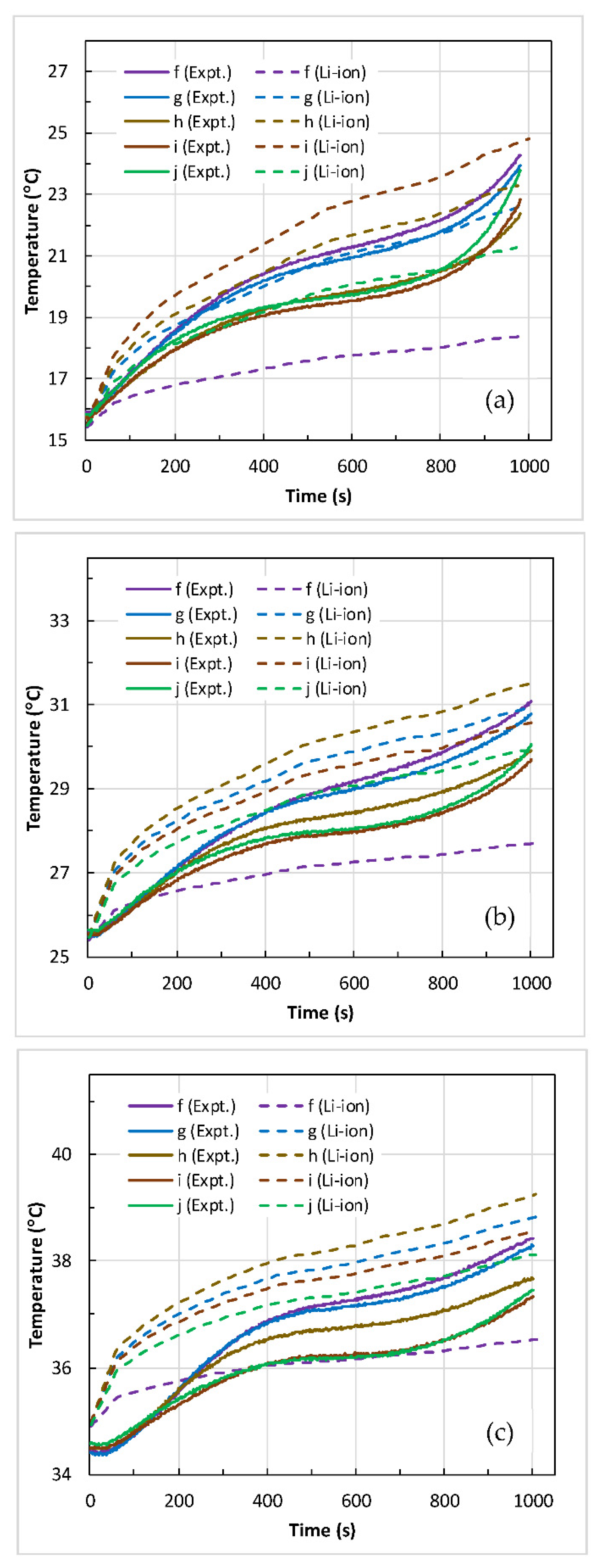
4.2. Battery Thermal Response
- The maximum temperature () and the temperature difference () across the battery surface rose with an increase in discharge C-rate at the given coolant inlet temperature (). At medium coolant inlet (25 °C), and at all C-rates, the predicted values of and are in good agreement with the measured values.
- At low coolant inlet (15 °C), the Li-ion model under-predicted the values of and at 1 C and 2 C. However, at high coolant inlet (35 °C), the model slightly over-predicted the values and at 4 C in comparison to the measured values.
- Furthermore, the percentage difference between the predicted and measured values of maximum surface temperature at all C-rates are within 2.6% at high coolant inlet (35 °C), within 4.8% at medium coolant inlet (25 °C), and within 14.6% at low coolant inlet (15 °C).
5. Summary
- Both and increase with an increase in the C-rate, and the rise in is high at low in contrast to high , and is attributed to more heat generation at low .
- increases linearly with an increase in . However, is more (i.e., non-uniformity) at low than at high .
- Predicted temperatures are in close agreement with the measured data at 3 C discharge rate. However, at low C-rates (1–2 C) the model slightly under-predicted the temperatures and slightly over-predicted at high C-rate (4 C).
- The current BTMS shows best performance meeting the desired operating range () at nominal discharge capacity (1 C) and at all coolant temperatures studied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xia, G.; Cao, L.; Bi, G. A review on battery thermal management in electric vehicle application. J. Power Sources 2017, 367, 90–105. [Google Scholar] [CrossRef]
- Shabani, B.; Biju, M. Theoretical modelling methods for thermal management of batteries. Energies 2015, 8, 10153–10177. [Google Scholar] [CrossRef]
- Xie, Y.; Shi, S.; Tang, J.; Wu, H.; Yu, J. Experimental and analytical study on heat generation characteristics of a lithium-ion power battery. Int. J. Heat Mass Transf. 2018, 122, 884–894. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.; Du, S.; Ai, L.; Ai, L.; Cheng, Y.; Tang, Y.; Jia, M. Insight into heat generation of lithium-ion batteries based on the electrochemical-thermal model at high discharge rates. Int. J. Hydrogen Energy 2015, 40, 13039–13049. [Google Scholar] [CrossRef]
- Liu, G.; Ouyang, M.; Lu, L.; Li, J.; Han, X. Analysis of the heat generation of lithium-ion battery during charging and discharging considering different influencing factors. J. Therm. Anal. Calorim. 2014, 116, 1001–1010. [Google Scholar] [CrossRef]
- Samba, A.; Omar, N.; Gualous, H.; Firouz, Y.; Van den Bossche, P.; Van Mierlo, J.; Boubekeur, T.I. Development of an advanced two-dimensional thermal model for large size lithium-ion pouch cells. Electrochim. Acta 2014, 117, 246–254. [Google Scholar] [CrossRef]
- Jiang, F.; Peng, P.; Sun, Y. Thermal analyses of LiFePO4/graphite battery discharge processes. J. Power Sources 2014, 243, 181–194. [Google Scholar] [CrossRef]
- Chen, K.; Unsworth, G.; Li, X. Measurements of heat generation in prismatic Li-ion batteries. J. Power Sources 2014, 261, 28–37. [Google Scholar] [CrossRef]
- Drake, S.J.; Martin, M.; Wetz, D.A.; Ostanek, J.K.; Miller, S.P.; Heinzel, J.M.; Jain, A. Heat generation rate measurement in a Li ion cell at large C-rates through temperature and heat flux measurements. J. Power Sources 2015, 285, 266–273. [Google Scholar] [CrossRef]
- Neupane, S.; Alipanah, M.; Barnes, D.; Li, X. Heat generation characteristics of LiFePO4 pouch cells with passive thermal management. Energies 2018, 11, 1243. [Google Scholar] [CrossRef] [Green Version]
- Schuster, E.; Ziebert, C.; Melcher, A.; Rohde, M.; Seifert, H.J. Thermal behaviour and electrochemical heat generation in a commercial 40 Ah lithium-ion pouch cell. J. Power Sources 2015, 286, 580–589. [Google Scholar] [CrossRef]
- Zhao, C.; Cao, W.; Dong, T.; Jiang, F. Thermal behavior study of discharging/charging cylindrical lithium-ion battery module cooled by channelled liquid flow. Int. J. Heat Mass Transf. 2018, 120, 751–762. [Google Scholar] [CrossRef]
- Bahiraei, F.; Ghalkhani, M.; Fartaj, A.; Nazri, G. A pseudo 3D electrochemical-thermal modeling and analysis of a lithium-ion battery for electric vehicle thermal management applications. Appl. Therm. Eng. 2017, 125, 904–918. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dubé, Y. A comprehensive review of lithium-ion batteries used in hybrid and electric vehicles at cold temperatures. Appl. Energy 2016, 164, 99–114. [Google Scholar] [CrossRef]
- Chalise, D.; Shah, K.; Halama, T.; Komsiyska, L.; Jain, A. An experimentally validated method for temperature prediction during cyclic operation of a Li-ion cell. Int. J. Heat Mass Transf. 2017, 112, 89–96. [Google Scholar] [CrossRef]
- Munoz, P.M.; Humana, R.M.; Falaguerra, T.; Correa, G. Parameter optimization of an electrochemical and thermal model for a lithium-ion commercial battery. J. Energy Storage 2020, 13, 100387. [Google Scholar] [CrossRef]
- An, Z.; Jia, L.; Wei, L.; Dang, C.; Peng, Q. Investigation on lithium-ion battery electrochemical and thermal characteristic based on electrochemical-thermal coupled mode. Appl. Therm. Eng. 2018, 137, 792–807. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, C.; Jiaqiang, E.; Zhua, H.; Chena, J.; Wen, M.; Yin, H. Effects of different coolants and cooling strategies on the cooling performance of the power lithium ion battery system: A review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar] [CrossRef]
- Arora, S. Selection of thermal management system for modular battery packs of electric vehicles: A review of existing and emerging technologies. J. Power Sources 2018, 400, 621–640. [Google Scholar] [CrossRef]
- Han, T.; Khalighi, B.; Yen, E.C.; Kaushik, S. Li-ion battery pack thermal management: Liquid vs. air cooling. J. Therm. Sci. Eng. Appl. 2019, 11, 021009. [Google Scholar] [CrossRef]
- Panchal, S.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Experimental and theoretical investigation of temperature distributions in a prismatic lithium-ion battery. Int. J. Therm. Sci. 2016, 99, 204–212. [Google Scholar] [CrossRef]
- Panchal, S.; Khasow, R.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Numerical modelling and experimental investigation of a prismatic battery subjected to water cooling. Numer. Heat Transf. A 2017, 17, 626–637. [Google Scholar] [CrossRef]
- Malika, M.; Dincer, I.; Rosen, M.A.; Mathew, M.; Fowler, M. Thermal and electrical performance evaluations of series connected Li-ion batteries in a pack with liquid cooling. Appl. Therm. Eng. 2018, 129, 472–481. [Google Scholar] [CrossRef]
- Basu, S.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Sohn, D.K.; Yeo, T. Coupled electrochemical thermal modelling of a novel Li-ion battery pack thermal management system. Appl. Energy 2016, 181, 1–13. [Google Scholar] [CrossRef]
- Chalise, D.; Shah, K.; Prasher, R.; Jain, A. Conjugate heat transfer analysis of thermal management of a li-ion battery pack. Trans. ASME J. Electrochem. Energy Convers. Storage 2018, 15, 011008. [Google Scholar] [CrossRef] [Green Version]
- Lan, C.; Xu, J.; Qiao, Y.; Ma, Y. Thermal management for high power lithium-ion battery by mini channel aluminum tubes. Appl. Therm. Eng. 2016, 101, 284–292. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Li, C.; Cui, N. Experimental investigation of water-cooling based thermal management for cylindrical li-ion batteries. In Proceedings of the IEEE 3rd Conference on Vehicle Control and Intelligence (CVCI), Hefei, China, 21–22 September 2019. [Google Scholar] [CrossRef]
- Huo, Y.; Rao, Z.; Liu, X.; Zhao, J. Investigation of power battery thermal management by using mini-channel cold plate. Energy Convers. Manag. 2015, 89, 387–395. [Google Scholar] [CrossRef]
- Alipoura, M.; Esena, E.; Kizilelb, R. Investigation of 3-D multi-layer approach in predicting the thermal behavior of 20 Ah Li-ion cells. Appl. Therm. Eng. 2019, 153, 620–632. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Peng, Q.; Zhang, C. A brief review on key technologies in the battery management system of electric vehicles. Front. Mech. Eng. 2019, 14, 47–64. [Google Scholar] [CrossRef] [Green Version]
- Panchal, S. Experimental Investigation and Modeling of Lithium-Ion Battery Cells and Packs for Electric Vehicles. Ph.D. Thesis, University of Ontario Institute of Technology, Oshawa, ON, Canada, 2016. Available online: http://ir.library.dc-uoit.ca/handle/10155/747 (accessed on 10 February 2021).
- Panchal, S. Impact of Vehicle Charge and Discharge Cycles on the Thermal Characteristics of Lithium-Ion Batteries. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2014. Available online: http://hdl.handle.net/10012/8423 (accessed on 10 February 2021).
- Battery Design Module User’s Guide, COMSOL Multiphysics® v.5.6; COMSOL AB: Stockholm, Sweden, 2020; pp. 231–371. Available online: https://doc.comsol.com/5.6/doc/com.comsol.help.battery/BatteryDesignModuleUsersGuide.pdf (accessed on 10 February 2021).
- Panchal, S.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Transient electrochemical heat transfer modelling and experimental validation of a large sized LiFePO4/graphite battery. Int. J. Heat Mass Transf. 2017, 109, 1239–1251. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.; Panchal, S.; Jee, S.; Lee, M. Investigation on thermal performance of water-cooled Li-ion pouch cell and pack at high discharge rate with U-turn type microchannel cold plate. Int. J. Heat Mass Transf. 2020, 155, 119728. [Google Scholar] [CrossRef]



| Discharge C-Rate | Maximum Surface Temperature (°C) | ||
|---|---|---|---|
| 3.5 Million Mesh Elements | 4.2 Million Mesh Elements | 5.4 Million Mesh Elements | |
| 1 C | 17.00 | 16.75 | 16.74 |
| 2 C | 19.90 | 19.56 | 19.50 |
| 3 C | 23.82 | 22.67 | 22.65 |
| Material Property (Unit) | Positive Electrode | Negative Electrode |
|---|---|---|
| Solid phase lithium diffusivity (m2/s) | 1 × 10−13 | 3.9 × 10−14 |
| Particle radius (m) | 12.5 × 10−6 | 8 × 10−6 |
| Electrolyte phase volume fraction | 0.444 | 0.357 |
| Electrode phase volume fraction | 0.297 | 0.471 |
| Filler phase volume fraction | 0.259 | 0.172 |
| Max solid phase concentration (mol/m3) | 22,806 | 31,370 |
| Initial concentration of active material (mol/m3) | 14,870 | 14,870 |
| Solid phase conductivity (S/m) | 3.8 | 100 |
| Thickness (µm) | 183 | 117 |
| Other data | ||
| Initial electrolyte salt concentration (mol/m3) | 1000 | |
| Bruggeman coefficient | 1 | |
| Thickness of separator (µm) | 52 | |
| Material/Property | Density (kg/m3) | Thermal Conductivity (W/m-K) | Specific Heat (J/kg-K) |
|---|---|---|---|
| Active battery | 2092 | 18.2 | 678 |
| Positive tab | 2719 | 202.0 | 871 |
| Negative tab | 8978 | 387.6 | 381 |
| Cold-plate | 2702 | 237.0 | 903 |
| Water Inlet T (°C) | Discharge C-Rate | Maximum Battery Surface Temperature, Tmax (°C) | Battery Surface Temperature Difference, ΔT | ||
|---|---|---|---|---|---|
| Experiments | Li-ion Model | Experiments | Li-ion Model | ||
| 15 | 1 C | 19.6 | 16.74 | 4.0 | 1.74 |
| 15 | 2 C | 22.9 | 20.46 | 7.3 | 5.46 |
| 15 | 3 C | 25.4 | 25.49 | 9.8 | 10.49 |
| 15 | 4 C | 28.0 | 31.14 | 12.4 | 16.14 |
| 25 | 1 C | 27.6 | 26.44 | 3.1 | 1.44 |
| 25 | 2 C | 30.4 | 29.3 | 5.9 | 4.3 |
| 25 | 3 C | 32.6 | 33.02 | 8.1 | 8.02 |
| 25 | 4 C | 35.2 | 36.88 | 10.7 | 11.88 |
| 35 | 1 C | 35.9 | 36.13 | 2.4 | 1.13 |
| 35 | 2 C | 38.2 | 38.15 | 4.7 | 3.15 |
| 35 | 3 C | 40.3 | 40.17 | 6.8 | 5.17 |
| 35 | 4 C | 42.3 | 43.38 | 8.8 | 8.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akkaldevi, C.; Chitta, S.D.; Jaidi, J.; Panchal, S.; Fowler, M.; Fraser, R. Coupled Electrochemical-Thermal Simulations and Validation of Minichannel Cold-Plate Water-Cooled Prismatic 20 Ah LiFePO4 Battery. Electrochem 2021, 2, 643-663. https://doi.org/10.3390/electrochem2040040
Akkaldevi C, Chitta SD, Jaidi J, Panchal S, Fowler M, Fraser R. Coupled Electrochemical-Thermal Simulations and Validation of Minichannel Cold-Plate Water-Cooled Prismatic 20 Ah LiFePO4 Battery. Electrochem. 2021; 2(4):643-663. https://doi.org/10.3390/electrochem2040040
Chicago/Turabian StyleAkkaldevi, Chaithanya, Sandeep Dattu Chitta, Jeevan Jaidi, Satyam Panchal, Michael Fowler, and Roydon Fraser. 2021. "Coupled Electrochemical-Thermal Simulations and Validation of Minichannel Cold-Plate Water-Cooled Prismatic 20 Ah LiFePO4 Battery" Electrochem 2, no. 4: 643-663. https://doi.org/10.3390/electrochem2040040
APA StyleAkkaldevi, C., Chitta, S. D., Jaidi, J., Panchal, S., Fowler, M., & Fraser, R. (2021). Coupled Electrochemical-Thermal Simulations and Validation of Minichannel Cold-Plate Water-Cooled Prismatic 20 Ah LiFePO4 Battery. Electrochem, 2(4), 643-663. https://doi.org/10.3390/electrochem2040040








