Modelling of Biotrickling Filters for Treatment of NOx Analytical Expressions for the NOx Concentration in Both Gas and Biofilm Phases
Abstract
:1. Introduction
2. Mathematical Formulation of the Problem
- The biofilm can be perceived as a planar surface owing to the radius of the packing particles, which is comparatively larger than the biofilm’s thickness; the gas flows through the crammed layer in a parallel pattern through a series of vertical channels;
- The gas phase is moved in a plug flow manner, with no consideration for axial diffusion. Molecule diffusion is used to transport NO in biofilms;
- The rate-limiting substrate is NO. Therefore, there is no depletion of oxygen or nutrients. It has been proven that the amount of oxygen in the environment is considered in excess, and hence the reaction of NO and molecular oxygen is pseudo-second-order in terms of the NO concentration;
- The consistent properties of the biofilm across the reactor and negligible biomass production in the packing materials result in a stable value of the biofilm kinetic constants. Here, the biofilm growth is depicted by Monod growth kinetics;
- Inside the biofilm, only one direction of diffusion/reaction occurs, which is perpendicular to the gas–biofilm boundary. Oxygen in the gas phase influences the partial oxidation of NO to NO2 and swiftly forms nitrates or nitrates by dissolving in water;
- Because of oxygen in the gas phase, NO is partially oxidized to NO2 and quickly dissolved in water to yield nitrite or nitrate. This portion of nitric oxide that has been converted to aqueous nitrogen compounds will not return to the gas phase, so it can be considered to be removed from the gas phase. In fact, nitrite or nitrate in water could be rapidly denitrified to N2 by denitrifiers.
2.1. Mass Balance in the Gas Phase
2.2. Mass Balance Equation in the Biofilm Phase
2.3. Dimensionless Form
3. Approximate Analytical Expression of the Concentration Using the Akbari–Ganji Method
4. Removal Efficiency of Nitric Oxide
5. Previous Analytical Results
6. Numerical Simulation
7. Results and Discussion
Limitation of This Model
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Description | Units |
| Specific surface area of the biofilm | ||
| a0 | Specific surface area of the medium | cm−1 |
| Cg | concentration in the gas phase | |
| concentration in the biofilm phase | ||
| Inlet concentration | ||
| Dimensionless concentration in the gas phase | None | |
| Dimensionless concentration in the biofilm phase | None | |
| Effective diffusion coefficient in the biofilm | ||
| Henry constant | None | |
| Monod half-saturation constant | ||
| Reaction rate constant | cm3 g−1 s−1 | |
| Biofilm thickness | ||
| Initial concentration in the gas phase | None | |
| Final concentration in the gas phase | None | |
| removal ratio ( removal efficiency) | None | |
| Superficial gas velocity | ||
| Microbial density of the biofilm | ||
| Coordinate axis calculated from the surface of the biofilm | ||
| Dimensionless height calculated from the base of the packing material | None | |
| Yield coefficient of microorganisms | ||
| Height value calculated from the base of the packing materials | ||
| Dimensionless parameter | None | |
| Growth rate of biomass | ||
| Maximum specific growth rate of biomass | ||
| Porosity ratio of biofilm-covered packing materials | None | |
| Porosity of medium | None | |
| Dimensionless parameters | None |
Appendix A. Analytical Expression of Concentration of Biofilm and Gas Phase
Appendix B. Solution of Bernulli Type Equations
| Symbols | Description | Units | Experimental Values |
|---|---|---|---|
| Porosity of the medium | None | ||
| Specific surface area of the medium | |||
| Effective diffusion coefficient in the biofilm | 5.21 × | ||
| Biofilm thickness | 0.1 | ||
| Characteristic length of the vertical channels | |||
| Reaction rate constant | |||
| Monod half-saturation constant | |||
| Henry constant | None | ||
| Microbial density of the biofilm | 0−7 | ||
| Maximum specific substrate utilization rate | |||
| Superficial gas velocity | 0.8 to 2.4 | ||
| concentration in the gas phase | |||
| Inlet concentration | |||
| Specific surface area of the biofilm | |||
| Porosity ratio of biofilm-covered packing materials | None | ||
| Dimensionless parameter | None | 0.1121 | |
| Dimensionless parameter | None | 0.629 | |
| Dimensionless parameter | None | 0.0126 | |
| Dimensionless parameter | None | 10.5 |
| Dimensionless Parameter | Experimental Value of Parameters Used in [13] | Value of the Parameter Used in Figure 2, Figure 3 and Figure 4 and Table 1 | Value of the Parameter Used in Figure 5 |
|---|---|---|---|
| 0.1121 | 0.01 to 20 | 0.1121 | |
| 0.629 | 0.01 to 500 | 0.629 | |
| 0.0126 | 0.01 to 250 | 0.0126 | |
| 10.5 | 0.01 to 10 | 10.5 |
Appendix C. MATLAB Code for the Numerical Solution of the Non-Linear Equation (10)
| function pdex4 |
| m = 0; |
| x = linspace(0,1); |
| t = linspace(0,10); |
| sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t); |
| u1 = sol(:,:,1); |
| figure |
| plot(x,u1(end,:)) |
| title(‘u1(x,t)’) |
| xlabel(‘Distance x’) |
| ylabel(‘u1(x,2)’) |
| %-------------------------------------------------------------- |
| function [c,f,s] = pdex4pde(x,t,u,DuDx) |
| c = [1]; |
| f = [1].* DuDx; |
| Alpha = 0.5; |
| Beta = 0.5; |
| F = −((alpha^2)*u(1))/(1+beta*u(1)); |
| s=[F]; |
| % ------------------------------------------------------------- |
| function u0 = pdex4ic(x); |
| %create a initial conditions |
| u0 = [1]; |
| % ------------------------------------------------------------- |
| function [pl,ql,pr,qr]=pdex4bc(xl,ul,xr,ur,t) |
| %create a boundary conditions |
| pl = [ul(1)−1]; |
| ql = [0]; |
| pr = [0]; |
| qr = [1]; |
References
- Deshusses, M.A.; Shareefdeen, Z. Modeling of Biofilters and Biotrickling Filters for Odor and VOC Control Applications. In Biotechnology for Odor and Air Pollution Control; Shareefdeen, Z., Singh, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Kalantar, M.; Zamir, S.M.; Ferdowsi, M.; Shojaosadati, S.A. Removal of toluene in a biotrickling filter in the presence of methanol vapors: Experimental study, mathematical modeling, and kinetic parameters optimization. J. Environ. Chem. Eng. 2021, 9, 104617. [Google Scholar] [CrossRef]
- San-Valero, P.; Penya-Roja, J.M.; Alvarez-Hornos, F.J.; Marzal, P.; Gabaldón, C. Dynamic mathematical modelling of the removal of hydrophilic vocs by biotrickling filters. Int. J. Environ. Res. Public Health 2015, 12, 746–766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Apel, W.A.; Turick, C.E. Use of Denitrifying bacteria for the removal of nitrogen oxides from combustion gases. Fuel 1993, 72, 1715–1718. [Google Scholar] [CrossRef]
- Du Plessis, C.A.; Kinney, K.A.; Schroeder, E.D.; Chang, D.P.Y.; Scow, K.M. Denitrification and nitric oxide reduction in an aerobic toluene-treating biofilter. Biotechnol. Bioeng. 1998, 58, 408–415. [Google Scholar] [CrossRef]
- Zhao, J.; Xia, Y.; Li, M.; Li, S.; Li, W.; Zhang, S. A biophysicochemical model for no removal by the chemical absorption−biological reduction integrated process. Environ. Sci. Technol. 2016, 50, 8705–8712. [Google Scholar] [CrossRef]
- Bogner, W.; Krämer, M.; Krutzsch, B.; Pischinger, S.; Voigtländer, D.; Wenninger, G.; Wirbeleit, F.; Brogan, M.S.; Brisley, R.J.; Webster, D.E. Removal of nitrogen oxides from the exhaust of a lean-tune gasoline engine. Appl. Catal. 1995, 7, 153–171. [Google Scholar] [CrossRef]
- Wang, J.; Wu, C.; Chen, J.; Zhang, H. Denitrification removal of nitric oxide in a rotating drum biofilter. Chem. Eng. J. 2006, 121, 45–49. [Google Scholar] [CrossRef]
- Chen, J.M.; Ma, J.F. Abiotic and biological mechanisms of nitric oxide removal from waste air in biotrickling filters. J. Air Waste Manag. Assoc. 2006, 56, 32–36. [Google Scholar] [CrossRef] [Green Version]
- Ramirez, M.; Gómez, J.M.; Aroca, G.; Cantero, D. Removal of hydrogen sulfide by immobilized Thiobacillus thioparus in a biotrickling filter packed with polyurethane foam. Bioresour. Technol. 2009, 100, 4989–4995. [Google Scholar] [CrossRef]
- Philip, L.; Deshusses, M.A. Sulfur dioxide treatment from flue gases using a biotrickling filter-bioreactor system. Environ. Sci. Technol. 2003, 37, 1978–1982. [Google Scholar] [CrossRef]
- Jiang, R.; Huang, S.; Chow, A.T.; Yang, J. Nitric oxide removal from flue gas with a biotrickling filter using Pseudomonas putida. J. Hazard. Mater. 2009, 164, 432–441. [Google Scholar] [CrossRef]
- Liang, W.; Huang, S.; Yang, Y.; Jiang, R. Experimental and modeling study on nitric oxide removal in a biotrickling filter using Chelatococcus daeguensis under thermophilic condition. Bioresour. Technol. 2012, 125, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, W.P.; Apel, W.A.; Barnes, J.M.; Lee, B.D. Development of gas phase bioreactors for the removal of nitrogen oxides from synthetic flue gas streams. Fuel 2002, 81, 1953–1961. [Google Scholar] [CrossRef]
- Lee, B.D.; Apel, W.A.; Smith, W.A. Oxygen effects on thermophilic microbial populations in biofilter treating nitric oxide containing off-gasstreams. Environ. Prog. 2001, 20, 157–166. [Google Scholar] [CrossRef]
- Caceres, M.; Silva, J.; Morales, M.; San, R.M.; Aroca, G. Kinetics of the biooxidation of volatile reduced sulphur compounds in a biotrickling filter. Bioresour. Technol. 2012, 118, 243–248. [Google Scholar] [CrossRef]
- Song, J.; Kinney, K.A. A model to predict long-term performance of vapor phase bioreactors: A cellular automation approach. Environ. Sci. Technol. 2002, 36, 2498–2507. [Google Scholar] [CrossRef]
- Zarook, S.M.; Shaikh, A.A. Analysis and comparison of biofilter modes. Chem. Eng. J. 1997, 65, 55–61. [Google Scholar] [CrossRef]
- Meena, V.; Rajendran, L. Analytical expression of concentration profiles of methanol and pinene in air stream and bio-film phase. J. Anal. Bioanal. Tech. 2014, 6, 1–8. [Google Scholar]
- Meena, V.; Rajendran, L.; Kumar, S.; Jansi Rani, P.G. Mathematical modeling of gas phase and biofilm phase biofilter performance. Egypt J. Basic Appl. Sci. 2016, 3, 94–105. [Google Scholar] [CrossRef] [Green Version]
- Deshusses, M.A.; Hamer, G.; Dunn, I.J. Behavior of biofilters for waste air biotreatment. 1. Dynamic model development. Environ. Sci. Technol. 1995, 29, 1048–1058. [Google Scholar] [CrossRef]
- Liao, Q.; Chen, R.; Zhu, X. Theoretical model for removal of volatile organic compound (VOC) air pollutant in trickling biofilter. Sci. China Ser. E 2003, 46, 245–258. [Google Scholar] [CrossRef]
- Manimegalai, B.; Lyons, M.E.G.; Rajendran, L. A kinetic model for amperometric immobilized enzymes at planar, cylindrical and spherical electrodes: The Akbari-Ganji method. J. Electroanal. Chem. 2021, 880, 114921. [Google Scholar] [CrossRef]
- Selvi, M.S.M.; Rajendran, L.; Abukhaled, M. Estimation of rolling motion of ship in random beam seas by efficient analytical and numerical approaches. J. Mar. Sci. Appl. 2021, 20, 55–66. [Google Scholar] [CrossRef]
- Chitra Devi, M.; Pirabaharan, P.; Rajendran, L.; Abukhaled, M. Amperometric biosensors in an uncompetitive inhibition process: A complete theoretical and numerical analysis. React. Kinet. Mech. Catal. 2021, 133, 655–668. [Google Scholar] [CrossRef]
- Saranya, K.; Mohan, V.; Rajendran, L. Steady state concentrations of carbon dioxide absorbed into phenyl glycidyl ether solutions by residual method. J. Math. Chem. 2020, 58, 1230–1246. [Google Scholar] [CrossRef]
- Joy Salomi, R.; Vinolyn Sylvia, S.; Rajendran, L.; Abukhaled, M. Electric potential and surface oxygen ion density for planar, spherical and cylindrical metal oxide grains. Sens. Actuators B Chem. 2020, 321, 128576. [Google Scholar] [CrossRef]
- Joy Salomi, R.; Vinolyn Sylvia, S.; Rajendran, L.; Lyons, M.E.G. Transient current, sensitivity and resistance of biosensors acting in a trigger mode: Theoretical study. J. Electroanal. Chem. 2021, 895, 115421. [Google Scholar] [CrossRef]
- Manimegalai, B.; Rajendran, L.; Lyons, M.E.G. Theory of the Transient Current Response for the Homogeneous Mediated Enzyme Catalytic Mechanism at the Rotating Disc Electrode. Int. J. Electrochem. Sci. 2021, 16, 210946. [Google Scholar] [CrossRef]
- Lyons, M.E.G. Understanding the kinetics of catalysed reactions in microheterogeneous thin film electrodes. J. Electroanal. Chem. 2020, 872, 114278. [Google Scholar] [CrossRef]
- Chitra Devi, M.; Pirabaharan, P.; Lyons, M.E.G.; Rajendran, L. Investigation of the Diffusion Impedance for an Irreversible Redox Reaction. Int. J. Electrochem. Sci. 2021, 16, 210639. [Google Scholar] [CrossRef]
- Akbari, M.R.; Ganji, D.D.; Nimafar, M.; Ahmadi, R. Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Front. Mech. Eng. 2014, 9, 390–401. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Lyons, M.E.G. Reaction-diffusion in a packed-bed reactors: Enzymatic isomerization with Michaelis-Menten Kinetics. J. Electroanal. Chem. 2022, 910, 116184. [Google Scholar] [CrossRef]
- Akbari, M.R.; Nimafar, M.; Ganji, D.D.; Karimi Chalmiani, H. Investigation on non-linear vibration in arched beam for bridges construction via AGM method. Appl. Math. Comput. 2017, 298, 95–110. [Google Scholar] [CrossRef]
- Meresht, N.B.; Ganji, D.D. Solving nonlinear differential equation arising in dynamical systems by AGM. Int. J. Appl. Comput. Math. 2017, 3, 1507–1523. [Google Scholar] [CrossRef]
- Rasi, M.; Kumar, S.; Rajendran, L. Analytical expressions for the concentration of nitric oxide removal in the gas and biofilm phase in a biotrickling filter. J. Assoc. Arab Univ. Basic Appl. Sci. 2015, 18, 19–28. [Google Scholar]
- Jeyabarathi, P.; Kannan, M.; Rajendran, L. Mathematical Model for Extracting Hollow Fiber Membrane Contactors from Carbon dioxide using Adomian decomposition method. Int. J. Sci. Res. 2020, 9, 6230–6233. [Google Scholar]
- He, J.H.; El-Dib, Y. Homotopy perturbation method for Fangzhu oscillator. J. Math. Chem. 2020, 58, 2245–2253. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y. Homotopy perturbation method with three expansions. J. Math. Chem. 2021, 59, 1139–1150. [Google Scholar] [CrossRef]
- Ali, M.; Anjum, N.; Ain, Q.T.; He, J.H. Homotopy perturbation method for the attachment oscillator arising in nanotechnology. Fibers Polym. 2021, 22, 1601–1606. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O.; Mady, A.A. Homotopy Perturbation Method for the Fractal Toda Oscillator. Fractal Fract. 2021, 5, 93. [Google Scholar] [CrossRef]
- He, J.H.; Ji, F.Y. Taylor series solution for Lane–Emden equation. J. Math. Chem. 2019, 57, 1932–1934. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Abukhaled, M.; Kannan, M. Semi-analytical expressions for the concentrations and effectiveness factor for the three general catalysts shapes. React. Kinet. Mech. Catal. 2022, 1–16. [Google Scholar] [CrossRef]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Rajendran, L.; Abukhaled, M. Solving nonlinear reaction–diffusion problem in electrostatic interaction with reaction-generated pH change on the kinetics of immobilized enzyme systems using Taylor series method. J. Math. Chem. 2019, 59, 1332–1347. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Optical bright and dark soliton solutions for coupled nonlinear Schrödinger (CNLS) equations by the variational iteration method. Optik 2020, 207, 164457. [Google Scholar] [CrossRef]
- Nirmala, K.; Manimegalai, B.; Rajendran, L. Steady-State Substrate and Product Concentrations for Non Michaelis-Menten Kinetics in an Amperometric Biosensor—Hyperbolic Function and Padé Approximants Method. Int. J. Electrochem. Sci. 2020, 15, 5682–5697. [Google Scholar] [CrossRef]
- Namihira, T.; Tsukamoto, S.; Wang, D.; Katsuki, S.; Hackam, R.; Akiyama, H.; Uchida, Y.; Koike, M. Imrovement of NOX removal efficiency using short-width pulsed power. IEEE Trans. Plasm. Sci. 2000, 28, 434–442. [Google Scholar] [CrossRef]
- Deshusses, M.A.; Webster, T.S. Construction and economics of a pilot/full-scale biological trickling filter reactor for the removal of volatile organic compounds from polluted air. J. Air Waste Manag. Assoc. 2000, 50, 1947–1956. [Google Scholar] [CrossRef] [Green Version]
- Hodge, D.S.; Devinny, J.S. Modeling removal of air contaminants by biofiltration. J. Environ. Eng. Sci. 1995, 121, 21–32. [Google Scholar] [CrossRef]
- Iranpour, R.; Cox, H.H.J.; Deshusses, M.A.; Schroeder, E.D. Literature review of air pollution control biofilters and biotrickling filters for odor and volatile organic compound removal. Environ. Prog. 2005, 24, 254–267. [Google Scholar] [CrossRef]
- Khan, F.I.; Ghoshal, A.K. Removal of volatile organic compounds from polluted ai. J. Loss Prev. Process. Ind. 2000, 13, 527–545. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, W.; Xu, J. A simplified mathematical model of multi-species biofilm for simultaneous removal of sulfur dioxide (SO2) and nitric oxide (NO) using a biotrickling-filter. Afr. J. Microbiol. Res. 2011, 5, 541–550. [Google Scholar]


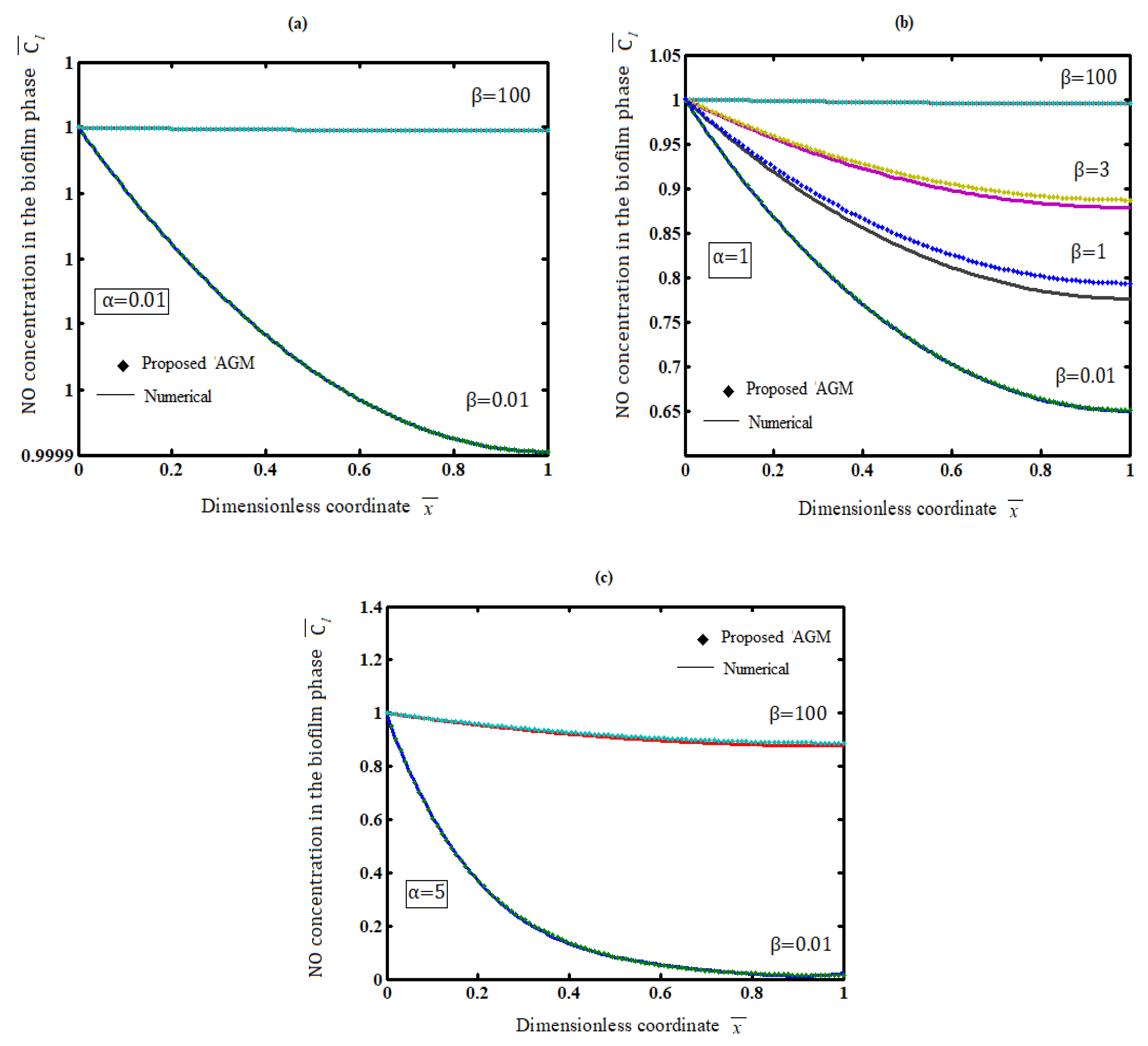

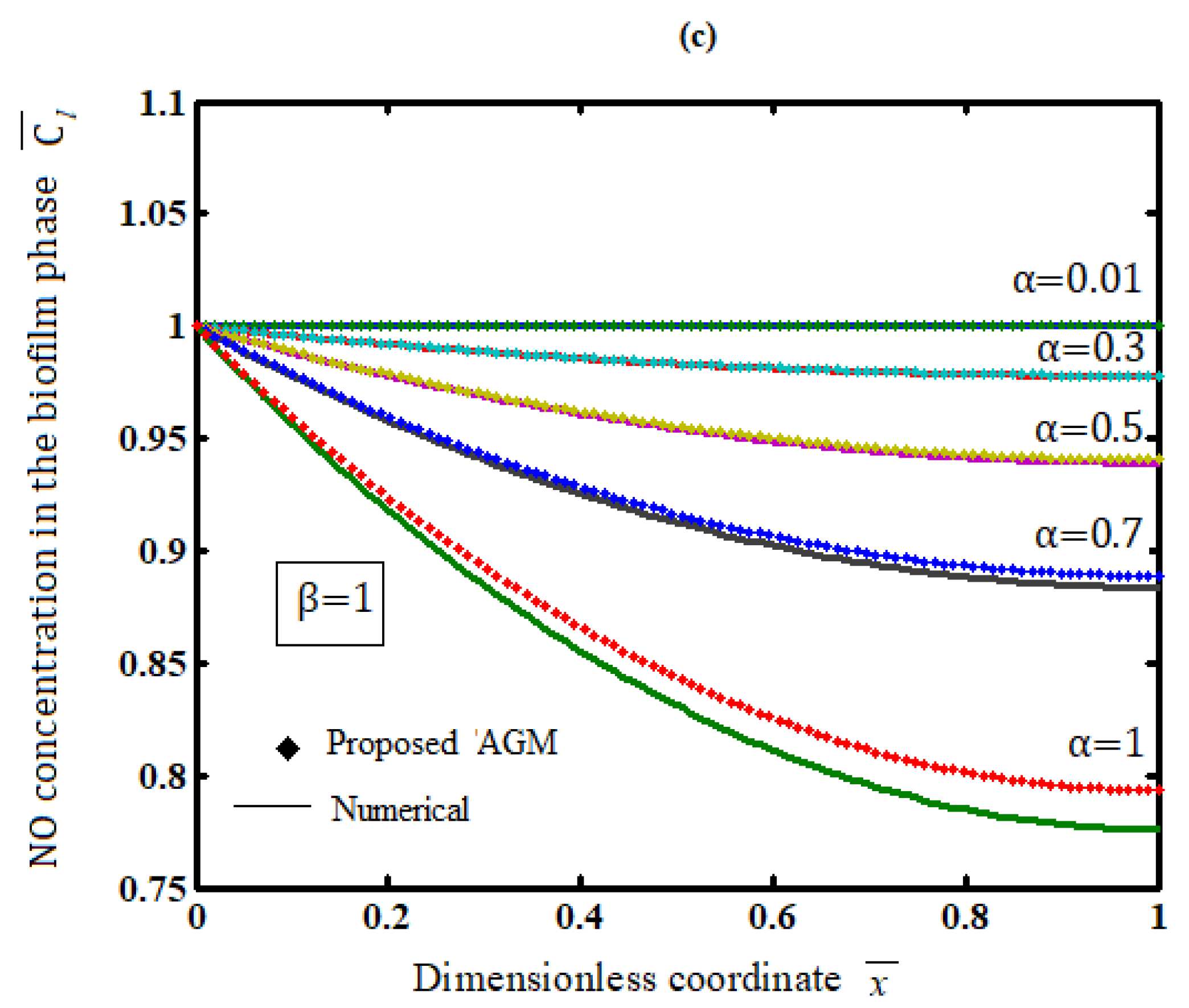

| Num. | Concentration in Biofim Phase | Error (%) | Num. | Concentration in Biofim Phase | Error (%) | Num. | Concentration in Biofim Phase | Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| This Work AGM Equation (15) | ADM [31] Equation (22) | This Work AGM Equation (15) | ADM [31] Equation (22) | This Work AGM Equation (15) | ADM [31] Equation (22) | This Work AGM Equation (15) | ADM [31] Equation (22) | This Work AGM Equation (15) | ADM [31] Equation (22) | AGM Equation (15) | ADM [31] Equation (22) | ||||
| 0 | 1.0000 | 1.0000 | 1.0000 | 0.00 | 0.00 | 1.0000 | 1.0000 | 1.0000 | 0.00 | 0.00 | 1.0000 | 1.0000 | 1.0000 | 0.00 | 0.00 |
| 0.2 | 0.9982 | 0.9982 | 0.9982 | 0.00 | 0.00 | 0.9587 | 0.9587 | 0.9591 | 0.00 | 0.04 | 0.8663 | 0.8666 | 0.8843 | 0.03 | 2.07 |
| 0.4 | 0.9968 | 0.9968 | 0.9968 | 0.00 | 0.00 | 0.9271 | 0.9271 | 0.9278 | 0.00 | 0.08 | 0.7678 | 0.7683 | 0.8019 | 0.06 | 4.44 |
| 0.6 | 0.9958 | 0.9958 | 0.9958 | 0.00 | 0.00 | 0.9049 | 0.9049 | 0.9058 | 0.00 | 0.09 | 0.7005 | 0.7011 | 0.7473 | 0.08 | 6.68 |
| 0.8 | 0.9953 | 0.9953 | 0.9953 | 0.00 | 0.00 | 0.8918 | 0.8918 | 0.8929 | 0.01 | 0.12 | 0.6617 | 0.6624 | 0.7165 | 0.11 | 8.28 |
| 1 | 0.9951 | 0.9951 | 0.9951 | 0.00 | 0.00 | 0.8877 | 0.8877 | 0.8889 | 0.01 | 0.13 | 0.6498 | 0.6605 | 0.7072 | 0.11 | 8.83 |
| Average error % | 0.00 | 0.00 | Average error % | 0.01 | 0.08 | Average error % | 0.06 | 5.05 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umadevi, R.; Jeyabarathi, P.; Venugopal, K.; Lyons, M.E.G.; Rajendran, L. Modelling of Biotrickling Filters for Treatment of NOx Analytical Expressions for the NOx Concentration in Both Gas and Biofilm Phases. Electrochem 2022, 3, 361-378. https://doi.org/10.3390/electrochem3030025
Umadevi R, Jeyabarathi P, Venugopal K, Lyons MEG, Rajendran L. Modelling of Biotrickling Filters for Treatment of NOx Analytical Expressions for the NOx Concentration in Both Gas and Biofilm Phases. Electrochem. 2022; 3(3):361-378. https://doi.org/10.3390/electrochem3030025
Chicago/Turabian StyleUmadevi, Ramasamy, Ponraj Jeyabarathi, Kothandapani Venugopal, Michael E. G. Lyons, and Lakshmanan Rajendran. 2022. "Modelling of Biotrickling Filters for Treatment of NOx Analytical Expressions for the NOx Concentration in Both Gas and Biofilm Phases" Electrochem 3, no. 3: 361-378. https://doi.org/10.3390/electrochem3030025
APA StyleUmadevi, R., Jeyabarathi, P., Venugopal, K., Lyons, M. E. G., & Rajendran, L. (2022). Modelling of Biotrickling Filters for Treatment of NOx Analytical Expressions for the NOx Concentration in Both Gas and Biofilm Phases. Electrochem, 3(3), 361-378. https://doi.org/10.3390/electrochem3030025







