Fractional Frequency Reuse Optimal SINR Threshold Selection Using NIR and ISODATA
Abstract
:1. Introduction
2. Literature Review
2.1. Cellular Network Model
2.2. FFR Network Layout
2.3. SINR
2.4. Throughput
2.5. Jain’s Index of Fairness
2.6. Proportionally Fair (PF) Scheduling
2.7. Native Integral Ratio (NIR) Method
2.8. The Iterative Self-Organizing Data Analysis (ISODATA) Method
2.9. ISODATA Algorithm
- ▪
- Select an initial threshold value, , for instance, half of the maximum dynamic range.
- ▪
- Loop
- ▪
- Divide the histogram into two such that one segment corresponds to the foreground and the other to the background.
- ▪
- Calculate the sample mean of gray values of foreground and background pixels ( and ).
- ▪
- Determine a new threshold value, ; this is the average of these two samples’ means.
- ▪
- Re-segment the histogram again into two.
- ▪
- Check if any mean value has changed. If so, go to loop or else terminate.
3. Methodology
System Algorithm
4. Results
4.1. UE Wideband SINR Distributions
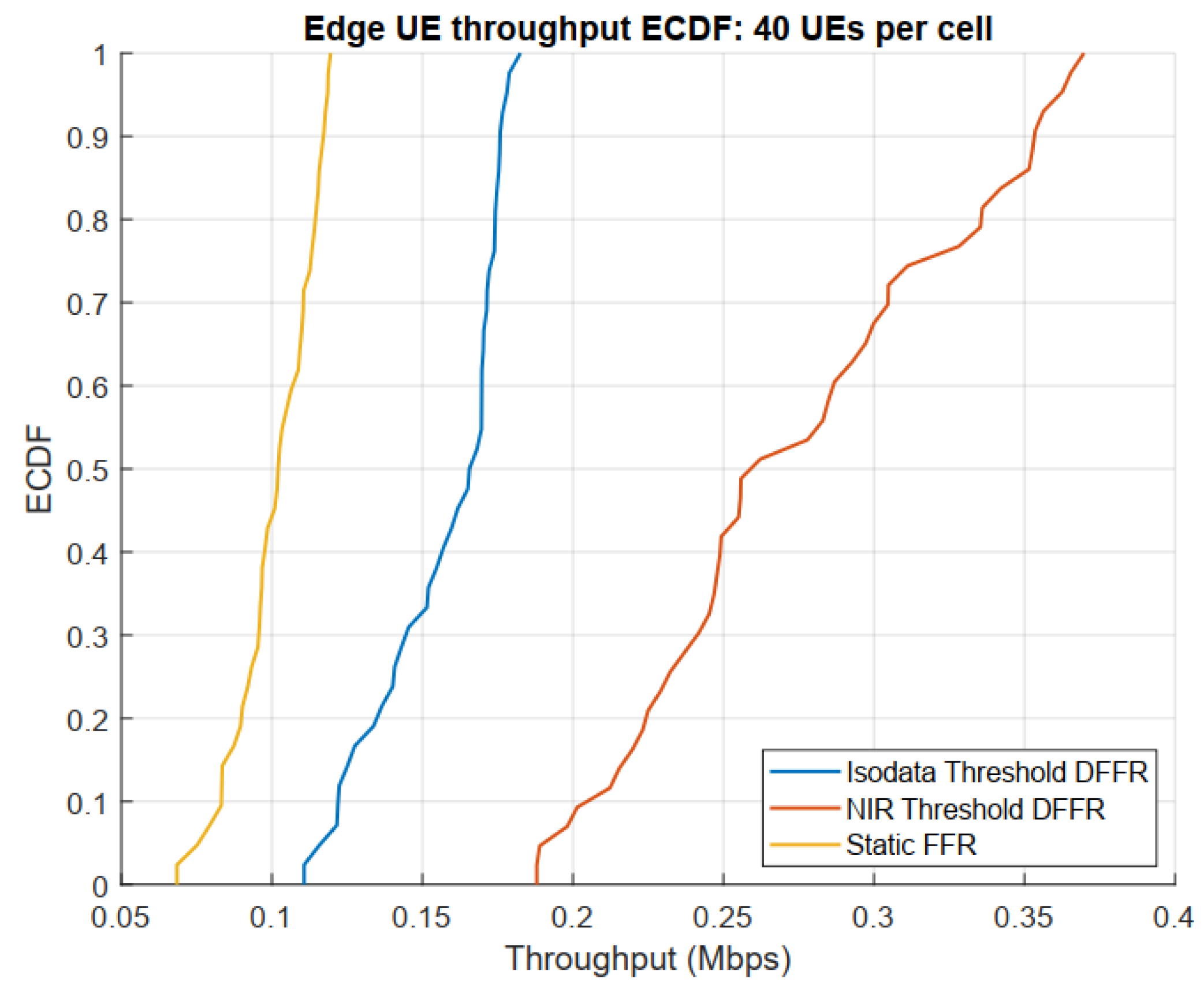
4.2. Empirical Cumulative Distributed Function (ECDF) Curves
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AMC | Adaptive Modulation and Coding |
| BS | Base Station |
| ECDF | Empirical Cumulative Distribution Function |
| CQI | Channel Quality Indicators |
| FFR | Fractional Frequency Reuse |
| FR | Full Reuse |
| ISODATA | Iterative Self-Organizing Data Analysis |
| LTE | Long-Term Evolution |
| LTE-A | Long-Term Evolution—Advanced |
| MCL | Maximum-Coupling Loss |
| MIMO | Multiple Input Multiple Output |
| MS | Mobile Station |
| NIR | Native Integral Ratio |
| OFDMA | Orthogonal Frequency Division Multiple Access |
| PF | Proportionally Fair |
| PMI | Precoding Matrix Indicator |
| PR | Partial Re-use |
| RI | Rank Indicator |
| RR | Round Robin |
| SINR | Signal-to-Interference-plus-Noise-Ratio |
| TTI | Transmission Time Interval |
| TU | Typical Urban |
| UE | User Equipment |
References
- Hamza, S.; Khalifa, S.S.; Hamza, H.S.; Elsayed, K. A survey on inter-cell interference coordination techniques in OFD-MA-based cellular networks. IEEE Commun. Surv. Tutor. 2013, 15, 1642–1670. [Google Scholar] [CrossRef] [Green Version]
- Afroz, F.; Sandrasegaran, K. Interference management in LTE downlink networks. Int. J. Wirel. Mobile Netw. 2015, 7, 91–106. [Google Scholar] [CrossRef]
- Novlan, T.D.; Ganti, R.K.; Ghosh, A.; Andrews, J.G. Analytical Evaluation of Fractional Frequency Reuse for OFDMA Cellular Networks. IEEE Trans. Wirel. Commun. 2011, 10, 4294–4305. [Google Scholar] [CrossRef] [Green Version]
- Senthilkumaran, N.; Vaithegi, S. Image segmentation by using thresholding techniques for medical images. Comput. Sci. Eng. Int. J. 2016, 6, 1–13. [Google Scholar]
- Bhargavi, K.; Jyothi, S. A survey on threshold based segmentation technique in image processing. Int. J. Innov. Res. Dev. 2014, 13, 234–239. [Google Scholar]
- Eesa, M.; Talib, H.R. Comparison of the Methods of Image Slicing after Initial Image Processing Using the Statistical Confidence Limits. Ann. Pure Appl. Math. 2021, 24, 53–64. [Google Scholar]
- Leedham, G.; Varma, S.; Patankar, A.; Govindaraju, V. Separating text and background in degraded document images—A comparison of global thresholding techniques for multi-stage thresholding. In Proceedings of the Eighth International Workshop on Frontiers in Handwriting Recognition (IWFHR’02), Niagara-on-the-Lake, ON, Canada, 6–8 August 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 244–249. [Google Scholar] [CrossRef]
- Solihin, Y.; Leedham, G. Integral ratio: A new class of global thresholding techniques for handwriting images. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 761–768. [Google Scholar] [CrossRef]
- Mapay, T.; Viriri, S.; Tapamo, J.R. Comparative study of retinal vessel segmentation based on global thresholding techniques. Comput. Math. Methods Med. 2015, 2015, 895267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ali, H.S.; Leung, V.C. Dynamic frequency allocation in fractional frequency reused OFDMA networks. IEEE Trans. Wirel. Commun. 2009, 8, 4286–4295. [Google Scholar] [CrossRef]
- AlAmmour, J.; Andrews, G.; Baccelli, F. SINR and throughput of dense cellular networks with stretched exponential path loss. IEEE Trans. Wirel. Commun. 2017, 17, 1147–1160. [Google Scholar] [CrossRef]
- Basilashvili, G. Study of spectral efficiency for LTE network. Acad. Sci. Res. J. Eng. Technol. Sci. 2017, 29, 21–32. [Google Scholar]
- Jain, R.K.; Chiu, D.M.; Hawe, W.R. A Quantitative Measure of Fairness and Discrimination; Eastern Research Laboratory, Digital Equipment Corporation: Hudson, MA, USA, 1984; p. 21. [Google Scholar]
- Kim, H.; Kim, K.; Han, Y.; Yun, S. A proportional fair scheduling for multicarrier transmission systems. IEEE Commun. Lett. 2005, 210–212. [Google Scholar] [CrossRef]
- Jawahar, C.; Biswas, P.; Ray, A. Investigations on fuzzy thresholding based on fuzzy clustering. Pattern Recognit. 1997, 30, 1605–1613. [Google Scholar] [CrossRef]
- Vimala, R.; Marimuthu, A.; Venkateswaran, S.; Poongodi, R. Unsupervised ISODATA algorithm classification used in the landsat image for predicting the expansion of Salem urban, Tamil, Nadu. Indian J. Sci. Technol. 2020, 13, 1619–1629. [Google Scholar]
- Ahmed, S. Comparison of Satellite Images Classification Techniques using Landsat-8 Data for Land Cover Extraction. Int. J. Intell. Comput. Inf. Sci. 2021, 21, 29–43. [Google Scholar] [CrossRef]
- Thieu, Q.-T.; Hsieh, H.-Y.; Wang, C.-H. A Wideband Scheduling Method for Non-Orthogonal Multiple Access in the Vienna LTE-A Downlink System-Level Simulator. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]













| Parameter | Value |
|---|---|
| UE speed | 5 Km/h |
| Number of cells | 21 |
| UEs per cell | 10, 20, 30, 40, 50 |
| Antenna pattern | TS 36.942 |
| Transmit power | 40 W |
| Feedback | AMC: CQI, MIMO: RI & PMI |
| Shadow fading | None |
| Minimum-coupling loss | 70 dB |
| Noise spectral density | −174 dBm/Hz |
| Simulation length | 50 sub frames (TTIs) |
| Receiver model | Zero forcing |
| Inter-eNodeB distance | 500 |
| Transmission bandwidth | 20 MHz (100 resource blocks) |
| Antennas (NTX × NRX) | 4 × 2 |
| Channel model | TU |
| Pathloss model | TS 36.942—Urban area, 70 dB MCL |
| Scheduling algorithm | Proportional fair |
| 1. INITIATE |
| 2. AFTER EVERY 50 TTIs DO |
| 3. for UEs |
| 4. IMPLEMENT NIR method to determine threshold, T |
| 5. ); #Note: T = isothresh for the case of ISODATA |
| 6. |
| 7. |
| 8. FFR UE MAPPING |
| 9. PR_zone_UEs = 0 |
| 10. FR_zone_UEs = 0 |
| 11. |
| 12. ALLOT User Equip to FR zone |
| 13. FR_zone_UEs++ |
| 14. else |
| 15. ALLOT User Equip to PR zone |
| 16. PR_zone_UEs++ |
| 17. end |
| 18. |
| 19. |
| 20. |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| Number of UEs per cell | 10 | 20 | 30 | 40 | 50 |
| Total number of UEs | 210 | 420 | 630 | 840 | 1050 |
| (dB) | 4.24 | 3.33 | 3.27 | 0.11 | 3.33 |
| 0.347 | 0.53 | 0.48 | 0.59 | 0.46 |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| Number of UEs per cell | 10 | 20 | 30 | 40 | 50 |
| Total number of UEs | 210 | 420 | 630 | 840 | 1050 |
| (dB) | 3.66 | 4.26 | 3.51 | 3.87 | 3.92 |
| 0.34 | 0.33 | 0.40 | 0.36 | 0.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kihato, P.; Musyoki, S.; Onim, A. Fractional Frequency Reuse Optimal SINR Threshold Selection Using NIR and ISODATA. Telecom 2022, 3, 433-447. https://doi.org/10.3390/telecom3030023
Kihato P, Musyoki S, Onim A. Fractional Frequency Reuse Optimal SINR Threshold Selection Using NIR and ISODATA. Telecom. 2022; 3(3):433-447. https://doi.org/10.3390/telecom3030023
Chicago/Turabian StyleKihato, Peter, Stephen Musyoki, and Antony Onim. 2022. "Fractional Frequency Reuse Optimal SINR Threshold Selection Using NIR and ISODATA" Telecom 3, no. 3: 433-447. https://doi.org/10.3390/telecom3030023
APA StyleKihato, P., Musyoki, S., & Onim, A. (2022). Fractional Frequency Reuse Optimal SINR Threshold Selection Using NIR and ISODATA. Telecom, 3(3), 433-447. https://doi.org/10.3390/telecom3030023





