Energy Consumption Modeling for Heterogeneous Internet of Things Wireless Sensor Network Devices: Entire Modes and Operation Cycles Considerations
Abstract
1. Introduction
Significance of the Contribution
2. Heterogeneous Scenarios and APT Transmission Scheme
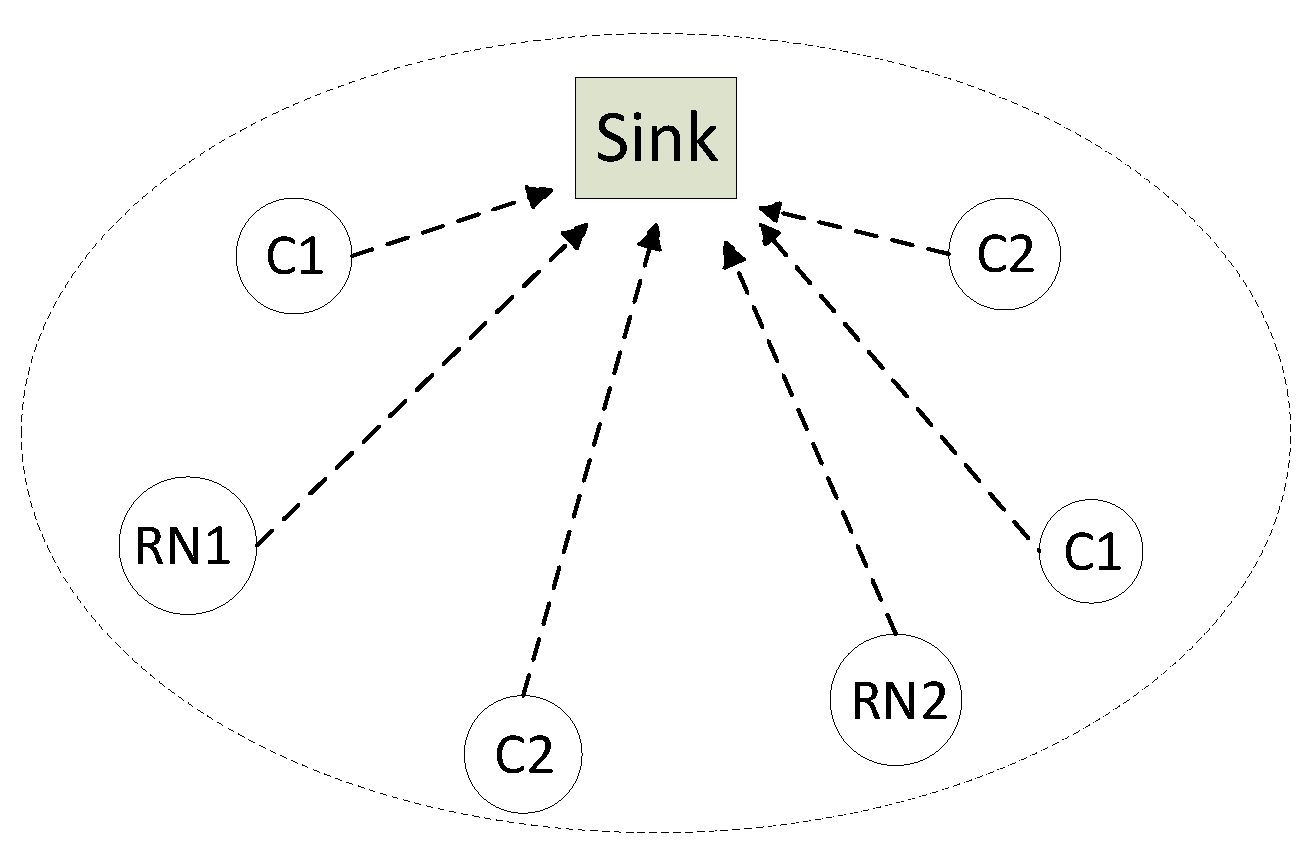
2.1. Network Assumptions
2.2. Transmission and Operation Modes
Prioritization Scheme
3. System Model
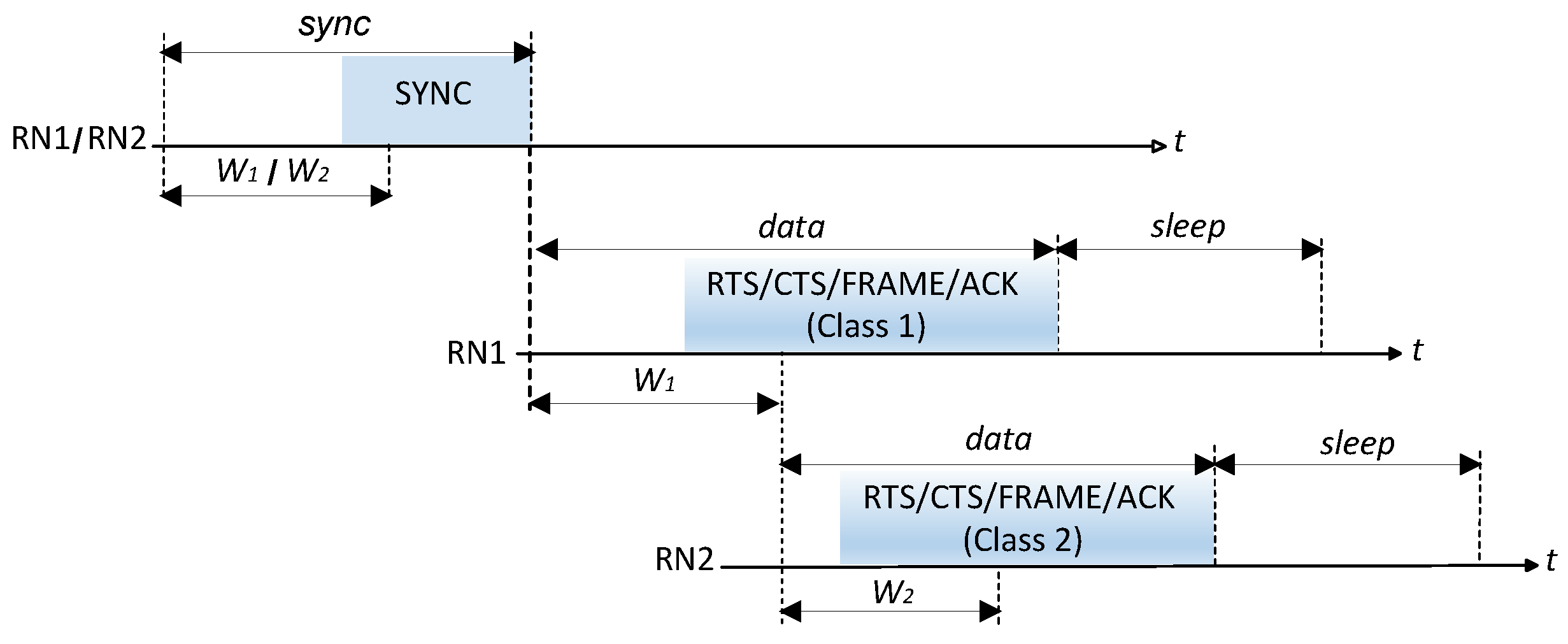
3.1. Medium Access
3.2. Definition of the 2D-DTMCs
3.3. Solution of the 2D-DTMCs
4. Energy Consumption
4.1. Average Energy Consumed by in the Sync Period
4.2. Average Energy Consumed by in the Data Period
4.3. Average Energy Consumed by in the Data Period
4.4. Average Energy Consumed by during Awake Cycles
- Cycle 1A: is active, .
- Zero or more SNs might also be active. When other SNs are active, in addition to , the following contention outcomes are possible: (i) completes a successful PF transmission; (ii) the PF from collides; (iii) another node completes a successful PF transmission, and (iv) other nodes different from collide.
- Cycle 1B: is inactive, .
- SNs access the channel while is awake. listens to the channel to decode the RTS packet and determine the duration of the PF transmission. The following contention outcomes are possible: (i) a SN completes a successful PF transmission; (ii) multiple PFs collide.
- Cycle 1C: All SNs remain inactive, including , .
- There are active SNs that access the channel while is awake, . listens to the channel, decodes the RTS packets in collision-free cycles and determines the duration of the PF transmissions. The following contention outcomes for SNs might be possible: (i) a SN completes a successful PF transmission; (ii) multiple PFs from different SNs collide.
- Cycle 1D: All and SNs remain inactive, , while is awake.
4.4.1. Average Energy Consumed by in Type 1A Cycles
4.4.2. Average Energy Consumed by in Type 1B Cycles
4.4.3. Energy Consumption in Type 1C Cycles
4.4.4. Energy Consumption in in Type 1D Cycles
4.4.5. Average Energy Consumed by in awake Cycles
4.5. Average Energy Consumed by during Awake Cycles
- Cycle 2A: SNs are inactive , but and other SNs are active . Either or any other active SNs will access the channel, while is awake in the same cycle. The possible contention outcomes are: (a) successfully transmits a PF; (b) a PF transmitted by collides; (c) another SN successfully transmits a PF; (d) other SNs collide.
- Cycle 2B: SNs are inactive, is also inactive, but other SNs are active, . SNs access the channel in the same cycle that is awake. The possible contention outcomes are: (a) a SN successfully transmits a PF; (b) multiple SNs collide.
- Cycle 2C: All SNs are active, , while SNs, including SNs, are inactive, . The possible contention outcomes are: (a) a SN successfully transmits a PF; (b) multiple SNs collide.
- Cycle 2D: and the rest of and SNs are inactive, . Please note that in cycles of type 2D, both and might simultaneously coincide in their respective awake cycles.
4.5.1. Energy Consumption in Type 2A Cycles
4.5.2. Energy Consumption in Type 2B Cycles
4.5.3. Energy Consumption in Type 2C Cycles
4.5.4. Energy Consumption in Type 2D Cycles
4.5.5. Average Energy Consumed by in Awake Cycles
4.6. Average Energy Consumption during Normal Cycles
4.6.1. Sensor Nodes
4.6.2. Sensor Nodes
4.7. Total Average Energy Consumed by an RN in a Cycle
5. Numerical Results
5.1. Scenario and Parameter Configuration
5.2. Analytical Model Validation
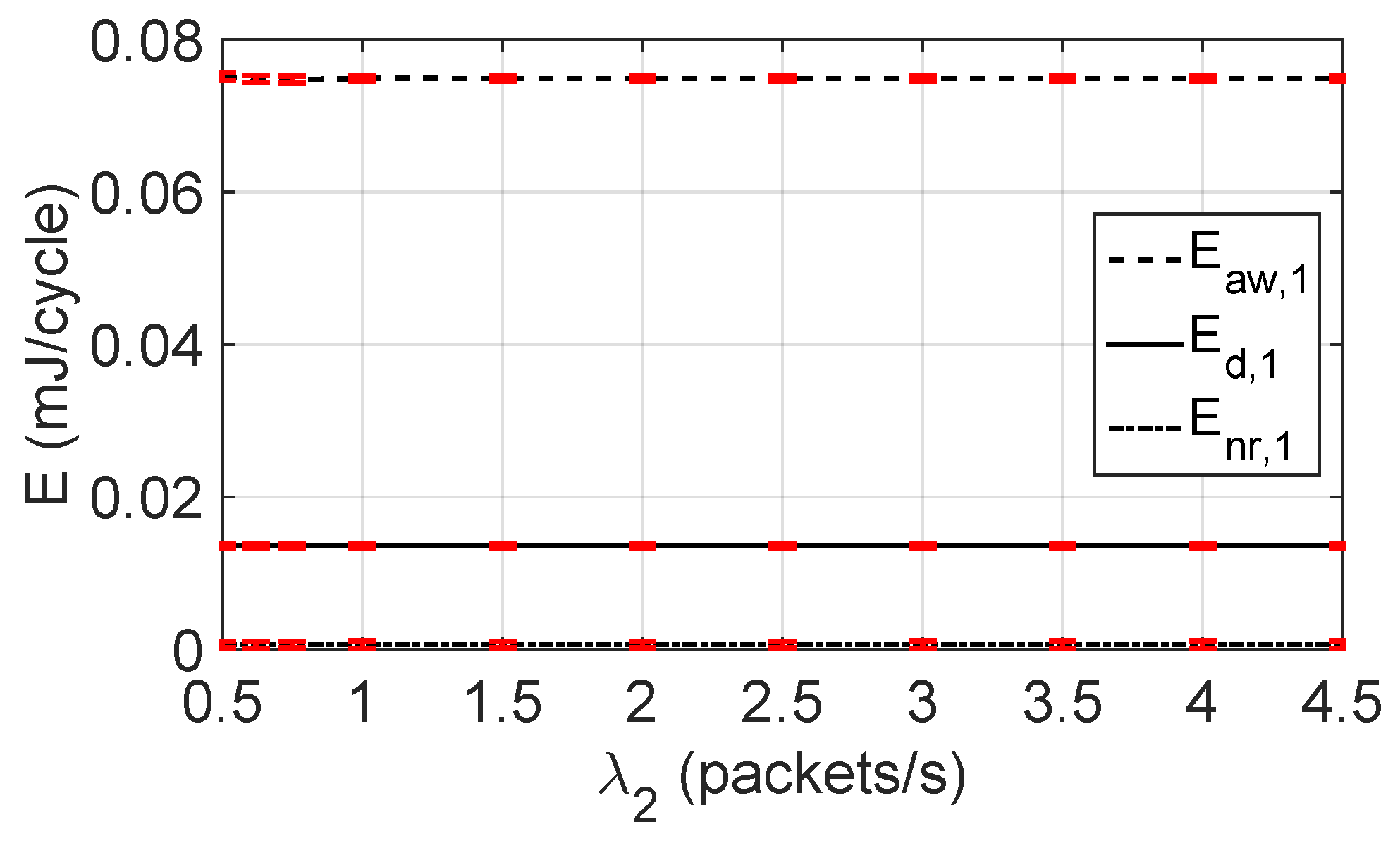
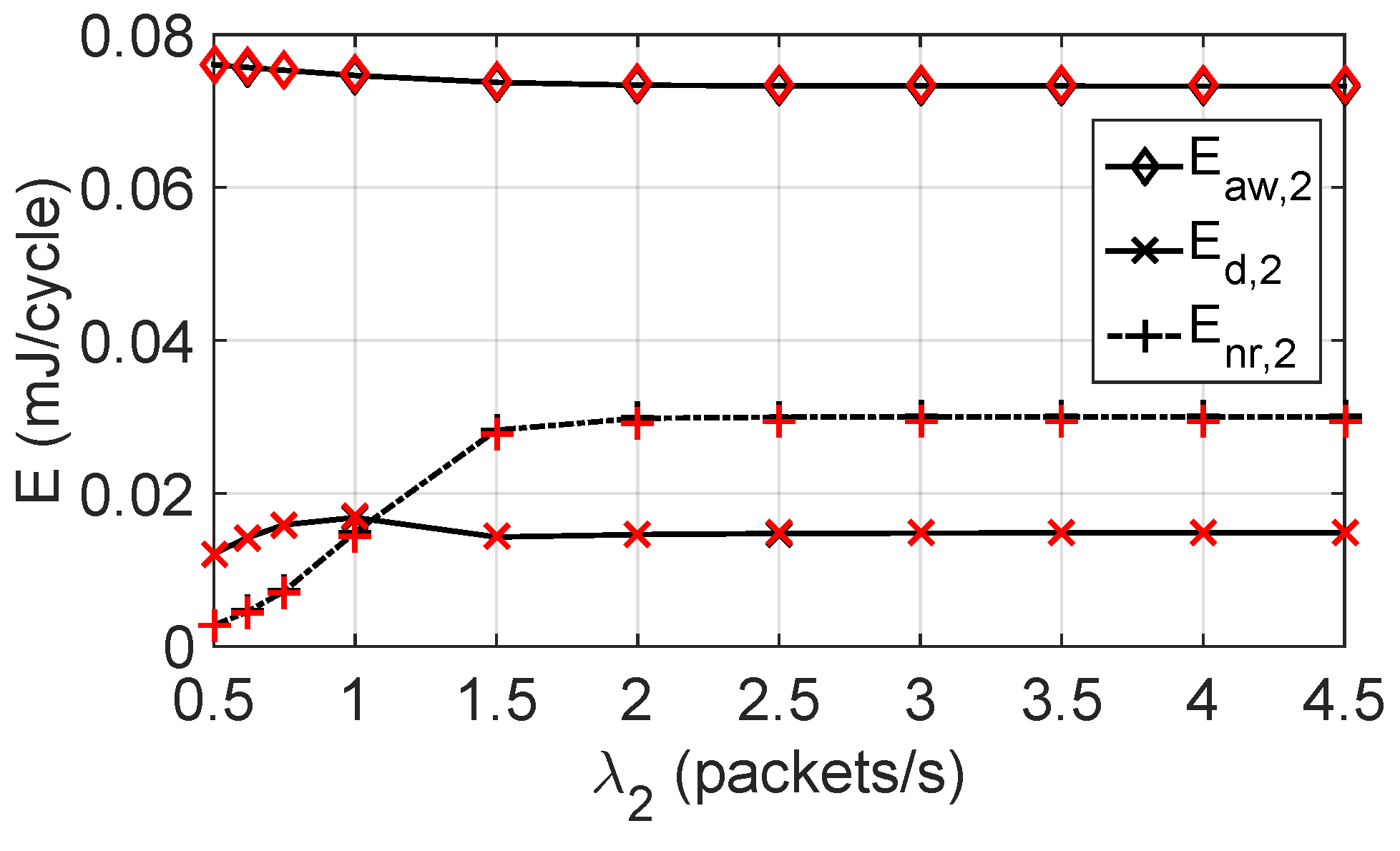
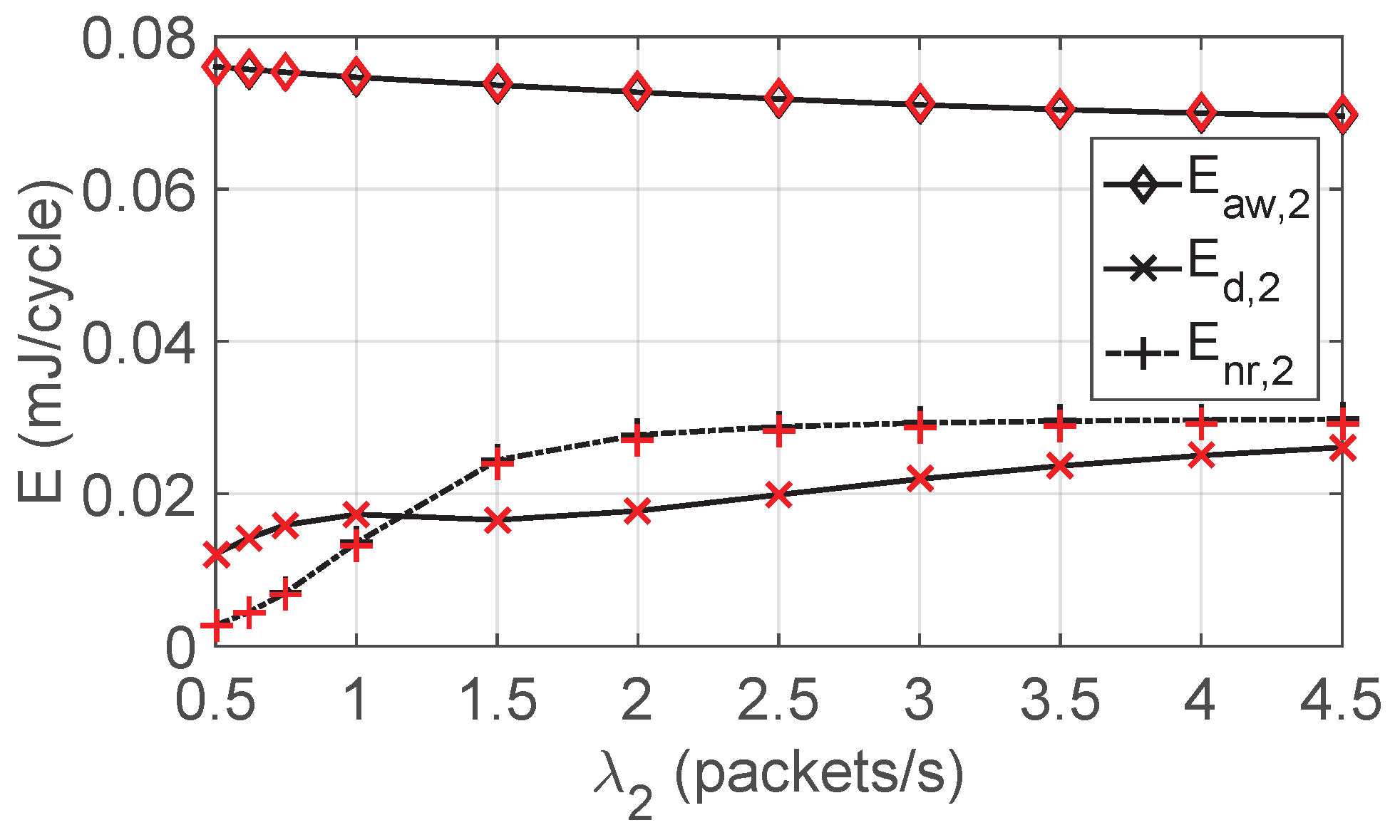
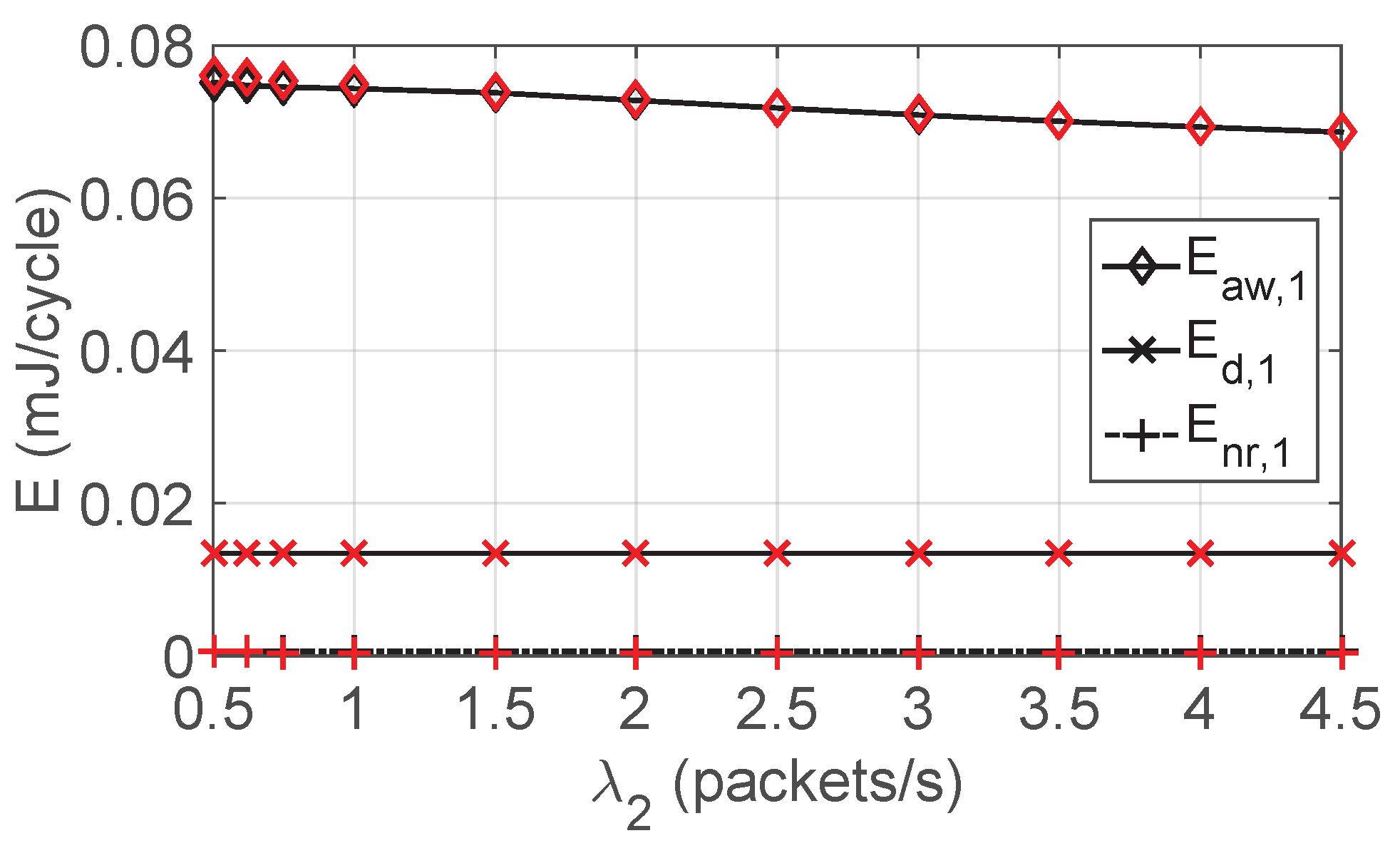
5.3. Energy Consumed by and in the Data Period, the Awake and Normal Cycles
5.4. Energy Consumed by Due to PF Transmissions with Success and Failure, and Due to Overhearing
5.5. Accuracy of the New Methodology to Determine Energy Consumption
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mansour, M.; Gamal, A.; Ahmed, A.I.; Said, L.A.; Elbaz, A.; Herencsar, N.; Soltan, A. Internet of Things: A Comprehensive Overview on Protocols, Architectures, Technologies, Simulation Tools, and Future Directions. Energies 2023, 16, 3465. [Google Scholar] [CrossRef]
- Ahmed, S. Energy Aware Software Defined Network Model for Communication of Sensors Deployed in Precision Agriculture. Sensors 2023, 23, 5177. [Google Scholar] [CrossRef] [PubMed]
- Pedditi, R.B.; Debasis, K. Energy Efficient Routing Protocol for an IoT-Based WSN System to Detect Forest Fires. Appl. Sci. 2023, 13, 3026. [Google Scholar] [CrossRef]
- Chi, H.R.; Wu, C.K.; Huang, N.; Tsang, K.; Radwan, A. A Survey of Network Automation for Industrial Internet-of-Things Toward Industry 5.0. IEEE Trans. Ind. Inform. 2023, 19, 2065–2077. [Google Scholar] [CrossRef]
- Li, B.; Zhao, Q.; Jiao, S.; Liu, X. DroidPerf: Profiling memory objects on android devices. In Proceedings of the 29th Annual International Conference on Mobile Computing and Networking (MobiCom 2023), Madrid, Spain, 2–6 October 2023; pp. 1–15. [Google Scholar]
- Raut, S.; Bhandari, C.; Jain, H. A Comparative Study of Power Optimization Techniques for Microcontroller based IoT Applications. In Proceedings of the 2024 Fourth International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 11–12 January 2024; pp. 1–8. [Google Scholar]
- Abdul-Qawy, A.; Alduais, N.; Saad, A.; Taher, M.; Nasser, A.; Saleh, S.; Khatri, N.B. An enhanced energy efficient protocol for large-scale IoT-based heterogeneous WSNs. Sci. Afr. 2023, 21, e01807. [Google Scholar] [CrossRef]
- Abdulzahra, A.; Al-Qurabat, A.; Abdulzahra, S. Optimizing energy consumption in WSN-based IoT using unequal clustering and sleep scheduling methods. Internet Things 2023, 22, 100765. [Google Scholar] [CrossRef]
- Banti, K.; Karampelia, I.; Dimakis, T.; Boulogeorgos, A.; Kyriakidis, T.; Louta, M. LoRaWAN Communication Protocols: A Comprehensive Survey under an Energy Efficiency Perspective. J. Telecom. 2022, 3, 322–357. [Google Scholar] [CrossRef]
- Ghaderi, M.R.; Amiri, N. LoRaWAN sensor: Energy analysis and modeling. Wirel. Netw. 2024, 30, 1013–1036. [Google Scholar] [CrossRef]
- Correia, F.; Alencar, M.; Assis, K. Stochastic Modeling and Analysis of the Energy Consumption of Wireless Sensor Networks. IEEE Lat. Am. Trans. 2023, 21, 434–440. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Nguyen, H.M.; Masaracchia, A.; Nguyen, C.V. Stochastic-Based Power Consumption Analysis for Data Transmission in Wireless Sensor Networks. EAI Endorsed Trans. Ind. Netw. Intell. Syst. 2019, 6, e5. [Google Scholar] [CrossRef][Green Version]
- Xu, D.; Wang, K. Stochastic Modeling and Analysis with Energy Optimization for Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2014, 10, 672494. [Google Scholar] [CrossRef]
- Rahimifar, A.; Kavian, Y.; Kaabi, H.; Soroosh, M. Predicting the energy consumption in software defined wireless sensor networks: A probabilistic Markov model approach. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 9053–9066. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W. Energy consumption analysis of a duty cycle wireless sensor network model. IEEE Access 2019, 7, 33405–33413. [Google Scholar] [CrossRef]
- Xiao, W.; Kaneko, M.; El Rachkidy, N.; Guitton, A. Integrating lora collision decoding and mac protocols for enabling iot massive connectivity. IEEE Internet Things Mag. 2022, 5, 166–173. [Google Scholar] [CrossRef]
- Wang, Y.; Vuran, M.C.; Goddard, S. Stochastic Analysis of Energy Consumption in Wireless Sensor Networks. In Proceedings of the 2010 7th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Boston, MA, USA, 21–25 June 2010; pp. 1–9. [Google Scholar]
- Gallucio, L.; Palazzo, S. End-to-End Delay and Network Lifetime Analysis in a Wireless Sensor Network Performing Data Aggregation. In Proceedings of the 2010 In 2009 IEEE Global Telecommunications Conference (GLOBECOM 2009), Honolulu, HI, USA, 30 November–4 December 2010; pp. 1–6. [Google Scholar]
- Li, Z.; Peng, Y.; Qiao, D.; Zhang, W. Joint Aggregation and MAC design to prolong sensor network lifetime. In Proceedings of the 2013 21st IEEE International Conference on Network Protocols (ICNP), Goettingen, Germany, 7–10 October 2013; pp. 1–10. [Google Scholar]
- Li, Z.; Peng, Y.; Qiao, D.; Zhang, W. LBA: Lifetime balanced data aggregation in low duty cycle sensor networks. In Proceedings of the 31st Annual IEEE International Conference on Computer Communications (IEEE INFOCOM 2012), Orlando, FL, USA, 25–30 March 2012; pp. 1844–1852. [Google Scholar]
- Guntupalli, L.; Martinez-Bauset, J.; Li, F.Y.; Weitnauer, A. Aggregated packet transmission in duty-cycled WSNs: Modeling and performance evaluation. IEEE Trans. Veh. Technol. 2016, 66, 563–579. [Google Scholar] [CrossRef]
- Portillo, C.; Martinez-Bauset, J.; Pla, V.; Casares-Giner, V. Energy Modeling and Analysis for IoT Sensor Devices: A DTMC-Based Approach. In Proceedings of the Workshop on Innovation on Information and Communication Technologies (ITACA-WIICT 2018), Valencia, Spain, 13 July 2018; pp. 126–142. [Google Scholar]
- Portillo, C.; Martinez-Bauset, J.; Pla, V.; Casares-Giner, V. Modeling of Duty-Cycled MAC Protocols for Heterogeneous WSN with Priorities. Electronics 2020, 9, 467. [Google Scholar] [CrossRef]
- Portillo, C.; Martinez-Bauset, J.; Pla, V.; Casares-Giner, V. Heterogeneous WSN Modeling: Packet Transmission with Aggregation of Traffic. In Proceedings of the Interdisciplinary Conference on Mechanics, Computers and Electrics (ICMECE 2022), Barcelona, Spain, 6–7 October 2022; pp. 278–283. [Google Scholar]
- Pereira, F.; Correia, R.; Carvalho, N.B. Comparison of active and passive sensors for IoT applications. In Proceedings of the 2018 IEEE Wireless Power Transfer Conference (WPTC), Montreal, QC, Canada, 3–7 June 2018; pp. 1–3. [Google Scholar]
- Guntupalli, L.; Martinez-Bauset, J.; Li, F.Y. Performance of Frame Transmissions and Event-triggered Sleeping in Duty-Cycled WSNs with Error-Prone Wireless Links. Comput. Netw. 2018, 134, 215–227. [Google Scholar] [CrossRef]
- Martinez-Bauset, J.; Guntupalli, L.; Li, F.Y. Performance analysis of synchronous duty-cycled MAC protocols. IEEE Wirel. Commun. Lett. 2015, 4, 469–472. [Google Scholar] [CrossRef]
- Portillo, C.; Martinez-Bauset, J.; Pla, V.; Casares-Giner, V. The State Transition Probabilities of the Two 2D-DTMC with Traffic Aggregation. Technical Note. Available online: https://personales.upv.es/jmartine/public/2DDTMC.pdf (accessed on 10 June 2024).
- MICAz Data Sheet. Crossbow Technology Incorporated, San Jose, CA, USA. Available online: http://courses.ece.ubc.ca/494/files/MICAz_Datasheet.pdf (accessed on 1 April 2024).
- Zhang, S. Modeling, Analysis and Design of Energy Harvesting Communication Systems. Ph.D. Thesis, University of Rochester, Rochester, NY, USA, 2013. [Google Scholar]
- Kramer, M.; Geraldy, A. Energy Measurements for Micaz Node; Technical Report KrGe06; University of Kaiserslautern: Kaiserslautern, Germany, 2006; pp. 1–6. [Google Scholar]
- Yang, O.; Heinzelman, W. Modeling and throughput analysis for SMAC with a finite queue capacity. In Proceedings of the 2009 International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Melbourne, Australia, 7–10 December 2009; pp. 409–414. [Google Scholar]
- Yang, O.; Heinzelman, W. Modeling and performance analysis for duty-cycled MAC protocols with applications to S-MAC and X-MAC. IEEE Trans. Mob. Comput. 2012, 11, 905–921. [Google Scholar] [CrossRef]
- Portillo, C.; Martinez-Bauset, J.; Pla, V. Modelling of S-MAC for Heterogeneous WSN. In Proceedings of the 2018 9th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Paris, France, 26–28 February 2018; pp. 1–6. [Google Scholar]







| Cycle time (T) | 60 ms | Propagation delay () | 0.1 s |
| , , and | 0.18 ms | Slot time () | 0.1 ms |
| 1.716 ms | Contention window (W) | 128 slots | |
| DATA packet size (S) | 50 bytes | Queue size (Q) | 10 packets |
| update supercycle () | 20 cycles | 80 supercycles | |
| Transmission power () | 52 mW | Reception power () | 59 mW |
| Sleep power consumption () | W | ||
| Maximum frame size | packets | ||
| Nodes number | Packets arrival rate (packets/s) | ||
| , | , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Portillo, C.; Martinez-Bauset, J.; Pla, V.; Casares-Giner, V. Energy Consumption Modeling for Heterogeneous Internet of Things Wireless Sensor Network Devices: Entire Modes and Operation Cycles Considerations. Telecom 2024, 5, 723-746. https://doi.org/10.3390/telecom5030036
Portillo C, Martinez-Bauset J, Pla V, Casares-Giner V. Energy Consumption Modeling for Heterogeneous Internet of Things Wireless Sensor Network Devices: Entire Modes and Operation Cycles Considerations. Telecom. 2024; 5(3):723-746. https://doi.org/10.3390/telecom5030036
Chicago/Turabian StylePortillo, Canek, Jorge Martinez-Bauset, Vicent Pla, and Vicente Casares-Giner. 2024. "Energy Consumption Modeling for Heterogeneous Internet of Things Wireless Sensor Network Devices: Entire Modes and Operation Cycles Considerations" Telecom 5, no. 3: 723-746. https://doi.org/10.3390/telecom5030036
APA StylePortillo, C., Martinez-Bauset, J., Pla, V., & Casares-Giner, V. (2024). Energy Consumption Modeling for Heterogeneous Internet of Things Wireless Sensor Network Devices: Entire Modes and Operation Cycles Considerations. Telecom, 5(3), 723-746. https://doi.org/10.3390/telecom5030036







