Phase Preserving Balanced Truncation for Order Reduction of Positive Real Systems
Abstract
:1. Introduction
2. Preliminaries
2.1. Balanced Truncation (BT)
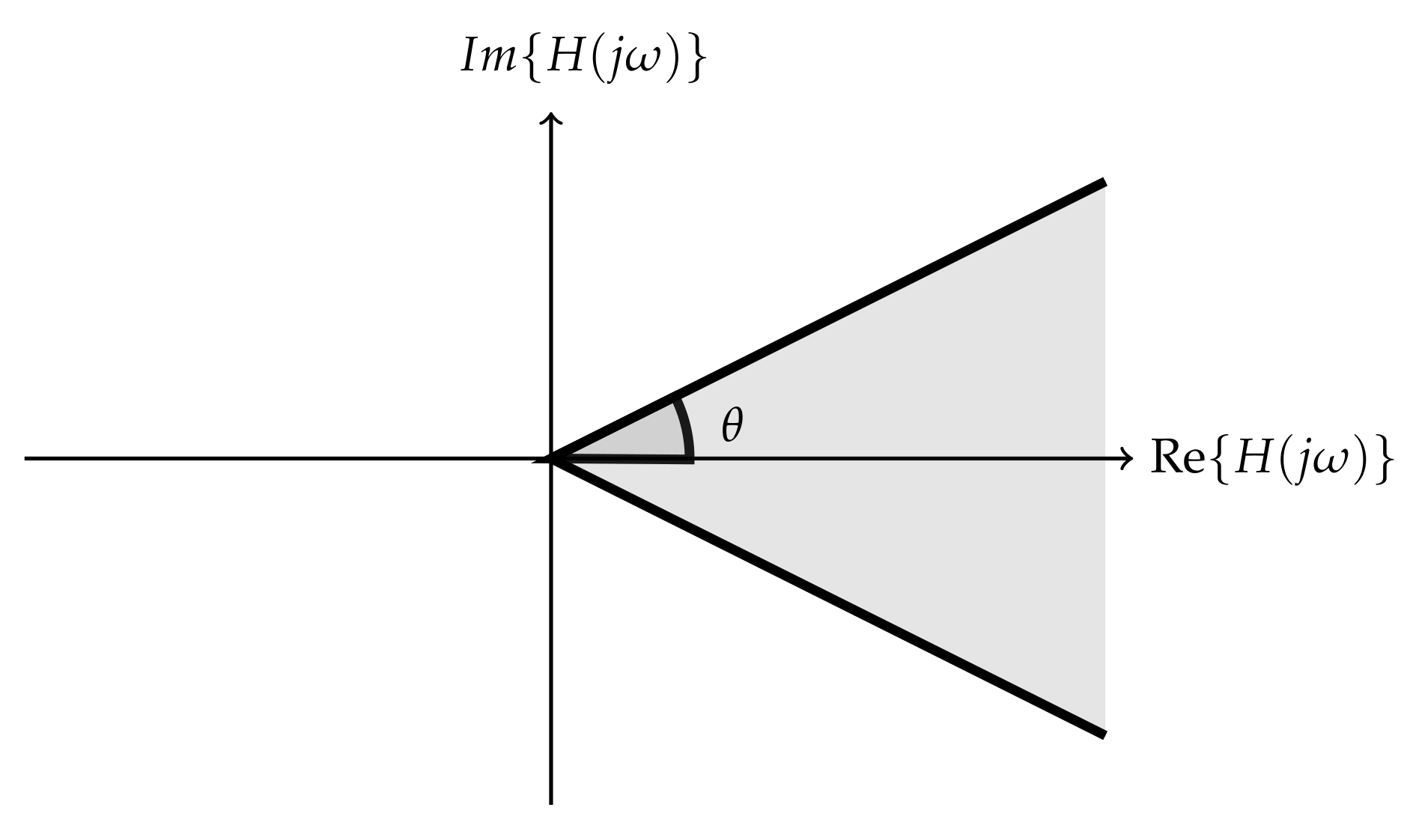
2.2. Conic Positive Real Balanced Truncation (CPRBT)
3. Phase Preserving Balanced Truncation
| Algorithm 1: Phase preserving balanced truncation |
|
4. Illustrative Examples
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moore, B. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Glover, K. All optimal Hankel-norm approximations of linear multivariable systems and their L∞ error bounds. Int. J. Control 1984, 39, 1115–1193. [Google Scholar] [CrossRef]
- Kavranoǧlu, D.; Bettayeb, M. Characterization of the solution to the optimal H∞ model reduction problem. Syst. Control Lett. 1993, 20, 99–107. [Google Scholar] [CrossRef]
- Feldmann, P.; Freund, R.W. Efficient linear circuit analysis by padé approximation via the Lanczos process. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1995, 14, 639–649. [Google Scholar] [CrossRef]
- Pillage, L.T.; Rohrer, R.A. Asymptotic waveform evaluation for timing analysis. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1990, 9, 352–366. [Google Scholar] [CrossRef] [Green Version]
- Chiprout, E.; Nakhla, M.S. Asymptotic Waveform Evaluation and Moment Matching for Interconnect Analysis; Kluwer: Norwell, MT, USA, 1994. [Google Scholar]
- Odabasioglu, A.; Celik, M.; Pileggi, L.T. PRIMA: Passive reduced-order interconnect macromodeling algorithm. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1998, 17, 645–654. [Google Scholar] [CrossRef] [Green Version]
- Enns, D.F. Model reduction with balanced realizations: An error bound and a frequency weighted generalization. In Proceedings of the 23rd IEEE Conference on Decision and Control, Las Vegas Hilton, LV, USA, 12–14 December 1984; pp. 127–132. [Google Scholar]
- Gawronski, W.; Juang, J.-N. Model reduction in limited time and frequency intervals. Int. J. Syst. Sci. 1990, 21, 349–376. [Google Scholar] [CrossRef]
- Wang, G.; Sreeram, V.; Liu, W. A new frequency-weighted balanced truncation method and an error bound. IEEE Trans. Autom. Control 1999, 44, 1734–1737. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.; Sreeram, V. Factorization-based frequency-weighted optimal Hankel-norm model reduction. Asian J. Control 2020, 22, 2106–2118. [Google Scholar] [CrossRef]
- Toor, H.I.; Imran, M.; Ghafoor, A.; Kumar, D.; Sreeram, V.; Rauf, A. Frequency limited model reduction techniques for discrete-time systems. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 345–349. [Google Scholar] [CrossRef]
- Haider, S.; Ghafoor, A.; Imran, M.; Malik, F.M. Time-limited Gramians-based model order reduction for second-order form systems. Trans. Inst. Meas. Control 2019, 41, 2310–2318. [Google Scholar] [CrossRef]
- Liang, W.; Chen, H.-B.; He, G.; Chen, J. Model order reduction based on dynamic relative gain array for mimo systems. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2507–2511. [Google Scholar] [CrossRef]
- Alsmadi, O.; Al-Smadi, A.; Gharaibeh, E. Firefly artificial intelligence technique for model order reduction with substructure preservation. Trans. Inst. Meas. Control 2019, 10, 2875–2885. [Google Scholar] [CrossRef]
- Lu, K.; Jin, Y.; Huang, P.; Zhang, F.; Zhang, H.; Fu, C.; Chen, Y. The applications of POD method in dual rotor-bearing systems with coupling misalignment. Mech. Syst. Signal Process. 2021, 150, 107236. [Google Scholar] [CrossRef]
- Bui-Thanh, T.; Willcox, K.; Ghattas, O. Model reduction for large-scale systems with high-dimensional parametric input space. SIAM J. Sci. Comput. 2008, 30, 3270–3288. [Google Scholar] [CrossRef]
- Opdenacker, P.C.; Jonckheere, E.A. A contraction mapping preserving balanced reduction scheme and its infinity norm error bounds. IEEE Trans. Circuits Syst. 1988, 35, 184–189. [Google Scholar] [CrossRef]
- Tu, K.; Du, X.; Fan, P. Negative imaginary balancing for mode reduction of LTI negative-imaginary systems. In Proceedings of the 26th Chinese Control and Decision Conference, Changsha, China, 31 May–2 June 2014; pp. 4234–4239. [Google Scholar]
- Phillips, J.R.; Daniel, L.; Silveira, L.M. Guaranteed passive balancing transformations for model order reduction. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2003, 22, 1027–1041. [Google Scholar] [CrossRef]
- Salehi, Z.; Karimaghaee, P.; Khooban, M.-H. Mixed positive-bounded balanced truncation. IEEE Trans. Circuits Syst. Ii: Express Briefs 2021, 68, 2488–2492. [Google Scholar] [CrossRef]
- Salehi, Z.; Karimaghaee, P.; Khooban, M.-H. A new passivity preserving model order reduction method: Conic positive real balanced truncation method. IEEE Trans. Syst. Man Cybern. Syst. 2021. [Google Scholar] [CrossRef]
- Huang, C.H.; Ioannou, P.A.; Maroulas, J.; Safonov, M.G. Design of strictly positive real systems using constant output feedback. IEEE Trans. Autom. Control 1999, 44, 569–573. [Google Scholar] [CrossRef]
- Liu, M.; Lam, J.; Zhu, B.; Kwok, K.W. On positive realness, negative imaginariness, and H∞ control of state-space symmetric systems. Automatica 2019, 101, 190–196. [Google Scholar] [CrossRef]
- Misgeld, B.J.; Hewing, L.; Liu, L.; Leonhardt, S. Closed-loop positive real optimal control of variable stiffness actuators. Control Eng. Pract. 2019, 82, 142–150. [Google Scholar] [CrossRef]
- Brogliato, B.; Lozano, R.; Maschke, B.; Egeland, O. Positive Real Systems. In Dissipative Systems Analysis and Control; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Salehi, Z.; Karimaghaee, P.; Khooban, M.-H. Model order reduction of positive real systems based on mixed gramian balanced truncation with error bounds. Circuits Syst. Signal Process. 2021, 40, 5309–5327. [Google Scholar] [CrossRef]
- Cheng, X.; Scherpen, J.M.; Besselink, B. Balanced truncation of networked linear passive systems. Automatica 2019, 104, 17–25. [Google Scholar] [CrossRef] [Green Version]
- Zulfiqar, U.; Imran, M.; Ghafoor, A.; Liaqat, M. Time/frequency-limited positive-real truncated balanced realizations. IMA J. Math. Control Inf. 2020, 37, 64–81. [Google Scholar] [CrossRef]
- Pernebo, L.; Silverman, L. Model reduction via balanced state space representations. IEEE Trans. Autom. Control 1982, 27, 382–387. [Google Scholar] [CrossRef]
- Anderson, B.D.; Vongpanitlerd, S. Network Analysis and Synthesis: A Modern Systems Theory Approach; Dover: New York, NY, USA, 2013. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehi, Z.; Karimaghaee, P.; Salehi, S.; Khooban, M.-H. Phase Preserving Balanced Truncation for Order Reduction of Positive Real Systems. Automation 2022, 3, 84-94. https://doi.org/10.3390/automation3010004
Salehi Z, Karimaghaee P, Salehi S, Khooban M-H. Phase Preserving Balanced Truncation for Order Reduction of Positive Real Systems. Automation. 2022; 3(1):84-94. https://doi.org/10.3390/automation3010004
Chicago/Turabian StyleSalehi, Zeinab, Paknoosh Karimaghaee, Shabnam Salehi, and Mohammad-Hassan Khooban. 2022. "Phase Preserving Balanced Truncation for Order Reduction of Positive Real Systems" Automation 3, no. 1: 84-94. https://doi.org/10.3390/automation3010004
APA StyleSalehi, Z., Karimaghaee, P., Salehi, S., & Khooban, M.-H. (2022). Phase Preserving Balanced Truncation for Order Reduction of Positive Real Systems. Automation, 3(1), 84-94. https://doi.org/10.3390/automation3010004






