Finite-Element Analysis of Adjacent Concrete Box Girders Transversely Post-Tensioned at the Top Flanges Only
Abstract
:1. Introduction
2. Experimental Program
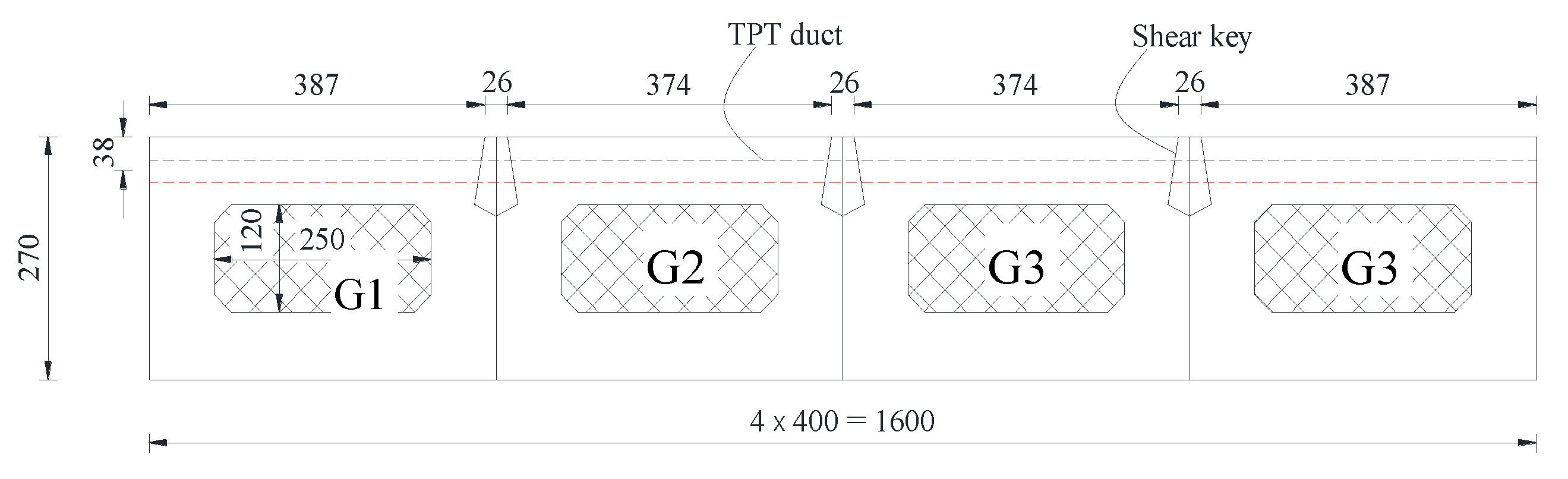
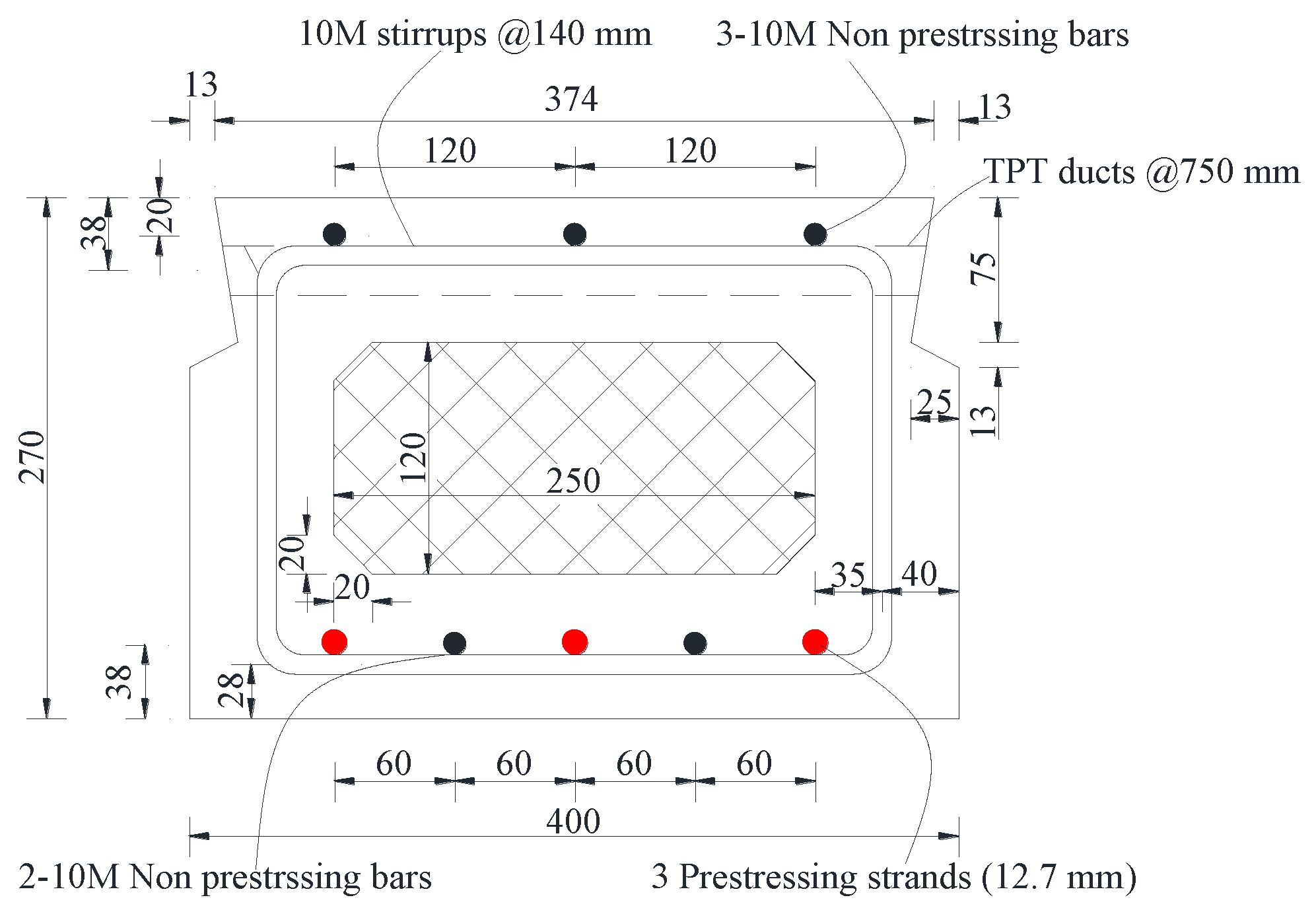
2.1. Details of Tested Bridge
2.2. Material Properties
2.3. Loading and Instrumentation
3. Characteristics of Finite-Element Model
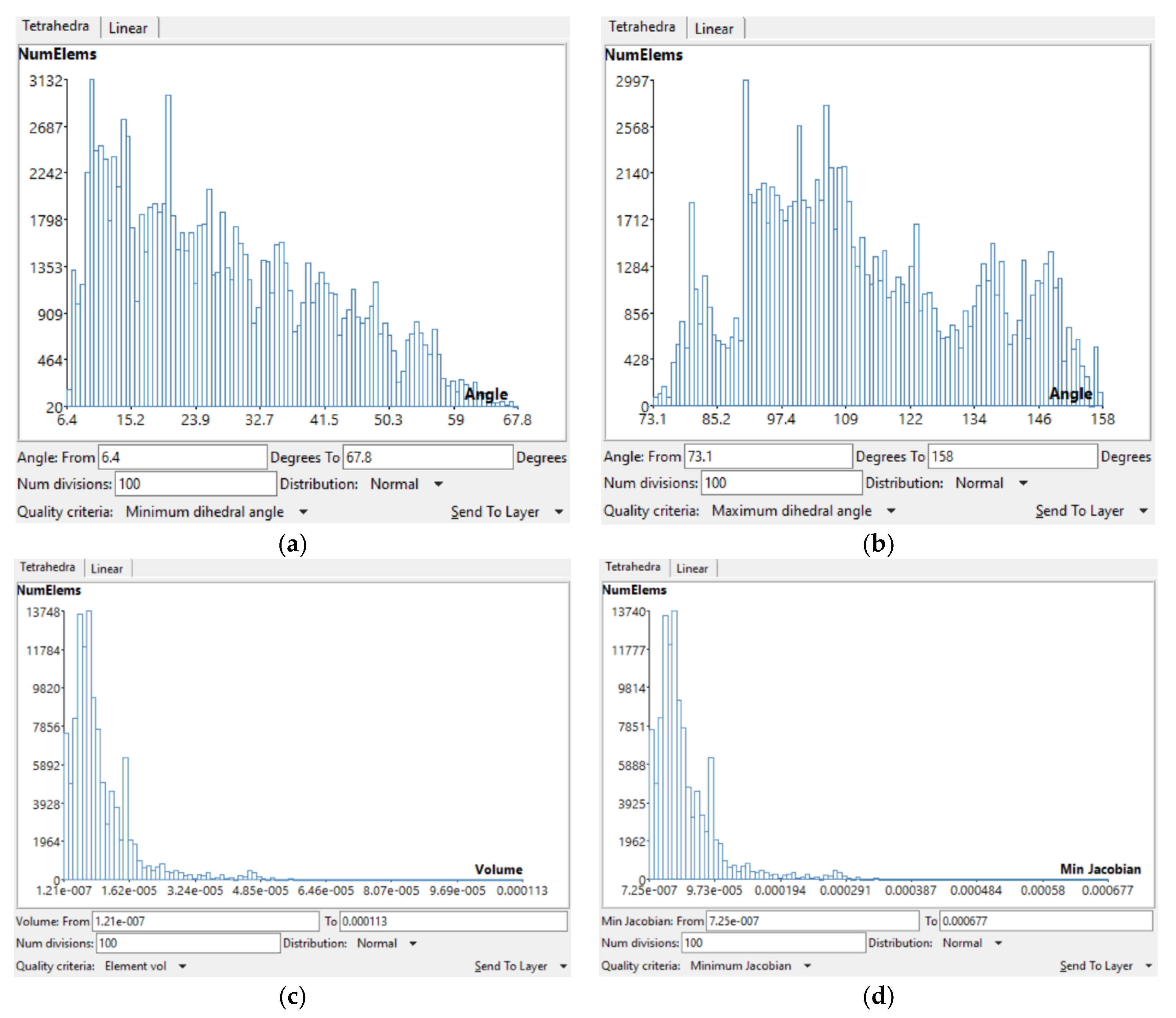
3.1. Geometry and Boundary Conditions
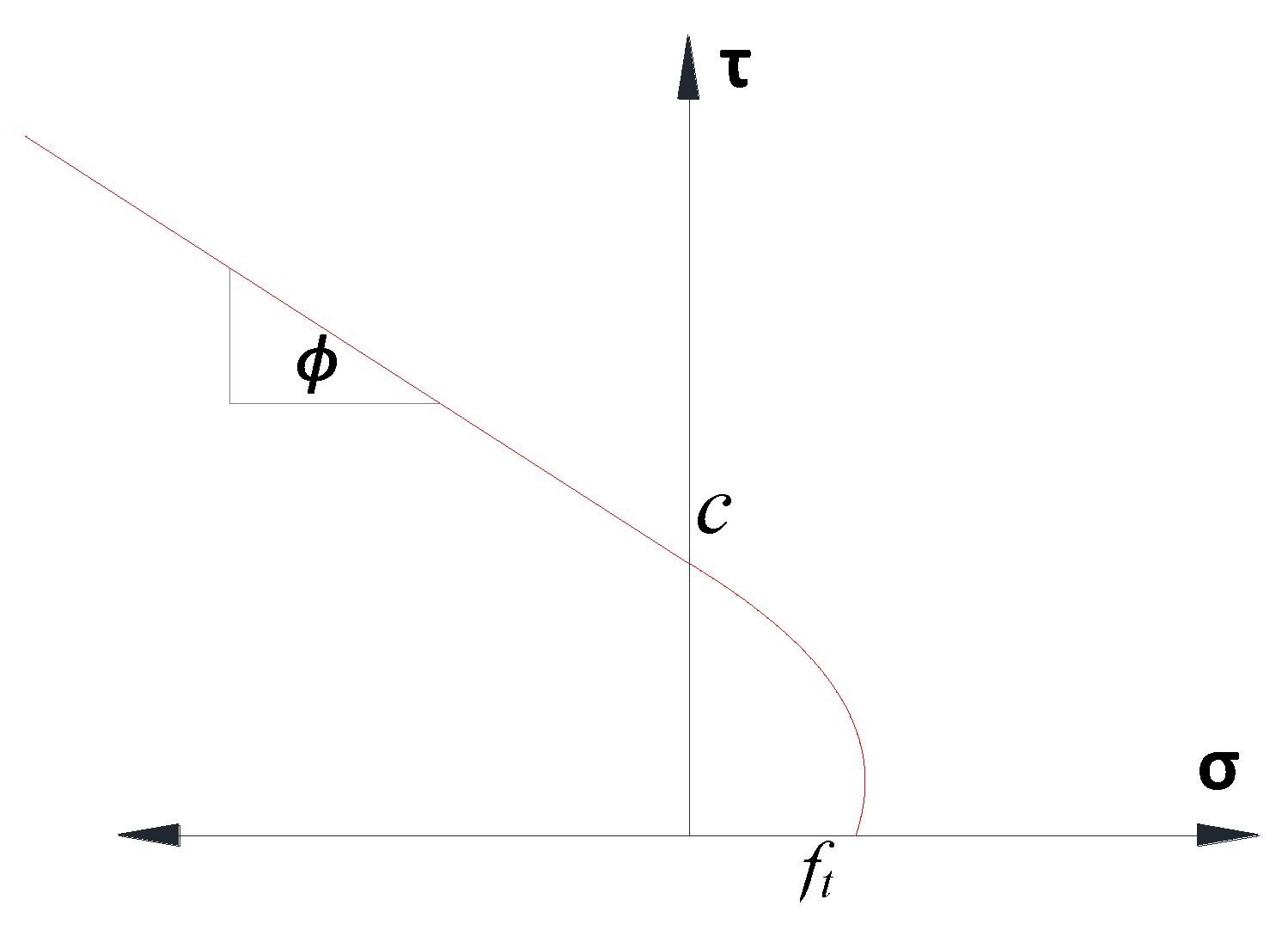
3.2. Concrete and Grout Material
3.3. Reinforcement Material
3.4. Loading and Bearing Plates
3.5. Bond Model
3.6. Interface and Bonding Materials
3.7. Continuum-Based Governing Equation
3.8. Load Application and Solution Method
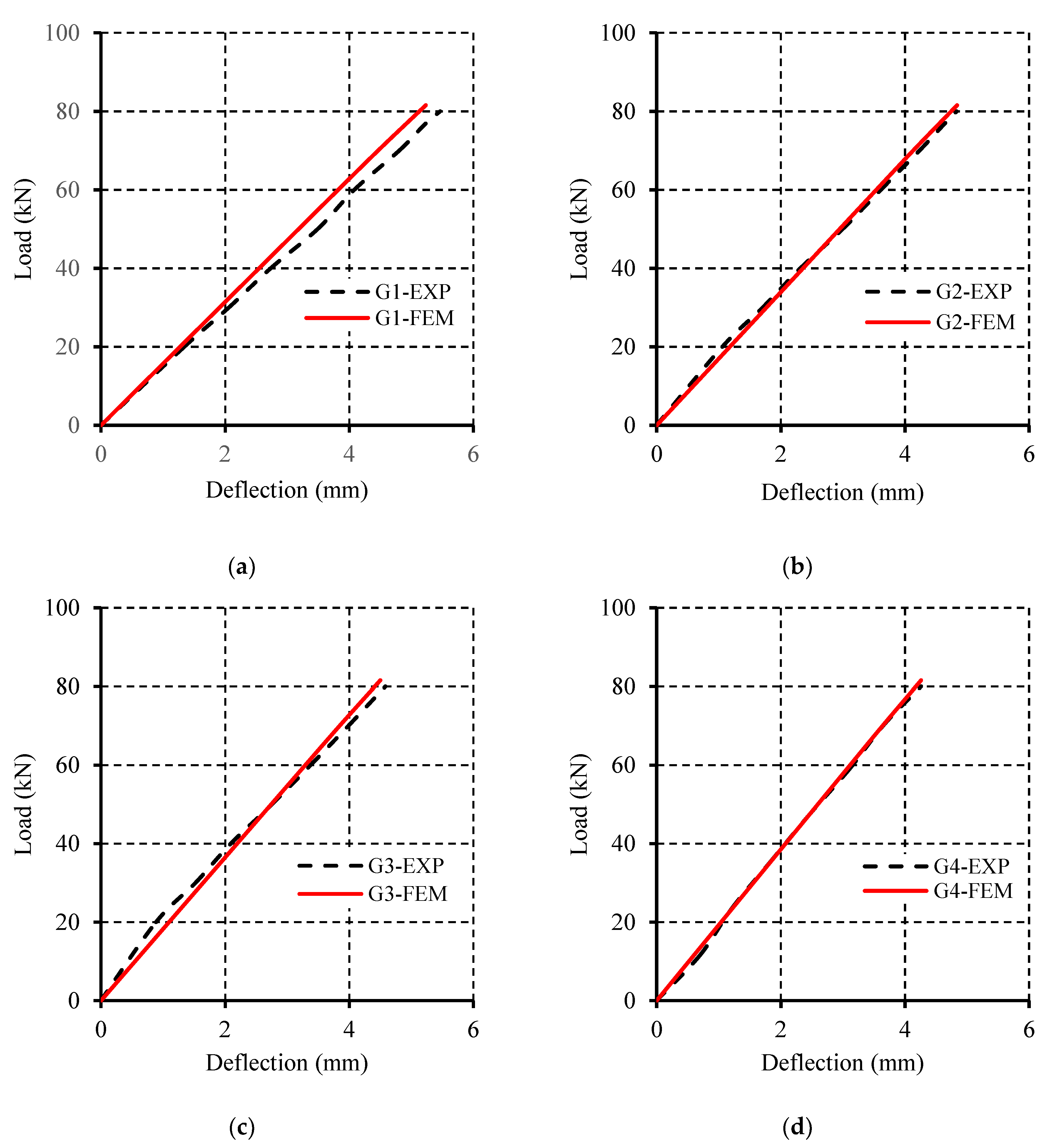
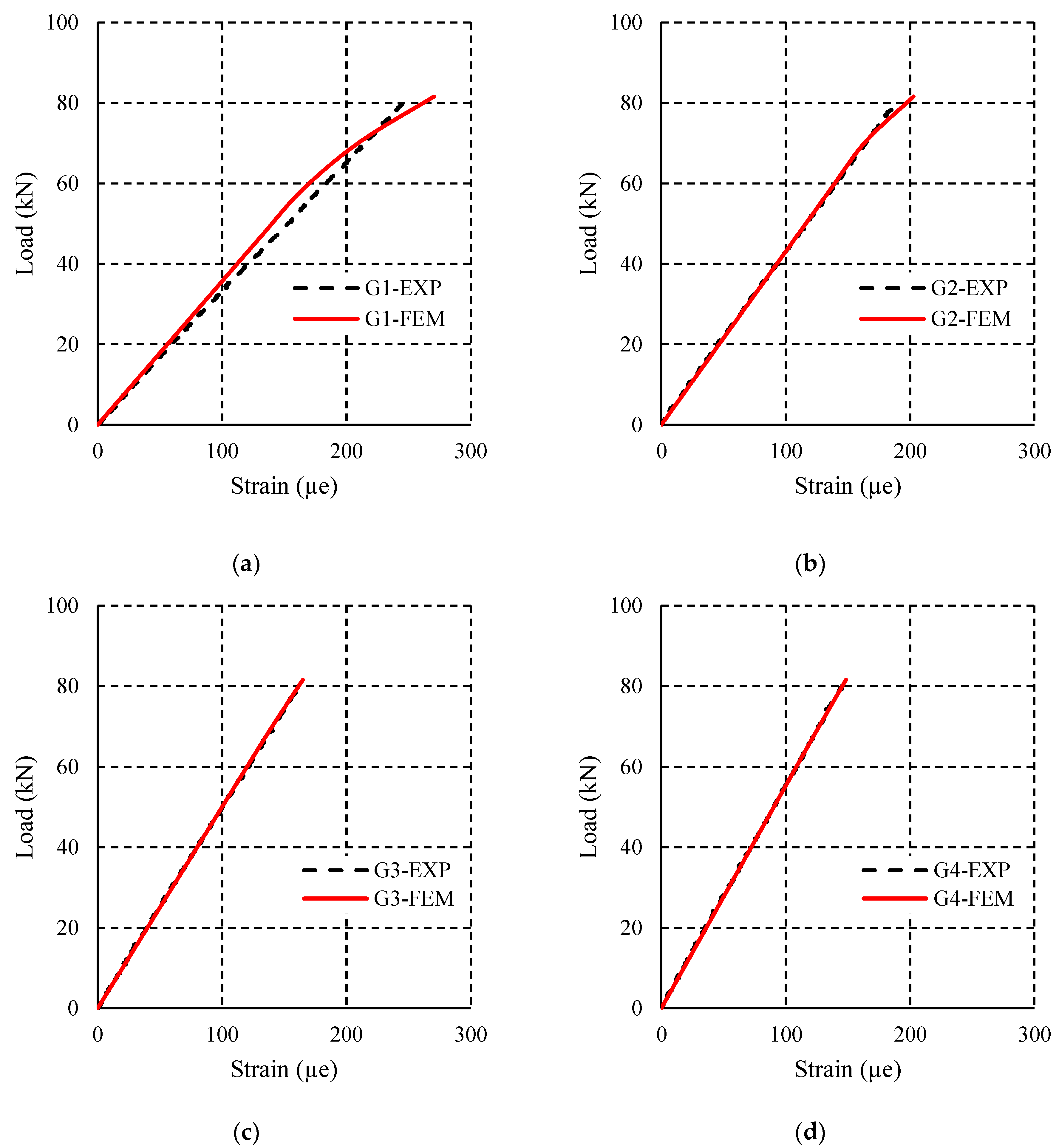
4. Model Validation
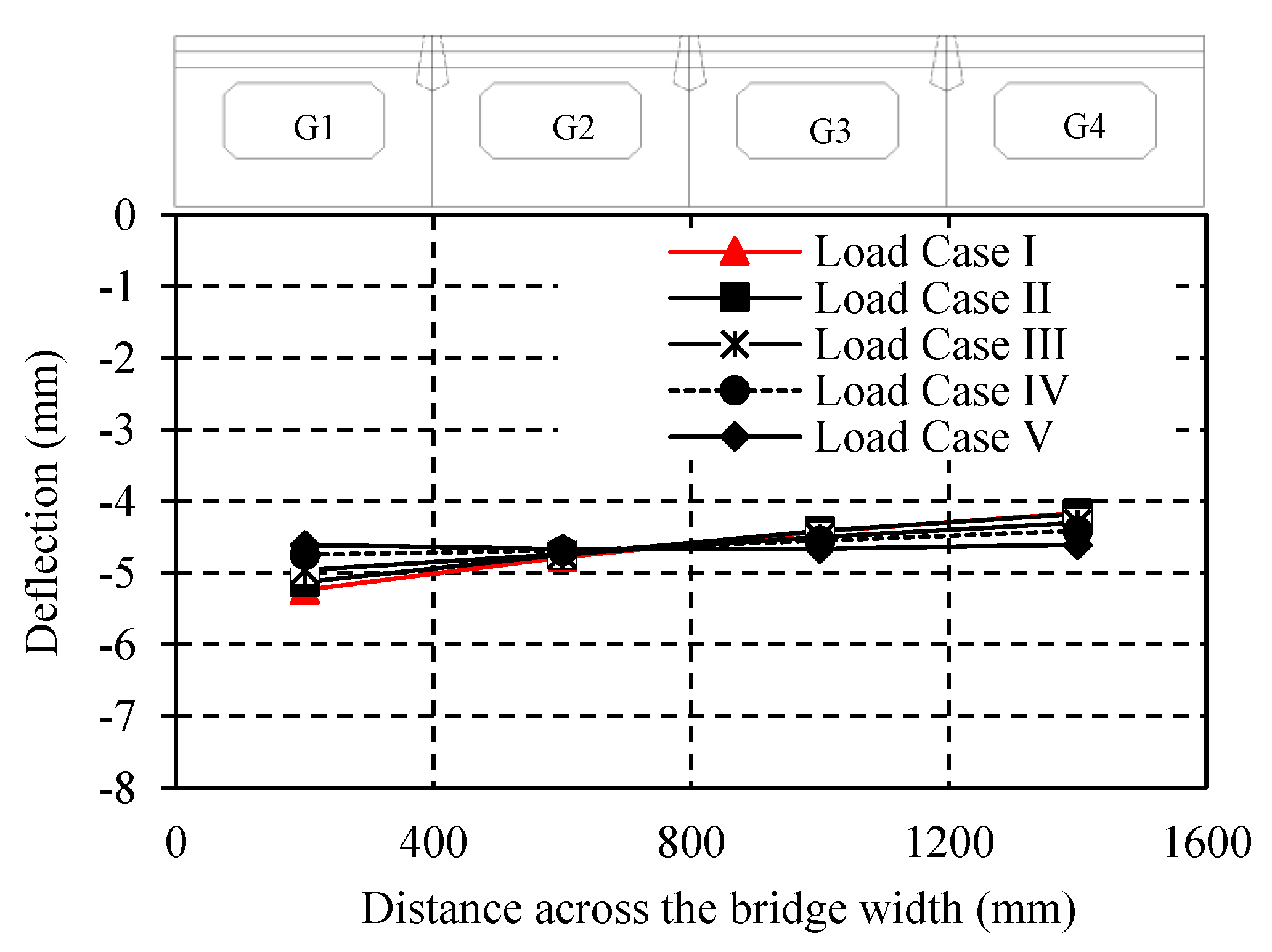
4.1. Service Load Validation
4.2. Ultimate Load Validation
5. Parametric Study and Discussion
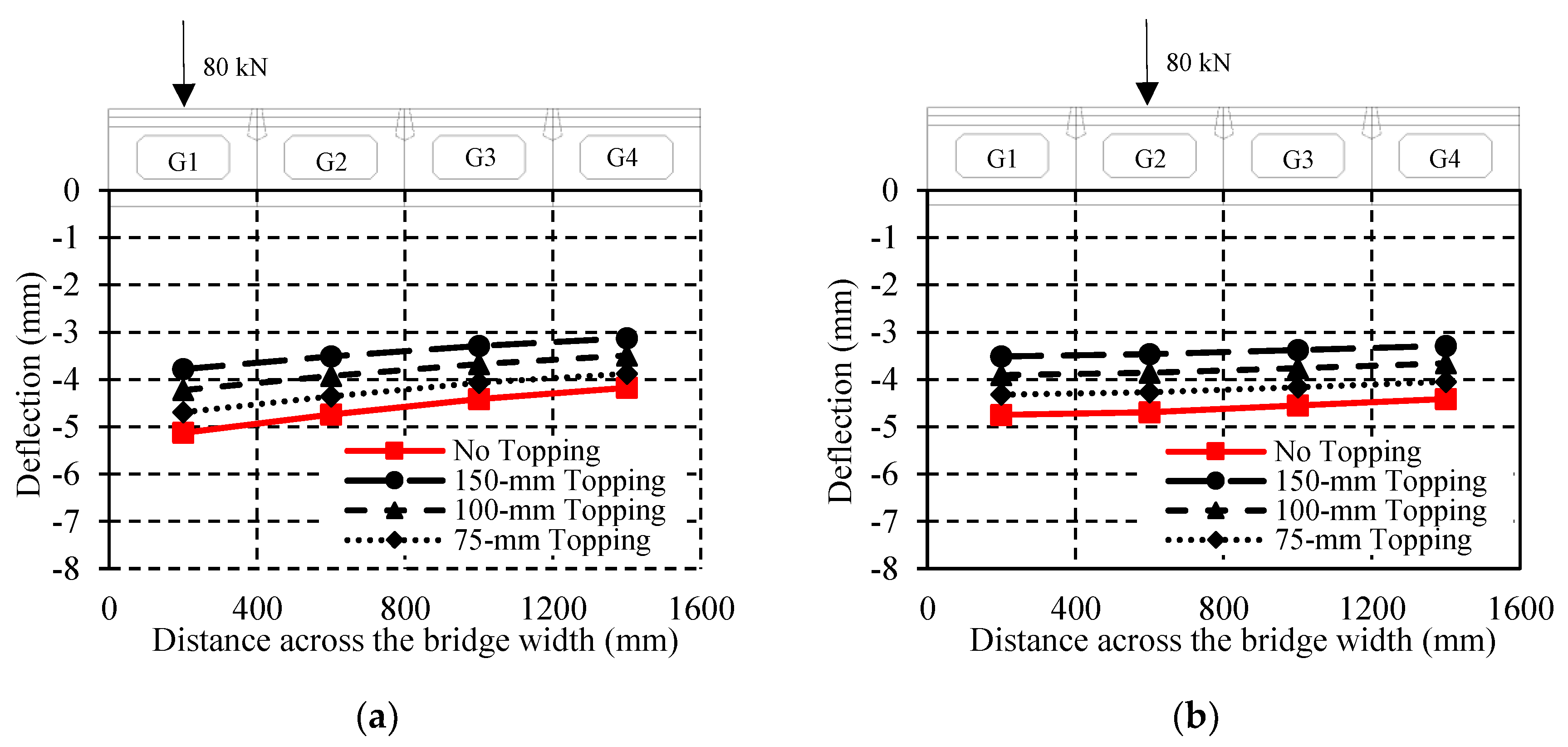
5.1. Effect of Adding Concrete Topping
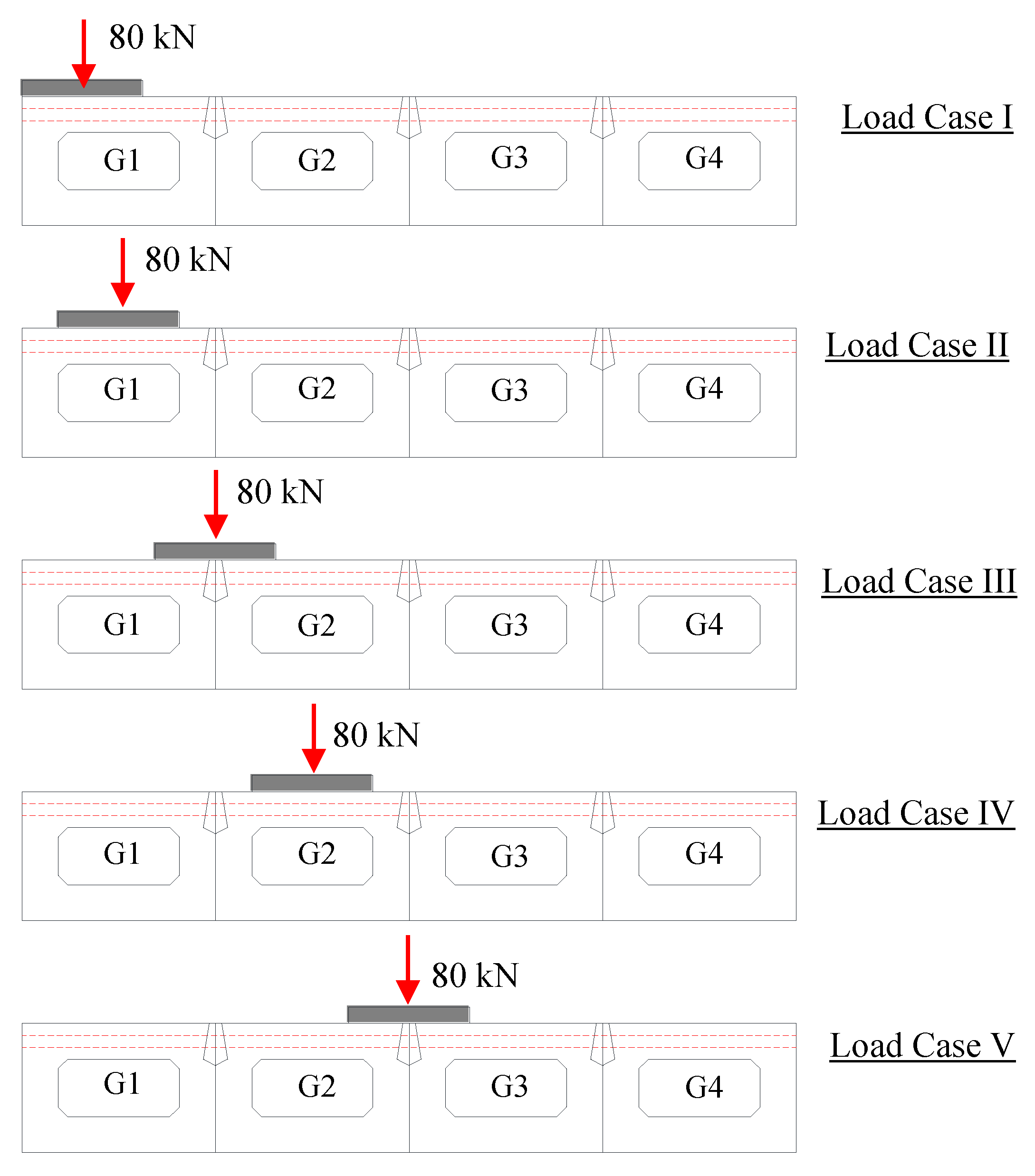
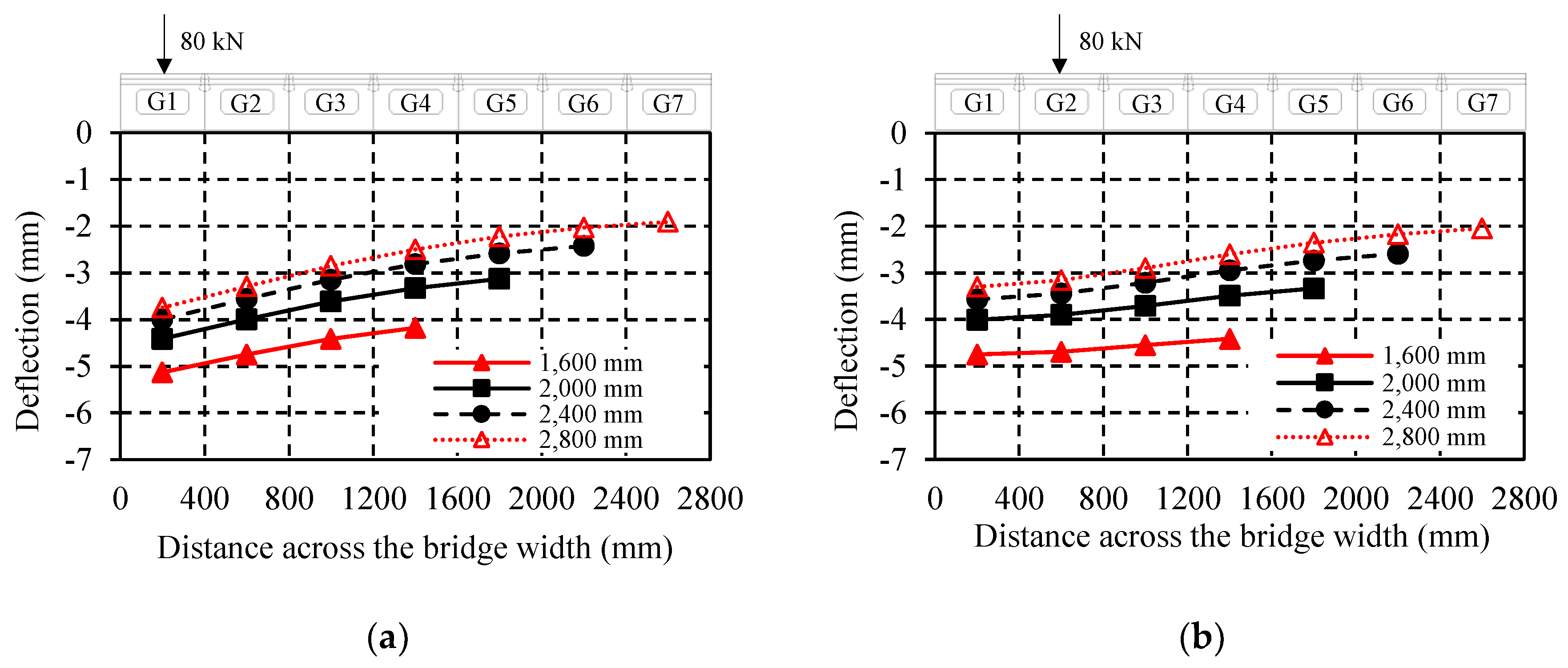
5.2. Effect of Load Location
5.3. Effect of Bridge Width
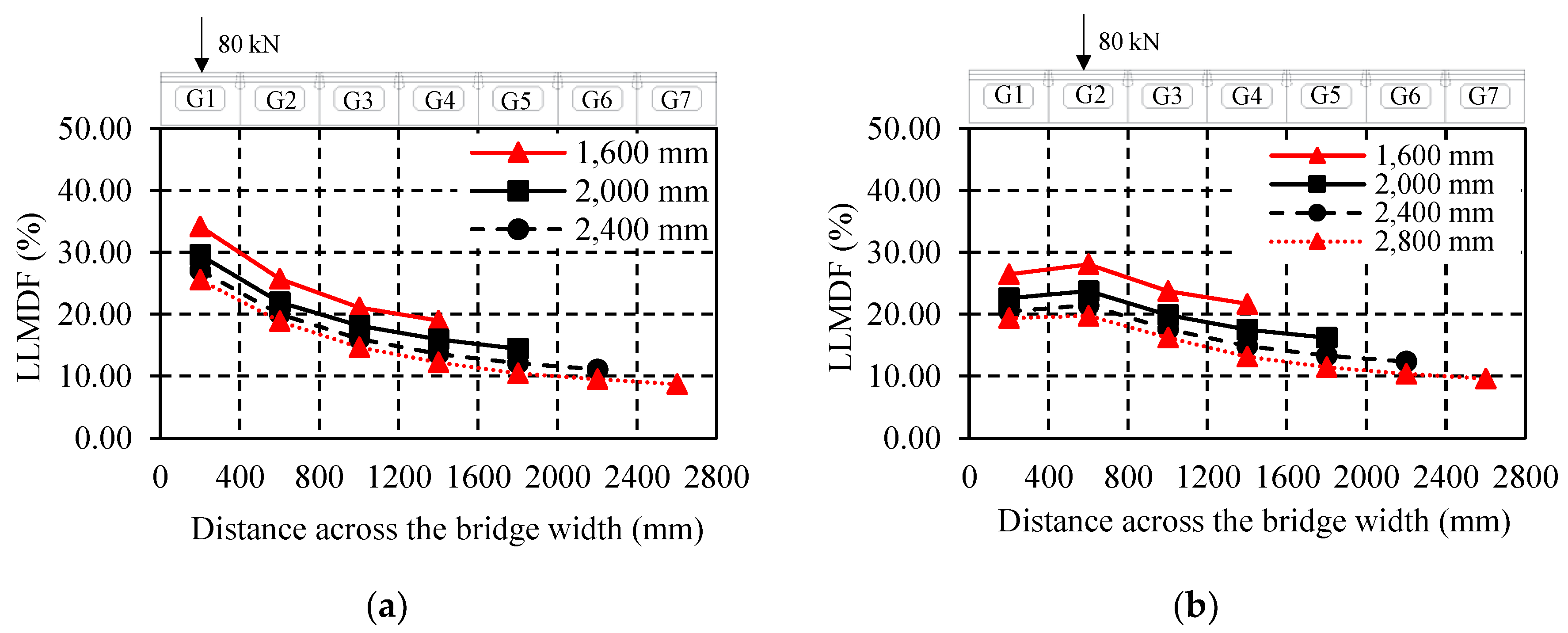
5.4. Evaluation of LLMDFs
6. Conclusions
- The presence of concrete topping enhanced the overall stiffness of the bridge model by limiting mid-span deflections. Mid-span deflections were reduced by 8, 17, and 25% when concrete topping of 75, 100 and 150-mm thickness, respectively, were used. Nevertheless, the LLMDFs were found to be insignificantly altered when a concrete topping was incorporated.
- The LLMDFs were evaluated for multiple wheel locations to determine the location associated with the maximum response. The exterior girder exhibited the maximum LLMDF when the load was placed at the farthest possible point across the bridge width. On the other hand, the interior girder G2 exhibited the maximum LLMDF when the wheel load was centered with the girder centerline (Load Case IV).
- To satisfy the minimum number of girders required to utilize the LLMDFs proposed by the AASHTO-LRFFD, different bridge widths consisting of five, six and seven girders were investigated. For each bridge width, the wheel load was placed transversely at different locations to estimate the maximum LLMDFs. The LLMDFs were found to be reduced when the bridge width was increased. The maximum LLMDF for the exterior girder dropped by 25% when the bridge width was increased to seven girders (2800 mm). A similar trend was observed for the interior girders.
- In lieu of size limitations dictated by the scaled bridge model, AASHTO LRFD-9 bridge design specifications were used to estimate the LLMDFs for both the exterior and the interior girders considering the actual dimensions of the one-third-scale bridge model. The obtained LLMDFs were found to be conservative by 39% and 16% for the interior and the exterior girders, respectively. This observation suggests that the existing LLMDFs proposed by AASHTO LRFD-9 could be used, as an initial step, to design the full-scale bridge structure of the tested bridge prototype.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, R.; Hlavacs, G.; Long, T.; Greuel, A. Full-scale testing of shear keys for adjacent box girder bridges. PCI J. 1999, 44, 80–90. [Google Scholar] [CrossRef] [Green Version]
- Hanna, K.; Morcous, G.; Tadros, M. Design, detailing, and testing of non-post-tensioned transverse connections in adjacent box-girder bridges. PCI J. 2011, 56, 94–107. [Google Scholar]
- Lall, J.; Alampalli, S.; DiCocco, E. Performance of full-depth shear keys in adjacent prestressed box beam bridges. PCI J. 1998, 43, 72–79. [Google Scholar] [CrossRef]
- Hanna, K.; Morcous, G.; Tadros, M. Transverse post-tensioning design and detailing of precast, prestressed concrete adjacent-box-girder bridges. PCI J. 2009, 54, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Hansen, J.; Hanna, K.; Tadros, M. Simplified transverse post-tensioning construction and maintenance of adjacent box girders. PCI J. 2012, 57, 64–79. [Google Scholar] [CrossRef]
- Sun, C.; Tadros, M.; Kopper, K.; Belill, T. Innovative precast concrete adjacent-box-beam system implemented in the St. Clair Road Bridge in Michigan. PCI J. 2018, 63, 41–50. [Google Scholar] [CrossRef]
- Labib, S.; El-Gendy, M.; El-Salakawy, E. Adjacent concrete box girders transversely post-tensioned at top flanges only: Experimental investigation. J. Bridge Eng. 2021, 26, 04021017. [Google Scholar] [CrossRef]
- Aktan, H.; Attanayake, U.; Ulku, E.; Ahlborn, T.; Deshpande, Y. Condition Assessment and Methods of Abatement of Prestressed Concrete Box-Beam Deterioration—Phase II; MDOT RC-1527; Michigan Department of Transportation: Detroit, MI, USA, 2007. [Google Scholar]
- Semendary, A.; Steinberg, E.; Walsh, K.; Barnard, E. Live-load moment-distribution factors for an adjacent precast prestressed concrete box beam bridge with reinforced UHPC shear key connections. J. Bridge Eng. 2017, 22, 04017088. [Google Scholar] [CrossRef]
- Grace, N.; Jensen, E.; Bebawy, M. Transverse post-tensioning arrangement for side-by-side box-beam bridges. PCI J. 2012, 57, 48–63. [Google Scholar] [CrossRef]
- Fu, C.; Pan, Z.; Ahmed, M. Transverse posttensioning design of adjacent precast solid multibeam bridges. J. Perform. Constr. Facil. 2011, 25, 223–230. [Google Scholar] [CrossRef]
- Hussein, H.; Sargand, S.; Al-Jhayyish, A.; Khoury, I. Contribution of transverse tie bars to load transfer in adjacent prestressed box-girder bridges with partial depth shear key. J. Perform. Constr. Facil. 2017, 31, 04016100. [Google Scholar] [CrossRef]
- Badwan, I.; Liang, R. Performance evaluation of precast posttensioned concrete multibeam deck. J. Perform. Constr. Facil. 2007, 21, 368–374. [Google Scholar] [CrossRef]
- Červenka, V.; Jendele, L.; Červenka, J. ATENA Program Documentation Part 1: Theory; Cevenka Consulting: Prague, Czech Republic, 2020. [Google Scholar]
- Coll, A.; Ribó, R.; Pasenau, M.; Escolano, E.; Perez, J.S.; Melendo, A.; Monros, A.; Gárate, J. GiD v.14 User Manual. 2018. Available online: www.gidhome.com (accessed on 25 January 2022).
- CSA. Canadian Highway Bridge Design Code (CHBDC), CSA S6-19; Canadian Standards Association (CSA): Toronto, ON, Canada, 2019. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 9th ed.; VR: Washington, DC, USA, 2020. [Google Scholar]
- Ghosn, M.; Moses, F.; Gobieski, J. Evaluation of steel bridges using in-service testing. Transp. Res. Rec. 1986, 1072, 71–78. [Google Scholar]
- CEB-FIP Model Code. First Draft, Committee Euro-International du Beton. Bull. D’inform. 1990, 195, 196. [Google Scholar]
- Vecchio, F.; Collins, M. Modified compression-field theory for reinforced concrete beams subjected to shear. ACI J. 1986, 83, 219–231. [Google Scholar]
- Dyngeland, T. Behavior of Reinforced Concrete Panels. Ph.D. Thesis, Trondheim University, Trondheim, Norway, 1989. [Google Scholar]
- Van Mier, J. Multiaxial strain-softening of concrete. Mater. Struct. 1986, 19, 179–190. [Google Scholar] [CrossRef]
- Bigaj, A. Structural Dependence of Rotation Capacity of Plastic Hinges. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1999. [Google Scholar]
- Jendele, L.; Cervenka, J. Finite element modelling of reinforcement with bond. Comput. Struct. 2006, 84, 1780–1791. [Google Scholar] [CrossRef]
- Mahmoud, K.; Anand, P.; El-Salakawy, E. 3-D Finite element modeling of prestressed hollow-core slabs strengthened with near surface mounted CFRP strips. Comput. Concr. 2018, 21, 607–622. [Google Scholar] [CrossRef]






| Bar Type | Bar Size | Diameter (mm) | Area (mm2) | Tensile Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|---|---|
| Non-prestressing bars | 10 M | 11.3 | 100 | 400 * | 200 |
| Prestressing strands | 13 | 12.7 | 98.7 | 1860 | 202 |
| Parameter | Concrete | Grout |
|---|---|---|
| Compressive strength, (MPa) | 55 | 85 |
| Modulus of elasticity, Ec (MPa) | 40,129 | 44,410 |
| Poisson’s ratio, µ | 0.2 | 0.2 |
| Fracture energy, Gf (N/m) | 97.5 | 130 |
| Tensile strength, ft (MPa) | 3.9 | 5.2 |
| Critical compressive displacement, wd (mm) | 0.5 | 0.5 |
| Crack model | Fixed | Fixed |
| Reduction in compressive strength factor, rc lim | 0.8 | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Labib, S.N.; El-Salakawy, E.F. Finite-Element Analysis of Adjacent Concrete Box Girders Transversely Post-Tensioned at the Top Flanges Only. CivilEng 2022, 3, 165-183. https://doi.org/10.3390/civileng3020011
Labib SN, El-Salakawy EF. Finite-Element Analysis of Adjacent Concrete Box Girders Transversely Post-Tensioned at the Top Flanges Only. CivilEng. 2022; 3(2):165-183. https://doi.org/10.3390/civileng3020011
Chicago/Turabian StyleLabib, Shady N., and Ehab F. El-Salakawy. 2022. "Finite-Element Analysis of Adjacent Concrete Box Girders Transversely Post-Tensioned at the Top Flanges Only" CivilEng 3, no. 2: 165-183. https://doi.org/10.3390/civileng3020011
APA StyleLabib, S. N., & El-Salakawy, E. F. (2022). Finite-Element Analysis of Adjacent Concrete Box Girders Transversely Post-Tensioned at the Top Flanges Only. CivilEng, 3(2), 165-183. https://doi.org/10.3390/civileng3020011







