Finite Element Framework for Efficient Design of Three Dimensional Multicomponent Composite Helicopter Rotor Blade System
Abstract
:1. Introduction
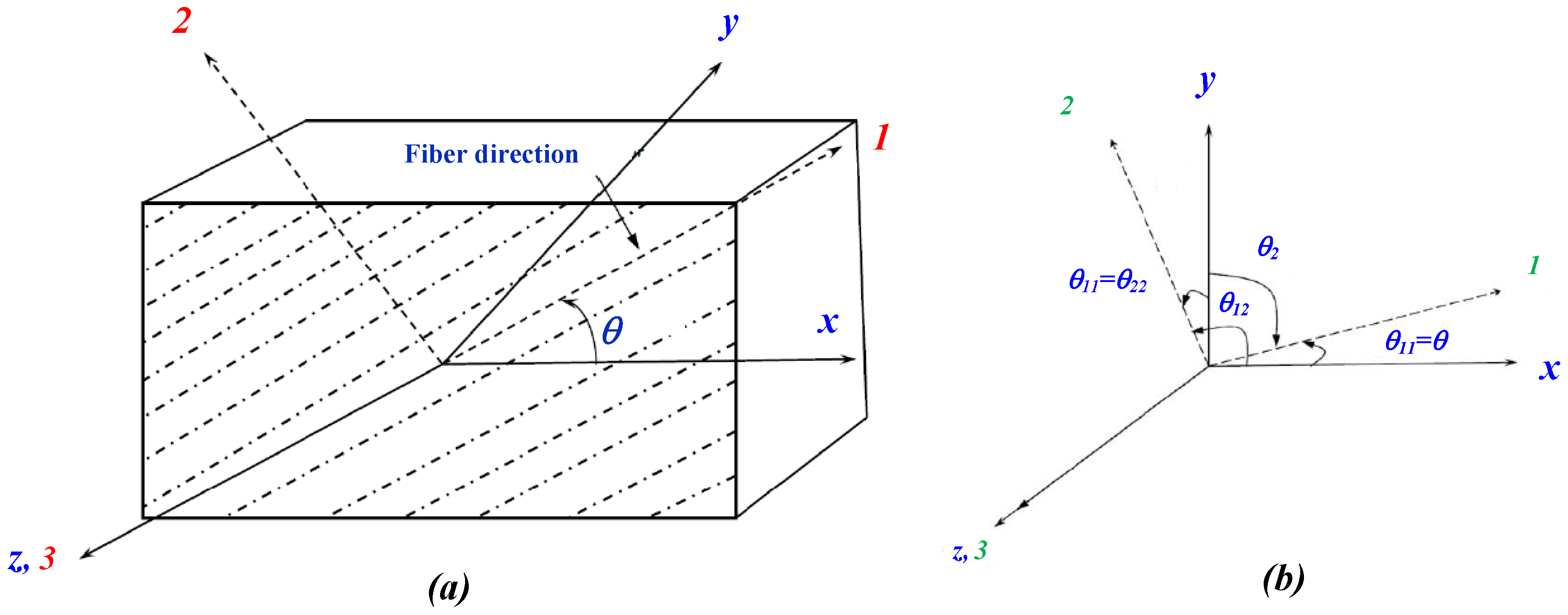
2. Constitutive Model for Composite Laminate
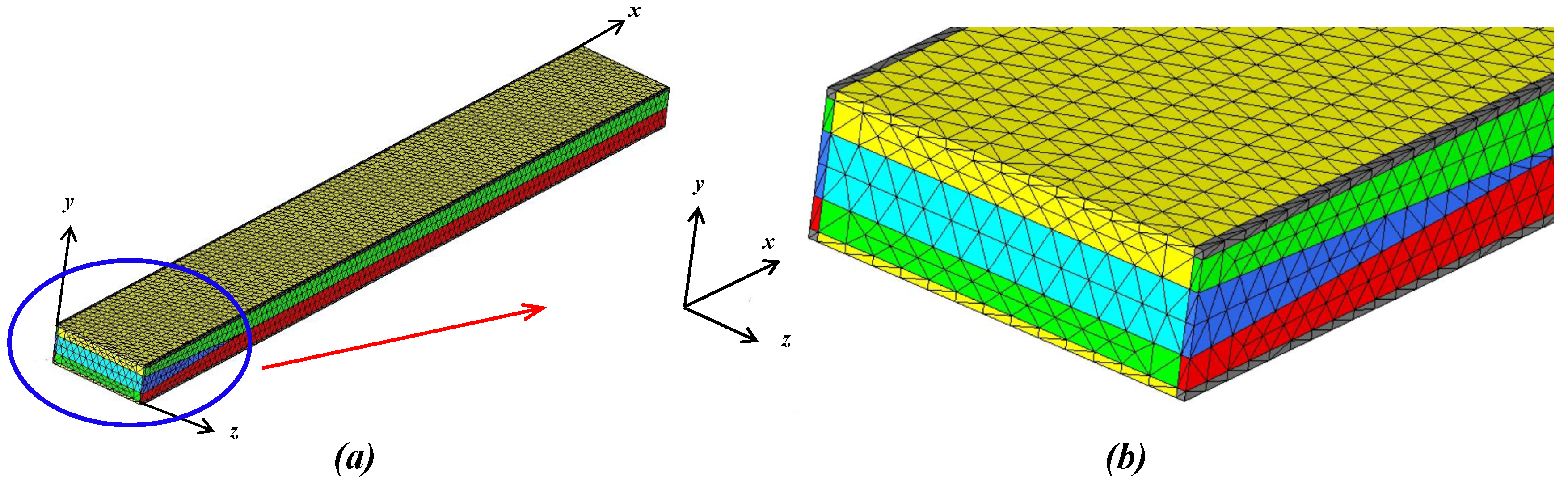
3. Finite Element Formulation
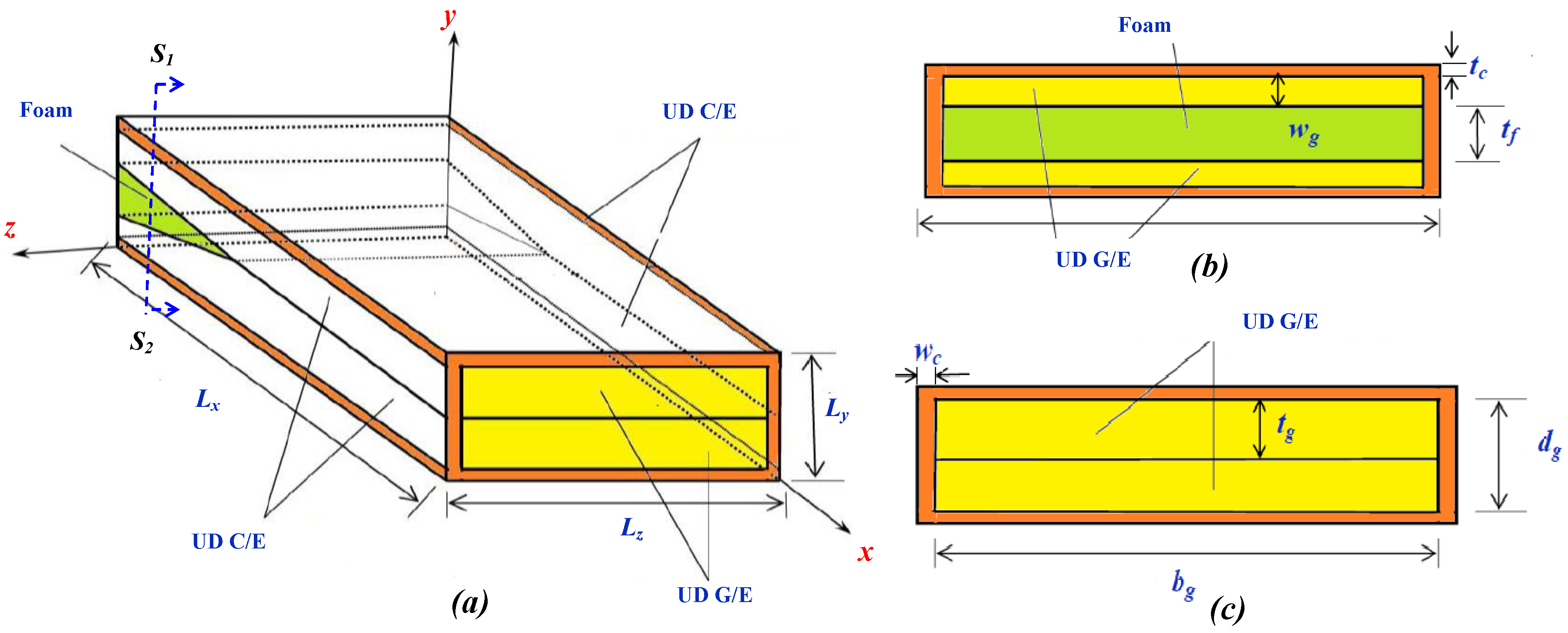
4. Beam Geometry and Material Parameters
5. Results and Discussions
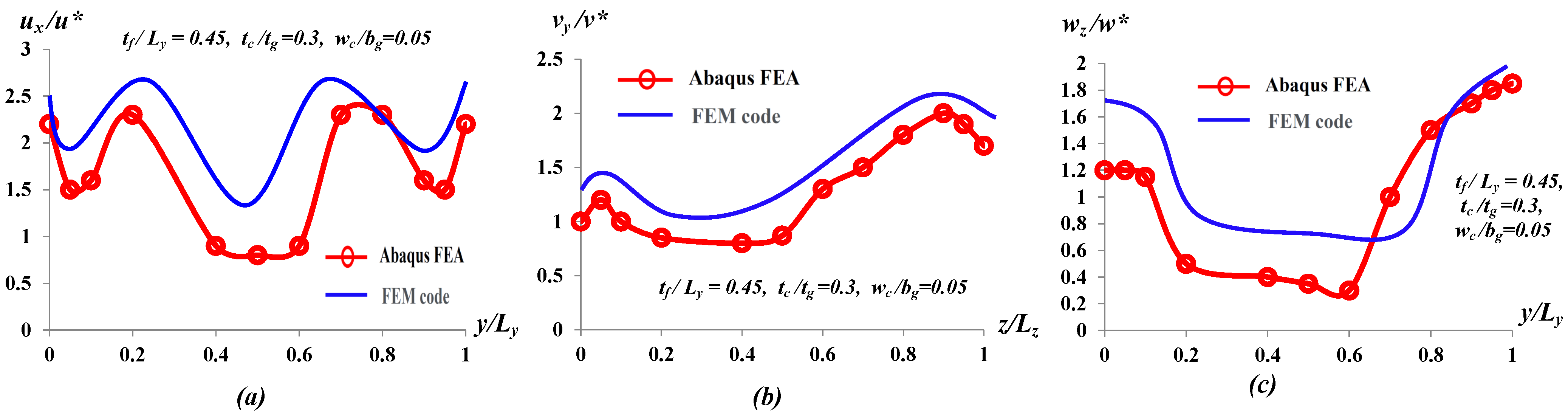
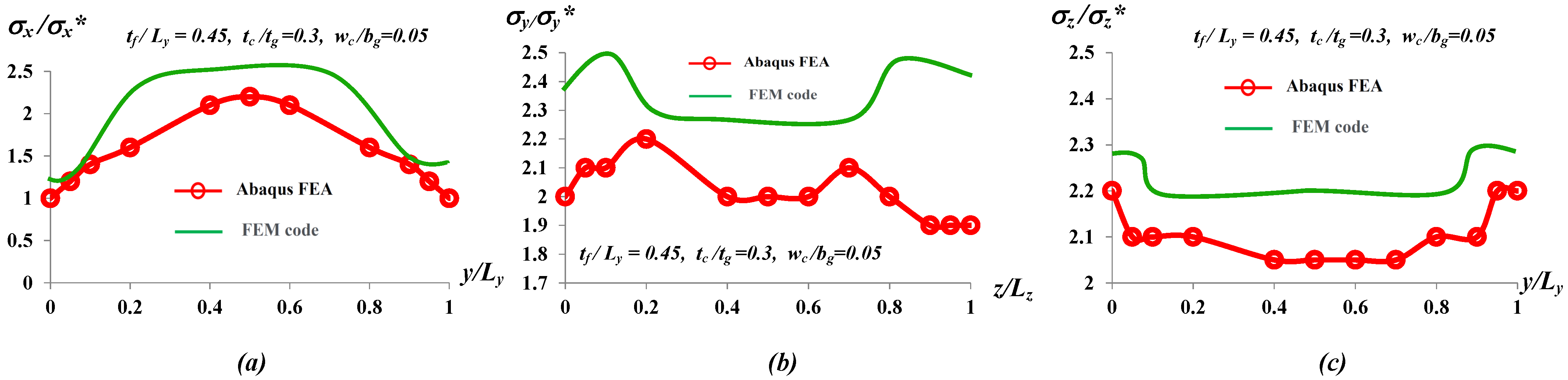
5.1. Tip Deformations and Stress Fields
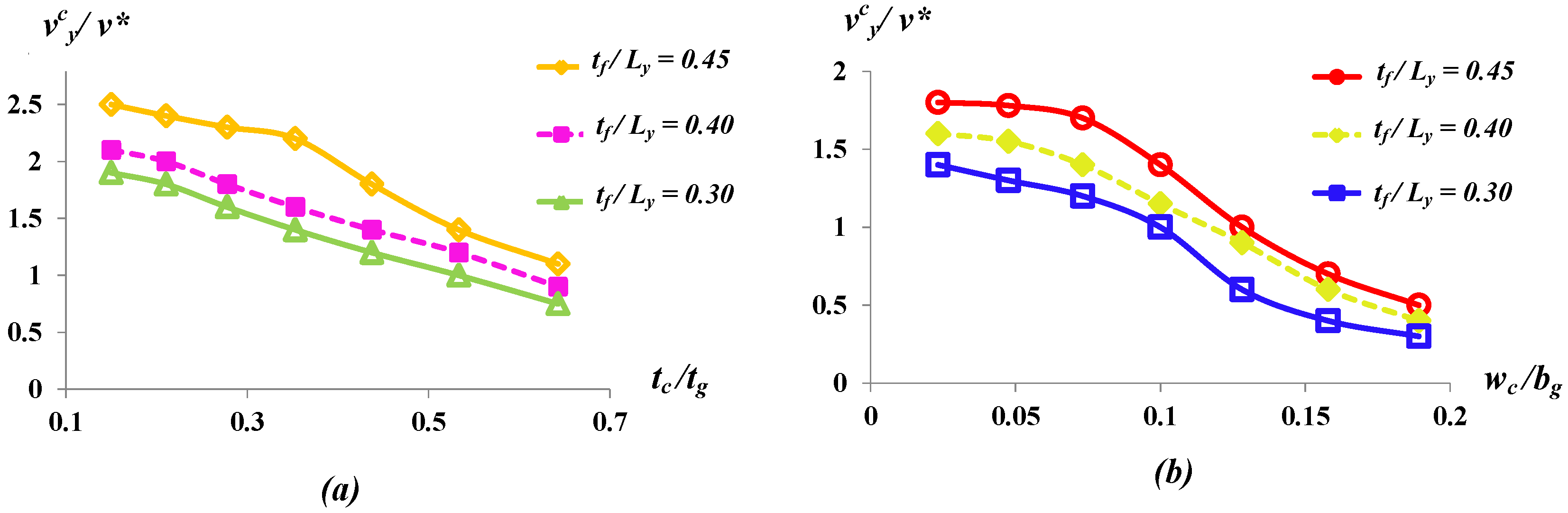
5.2. Efficient Design of Rotor Blade Geometry
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herakovich, C.T. Mechanics of Fibrous Composites; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Chaboche, J.-L. Comprehensive Structural Integrity; Elsevier Pergamon: Amsterdam, The Netherlands; San Diego, CA, USA, 2003. [Google Scholar]
- Barbero, E.J. Introduction to Composite Materials Design; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Seddon, J.M.; Simon, N. Basic Helicopter Aerodynamics; John Wiley and Sons: New York, NY, USA, 2011; Volume 40. [Google Scholar]
- Maksimovic, S.; Kozic, M.; Stetic-Kozic, S.; Maksimović, K.; Vasović, I.; Maksimovic, M. Determination of load distributions on main helicopter rotor blades and strength analysis of its structural components. J. Aero. Eng. 2014, 27, 0401–0432. [Google Scholar] [CrossRef]
- Alkahe, J.; Rand, O. Analytic extraction of the elastic coupling mechanisms in composite blades. Compos. Struct. 2000, 49, 399–413. [Google Scholar] [CrossRef]
- Ghiringhelli, G.L.; Masarati, P.; Mantegazza, P. Analysis of an actively twisted rotor by multibody global modeling. Compos. Struct. 2001, 52, 113. [Google Scholar] [CrossRef]
- Morozov, E.V.; Sylantiev, S.A.; Evseev, E.G. Impact damage tolerance of laminated composite helicopter blades. Compos. Struct. 2003, 62, 367–371. [Google Scholar] [CrossRef]
- Conlisk, A.T. Modern helicopter rotor aerodynamics. Prog. Aero. Sci. 2001, 37, 419–476. [Google Scholar] [CrossRef]
- Sirohi, J.; Michael, S.L. Measurement of helicopter rotor blade deformation using digital image correlation. Optic. Eng. 2012, 51, 043603. [Google Scholar] [CrossRef]
- Brocklehurst, A.; Barakos, G.N. A review of helicopter rotor blade tip shapes. Prog. Aero. Sci. 2013, 56, 35–74. [Google Scholar] [CrossRef]
- Kang, H.; Hossein, S.; Gandhi, F. Dynamic blade shape for improved helicopter rotor performance. J. Am. Heli. Soc. 2010, 55, 32008. [Google Scholar] [CrossRef]
- Kumar, A.A.; Viswamurthy, S.R.; Ganguli, R. Correlation of helicopter rotor aeroelastic response with HART-II wind tunnel test data. Air. Eng. Aero. Tech. 2010, 82, 237–248. [Google Scholar] [CrossRef]
- Rasuo, B. Experimental techniques for evaluation of fatigue characteristics of laminated constructions from composite materials: Full-scale testing of the helicopter rotor blades. J. Test. Eval. 2011, 39, 237–242. [Google Scholar]
- Ganguli, R.; Chopra, I.; Haas, D.J. Simulation of helicopter rotor-system structural damage, blade mistracking, friction and freeplay. J. Aircraft 1998, 35, 591. [Google Scholar] [CrossRef]
- Yang, M.; Chopra, I.; Haas, D.J. Sensitivity of rotor-fault-induced vibrations to operational and design parameters. J. Am. Heli. Soc. 2004, 49, 328–339. [Google Scholar] [CrossRef]
- Jones, R.M. Mechanics of Composite Materials, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Lemaitre, J.; Chaboche, J.-L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990; pp. 346–450. [Google Scholar]
- Mansoor, R.; Hosseini, S.M. An ILU preconditioner for nonsymmetric positive definite matrices by using the conjugate Gram-Schmidt process. J. Comp. App. Math. 2006, 188, 150–164. [Google Scholar]
- Straubhaar, J. Preconditioners for the conjugate gradient algorithm using Gram-Schmidt and least squares methods. Int. J. Comp. Math. 2007, 84, 89–108. [Google Scholar] [CrossRef]
- Levitas, V.I.; Roy, A.M.; Preston, D.L. Multiple twinning and variant-variant transformations in martensite: Phase-field approach. Phys. Rev. B 2013, 88, 054113. [Google Scholar] [CrossRef] [Green Version]
- Levitas, V.I.; Roy, A.M. Multiphase phase field theory for temperature-and stress-induced phase transformations. Phys. Rev. B 2015, 91, 174109. [Google Scholar] [CrossRef] [Green Version]
- Levitas, V.I.; Roy, A.M. Multiphase phase field theory for temperature-induced phase transformations: Formulation and application to interfacial phases. Acta Mater. 2016, 105, 244–257. [Google Scholar] [CrossRef] [Green Version]
- Roy, A.M. Multiphase phase field approach for solid-solid phase transformations via propagating interfacial phase in HMX. J. App. Phys. 2021, 129, 025103. [Google Scholar] [CrossRef]
- Roy, A.M. Influence of Interfacial Stress on Microstructural Evolution in NiAl Alloys. JETP Lett. 2020, 112, 173–179. [Google Scholar] [CrossRef]
- Roy, A.M. Effects of interfacial stress in phase field approach for martensitic phase transformation in NiAl shape memory alloys. App. Phys. A 2020, 126, 576. [Google Scholar] [CrossRef]
- Roy, A.M. Evolution of Martensitic Nanostructure in NiAl Alloys: Tip Splitting and Bending. Mat. Sci. Res. Ind. 2020, 17, 3–6. [Google Scholar] [CrossRef]
- Roy, A.M. Barrierless melt nucleation at solid-solid interface in energetic nitramine octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazocine. Materialia 2021, 15, 101000. [Google Scholar] [CrossRef]
- Roy, A.M. Influence of nanoscale parameters on solid-solid phase transformation in Octogen crystal: Multiple solution and temperature effect. JETP Lett. 2021. [Google Scholar] [CrossRef]
- Roy, A.M. Phase Field Approach for Multiphase Phase Transformations, Twinning, and Variant-Variant Transformations in Martensite. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2015. [Google Scholar] [CrossRef]
- Solomon, E.; Natarajan, A.; Roy, A.M.; Sundararaghavan, V.; Van der Ven, A.; Marquis, E. Stability and strain-driven evolution of precipitate in Mg-Y alloys. Acta Mater. 2019, 166, 148–157. [Google Scholar] [CrossRef]
- Gusev, A.A.; Peter, J.H.; Ian, M. Fiber packing and elastic properties of a transversely random unidirectional glass/epoxy composite. Compos. Sci. Tech. 2000, 60, 535–541. [Google Scholar] [CrossRef]
- Younes, R.; Hallal, A.; Fardoun, F.; Chehade, F.H. Comparative review study on elastic properties modeling for unidirectional composite materials. Comp. Prop. 2012, 17, 391–408. [Google Scholar]
- Burlayenko, V.N.; Sadowski, T. Effective elastic properties of foam-filled honeycomb cores of sandwich panels. Compos. Struct. 2010, 92, 2890–2900. [Google Scholar] [CrossRef]
- Zhu, H.X.; Knott, J.F.; Mills, N.J. Analysis of the elastic properties of open-cell foams with tetrakaidecahedral cells. J. Mech. Phy. Sol. 1997, 45, 319–343. [Google Scholar] [CrossRef]
- HyperMesh. Available online: www.altair.com/hypermesh (accessed on 1 August 2020).
- MATLAB. Version 7.10.0 (R2010a); The MathWorks Inc.: Natick, MA, USA, 2010. [Google Scholar]
- ABAQUS. Dassault System; Version 6.9; Simulia Corp: Johnston, RI, USA, 2010. [Google Scholar]
- Bruno, D.; Greco, F.; Lonetti, P. A coupled interface-multilayer approach for mixed mode delamination and contact analysis in laminated composites. Int. J. Sol. Struct. 2003, 40, 7245–7268. [Google Scholar] [CrossRef]
- de Borst, R.; Remmers, J.J.C. Computational modeling of delamination. Compos. Sci. Technol. 2006, 66, 713–722. [Google Scholar] [CrossRef]
- Abisset, E.; Daghia, F.; Ladeveze, P. On the validation of a damage mesomodel for laminated composites by means of open-hole tensile tests on quasi-isotropic laminates. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1515–1524. [Google Scholar] [CrossRef]
- Georgantzinos, S.K.; Giannopoulos, G.I.; Markolefas, S.I. Vibration Analysis of Carbon Fiber-Graphene-Reinforced Hybrid Polymer Composites Using Finite Element Techniques. Materials 2020, 13, 4225. [Google Scholar] [CrossRef]
- Georgantzinos, S.K.; Stamoulis, K.P.; Markolefas, S.I. Mechanical Response of Hybrid Laminated Polymer Nanocomposite Structures: A Multilevel Numerical Analysis. SAE Int. J. Aerosp. 2020, 13, 243–256. [Google Scholar] [CrossRef]
- Yu, W.; Hodges, D.H. Elasticity solutions versus asymptotic sectional analysis of homogeneous, isotropic, prismatic beams. J. App. Mech. 2004, 71, 15–23. [Google Scholar] [CrossRef]
- Yu, W.; Hodges, D.H.; Ho, J.C. Variational asymptotic beam sectional analysis—An updated version. Int. J. Eng. Sci. 2012, 59, 40–64. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, A.M. Finite Element Framework for Efficient Design of Three Dimensional Multicomponent Composite Helicopter Rotor Blade System. Eng 2021, 2, 69-79. https://doi.org/10.3390/eng2010006
Roy AM. Finite Element Framework for Efficient Design of Three Dimensional Multicomponent Composite Helicopter Rotor Blade System. Eng. 2021; 2(1):69-79. https://doi.org/10.3390/eng2010006
Chicago/Turabian StyleRoy, Arunabha M. 2021. "Finite Element Framework for Efficient Design of Three Dimensional Multicomponent Composite Helicopter Rotor Blade System" Eng 2, no. 1: 69-79. https://doi.org/10.3390/eng2010006
APA StyleRoy, A. M. (2021). Finite Element Framework for Efficient Design of Three Dimensional Multicomponent Composite Helicopter Rotor Blade System. Eng, 2(1), 69-79. https://doi.org/10.3390/eng2010006






