Neural Network Optimization Algorithms to Predict Wind Turbine Blade Fatigue Life under Variable Hygrothermal Conditions

Abstract

Moisture and temperature are the most important environmental factors that affect the degradation of wind turbine blades, and their influence must be considered in the design process. They will first affect the resin matrix and then, possibly, the interface with the fibers. This work is the first to use a series of metaheuristic approaches to analyze the most recent experimental results database and to identify which resins are the most robust to moisture/temperature in terms of fatigue life. Four types of resin are compared, representing the most common types used for wind turbine blades manufacturing. Thermoset polymer resins, including polyesters and vinyl esters, were machined as coupons and tested for the fatigue in air temperatures of 20 °C and 50 °C under “dry” and “wet” conditions. The experimental fatigue data available from Sandia National Laboratories (SNL) for wind turbine-related materials have been used to build, train, and validate an artificial neural network (ANN) to predict fatigue life under different environmental conditions. The performances of three algorithms (Backpropagation BP, Particle Swarm Optimization PSO, and Cuckoo Search CS) are compared for adjusting the synaptic weights of the ANN and evaluating the efficiency in predicting the fatigue life of the materials studied, under the conditions mentioned above. For accuracy evaluation, the mean square error (MSE) is used as an objective function to be optimized by the three algorithms.

1. Introduction

Blades are one of the most critical components of wind turbines. They capture wind energy and convert it into mechanical energy for the production of electricity. Defective blades significantly affect the energy conversion efficiency of the wind turbines, and blade failures have a significant impact on the cost of energy (repair, maintenance, etc.). Therefore, the increased reliability and lifetime of wind turbine blades are important for the cost of energy reduction.

Approximately 95% of the modern wind turbine blades are made of fiber-reinforced composites because of their good mechanical characteristics: high stiffness, low density, and long fatigue life [1]. Compared to alternative materials, fiber-reinforced composites have other advantages in terms of weight, cost, quality, technical feasibility, market expectation, environmental impact, and health and safety. Several key properties are dictated by the matrix resin, including fatigue strength, which is a dominant failure mode in composite material structures, leading to the breakdown of structural integrity in areas such as the trailing edge, spars, and root connections [2,3].

Hygrothermal effects on composite materials should be considered in the early phases of design; otherwise, design iterations and failures will result in a waste of time, energy, and money. Usually, the degree of sensitivity of composites to individual environmental factors is quite different. Temperature and moisture are the most significant variables to consider for the design of wind turbine blades. The primary environmental effects are on the matrix material and then, possibly, on the interface with the fibers.

The purpose of this paper is to identify resins that have good resistance to temperature/moisture while providing better fatigue life. The resins studied are thermosetting polymers, including unsaturated polyesters and vinyl esters. They are both suitable for manufacturing wind turbine blades in terms of cost and low viscosity for ductile processing by resin transfer molding (RTM) [2].

This study also proposes and compares three algorithms, namely Backpropagation (BP) Levenberg Marquardt, Particle Swarm Optimization (PSO), and Cuckoo Search (CS), in combination with the popular feedforward neural network (FNN) for the prediction of fatigue life of wind turbine blades. These new combinations were used in the training of SNL/MSU database [4], developed by SNL in collaboration with Montana State University (MSU). The dataset we used is collected from their large public database build for comparative analysis of fatigue life for five resin systems. All the materials studied are used for wind turbine blades by most wind turbine manufacturers, owners, and contractors. The glass-fiber-reinforced plastic (GFRP) from E-glass fibers and thermoset polymers were the most appropriate choices for our analysis [5].

This database is the latest of a series of tests that the SNL has been publishing over the years. The novelty of our work is that it applies these combinations (BPNN, PSO-ANN, and CSNN) on this newly published data and creates a model that is capable of predicting the fatigue life of the different resin systems studied. Indeed, this study is based on a portion of the data used with the BP algorithm by [6], in order to improve the results already found. In contrast, this new model could be used in the future as an alternative to the costly lab tests, as well as to validate new experimental results.

Following this introductory section, the rest of the paper is organized as follows: Section 2 explains the hygrothermal effects on wind turbine blade composite; Section 3 presents the experimental fatigue data conducted with wind turbine blades related materials; Section 4 gives a brief overview of the BP, PSO, and CS and their implementation as a training algorithm of the NN; Section 5 describes how the CSNN accurately predicts the fatigue life of wind turbine blade materials; finally, some conclusions are drawn in Section 6.

2. Hygro-Thermo-Mechanics of Wind Turbine Blades

Offshore and onshore wind turbines are exposed, depending on the climatology of the region, to climatic constraints such as variations in temperature, moisture, and sand grains associated with storms. These natural phenomena can easily damage the skin of the blade (gelcoat) [7]. However, a composite wind turbine blade is highly durable if the layer of gelcoat that protects it from the external environment has good physicochemical characteristics.

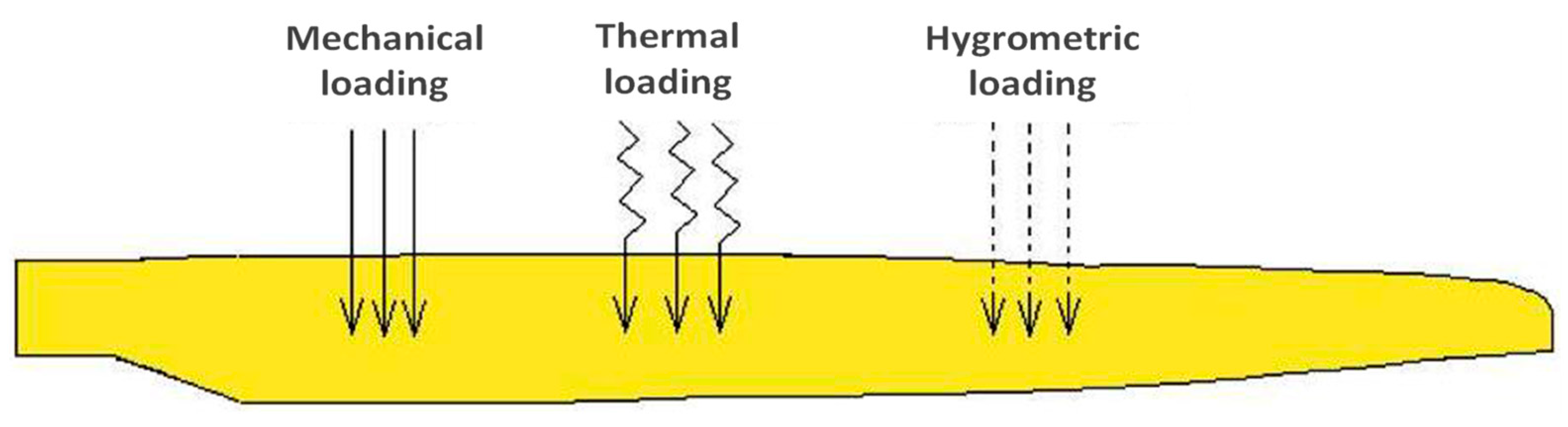
The state of the problem illustrated by Figure 1 is of the hygro-thermomechanical type, because the structure of the blade is subjected to three types of loadings of origin [8]:

• Mechanical (wind gust, storms...);
• Thermal (temperature variation);
• Hygrometric (moisture variation).

The constitutive equations governing the hygro-thermomechanical behavior of a stratified composite (upper and lower surfaces) and without taking into account the transverse shear are expressed according to [7] by the following compact matrix form:

$${\left[\begin{array}{c}N\\ \cdots \\ M\end{array}\right]}_{xy}=\left[\begin{array}{ccc}A& ⋮& B\\ \cdots & & \cdots \\ B& ⋮& D\end{array}\right]{\left[\begin{array}{c}{\epsilon }_0\\ \cdots \\ \kappa \end{array}\right]}_{xy}-{\left[\begin{array}{c}{N}^{\Delta T}\\ \cdots \\ M^{\Delta T}\end{array}\right]}_{xy}-\left[\begin{array}{c}{N}^{\Delta m}\\ \cdots \\ M^{\Delta m}\end{array}\right],$$

(1)

where ΔT and Δm, respectively, represent the variations of temperature and moisture. During the design process, the behavior of the gelcoat to climatic phenomena, as well as hygro-thermomechanical stresses, must be considered in order to predict the undesirable effects in the short- and/or long-term [7,8].

Once the plates are fabricated and nailed, the specimens can be cut. The geometry of the specimen can strongly affect the experimental results, and it is important to decide which one to use for testing. All samples were prepared using RTM. The fabrics were cut by a rolling knife and stacked in the mold following the stacking sequence “lay-up” given in each case.

All specimens were machined from the plates using a water-cooled diamond saw, and their edges were sanded before conditioning. Dry specimens were stored in ambient laboratory air at an ambient temperature of 23 °C with low humidity. Other dry specimens were stored in an oven at 50 °C, and they are defined as “50 °C dry”. Additionally, the wet specimens were stored in a plastic container of distilled water at 50 °C; they are defined as “50 °C wet” [2,6].

3. Data and Method

During its operation, the blade is subject to stress variation from one cycle to another. This variation can result in a degradation of the structural resistance through the phenomena of accumulation of stresses and fatigue.

A number of specimens (sections) must be manufactured in accordance with the blade structure itself. These specimens are tested under sufficient alternating load levels until rupture. A testbed and strain gauges for performing the tests are required. The experimental results obtained by Sandia National Laboratories [4] make it possible to estimate the life of the blade with a sufficiently acceptable degree of confidence. On average, this lifetime is estimated at 20 years [7].

3.1. Fatigue Data

The purpose of the neural networks and optimization algorithms used in this paper is to predict the fatigue behavior of wind turbine blade composites under the hygrothermal effect and in extreme conditions (dry/wet). The specimens used for this process were tested in air temperatures of 20 °C and 50 °C. The experiments have been carried out by SNL with wind turbine-related materials and released on their website [4]. In addition, a wide variety of prospective blade materials were included in this work, including E-glass-fiber/polyester and vinyl ester resins in the form of a multidirectional laminate constructions [0/±45/0]_s, fiber contents (35–36%), and many stitched fabrics.

Table 1. Different resins investigated.

Laminate			Matrix Materials
General Material Name	Lay-Up	Volume Fiber (%)	Resin	Description		Resin Trade Name		Supplier
MD-DD5P-UP2	[0/±45/0]S	35–36	Ortho-polyester	Orthophthalic		CoRezyn 63-AX-051		Interplastics Corporation
			Iso-polyester	Isophthalic		CoRezyn 75-AQ-010
MD-DD5P-VE	[0/±45/0]S	35–36	Vinyl ester 411C-50	Unmodified		Derakane 411C-50		Dow Chemical
			Vinyl ester 8084	Rubber toughened		Derakane 8084
Fiber reinforcing fabrics
E-glass fabric	Fabric orientation		Type		Areal weight (g/m2)		Supplier
Knytex D155	0° unidirectional fabrics		Stitched unidirectional		527		Owens corning fabrics
Knytex DB120	±45 fabrics		Bias, stitched		393		Owens corning fabrics

lists the types and sources of resins and reinforcement used during the manufacturing process. All materials were treated in closed molds with the RTM process, which were molded into their final dog-bone shape without machining. The laminate nomenclature corresponds to the Sandia National Laboratories. Therefore, the fabric details given indicate the content of stitching and transverse strands or mat to which the primary strands are stitched. Laminates were processed by RTM through resin distribution layers [9,10]; a more detailed description of the fabrication process may be found in [6,11].

3.2. Backpropagation Neural Network BPNN

Artificial neural networks (ANNs) have been shown to be useful for a variety of engineering applications, including the characterization of fatigue behavior. Due to their massively parallel structure, they can solve many nonlinear and multivariate problems, for which an accurate analytical solution is difficult to obtain.

The popular topology of a neural network model is illustrated in Figure 2, which typically consists of one or more input layers, output layers, and hidden layers where weights are trained. Each layer comprises one or more neurons; the neurons are interconnected so that the information passes from one layer to another, from the input layer to the output layer, through the hidden layers. Various transfer functions such as sigmoidal, linear, or triangular have been used to model neuronal activity [12,13].

In Figure 2, w_i is the synaptic weight matrix linking the input with the hidden layer, and w_s is the synaptic weight matrix linking the hidden layer with the output, according to Equation (2) [6,12,13,14]:

$$ne{t}_{i,k}=\left[{\displaystyle \sum }_j{w}_{i,j,k}ou{t}_{j,k-1}\right]+{\theta }_{i,k},$$

(2)

where w_i,j,k represents the weight connection strengths for node j in the (k − 1)th layer to node i in the kth layer; out_j,k is the output of node i in the kth layer and θ_i,k is the threshold associated with node i in the kth layer.

In Equation (3), the MSE was used as an objective function to optimize, and weights were tuned to minimize their values throughout the prediction process, defined as follows:

$$j\left(W\right)=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{\left(y^i-y_d^i\right)}^2.$$

(3)

where j is the objective function, performance, or cost function; N is the number of nodes; W is the weight matrix; y is the output obtained by the neural network; y_d is the desired output.

In this study, two other metaheuristic algorithms (PSO and CS) were used to avoid the local optimum trap. Both were deployed to optimize MSE by adjusting the neural network weights. The details of these two proposed algorithms are described in the next sections.

3.3. Particle Swarm Optimization PSO

Particle swarm optimization or PSO is an intelligent optimization algorithm; it belongs to a class of optimization algorithms called metaheuristics. PSO is based on the intelligence paradigm of swarms and is inspired by the social behavior of animals, such as fish and birds. PSO is a simple yet powerful algorithm, which has been successfully applied to various fields of science and engineering. Initially, PSO was introduced by Kennedy and Eberhart [15], where they sought to model social interactions between “particles” to achieve a given goal in a common search space, each particle having a certain capacity for memorizing and processing information. The basic rule was that there should be no conductor, or even any knowledge by the particles of all information, only local knowledge. A simple model was then developed.

The algorithm works by initializing a flock of birds randomly over the searching space, where every bird is called a “particle”. These particles fly with a certain velocity and find the global best position after some iteration [16]. During the flight, each particle updates its velocity vector, based on its momentum and the influence of its best position (P_b) as well as the best position of its neighbors (P_g), and then computes a new position [14]. Figure 3 briefly illustrates the concept of PSO.

In a search space of dimension d, the particle i of the swarm is modeled by its vector position ${\overrightarrow{x}}_i={\left(x_{i1}, x_{i2},\dots x_{id}\right)}^T$, and by its velocity vector ${\overrightarrow{v}}_i={\left(v_{i1}, v_{i2 },\dots v_{id}\right)}^T$, designating by A^T the transpose of a matrix A. The quality of its position is determined by the value of the objective function at this point. This particle keeps in memory the best position by which it has already passed, which we note ${\overrightarrow{p}}_i={\left(p_{i1},p_{i2},\dots p_{id}\right)}^T$. The best position reached by its neighboring particles is noted ${\overrightarrow{g}}_i={\left(g_{i1}, g_{i2},\dots g_{id}\right)}^T$. At time t, the velocity vector is calculated from Equation (4):

$$v_{id}\left(t+1\right)=w{v}_{id}\left(t\right)+c_1{r}_1\left(p_{id}\left(t\right)-x_{id}\left(t\right)\right)+c_2{r}_2\left(g_{id}\left(t\right)-x_{id}\left(t\right)\right)$$

(4)

In Equation (4), v_id and p_id are the velocity and position of particle i (i = 1, 2, … n), where n is the number of particles; d = 1, 2, … m, and m is the number of input variables to be optimized; w is usually a constant, called the “inertia weight factor”; c₁ and c₂ are cognitive and social acceleration factors, respectively, that scale the old velocity and increase new velocity toward P_best (local best result) or G_best (global best result); r₁ and r₂ represent random numbers that are uniformly distributed in the interval [0,1] [8,14].

3.4. Cuckoo Search Algorithm

The cuckoo search (CS) algorithm was inspired by the brood parasitism of cuckoo birds. In fact, their breeding strategy is characterized by the laying of their eggs in the nests of other species (host birds). If the host bird discovers that the eggs are not its, it will throw them away. Otherwise, its will simply abandon its nest and build another elsewhere. CS is a metaheuristic optimization algorithm based on the following rules:

• Every cuckoo lays solely one egg at a time, and the eggs are exactly set in a nest (randomly selected nest);
• The nest has better quality eggs, which are carried onto the next round;
• The number of the nest is fixed, and the quality of the nest is static and not alterable.

In CS, each egg in a nest represents a solution, and each cuckoo can lay a single egg (which represents a solution). The goal is to use the new and potentially better solution to replace a less good solution in a nest. This metaheuristic is thus based on this parasitic behavior of the species of cuckoos associated with a logic of displacement of the “Lévy flight” type, which is specific to certain birds and certain fly species [17].

The Lévy flight is a random process in which a sequence of random steps is performed [17]. Two sequential procedures must be completed to produce random numbers with Lévy flights: step generation and selection of a random direction. One of the more efficient methods for doing so is to employ the so-called Mantegna algorithm, in which the step length s can be calculated as in Equation (5) [17,18]:

$$s=\frac{u}{{\left|v\right|}^{1/\beta }}$$

(5)

Here, u and v are random values from centered Gaussian distributions; β is the scale parameter, and its recommended range is [1,2].

In the process of the cuckoo search algorithm, n randomly chosen nests come into being and the ith nest is set nest_i = (x_i1, x_i2, … x_id), where d is the dimension of the problem. The fitness of each nest can be determined according to their own location information [17,18]. The nests are updated according to Equation (6):

$$nes{t}_i^{t+1}+\alpha \otimes lévy\left(\beta \right),1\le i\le n,$$

(6)

where α is the step size according to the scale of the problem. The produce ⊗ is the entry-wise multiplications. The random walk via Lévy flight is more efficient in exploring the search space as its step length is much longer in the long run [18]. Each nest has a certain probability (P_a) to be abandoned. If a nest is abandoned, a new nest will be created according to Equation (7):

$$nes{t}_i^{t+1}=nes{t}_i^t+r\left(nes{t}_j^t-nes{t}_k^t\right),$$

(7)

where r is a scale factor uniformly distributed between 0 and 1; $nes{t}_j^t$ and $nes{t}_k^t$ are other nests, randomly selected in ith generation [18].

3.5. Data Preparation

Data preparation is important for ensuring the built model’s accuracy and robustness. The accuracy of the collected data influences the precision, and the amount of data used to train the model affects robustness [19]. As mentioned above, the data were collected from the extensive database of Sandia National Laboratories to compare four types of thermosetting resins (cited in Table 1) in terms of fatigue lives and hygrothermal effect. The size of the database collected is 122 sets distributed over the four resins in question (ortho-polyester, iso-polyester, vinyl ester 411C-50 and vinyl ester 8084). Before we began to model the data, we had to normalize it to be in a range from 0 to 1. Since the number of cycles to failure ranged from 16 to 6,000,000 cycles, and the maximum applied compressive stress was −13.8 to −41.4 MPa, we used the range-normalized absolute difference method based on the Equation (8):

$$Normalized value=\left(value-minValue\right)/\left(maxValue-minValue\right).$$

(8)

This method was applied to both data ranges (number of cycles and max stress). Indeed, the starting point of the parameter optimization process starts with error estimation as a difference between real and predicted values. These two sets of values must, therefore, have the same range. The normalization of inputs in neural networks can, for practical reasons, make learning faster and reduce the chances of being trapped in local minima.

We used Excel to process the data from

Table 2. Sample parameters of ortho-polyester 63-AX-051.

Testing Temperature T (°C)	Stress Ratio R	UCS * (MPa)	Hygrometric Conditions
50 °C Wet	10	−34.5	Wet coupons (1.0% distilled water)
50 °C Dry	10	−34.5
20 °C Wet	10	−31
50 °C Dry	10	−37.9

* UCS: ultimate compressive stress.

, and the results are shown in Figure 4. We started sorting the data in ascending order based on hygrothermal conditions and the resin types. We then normalized them to allow the application of the proposed neural network combinations mentioned earlier. We identified the properties extracted from the prediction for each resin, such as MSE, number of epochs, etc. This Excel file (Figure 4) synthesizes all the data and allows us to process the simulations efficiently.

4. Proposed Hybrid Models for Fatigue Life Prediction

In order to create a model that can predict the fatigue life of the various resins investigated with reasonable accuracy, a total number of 122 experimental fatigue data entries were used in the training process; the parameters of input and output are tabulated in

Table 3. Input and output parameters.

Input Parameters	Output Parameters
Normalized maximum compressive stress σmax	Normalized number of cycles to failure N

.

The training data were split into three different sets to fulfill the training requirements and improve accuracy, according to the “early stopping” method, integrated by default in the Matlab software (R2016b). Accordingly, 60% of the data serve as the training set, 20% for validation, and the remaining 20% for testing purposes.

The NN used to predict the fatigue life of all resin matrices is a two-layer feedforward network with one input, the normalized maximum compressive stress σ_max, and one output, the normalized number of cycles to failure N. The network consists of a single hidden layer of 10 neurons using a sigmoid activation function, while the output uses a linear activation function with one computation neuron. It is a fixed architecture for all our proposed combinations, and we try each time to replace the BP algorithm (Levenberg-Marquardt) with one of the suggested algorithms (PSO and CS). Since we have only one input and one output, data scaling was achieved by normalizing/standardizing real-valued input and output variables.

The effect of varying the number of hidden neurons on the prediction of fatigue life was investigated. In each test, the number of neurons in the hidden layer was changed to obtain the lowest root mean square error (RMSE). Figure 5 shows the variations of RMSE according to the number of hidden neurons for 14 trials.

4.1. PSO-Based ANN

A neural network optimized by a particle swarm algorithm is also called a PSO-ANN (particle swarm optimization-based artificial neural network) combination. This algorithm takes the weights and biases of the trained neural network as a single particle. For training a neural network using the PSO, the fitness value of each swarm particle (member) is the value of the error function evaluated at the particle’s current position, and the particle’s position vector corresponds to the network’s weight matrix [14,20]. The number of PSO dimensions is taken as the total number of neural network weights and biases. The PSO-ANN combination procedure is illustrated in the flowchart of Figure 6.

Returning to the parameters, to improve the convergence rate and the learning process, the parameters presented in

Table 4. Parameters of PSO algorithm.

Parameters	Values
Number of particles	20
Number of generations (max iterations)	1000
Maximum velocity Vmax	0.9
Minimum velocity Vmin	0.4
Cognitive and social acceleration factors c1 and c2	2
Search space range	[−100, 100]
Inertia weight factor w	0.72

were better suited for the execution of the PSO algorithm.

In this combination, the number of dimensions of the PSO domain corresponds to the number of weights and biases of the neural network, from which each PSO dimension corresponds to a weight or bias of the neural network. Since it is not possible to display more than three dimensions, we will only show the first and the last dimension in the x and y axes. The z-axis corresponds to the performance function of the neural network, which also represents the objective function of the PSO (Figure 7). The goal of PSO will be to optimize the MSE of our network.

For our topology, we have 31 dimensions where the PSO particles search an optimum. These 31 dimensions correspond to the weights and biases of our neural network (two layers, one of 10 and the other of a single neuron, give 20 weights and 11 biases). In this search space, each particle will have projections on the dimensions that correspond to the parameters (weight and bias) of the NN. In our case, the number of parameters is 31 (20 weights and 11 biases). Therefore, if we want to follow the evolution of the position of a particle (choose a particle among the 20 used in our PSO-ANN combination), we will see that this evolution will have 31 projections. Each projection corresponds to a parameter (weight or bias) of the NN.

Figure 8 represents the change of the position of particle 9 in projection on the 31 parameters (or dimensions); dim1…dim31 represent the parameters of the NN (weight and bias).

Similarly, if we want to follow the value of the objective function of a particle, the projection on the z-axis will give us the value of the objective function at any iteration. This value converges when the particles are clustered near an optimum. Figure 9 shows the evolution of the objective function according to particle 9.

4.2. CS-Based NN (CSNN)

In CSNN, CS is used to optimize the backpropagation (BP) network’s initial weights and biases. More precisely, the BP network is regarded as the objective function (fitness function), and the weights and biases are calculated by the CS algorithm to maximize the objective function [21]. It is expected that these optimal weights and biases used for the BP network will be significantly higher than the default BP network. In the first epoch, CS initializes the best weights and biases and then transfers it to the BPNN. Then, BPNN weights are calculated and compared with the best solution in the backward direction. In the next cycle, CS will update the weights with the best possible solution, and CS will continue to search for the best weights until the network’s last cycle/epoch is reached or the MSE is achieved [22]. The flowchart of the CSNN combination is described in Figure 10.

CS performance is tested with a discovery rate pa = 0.15 to optimize weights and bias and a small population size of 20. For each prediction, the trial is limited to 1000 epochs, and the minimum error is kept close to 0. As intelligent algorithms always have certain randomness, different results will be generated by each run. For each case, 10 tests are run to obtain a standard statistical result. The results of the network will be saved for each test.

5. Results and Discussion

In this section, we have used neural networks combined with three different algorithms (BP, PSO, and CS), called BPNN, PSO-ANN, and CSNN, respectively, as described in Section 4. These three hybrid models have been exploited to evaluate their effectiveness in predicting the fatigue life of wind turbine blade materials. The materials in question are composites based on thermosetting resins, namely the ortho-polyester resin (CoRezyn 63-AX-051), the iso-polyester resin (CoRezyn 75-AQ-010), and the two vinyl ester resins (Derakane 411C-50 and Derakane 8084). In the first step, we have trained our NN with the BP algorithm with three different temperatures: 50 °C wet, 20 °C dry, and 20 °C wet, in order to preselect the best architecture for our network, as it will follow us throughout the evaluation and prediction process. The choice of a suitable architecture ends when the network converges or reaches a global minimum already predefined as an objective function (MSE). For the materials considered, both experimental and predicted results obtained with BPNN, PSO-ANN and CSNN are compared in Figure 11, Figure 12, Figure 13 and Figure 14 and show the relationship between the maximum applied compressive stress (σ_max) and the number of cycles to failure (N). For illustration and comparative purposes, we have presented in the same figure and for each studied temperature, four plots for different experimental and predicted values obtained with BPNN, PSO-ANN, and CSNN, where they show typical fatigue life predictions. We did not have enough data to predict scenarios for 50 °C wet conditions. All the data originates from SNL, who performed the experiments and made their database publicly available. Therefore, we have not being able to test the 50 °C wet with the following materials: Derakane 8084, CoRezyn 75-AQ-010 and Derakane 411C-50.

In all these figures, it can be noted that the prediction plots follow their experimental reference, which demonstrates the efficiency of the combinations we propose. However, the CSNN plot is almost superimposed on that of the experimental, because of its simplicity in using mathematical models in comparison with PSO-ANN, as well as its ability to adjust weights without determining a gradient by comparing with BPNN. In the training process, we found that BPNN and CSNN converged more quickly to a minimal error, whereas PSO-ANN requires a considerable number of iterations to do so. In fact, this paper is the result of the sum of our experiences, which allowed us to overcome the shortcomings of our previous work [6,14,23].

In terms of error, we further evaluated the erroneously predicted values for the three combinations and presented their prediction errors in

Table 5. RMSE, MAE, epochs, CPU time and prediction accuracies for all materials and combinations.

Material	Environmental Conditions	BPNN					PSO-ANN					CSNN
		RMSE	MAE	Epochs	CPU Time (s)	Accuracy (%)	RMSE	MAE	Epochs	CPU Time (s)	Accuracy (%)	RMSE	MAE	Epochs	CPU Time (s)	Accuracy (%)
Ortho-polyester (CoRezyn 63-AX-051)	50 °C wet	0.0175	0.0259	277	9.371	94.443	0.0181	0.0316	228	227.73	94.394	0.0141	0.0079	62	6.632	94.761
	50 °C dry	0.0316	0.0342	54	7.453	92.006	0.0331	0.0284	112	111.50	93.115	0.0309	0.0282	23	2.961	92.138
	20 °C wet	0.036	0.0387	18	5.820	92.878	0.0206	0.0235	32	31.71	93.618	0.0199	0.0165	3	0.267	94.204
	20 °C dry	0.0374	0.0298	14	5.158	92.867	0.0374	0.0295	11	10.95	92.869	0.0387	0.0271	10	1.292	92.655
Iso-polyester (CoRezyn 75-AQ-010)	50 °C wet	0.1256	0.0917	1000	28.886	81.330	0.1256	0.0961	1000	909.09	81.333	0.1256	0.083	1000	32.490	81.322
	20 °C dry	0.2996	0.206	152	8.674	63.117	0.2886	0.188	381	379.32	63.975	0.0412	0.0361	144	8.769	91.630
	20 °C wet	0.0519	0.0375	5	2.051	87.675	0.0447	0.0323	16	15.54	91.052	0.04	0.0282	16	1.39	91.750
Vinyl ester (Derakane 411C-50)	50 °C wet	0.1126	0.0825	98	7.903	82.366	0.064	0.058	157	152.09	88.088	0.0424	0.0397	131	7.277	91.243
	20 °C dry	0.0655	0.0694	1000	28.760	86.078	0.0479	0.0431	1000	991.07	90.894	0.0469	0.046	1000	32.327	90.113
	20 °C wet	0.0979	0.0637	133	8.342	84.611	0.0655	0.0429	416	414.17	87.879	0.0196	0.0257	327	11.168	94.131
Vinyl ester (Derakane 8084)	50 °C wet	0.019	0.0253	122	8.197	94.248	0.0186	0.0241	169	158.43	94.312	0.0184	0.0151	112	8.023	94.344
	20 °C dry	0.0529	0.0524	195	8.847	87.141	0.0608	0.0554	217	210.21	88.496	0.0314	0.0293	259	10.806	92.018
	20 °C wet	0.1558	0.1268	599	17.299	77.753	0.1392	0.1144	627	621.40	79.504	0.1268	0.0759	1000	32.112	81.102

. The table contains the values of the RMSE, mean absolute error (MAE), number of epochs, CPU times, and the prediction accuracies. It is clear that the prediction performance of CSNN is better than that of PSO-ANN and BPNN, with the exception of certain prediction values mentioned above. In the case of ortho-polyester, the maximum RMSE at 20 °C dry reaches 0.0373 for BPNN, 0.0374 for PSO-ANN and 0.0387 for CSNN. At 20 °C dry in the case of iso-polyester, the maximum RMSE is about 0.299 for BPNN, 0.288 for PSO-ANN and 0.041 for CSNN. As for the case of vinyl ester (Derakane 411C-50), the maximum error reaches at 50 °C wet 0.112 for BPNN, 0.064 for PSO- ANN and 0.042 for CSNN. At the same time, the max RMSE at 20 °C wet of the vinyl ester (Derakane 8084) is 0.155 for BPNN, 0.139 for PSO-ANN and 0.128 for CSNN. In the same table, we can note that the lowest number of epochs corresponds to the CSNN combination, with the shortest calculation times and best prediction accuracies. Both BPNN and PSO-ANN have higher RMSE values than CSNN. The CSNN approach gives better results than PSO-ANN due to its simplicity in using mathematical models. Additionally, CSNN adjusts the weights without determining a gradient, as is the case with BPNN. We found that CSNN converged faster to a minimum error in the training process, whereas PSO-ANN requires a considerable number of iterations.

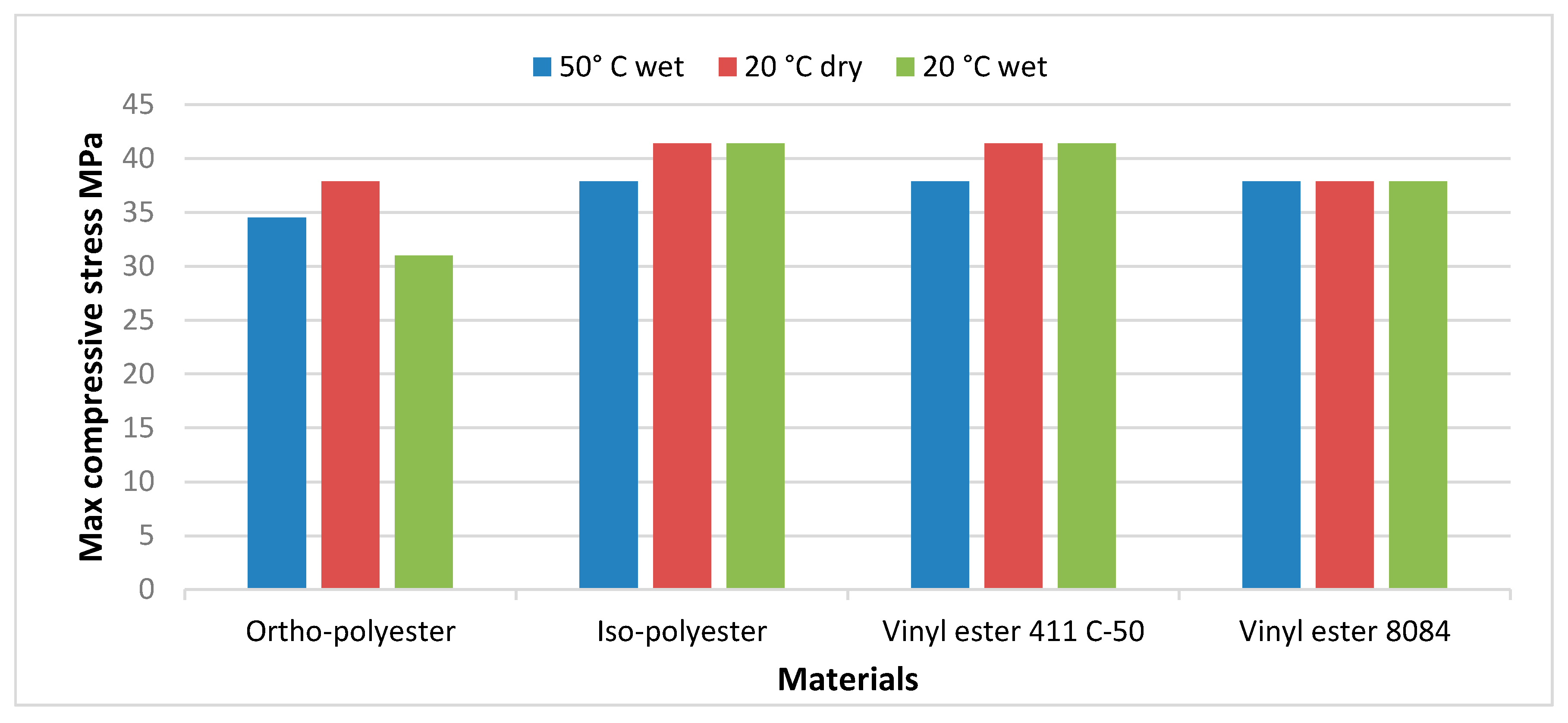
To make these results more precise, we had to use a bar chart to quantify the comparison. The different materials studied were compared in Figure 15 in terms of the maximum compressive stress and according to the hygrothermal conditions. The values shown in the figure were taken directly from the source database without normalization. According to the figure, the iso-polyester and the vinyl ester 411 C-50 have a high fatigue strength compared to the two remaining. The decrease in fatigue strength is very significant for the ortho-polyester at 20 °C. On the other hand, the vinyl ester 8084 still retains the same fatigue strength, regardless of the hygrothermal effect. All materials showed a significant decrease at 50 °C wet.

6. Conclusions

The use of artificial neural networks in the evaluation of composite materials of wind turbine blades will be considered as an alternative and economical solution. This will also allow us to reduce the duration of laboratory tests and let the network predict fatigue life. Depending on the results obtained, it is possible to propose iso-polyester and vinyl ester 411 C-50 as the most appropriate resins for an eventual design of wind turbine blades, under the hydrothermal effect, and this, from a lifetime and strength standpoint.

The proposed hybrid neural network models BPNN, PSO-ANN and CSNN reproduce the same nonlinear characteristics obtained in the laboratory with an acceptable error. The critical element that can decide the quality of prediction and learning is simply the database, which must be relatively consistent for the network to predict future values with minimal error. The ANN architecture (number of neurons, topology, etc.) is also considered as an important factor deciding the quality of learning more than the learning parameters. We have pointed out that the CSNN is better than the BPNN and PSO-ANN in terms of prediction because of its simplicity in using mathematical models, as well as its ability to adjust weights without determining a gradient. CSNN gave us better fatigue life predictions, faster computation, more accuracy, and above all, a high convergence rate toward the actual global minimum.

More research is needed to determine the possibility of finding specific combinations that always leads to the best predictions of fatigue life, as well as improving the accuracy of ANN using other optimization algorithms in the phase of learning.