An Analytical Method to Estimate Supersaturation in Gas–Liquid Systems as a Function of Pressure-Reduction Step and Waiting Time
Abstract
:1. Introduction
2. Methodology
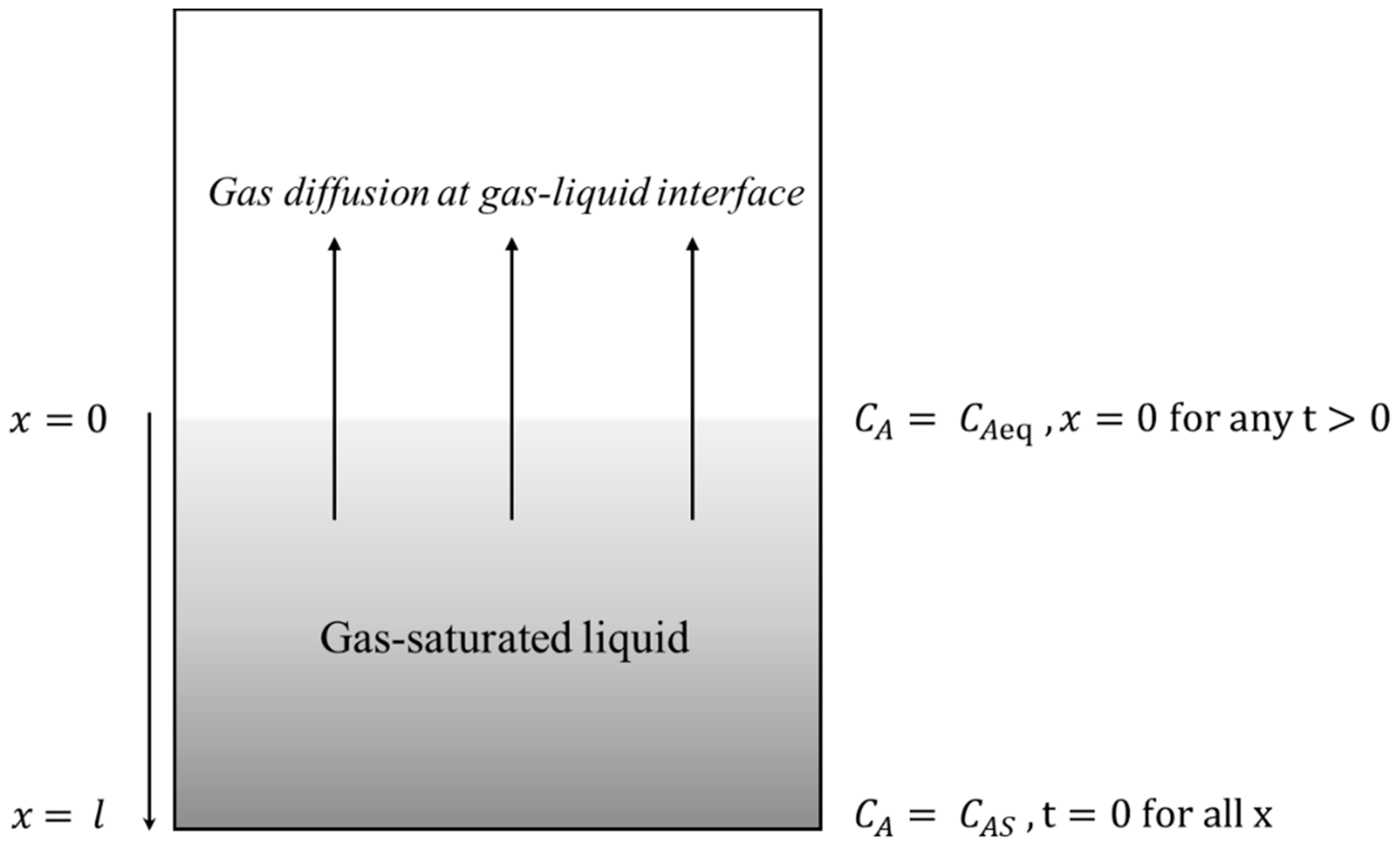
2.1. Derivation of Supersaturation Equation
2.2. Validation of Waiting Time after Each Pressure Reduction Step with ‘Characteristic Time’
3. Results and Discussion
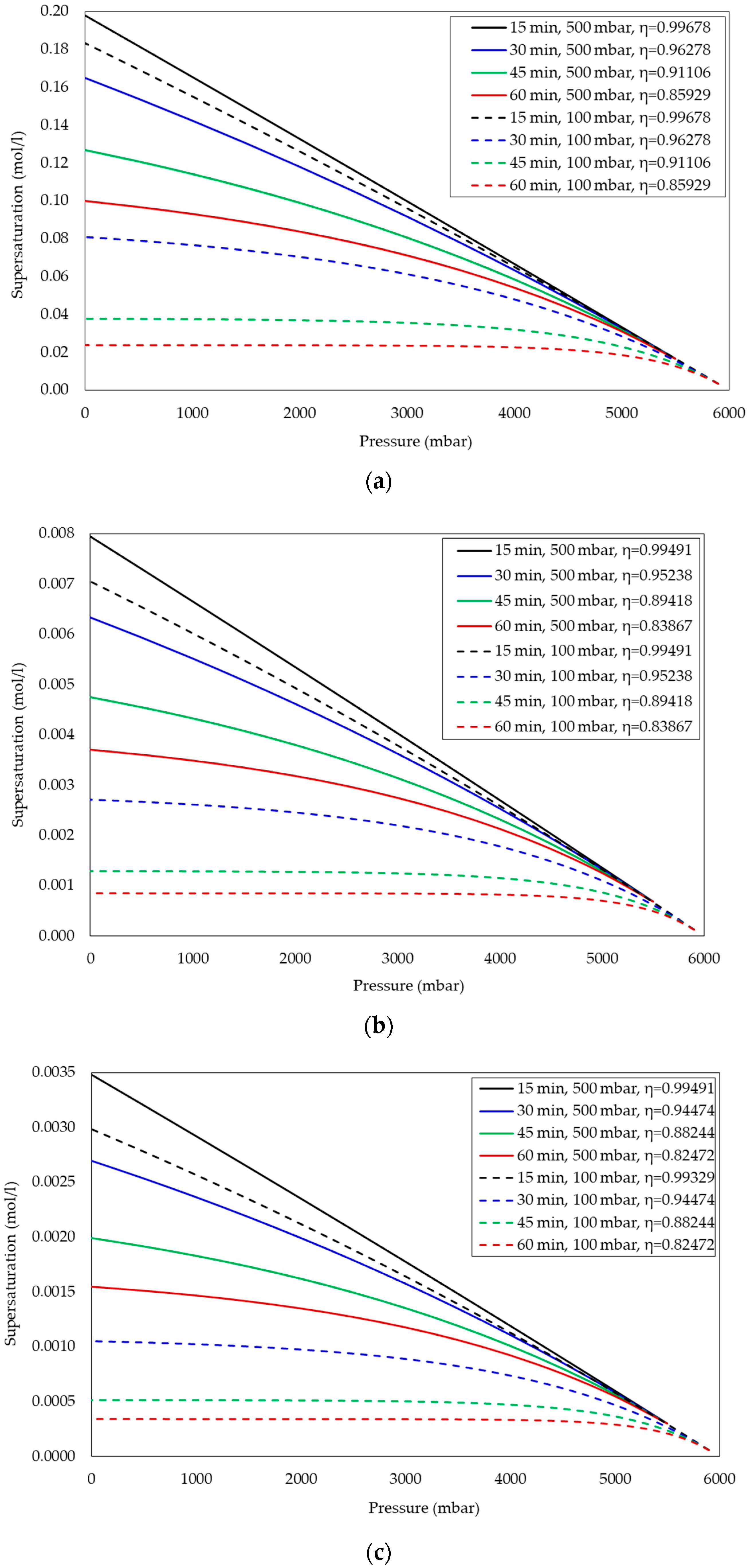
Effect of Waiting Time on Supersaturation after Each Pressure Reduction Step
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bikkina, P.K.; Pradhan, S. A potential solution for boiling crisis. In Proceedings of the 18th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH 18), Portland, Oregon, OR, USA, 18–23 August 2019; American Nuclear Society: Portland, OR, USA, 2019; pp. 1383–1396. [Google Scholar]
- Pradhan, S.; Qader, R.J.; Sedai, B.R.; Bikkina, P.K. Influence of wettability on pressure-driven bubble nucleation: A potential method for dissolved gas separation. Sep. Purif. Technol. 2019, 217, 31–39. [Google Scholar] [CrossRef]
- Baillon, F.; Espitalier, F.; Cogne, C.; Peczalski, R.; Louisnard, O. Crystallization and Freezing Processes Assisted by power Ultrasound, in Power Ultrasonics; Elsevier: Amsterdam, The Netherlands, 2015; pp. 845–874. [Google Scholar]
- Zuo, L.; Krevor, S.; Falta, R.W.; Benson, S.M. An experimental study of CO2 exsolution and relative permeability measurements during CO2 saturated water depressurization. Transp. Porous Media 2012, 91, 459–478. [Google Scholar] [CrossRef]
- Liger-Belair, G.; Parmentier, M.; Jeandet, P. Modeling the kinetics of bubble nucleation in champagne and carbonated beverages. J. Phys. Chem. B 2006, 110, 21145–21151. [Google Scholar] [CrossRef] [PubMed]
- Schmid, M.; Lorke, A.; Wuest, A.; Halbwachs, M.; Tanyileke, G. Development and sensitivity analysis of a model for assessing stratification and safety of lake nyos during artificial degassing. Ocean Dyn. 2003, 53, 288–301. [Google Scholar] [CrossRef] [Green Version]
- Kusakabe, M. Lakes nyos and monoun gas disasters (Cameroon)—Limnic eruptions caused by excessive accumulation of magmatic CO2 in crater lakes. Geochem. Monogr. Ser. 2017, 1, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Vaselli, O.; Tedesco, D.; Cuoco, E.; Tassi, F. Are limnic eruptions in the CO2–CH4-rich gas reservoir of lake kivu (Democratic Republic of the Congo and Rwanda) possible? Insights from physico-chemical and isotopic data. In Volcanic Lakes; Springer: New York, NY, USA, 2015; pp. 489–505. [Google Scholar]
- Jones, N. How dangerous is Africa’s explosive lake kivu? Nature 2021, 597, 466–469. [Google Scholar] [CrossRef] [PubMed]
- Hawtin, R.W.; Quigley, D.; Rodger, P.M. Gas hydrate nucleation and cage formation at a water/methane interface. Phys. Chem. Chem. Phys. 2008, 10, 4853–4864. [Google Scholar] [CrossRef] [PubMed]
- Sharp, R.; Khunjar, W.; Daly, D.; Perez-Terrero, J.; Chandran, K.; Niemiec, A.; Pace, G. Nitrogen removal from water resource recovery facilities using partial nitrification, denitratation-anaerobic ammonia oxidation (PANDA). Sci. Total Environ. 2020, 724, 138283. [Google Scholar] [CrossRef] [PubMed]
- Bergeron, V.; Walstra, P. Foams, in Fundamentals of Interface and Colloid Science; Elsevier: Amsterdam, The Netherlands, 2005; pp. 7.1–7.38. [Google Scholar]
- Pradhan, S. Influence of Wettability on Dissolved Gas Separation, Nucleate Boiling, and Enhanced Oil Recovery, in School of Chemical Engineering. Ph.D. Dissertation, Oklahoma State University, Stillwater, OK, USA, 2021. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena 2002; JohnWiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Conrad, K. The Gaussian Integral; University of Connecticut: Storrs, CT, USA, 2016; pp. 1–2. [Google Scholar]
- Smith, J.M. Introduction to Chemical Engineering Thermodynamics; ACS Publications: Washington, DC, USA, 1950. [Google Scholar]
- Berthier, J.; Silberzan, P. Microfluidics for Biotechnology; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
- Himmelblau, D. Diffusion of dissolved gases in liquids. Chem. Rev. 1964, 64, 527–550. [Google Scholar] [CrossRef]
- Witherspoon, P.; Saraf, D. Diffusion of methane, ethane, propane, and n-butane in water from 25 to 43. J. Phys. Chem. 1965, 69, 3752–3755. [Google Scholar] [CrossRef]
- Ferrell, R.T.; Himmelblau, D.M. Diffusion coefficients of nitrogen and oxygen in water. J. Chem. Eng. Data 1967, 12, 111–115. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradhan, S.; Bikkina, P.K. An Analytical Method to Estimate Supersaturation in Gas–Liquid Systems as a Function of Pressure-Reduction Step and Waiting Time. Eng 2022, 3, 116-123. https://doi.org/10.3390/eng3010010
Pradhan S, Bikkina PK. An Analytical Method to Estimate Supersaturation in Gas–Liquid Systems as a Function of Pressure-Reduction Step and Waiting Time. Eng. 2022; 3(1):116-123. https://doi.org/10.3390/eng3010010
Chicago/Turabian StylePradhan, Sushobhan, and Prem Kumar Bikkina. 2022. "An Analytical Method to Estimate Supersaturation in Gas–Liquid Systems as a Function of Pressure-Reduction Step and Waiting Time" Eng 3, no. 1: 116-123. https://doi.org/10.3390/eng3010010
APA StylePradhan, S., & Bikkina, P. K. (2022). An Analytical Method to Estimate Supersaturation in Gas–Liquid Systems as a Function of Pressure-Reduction Step and Waiting Time. Eng, 3(1), 116-123. https://doi.org/10.3390/eng3010010







