Far-Field Radiation Characteristics of Folded Monopole Antennas over a Conducting Ground Plane
Abstract
:1. Introduction
2. Materials and Methods
3. Results
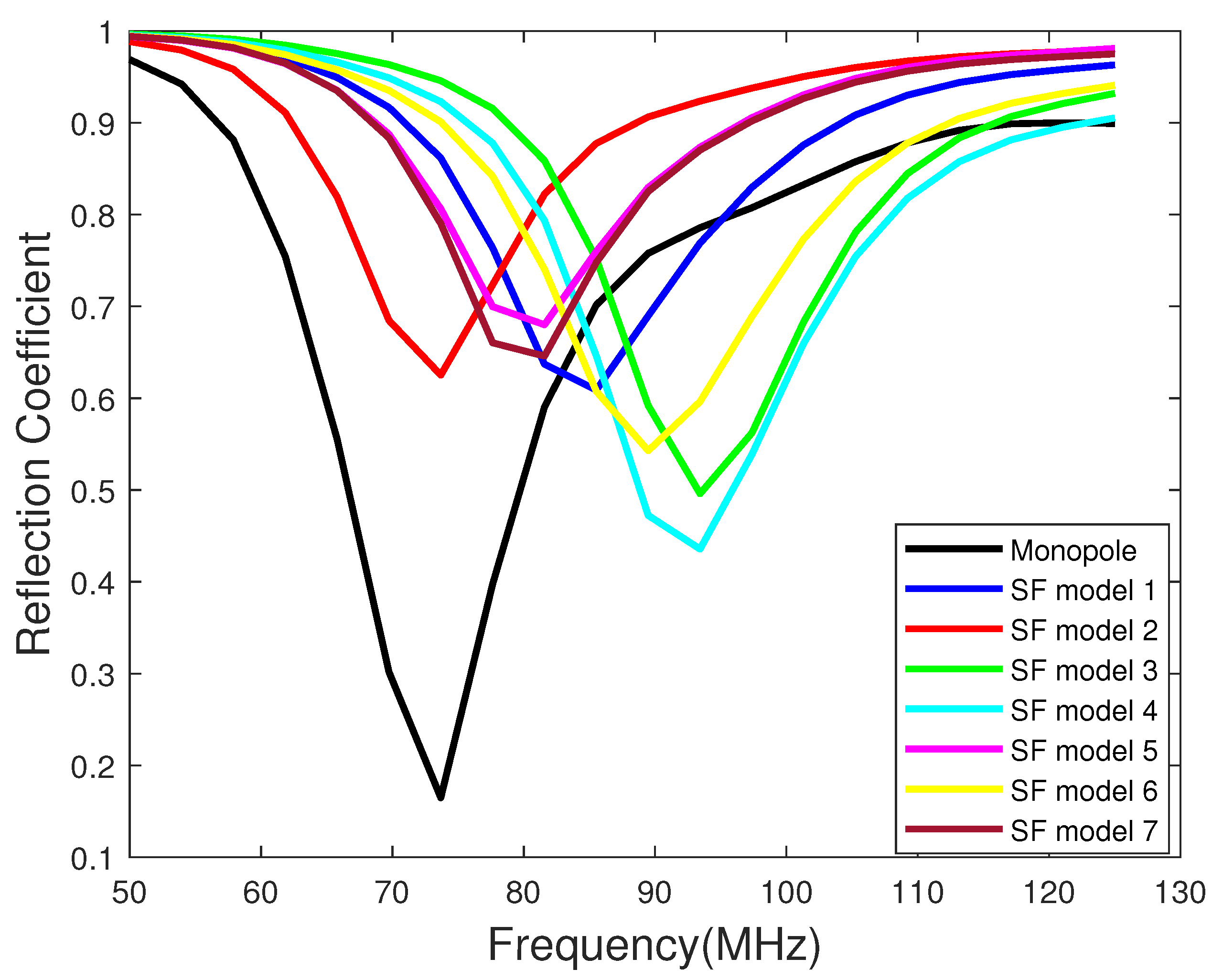
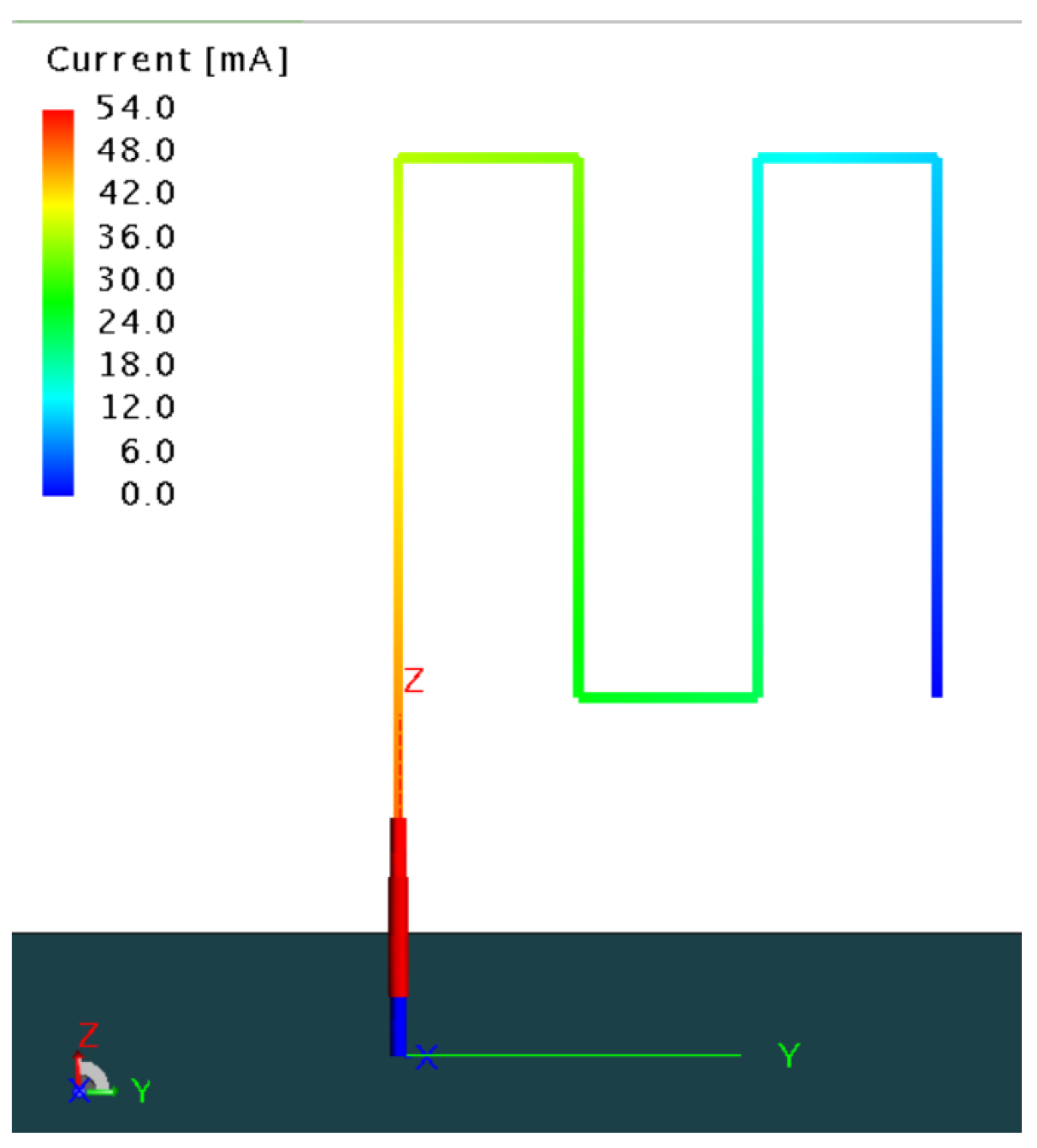
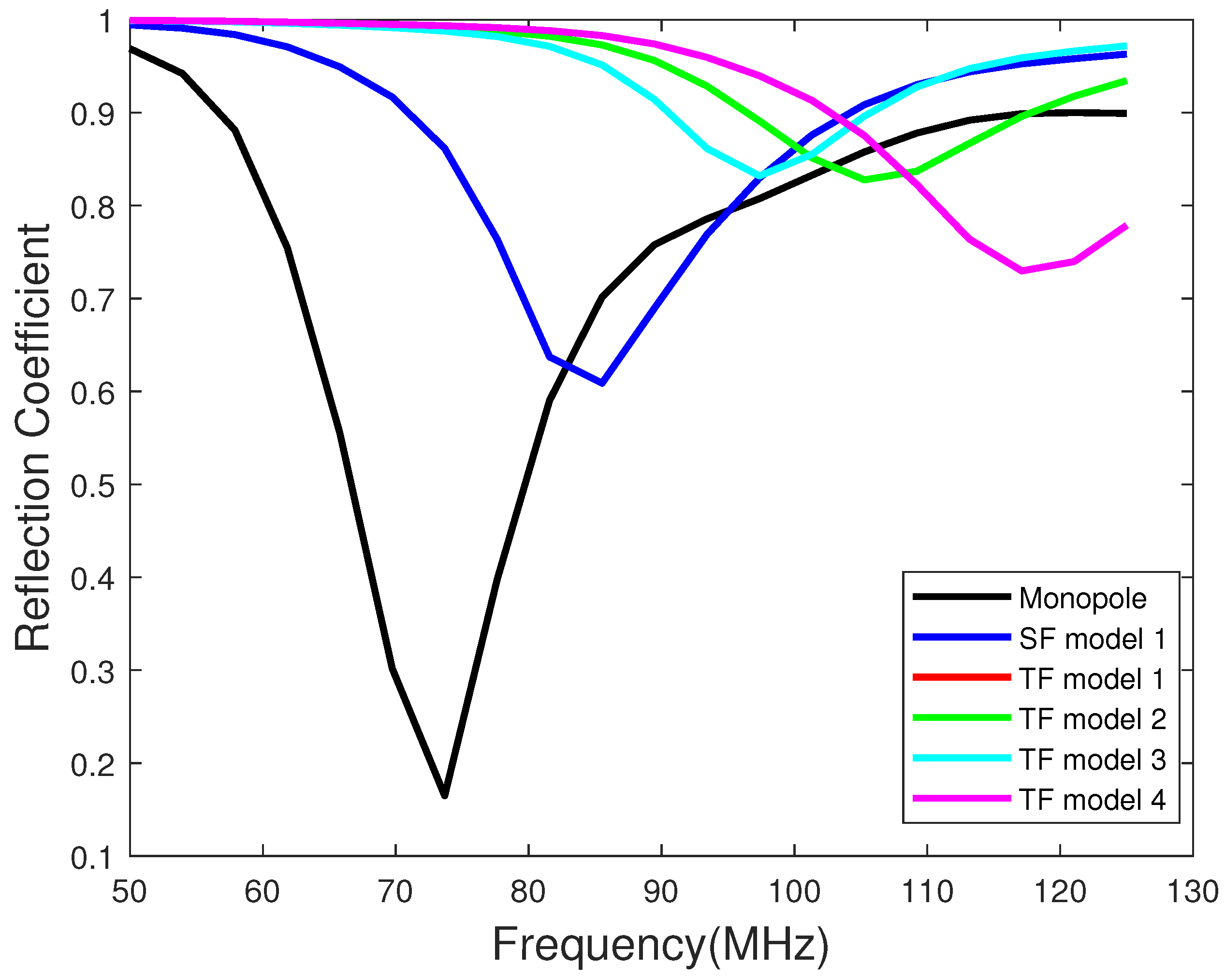
3.1. The Single-Fold Monopole
3.2. The Two-Fold Monopole
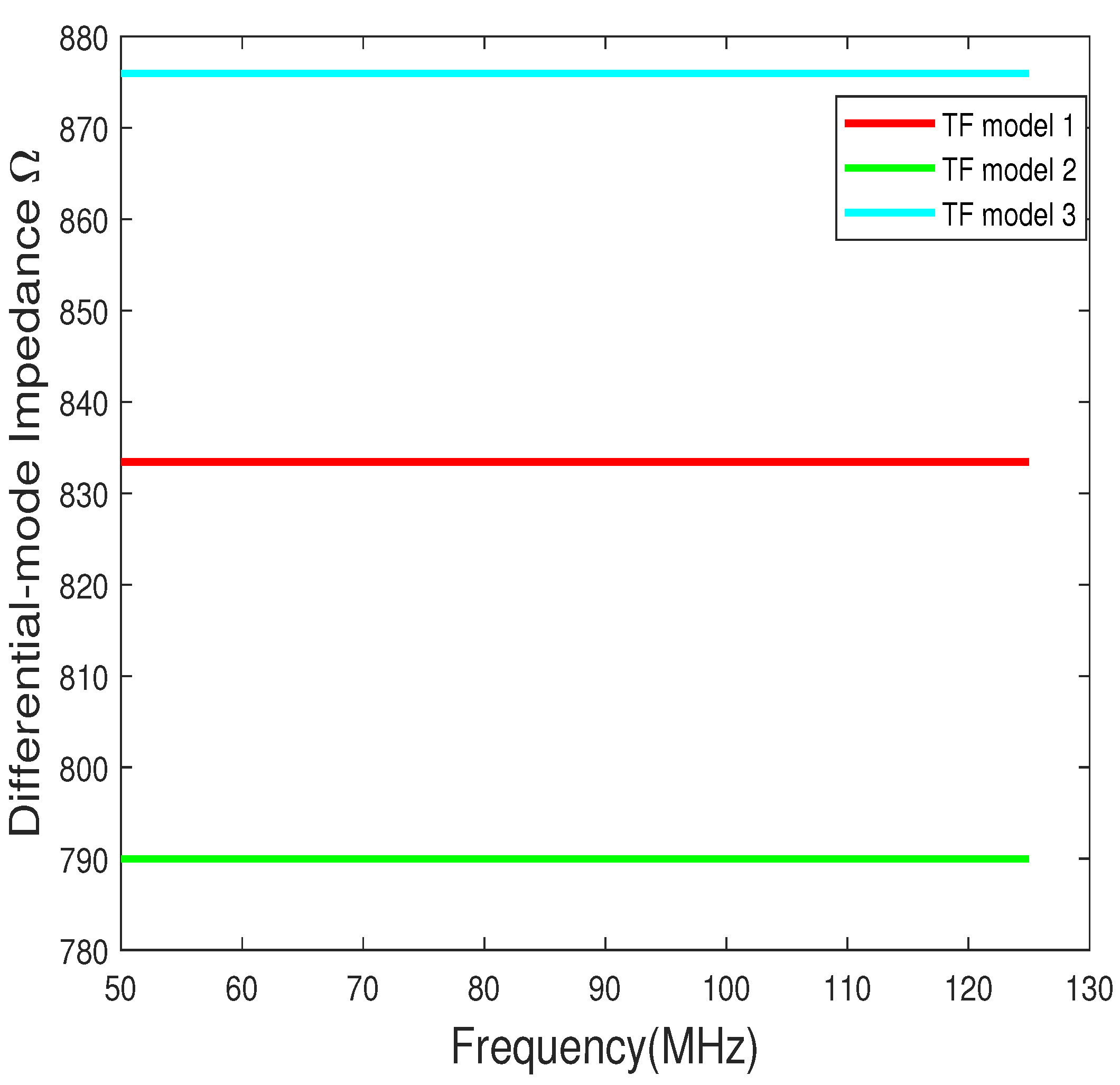
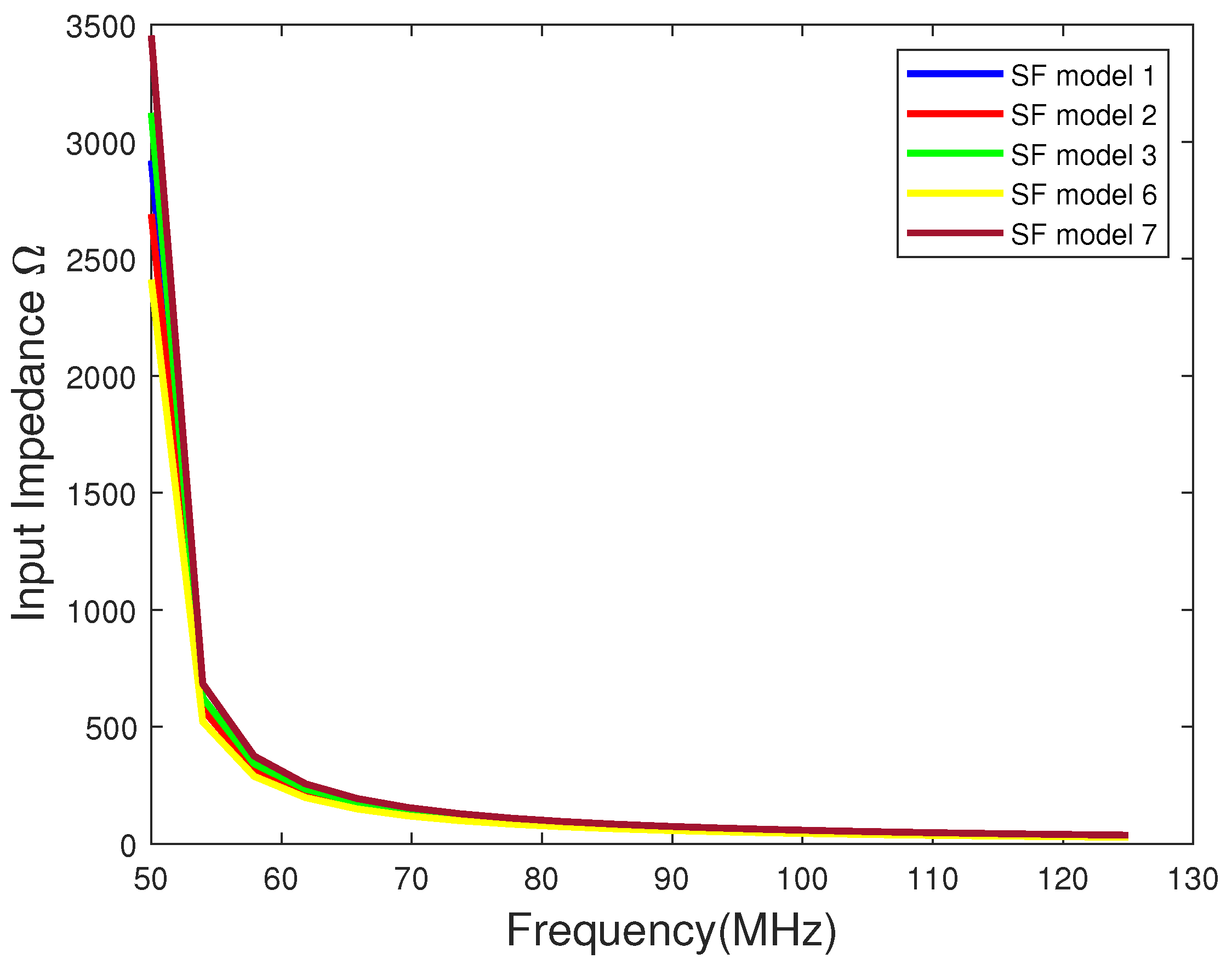
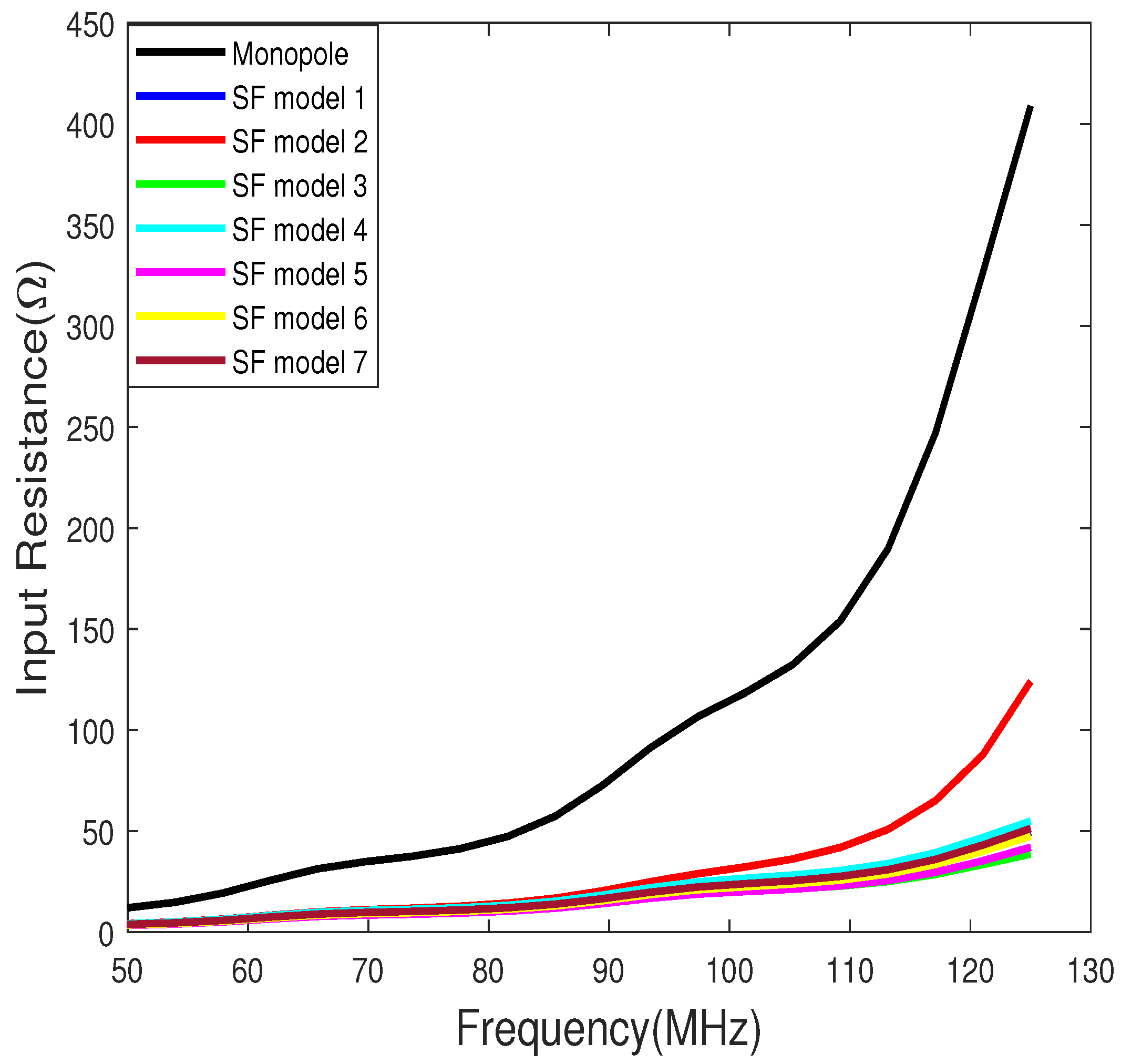
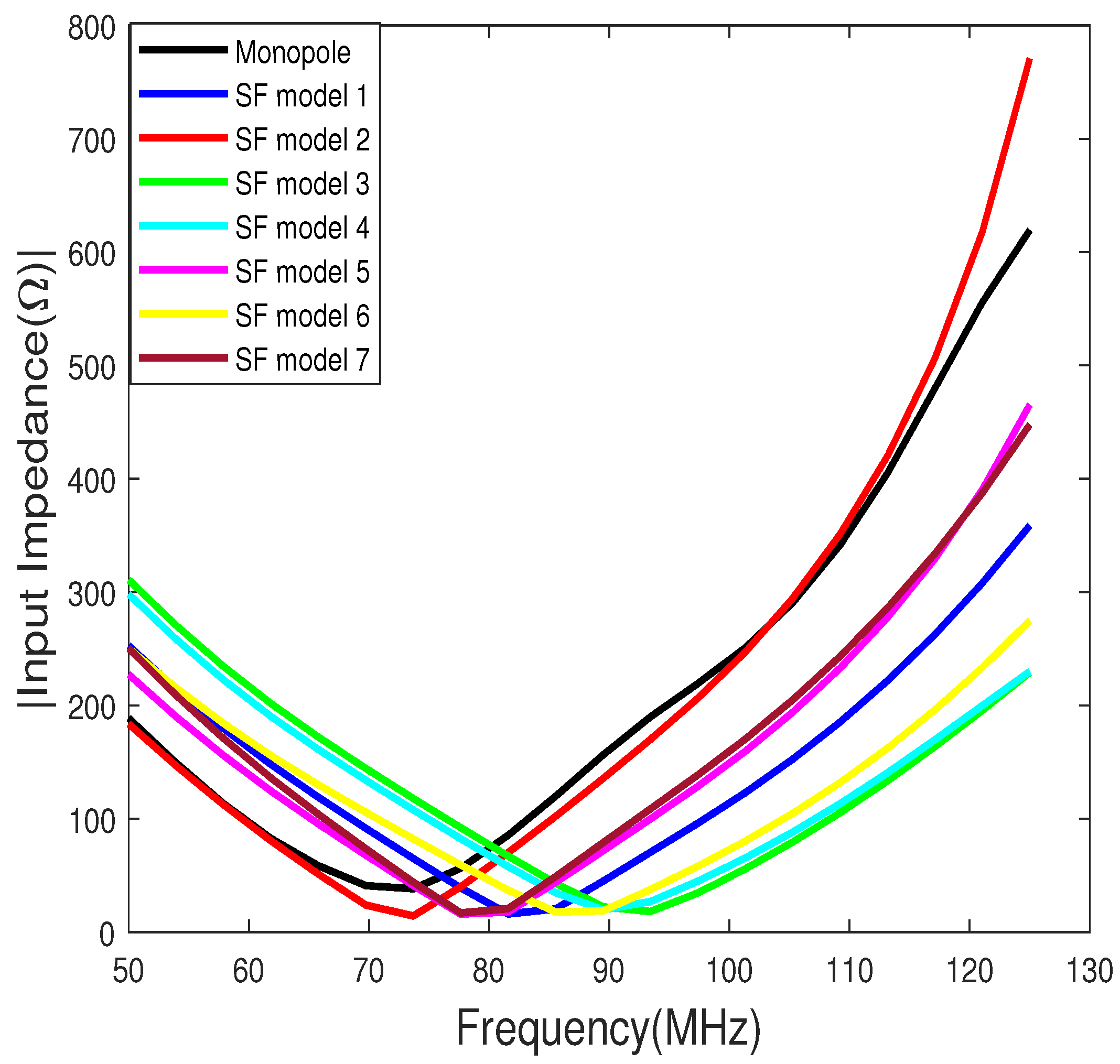
4. Discussion
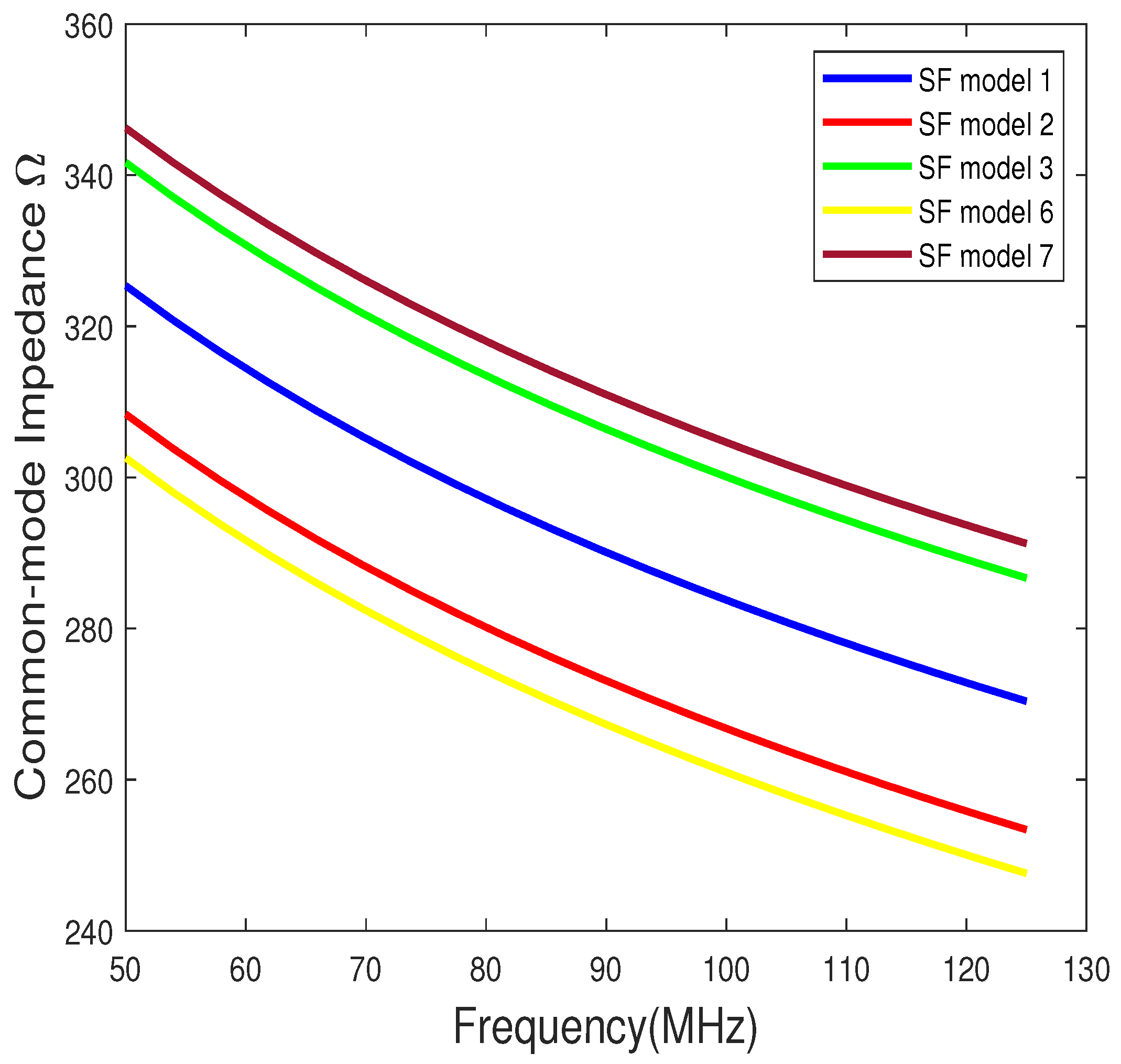
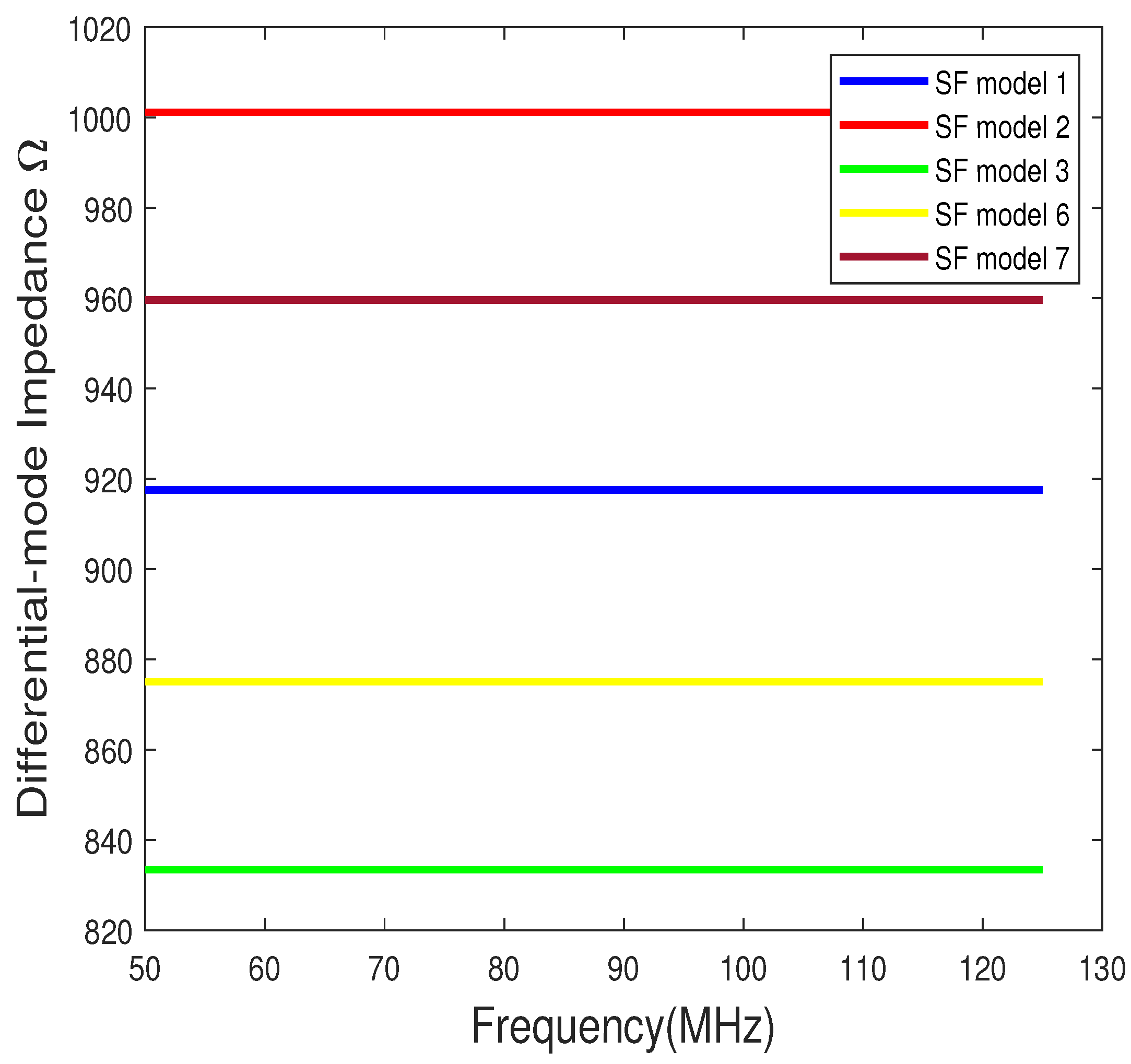
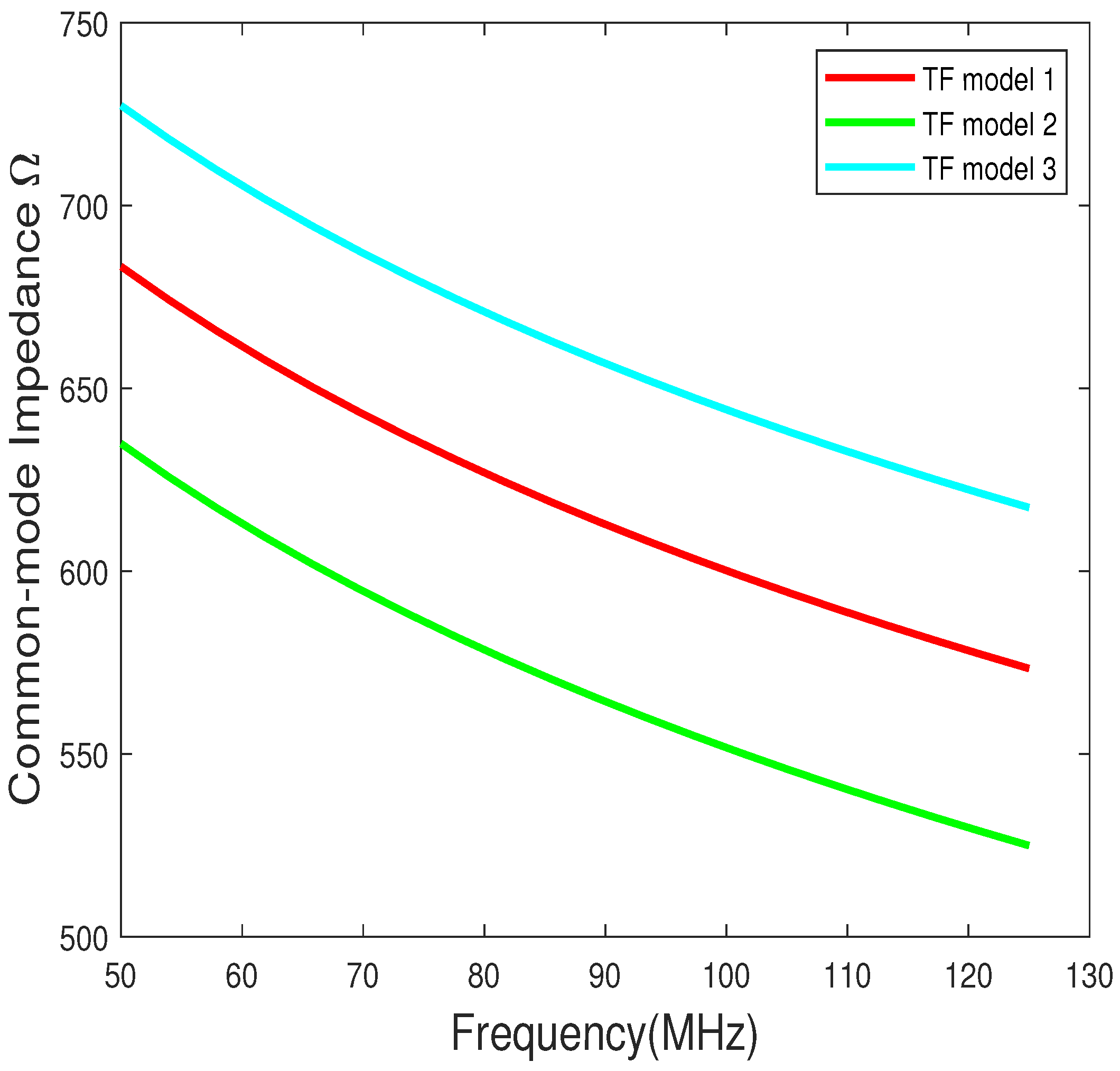
4.1. Characteristic and Input Impedance
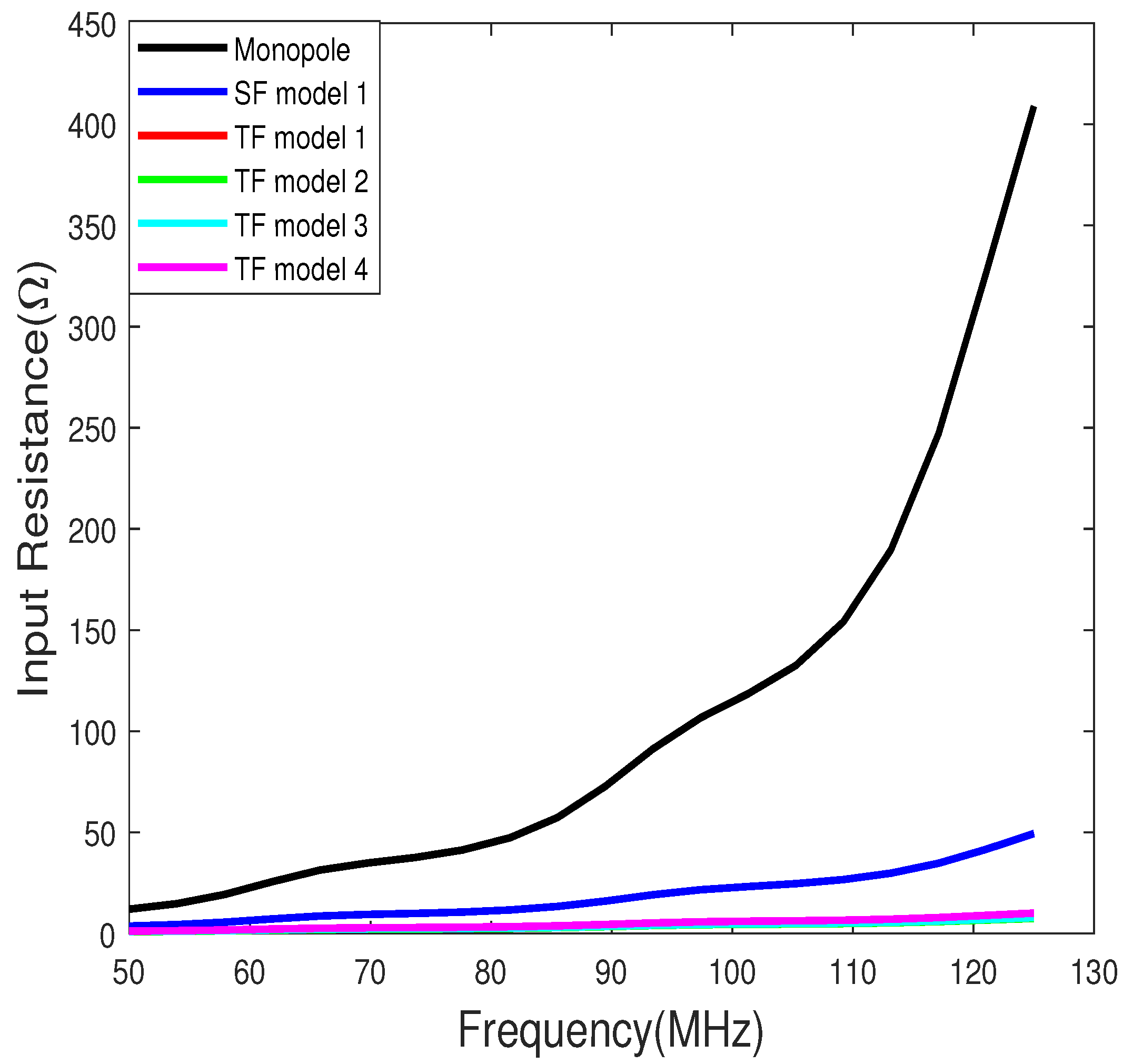
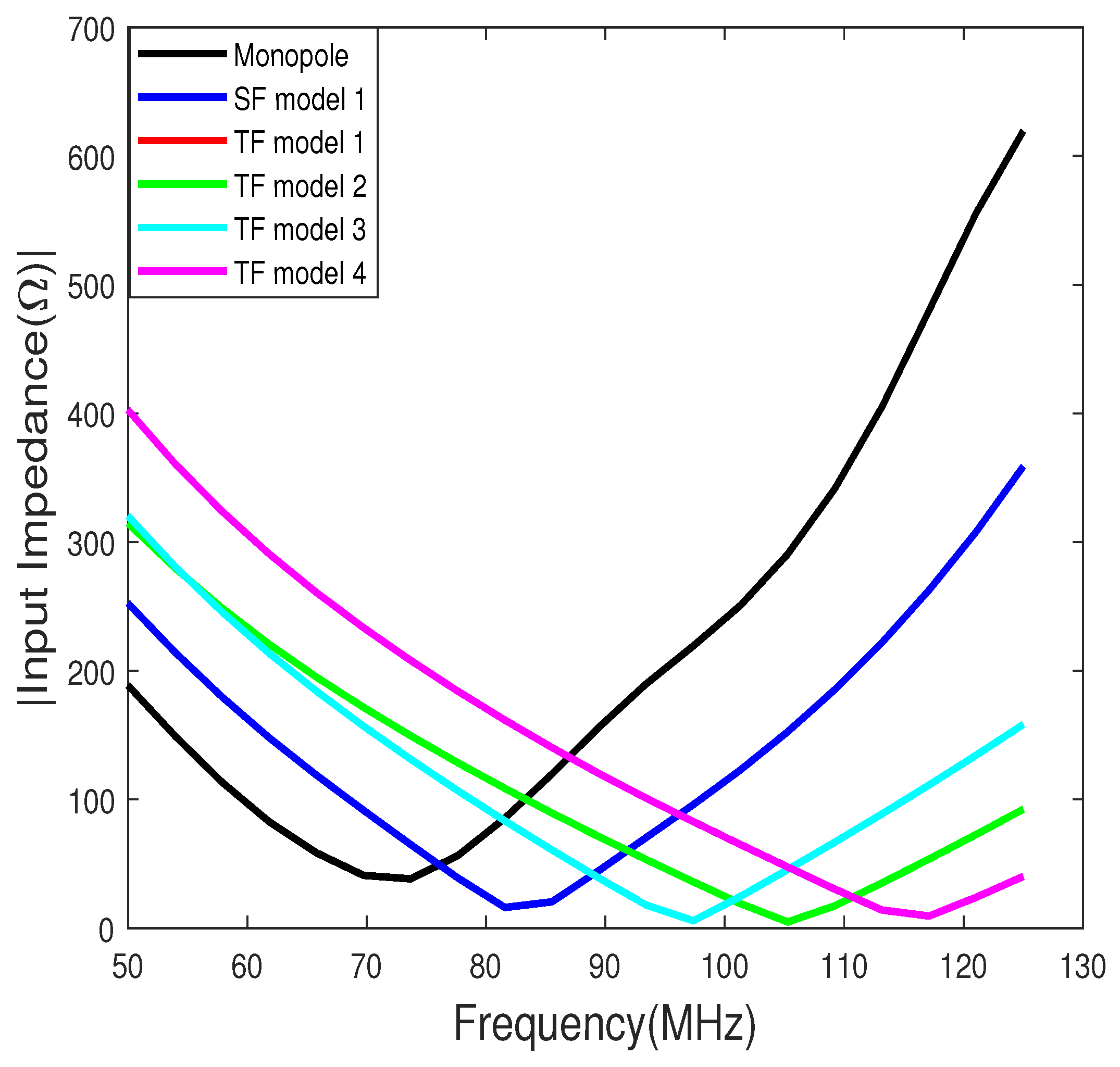
4.2. Numerical and Simulated Input Impedance
5. Conclusions
- Folded antennas are good candidates when antenna height is restricted, since folding the antenna increases the resonance length of the antenna without increasing the physical height of the antenna.
- Folding the antennas changes the resonance frequency of the antennas compared to a monopole. At the same time, folding the antennas introduces additional parameters and all those parameters affect the resonance frequency of the antenna differently. By adjusting these parameters, a folded antenna model can be designed to have the same resonance frequency as a monopole.
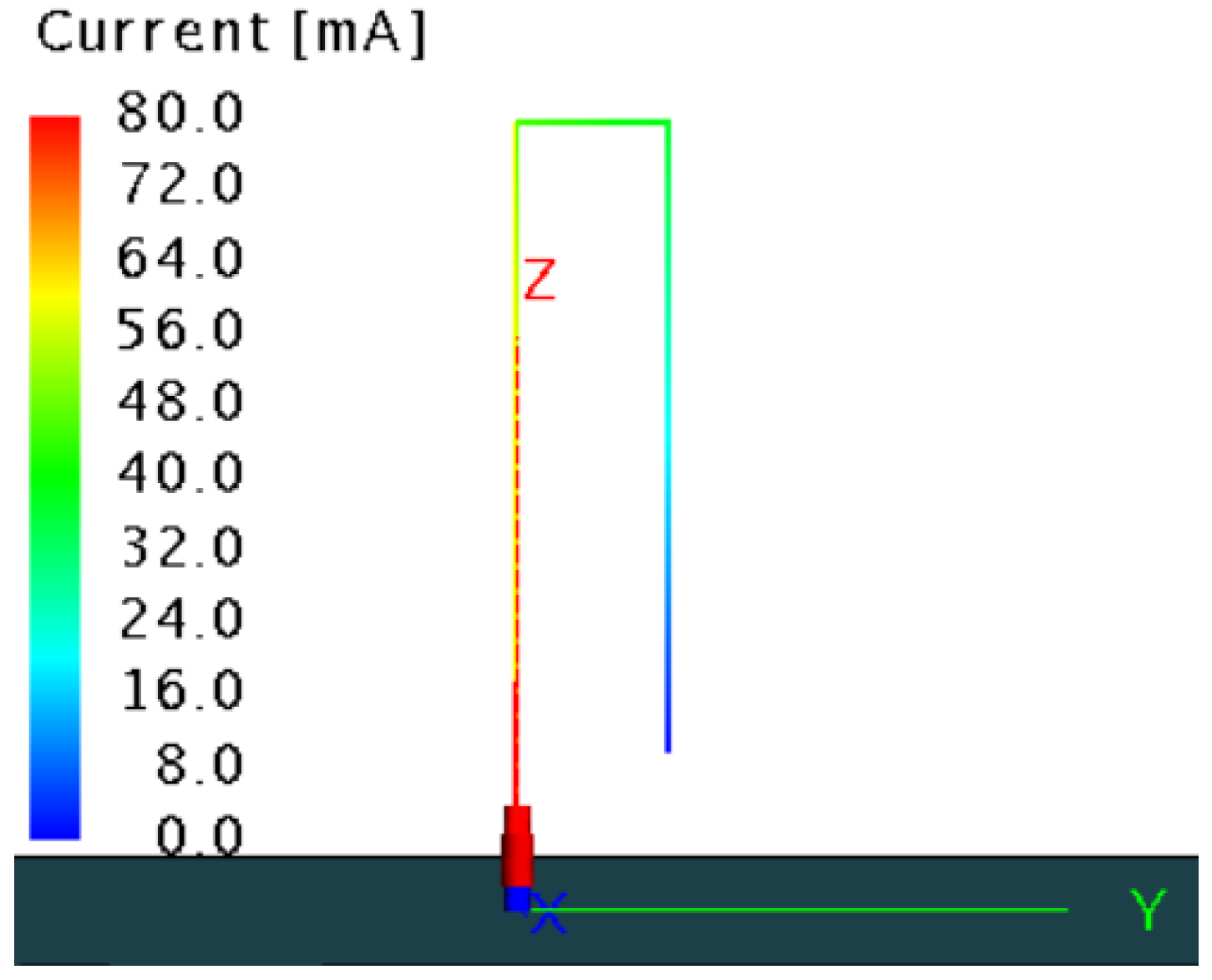
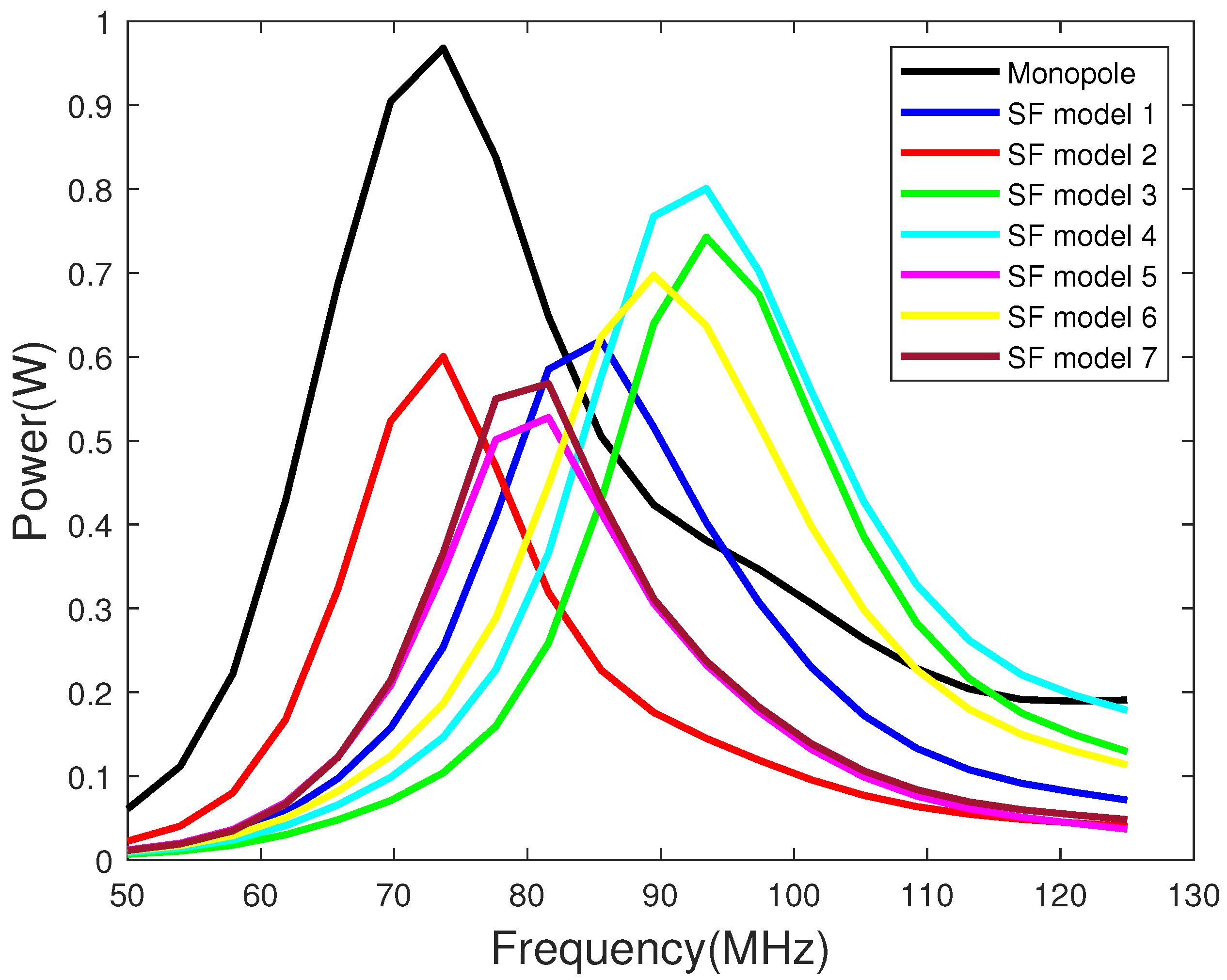
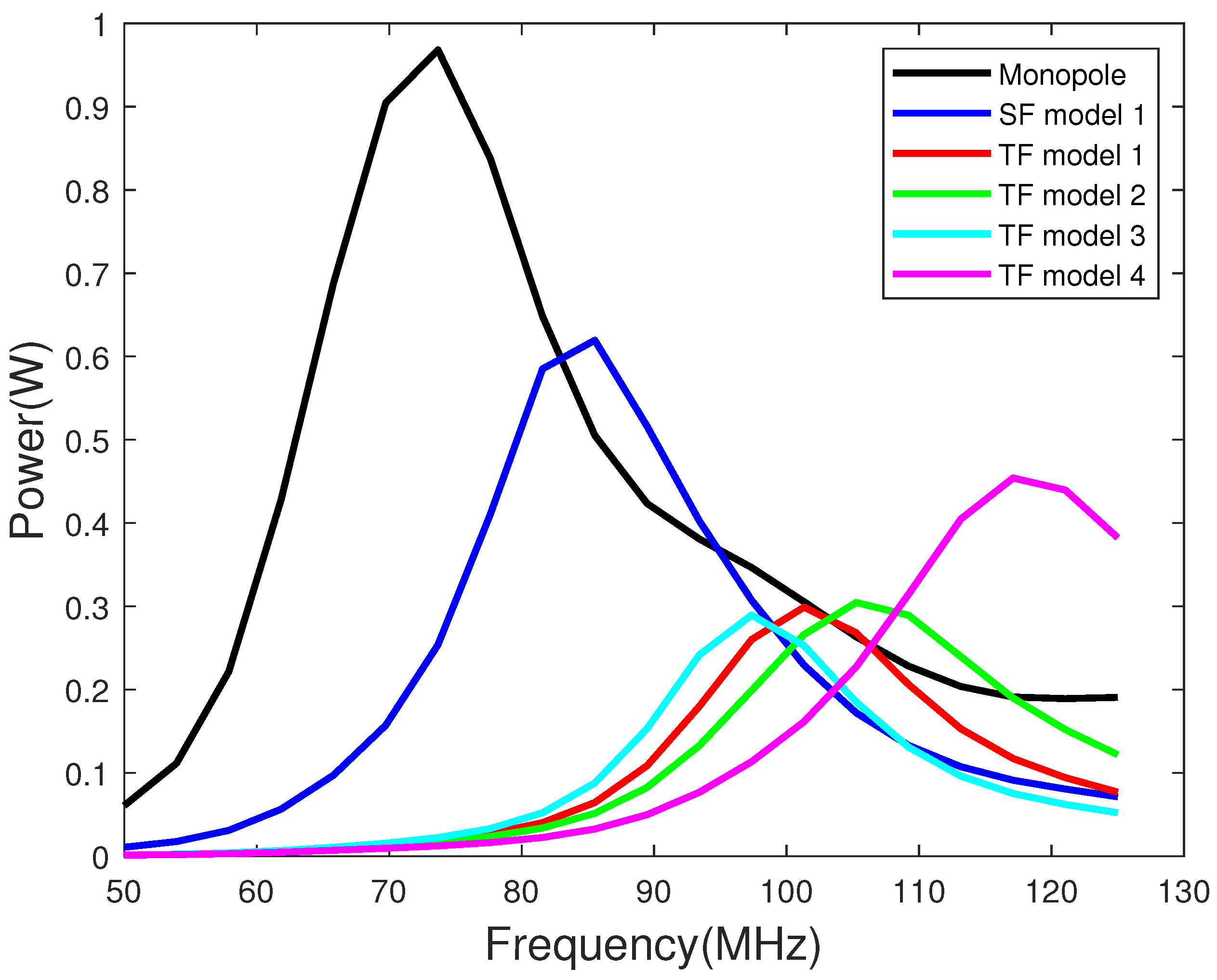
- With every fold, the far-field radiation power decreases. With every halving of the antenna height, and the radiation power also halves.
- For single-fold antenna models, the biggest effect on the far-field radiation power is attained by reducing the wire-to-wire separation (d) and by increasing the ground-to-wire separation (w). The highest far-field radiated power is obtained by increasing the ground-to-wire separation.
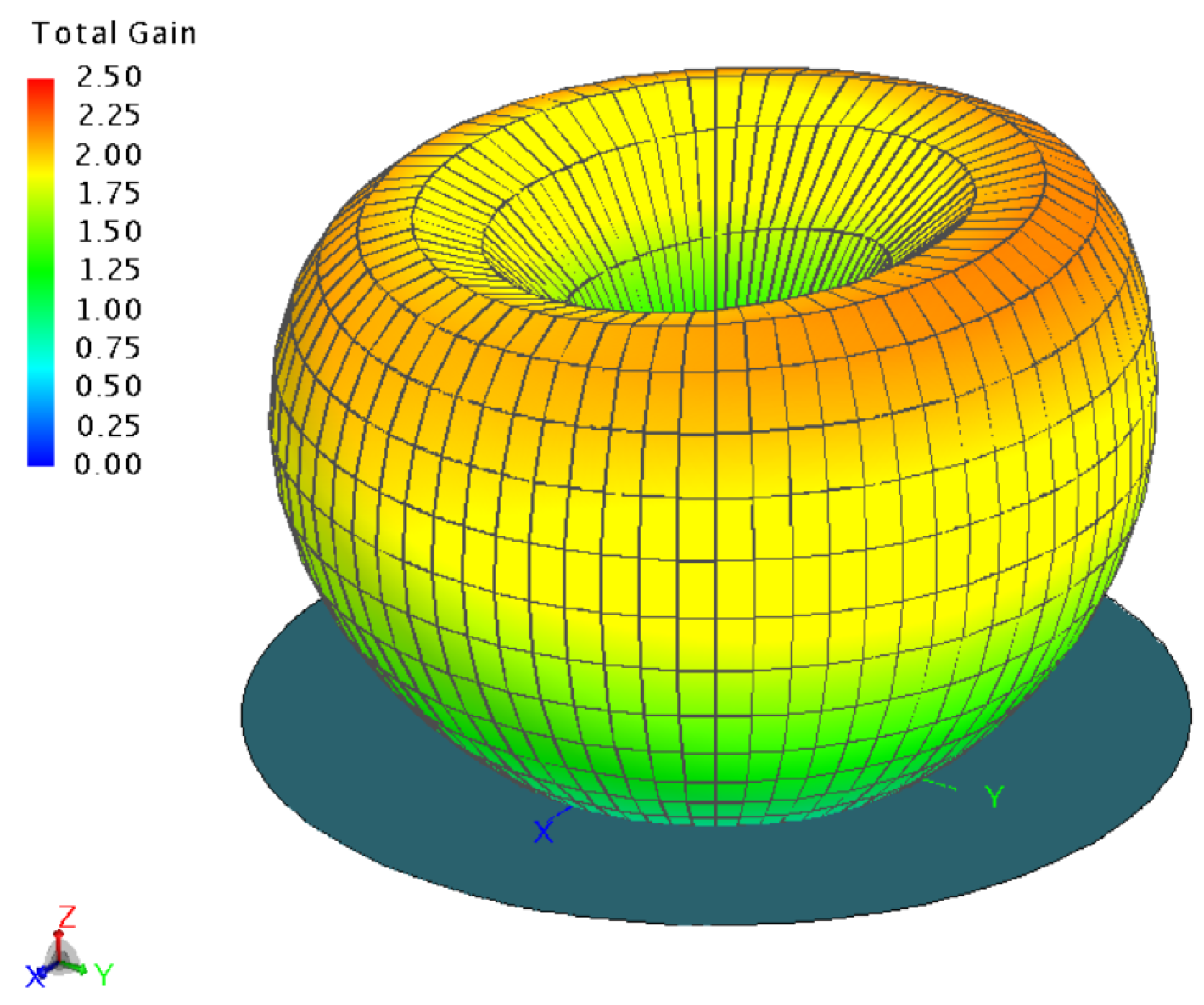
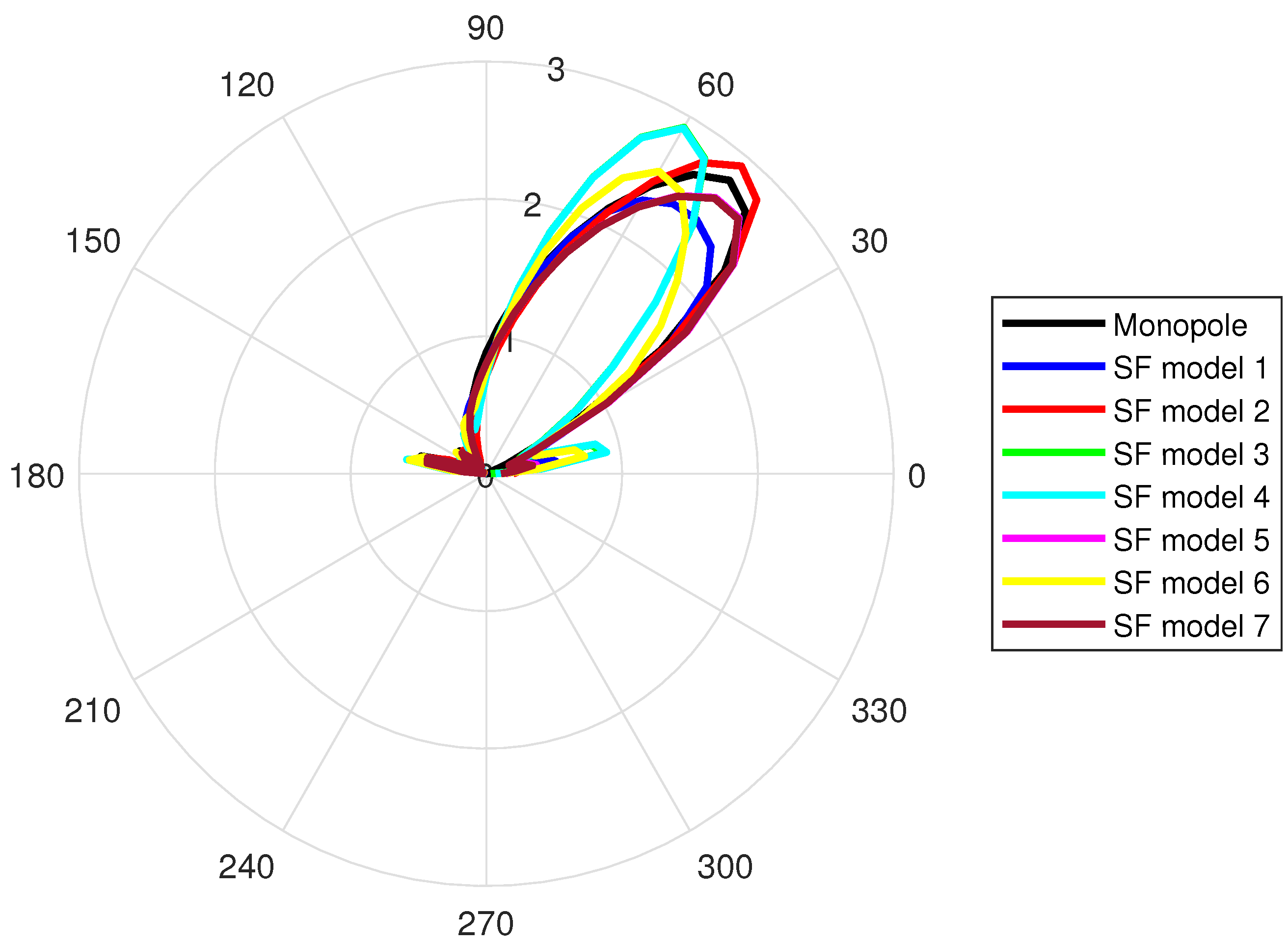
- The beam widths achieved from the single-fold monopoles and the traditional monopole are the same and there were no significant differences between the gains either.
- For the two-fold monopoles, the far-field radiation power can be increased by increasing the ground-to-wire separation similar to the single-fold monopoles.
- In both single-fold and two-fold cases, doubling the ground-to-wire separation increased the radiated power by 0.2 W compared to other single- and two-fold models.
- The two-fold antenna models show more directivity compared to the other models.
- There are significant differences between the calculated and simulated input impedance. Hence, appropriate measurements are needed to validate the models and equations.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Balanis, C.A. Antenna Theory: Analysis and Design; Harper and Row: New York, NY, USA, 1982. [Google Scholar]
- Kraus, J.D.; Marhefka, R.J. Antennas for All Applications; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Stutzman, W.L.; Thiele, G.A. Antenna Theory and Design, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Bell, T.F.; Inan, U.S.; Kimura, I.; Matsumoto, H.; Hashimoto, K. EXOS-B/Siple VLF wave-particle interaction experiments: 2. Transmitter signals and associated emission. J. Geophys. Res. 1983, 88, 295–309. [Google Scholar] [CrossRef]
- Helliwell, R.A. Siple station experiments on wave-particle interactions in the magnetosphere. In Wave Instabilities in Space Plasmas; Palmadesso, P.J., Papadopoulos, K., Eds.; Springer: Berlin, Germany, 1979; pp. 191–203. [Google Scholar]
- Helliwell, R.A. Controlled stimulation of VLF emissions from Siple Station, Antarctica. Radio Sci. 1983, 6, 801–814. [Google Scholar] [CrossRef]
- Helliwell, R.A. VLF wave-injection experiments from Siple Station, Antarctica. Adv. Space Res. 1988, 8, 279–289. [Google Scholar] [CrossRef] [Green Version]
- Maxworth, A.S. Multistation observations of the azimuth, polarization, and frequency dependence of ELF/VLF waves generated by electrojet modulation. Radio Sci. 2015, 50, 1008–1026. [Google Scholar] [CrossRef]
- Mielke, T.A.; Elkins, C.J.; Helliwell, R.A.; Inan, U.S. Excitation of whistler mode signals via injection of polarized VLF waves with the Siple transmitter. Radio Sci. 1992, 27, 31–46. [Google Scholar] [CrossRef]
- Barros, P.A. Design and Analysis of a Folded Meander Dipole Antenna Using the MININEC Program. Available online: https://digitalcommons.fiu.edu/cgi/viewcontent.cgi?article=2630context=etd (accessed on 29 November 2021).
- Raines, J.K. Folded Unipole Antennas Theory and Applications; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Raines Engineering. Available online: https://www.rainesengineering.com/articles/SimpleFormulasFoldedAntennas.pdf (accessed on 29 November 2021).
- Esnagari, A.K.; Anantha, B. A Compact Microstrip-Line Fed Meandered Inverted-F MIMO Antenna. In Proceedings of the 2018 IEEE Indian Conference on Antennas and Propogation (InCAP), Hyderabad, India, 16–19 December 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Hashmi, M.S.; Sharma, D. A meandered rectangular monopole antenna for quad-band applications. In Proceedings of the 2015 IEEE MTT-S International Microwave and RF Conference (IMaRC), Hyderabad, India, 10–12 December 2015; pp. 61–63. [Google Scholar] [CrossRef]
- Misman, D.; Aziz, M.Z.A.A.; Husain, M.N.; Soh, P.J. Design of planar meander line antenna. In Proceedings of the 2009 3rd European Conference on Antennas and Propagation, Berlin, Germany, 23–27 March 2009; pp. 2420–2424. [Google Scholar]
- Noordin, N.H.; Wong, Y.C.; Erdogan, A.T.; Flynn, B.; Arslan, T. Meandered inverted-F antenna for MIMO mobile devices. In Proceedings of the 2012 Loughborough Antennas and Propagation Conference (LAPC), Loughborough, UK, 12–13 November 2012; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Best, S.R. Improving the Performance Properties of a Dipole Element Closely Spaced to a PEC Ground Plane. IEEE Antennas Wirel. Propag. Lett. 2004, 3, 359–363. [Google Scholar] [CrossRef]
- Hung, T.; Hirayama, M.; Nagatoshi, M.; Morishita, H. Characteristics of U-shaped folded dipole antenna on a small ground plane. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar] [CrossRef]
- FEKO Software. Available online: https://www.altair.com/feko/ (accessed on 23 February 2022).
- MATLAB Software. Available online: https://www.mathworks.com/products/matlab.html (accessed on 3 March 2022).
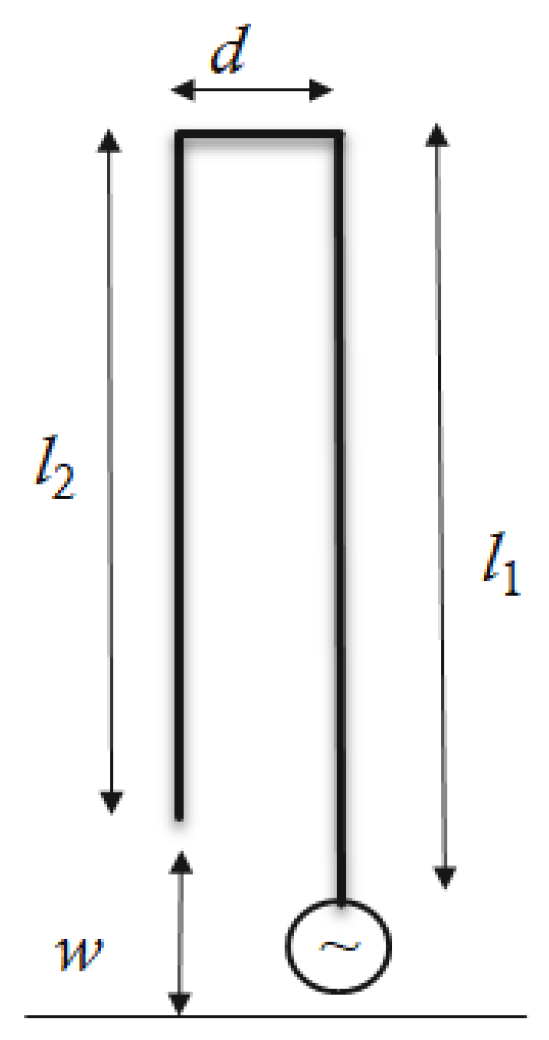







| Model | (cm) | (cm) | d (cm) | w (cm) | (mm) | (mm) |
|---|---|---|---|---|---|---|
| Monopole | 100 | - | - | - | 1.5 | - |
| SF model 1 | 50 | 40 | 10 | 10 | 1.5 | 1.5 |
| SF model 2 | 50 | 40 | 20 | 10 | 1.5 | 1.5 |
| SF model 3 | 50 | 40 | 5 | 10 | 1.5 | 1.5 |
| SF model 4 | 50 | 30 | 10 | 20 | 1.5 | 1.5 |
| SF model 5 | 50 | 45 | 10 | 5 | 1.5 | 1.5 |
| SF model 6 | 50 | 40 | 10 | 10 | 3.0 | 1.5 |
| SF model 7 | 50 | 40 | 10 | 10 | 0.75 | 1.5 |
| Model | (cm) | (cm) | d (cm) | w (cm) | (mm) | (mm) |
|---|---|---|---|---|---|---|
| TF model 1 | 25 | 20 | 5 | 5 | 1.5 | 1.5 |
| TF model 2 | 25 | 20 | 5 | 5 | 3.0 | 1.5 |
| TF model 3 | 25 | 20 | 5 | 5 | 0.75 | 1.5 |
| TF model 4 | 25 | 15 | 5 | 10 | 1.5 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maxworth, A. Far-Field Radiation Characteristics of Folded Monopole Antennas over a Conducting Ground Plane. Eng 2022, 3, 142-160. https://doi.org/10.3390/eng3010012
Maxworth A. Far-Field Radiation Characteristics of Folded Monopole Antennas over a Conducting Ground Plane. Eng. 2022; 3(1):142-160. https://doi.org/10.3390/eng3010012
Chicago/Turabian StyleMaxworth, Ashanthi. 2022. "Far-Field Radiation Characteristics of Folded Monopole Antennas over a Conducting Ground Plane" Eng 3, no. 1: 142-160. https://doi.org/10.3390/eng3010012
APA StyleMaxworth, A. (2022). Far-Field Radiation Characteristics of Folded Monopole Antennas over a Conducting Ground Plane. Eng, 3(1), 142-160. https://doi.org/10.3390/eng3010012






