Similarity of Musical Timbres Using FFT-Acoustic Descriptor Analysis and Machine Learning
Abstract
:1. Introduction
2. Acoustic Descriptors and Timbral Representation
2.1. Fundamental Frequency Descriptors
2.2. Distribution Statistics
2.3. Descriptors of the Frequency Distribution
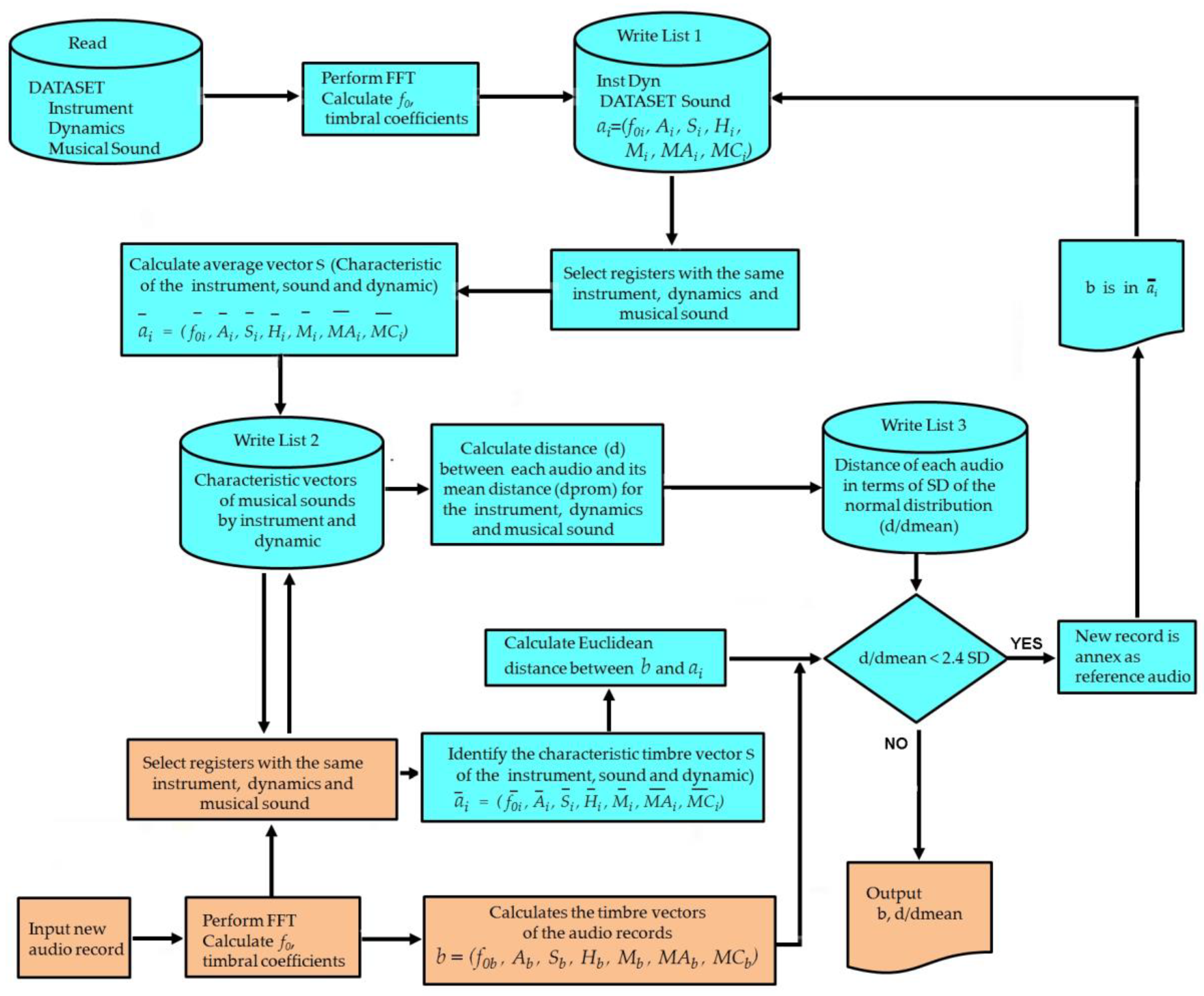
3. Timbre Similarities in Musical Instruments
4. Results
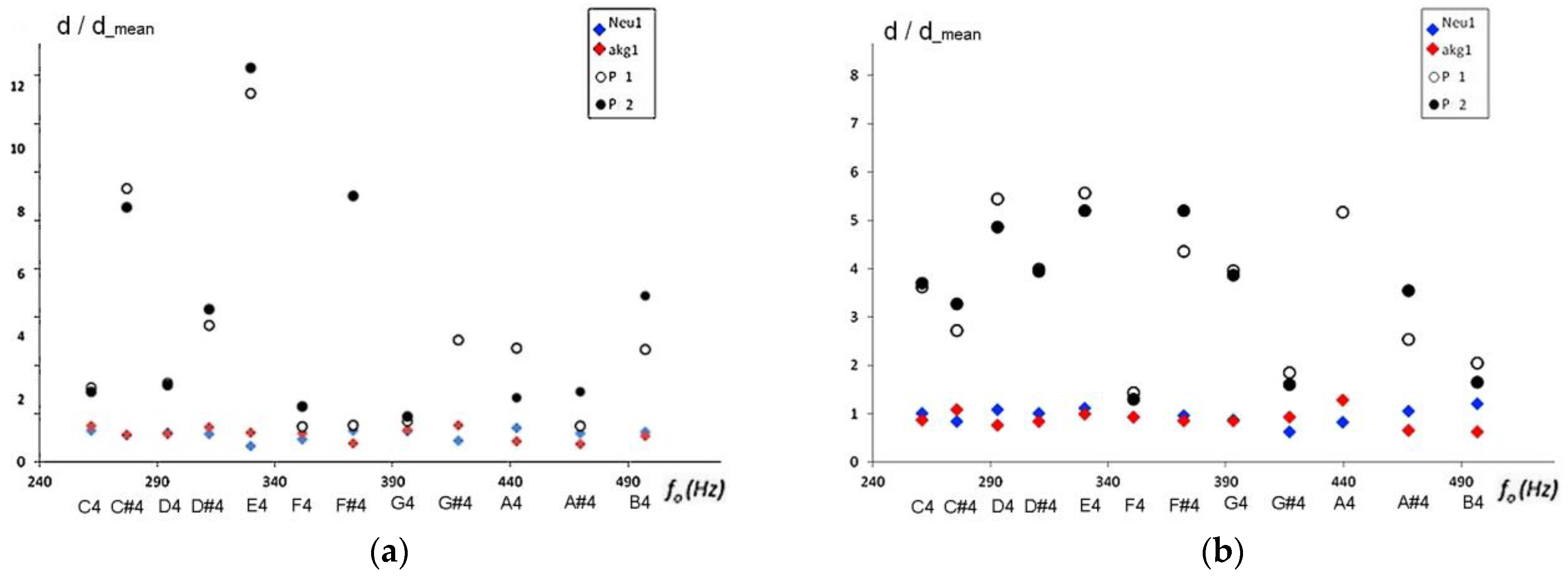
4.1. Variations Due to the Musical Instrument
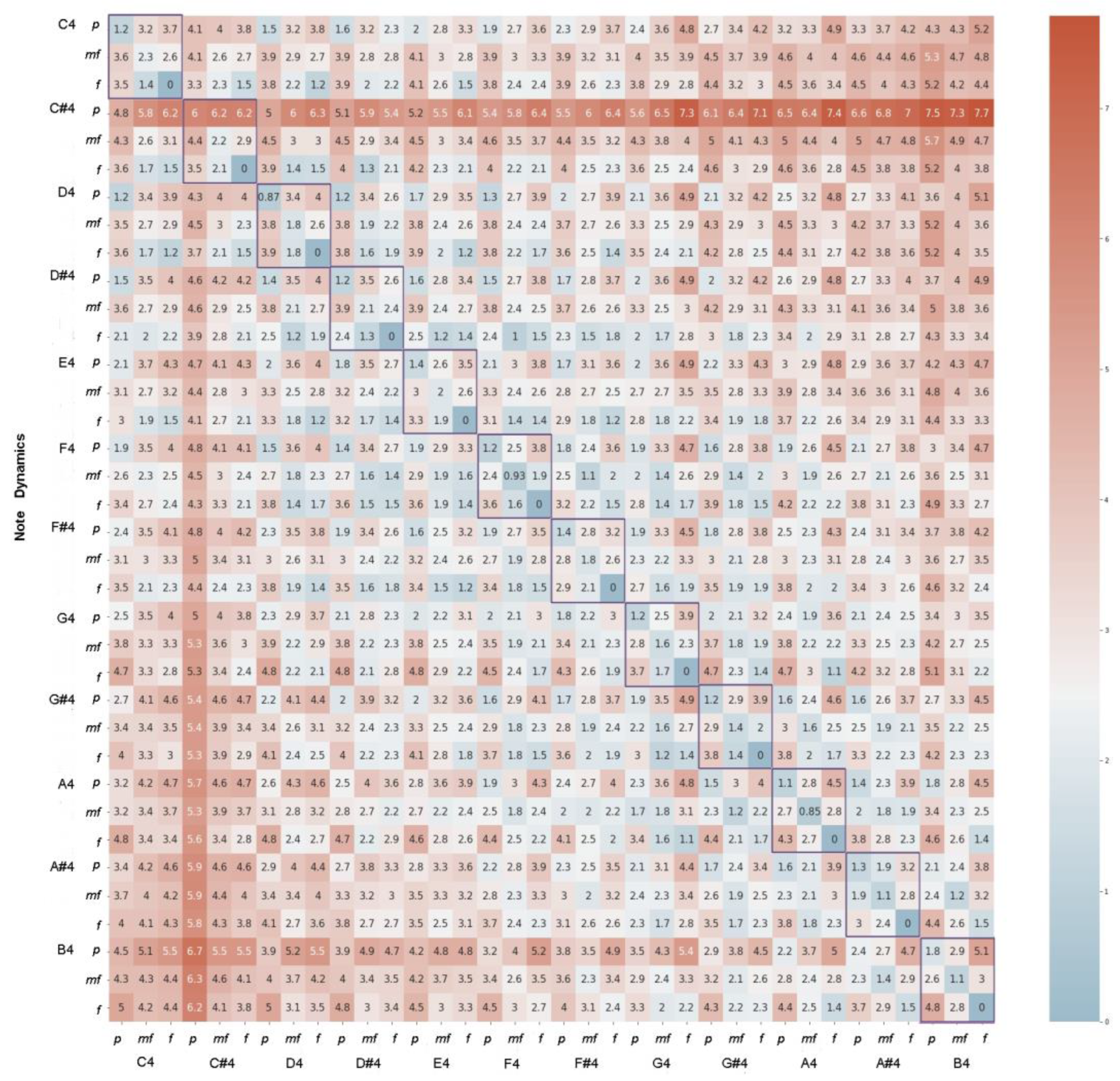
4.2. Variations Due Musical Dynamics
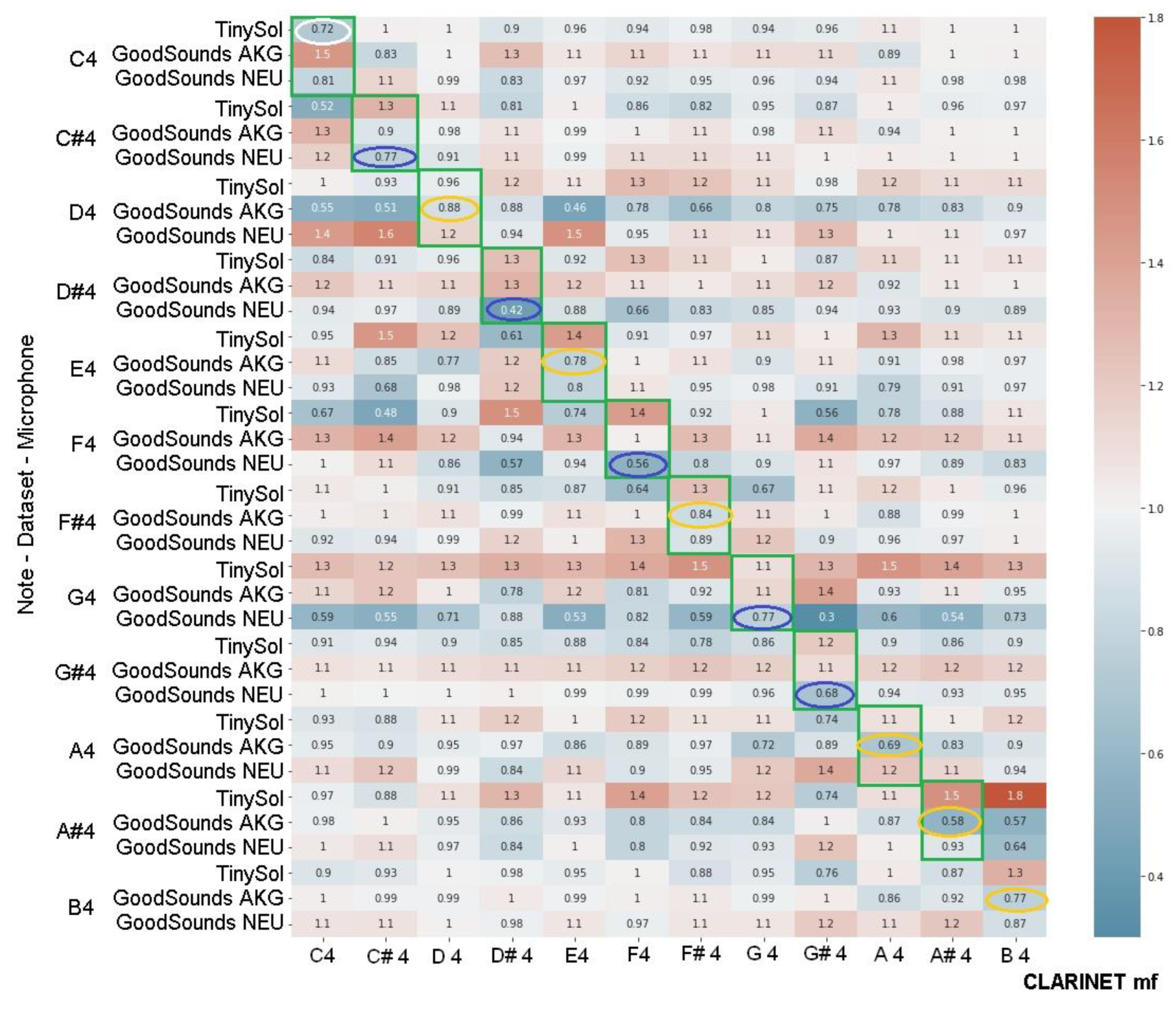
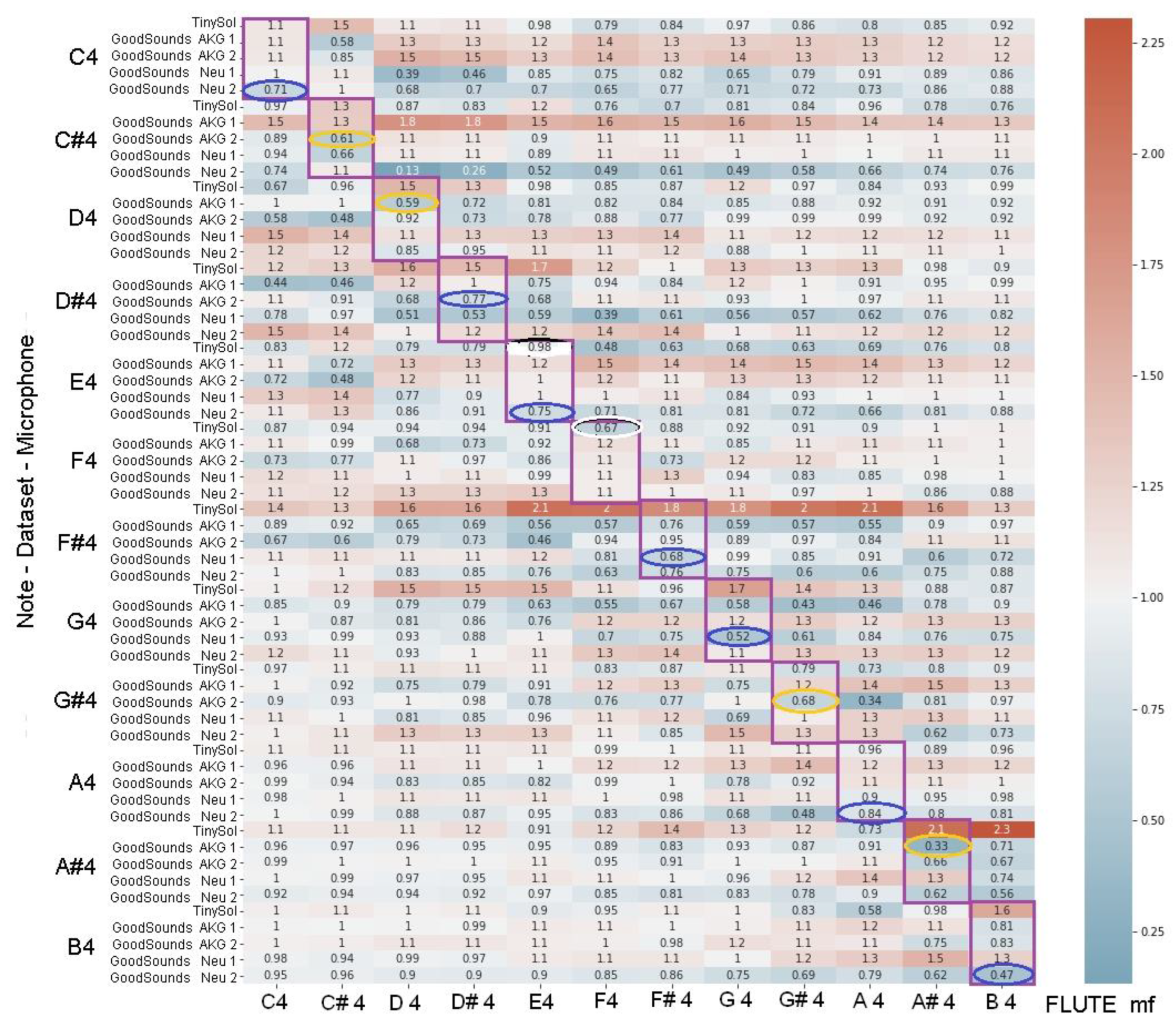
4.3. Variations Due to the Tinysol and GoodSounds Database
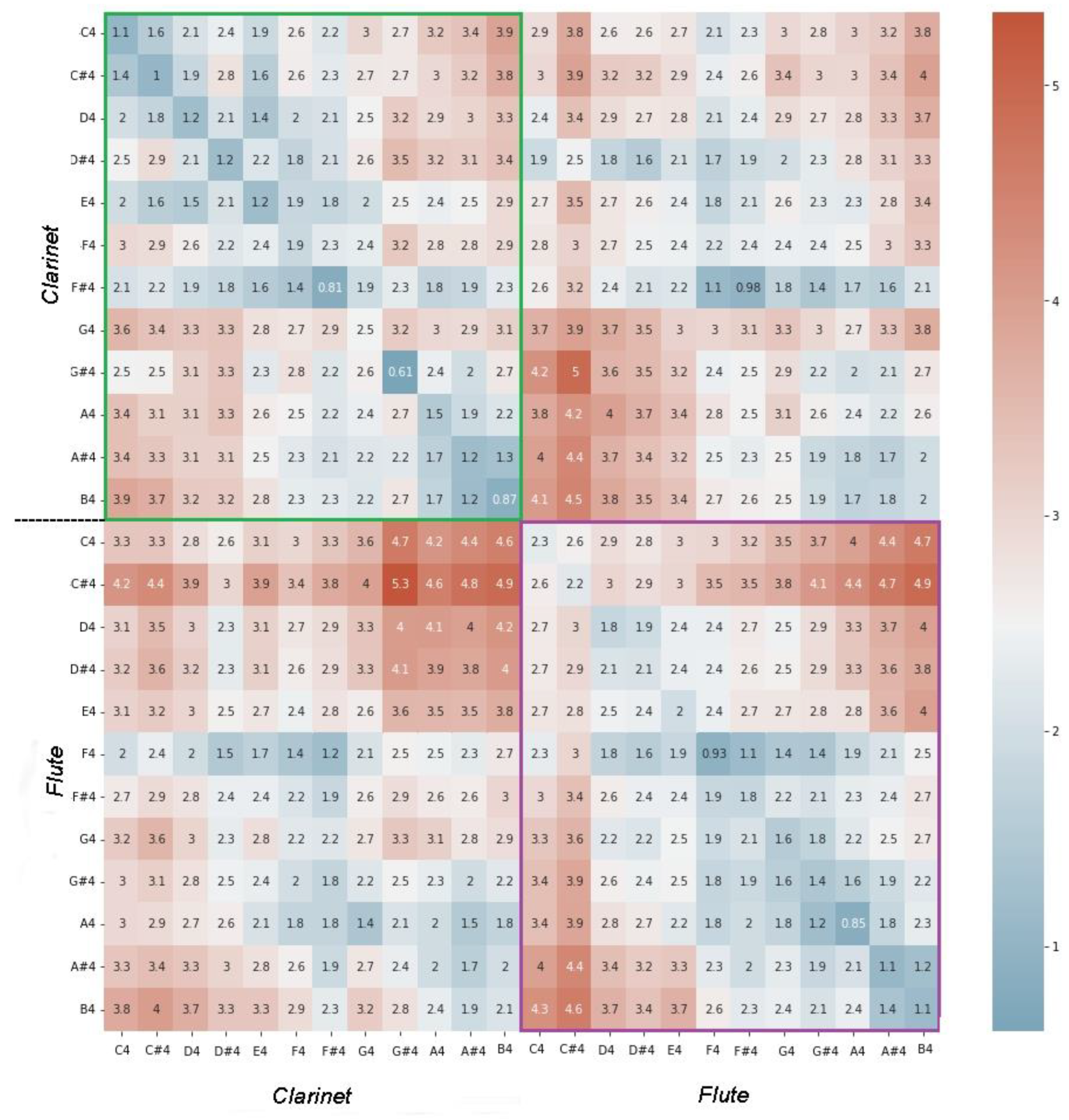
4.4. Timbral Similarity between Clarinet and Transverse Flute
5. Conclusions
- -
- Audios of different sounds and different instruments (Section 4.1).
- -
- Audios of the same type of sound and instrument with different relative musical dynamics (Section 4.2).
- -
- Audios of different databases (Section 4.3).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, W.; Liu, J.; Zhang, X.; Wang, S.; Jiang, Y. Analysis and Modeling of Timbre Perception Features in Musical Sounds. Appl. Sci. 2020, 10, 789. [Google Scholar] [CrossRef]
- Guven, E.; Ozbayoglu, A.M. Note and Timbre Classification by Local Features of Spectrogram. Procedia Comput. Sci. 2012, 12, 182–187. [Google Scholar] [CrossRef]
- Fourer, D.; Rouas, J.L.; Hanna, P.; Robine, M. Automatic timbre classification of ethnomusicological audio recordings. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR 2014), Taipei, Taiwan, 27–31 October 2013. [Google Scholar]
- McAdams, S. The perceptual representation of timbre. In Timbre: Acoustics, Perception, and Cognition; Springer: Cham, Switzerland, 2019; pp. 23–57. [Google Scholar]
- Liu, J.; Zhao, A.; Wang, S.; Li, Y.; Ren, H. Research on the Correlation Between the Timbre Attributes of Musical Sound and Visual Color. IEEE Access 2021, 9, 97855–97877. [Google Scholar]
- Reymore, L.; Huron, D. Using auditory imagery tasks to map the cognitive linguistic dimensions of musical instrument timbre qualia. Psychomusicol. Music. Mind Brain 2020, 30, 124–144. [Google Scholar] [CrossRef]
- Reymore, L. Characterizing prototypical musical instrument timbres with Timbre Trait Profiles. Musicae Sci. 2022, 26, 648–674. [Google Scholar] [CrossRef]
- Muller, M.; Ewert, S.; Kreuzer, S. Making chroma features more robust to timbre changes. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 1877–1880. [Google Scholar] [CrossRef]
- Muller, M. Fundamentals of Music Processing; Springer: Erlangen, Germany, 2021. [Google Scholar]
- Muller, M.; Ewert, S. Towards Timbre-Invariant Audio Features for Harmony-Based Music. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 649–662. [Google Scholar] [CrossRef]
- Lartillot, O.; Toiviainen, P.; Eerola, T. A Matlab Toolbox for music information retrieval. In Data Analysis, Machine Learning and Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 261–268. [Google Scholar]
- Peeters, G.; Giordano, B.L.; Susini, P.; Misdariis, N.; McAdams, S. The timbre toolbox: Extracting audio descriptors from musical signals. J. Acoust. Soc. Am. 2011, 130, 2902–2916. [Google Scholar] [PubMed]
- Barbedo, J.G.; Tzanetakis, G. Musical instrument classification using individual partials. In IEEE Transactions on Audio, Speech, and Language Processing; IEEE: New York, NY, USA, 2010; Volume 19, pp. 111–122. [Google Scholar]
- Joshi, S.; Chitre, A. Identification of Indian musical instruments by feature analysis with different classifiers. In Proceedings of the Sixth International Conference on Computer and Communication Technology 2015, Allahabad, India, 25–27 September 2015; pp. 110–114. [Google Scholar] [CrossRef]
- Ezzaidi, H.; Bahoura, M.; Hall, G.E. Towards a characterization of musical timbre based on chroma contours. In Proceedings of the International Conference on Advanced Machine Learning Technologies and Applications, Cairo, Egypt, 8–10 December 2012; pp. 162–171. [Google Scholar]
- Böck, S.; Korzeniowski, F.; Schlüter, J.; Krebs, F.; Widmer, G. Madmom: A new python audio and music signal processing library. In Proceedings of the 24th ACM International Conference on Multimedia, Santa Barbara, CA, USA, 23–27 October 2016; pp. 1174–1178. [Google Scholar]
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.P.; McVicar, M.; Battenberg, E.; Nieto, O. Librosa: Audio and music signal analysis in python. In Proceedings of the 14th Python in Science Conference, Austin, TX, USA, 6–12 July 2015; Volume 8, pp. 18–25. [Google Scholar]
- Krimphoff, J.; McAdams, S.; Winsberg, S. Characterization of the timbre of complex sounds. II Acoustical analysis and psychophysical quantification. J. Phys. 1994, 4, 625–628. [Google Scholar]
- Johnston, J. Transform coding of audio signals using perceptual noise criteria. IEEE J. Sel. Areas Commun. 1988, 6, 314–323. [Google Scholar]
- Gaikwad, S.; Chitre, A.V.; Dandawate, Y.H. Classification of Indian Classical Instruments using Spectral and Principal Component Analysis based Cepstrum Features. In Proceedings of the IEEE International Conference on Electronic Systems, Signal Processing and Computing Technologies (ICESC), Nagpur, India, 9–11 January 2014. [Google Scholar]
- Joder, C.; Slim Essid, S. Temporal Integration for Audio Classification with Application to Musical Classification. In IEEE Transaction on Speech and Audio Processing; IEEE: New York, NY, USA, 2009; Volume 17, pp. 174–186. [Google Scholar]
- Pollard, H.F.; Jansson, E.V. A tristimulus method for the specification of musical timbre. Acta Acust. United Acust. 1982, 51, 162–171. [Google Scholar]
- Burred, J.J.; Röbel, A.; Sikora, T. Dynamic spectral envelope modeling for timbre analysis of musical instrument sounds. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 663–674. [Google Scholar]
- Gonzalez, Y.; Prati, R.C. Acoustic Descriptors for Characterization of Musical Timbre Using the Fast Fourier Transform. Electronics 2022, 11, 1405. [Google Scholar] [CrossRef]
- Gonzalez, Y.; Prati, R.C. Applications of FFT for timbral characterization in woodwind instruments. In Proceedings of the Brazilian Symposia On Computer Music (SBCM), Recipe, PE, Brazil, 24–27 October 2021. [Google Scholar] [CrossRef]
- Gonzalez, Y.; Prati, R.C. Acoustic Analysis of Musical Timbre of Wooden Aerophones. Rom. J. Acoust. Vib. 2022; in press. [Google Scholar]
- Cella, C.E.; Ghisi, D.; Lostanlen, V.; Lévy, F.; Fineberg, J.; Maresz, Y. OrchideaSOL: A dataset of extended instrumental techniques for computer-aided orchestration. arXiv 2020, arXiv:2007.00763. [Google Scholar]
- Awodey, S. Category Theory; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Mannone, M.; Arias-Valero, J.S. Some Mathematical and Computational Relations Between Timbre and Color. In Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science; Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B., Eds.; Springer: Cham, Switzerland, 2022; Volume 13267, pp. 127–139. [Google Scholar]
- Grey, J.M. Multidimensional perceptual scaling of musical timbres. J. Acoust. Soc. Am. 1977, 61, 1270–1277. [Google Scholar] [PubMed] [Green Version]
- McAdams, S. Perception et Cognition de la Musique. 2015. Available online: https://www.erudit.org/en/journals/sqrm/2016-v17-n2-sqrm03970/1052743ar/ (accessed on 10 November 2022).
- Carmine, E.; Ghisi, D.; Lostanlen, V.; Lévy, F.; Fineberg, J.; Maresz, Y. TinySOL: An Audio Dataset of Isolated Musical Notes. Zenodo 2020. Available online: https://zenodo.org/record/3632193#.Y-QrSnbMLIU (accessed on 15 May 2022).
- Romaní Picas, O.; Parra-Rodriguez, H.; Dabiri, D.; Tokuda, H.; Hariya, W.; Oishi, K.; Serra, X. A real-time system for measuring sound goodness in instrumental sounds. In Proceedings of the 138th Audio Engineering Society Convention, AES 2015, Warsaw, Poland, 7–10 May 2015; Audio Engineering Society: New York, NY, USA, 2015; pp. 1106–1111. [Google Scholar]

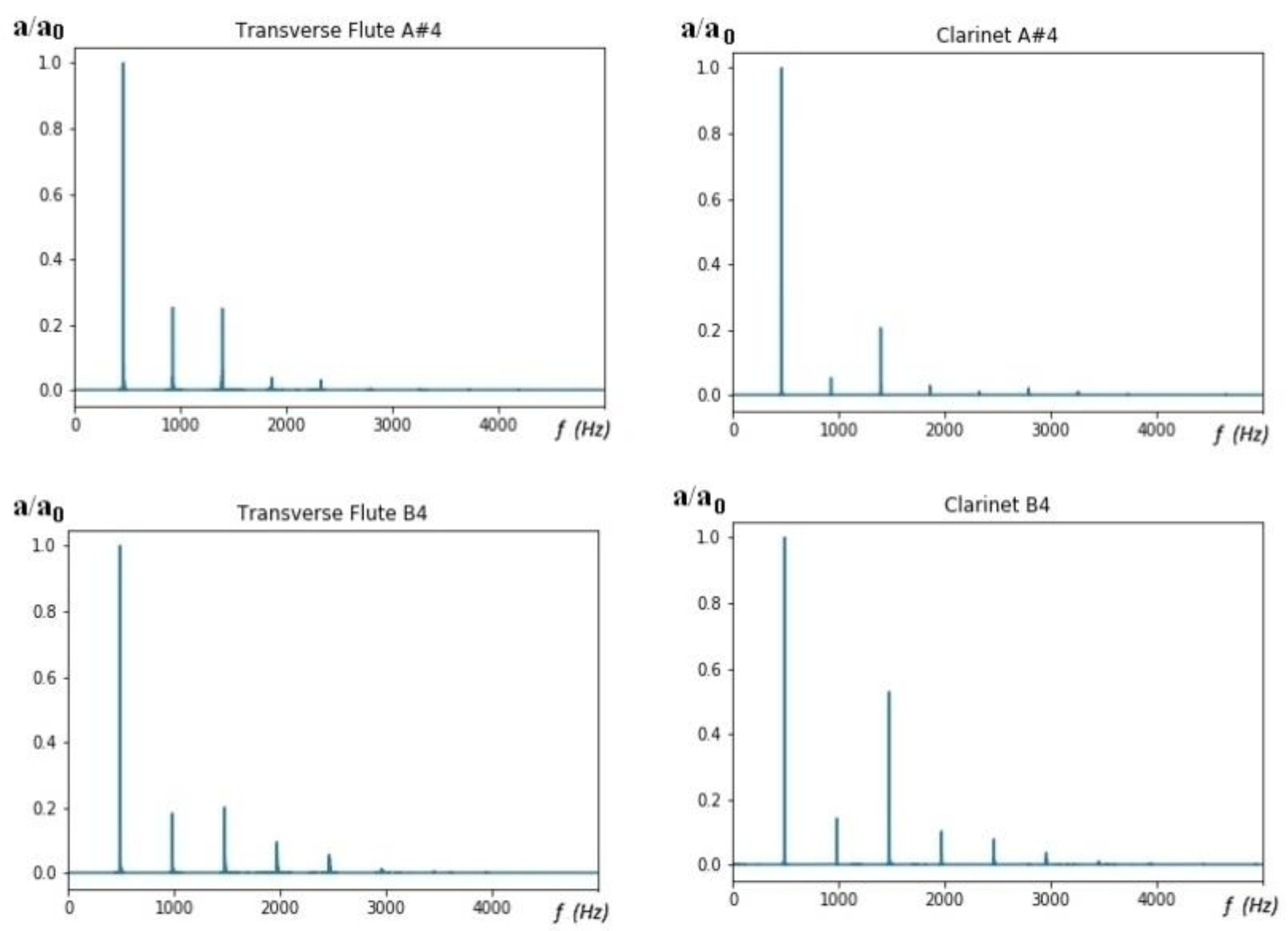
| ClBb A#4 | ClBb B4 | Fl A#4 | Fl B4 | |
|---|---|---|---|---|
| ClBb A#4 | 1.198 | 1.314 | 1.667 | 1.985 |
| ClBb B4 | 1.184 | 0.867 | 1.807 | 2.015 |
| Fl A#4 | 1.665 | 2.026 | 1.091 | 1.247 |
| Fl B4 | 1.936 | 2.141 | 1.362 | 1.127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez, Y.; Prati, R.C. Similarity of Musical Timbres Using FFT-Acoustic Descriptor Analysis and Machine Learning. Eng 2023, 4, 555-568. https://doi.org/10.3390/eng4010033
Gonzalez Y, Prati RC. Similarity of Musical Timbres Using FFT-Acoustic Descriptor Analysis and Machine Learning. Eng. 2023; 4(1):555-568. https://doi.org/10.3390/eng4010033
Chicago/Turabian StyleGonzalez, Yubiry, and Ronaldo C. Prati. 2023. "Similarity of Musical Timbres Using FFT-Acoustic Descriptor Analysis and Machine Learning" Eng 4, no. 1: 555-568. https://doi.org/10.3390/eng4010033
APA StyleGonzalez, Y., & Prati, R. C. (2023). Similarity of Musical Timbres Using FFT-Acoustic Descriptor Analysis and Machine Learning. Eng, 4(1), 555-568. https://doi.org/10.3390/eng4010033






