Minimum Shear Reinforcement for Reactive Powder Concrete Beams
Abstract
:1. Introduction
2. Design Guidelines for the Shear of RC Beams
2.1. Shear Design of RC Beams under ACI318-2014 Code
2.2. The ACI318-2014 Code for RC Beams Specifies the Minimal Amount of Shear Reinforcement
2.3. Limits of Spacing for Shear Reinforcement
2.4. Design Recommendations for RPC Beams in Regard to Shear
2.5. The France Association of Civil Engineers (AFGC-2013)
2.6. Korea Concrete Institute (KCI-2012)
3. Materials and Methods
3.1. Materials Used
3.2. Concrete Mix Proportions and Specimen Casting
3.3. Experimental Program for the RPC Beams
4. Analysis Software and Model Calibration
4.1. Concrete and Reinforcement Constitutive Models
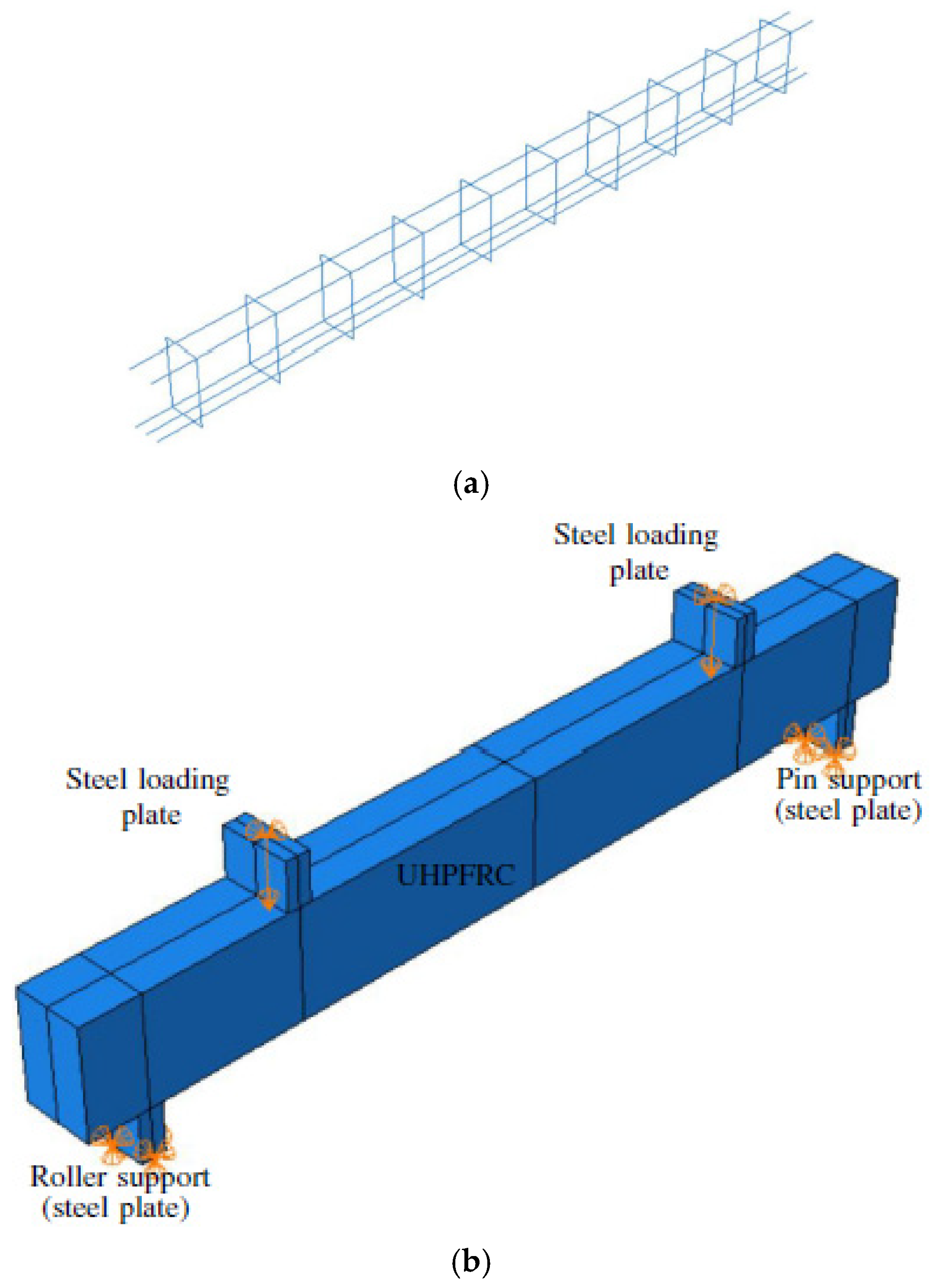
4.2. Finite Element Modelling and Analysis Procedure
5. Results and Discussion
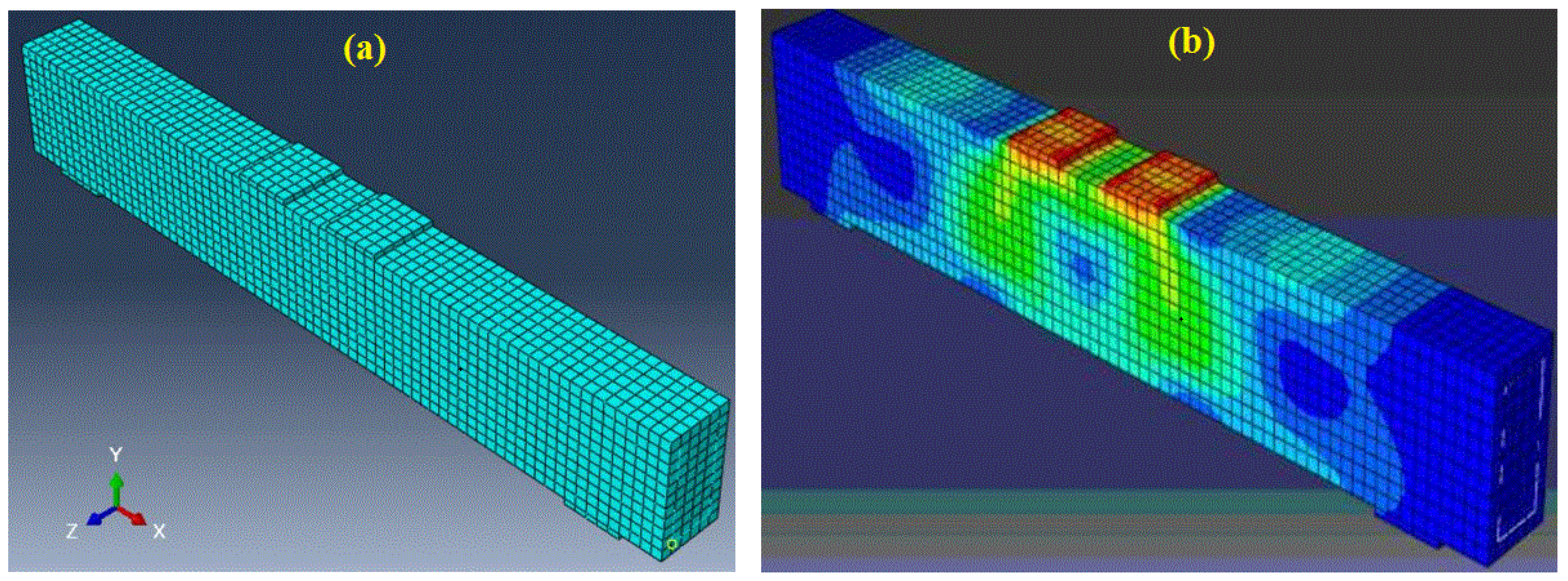
5.1. Damage and Crack Patterns
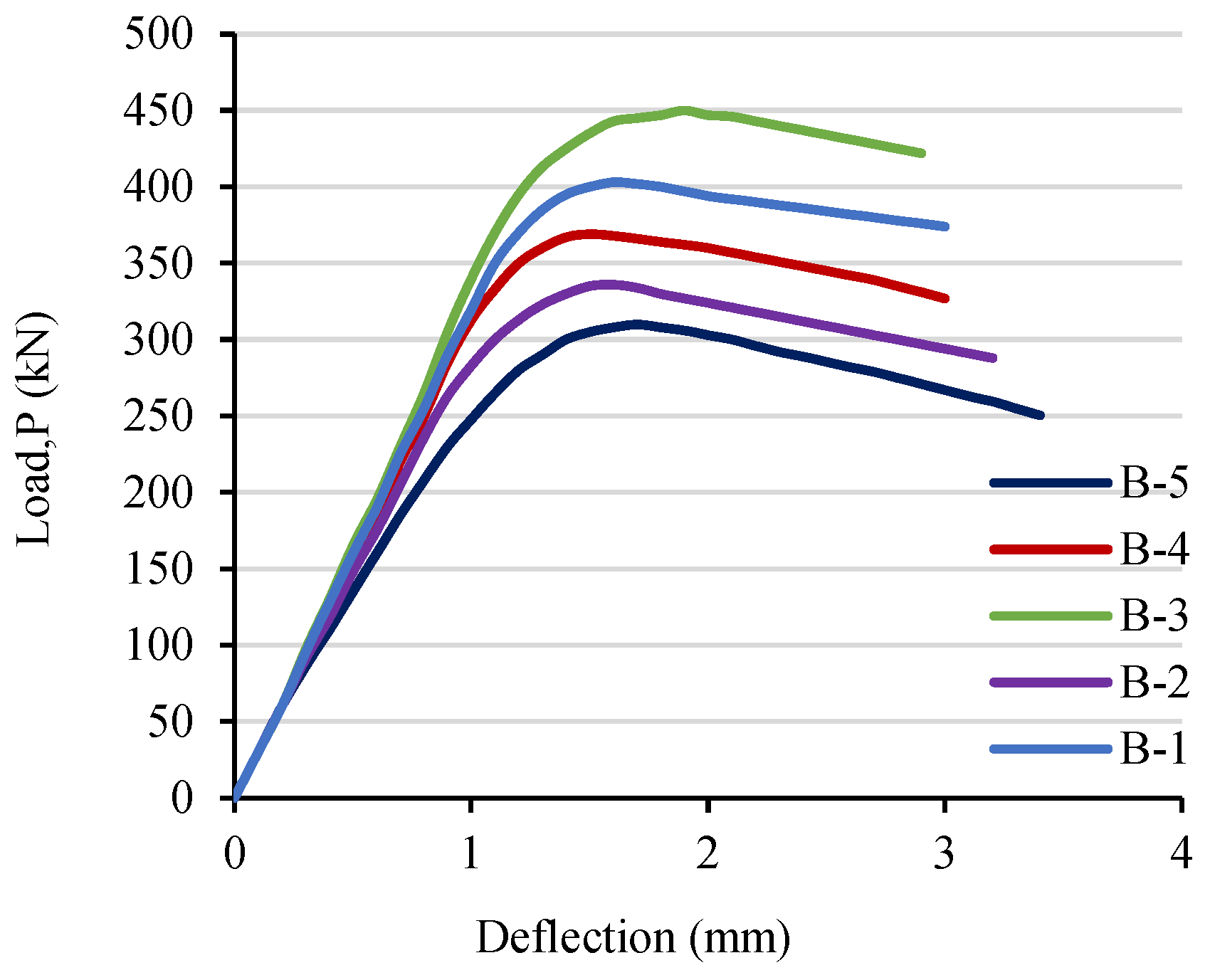
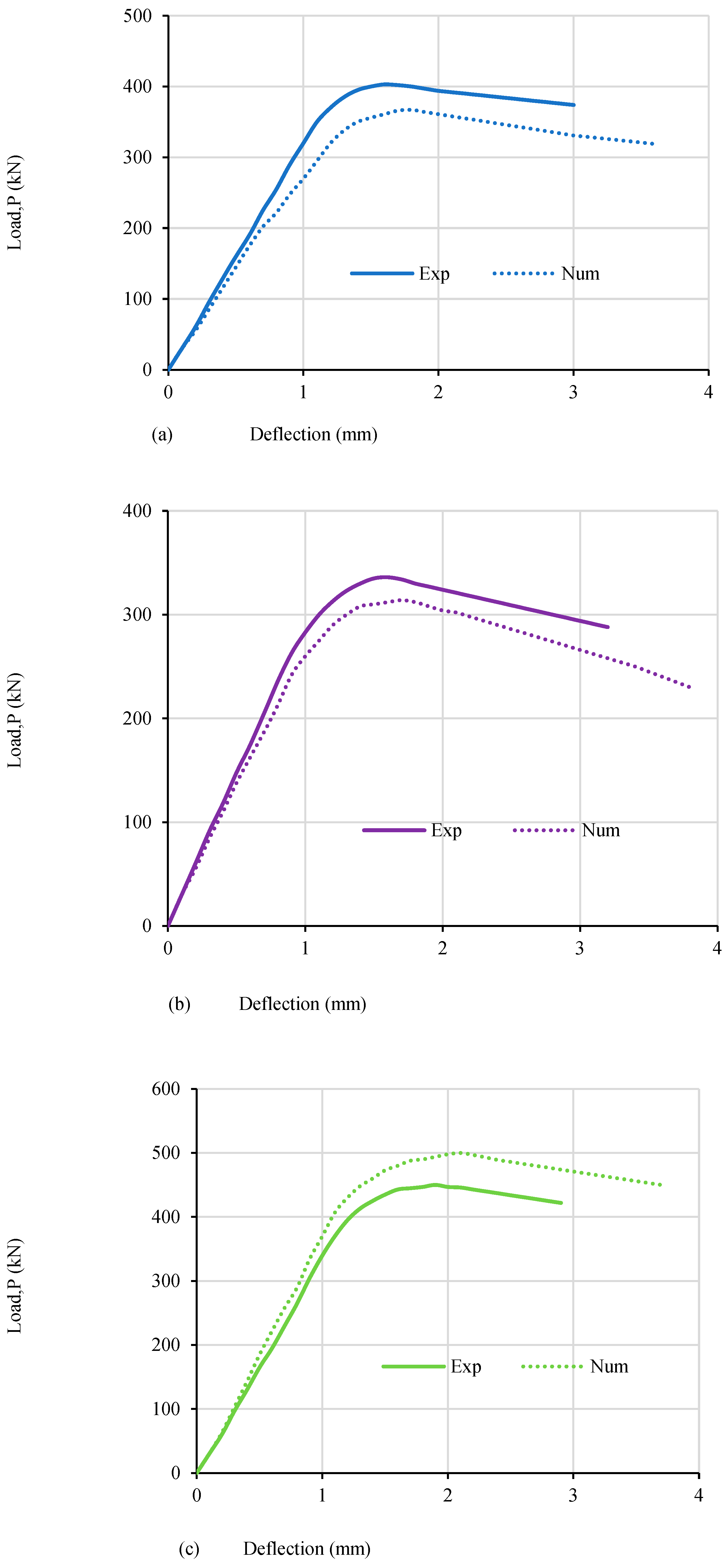
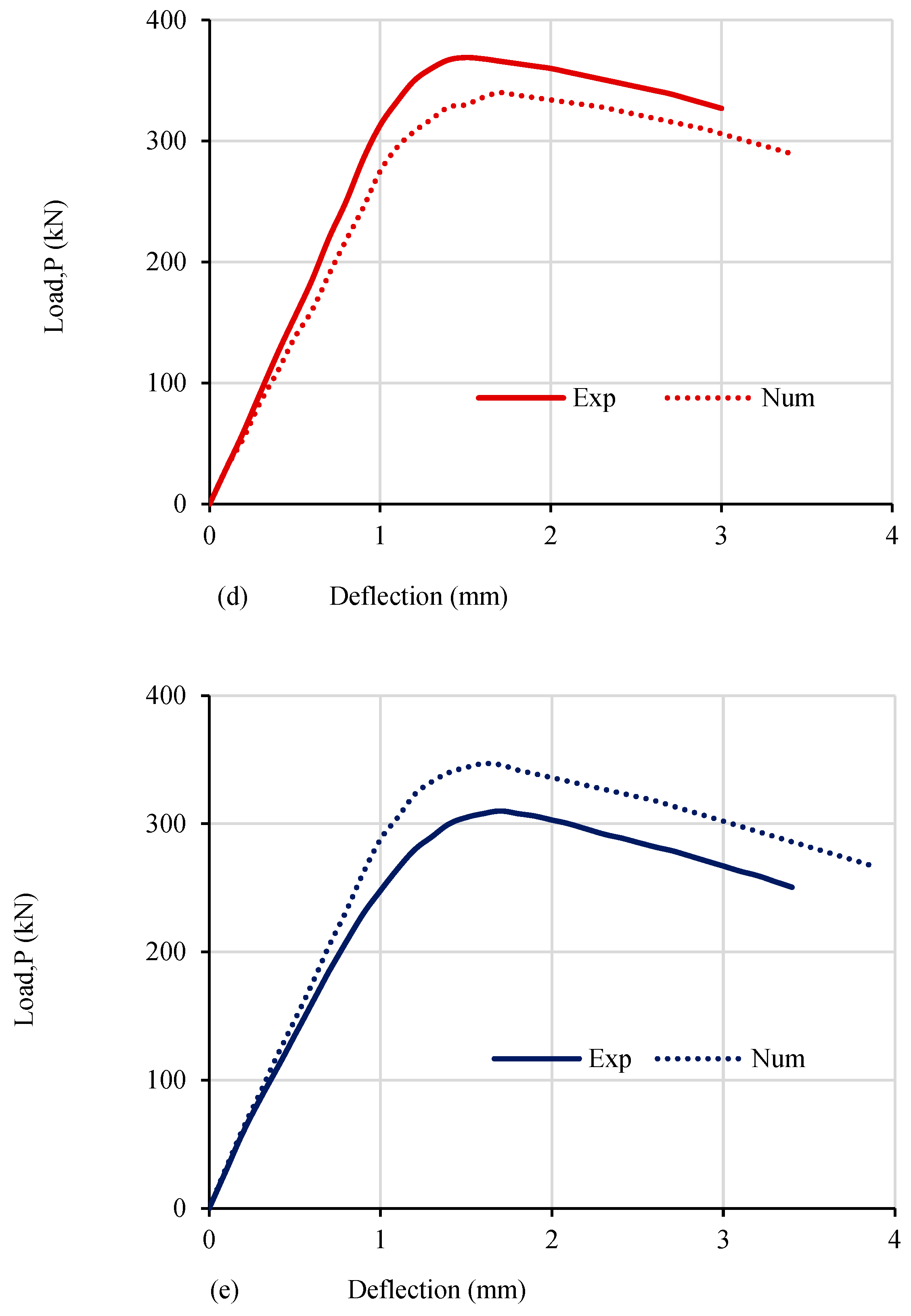
5.2. Load–Displacement Relationships
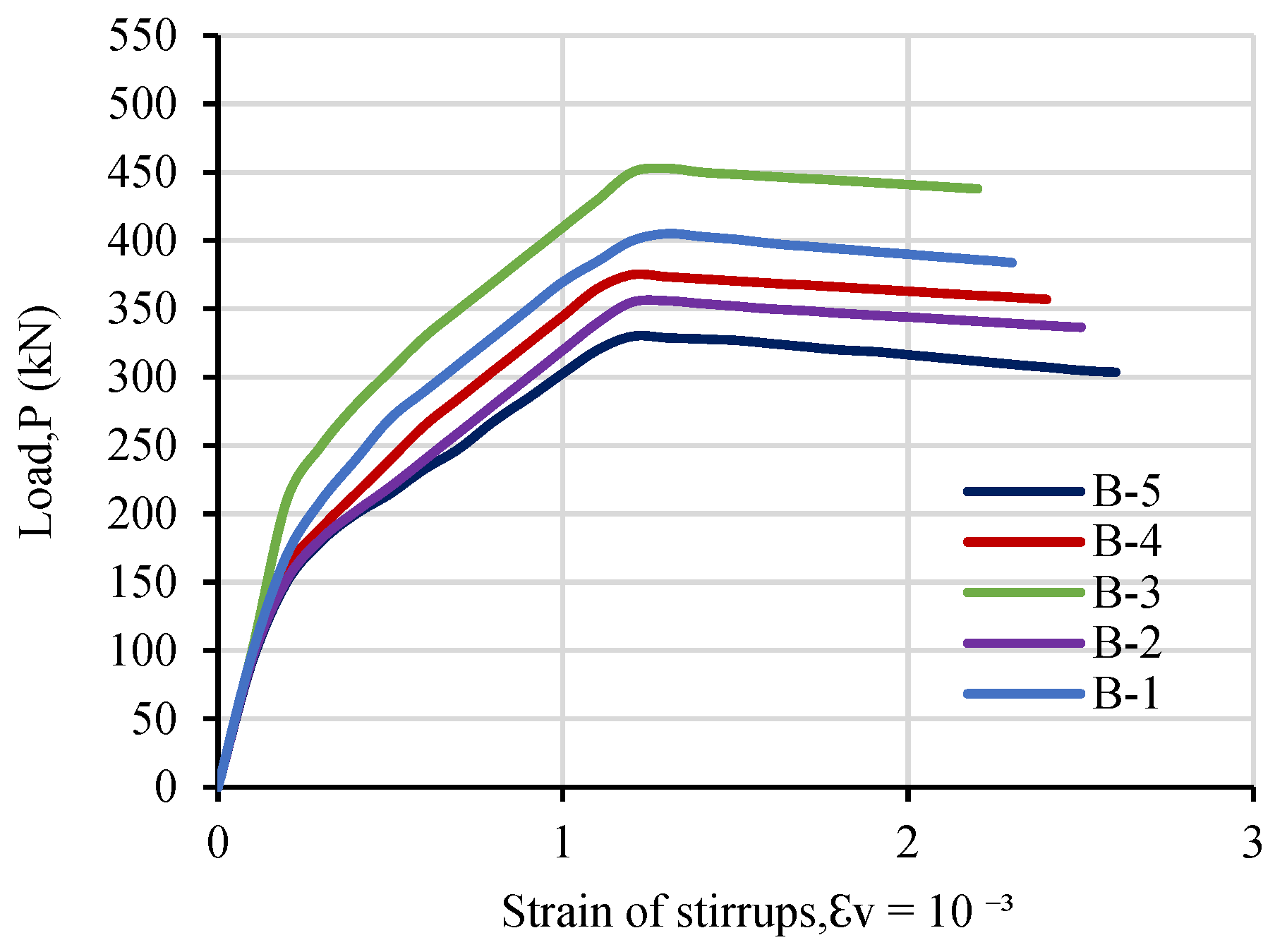
5.3. Strain Response
5.4. Effect of Web Reinforcement Ratio
5.5. Analyzing the RPC Beam Test Results in Relation to the ACI 318-2014 Code’s Shear Requirements
5.6. Comparison of Test Results for RPC Beams with AFGC-2013 and KCI-2012 Design Recommendations
5.7. RPC Beam Analytical Modeling Utilizing Finite Element Software
6. Conclusions
- i
- The offered shear reinforcement barely affects the maximum shear strength of the tested RPC beams with a volume content of 2.0% steel fibers. These steel fibers are crucial in helping RPC beams endure shear loads. Despite the fact that the examined RPC shallow beams’ vertical web reinforcement ratio was far below the smallest proportion specified by ACI 318-14, all of the examined RPC shallow beams displayed excellent performance in general.
- ii
- ACI 318-14’s shear strength calculation formulas significantly understate the shear strength of the examined RPC beams that have a minimal vertical web reinforcement ratio. As a result, these formulas are not suitable for RPC beams as they do not account for the significant role that steel fibers play in resisting shear stresses. For RPC beams with relatively low heights, the highest distance between stirrups (sv,max) specified according to the ACI 318-14 guidelines can safely be extended from 0.50 d to 0.75 d.
- iii
- In light of the predicted ultimate shear strengths of the examined beams, the design suggestions for RPC specified by KCI-2012 and AFGC-2013 are secure and restrained. The ultimate shearing strength forecasts made by KCI-2012 and AFGC-2013 are roughly equivalent (the mean proportion of the experimental ultimate shearing strength and the predicted ultimate shearing strength utilizing KCI-2012 and AFGC-2013 are approximately 1.462 and 1.446, respectively).
- iv
- According to the AFGC-2013 criteria, the mean proportion of Vfb to projected Vu,AFGC is roughly 58.3%, whereas the mean proportion of Vs to Vc is just 41.7%.
- v
- The deformation response and the ultimate shear strength of the examined RPC beams with vertical reinforcement of the web ratio much below the lowest value permitted by the code were reliably predicted by the suggested FEM when steel fibers were taken into account.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hou, X.M.; Cao, S.J.; Rong, Q.; Zheng, W.Z.; Li, G. Effects of steel fiber and strain rate on the dynamic compressive stress-strain relationship in reactive powder concrete. Constr. Build. Mater. J. 2018, 170, 570–581. [Google Scholar] [CrossRef]
- Shen, L.; Ding, M.; Chen, K.; Feng, C.; Yang, B.; Elchalakani, M. The mechanical behavior of RPC under combined shear and compressive loads. Cem. Concr. Compos. 2021, 121, 104071. [Google Scholar] [CrossRef]
- Hiremath, P.N.; Yaragal, S.C. Performance evaluation of reactive powder concrete with polypropylene fibers at elevated temperatures. Constr. Build. Mater. J. 2018, 169, 499–512. [Google Scholar] [CrossRef]
- Abid, M.; Hou, X.; Zheng, W.; Hussain, R.R. High temperature and residual properties of reactive powder concrete—A review. Constr. Build. Mater. J. 2017, 147, 339–351. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.Q.; Tang, Y.C.; Liu, T.X.; Gao, Y.F.; Zhang, J. Seismic behavior of precast segmental UHPC bridge columns with replaceable external cover plates and internal dissipaters. Eng. Struct. 2018, 177, 540–555. [Google Scholar] [CrossRef]
- Paschalis, S.A.; Lampropoulos, A.P. Ultra-high-performance fiber reinforced concrete under cyclic loading. ACI Mater. J. 2016, 113, 419–427. [Google Scholar] [CrossRef]
- Xu, S.C.; Wu, C.Q.; Liu, Z.X.; Han, K.P.; Su, Y.; Zhao, J.; Li, J.C. Experimental investigation of seismic behavior of ultra-high performance steel fiber reinforced concrete columns. Eng. Struct. 2017, 152, 129–148. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H.J.H. Energy absorption capacity of a sustainable Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) in quasi-static mode and under high velocity projectile impact. Cement Concr. Compos. 2016, 68, 109–122. [Google Scholar] [CrossRef]
- ACI Committee 363; Ultra-High Performance Concrete, A State-of-the-Art Report for the Bridge Community, Publication No. FHWA-HRT-13-060. Federal Highway Administration: Washington, DC, USA, 2013; pp. 13–44.
- Ji, W.Y.; Li, W.W.; An, M.Z.; Zhu, L. Shear capacity of T-section girders made of reactive powder concrete. J. Bridge Eng. 2018, 23, 04018041. [Google Scholar] [CrossRef]
- Zinkaah, O.H.; Sultan, H.K.; Al-Rifaie, A.; Alridha, Z. Influence of Strut Geometry on the Size Effect of FRP Reinforced Simply Supported Deep Beams: A Theoretical Analysis. Math. Model. Eng. Probl. 2022, 9, 411–417. [Google Scholar] [CrossRef]
- Zheng, H.; Fang, Z.; Chen, B. Experimental study on shear behavior of prestressed reactive powder concrete I-girders. Front. Struct. Civ. Eng. 2019, 13, 618–627. [Google Scholar] [CrossRef]
- Kaufmann, W.; Amin, A.; Beck, A.; Lee, M. Shear transfer across cracks in steel fibre reinforced concrete. Eng. Struct. 2019, 186, 508–524. [Google Scholar] [CrossRef]
- Sultan, H.K.; Alyaseri, I. Effects of elevated temperatures on mechanical properties of reactive powder concrete elements. Constr. Build. Mater. 2020, 261, 120555. [Google Scholar] [CrossRef]
- Sultan, H.K.; Zinkaah, O.H.; Rasheed, A.A.; Alridha, Z.; Alhawat, M. Producing Sustainable Modified Reactive Powder Concrete Using Locally Available Materials. Innov. Infrastruct. Solut. 2022, 7, 342. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L. How do steel fibers improve the shear capacity of reinforced concrete beams without stirrups? Compos. B Eng. 2019, 175, 107079. [Google Scholar] [CrossRef]
- Biswas, R.K.; Bin Ahmed, F.; Haque, M.E.; Provasha, A.A.; Hasan, Z.; Hayat, F.; Sen, D. Effects of steel fiber percentage and aspect ratios on fresh and harden properties of ultra-high performance fiber reinforced concrete. Appl. Mech. 2021, 2, 501–515. [Google Scholar] [CrossRef]
- He, J.; Chen, W.; Zhang, B.; YU, J.; Liu, H. The mechanical properties and damage evolution of UHPC Reinforced with glass fibers and high-performance polypropylene fibers. Materials 2021, 14, 2455. [Google Scholar] [CrossRef] [PubMed]
- Yoo, D.Y.; Yang, J.M. Effects of stirrup, steel fiber, and beam size on shear behavior of high-strength concrete beams. Cement Concr. Compos. 2018, 87, 137–148. [Google Scholar] [CrossRef]
- Głodkowska, W.; Ziarkiewicz, M. Cracking behavior of steel fiber reinforced waste sand concrete beams in flexure-experimental investigation and theoretical analysis. Eng. Struct. 2018, 176, 1–10. [Google Scholar] [CrossRef]
- Wille, K.; Naaman, A.E.; Parra-Montesions, G.J. Ultra-High-Performance Concrete with Compressive Strength Exceeding 150 MPa (22 ksi), A simpler Way. ACI Mater. J. 2011, 108, 46–54. [Google Scholar]
- Sultan, H.K. Designing reinforced HSC rectangular beams using optimization techniques. Pollack Period. J. 2023, 18, 20–25. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, J.; Liu, W.; Ma, Z. Unloading and reloading stress-strain relationship of recycled aggregate concrete reinforced with steel/polypropylene fibers under uniaxial low-cycle loadings. Cem. Concr. Compos. 2022, 131, 104597. [Google Scholar] [CrossRef]
- Wang, C.; Wu, H.; Li, C. Hysteresis and damping properties of steel and polypropylene fiber reinforced recycled aggregate concrete under uniaxial low-cycle loadings. Constr. Build. Mater. 2022, 319, 126191. [Google Scholar] [CrossRef]
- Samadi, M.; Baghban, M.H.; Kubba, Z.; Faridmehr, I.; Abdul Shukor Lim, N.H.; Benjeddou, O.; Huseien, G.F. Flexural behavior of reinforced concrete beams under instantaneous loading: Effects of recycled ceramic as cement and aggregates replacement. Buildings 2022, 12, 439. [Google Scholar] [CrossRef]
- Wang, C.; Wu, H.; Li, C. Hysteretic deteriorating behaviors of fiber-reinforced recycled aggregate concrete composites subjected to cyclic compressive loadings. J. Build. Eng. 2022, 49, 104087. [Google Scholar] [CrossRef]
- Sultan, H.K. Hysteresis Damping Ratio for Moment Steel Frame Evaluation Using DDBD. Pollack Period. J. 2024, 19, 33–40. [Google Scholar] [CrossRef]
- Sultan, H.K.; Mohammed, A.T. Assessing of the common strengthening methods for existing RC buildings. Pollack Period. J. 2023, 18, 6–11. [Google Scholar] [CrossRef]
- Yahy Al-Radi, H.H.; Dejian, S.; Sultan, H.K. Performance of Fiber Self-Compacting Concrete at High Temperatures. Civ. Eng. J. 2021, 7, 2083–2098. [Google Scholar] [CrossRef]
- Sultan, H.K.; Mohammed, A.T.; Qasim, O.D.; Maula, B.H.; Aziz, H.Y. Ductility Factor Evaluation of Concrete Moment Frame Retrofitted by FRP Subjected to Seismic Loads. Int. Rev. Civ. Eng. (IRECE) 2020, 11, 275–282. [Google Scholar] [CrossRef]
- Qasim, O.A.; Sultan, H.K. Experimental Investigation of Effect of Steel Fiber on Concrete Construction Joints of Prism. IOP Conf. Ser. Mater. Sci. Eng. 2020, 745, 012170. [Google Scholar] [CrossRef]
- Voo, Y.; Poon, W.K.; Foster, S.J. Shear strength of steel fiber-reinforced ultrahigh-performance concrete beams without stirrups. J. Struct. Eng. 2010, 136, 1393–1400. [Google Scholar] [CrossRef]
- Aziz, O.Q.; Hasan, M.; Ali, H. Shear Strength and Behavior of Ultra-High Performance Fiber Reinforced Concrete (UHPC) Deep Beams without Web Reinforcement. Int. J. Civ. Eng. (IJCE) 2013, 2, 85–96. [Google Scholar]
- Baby, F.; Marchand, P.; Toutlemonde, F. Shear Behavior of Ultra-High Performance Fiber-Reinforced Concrete Beams, I: Experimental investigation. J. Struct. Eng. 2014, 140, 04013111. [Google Scholar] [CrossRef]
- Lim, W.-Y.; Hong, S.-G. Shear Test for Ultra-High Performance Fiber Reinforced concrete (UHPFRC) Beams with shear reinforcement. Int. J. Concr. Struct. Mater. 2016, 10, 177–188. [Google Scholar] [CrossRef]
- Qi, J.; Ma, Z.J.; Wang, J. Shear Strength of UHPFRC Beams: Mesoscale Fiber Matrix Discrete Model. J. Struct. Eng. 2016, 143, 1–10. [Google Scholar] [CrossRef]
- European Committee for Standardization. Eurocode 2: Design of Concrete Structures—Part 1; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- ACI Committee 318; Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary (ACI 318R-14). American Concrete Institute: Farmington Hills, MI, USA, 2014.
- Association Francaise du Genil Civil (AFGC). Ultra-High Performance Fiber Reinforced Concrete; AFGC: Paris, France, 2002. [Google Scholar]
- Association Francaise du Genil Civil (AFGC). Ultra-High Performance Fiber Reinforced Concrete; AFGC: Paris, France, 2013. [Google Scholar]
- Japan Society of Civil Engineers (JSCE). Recommendations for Design and Construction of Ultra-High-Strength Fiber Reinforced Concrete Structures; Concrete Engineering Series; Japan Society of Civil Engineers: Tokyo, Japan, 2008. [Google Scholar]
- Korea Concrete Institute. Design Recommendations for Ultra High Performance Concrete (K-UHPC), KCI-M-12-003; Korea Concrete Institute: Seoul, Republic of Korea, 2012. [Google Scholar]
- ASTM C109/C109M-20b; Standard Test Method for Compressive Strength of Hydraulic Cement Mortars (Using 2-in. or [50 mm] Cube Specimens). ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM C496; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. American Society for Testing and Materials Standard Practice C496. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM C78; Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Center Point Loading). ASTM International: West Conshohocken, PA, USA, 2010.
- ABAQUS: Abaqus Analysis User’s Manual, Version 6.9; Dassault Systems Corp.: Providence, RI, USA, 2009.
- Katsamakas, A.A.; Papanikolaou, V.K.; Thermou, G.E. Tree-dimensional numerical modeling of RC beam strengthened in shear with steel reinforced grout (SRG). In Proceedings of the 1st Fib Italy YMG Symposium on Concrete and Concrete Structures, Krakow, Poland, 27–29 May 2019; pp. 64–71. [Google Scholar]
- Ombres, L.; Verre, S. Shear strengthening of reinforced concrete beams with SRG (Steel Reinforced Grout) composites: Experimental investigation and modeling. J. Build. Eng. 2021, 42, 103047. [Google Scholar] [CrossRef]
- Bahij, S.; Adekunle, S.K.; Al-Osta, M.; Ahmad, S.; Al-Dulaijan, S.U.; Rahman, M.K. Numerical investigation of the shear behavior of reinforced ultra-high-performance concrete beams. Struct Concr. 2018, 19, 305–317. [Google Scholar] [CrossRef]
- Ahmad, S.; Bahij, S.; Al-Osta, M.; Adekunle, S.K.; Al-Dulaijan, S.U. Shear behavior of ultra-high-performance concrete beams reinforced with high-strength steel bars. ACI Struct. J. 2019, 116, 3–14. [Google Scholar] [CrossRef]



| C a, kg | FS b, kg | QP c, kg | SF d, kg | W e, kg | SP f, kg |
|---|---|---|---|---|---|
| 760 | 1026 | 228 | 190 | 144.4 | 30.4 |
| Beam | fcu, MPa | b × h (mm) | a/d Ratio | Main Longitudinal Bars | Provided Stirrups (Vertical Web Reinforcement) | Requirements of ACI 318-14 for sv,max and ρv,min | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Upper | sv, (mm) | dv, (mm) | ρv, (%) | sv,max, (mm) | ρv,min (%) | ||||
| B-1 | 157 | 140 × 220 | 3.0 | 6Φ18 | 2Φ10 | 100 | 6 | 0.20 | 90 | 0.235 |
| B-2 | 157 | 140 × 220 | 3.0 | 6Φ18 | 2Φ10 | 200 | 6 | 0.10 | 90 | 0.235 |
| B-3 | 157 | 140 × 220 | 3.0 | 6Φ18 | 2Φ10 | 100 | 8 | 0.36 | 90 | 0.25 |
| B-4 | 157 | 140 × 220 | 3.0 | 6Φ18 | 2Φ10 | 200 | 8 | 0.18 | 90 | 0.25 |
| B-5 | 157 | 140 × 220 | 3.2 | 6Φ18 | 2Φ10 | 200 | 8 | 0.18 | 90 | 0.25 |
| Details | ||
|---|---|---|
| Concrete | Finite element type | 8-node isoparametric solid elements |
| Failure mode | Fracture under tension, plasticity under compression | |
| Crack formulation | Smeared | |
| Numerical modification | Shear factor reduction | |
| Reinforcement | Finite element type | 2-node truss elements |
| Constitutive model | Uniaxial multilinear law | |
| Modeling type | Embedded reinforcement | |
| Bond type | Full reinforcement–concrete bond | |
| Beam | a/d | 2Vcr (kN) | 2Vu,exp (kN) | Vcr (kN) | Vu,exp (kN) | ||
|---|---|---|---|---|---|---|---|
| B-1 | 3.0 | 130 | 403 | 65 | 201.5 | 0.323 | 0.638 |
| B-2 | 3.0 | 110 | 369 | 55 | 184.5 | 0.298 | 0.584 |
| B-3 | 3.0 | 170 | 450 | 85 | 225 | 0.378 | 0.713 |
| B-4 | 3.0 | 120 | 369 | 60 | 184.5 | 0.325 | 0.584 |
| B-5 | 3.2 | 110 | 310 | 55 | 155 | 0.355 | 0.491 |
| Beam | Vu,exp (kN) | ACI 318-14 Code | |||
|---|---|---|---|---|---|
| Vc (kN) | Vs (kN) | Vu,cal (kN) | |||
| B-1 | 201.5 | 45.6 | 32.3 | 77.9 | 0.387 |
| B-2 | 184.5 | 45.6 | 16.2 | 61.8 | 0.335 |
| B-3 | 225 | 45.6 | 52.7 | 98.3 | 0.437 |
| B-4 | 184.5 | 45.6 | 26.4 | 72 | 0.390 |
| B-5 | 155 | 45.6 | 26.4 | 72 | 0.465 |
| Beam | Vu,exp (kN) | KCI-2012 | AFGC-2013 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Vc (kN) | Vfb (kN) | Vs (kN) | Vu,KCI (kN) | Vc (kN) | Vfb (kN) | Vs (kN) | Vu,AFGC (kN) | ||||
| B-1 | 201.5 | 37.2 | 87.4 | 24.9 | 149.5 | 1.348 | 37.6 | 90.4 | 29.1 | 157.1 | 1.283 |
| B-2 | 184.5 | 37.2 | 87.4 | 12.5 | 137.1 | 1.346 | 37.6 | 90.4 | 14.5 | 142.5 | 1.295 |
| B-3 | 225 | 37.2 | 87.4 | 40.6 | 165.2 | 1.362 | 37.6 | 90.4 | 47.4 | 175.4 | 1.283 |
| B-4 | 184.5 | 37.2 | 87.4 | 20.3 | 144.9 | 1.273 | 37.6 | 90.4 | 23.7 | 151.7 | 1.216 |
| B-5 | 155 | 37.2 | 87.4 | 20.3 | 144.9 | 1.07 | 37.6 | 90.4 | 23.7 | 151.7 | 1.022 |
| Beam | Cracking Load and Ultimate Load | Cracking Displacement and Maximum Displacement | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (kN) | (kN) | (kN) | (kN) | (mm) | (mm) | (mm) | (mm) | |||||
| B-1 | 72 | 76.5 | 1.06 | 201.5 | 185 | 1.089 | 0.5 | 0.34 | 0.68 | 1.75 | 1.95 | 0.897 |
| B-2 | 51 | 57 | 1.12 | 184.5 | 178 | 1.037 | 0.48 | 0.4 | 0.83 | 1.85 | 2.1 | 0.881 |
| B-3 | 88 | 83.5 | 0.95 | 225 | 255 | 0.882 | 0.31 | 0.33 | 1.07 | 2.2 | 1.98 | 1.11 |
| B-4 | 58 | 65 | 1.12 | 184.5 | 174 | 1.06 | 0.24 | 0.26 | 1.08 | 1.78 | 1.88 | 0.947 |
| B-5 | 60 | 55 | 0.92 | 155 | 160.5 | 0.966 | 0.47 | 0.44 | 0.94 | 2.1 | 1.98 | 1.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultan, H.K.; Huseien, G.F. Minimum Shear Reinforcement for Reactive Powder Concrete Beams. Eng 2024, 5, 801-818. https://doi.org/10.3390/eng5020043
Sultan HK, Huseien GF. Minimum Shear Reinforcement for Reactive Powder Concrete Beams. Eng. 2024; 5(2):801-818. https://doi.org/10.3390/eng5020043
Chicago/Turabian StyleSultan, Hussein Kareem, and Ghasan Fahim Huseien. 2024. "Minimum Shear Reinforcement for Reactive Powder Concrete Beams" Eng 5, no. 2: 801-818. https://doi.org/10.3390/eng5020043
APA StyleSultan, H. K., & Huseien, G. F. (2024). Minimum Shear Reinforcement for Reactive Powder Concrete Beams. Eng, 5(2), 801-818. https://doi.org/10.3390/eng5020043







