An Efficient Approach for Damage Identification of Beams Using Mid-Span Static Deflection Changes
Abstract
:1. Introduction
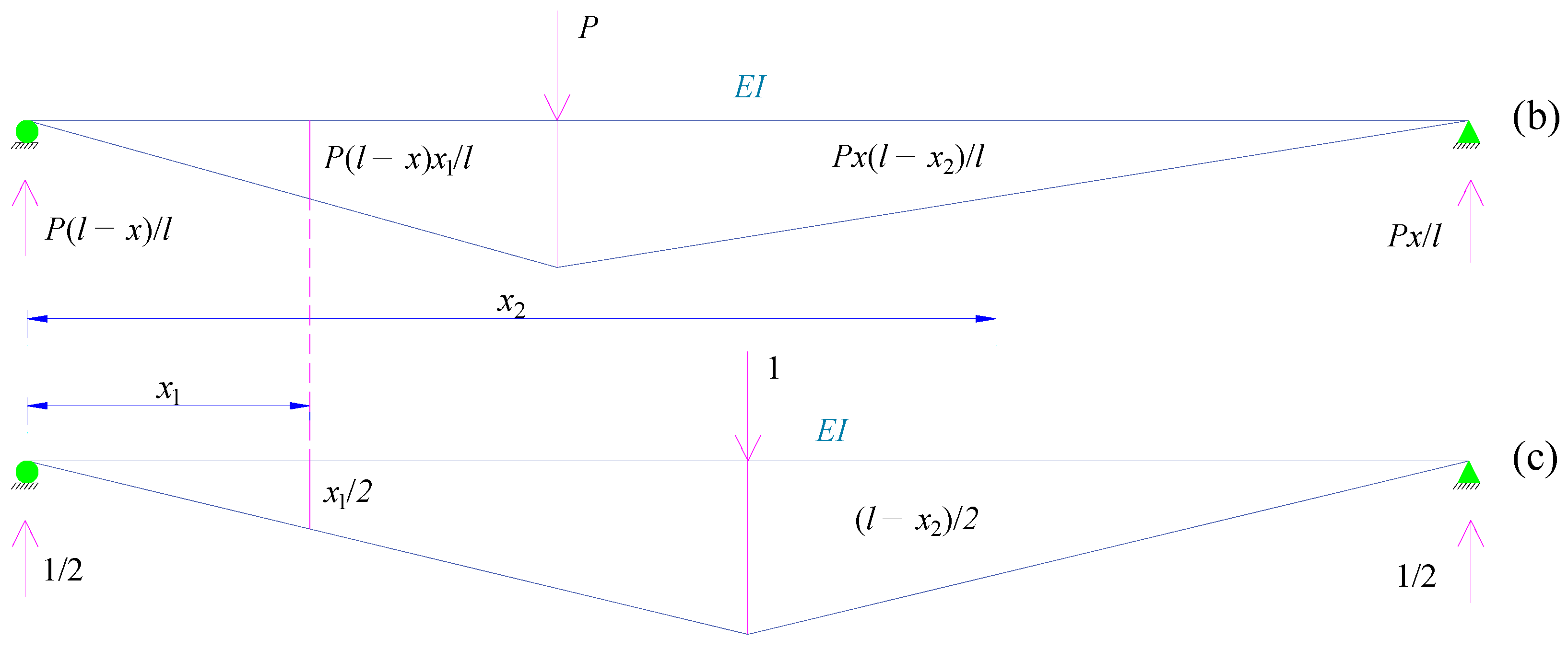
2. Governing Equations of Mid-Span Deflection of Simply Supported Beams with Local Damage
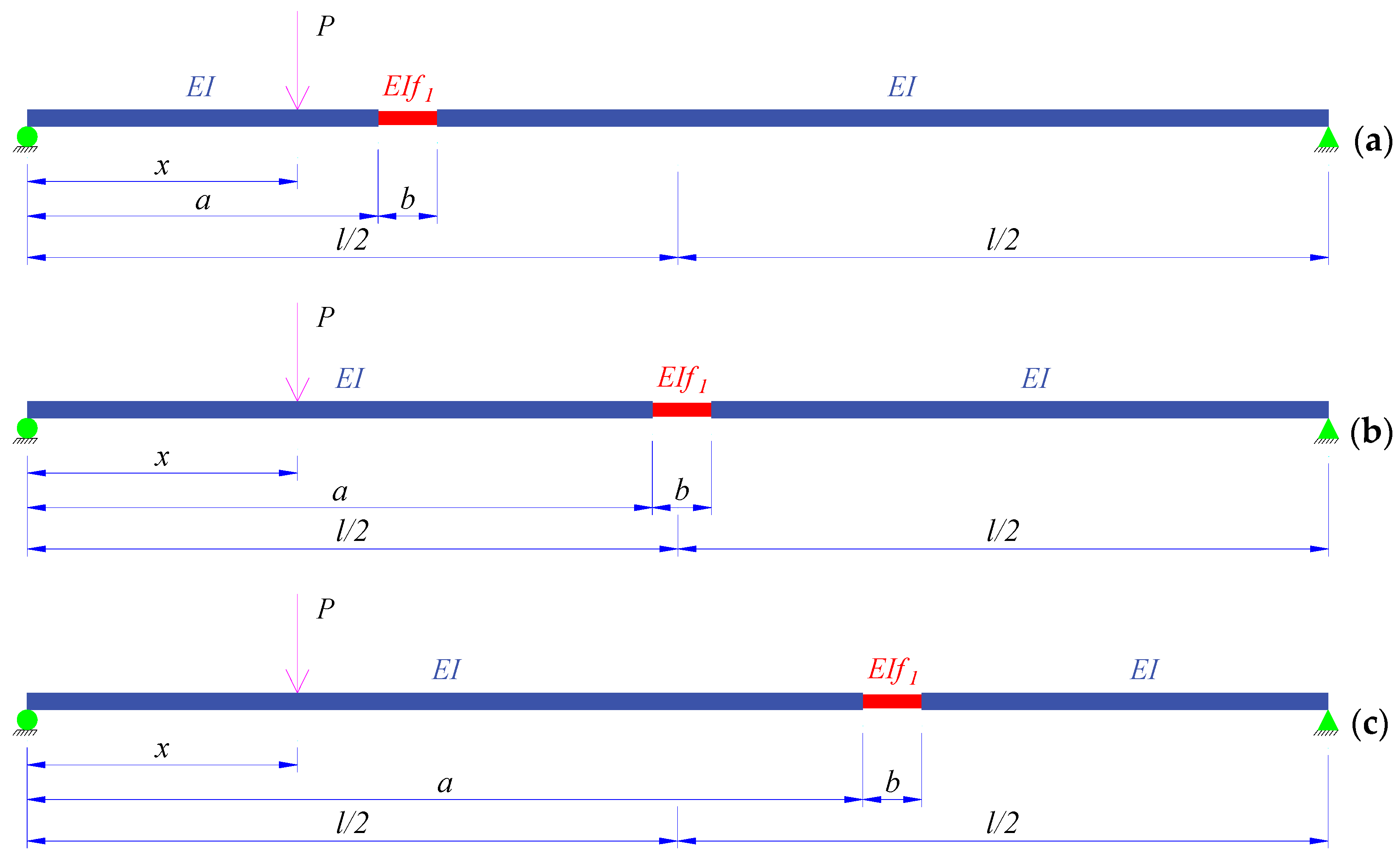
2.1. Mid-Span Deflection of the Simply Supported Beam with a Single Damaged Location
- The damage zone is located on the left-half beam:
- The damage zone is located at the mid-span point:
- The damage zone is located on the right-half beam:
2.2. Damage Index
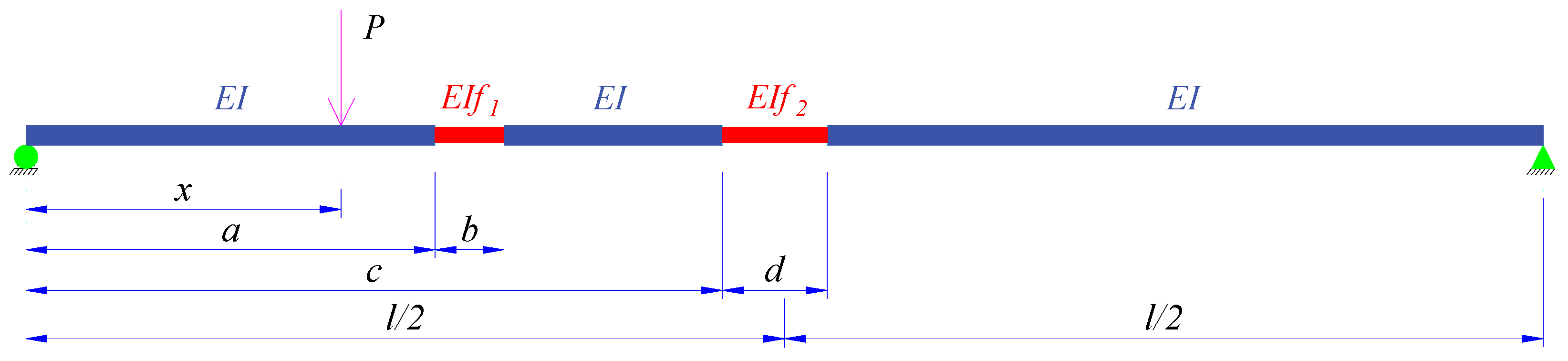
2.3. Mid-Span Deflection of the Simply Supported Beam with Two Damaged Locations
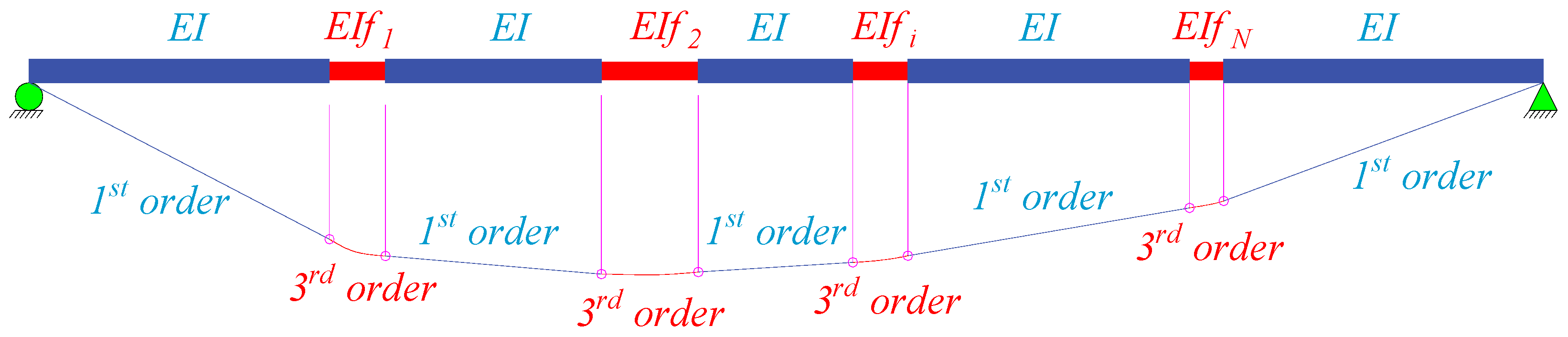
2.4. Mid-Span Deflection of the Simply Supported Beam with Many Damaged Locations
2.5. The Proposed Framework of Identification of Damage Zones in SS Beam
- Step 1: Calculate yN, representing the mid-span deflection at the second structural state, by applying a static load P at various positions along the beam.
- Step 2: Determine ΔyN0 = yN − y0 where y0 denotes the mid-span deflection at the first structural state.
- Step 3: Plot the ΔyN0 diagram.
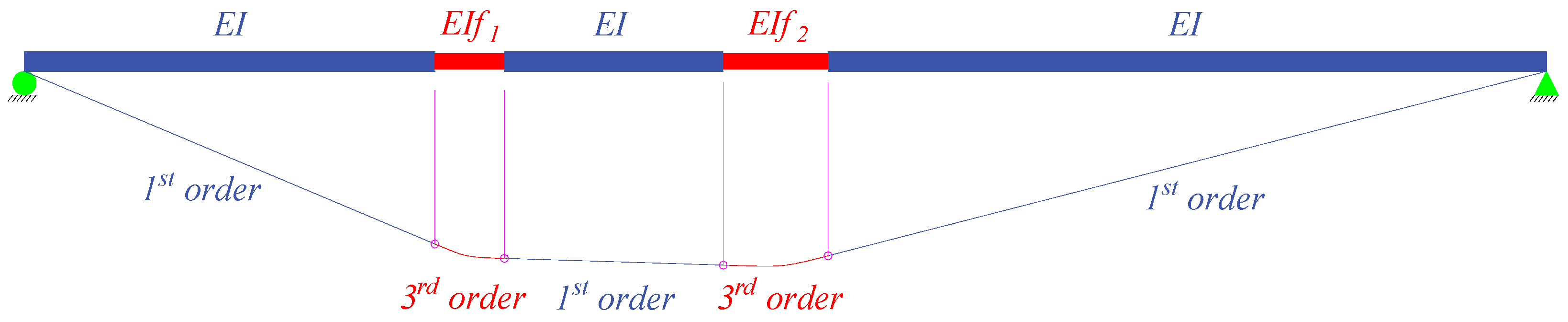
- Step 4: Identify the new damage zones following these fundamental principles:
- New damage zones exhibit cubic curve shapes, while the remaining zones display straight-line shapes.
- New damaged positions are typically found near the intersection of two consecutive first-order lines on the diagram, and new damage zones are discerned through the two consecutive intersection points between the first-order line and the cubic curve.
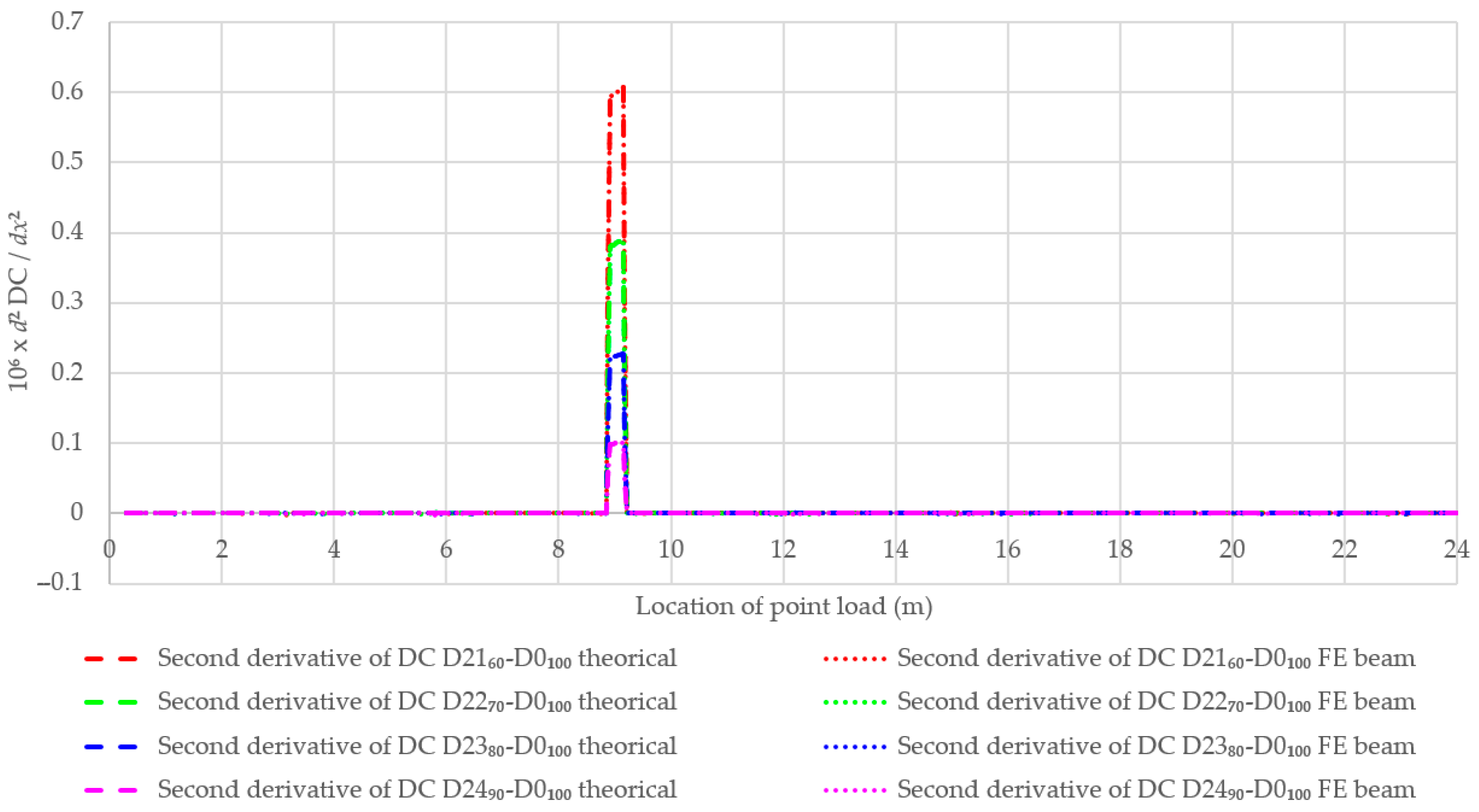
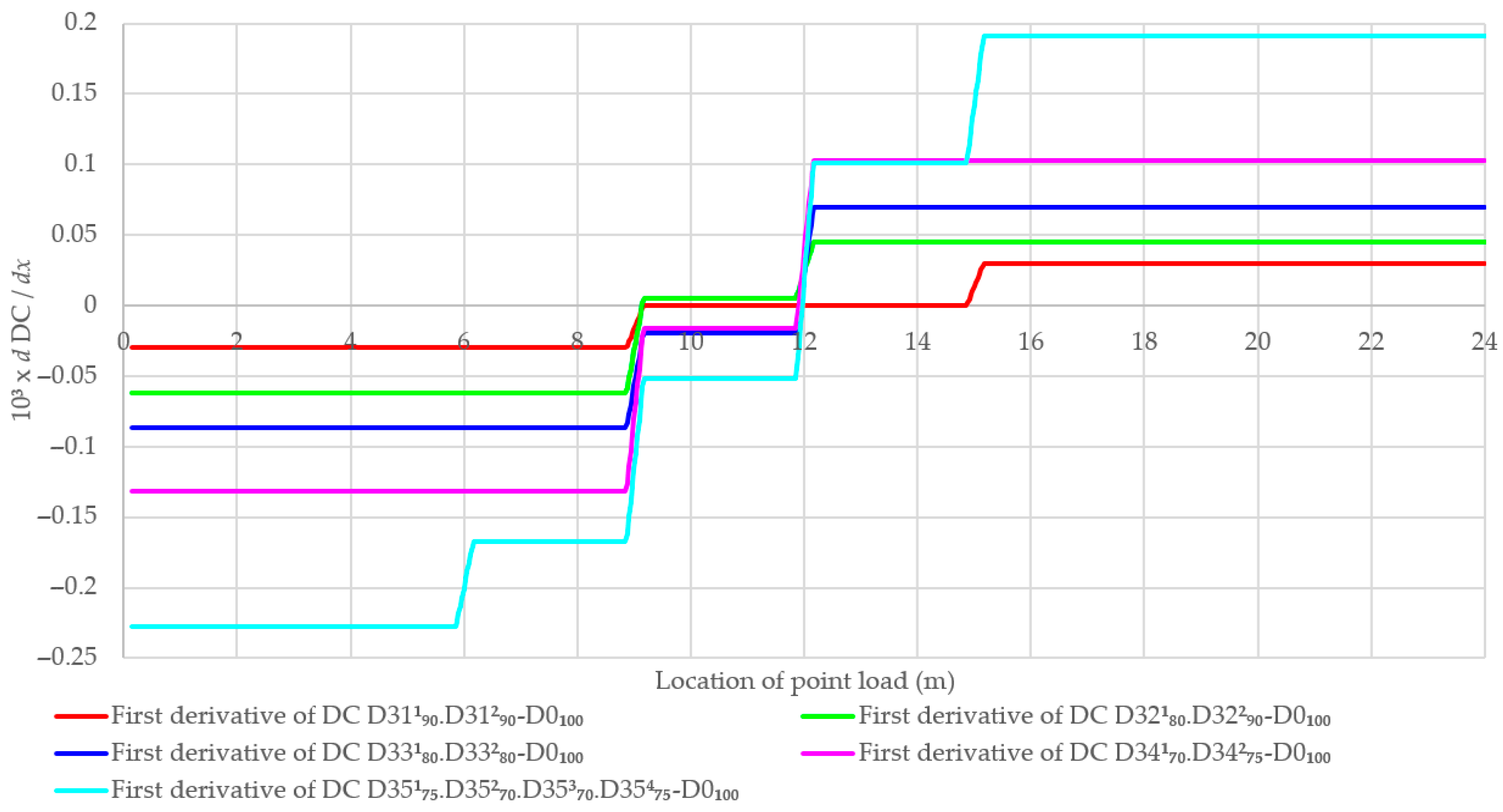
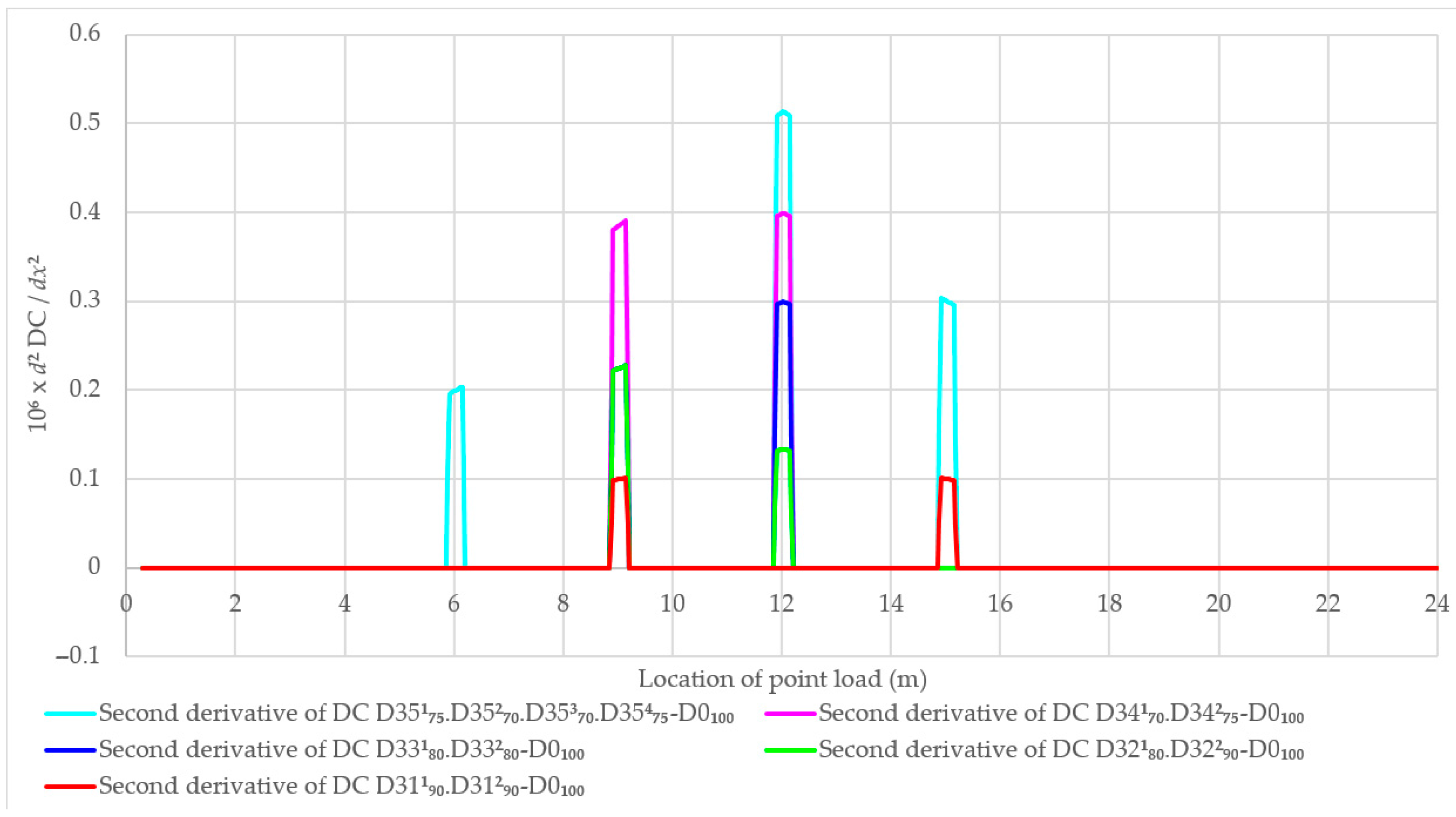
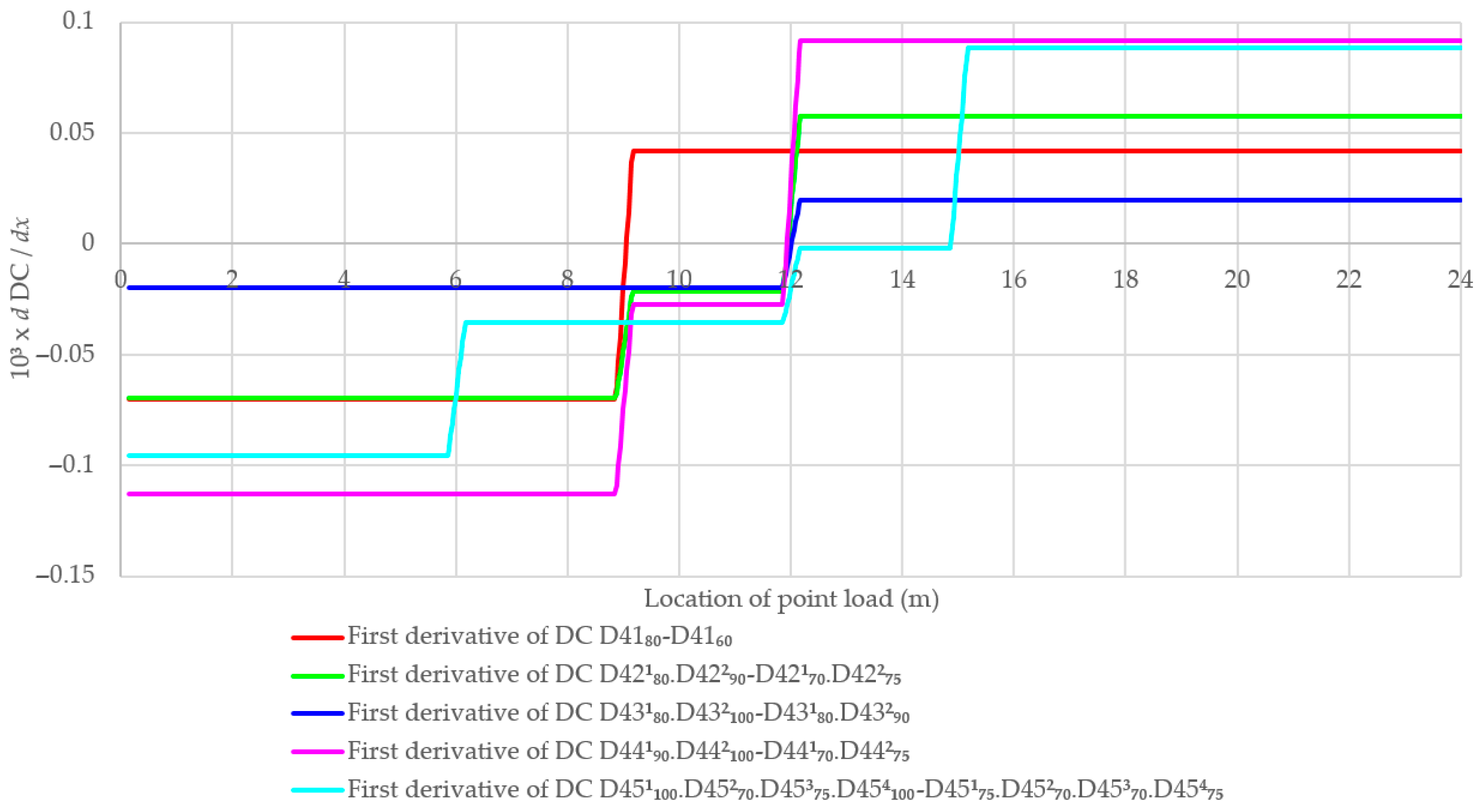
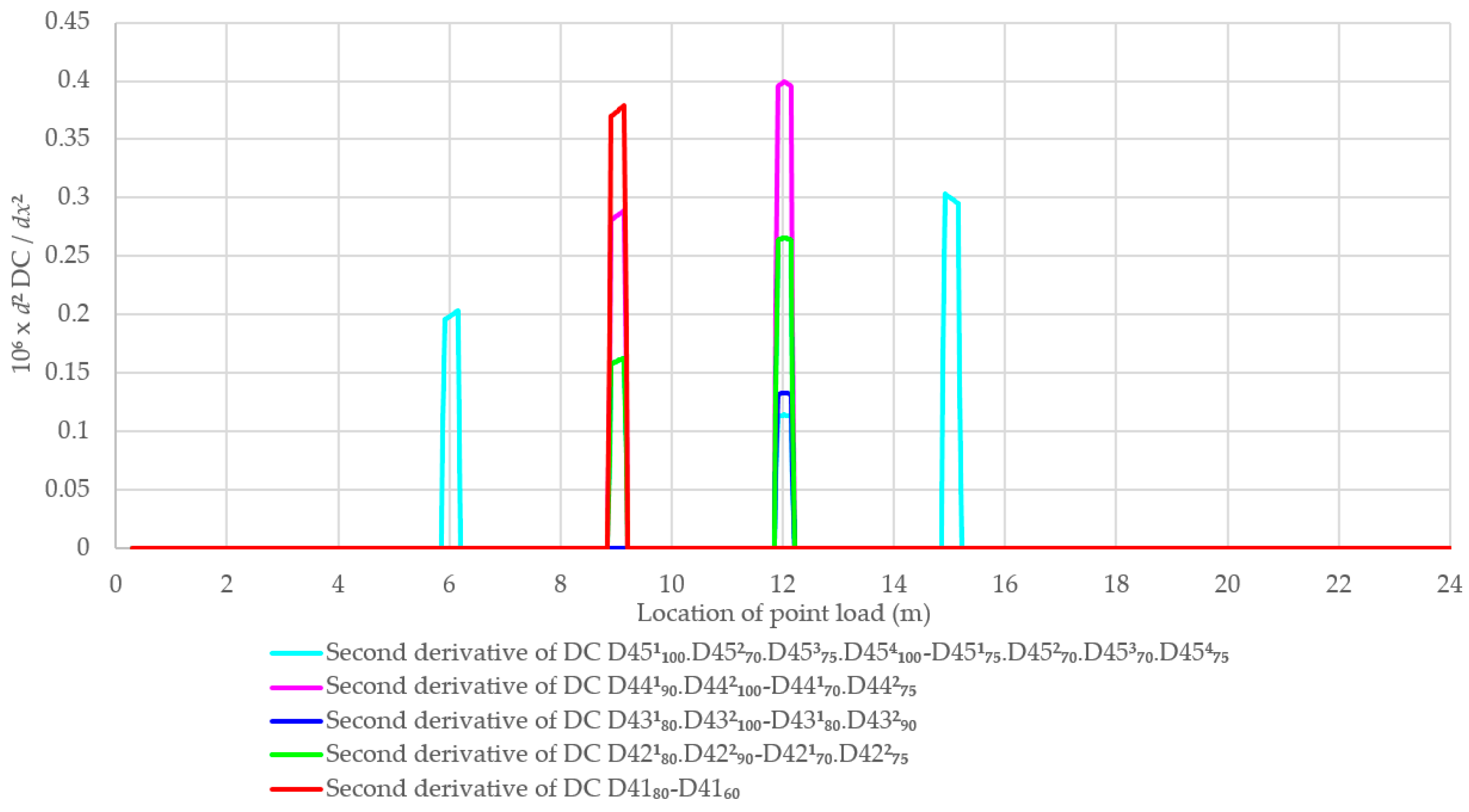
- The first and second derivatives of DC can also aid in determining the damage location and the damage index.
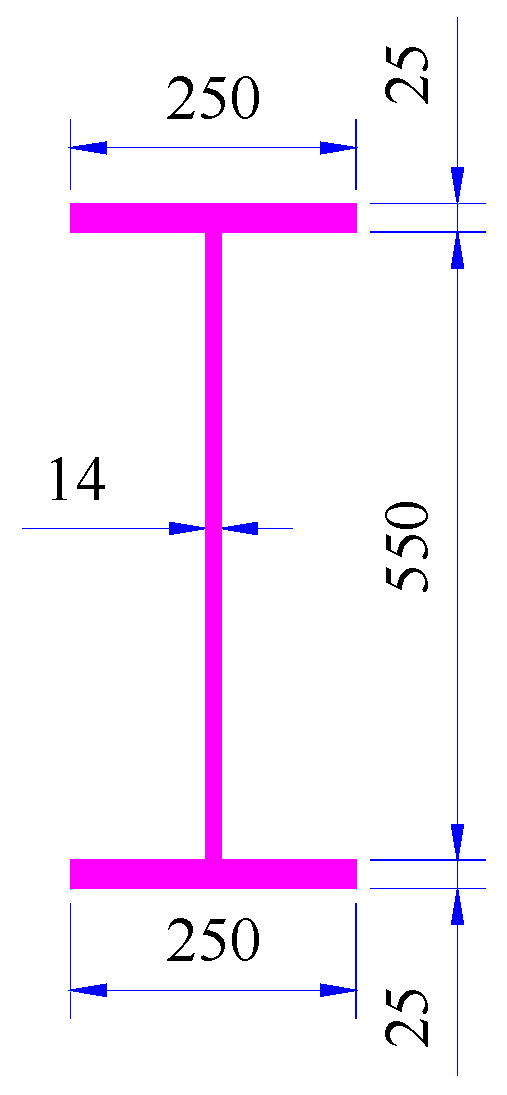
3. Description of Case Studies
3.1. Single-Damage Beams with Different Positions and the Same Remaining Stiffness
3.2. Single-Damage Beam at the Same Positions with Different Remaining Stiffness
3.3. Beam with Multiple Damage Zones Compared to Intact Beam
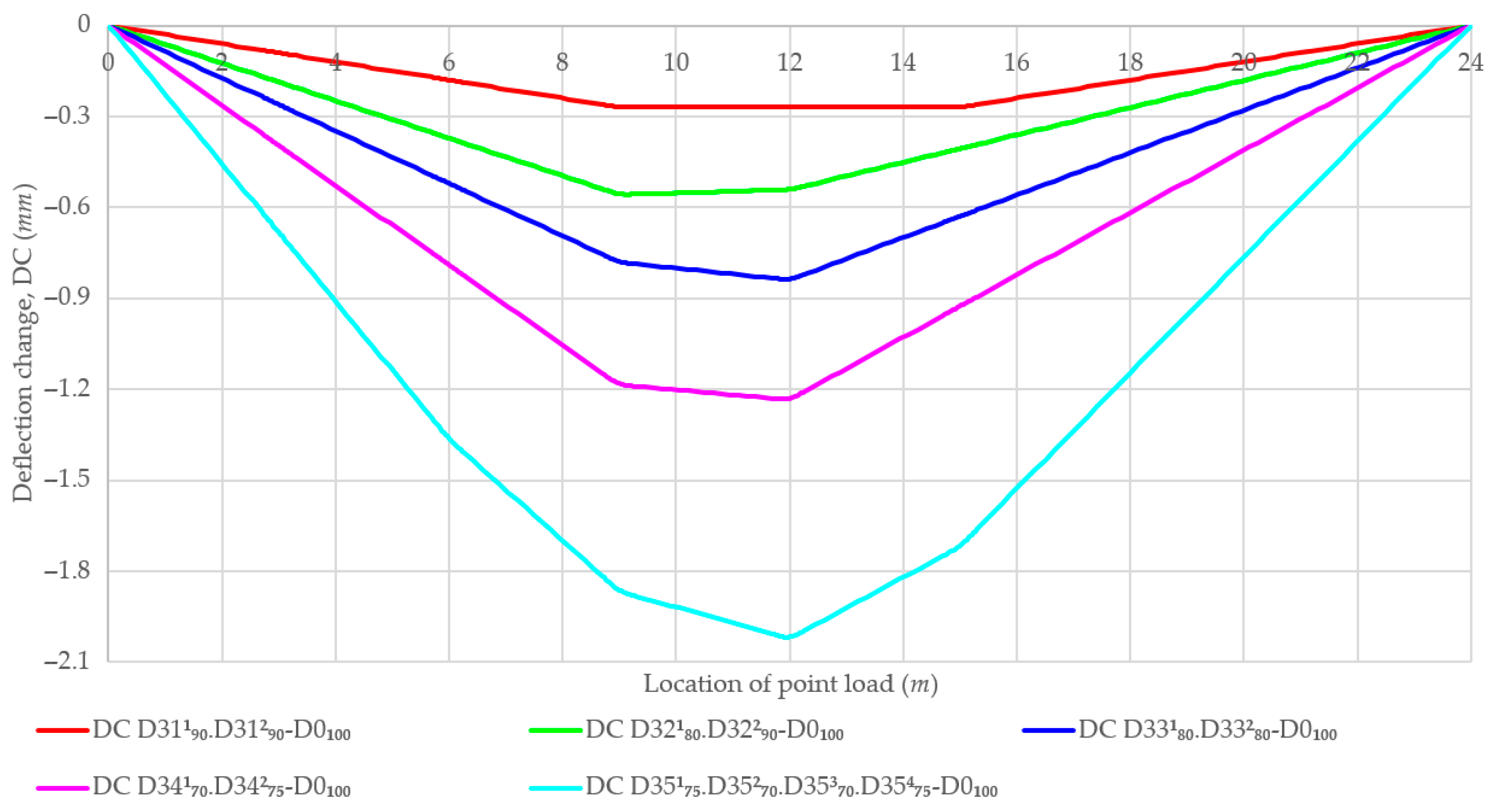
3.4. Beam with Multiple Damage Zones Considering New Damages and Development of Existing Damage
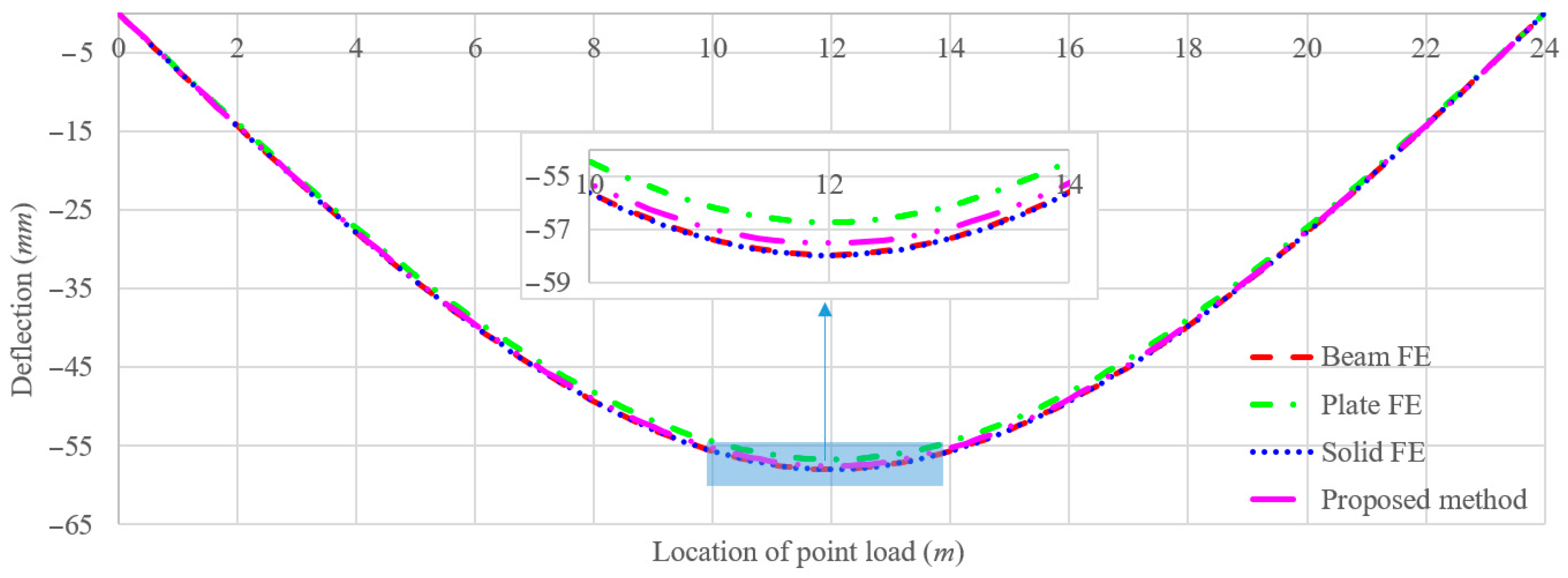
4. Results and Discussion
4.1. Single-Damage Beams with Different Positions and Same Remaining Stiffness
4.2. Single-Damage Beam with the Same Positions and Different Remaining Stiffness
4.3. Beam with Multiple Damage Zones Compared to Intact Beam
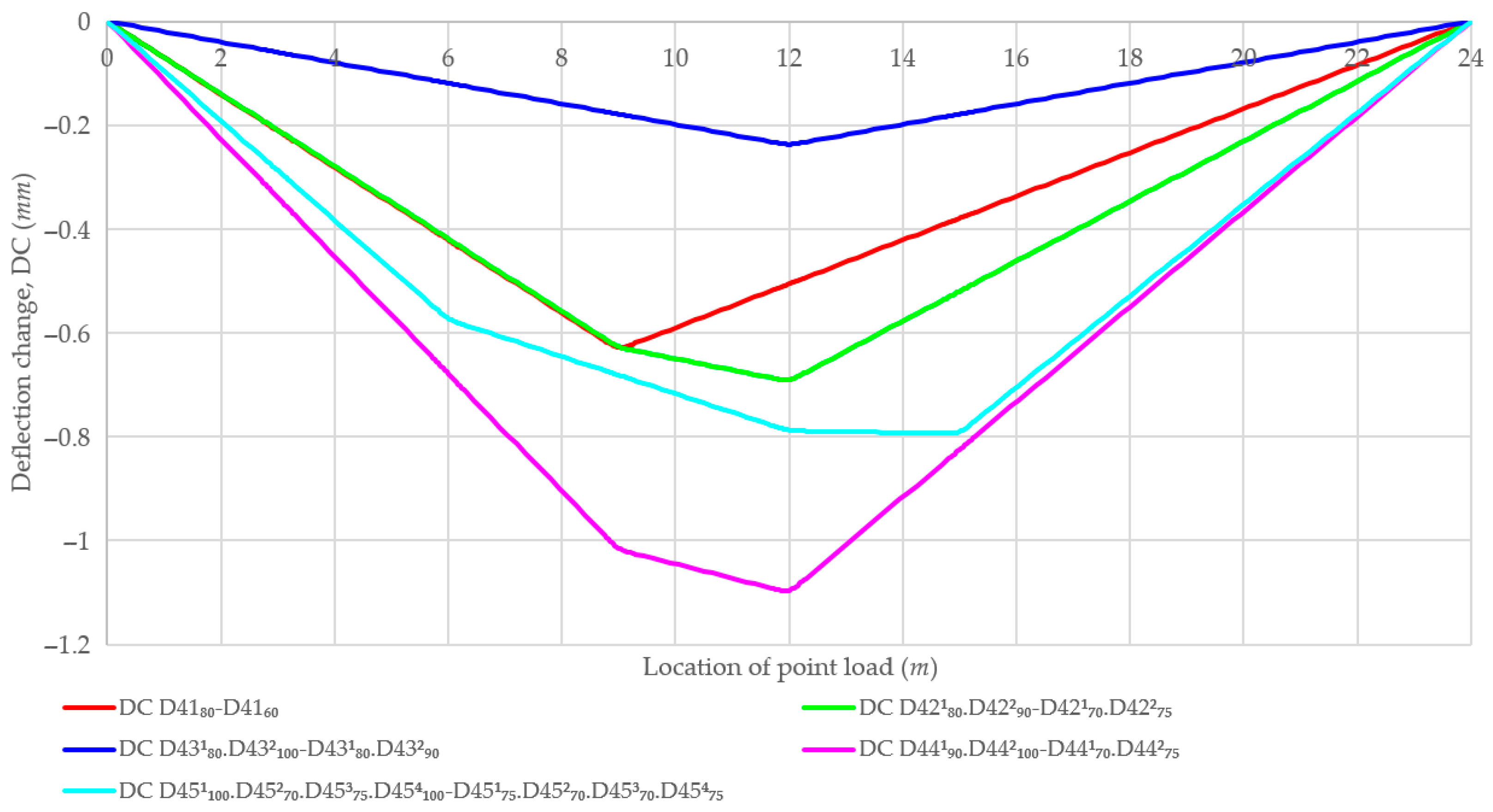
4.4. Beam with Multiple Damage Zones Considering New Damages and Development of Existing Damages
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- Case of a single damage zone located on the left half of the SS beam:
- Case of a single damage zone located at the mid-span point of the SS beam:
- Case of a single damage zone located on the right half of the SS beam:
- Case of a single damage zone located on the left half of the SS beam:
- Case of a single damage zone located at the mid-span point of the SS beam:
- Case of a single damage zone located on the right half of the SS beam:
References
- Chan, T.; Thambiratnam, D.P. (Eds.) Structural Health Monitoring in Australia; UK ed. Edition; Nova Science: New York, NY, USA, 2011; pp. 1–193. [Google Scholar]
- Farrar, C.; Worden, K. Structural Health Monitoring A Machine Learning Perspective, 1st ed.; Wiley: West Sussex, UK, 2012; pp. 1–656. [Google Scholar]
- Balageas, D.; Fritzen, C.P.; Güemes, A. Structural Health Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 1–496. [Google Scholar]
- Yan, R.; Chen, X.; Mukhopadhyay, S.C. Structural Health Monitoring: An Advanced Signal Processing Perspective; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 1–375. [Google Scholar]
- Zhang, W.; Li, J.; Hao, H.; Ma, H. Damage detection in bridge structures under moving loads with phase trajectory change of multi-type vibration measurements. Mech. Syst. Signal Process. 2017, 87, 410–425. [Google Scholar] [CrossRef]
- Wickramasinghe, W.R.; Thambiratnam, D.P.; Chan, T.H.T.; Nguyen, T. Vibration characteristics and damage detection in a suspension bridge. J. Sound Vib. 2016, 375, 254–274. [Google Scholar] [CrossRef]
- Baba, S.; Kondoh, J. Damage evaluation of fixed beams at both ends for bridge health monitoring using a combination of a vibration sensor and a surface acoustic wave device. Eng. Struct. 2022, 262, 114323. [Google Scholar] [CrossRef]
- Seyedpoor, S.M.; Yazdanpanah, O. An efficient indicator for structural damage localization using the change of strain energy based on static noisy data. Appl. Math. Model. 2014, 38, 2661–2672. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Nguyen, Q.B.; Bui-Tien, T.; De Roeck, G.; Wahab, M.A. Damage detection in girder bridges using modal curvatures gapped smoothing method and Convolutional Neural Network: Application to Bo Nghi bridge. Theor. Appl. Fract. Mech. 2020, 109, 102728. [Google Scholar] [CrossRef]
- Wan, H.; Gao, L.; Yuan, Z.; Qu, H.; Sun, Q.; Cheng, H.; Wang, R. A novel transformer model for surface damage detection and cognition of concrete bridges. Expert Syst. Appl. 2023, 213, 119019. [Google Scholar] [CrossRef]
- Gordan, M.; Razak, H.A.; Ismail, Z.; Ghaedi, K.; Tan, Z.X.; Ghayeb, H.H. A hybrid ANN-based imperial competitive algorithm methodology for structural damage identification of slab-on-girder bridge using data mining. Appl. Soft Comput. 2020, 88, 106013. [Google Scholar] [CrossRef]
- Chen, L.; Chen, W.; Wang, L.; Zhai, C.; Hu, X.; Sun, L.; Tian, Y.; Huang, X.; Jiang, L. Convolutional neural networks (CNNs)-based multi-category damage detection and recognition of high-speed rail (HSR) reinforced concrete (RC) bridges using test images. Eng. Struct. 2023, 276, 115306. [Google Scholar] [CrossRef]
- Kamariotis, A.; Chatzi, E.; Straub, D. A framework for quantifying the value of vibration-based structural health monitoring. Mech. Syst. Signal Process. 2023, 184, 109708. [Google Scholar] [CrossRef]
- Kouhpangi, M.Z.; Yaghoubi, S.; Torabipour, A. Improved Structural Health Monitoring Using Mode Shapes: An Enhanced Framework for Damage Detection in 2D and 3D Structures. Eng 2023, 4, 1742–1760. [Google Scholar] [CrossRef]
- Doebling, S.; Farrar, C.; Prime, M. A Summary Review of Vibration-Based Damage Identification Methods. Shock. Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Farrar, C.; Czarnecki, J.J.; Sohn, H.; Hemez, F. A Review of Structural Health Monitoring Literature: 1996–2001; Los Alamos National Laboratory: Santa Fe, NM, USA, 2004; pp. 1–301. [Google Scholar]
- Fan, W.; Qiao, P. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2010, 10, 83–111. [Google Scholar] [CrossRef]
- Cuadrado, M.; Pernas-Sánchez, J.; Artero-Guerrero, J.A.; Varas, D. Detection of barely visible multi-impact damage on carbon/epoxy composite plates using frequency response function correlation analysis. Measurement 2022, 196, 111194. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Q.; Xu, W.; Xiong, K. Damage evaluation of complex composite structures using acousto-ultrasonic detection combined with phase-shifted fiber Bragg grating and dual-frequency based data processing. Compos. Struct. 2022, 281, 115000. [Google Scholar] [CrossRef]
- Moughty, J.J.; Casas, J.R. A State of the Art Review of Modal-Based Damage Detection in Bridges: Development, Challenges, and Solutions. Appl. Sci. 2017, 7, 510. [Google Scholar] [CrossRef]
- Le, N.T.; Thambiratnam, D.P.; Nguyen, A.; Chan, T.H.T. A new method for locating and quantifying damage in beams from static deflection changes. Eng. Struct. 2019, 180, 779–792. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, T.; Liu, X.; Lu, Z.; Guo, T. Distance-restrained atmospheric parameters correction (DR-APC) model for GB-SAR transmission power attenuation compensation in bridges dynamic deflection measurement. Measurement 2022, 205, 112192. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, C.; Lu, Z.; Li, X. A multi-resolution deep feature framework for dynamic displacement measurement of bridges using vision-based tracking system. Measurement 2021, 183, 109847. [Google Scholar] [CrossRef]
- White, R.E.; Alexander, N.A.; Macdonald, J.H.G.; Bocian, M. Characterisation of crowd lateral dynamic forcing from full-scale measurements on the Clifton Suspension Bridge. Structures 2020, 24, 415–425. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, Z.; Zhang, J. Measurement of Vehicle-Bridge-Interaction force using dynamic tire pressure monitoring. Mech. Syst. Signal Process. 2018, 104, 370–383. [Google Scholar] [CrossRef]
- Rana, S.; Adhikary, S.; Tasnim, J. A statistical index based damage identification method of a bridge using dynamic displacement under moving vehicle. Structures 2022, 43, 79–92. [Google Scholar] [CrossRef]
- Hu, H.; Wang, J.; Dong, C.Z.; Chen, J.; Wang, T. A hybrid method for damage detection and condition assessment of hinge joints in hollow slab bridges using physical models and vision-based measurements. Mech. Syst. Signal Process. 2023, 183, 109631. [Google Scholar] [CrossRef]
- Ma, L.L.; Wu, H.; Fang, Q. Damage mode and dynamic response of RC girder bridge under explosions. Eng. Struct. 2021, 243, 112676. [Google Scholar] [CrossRef]
- Alemu, Y.L.; Lahmer, T.; Walther, C. Damage Detection with Data-Driven Machine Learning Models on an Experimental Structure. Eng 2024, 5, 629–656. [Google Scholar] [CrossRef]
- Pan, B.; Tian, L.; Song, X. Real-time, non-contact and targetless measurement of vertical deflection of bridges using off-axis digital image correlation. NDT E Int. 2016, 79, 73–80. [Google Scholar] [CrossRef]
- Pan, P.; Xing, C.; Bai, J.; Yu, S.; Xu, Y.; Zhou, J.; Yu, J. A remote deflection detection method for long-span bridges using adaptive mask and high-resolution camera. Measurement 2022, 201, 111774. [Google Scholar] [CrossRef]
- Sung, S.H.; Koo, K.Y.; Jung, H.Y.; Jung, H.J. Damage-induced deflection approach for damage localization and quantification of shear buildings: Validation on a full-scale shear building. Smart Mater. Struct. 2012, 21, 115013. [Google Scholar] [CrossRef]
- Ma, Q.; Solís, M.; Galvín, P. Wavelet analysis of static deflections for multiple damage identification in beams. Mech. Syst. Signal Process. 2021, 147, 107103. [Google Scholar] [CrossRef]
- Cao, M.; Ye, L.; Zhou, L.; Su, Z.; Bai, R. Sensitivity of fundamental mode shape and static deflection for damage identification in cantilever beams. Mech. Syst. Signal Process. 2011, 25, 630–643. [Google Scholar] [CrossRef]
- Ghali, A.; Neville, A.; Brown, T. Structural Analysis: A Unified Classical and Matrix Approach, 7th ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–962. [Google Scholar]
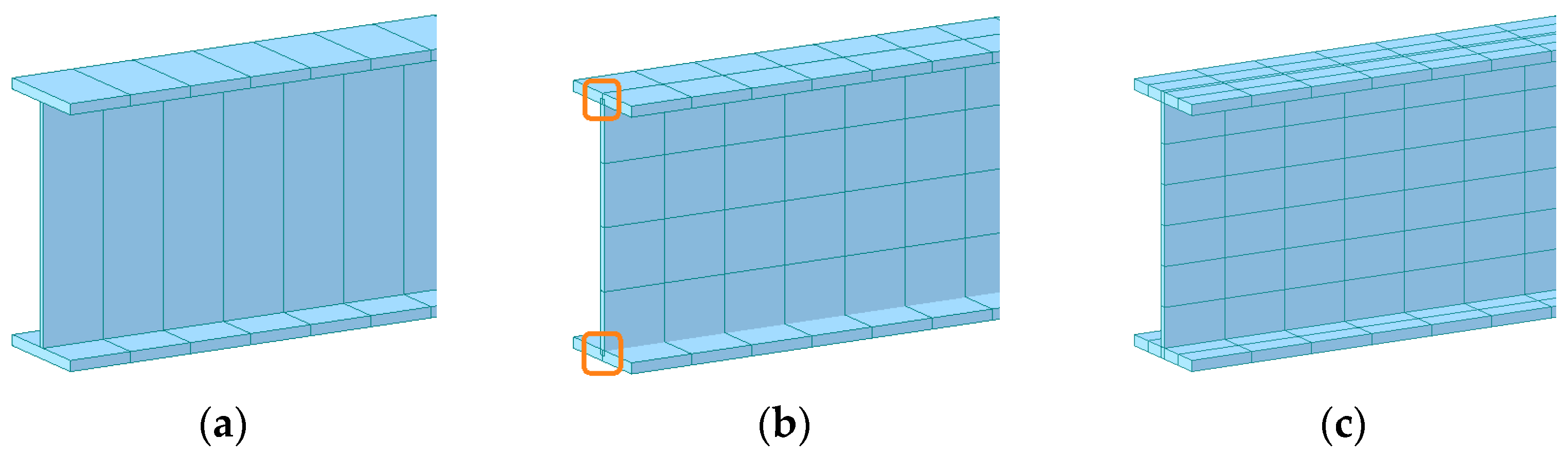
- Midas FEA NX 2020 (v1.1), User Manual; MIDAS Information Technology Co., Ltd.: New York, NY, USA, 2020.





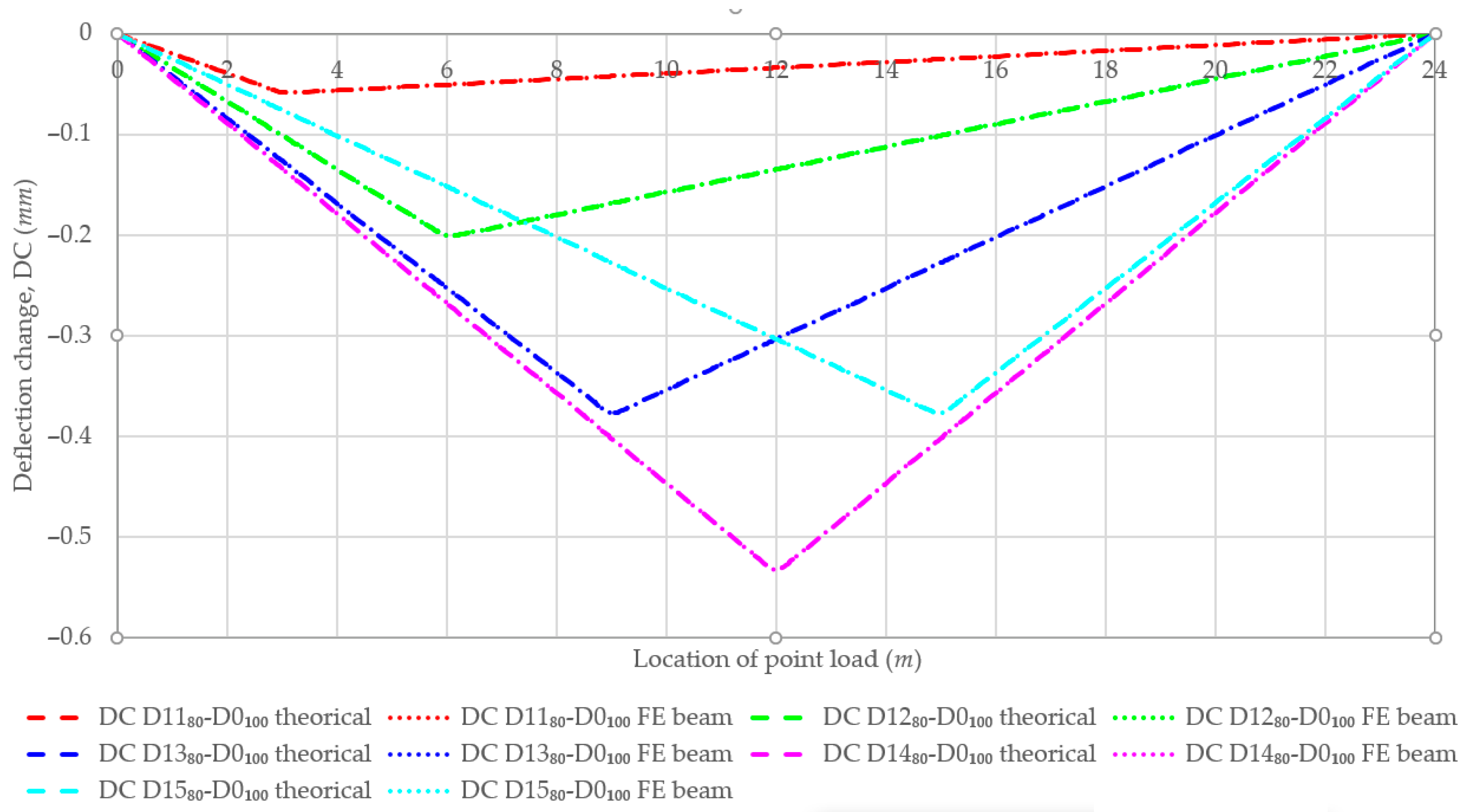

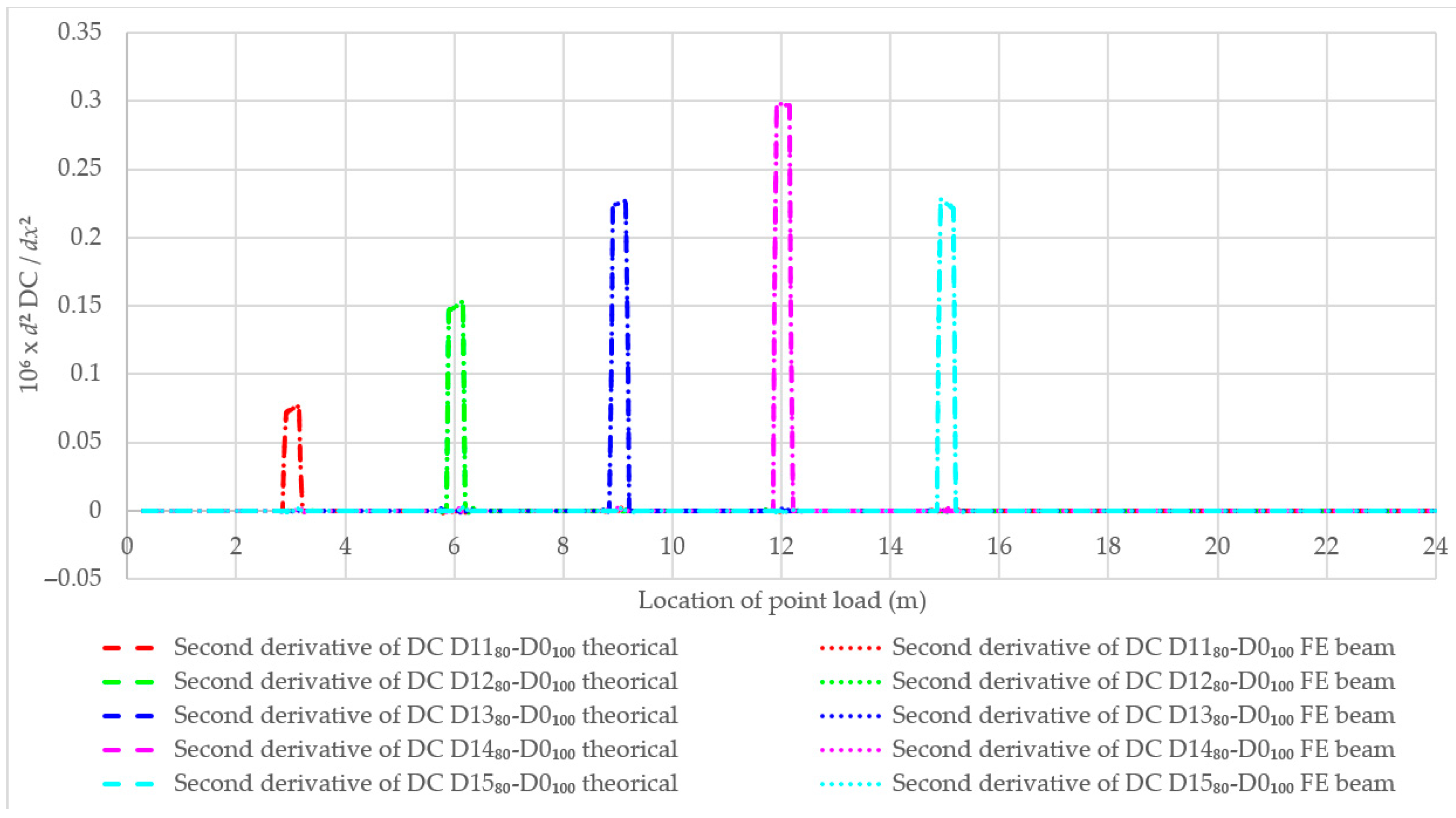
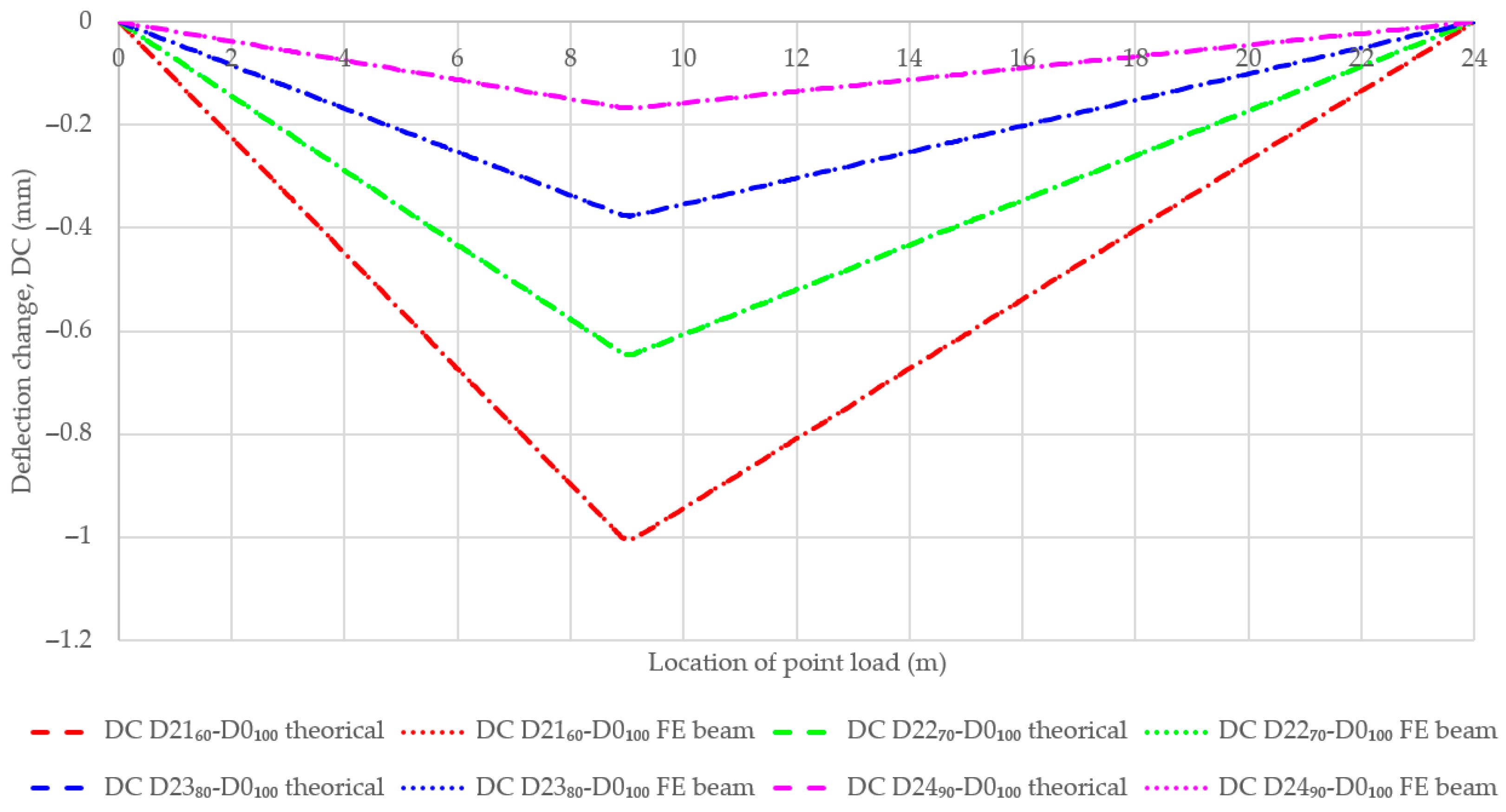
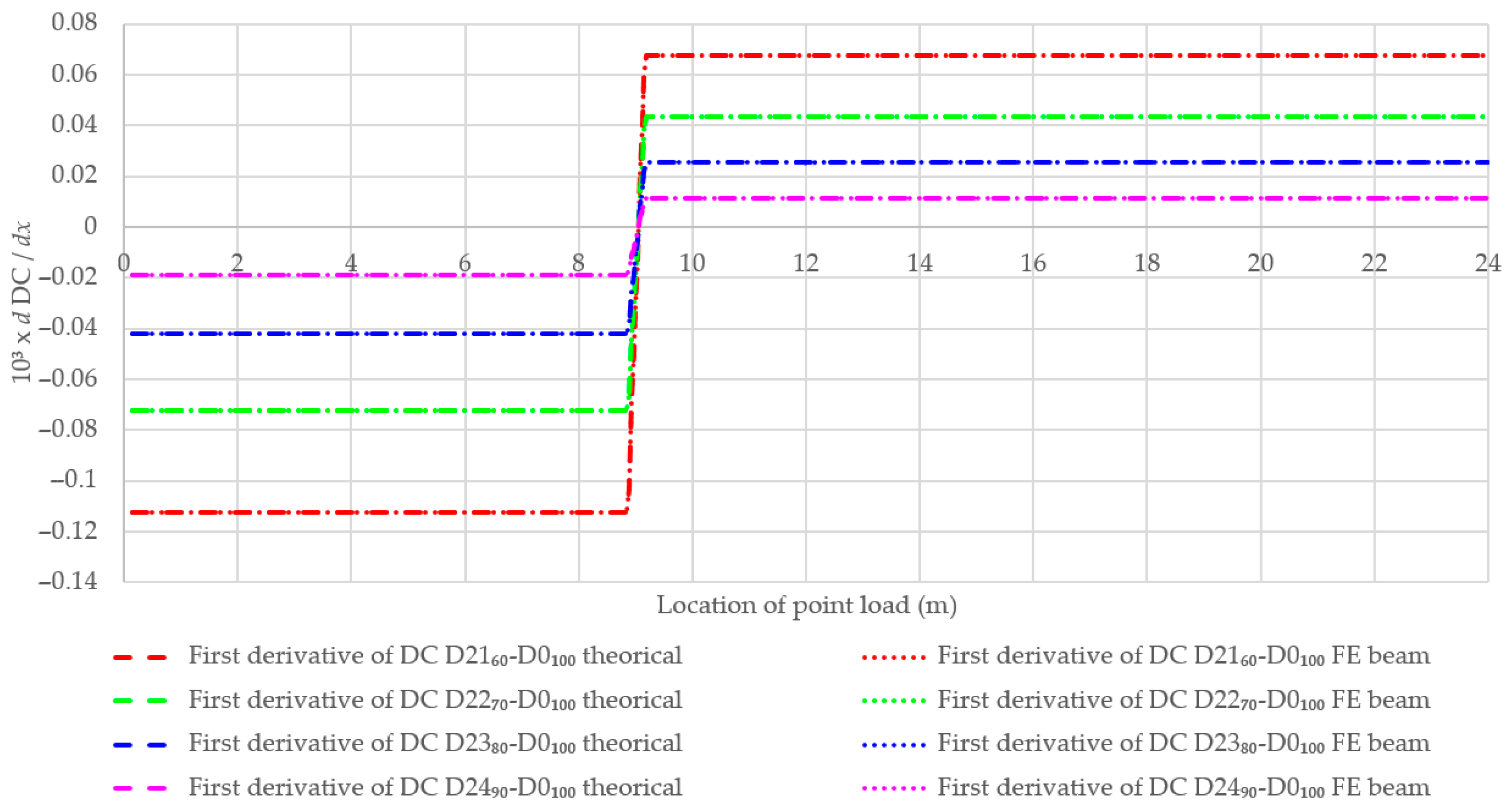
| No | Damage Case | Damage Location | Remaining Stiffness of the Damage Zone | Remarks |
|---|---|---|---|---|
| 1-0 | D0100% | Intact beam | ||
| 1-1 | D1180% | 2850–3150 mm | 80% | One new damage zone |
| 1-2 | D1280% | 5850–6150 mm | 80% | One new damage zone |
| 1-3 | D1380% | 8850–9150 mm | 80% | One new damage zone |
| 1-4 | D1480% | 11,850–12,150 mm | 80% | One new damage zone |
| 1-5 | D1580% | 14,850–15,150 mm | 80% | One new damage zone |
| No | Damage Case | Damage Location | Remaining Stiffness of the Damage Zone | Remarks |
|---|---|---|---|---|
| 2-1 | D2160% | 8850–9150 mm | 60% | One new damage zone |
| 2-2 | D2270% | 8850–9150 mm | 70% | One new damage zone |
| 2-3 | D2380% | 8850–9150 mm | 80% | One damage zone, same case of D1380% |
| 2-4 | D2490% | 8850–9150 mm | 90% | One new damage zone |
| No | Damage Case | Damage Location | Remaining Stiffness of the Damage Zone | Remarks |
|---|---|---|---|---|
| 3-1 | D31190%.D31290% | D311: 8850–9150 mm | 90% | Two new damage zones |
| D314: 14,850–15,150 mm | 90% | |||
| 3-2 | D32180%.D32290% | D321: 8850–9150 mm | 80% | Two new damage zones |
| D322: 11,850–12,150 mm | 90% | |||
| 3-3 | D33180%.D33280% | D331: 8850–9150 mm | 80% | Two new damage zones |
| D332: 11,850–12,150 mm | 80% | |||
| 3-4 | D34170%.D34275% | D341: 8850–9150 mm | 70% | Two new damage zones |
| D342: 11,850–12,150 mm | 75% | |||
| 3-5 | D35175%.D35270%.D35370%.D35475% | D351: 5850–6150 mm | 75% | Four new damage zones |
| D352: 8850–9150 mm | 70% | |||
| D353: 11,850–12,150 mm | 70% | |||
| D354: 14,850–15,150 mm | 75% |
| No | Damage Case | Damage Location | Remaining Stiffness | Remarks | |
|---|---|---|---|---|---|
| 1st Structural State | 2nd Structural State | ||||
| 4-1 | D4180% → D4160% | D41: 8850–9150 mm | 80% | 60% | One existing damage zone is developing. |
| 4-2 | D42180%.D42290% → D42170%.D42275% | D421: 8850–9150 mm | 80% | 70% | Two existing damage zones are developed simultaneously. |
| D422: 11,850–12,150 mm | 90% | 75% | |||
| 4-3 | D43180%.D432100% → D43180%.D43290% | D431: 8850–9150 mm | 80% | 80% | The existing damage is not developed, but new damage appears. |
| D432: 11,850–12,150 mm | 100% | 90% | |||
| 4-4 | D44190%.D442100% → D44170%.D44275% | D441: 8850–9150 mm | 90% | 70% | The existing damage is developing, while new damage appears. |
| D442: 11,850–12,150 mm | 100% | 75% | |||
| 4-5 | D451100%.D45270%.D45375%.D454100% → D45175%.D45270%.D45370%.D45475% | D451: 5850–6150 mm | 100% | 75% | One existing damage zone is developing and one other is not, while two new damage zones appear. |
| D452: 8850–9150 mm | 70% | 70% | |||
| D453: 11,850–12,150 mm | 75% | 70% | |||
| D454: 14,850–15,150 mm | 100% | 75% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, Q.-B.; Nguyen, H.-H. An Efficient Approach for Damage Identification of Beams Using Mid-Span Static Deflection Changes. Eng 2024, 5, 895-917. https://doi.org/10.3390/eng5020048
Nguyen Q-B, Nguyen H-H. An Efficient Approach for Damage Identification of Beams Using Mid-Span Static Deflection Changes. Eng. 2024; 5(2):895-917. https://doi.org/10.3390/eng5020048
Chicago/Turabian StyleNguyen, Quoc-Bao, and Huu-Hue Nguyen. 2024. "An Efficient Approach for Damage Identification of Beams Using Mid-Span Static Deflection Changes" Eng 5, no. 2: 895-917. https://doi.org/10.3390/eng5020048






