Carbon Fiber-Reinforced Polymer Composites Integrated Beam–Column Joints with Improved Strength Performance against Seismic Events: Numerical Model Simulation
Abstract
:1. Introduction
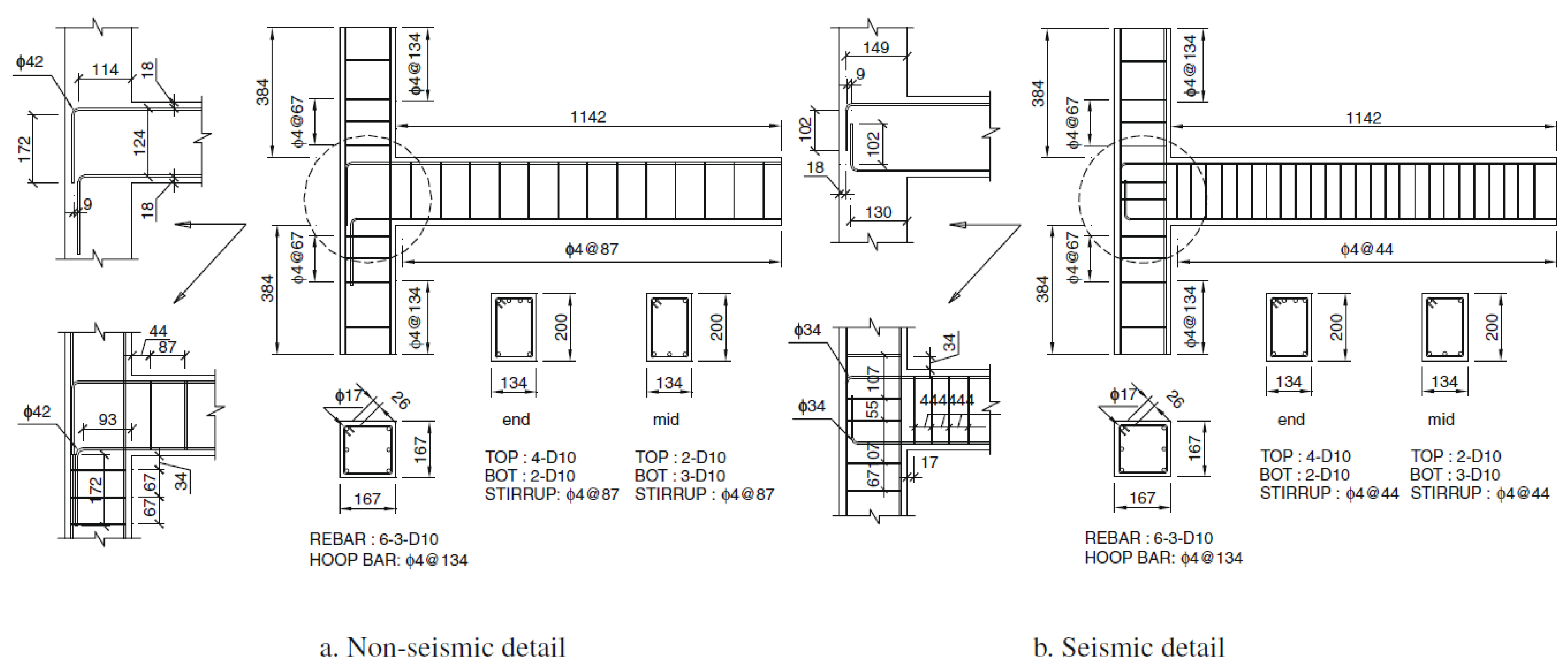
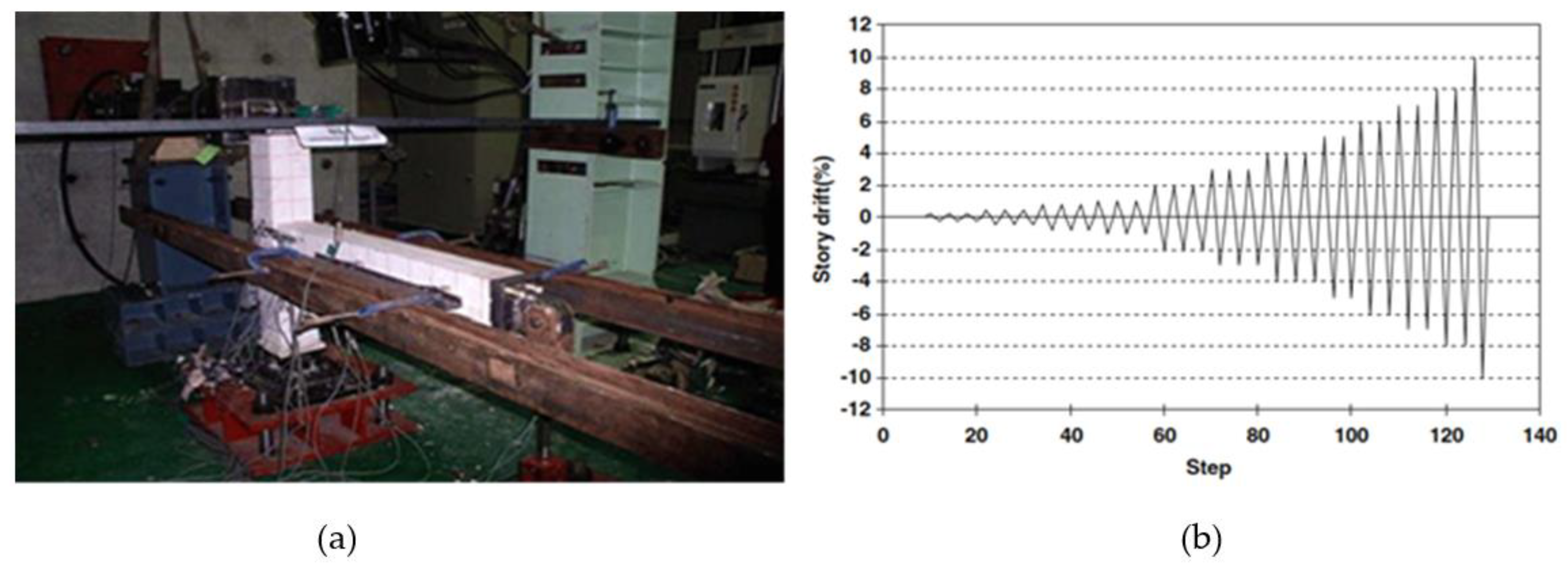
2. Experimental Work
3. Model Simulation Using Abacus
3.1. Element Type
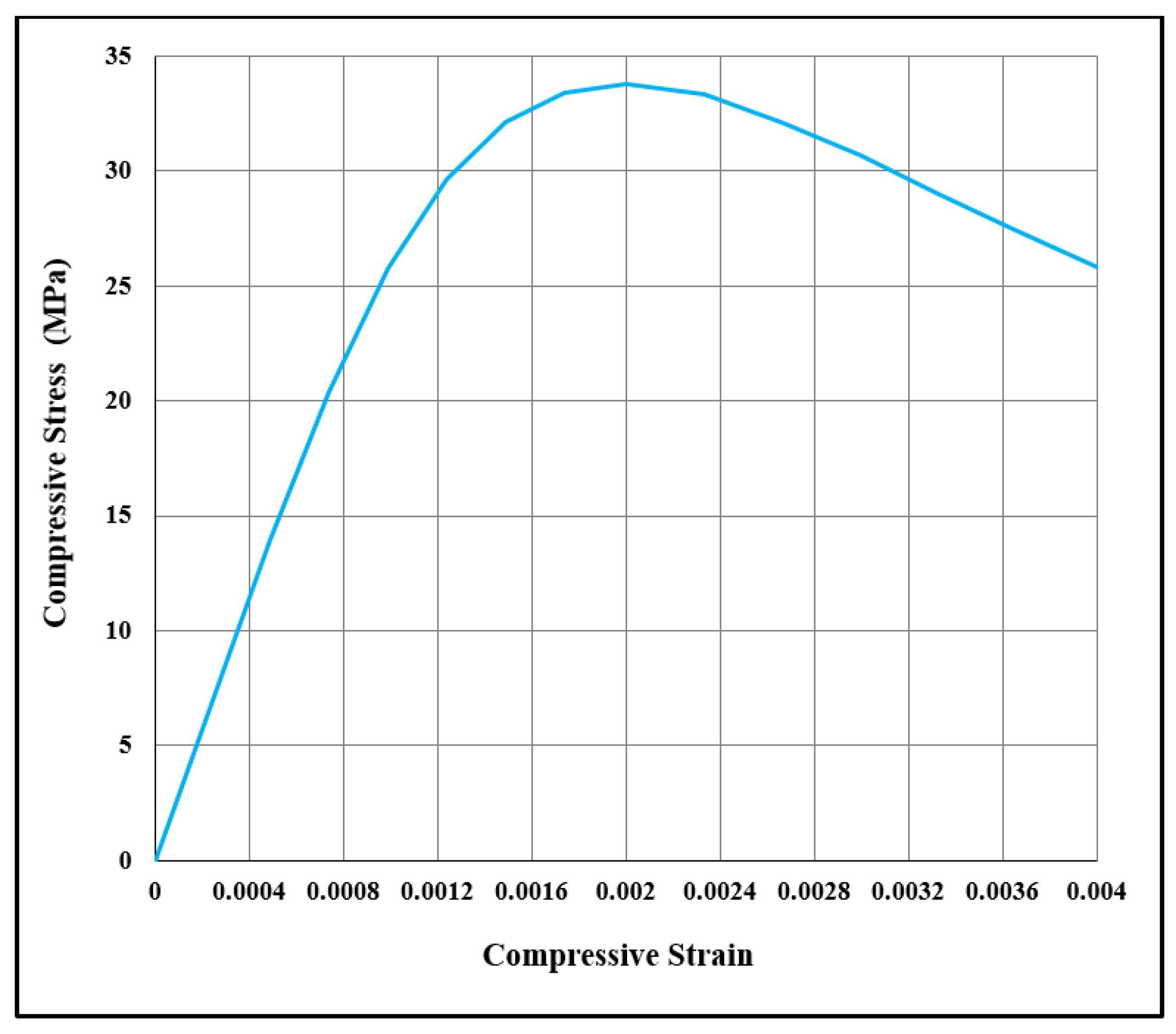
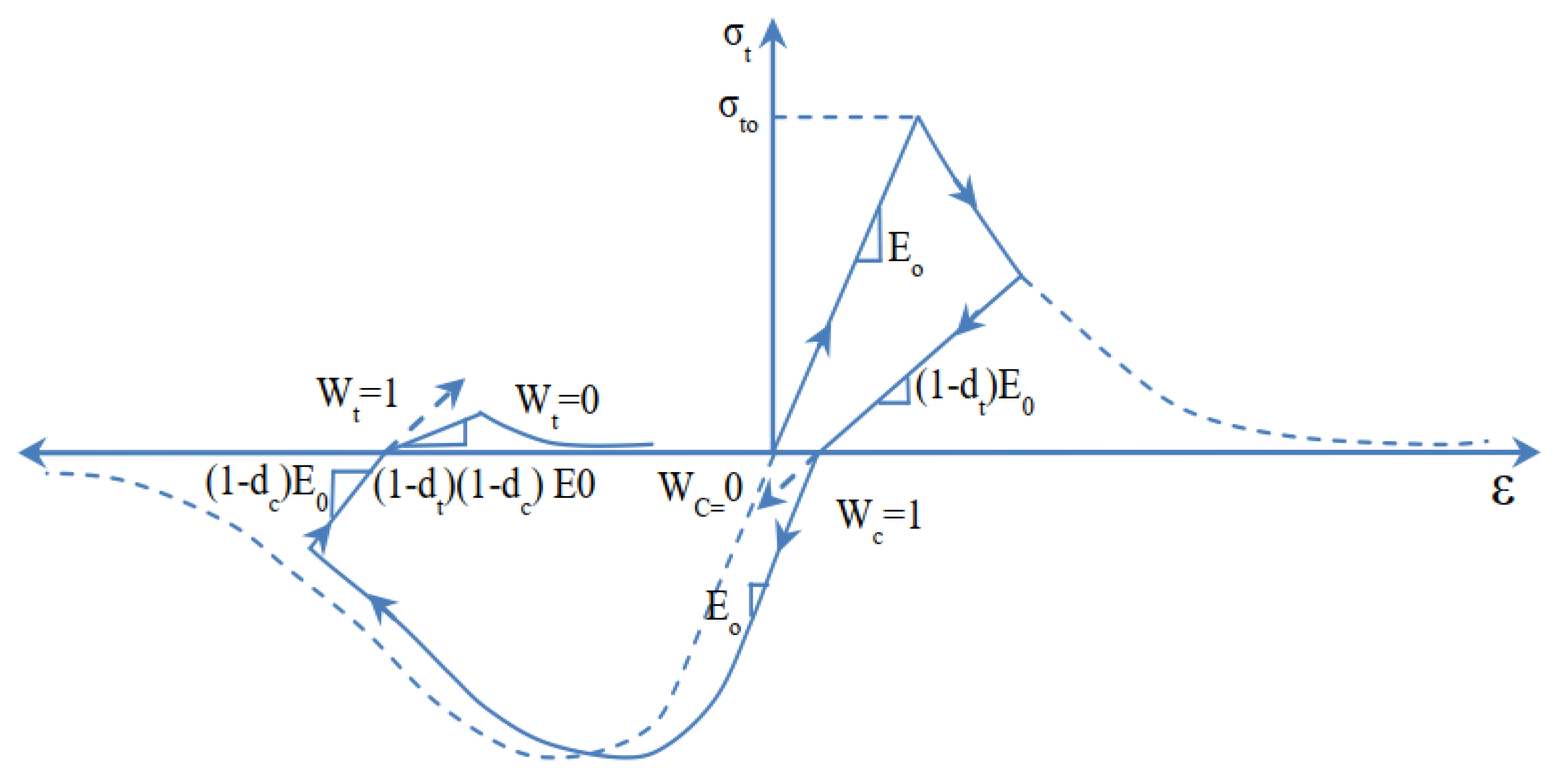
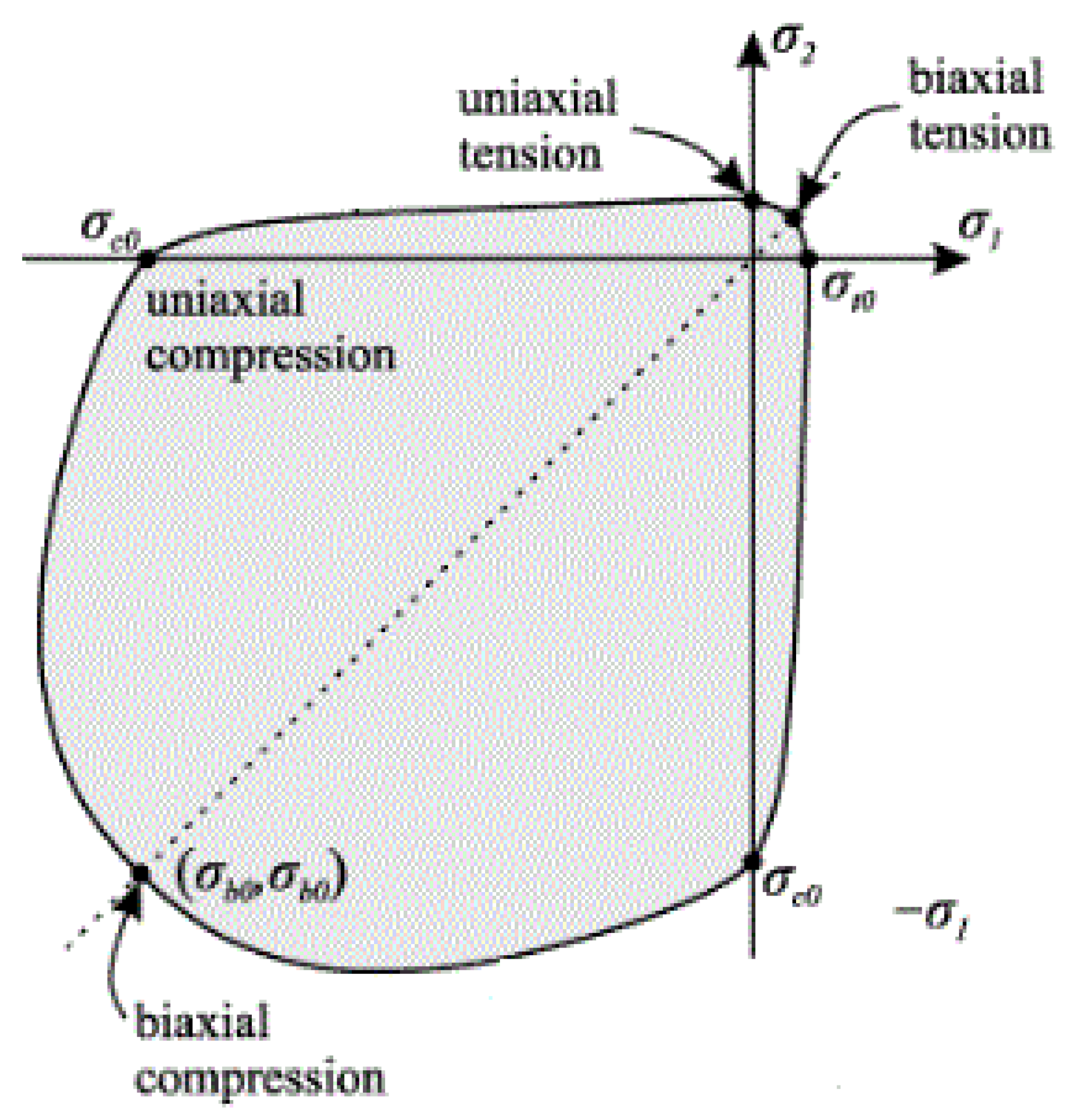
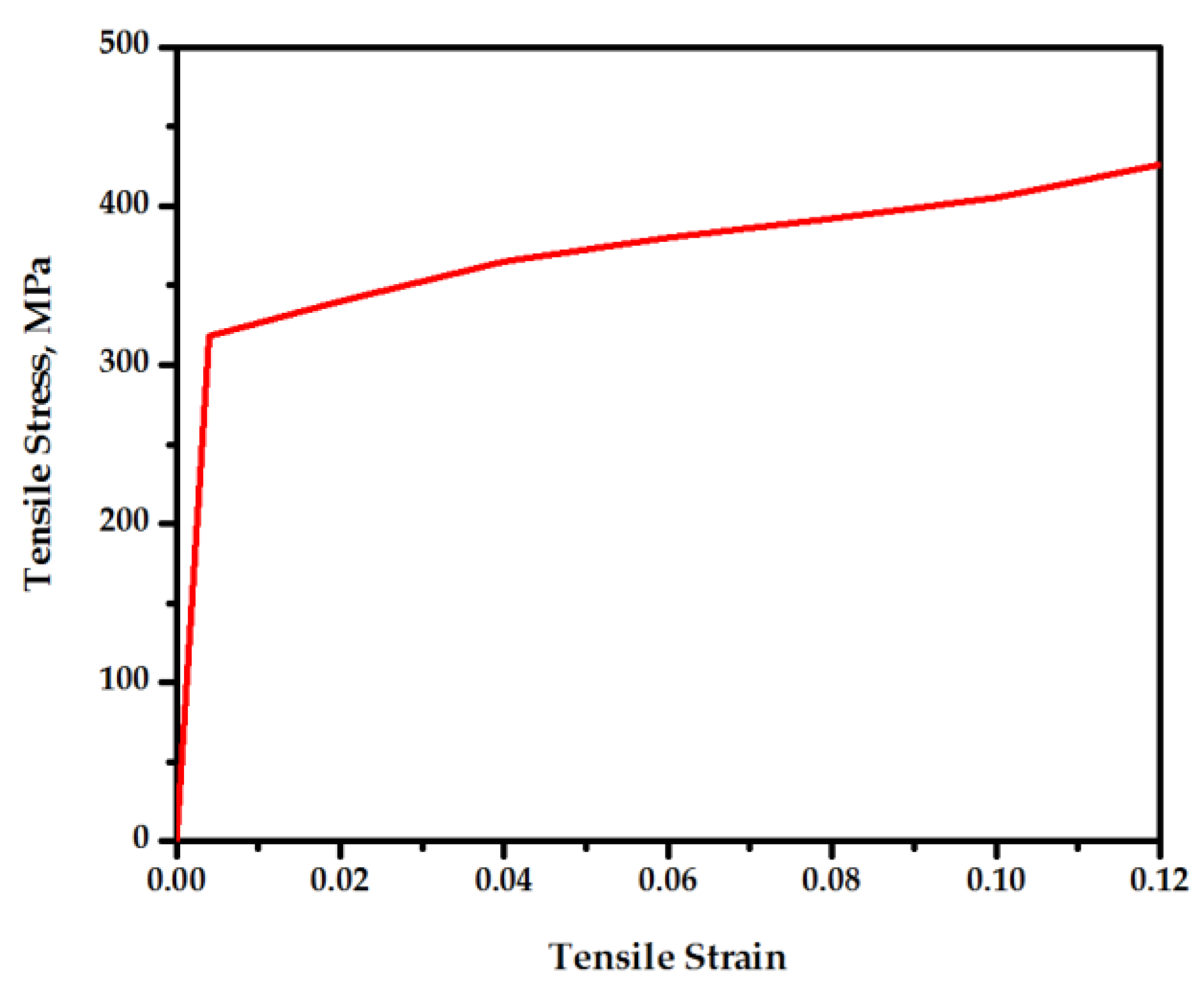
3.2. Material Properties
3.3. Geometry
3.4. Boundary Condition
4. Results and Discussion
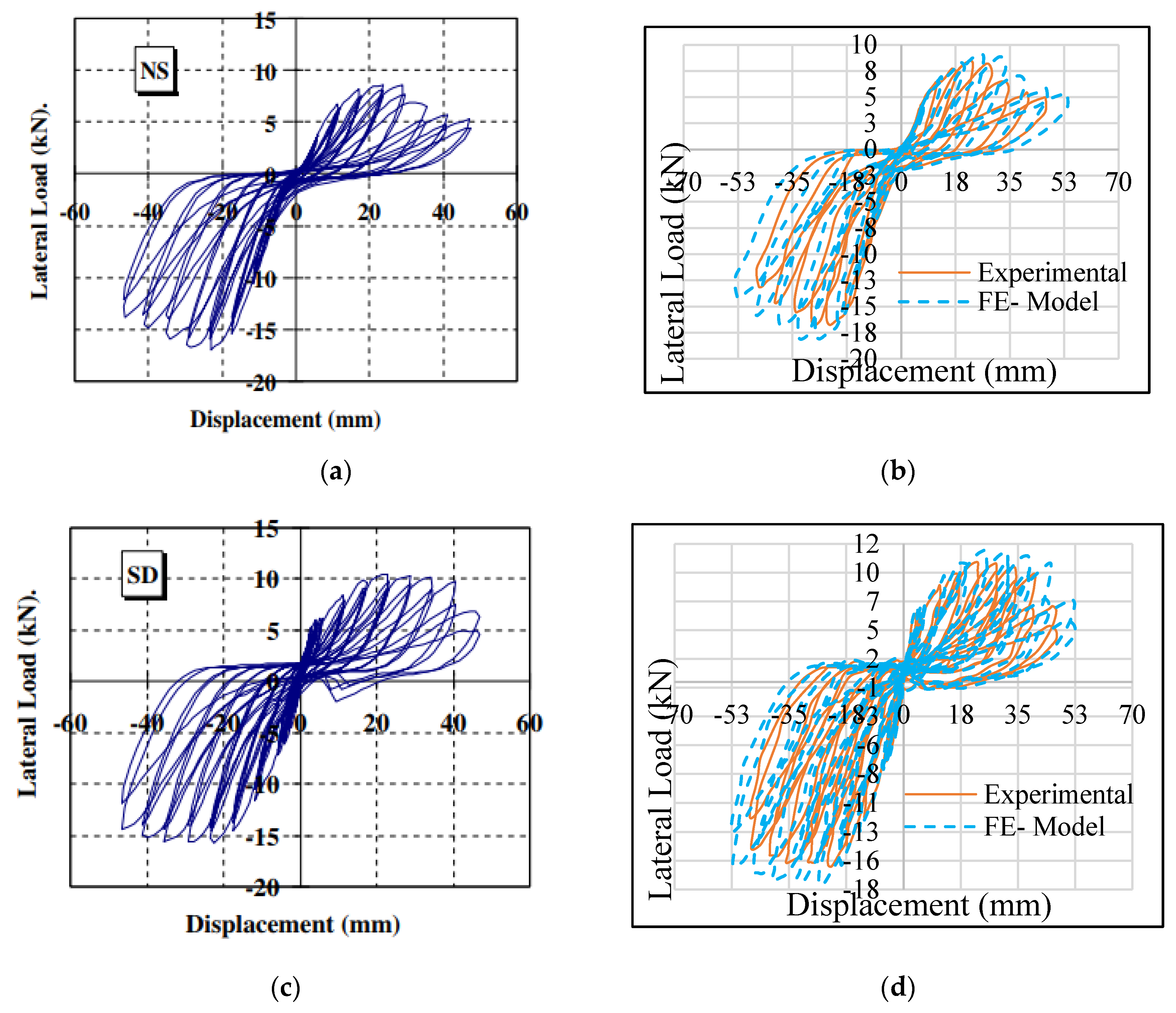
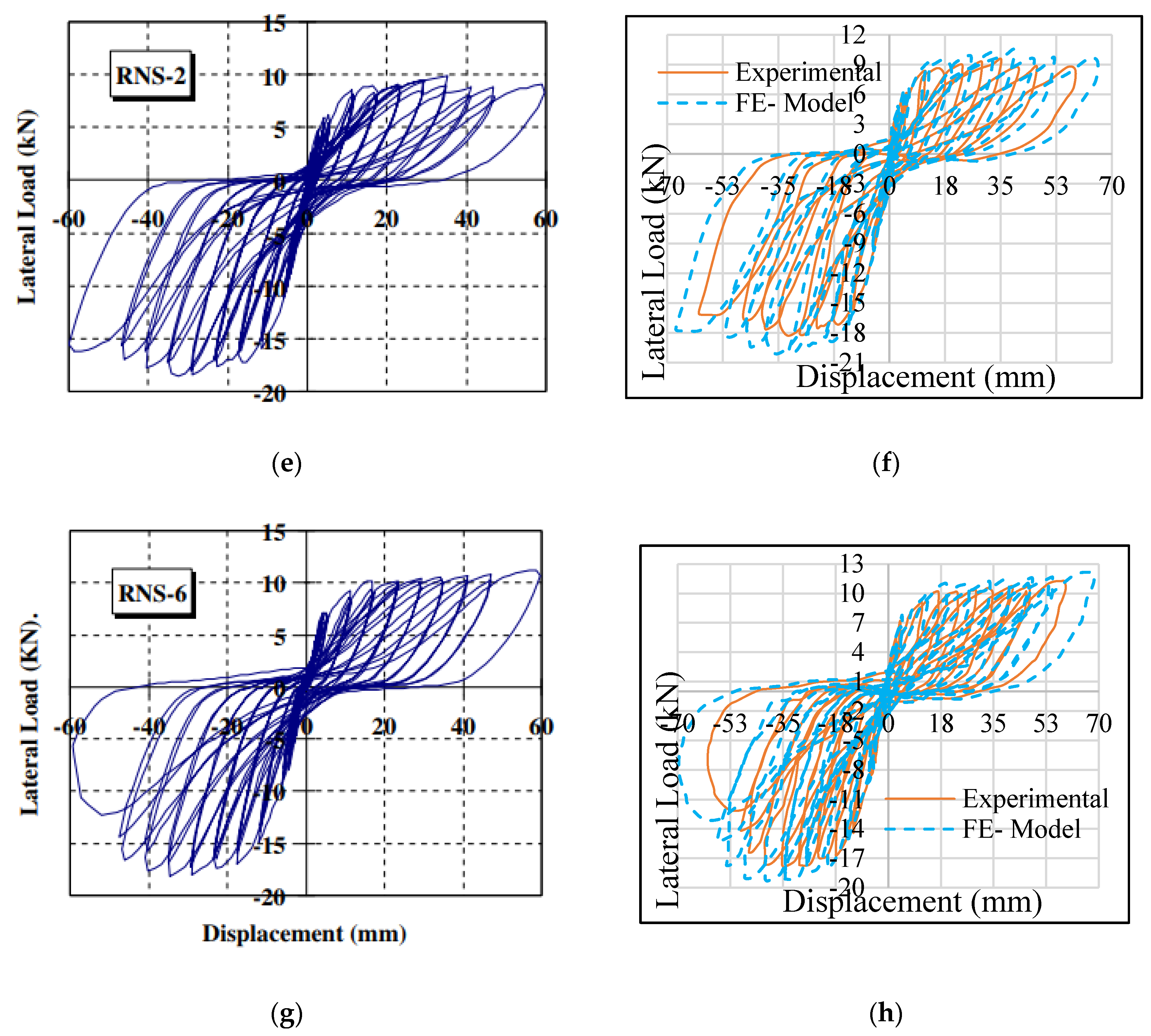
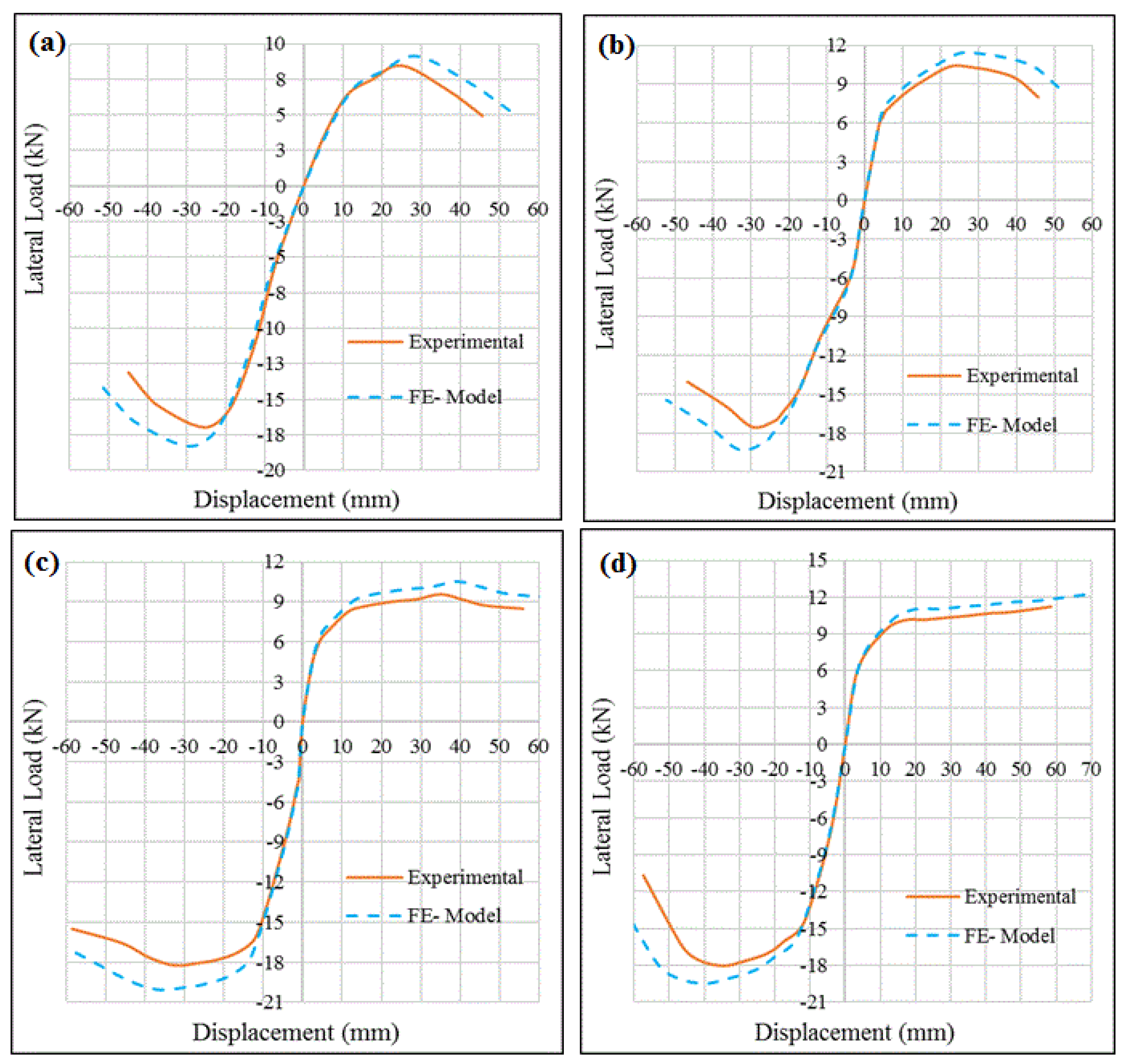
4.1. Verification of the Finite Element Models with Experiments
4.1.1. Force versus Displacement Curves
4.1.2. Failure Modes
4.2. Requirement of ACI 374.1-05
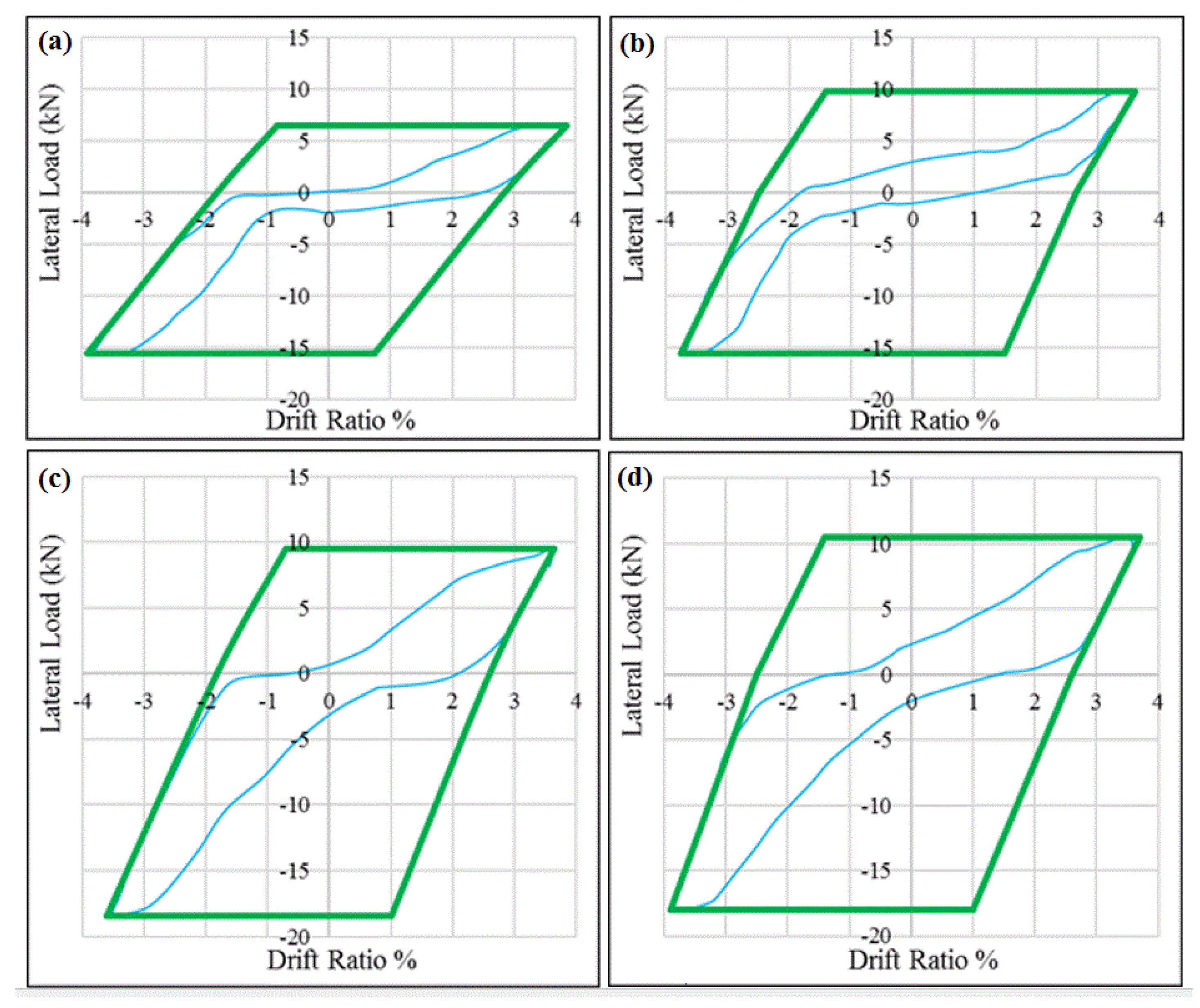
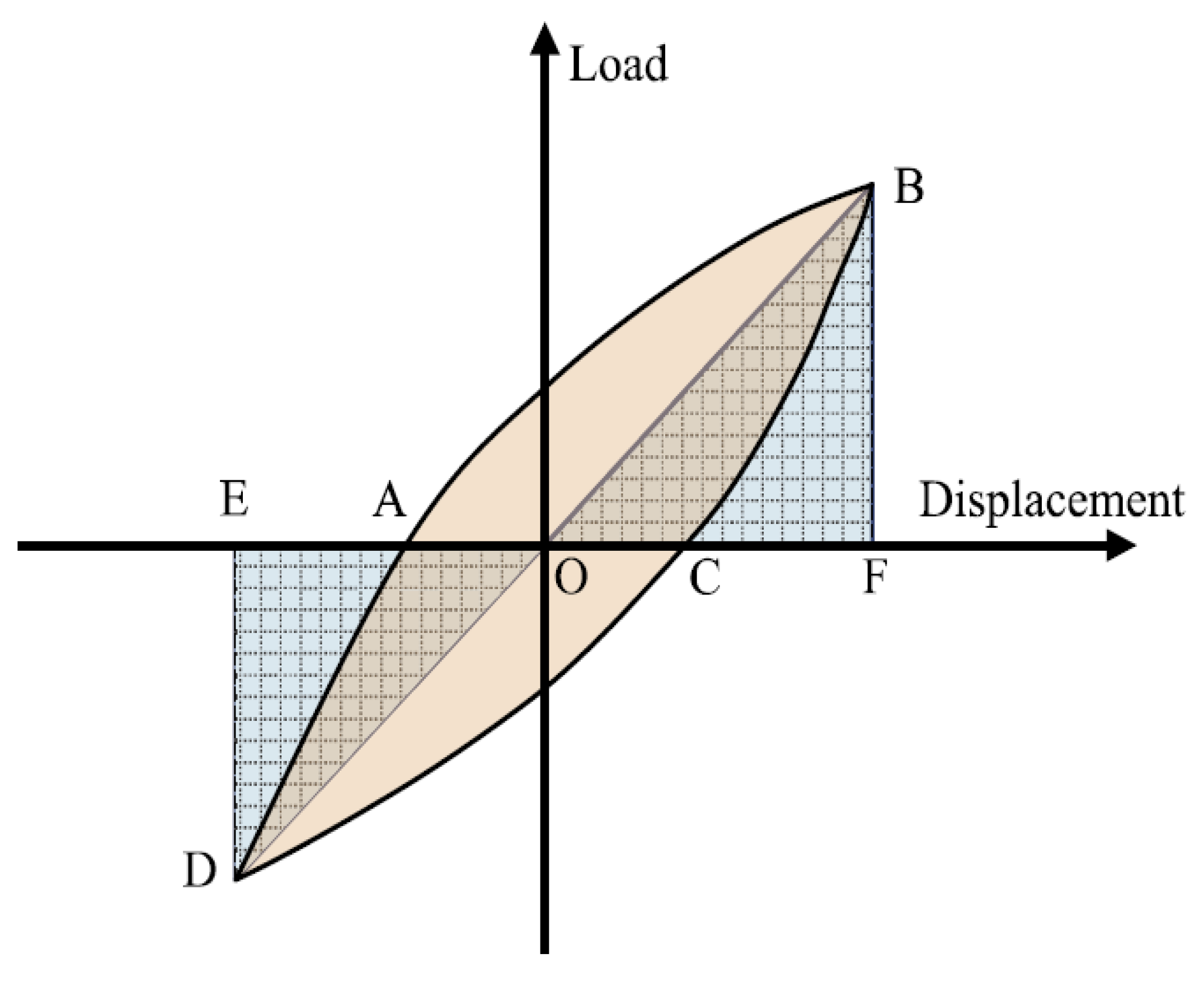
4.2.1. Relative Energy Dissipation
4.2.2. Strength Criteria
4.2.3. Stiffness Criteria
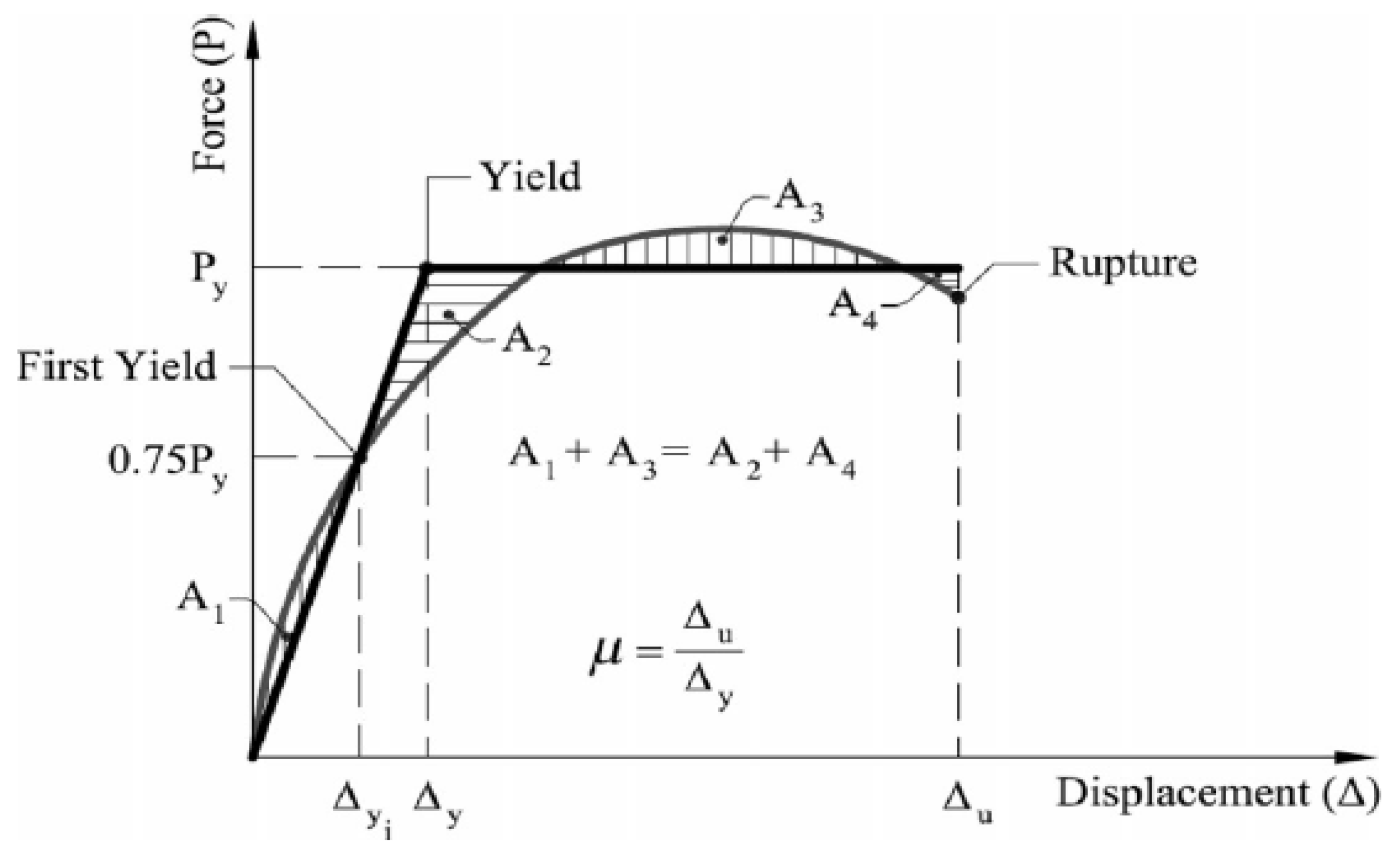
4.2.4. Effective Elastic Stiffness and Displacement Capacity
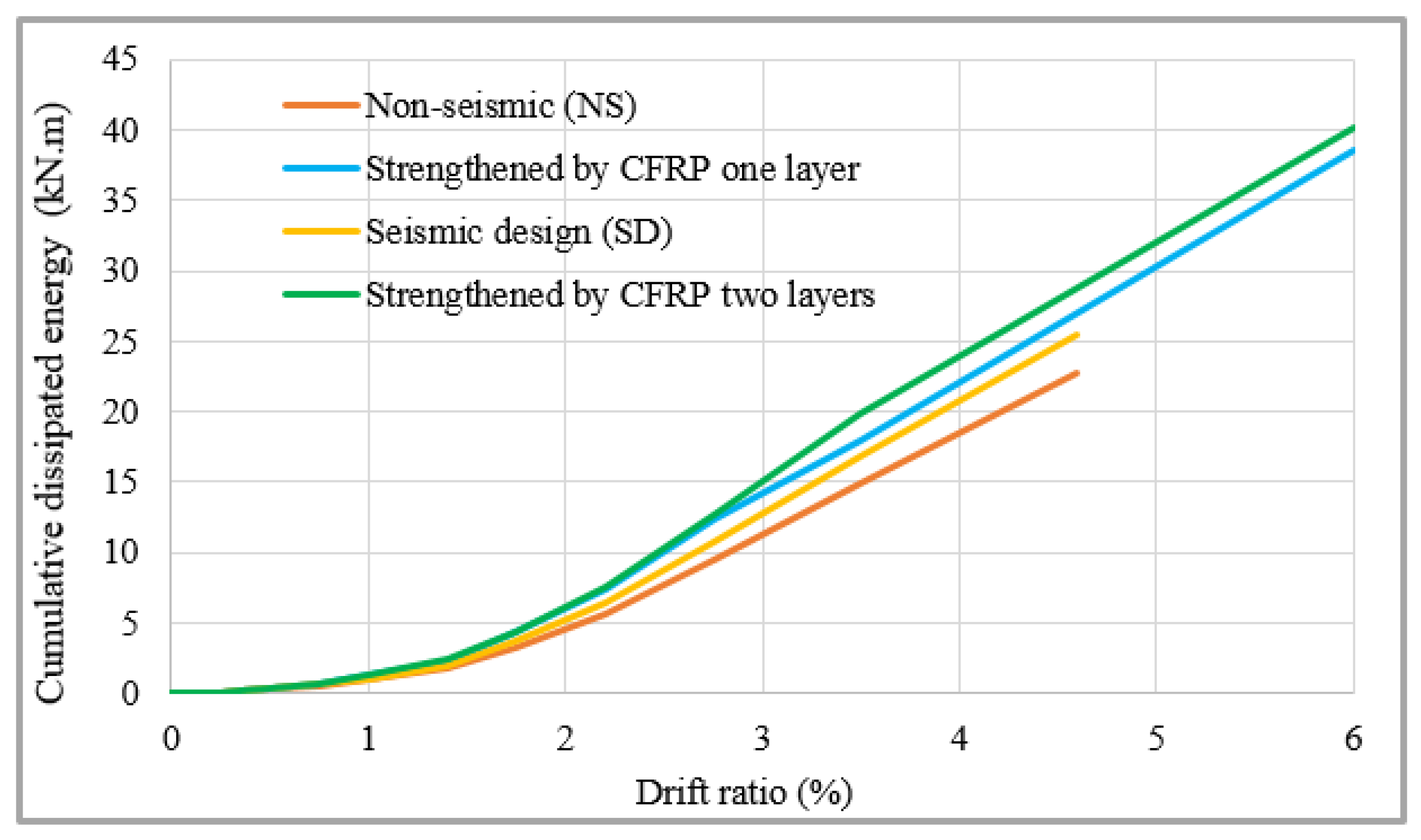
4.2.5. Damping Ratio and Energy Dissipation
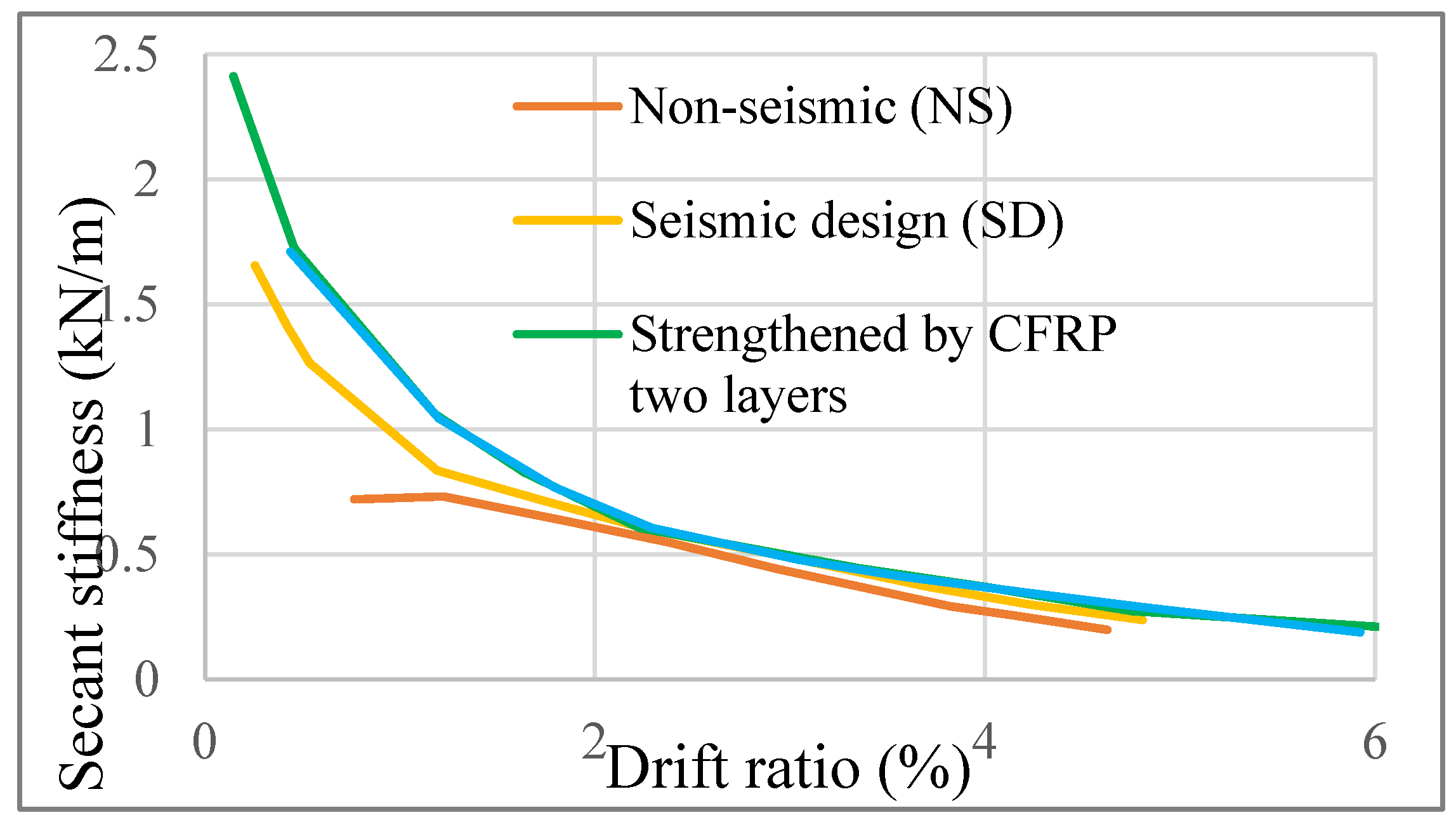
4.3. Stiffness Degradation
5. Conclusions
- The strengthening of NSCBCJs using CFRPC reinforcement enabled us to reduce crack formation in the plastic hinge location, thus leading to a reduced risk of building collapse during seismic events. The plastic hinges for the frame of the reinforced concrete building were placed near the column and beam joint.
- The strengthening of the NSCBCJs was appropriate when assessing the behavior of non-seismic details due to the overall lateral displacement increase that produces an increase in ductility demand.
- The NSCBCJs being non-ductile meant that they could display large lateral displacement which can be attributed to the significant cracks and deformation of the joint area. Consequently, the observed large lateral displacement can cause severe failure in the frame building during strong seismic vibration.
- The proposed NSCBCJs showed significant joint shear failure together with the beam and column flexural failure. However, the seismic joint failure was beam flexural, while CFRPC-integrated joints showed beam flexural failure with the debonding of the CFRPC sheet. Since the studied joints had beam flexural strength, the lateral load capacity difference can be mainly ascribed to the transverse reinforcement and strengthening of the joint.
- Both seismic and CFRPC-strengthened joints revealed good strength, stiffness, ductility, and energy-dissipation capabilities.
- Both seismic and CFRPC-strengthened joints achieved the required seismic code provisions of ACI 374.1-05. Conversely, the NSCBCJs failed to satisfy the desired requirement due to a failure in achieving the strength criteria.
- The finite element model simulation results for the stress and strain response demonstrated the considerable impact of CFRPC integration into NSCBCJs, leading to a reasonable strength capacity enhancement in the joints, thereby reducing the joint cracks.
- It is established that the present comprehensive numerical modeling and simulation study may contribute to the development of CFRPC-reinforced high-performance anti-seismic CBCJs, thus contributing towards the sustainable construction sector.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sultan, H.K.; Huseien, G.F. Minimum Shear Reinforcement for Reactive Powder Concrete Beams. Eng 2024, 5, 801–818. [Google Scholar] [CrossRef]
- Cascardi, A.; Verre, S.; Sportillo, A.; Giorgio, G. A Multiplex Conversion of a Historical Cinema. Adv. Civ. Eng. 2022, 2022, 2191315. [Google Scholar] [CrossRef]
- Sultan, H.K.; Noor, A.A.A.; Huseien, G.F. Performance Evaluation of Self-Compacting Glass Fiber Concrete Incorporating Silica Fume at Elevated Temperatures. Eng 2024, 5, 1043–1066. [Google Scholar] [CrossRef]
- Saleh, S.M.; Majeed, F.H. Shear strength of headed stud connectors in self-compacting concrete with recycled coarse aggregate. Buildings 2022, 12, 505. [Google Scholar] [CrossRef]
- Falih, Z.F.M.; Dakhi, A.J.; Saleh, S.M. Numerical Solution for Masonry Wall Using General Static Step with ABAQUS/Standard. Math. Model. Eng. Probl. 2023, 10, 2142–2148. [Google Scholar] [CrossRef]
- Saleh, S.M.; Majeed, F.H.; Al-Salih, O.; Hussain, H.K. Torsional Behavior of Steel-Concrete-Steel Sandwich Beams with Welded Stirrups as Shear Connectors. Civ. Eng. J. 2023, 9, 208–219. [Google Scholar] [CrossRef]
- Karim, A.A.; Abd Matooq, J.; Abdulrazzaq, O.A.; Majeed, F.H.; Saleh, S.M. The behavior of Shear Connectors in Steel-Normal Concrete Composite Structure under Repeated Loads. Civ. Eng. J. 2024, 10, 210–221. [Google Scholar] [CrossRef]
- Deaton, J.B. Nonlinear Finite Element Analysis of Reinforced Concrete Exterior Beam-Column Joints with Nonseismic Detailing. 2013. Available online: https://repository.gatech.edu/entities/publication/78302263-8d44-44c4-bbc2-c064816bf6de (accessed on 10 May 2024).
- Tahnat, Y.B.A.; Samaaneh, M.A.; Dwaikat, M.M.; Halahla, A.M. Simple equations for predicting the rotational ductility of fiber-reinforced-polymer strengthened reinforced concrete joints. Structures 2020, 24, 73–86. [Google Scholar] [CrossRef]
- Gao, F.; Tang, Z.; Mei, S.; Hu, B.; Huang, S.; Chen, J. Seismic behavior of exteriorbeam–column joints with high-performance steel rebar: Experimental and numerical investigations. Adv. Struct. Eng. 2021, 24, 90–106. [Google Scholar] [CrossRef]
- Yu, F.; Wu, C.; Xu, B.; Guan, Y.; Zhu, X.; Fang, Y. Study on shear bearing capacity of PVC-CFRP confined concrete column-RC beam exterior joint with core steel tube. Constr. Build. Mater. 2024, 410, 134197. [Google Scholar] [CrossRef]
- Samadi, M.; Baghban, M.H.; Kubba, Z.; Faridmehr, I.; Abdul Shukor Lim, N.H.; Benjeddou, O.; Ariffin, N.F.B.; Huseien, G.F. Flexural behavior of reinforced concrete beams under instantaneous loading: Effects of recycled ceramic as cement and aggregates replacement. Buildings 2022, 12, 439. [Google Scholar] [CrossRef]
- Kularni, S.; Patil, Y.D. A novel reinforcement pattern for exterior reinforced concrete beam-column joint. Procedia Eng. 2013, 51, 184–193. [Google Scholar] [CrossRef]
- Abdalla, K.M.; Al-Rousan, R.; Alhassan, M.A.; Lagaros, N.D. Finite-element modelling of concrete-filled steel tube columns wrapped with CFRP. Proc. Inst. Civ. Eng.-Struct. Build. 2020, 173, 844–857. [Google Scholar] [CrossRef]
- Kaliluthin, A.; Kothandaraman, S.; Ahamed, T.S. A review on behavior of reinforced concrete beam column joint. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 11299–11312. [Google Scholar]
- Kiran, R.; Genesio, G. A case study on pre 1970s constructed concrete exterior beam-column joints. Case Stud. Struct. Eng. 2014, 1, 20–25. [Google Scholar] [CrossRef]
- Rajagopal, S.; Prabavathy, S. Exterior beam-column joint study with non-conventional reinforcement detailing using mechanical anchorage under reversal loading. Sadhana 2014, 39, 1185–1200. [Google Scholar] [CrossRef]
- Rajagopal, S.; Prabavathy, S. Seismic behavior of exterior beam-column joint using mechanical anchorage under reversal loading: An experimental study. Iran. J. Sci. Technol. Trans. Civ. Eng. 2014, 38, 345. [Google Scholar]
- Fan, G.; Song, Y.; Wang, L. Experimental study on the seismic behavior of reinforced concrete beam-column joints under various strain rates. J. Reinf. Plast. Compos. 2014, 33, 601–618. [Google Scholar] [CrossRef]
- Al-Rousan, R.Z.; Alhassan, M.A.; Al-omary, R.J. Response of interior beam-column connections integrated with various schemes of CFRP composites. Case Stud. Constr. Mater. 2021, 14, e00488. [Google Scholar] [CrossRef]
- Patel, R.S.; Nambiyanna, B.; Prabhakara, R. An experimental study on effect of diameter of rebar on exterior beam column joint. Int. J. Innov. Res. Sci. 2015, 4, 5984–5991. [Google Scholar]
- Rodríguez, V.; Guerrero, H.; Alcocer, S.M.; Tapia-Hernández, E. Rehabilitation of heavily damaged beam-column connections with CFRP wrapping and SFRM casing. Soil Dyn. Earthq. Eng. 2021, 145, 106721. [Google Scholar] [CrossRef]
- Moskaleva, A.; Safonov, A.; Hernández-Montes, E. Fiber-reinforced polymers in freeform structures: A review. Buildings 2021, 11, 481. [Google Scholar] [CrossRef]
- Al-Rousan, R.Z.; Alkhawaldeh, A. Behavior of heated damaged reinforced concrete beam-column joints strengthened with FRP. Case Stud. Constr. Mater. 2021, 15, e00584. [Google Scholar] [CrossRef]
- Ruiz-Pinilla, J.G.; Pallarés, F.; Gimenez, E.; Calderón, P. Experimental tests on retrofitted RC beam-column joints underdesigned to seismic loads. General approach. Eng. Struct. 2014, 59, 702–714. [Google Scholar] [CrossRef]
- Yurdakul, Ö.; Avşar, Ö. Strengthening of substandard reinforced concrete beam-column joints by external post-tension rods. Eng. Struct. 2016, 107, 9–22. [Google Scholar] [CrossRef]
- Ong, C.; Chin, C.; Ma, C.; Tan, J.; Awang, A.; Omar, W. Seismic retrofit of reinforced concrete beam-column joints using various confinement techniques: A review. Structures 2022, 42, 221–243. [Google Scholar] [CrossRef]
- Abdalla, J.A.; Mhanna, H.H.; Hawileh, R.A.; Sharafi, M.; Al-Marzouqi, A.; Al-Teneiji, S.; Al-Ali, K. Shear Strengthening of Reinforced Concrete T-Beams using Carbon Fiber Reinforced Polymer (CFRP) Anchored with CFRP Spikes. Procedia Struct. Integr. 2022, 42, 1223–1230. [Google Scholar] [CrossRef]
- Fang, H.; Bai, Y.; Liu, W.; Qi, Y.; Wang, J. Connections and structural applications of fibre reinforced polymer composites for civil infrastructure in aggressive environments. Compos. Part B Eng. 2019, 164, 129–143. [Google Scholar] [CrossRef]
- Jia, J.; Zandi, Y.; Rahimi, A.; Pourkhorshidi, S.; Khadimallah, M.A.; Ali, H.E. Numerical performance evaluation of debonding strength in fiber reinforced polymer composites using three hybrid intelligent models. Adv. Eng. Softw. 2022, 173, 103193. [Google Scholar] [CrossRef]
- Zhang, J.-g.; Yang, G.-c.; Ma, Z.-h.; Zhao, G.-l.; Song, H.-y. A stacking-CRRL fusion model for predicting the bearing capacity of a steel-reinforced concrete column constrained by carbon fiber-reinforced polymer. Structures 2023, 55, 1793–1804. [Google Scholar] [CrossRef]
- Vatani-Oskouei, A. Repairing of seismically damaged RC exterior beam—Column connection using CFRP. J. Reinf. Plast. Compos. 2010, 29, 3257–3274. [Google Scholar] [CrossRef]
- Eslami, A.; Ronagh, H.R. Experimental investigation of an appropriate anchorage system for flange-bonded carbon fiber–reinforced polymers in retrofitted RC beam–column joints. J. Compos. Constr. 2014, 18, 04013056. [Google Scholar] [CrossRef]
- Zgür Yurdakul, Ö.; Avşar, Ö. Structural repairing of damaged reinforced concrete beam-column assemblies with CFRPs. Struct. Eng. Mech. 2015, 54, 521–543. [Google Scholar] [CrossRef]
- Sasmal, S.; Novák, B.; Ramanjaneyulu, K.; Srinivas, V.; Roehm, C.; Lakshmanan, N.; Iyer, N.R. Seismic retrofitting of damaged exterior beam–column joints using fibre reinforced plastic composite–steel plate combined technique. Struct. Infrastruct. Eng. 2013, 9, 116–129. [Google Scholar] [CrossRef]
- Agarwal, P.; Gupta, A.; Angadi, R.G. Effect of FRP wrapping on axial behavior of concrete and cyclic behavior of external RC beam column joints. KSCE J. Civ. Eng. 2014, 18, 566–573. [Google Scholar] [CrossRef]
- Granata, P.J.; Parvin, A. An experimental study on Kevlar strengthening of beam–column connections. Compos. Struct. 2001, 53, 163–171. [Google Scholar] [CrossRef]
- Zhoudao, L.; Lei, S.; Jiangtao, Y. Experimental study on the seismic behaviour of strengthened concrete column-beam joints by simulated earthquake. Procedia Eng. 2011, 14, 1871–1878. [Google Scholar] [CrossRef]
- Allam, K.; Mosallam, A.S.; Salama, M.A. Experimental evaluation of seismic performance of interior RC beam-column joints strengthened with FRP composites. Eng. Struct. 2019, 196, 109308. [Google Scholar] [CrossRef]
- Mosallam, A. Strength and ductility of reinforced concrete moment frame connections strengthened with quasi-isotropic laminates. Compos. Part B Eng. 2000, 31, 481–497. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Y.; Li, J. Study of seismic behavior of RC beam-column joints strengthened by sprayed FRP. Adv. Mater. Sci. Eng. 2018, 2018, 3581458. [Google Scholar] [CrossRef]
- Mukherjee, A.; Joshi, M. FRPC reinforced concrete beam-column joints under cyclic excitation. Compos. Struct. 2005, 70, 185–199. [Google Scholar] [CrossRef]
- Alshamrani, S.; Rasheed, H.A.; Salahat, F.H.; Borwankar, A.; Divilbiss, N. Seismic flexural behavior of CFRP strengthened reinforced concrete beams secured with fiber anchors. Eng. Struct. 2024, 305, 117728. [Google Scholar] [CrossRef]
- Smith, S.T.; Rasheed, H.A.; Kim, S.J. Full-range load-deflection response of FRP-strengthened RC flexural members anchored with FRP anchors. Compos. Struct. 2017, 167, 207–218. [Google Scholar] [CrossRef]
- Rasheed, H.A.; Pervaiz, S. Bond slip analysis of fiber-reinforced polymer-strengthened beams. J. Eng. Mech. 2002, 128, 78–86. [Google Scholar] [CrossRef]
- Gao, W.; Teng, J.; Dai, J.-G. Effect of temperature variation on the full-range behavior of FRP-to-concrete bonded joints. J. Compos. Constr. 2012, 16, 671–683. [Google Scholar] [CrossRef]
- Khodadadi, N.; Roghani, H.; Harati, E.; Mirdarsoltany, M.; De Caso, F.; Nanni, A. Fiber-reinforced polymer (FRP) in concrete: A comprehensive survey. Constr. Build. Mater. 2024, 432, 136634. [Google Scholar] [CrossRef]
- Azuwa, S.B.; Yahaya, F.B.M. Experimental investigation and finite element analysis of reinforced concrete beams strengthened by fibre reinforced polymer composite materials: A review. Alex. Eng. J. 2024, 99, 137–167. [Google Scholar] [CrossRef]
- Laseima, S.Y.; Mutalib, A.; Osman, S.; Hamid, N. Seismic behavior of exterior rc beam-column joints retrofitted using CFRP sheets. Lat. Am. J. Solids Struct. 2020, 17, e263. [Google Scholar] [CrossRef]
- Saqan, E.I.; Rasheed, H.A.; Alkhrdaji, T. Seismic Behavior of Carbon Fiber-Reinforced Polymer-Strengthened Reinforced Concrete Members with Various Anchors. ACI Struct. J. 2020, 117, 3–14. [Google Scholar]
- Karayannis, C.G.; Golias, E. Full-scale experimental testing of RC beam-column joints strengthened using CFRP ropes as external reinforcement. Eng. Struct. 2022, 250, 113305. [Google Scholar] [CrossRef]
- Lim, C.; Jeong, Y.; Kim, J.; Kwon, M. Experimental study of reinforced concrete beam-column joint retrofitted by CFRP grid with ECC and high strength mortar. Constr. Build. Mater. 2022, 340, 127694. [Google Scholar] [CrossRef]
- Attari, N.; Youcef, Y.S.; Amziane, S. Seismic performance of reinforced concrete beam–column joint strengthening by frp sheets. Structures 2019, 20, 353–364. [Google Scholar] [CrossRef]
- Golias, E.; Zapris, A.G.; Kytinou, V.K.; Osman, M.; Koumtzis, M.; Siapera, D.; Chalioris, C.E.; Karayannis, C.G. Application of X-shaped CFRP ropes for structural upgrading of reinforced concrete beam–column joints under cyclic loading–experimental study. Fibers 2021, 9, 42. [Google Scholar] [CrossRef]
- Mady, M.H.A. Seismic Behaviour of Exterior Beam-Column Joints Reinforced with Frp Bars and Stirrups; University of Manitoba (Canada): Winnipeg, MB, Canada, 2011. [Google Scholar]
- Bsisu, K.; Hiari, B.O. Finite element analysis of retrofitting techniques for reinforced concrete beam-column joint. J. Am. Sci. 2015, 11, 48–56. [Google Scholar]
- Ercan, E.; Arisoy, B.; Ertem, O.B. Experimental assessment of RC beam-column connections with internal and external strengthening techniques. Adv. Civ. Eng. 2019, 2019, 2828353. [Google Scholar] [CrossRef]
- Le-Trung, K.; Lee, K.; Lee, J.; Lee, D.H.; Woo, S. Experimental study of RC beam–column joints strengthened using CFRP composites. Compos. Part B Eng. 2010, 41, 76–85. [Google Scholar] [CrossRef]
- ACI Committee. Building Code Requirements For Structural Concrete (ACI 318-02) and Commentary (ACI 318R-02). Available online: https://agussugiantocom.files.wordpress.com/2016/07/aci318-02-building-code-for-structural-concrete.pdf (accessed on 10 May 2024).
- Tao, Y.; Chen, J.-F. Concrete damage plasticity model for modeling FRP-to-concrete bond behavior. J. Compos. Constr. 2015, 19, 04014026. [Google Scholar] [CrossRef]
- Chen, G.; Chen, J.; Teng, J. On the finite element modelling of RC beams shear-strengthened with FRP. Constr. Build. Mater. 2012, 32, 13–26. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Neuberger, Y.M.; Andrade, M.V.; de Sousa, A.M.D.; Bandieira, M.; da Silva Júnior, E.P.; dos Santos, H.F.; Catoia, B.; Bolandim, E.A.; de Moura Aquino, V.B.; Christoforo, A.L. Numerical Analysis of Reinforced Concrete Corbels Using Concrete Damage Plasticity: Sensitivity to Material Parameters and Comparison with Analytical Models. Buildings 2023, 13, 2781. [Google Scholar] [CrossRef]
- Narayanan, R.; James, R. Microwave nondestructive testing of galvanic corrosion and impact damage in carbon fiber reinforced polymer composites. Int. J. Microw. Appl 2018, 7, 1. [Google Scholar] [CrossRef]
- GangaRao, H.V.; Vijay, P. Bending behavior of concrete beams wrapped with carbon fabric. J. Struct. Eng. 1998, 124, 3–10. [Google Scholar] [CrossRef]
- Torabi, A.; Maheri, M.R. Seismic repair and retrofit of RC beam–column joints using stiffened steel plates. Iran. J. Sci. Technol. Trans. Civ. Eng. 2017, 41, 13–26. [Google Scholar] [CrossRef]
- Peng, Z.; Dai, S.-B.; Pi, Y.-L.; Zhang, Y.-C.; Huang, J. Seismic performance of end-plate connections between T-shaped CFST columns and RC beams. J. Constr. Steel Res. 2018, 145, 167–183. [Google Scholar] [CrossRef]










| Properties of Used Materials | |||
|---|---|---|---|
| Concrete | Compressive strength, MPa | Water curing | 33.8 |
| Air curing | 36.5 | ||
| Tensile strength, MPa | Water curing | 4.0 | |
| Air curing | 3.8 | ||
| Steel bars | Yield strength, MPa | D10 | 324 |
| Ø4 | 459 | ||
| CFRP (CF720) | Tensile strength 0°, MPa | 4965.8 | |
| Elastic modulus, GP | 240.5 | ||
| Elastic modulus 90°, GPa | 10 | ||
| In-plane shear modulus, GPa | 5 | ||
| Tensile strength 90°, MPa | 50 | ||
| Compressive strength 0°, MPa | 1200 | ||
| Compressive strength 90°, MPa | 250 | ||
| In-plane shear strength, MPa | 70 | ||
| Sheet thickness, mm | 0.33 | ||
| Major Poisson’s ratio | 0.3 | ||
| Density, g/cm3 | 1.6 | ||
| Epoxy topcoat (CLR67) | Tensile strength, MPa | 59.5 | |
| Elastic modulus, GP | 3.7 | ||
| Epoxy primer (CLR67) | Tensile strength, MPa | 56.8 | |
| Elastic modulus, GP | 3.7 | ||
| Model Number | Materials | Material Properties | ||
|---|---|---|---|---|
| 1 | Deformed steel bar (10 mm) | Linear isotropic | Young’s modulus, MPa | 200,000 |
| Poisson’s ratio | 0.3 | |||
| Bilinear kinematic | Strain–stress, MPa | 0—0 | ||
| 0.00162—324 | ||||
| 0.12—420 | ||||
| 2 | Deformed steel bar (4 mm) | Linear isotropic | Young’s modulus, MPa | 200000 |
| Poisson’s ratio | 0.3 | |||
| Bilinear kinematic | Strain–stress, MPa | 0—0 | ||
| 0.0022—459 | ||||
| 0.008—620 | ||||
| Specimen | Loading Direction | Yield Lateral Resistance (kN) | Ultimate Lateral Resistance (kN) | ||||
|---|---|---|---|---|---|---|---|
| Non-seismic (NS) | Positive | 5.40 | 5.925 | 1.09 | 7.3 | 7.9 | 1.08 |
| Negative | 11.70 | 12.9 | 1.10 | 15.76 | 17.2 | 1.09 | |
| Seismic design (SD) | Positive | 7.30 | 7.82 | 1.07 | 9.7 | 10.75 | 1.10 |
| Negative | 13.15 | 13.85 | 1.05 | 16.15 | 18.23 | 1.13 | |
| Strengthened by CFRP (one layer) | Positive | 6.75 | 7.42 | 1.09 | 9.10 | 10.15 | 1.12 |
| Negative | 12.95 | 14.25 | 1.10 | 17.23 | 19.07 | 1.11 | |
| Strengthened by CFRP (two layers) | Positive | 7.95 | 8.4 | 1.05 | 10.6 | 11.20 | 1.06 |
| Negative | 13.80 | 14.35 | 1.04 | 16.80 | 17.80 | 1.06 | |
| Specimen | Drift Ratio (%) | Parallelograms Area | Area of Hysteretic Loop | Relative Energy Dissipation Ratio β | Check to Meet the Criteria ≥ 0.125 |
|---|---|---|---|---|---|
| NS | 3.5 | 91.75 | 18.30 | 0.20 | Ok |
| SD | 3.5 | 130.33 | 41.20 | 0.32 | Ok |
| 1-layer CFRPC-integrated | 3.5 | 124.64 | 43.87 | 0.35 | Ok |
| 2-layer CFRPC-integrated | 3.5 | 144.08 | 72.60 | 0.5 | Ok |
| Specimen | λ | (kN) | (kN) | (kN) | Remarks |
|---|---|---|---|---|---|
| NS | 1.31 | 8.4 | 11.00 | 8.65 | Ok |
| SD | 1.31 | 8.4 | 11.00 | 10.42 | Ok |
| 1-layer CFRPC-integrated | 1.31 | 12.65 | 16.57 | 9.87 | Ok |
| 2-layer CFRPC-integrated | 1.31 | 16.02 | 20.98 | 11.27 | Ok |
| Specimen | Direction | Ultimate Lateral Force in kN | 3.5% (Drift Ratio) | |
|---|---|---|---|---|
| Force in kN | Ratio of the Strength > 0.75 | |||
| NS | Positive | 8.56 | 6.30 | 0.73 * |
| Negative | 16.77 | 15.50 | 0.92 | |
| SD | Positive | 10.42 | 10.01 | 0.96 |
| Negative | 16.20 | 15.67 | 0.96 | |
| 1-layer CFRPC-integrated | Positive | 9.87 | 9.58 | 0.97 |
| Negative | 18.23 | 18.00 | 0.98 | |
| 2-layer CFRPC-integrated | Positive | 11.27 | 10.50 | 0.93 |
| Negative | 17.86 | 17.98 | 0.99 | |
| Specimen | Direction | Drift Ratio | δ (mm) | F (kN) | Secant Stiffness (kN/mm) | Initial Stiffness (kN/mm) | Ratio between Secant Stiffness and Initial Stiffness | Check to Meet the Criteria ≥ 0.05 |
|---|---|---|---|---|---|---|---|---|
| NS | Positive | 3.5 | 33.88 | 6.30 | 0.18 | 0.66 | 0.27 | Ok |
| Negative | 33.88 | 15.50 | 0.45 | 0.76 | 0.59 | Ok | ||
| SD | Positive | 3.5 | 33.88 | 10.01 | 0.29 | 1.53 | 0.19 | Ok |
| Negative | 33.88 | 15.67 | 0.46 | 1.83 | 0.25 | Ok | ||
| 1-layer CFRPC-integrated | Positive | 3.5 | 33.88 | 9.58 | 0.28 | 1.82 | 0.15 | Ok |
| Negative | 33.88 | 18.00 | 0.53 | 1.84 | 0.28 | Ok | ||
| 2-layer CFRPC-integrated | Positive | 3.5 | 33.88 | 10.50 | 0.31 | 1.70 | 0.18 | Ok |
| Negative | 33.88 | 17.80 | 0.53 | 1.71 | 0.31 | Ok |
| Specimen | Direction | (kN) | (mm) | (KN/m) | (KN/m) | (mm) | (mm) | µ | Average µ |
|---|---|---|---|---|---|---|---|---|---|
| NS | Positive | 5.47 | 8.77 | 623 | 745.5 | 11.70 | 45.72 | 3.9 | 3.10 |
| Negative | 11.75 | 13.5 | 870 | 19.70 | 44.79 | 2.3 | |||
| SD | Positive | 7.30 | 7.12 | 1025 | 973.5 | 9.50 | 45.90 | 4.83 | 3.63 |
| Negative | 13.15 | 14.25 | 922 | 19.10 | 46.55 | 2.43 | |||
| 1-layer CFRPC-integrated | Positive | 6.75 | 6.375 | 1059 | 1262 | 8.50 | 56.03 | 6.59 | 5.95 |
| Negative | 12.95 | 8.80 | 1465 | 11.00 | 58.59 | 5.32 | |||
| 2-layer CFRPC-integrated | Positive | 7.95 | 6.97 | 1140 | 1301 | 9.30 | 58.50 | 6.29 | 6.16 |
| Negative | 13.80 | 9.30 | 1462 | 9.52 | 57.53 | 6.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljabbri, N.A.S.; Karim, A.A.; Majeed, F.H. Carbon Fiber-Reinforced Polymer Composites Integrated Beam–Column Joints with Improved Strength Performance against Seismic Events: Numerical Model Simulation. Eng 2024, 5, 1112-1139. https://doi.org/10.3390/eng5020061
Aljabbri NAS, Karim AA, Majeed FH. Carbon Fiber-Reinforced Polymer Composites Integrated Beam–Column Joints with Improved Strength Performance against Seismic Events: Numerical Model Simulation. Eng. 2024; 5(2):1112-1139. https://doi.org/10.3390/eng5020061
Chicago/Turabian StyleAljabbri, Noor Alhuda Sami, Abdulamir Atalla Karim, and Fareed Hameed Majeed. 2024. "Carbon Fiber-Reinforced Polymer Composites Integrated Beam–Column Joints with Improved Strength Performance against Seismic Events: Numerical Model Simulation" Eng 5, no. 2: 1112-1139. https://doi.org/10.3390/eng5020061
APA StyleAljabbri, N. A. S., Karim, A. A., & Majeed, F. H. (2024). Carbon Fiber-Reinforced Polymer Composites Integrated Beam–Column Joints with Improved Strength Performance against Seismic Events: Numerical Model Simulation. Eng, 5(2), 1112-1139. https://doi.org/10.3390/eng5020061






