Comparative Study on Housing Defect Repair Cost through Linear Regression Model
Abstract
1. Introduction
2. Literature Study
2.1. Housing Defects and Repair Cost
2.2. Prediction of Repair Cost
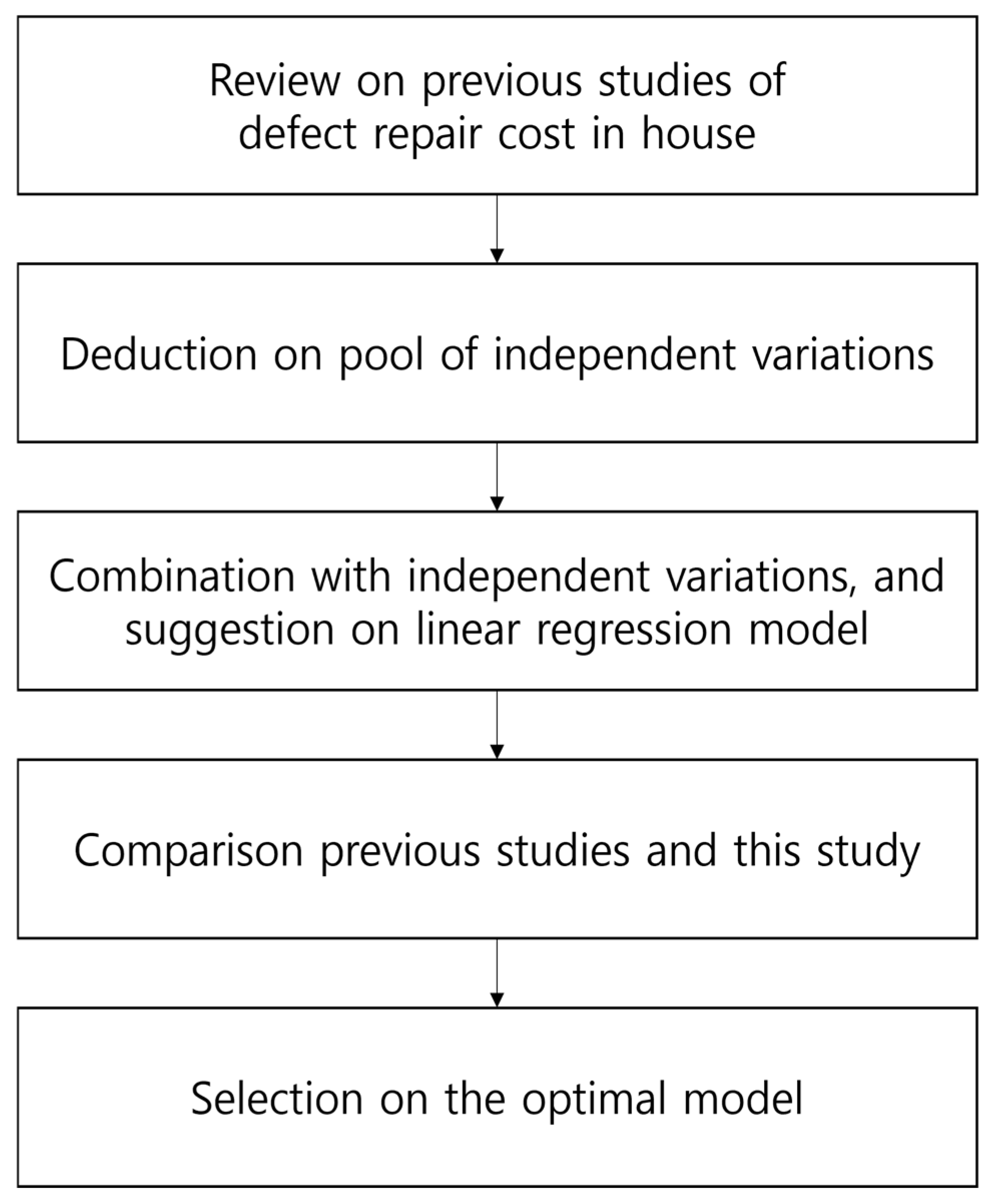
3. Materials and Methods
3.1. Scope
3.2. Data Collection
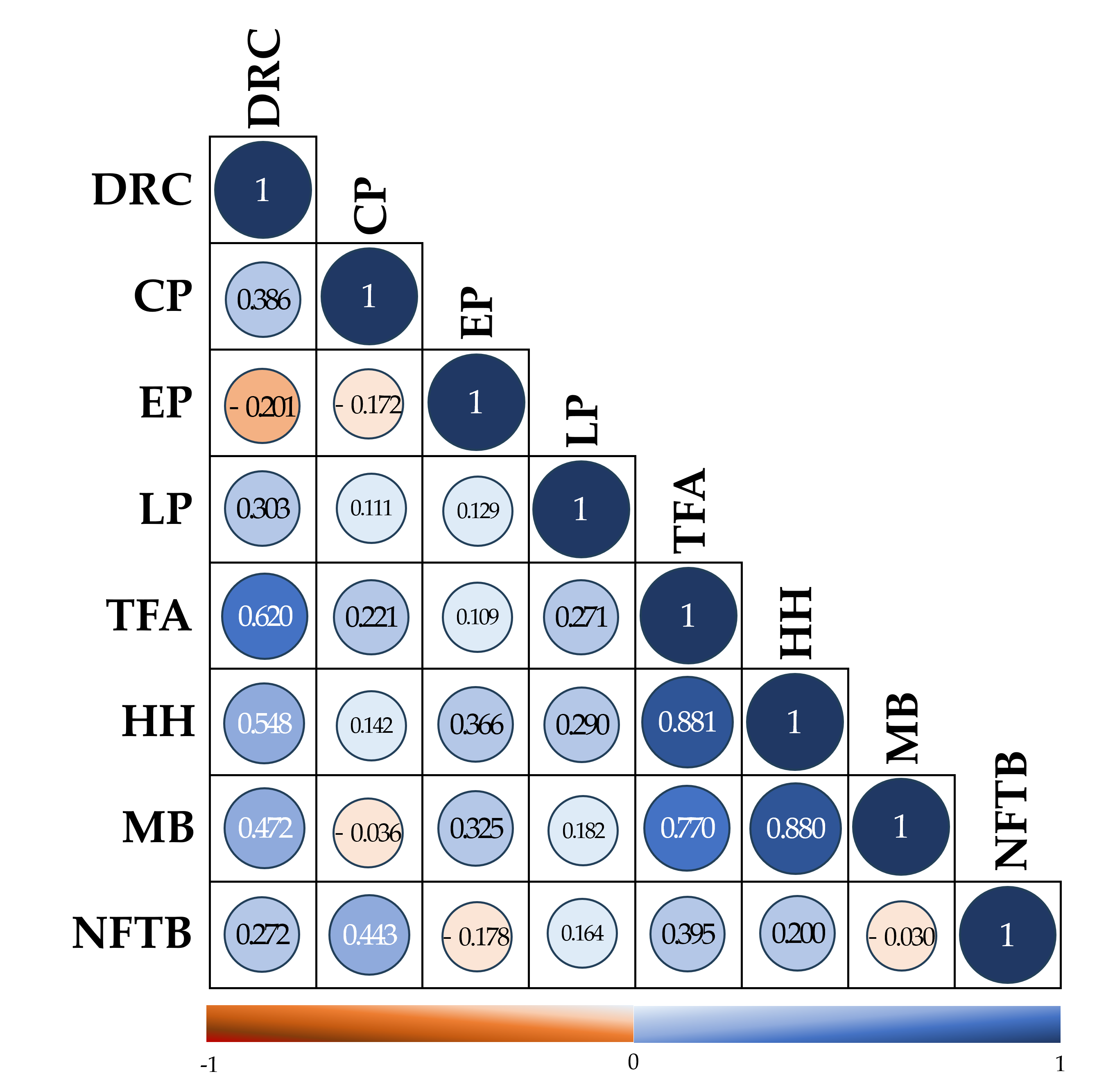
3.3. Linear Regression Analysis
4. Results
4.1. Outline
4.2. Comparison
4.3. Suggested Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gurmu, A.; Krezel, A.; Ongkowijoyo, C. Fuzzy Stochastic Model to Assess Defects in Low-rise Residential Buildings. J. Build. Eng. 2021, 40, 102318. [Google Scholar] [CrossRef]
- Tazelaar, F.; Snijders, C. Dispute Resolution and Litigation in the Construction Industry. Evidence on conflicts and conflict resolution in the Netherlands and Germany. J. Purch. Supply Manag. 2010, 16, 221–229. [Google Scholar] [CrossRef]
- Taggart, M.; Koskela, L.; Rooke, J. The Role of the Supply Chain in the Elimination and Reduction of Construction Rework and Defects: An Action Research Approach. Constr. Manag. Econ. 2014, 32, 829–842. [Google Scholar] [CrossRef]
- Lall, P.; Sakalaukus, P.; Davis, L. Reliability and Failure Modes of Solid-State Lighting Electrical Drivers Subjected to Accelerated Aging. IEEE Access 2015, 3, 531–542. [Google Scholar] [CrossRef]
- Kang, K.; Seo, D. An Analysis Study on the Initial Defects Raised in Apartment House of Korea. J. Archit. Inst. Korea Struct. Constr. 1998, 14, 137–145. [Google Scholar]
- Georgiou, J.; Smith, J.; Love, P. A Benchmark Study on Housing Defects in Victoria, Australia. Int. J. Constr. Manag. 2004, 4, 89–100. [Google Scholar] [CrossRef]
- Love, P.; Teo, P.; Morrison, J. Revisiting Quality Failure Costs in Construction. J. Constr. Eng. Manag. 2017, 144, 05017020. [Google Scholar] [CrossRef]
- Josephson, P.; Larsson, B.; Li, H. Illustrative Benchmarking Rework and Rework Costs in Swedish Construction Industry. J. Constr. Eng. Manag. 2002, 18, 76–83. [Google Scholar] [CrossRef]
- Abdul-Rahman, H.; Thompson, P.; Whyte, I. Capturing the Cost of non-Conformance on Construction Sites: An Ap-plication of the Quality Cost Matrix. Int. J. Qual. Reliab. Manag. 1996, 13, 48–60. [Google Scholar] [CrossRef]
- Plebankiewicz, E.; Malara, J. Analysis of Defects in Residential Buildings reported During the Warranty Period. Appl. Sci. 2020, 10, 6123. [Google Scholar] [CrossRef]
- Balouchi, M.; Gholhaki, M. Reworks Causes and related Costs in Construction: Case of Parand Mass Housing Project in Iran. Int. J. Qual. Reliab. Manag. 2019, 36, 1392–1408. [Google Scholar] [CrossRef]
- Liu, Q.; Ye, G.; Feng, Y.; Wang, C.; Peng, Y. Case-based Insights into Rework Costs of Residential Building Projects in China. Int. J. Constr. Manag. 2018, 20, 347–355. [Google Scholar] [CrossRef]
- Kang, Y.; Kim, B.; Park, J.; Seo, J.; Kim, O. Regression Analysis on the Dispute Cost Property in Apartment Housing Claims. In Proceedings of the 2010 Spring Conference of Korean Institute of Building Construction, Seoul, Republic of Korea, 14 May 2010; pp. 225–228. [Google Scholar]
- Josephson, P.; Hammarlund, Y. The Causes and Costs of Defects in Construction. A Study of Seven Building Projects. Autom. Constr. 1999, 8, 681–687. [Google Scholar] [CrossRef]
- Rotimi, F.; Tookey, J.; Rotimi, J. Evaluating Defect Reporting in New Residential Buildings in New Zealand. Buildings 2015, 5, 39–55. [Google Scholar] [CrossRef]
- Seo, J. Model for Predicting the Occurrence of Defects in High-Rise Residential Building. Ph.D. Dissertation, Korea University, Seoul, Republic of Korea, 2009. Available online: https://dcollection.korea.ac.kr/public_resource/pdf/000000008907_20240722132316.pdf (accessed on 2 September 2024).
- Park, J.; Seo, D. Defect Index of Timberwork in House, Korea. Forests 2021, 12, 896. [Google Scholar] [CrossRef]
- Mills, A.; Love, P.; Williams, P. Defect Costs in Residential Construction. J. Constr. Eng. Manag. 2009, 135, 12–16. [Google Scholar] [CrossRef]
- Park, J.; Seo, D. Defect Repair Cost and Home Warranty Deposit, Korea. Buildings 2022, 12, 1027. [Google Scholar] [CrossRef]
- Seo, D.; Lee, U. Characteristic Analysis of Utilization of Security Deposit for Repairing Defects Using Statistical Analysis. J. Korea Inst. Build. Constr. 2015, 15, 209–215. [Google Scholar] [CrossRef][Green Version]
- Choi, J. Evaluation of Defect Repairing Bond Ratio through Defect Lawsuit Case Study in Apartment Building. Ph.D. Dissertation, Chungbuk National University, Cheongju, Republic of Korea, 2017. Available online: https://chungbuk.dcollection.net/public_resource/pdf/200000766489_20240722132236.pdf (accessed on 2 September 2024).
- Forcada, N.; Gangolells, M.; Casals, M.; Macarulla, M. Factors Affecting Rework Costs in Construction. J. Constr. Eng. Manag. 2017, 143, 04017032. [Google Scholar] [CrossRef]
- Kim, Y. Regression Models for Defect Repair Cost Predictions Year and Wet Construction of Apartment House. Master’s Thesis, University of Seoul, Seoul, Republic of Korea, 2019. Available online: https://dcollection.uos.ac.kr/public_resource/pdf/000000031146_20240722132138.pdf (accessed on 2 September 2024).
- Kovačević, M.; Hadzima-Nyarko, M.; Grubeša, I.N.; Radu, D.; Lozančić, S. Application of Artificial Intelligence Methods for Predicting the Compressive Strength of Green Concretes with Rice Husk Ash. Mathematics 2024, 12, 66. [Google Scholar] [CrossRef]
- HomeOwners Alliance. Homeowner Survey 2019: Top UK Housing Concerns Revealed. Available online: https://hoa.org.uk/2019/08/homeowner-survey-2019 (accessed on 30 June 2024).
- Konno, Y. An Empirical Analysis of the Exit of SMEs Rendering for Public Works in the Japanese Construction Industry. J. Financ. Manag. Prop. Constr. 2014, 19, 101–116. [Google Scholar] [CrossRef]
- Choi, J.; Park, J.; Seo, D.; Jo, J.; Park, K.; Kim, O. A Study on Legal Issues about Defect Repair Claim on Apartment Building. J. Archit. Inst. Korea 2009, 25, 145–153. [Google Scholar]
- Apartment Defect Dispute Mediation Committee. Defect Management Information System. Available online: https://www.adc.go.kr (accessed on 30 June 2024).
- Seo, D.; Park, J. Analysis of Consulting Reports on Defect Disputes in Apartment Building. J. Korea Inst. Build. Constr. 2013, 13, 498–505. [Google Scholar] [CrossRef]
- Korean Ministry of Land, Infrastructure and Transport. Seumter. Architectural Administrative System. Available online: https://cloud.eais.go.kr (accessed on 30 June 2024).
- Bank of Korea. Korea Government Bond(3Y). Available online: https://ecos.bok.or.kr (accessed on 30 June 2024).
- Bank of Korea. Won per United States Dollar(Open). Available online: https://ecos.bok.or.kr (accessed on 30 June 2024).
- Kovačević, M.; Antoniou, F. Machine-Learning-Based Consumption Estimation of Prestressed Steel for Prestressed Concrete Bridge Construction. Buildings 2023, 13, 1187. [Google Scholar] [CrossRef]
| Researcher | Independent Variable | R2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EP | LP | VL | HWD | TFA | HH | MB | CC | Lo | NFTB | ||
| Kang et al. [13] | ● | ● | ● | ● | 0.700 | ||||||
| Seo and Lee [20] | ● | ● | ● | 0.691 | |||||||
| Choi [21] | ● | ● | ● | 0.719 | |||||||
| Focarda et al. [22] | ● | ● | 0.561 | ||||||||
| Kim [23] | ● | ● | ● | ● | 0.865 | ||||||
| Acronym | Variable | Definition | Unit | Variable Type |
|---|---|---|---|---|
| DRC | Defect repair cost | Defect repair cost to the housing complex | USD | Continuous variable |
| CP | Construction period | The period from construction start to completion | Month | Continuous variable |
| EP | Elapsed period | The period from building completion to initiation of a lawsuit | Month | Continuous variable |
| LP | Lawsuit period | The period from initiating a lawsuit to the end of the lawsuit | Month | Continuous variable |
| TFA | Total floor area | Sum of floor area to public space and private space | Thousand m2 | Continuous variable |
| HH | Households | Households living in a housing complex | Household | Continuous variable |
| MB | Main buildings’ quantity | Main building’s quantity in a housing complex | Building | Continuous variable |
| NFTB | Number of floors in the tallest building | Number of floors in the tallest building in a housing complex | Floor | Continuous variable |
| Lo1 | Distance from the developer’s headquarters to the housing complex | Distance from the developer’s headquarters to the housing complex, whether in the same municipality, in the same metropolitan region, or between other metropolitan regions | Nominal variable | |
| Lo1-1 | Dummy 1 of Lo1 | Same local municipality or not | Nominal variable | |
| Lo1-2 | Dummy 2 of Lo1 | Same metropolitan region or not | Nominal variable | |
| Lo1-3 | Dummy 3 of Lo1 | Between other metropolitan regions or not | Nominal variable | |
| Lo2 | Location from builder’s headquarters to housing complex | Location of builder’s headquarters and housing complex, whether in the same basic local municipality, in the same metropolitan region, or between other metropolitan regions | Nominal variable | |
| Lo2-1 | Dummy 1 of Lo2 | Same basic local municipality or not | Nominal variable | |
| Lo2-2 | Dummy 2 of Lo2 | Same metropolitan region or not | Nominal variable | |
| Lo2-3 | Dummy 3 of Lo2 | Between other metropolitan regions or not | Nominal variable | |
| Lo3 | Location of the housing complex | Capital area or non-capital area | Nominal variable | |
| Lo3-1 | Dummy 1 of Lo3 | Capital area or not | Nominal variable | |
| Lo3-2 | Dummy 2 of Lo3 | Non-capital area or not | Nominal variable |
| Variable (Unit) | Minimum | Mean | Maximum | Standard Deviation | Variance |
|---|---|---|---|---|---|
| DRC (USD) | 84,455 | 886,415 | 4,271,102 | 752,318.93 | 5.660 × 1011 |
| CP (Month) | 19.63 | 32.0930 | 100.33 | 10.84 | 117.51 |
| EP (Month) | 14.67 | 157.13 | 73.18 | 34.41 | 1184.00 |
| LP (Month) | 10.43 | 23.85 | 55.83 | 7.20 | 51.88 |
| TFA (Thousand m2) | 11.53 | 100.10 | 297.84 | 59.37 | 3,524,566.98 |
| HH (Households) | 96 | 814.31 | 3129 | 473.50 | 224,206.64 |
| MB (Buildings) | 1 | 9.91 | 39 | 5.69 | 32.35 |
| NFTB (Floors) | 12 | 19.80 | 40 | 5.51 | 30.38 |
| Model | R2 | Adjusted R2 | Durbin–Watson | Independent Variable | Standardized Coefficient (Beta) | t | p-Value | Multicollinearity Statistics | |
|---|---|---|---|---|---|---|---|---|---|
| Tolerance | VIF | ||||||||
| Kang et al. [13] | 0.150 | 0.133 | 2.162 | EP | −0.244 | −2.583 | 0.011 | 0.983 | 1.017 |
| LP | 0.334 | 3.540 | 0.001 | 0.983 | 1.017 | ||||
| Seo and Lee [20] | 0.385 | 0.365 | 1.993 | TFA | 0.611 | 3.608 | 0.000 | 0.223 | 4.481 |
| HH | 0.038 | 0.166 | 0.869 | 0.124 | 8.047 | ||||
| MB | −0.191 | −0.191 | 0.849 | 0.226 | 4.418 | ||||
| Choi [21] | 0.384 | 0.372 | 1.996 | HH | 0.009 | 0.052 | 0.958 | 0.223 | 4.479 |
| TFA | 0.612 | 3.631 | 0.000 | 0.223 | 4.479 | ||||
| Forcada et al. [22] | 0.021 | −0.020 | 1.867 | Lo 1-1 | −0.085 | −0.788 | 0.433 | 0.884 | 1.131 |
| Lo 1-2 | −0.023 | −0.197 | 0.844 | 0.765 | 1.307 | ||||
| Lo 2-1 | 0.084 | 0.825 | 0.411 | 0.993 | 1.007 | ||||
| Lo 2-2 | 0.110 | 0.959 | 0.340 | 0.790 | 1.266 | ||||
| Kim [23] | 0.387 | 0.361 | 1.978 | TFA | 0.588 | 3.205 | 0.003 | 0.171 | 5.857 |
| HH | 0.027 | 0.147 | 0.884 | 0.196 | 5.100 | ||||
| Lo 3 | −0.044 | −0.535 | 0.594 | 0.975 | 1.025 | ||||
| NFTB | 0.037 | 0.396 | 0.693 | 0.745 | 1.342 | ||||
| This Study 1 | 0.523 | 0.503 | 2.285 | TFA | 0.559 | 7.385 | 0.000 | 0.877 | 1.140 |
| CP | 0.202 | 2.718 | 0.008 | 0.907 | 1.103 | ||||
| EP | −0.248 | −3.380 | 0.001 | 0.934 | 1.070 | ||||
| LP | 0.161 | 2.168 | 0.033 | 0.911 | 1.097 | ||||
| Model | Unstandardized Coefficients | Standardized Coefficients (Beta) | t | Sig. | ||
|---|---|---|---|---|---|---|
| B | Std. Error | |||||
| 1 | (Constant) | −277,561.179 | 260,242.528 | −1.067 | 0.289 | |
| TFA | 7.081 | 0.959 | 0.559 | 7.385 | 0.000 | |
| CP | 14,037.694 | 5164.691 | 0.202 | 2.718 | 0.008 | |
| EP | −5417.073 | 1602.755 | −0.248 | −3.380 | 0.001 | |
| LP | 16,809.405 | 7752.889 | 0.161 | 2.168 | 0.033 | |
| Model | R2 | Adjusted R2 | Durbin–Watson | Independent Variable | Standardized Coefficient (Beta) | t | p-Value | Multicollinearity Statistics | |
|---|---|---|---|---|---|---|---|---|---|
| Tolerance | VIF | ||||||||
| This Study 1 | 0.523 | 0.503 | 2.285 | TFA | 0.559 | 7.385 | 0.000 | 0.877 | 1.140 |
| CP | 0.202 | 2.718 | 0.008 | 0.907 | 1.103 | ||||
| EP | −0.248 | −3.380 | 0.001 | 0.934 | 1.070 | ||||
| LP | 0.161 | 2.168 | 0.033 | 0.911 | 1.097 | ||||
| This Study 2 | 0.523 | 0.508 | 2.287 | HH × CP | 0.822 | 9.522 | 0.000 | 0.667 | 1.500 |
| CP × LP | −0.467 | −5.467 | 0.000 | 0.682 | 1.467 | ||||
| LP × LP | 0.169 | 2.349 | 0.021 | 0.965 | 1.036 | ||||
| Model | Unstandardized Coefficients | Standardized Coefficients (Beta) | t | Sig. | ||
|---|---|---|---|---|---|---|
| B | Std. Error | |||||
| 1 | (Constant) | 606,179.675 | 136,035.969 | 4.456 | 0.000 | |
| HH × CP | 30.554 | 3.209 | 0.822 | 9.522 | 0.000 | |
| CP × LP | −314.700 | 57.560 | −0.467 | −5.467 | 0.000 | |
| LP × LP | 288.129 | 122.684 | 0.169 | 2.349 | 0.021 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Seo, D. Comparative Study on Housing Defect Repair Cost through Linear Regression Model. Eng 2024, 5, 2328-2344. https://doi.org/10.3390/eng5030121
Park J, Seo D. Comparative Study on Housing Defect Repair Cost through Linear Regression Model. Eng. 2024; 5(3):2328-2344. https://doi.org/10.3390/eng5030121
Chicago/Turabian StylePark, Junmo, and Deokseok Seo. 2024. "Comparative Study on Housing Defect Repair Cost through Linear Regression Model" Eng 5, no. 3: 2328-2344. https://doi.org/10.3390/eng5030121
APA StylePark, J., & Seo, D. (2024). Comparative Study on Housing Defect Repair Cost through Linear Regression Model. Eng, 5(3), 2328-2344. https://doi.org/10.3390/eng5030121






