Modeling and Control of a Permanent Magnet DC Motor: A Case Study for a Bidirectional Conveyor Belt’s Application
Abstract
1. Introduction
- A feedforward control scheme based on a low-order and causal filter is developed using frequency domain analysis, which is considered to reject external perturbations without using direct cancellation to compensate them;
- A state observer is proposed to estimate mechanical variables, such as angular velocity and torque load, and is used to develop a sensorless velocity regulator using only measurements of the DC motor’s armature current.
2. Related Works
3. Materials and Methods
3.1. Modeling Process
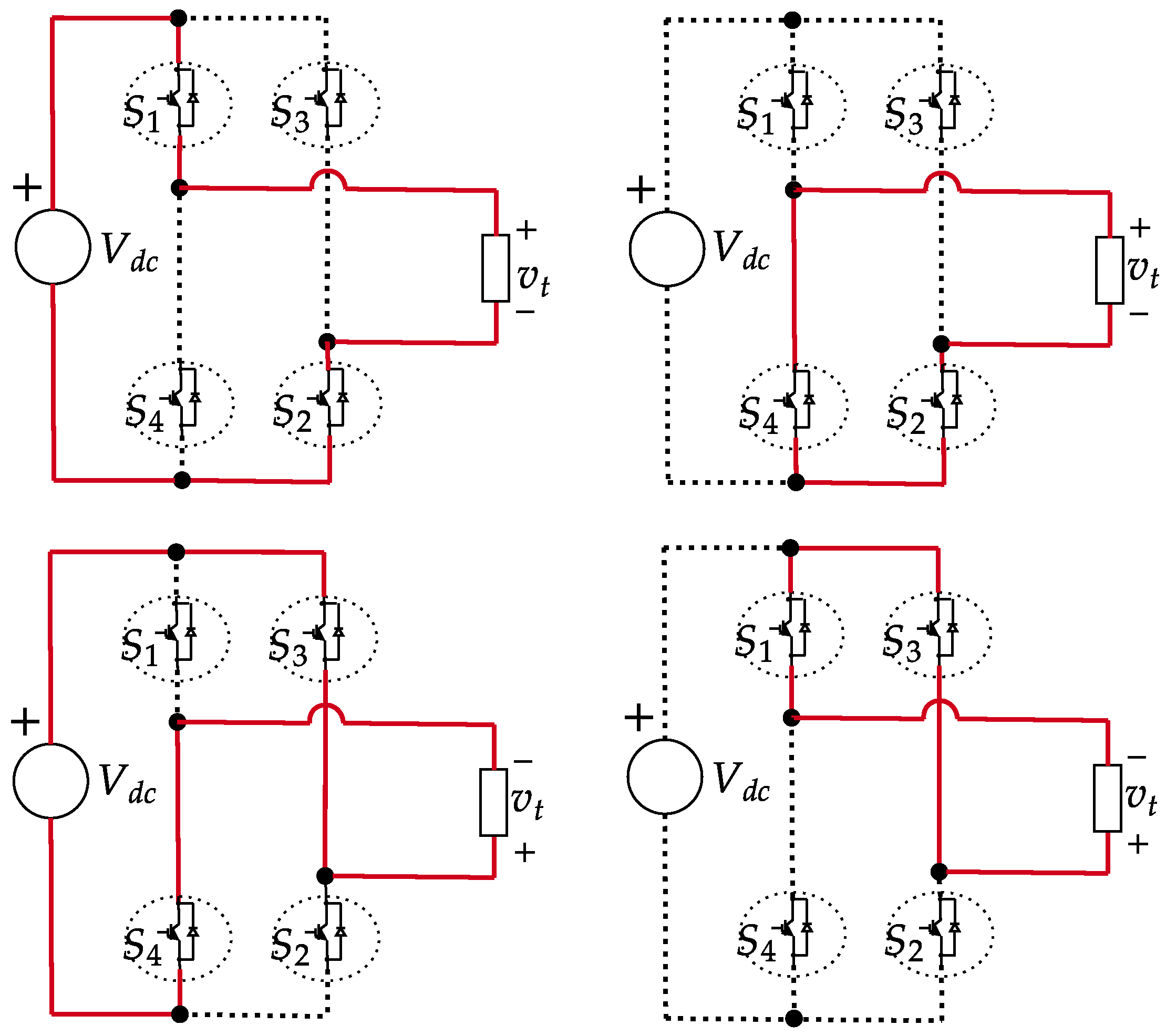
3.1.1. Model of the Power Converter
- The semiconductor devices are considered as short circuits when they are in the on-state;
- The semiconductor devices are considered as open circuits when they are in the off-state;
- The dynamics associated with the switching transitions of the semiconductor devices are neglected.
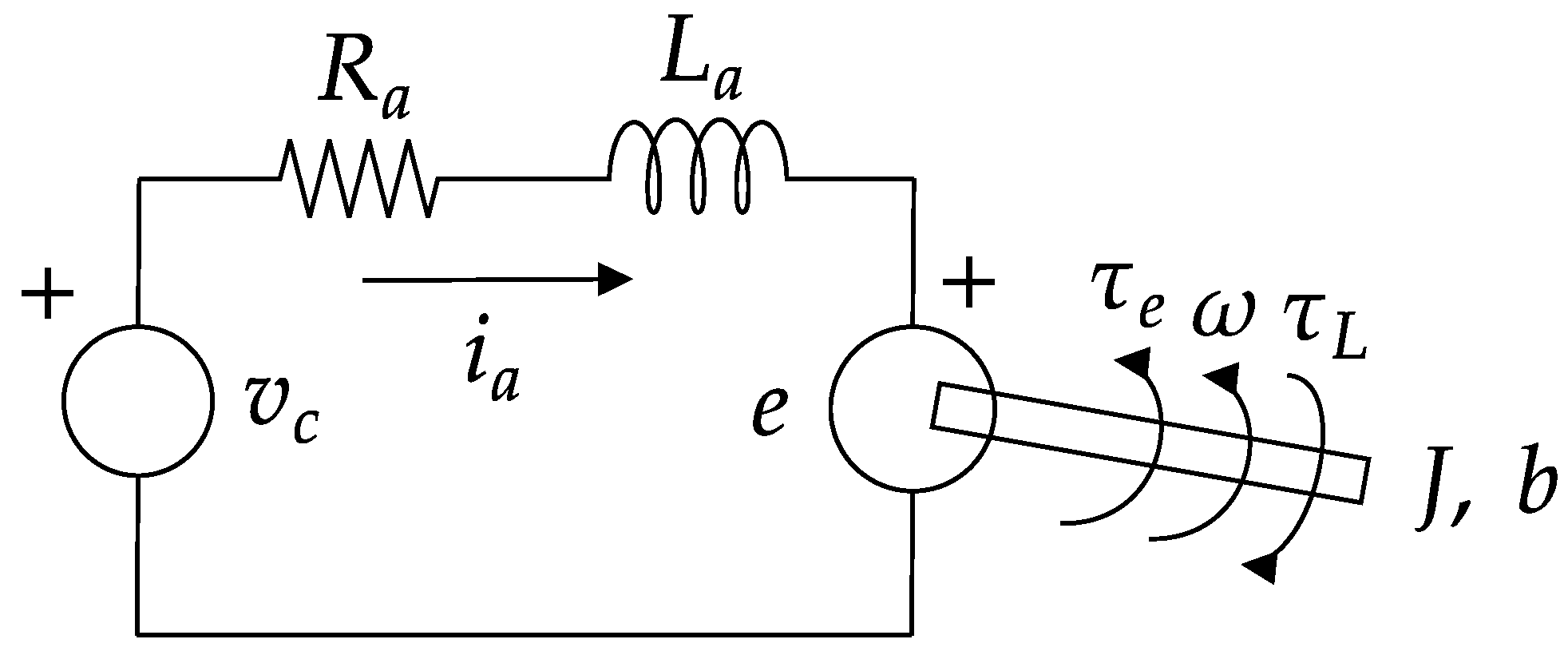
3.1.2. Model of the DC Motor
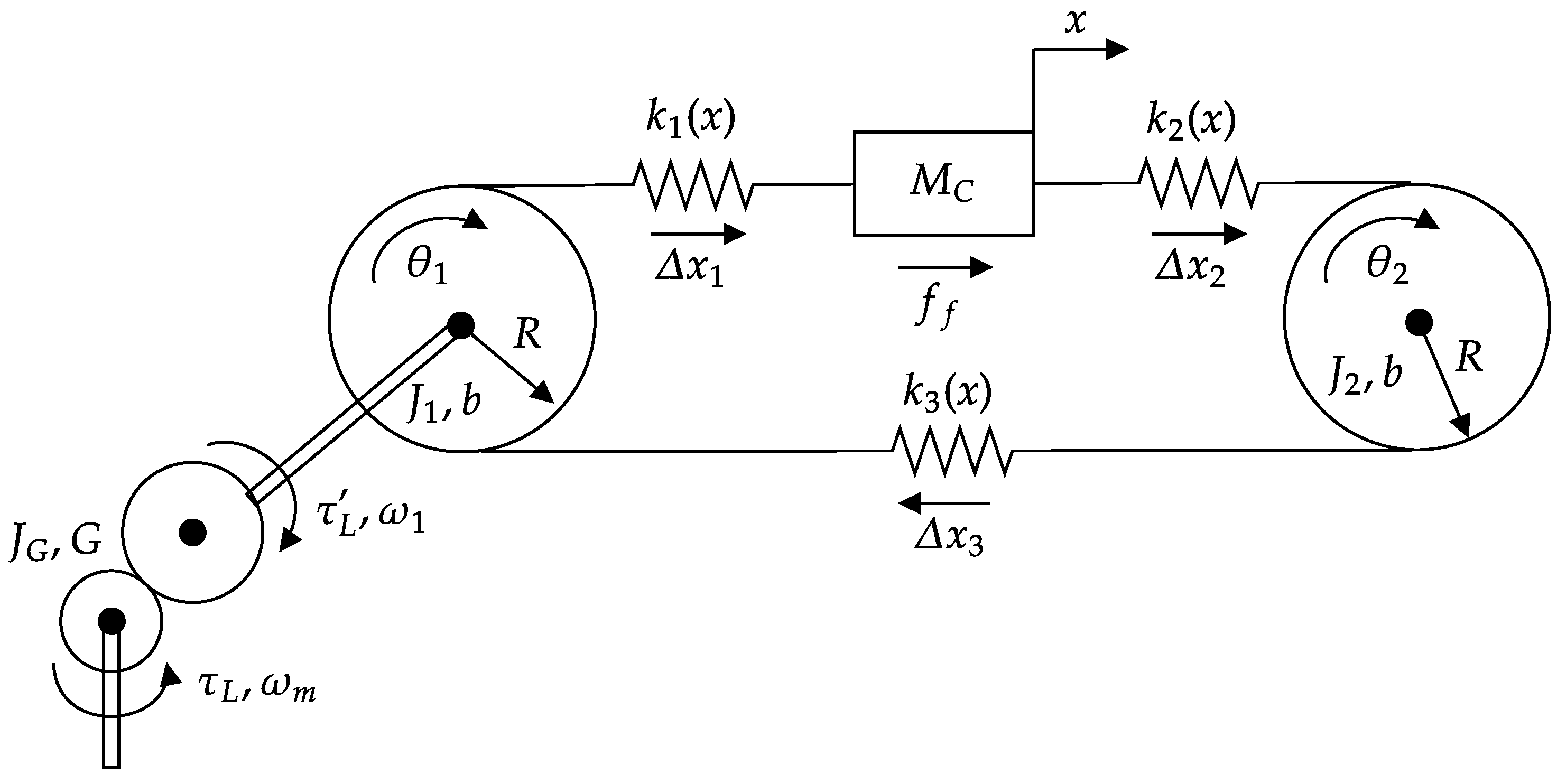
3.1.3. Space-State-Based Model of the Conveyor
- The link between the motor shaft and the driving pulley is rigid;
- No backlash is present in the system;
- The belt can be modeled by a constant mass ();
- The density of sugarcane’s mass is maintained as constant along the conveyor belt.
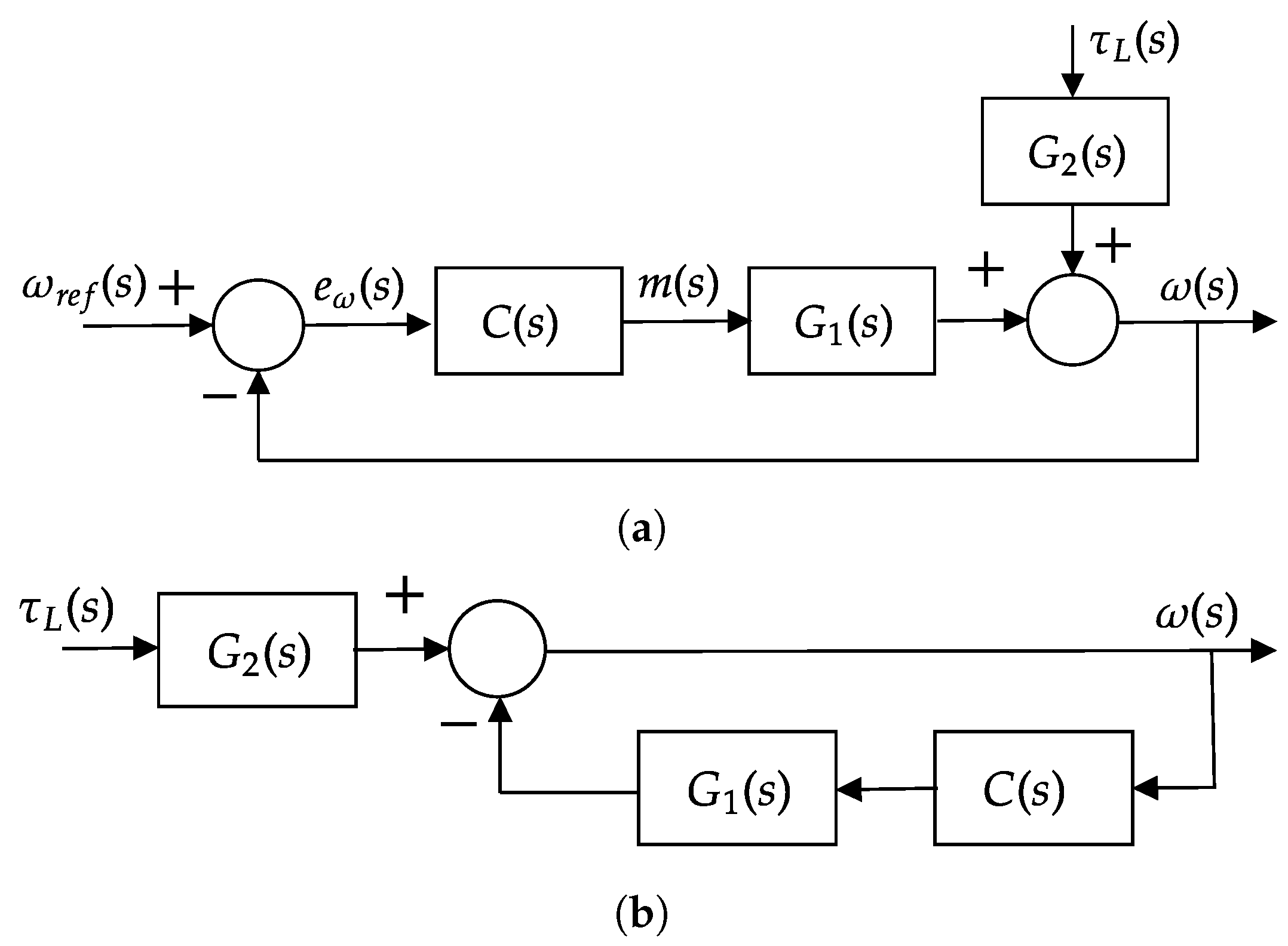
3.1.4. Unified Analytical Model
3.2. Case Study Parameters
3.2.1. Conveyor Belt
3.2.2. DC Motor
3.2.3. Ripple Filter
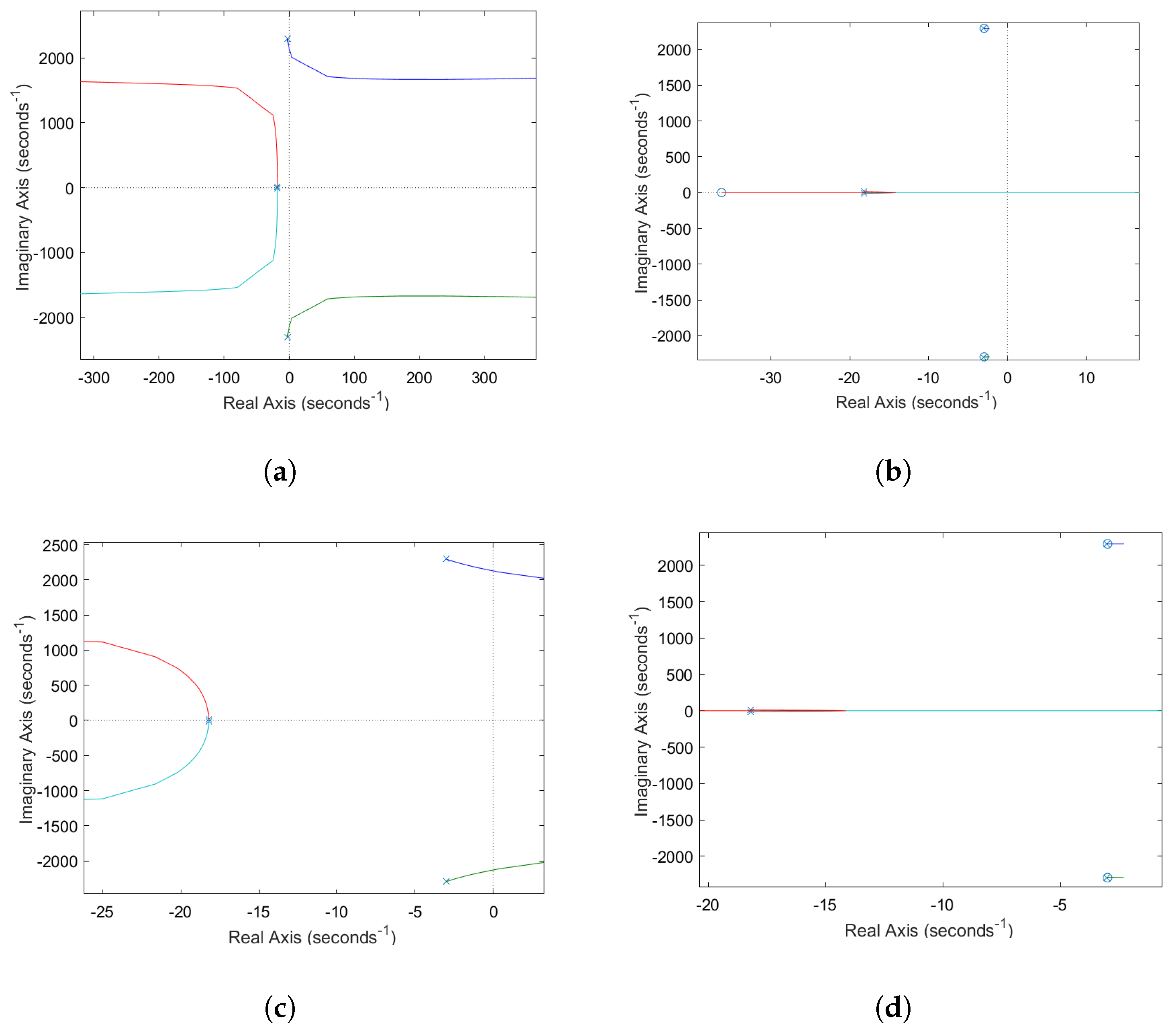
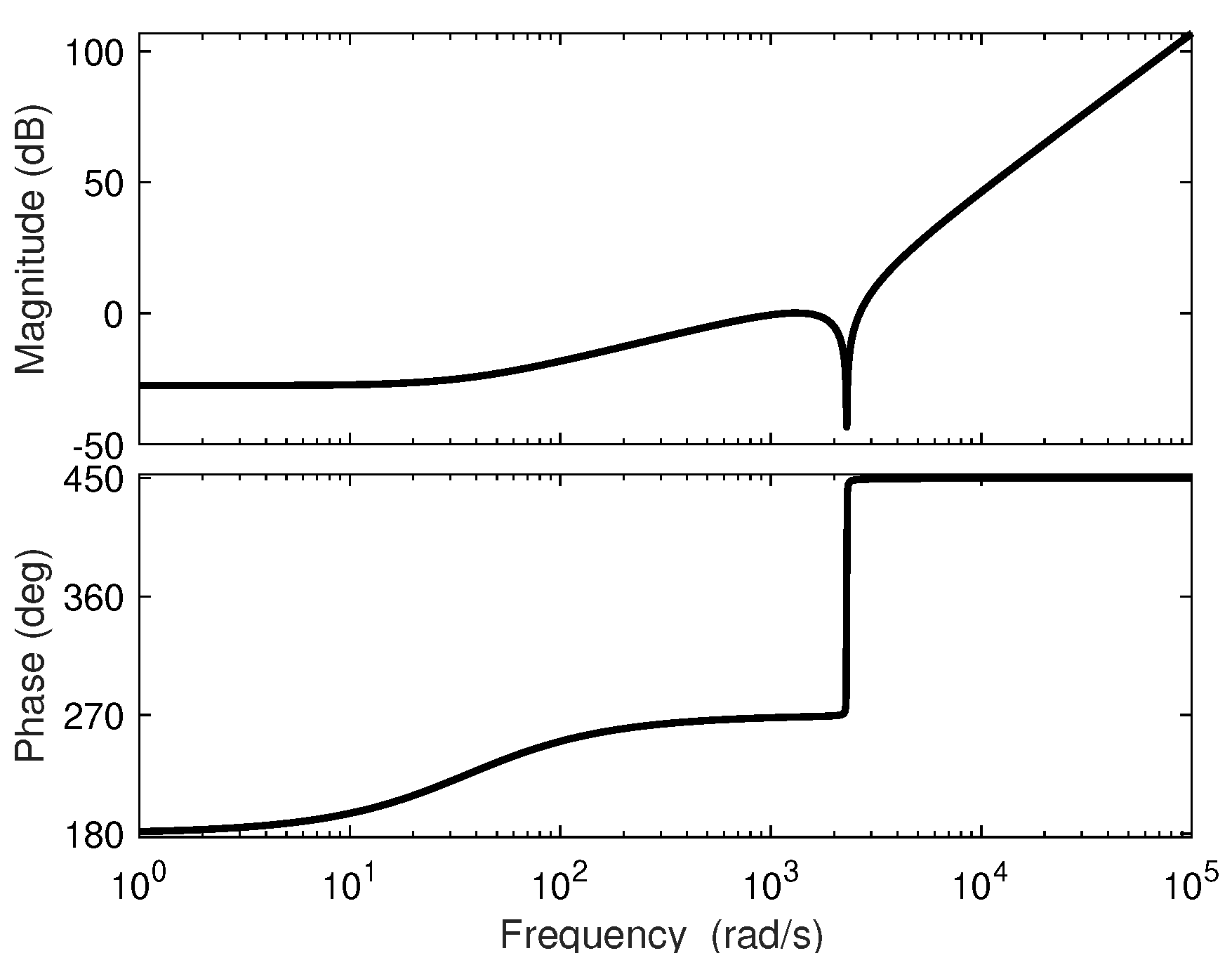
3.3. Characteristics of the Transfer-Function-Based Models
3.4. Emulation of the System Using the Space-State-Based Model
3.5. Index Criteria Used
4. Results
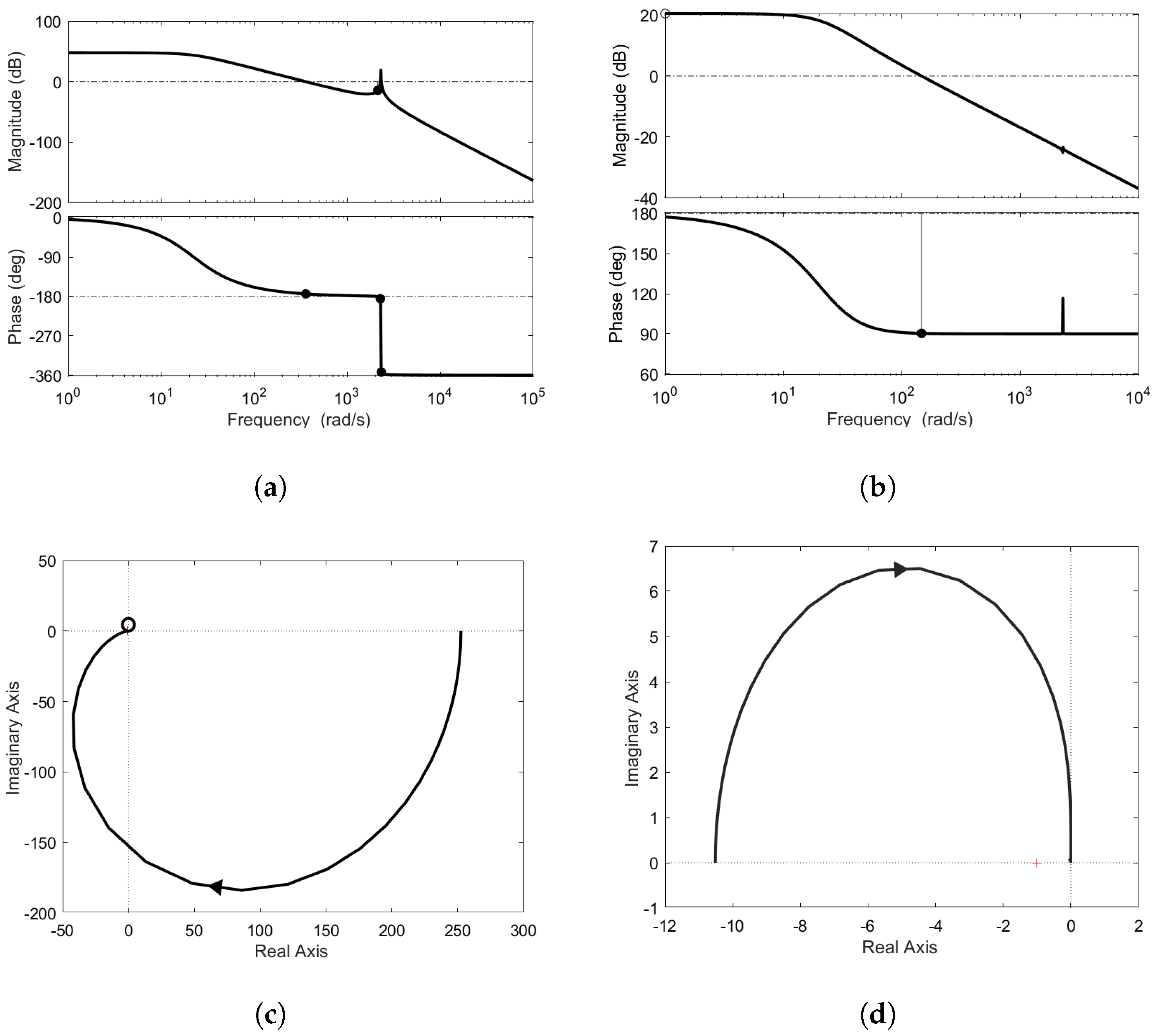
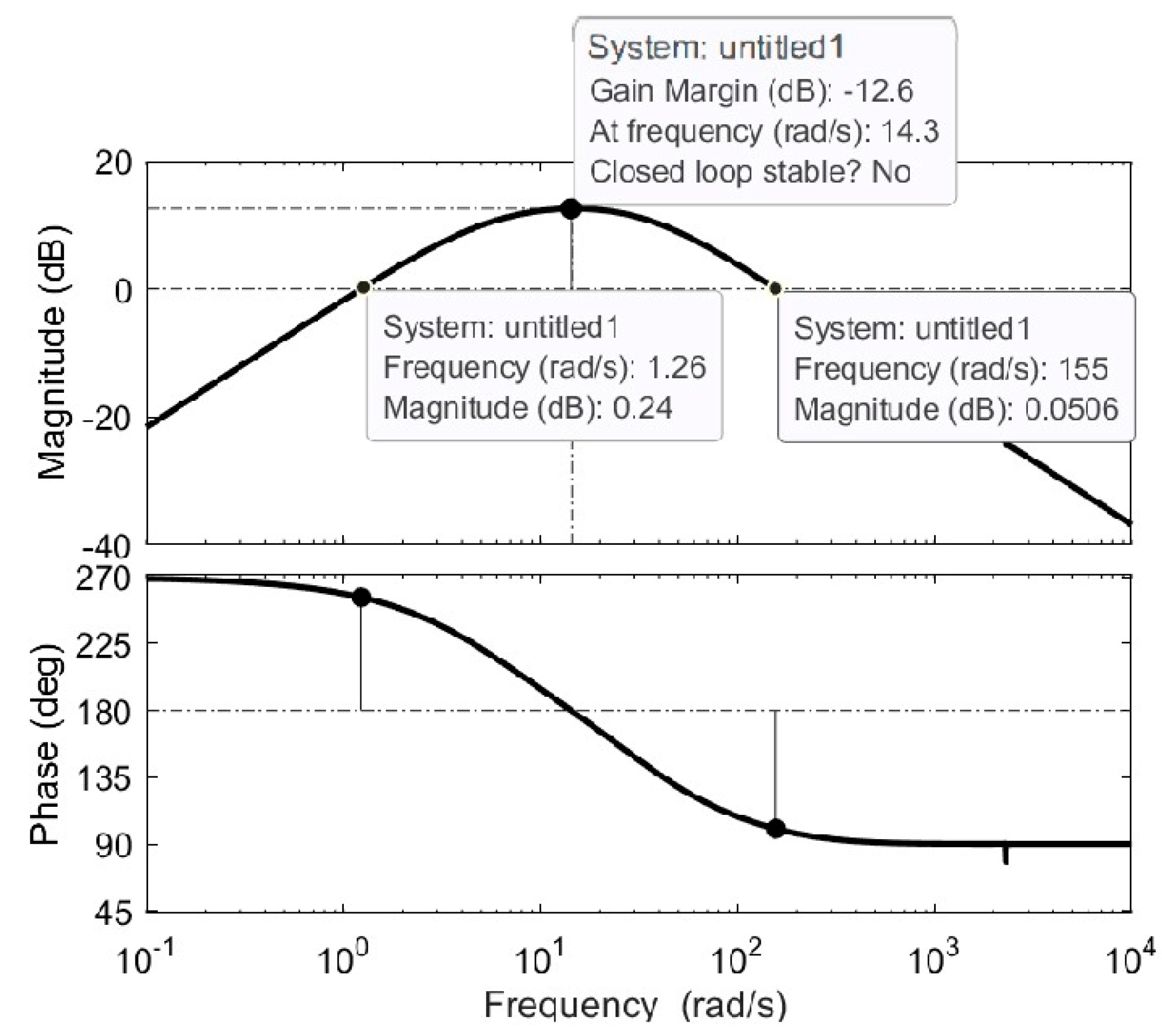
4.1. Design of the Regulator of the Control Scheme
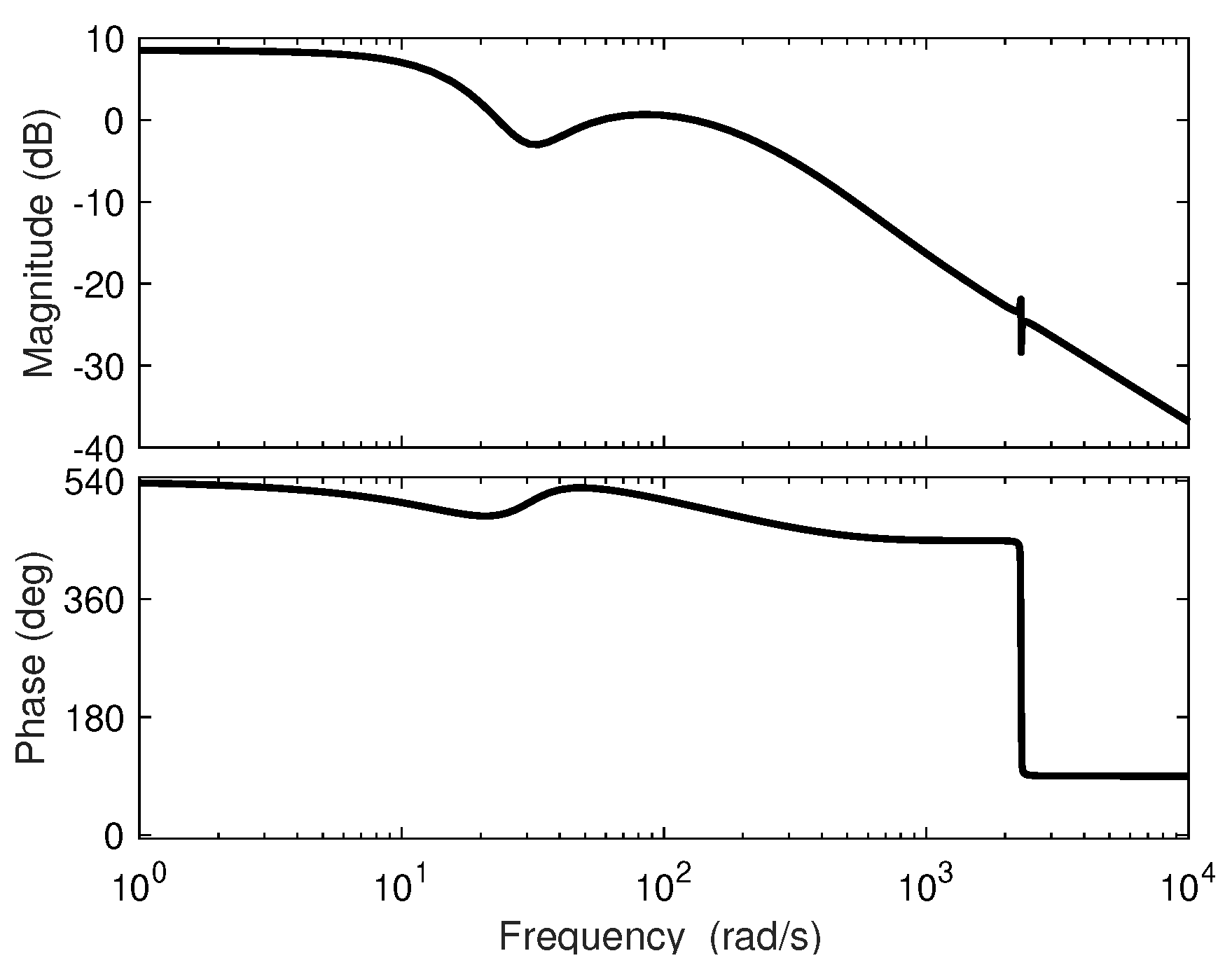
4.2. Analysis of the Sensibility Transfer Function
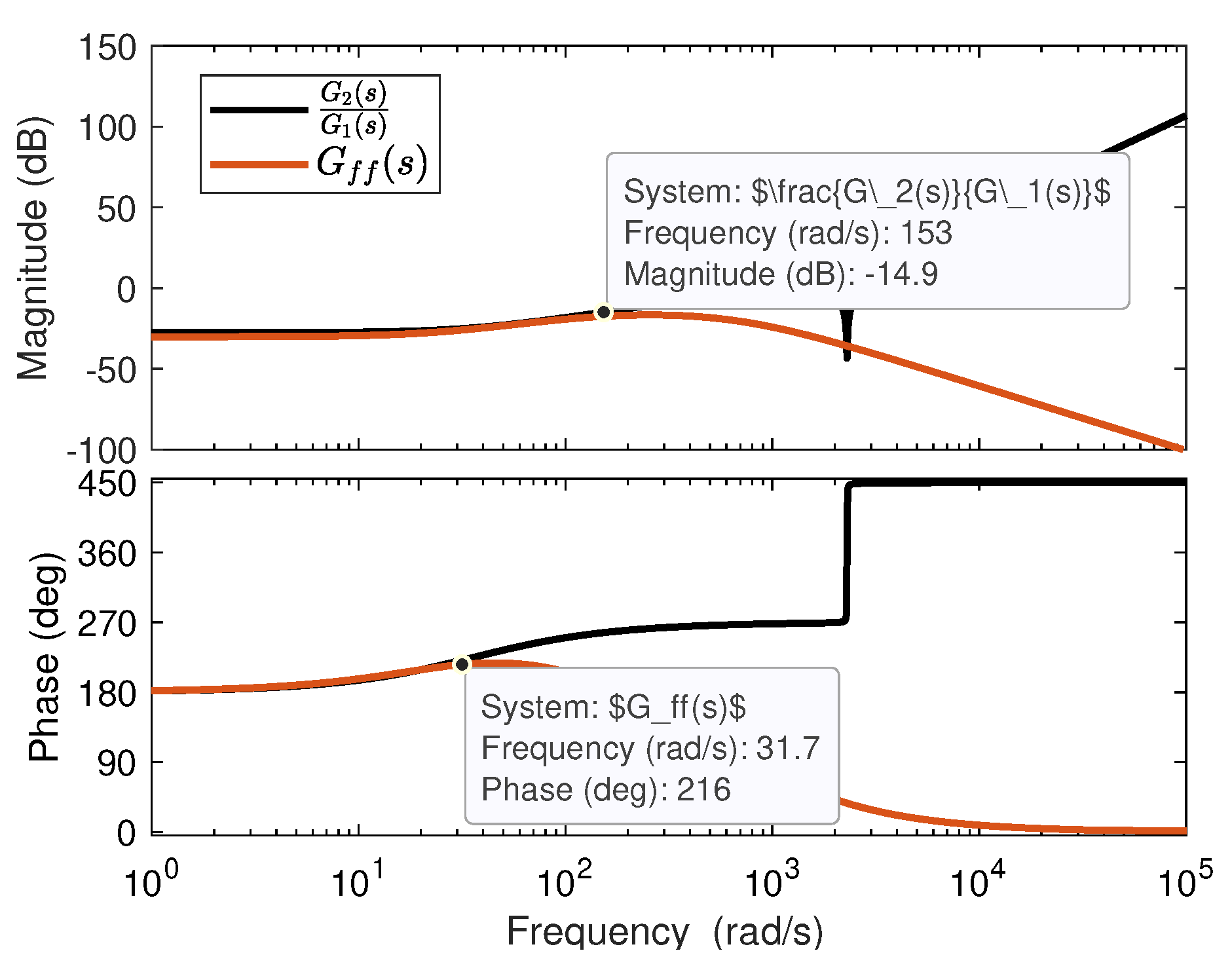
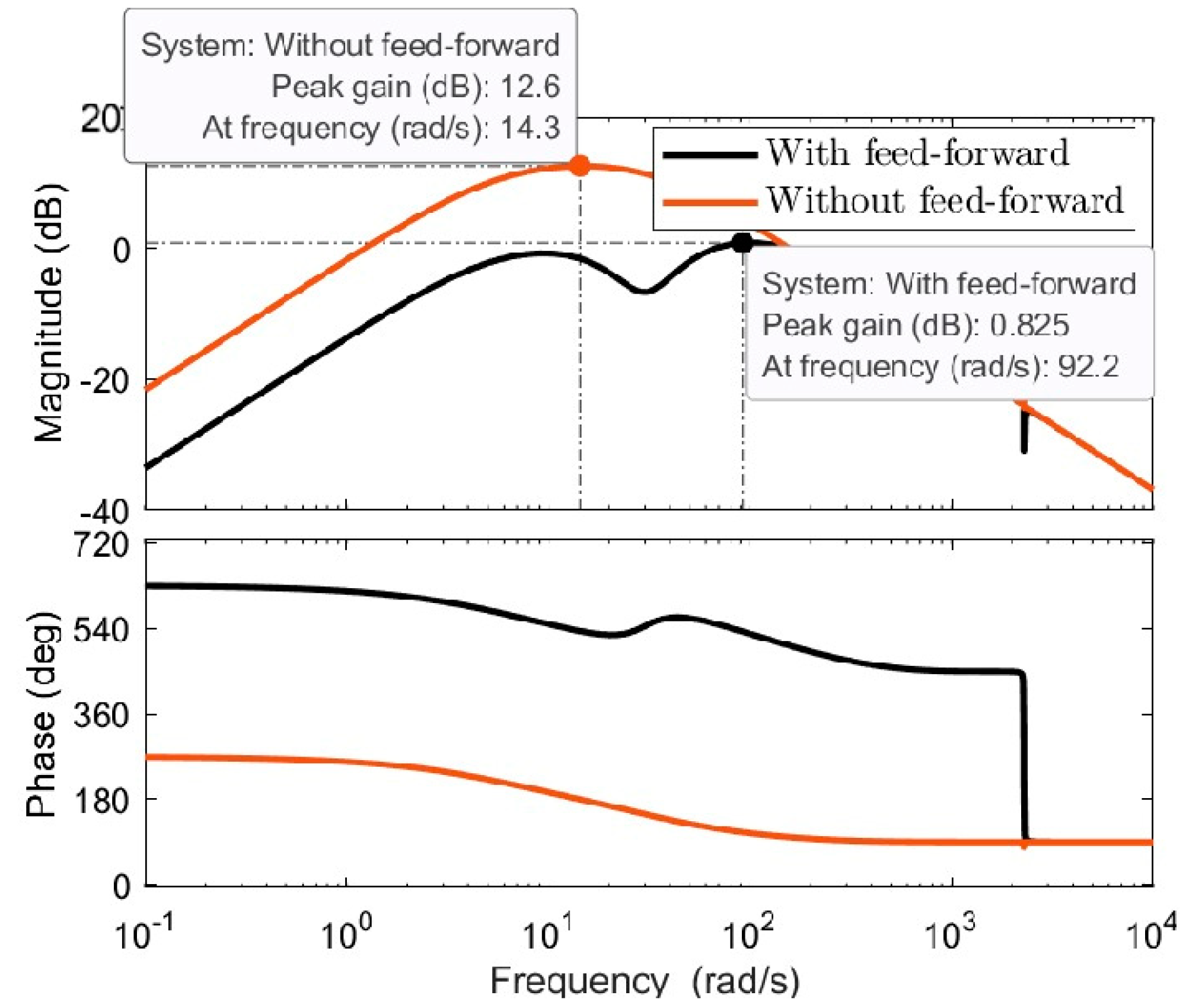
4.3. Feedforward Control Scheme’s Design
4.4. Design of the Linear State Observer
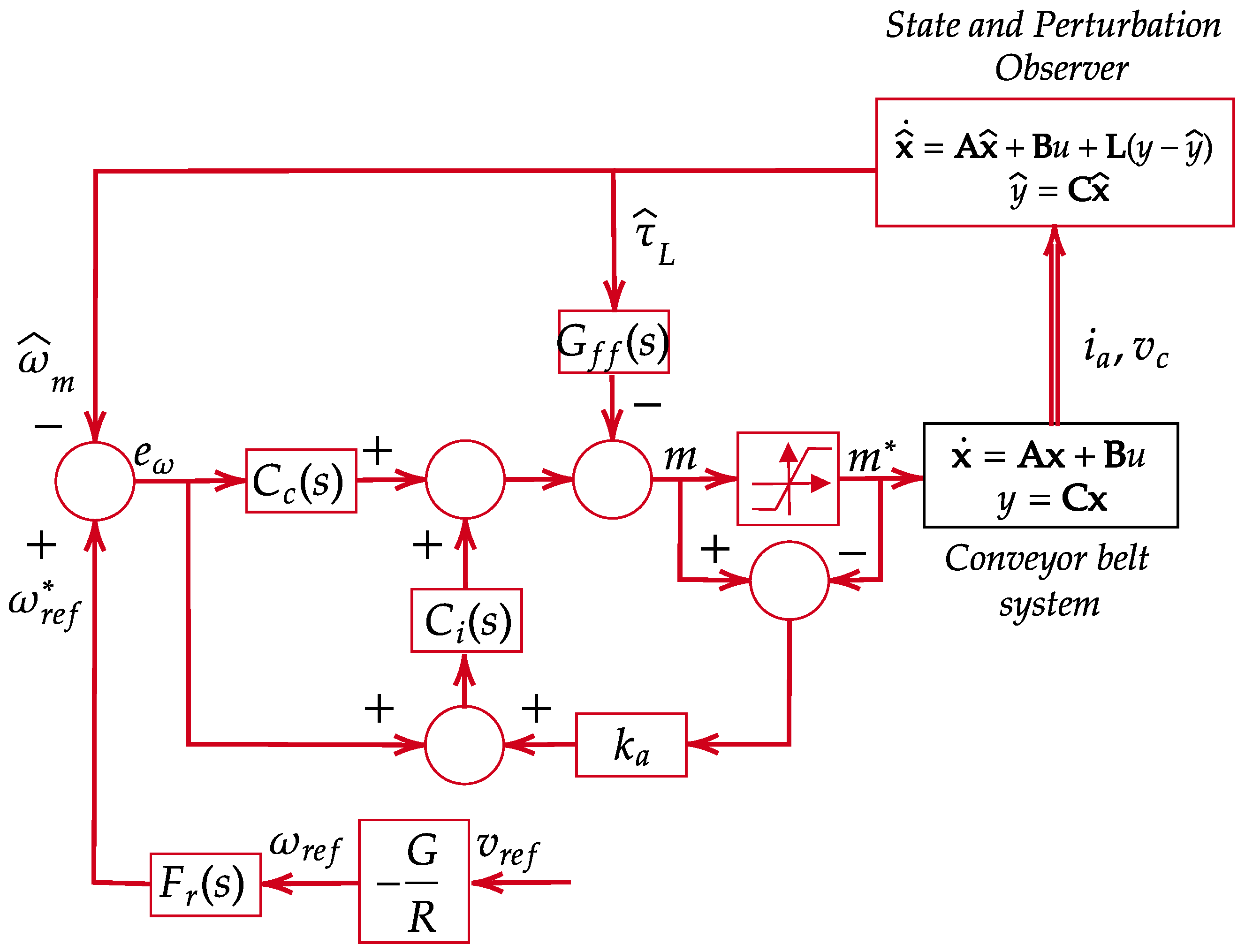
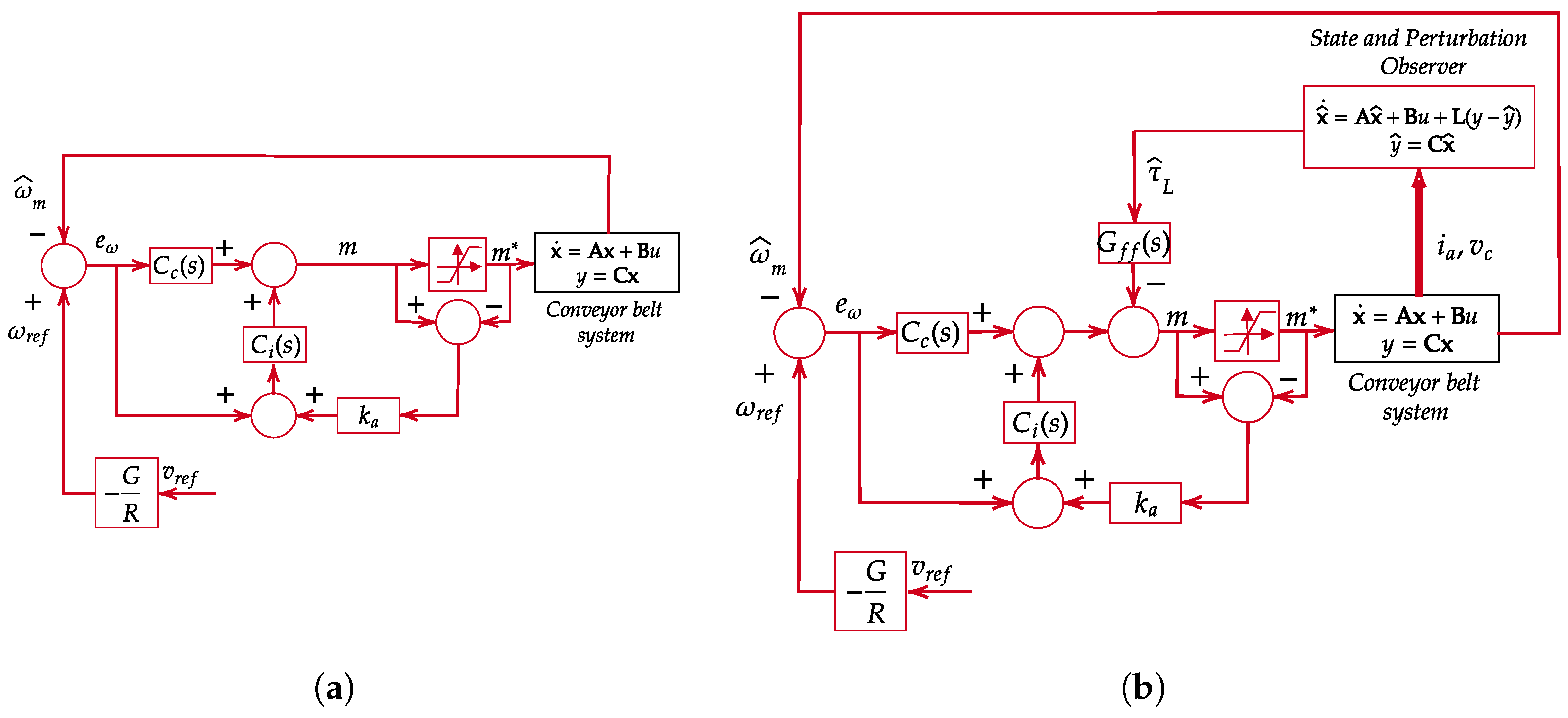
4.5. Proposed Control Scheme
5. Discussion
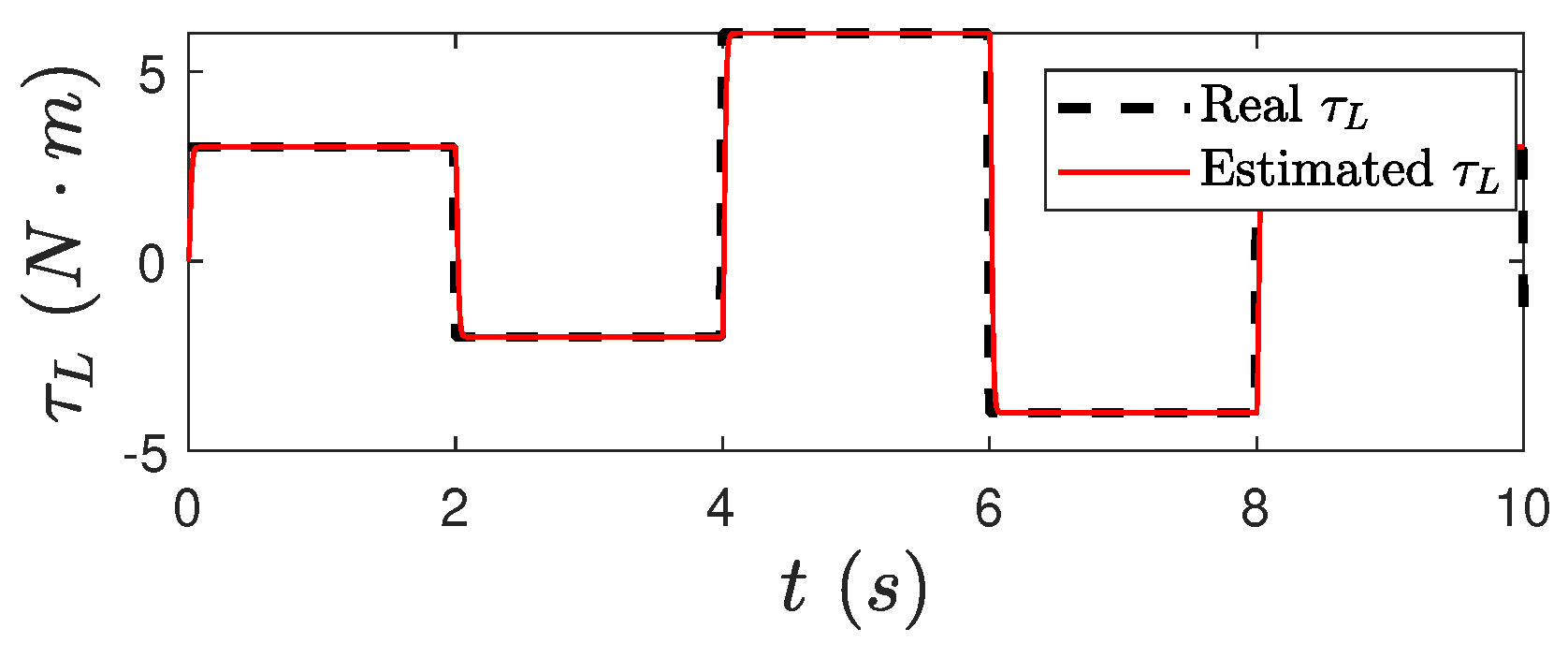
5.1. Performance Evaluation of the Proposed Observer
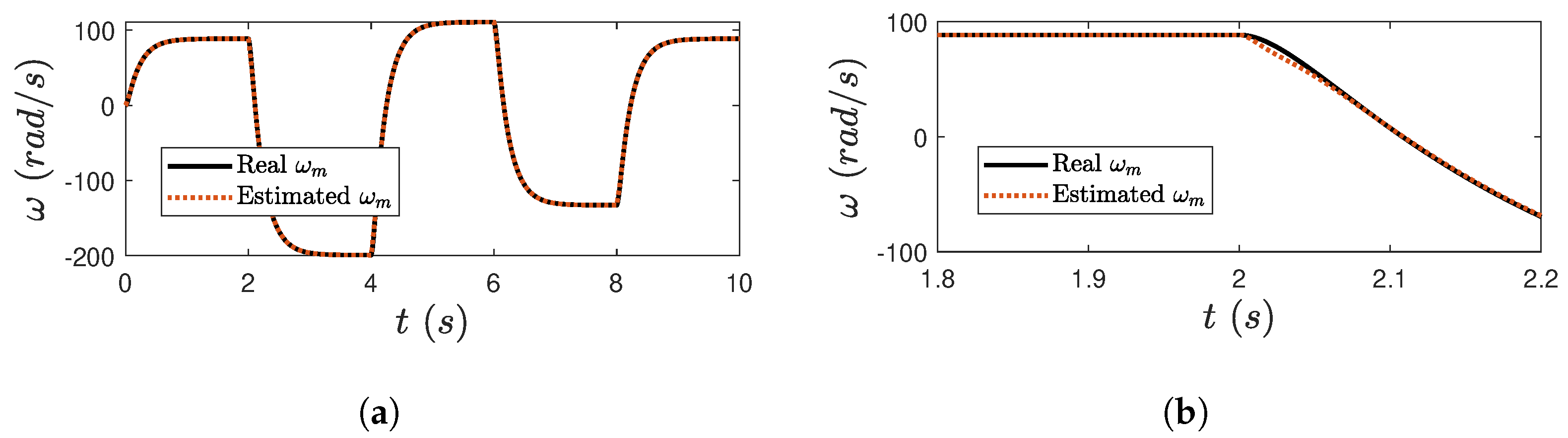
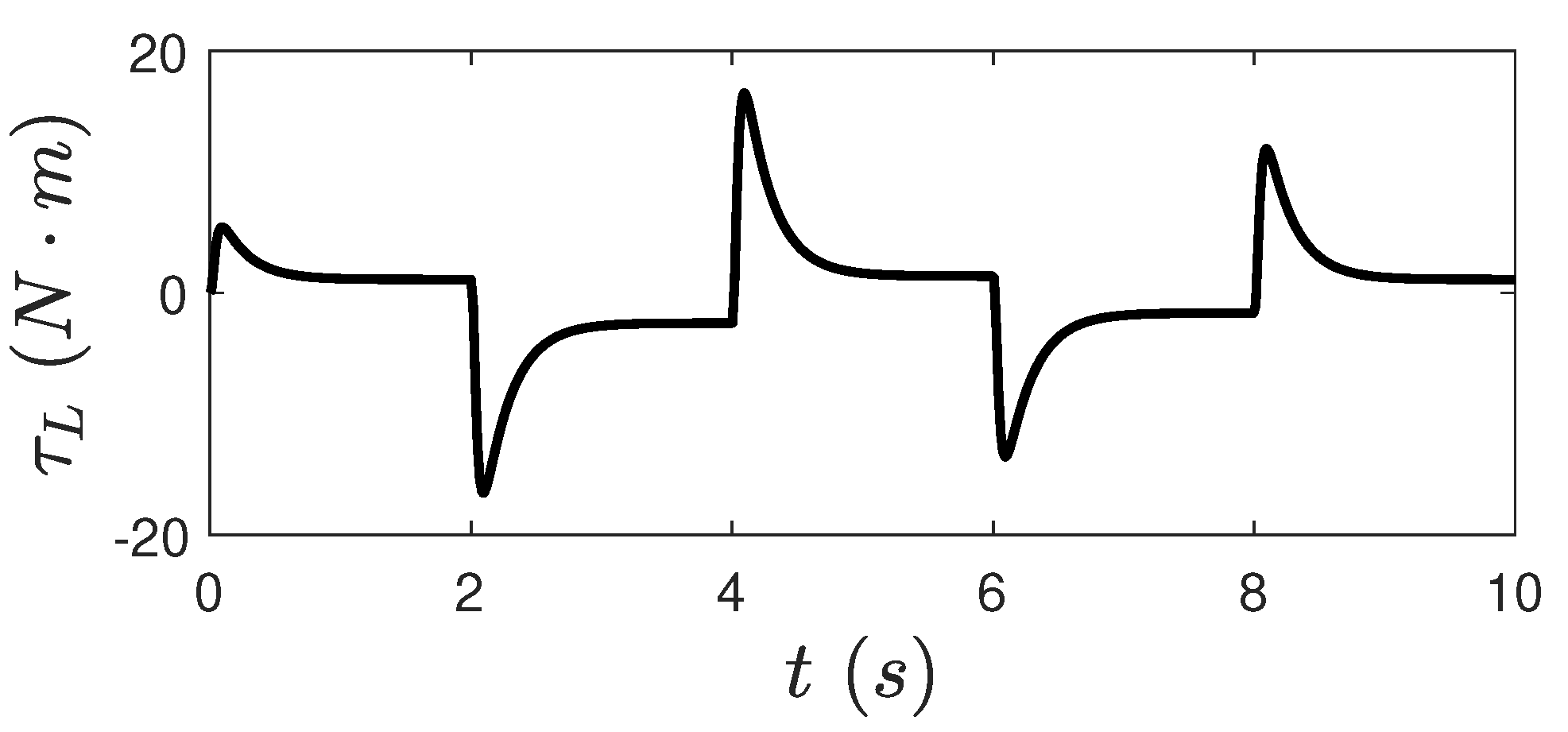
5.1.1. Test 1: Estimation Process Under Ideal Conditions
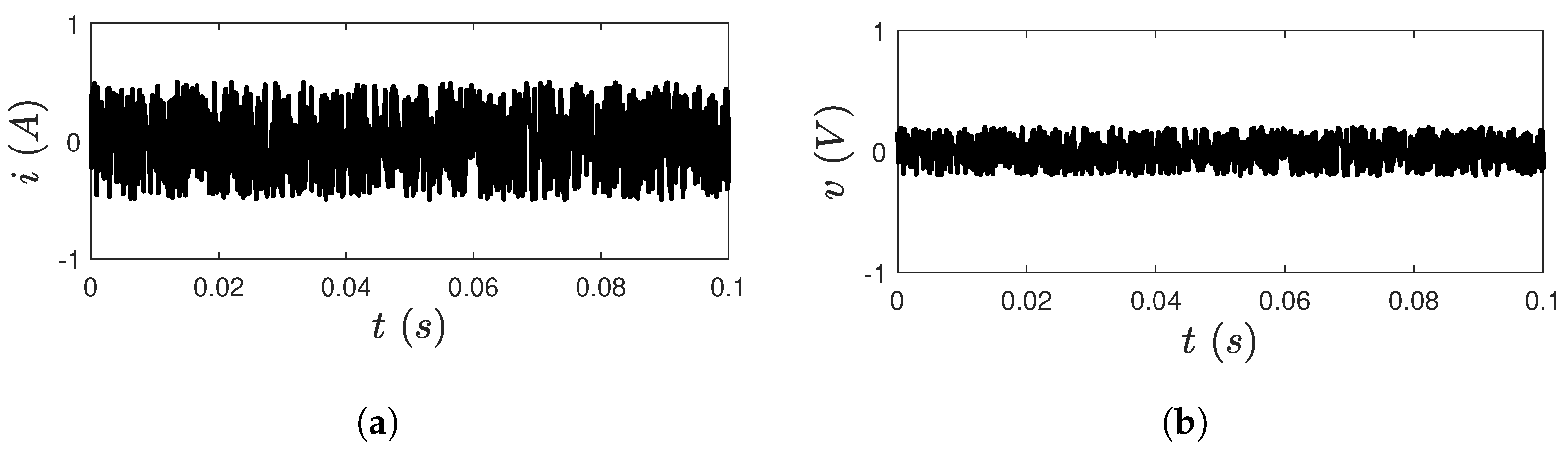
5.1.2. Test 2: Estimation Process Considering Parameter Uncertainties and Measurement Noises
5.2. Sensorless Control Scheme’s Evaluation
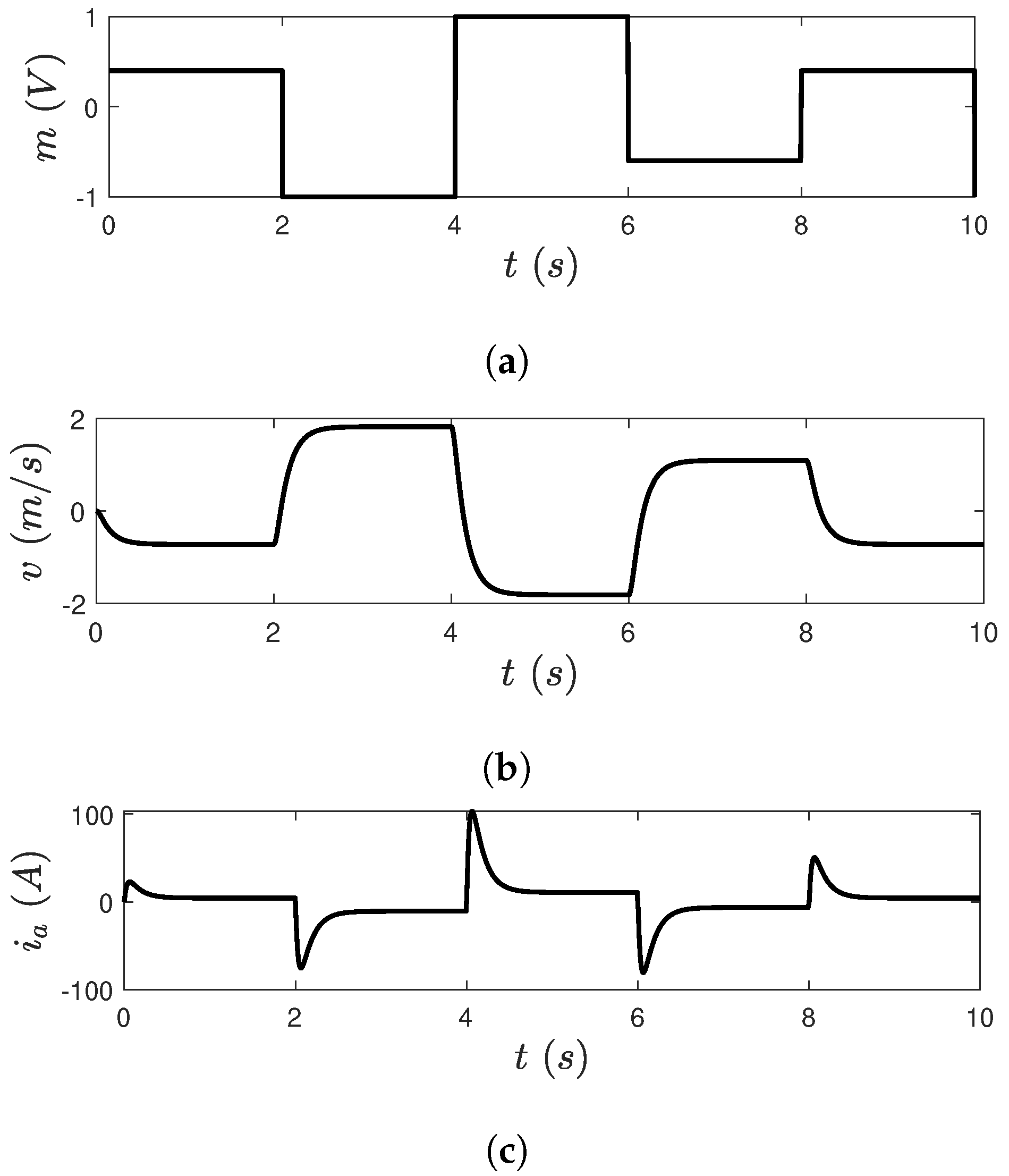
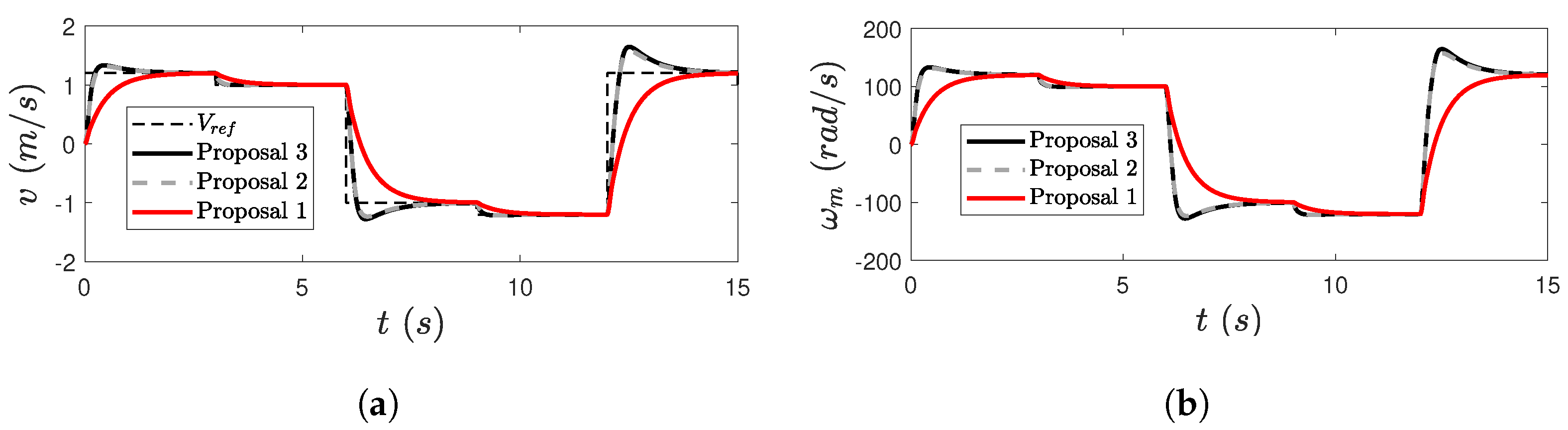
5.2.1. Test 1: Changes in the Velocity Reference’s Value
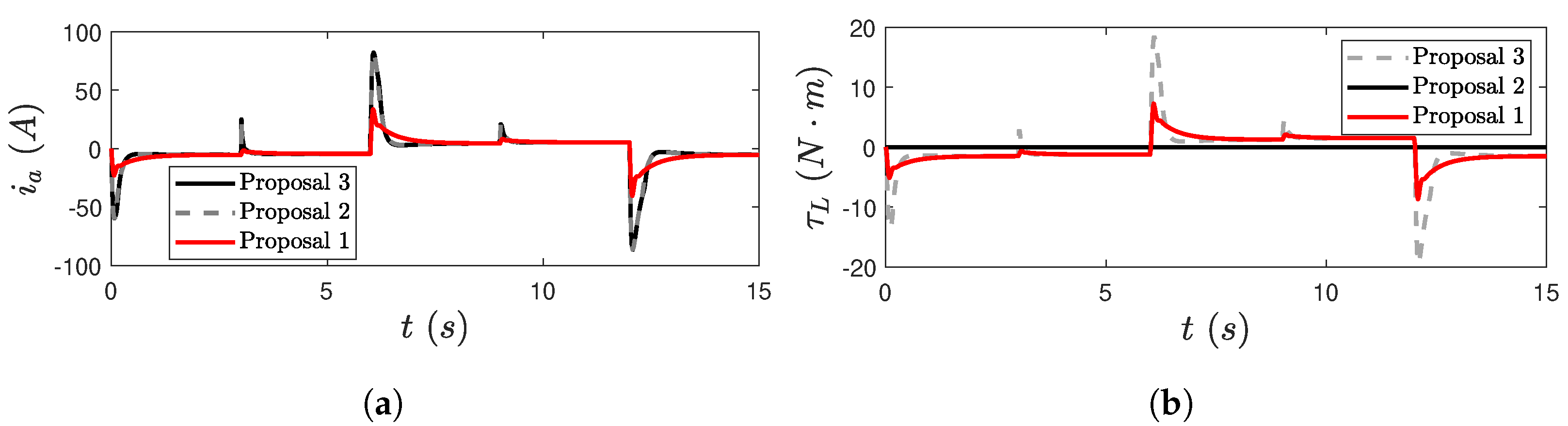
5.2.2. Test 2: Abrupt Changes in the Torque Load at a Constant Velocity Reference Value
5.2.3. Test 3: Non-Ideal Operational Conditions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sankardoss, V.; Geethanjali, P. PMDC Motor Parameter Estimation Using Bio-Inspired Optimization Algorithms. IEEE Access 2017, 5, 11244–11254. [Google Scholar] [CrossRef]
- Barkas, D.A.; Ioannidis, G.C.; Psomopoulos, C.S.; Kaminaris, S.D.; Vokas, G.A. Brushed DC Motor Drives for Industrial and Automobile Applications with Emphasis on Control Techniques: A Comprehensive Review. Electronics 2020, 9, 887. [Google Scholar] [CrossRef]
- Coral-Enriquez, H.; Pulido-Guerrero, S.; Cortés-Romero, J. Robust disturbance rejection based control with extended-state resonant observer for sway reduction in uncertain tower-cranes. Int. J. Autom. Comput. 2019, 16, 812–827. [Google Scholar] [CrossRef]
- Baidya, D.; Dhopte, S.; Bhattacharjee, M. Sensing System Assisted Novel PID Controller for Efficient Speed Control of DC Motors in Electric Vehicles. IEEE Sens. Lett. 2023, 7, 6000604. [Google Scholar] [CrossRef]
- Silva-Ortigoza, R.; Hernández-Márquez, E.; Roldán-Caballero, A.; Tavera-Mosqueda, S.; Marciano-Melchor, M.; García-Sánchez, J.R.; Hernández-Guzmán, V.M.; Silva-Ortigoza, G. Sensorless Tracking Control for a “Full-Bridge Buck Inverter–DC Motor” System: Passivity and Flatness-Based Design. IEEE Access 2021, 9, 132191–132204. [Google Scholar] [CrossRef]
- García-Chávez, R.E.; Silva-Ortigoza, R.; Hernández-guzmáN, V.M.; Marciano-Melchor, M.; Orta-Quintana, A.A.; García-Sánchez, J.R.; Taud, H. A Robust Sliding Mode and PI-Based Tracking Control for the MIMO “DC/DC Buck Converter–Inverter–DC Motor” System. IEEE Access 2023, 11, 119396–119408. [Google Scholar] [CrossRef]
- Ismail, A.A.A.; Elnady, A. Advanced Drive System for DC Motor Using Multilevel DC/DC Buck Converter Circuit. IEEE Access 2019, 7, 54167–54178. [Google Scholar] [CrossRef]
- Chen, J.; Maksimovic, D.; Erickson, R. Buck-boost PWM converters having two independently controlled switches. In Proceedings of the 2001 IEEE 32nd Annual Power Electronics Specialists Conference (IEEE Cat. No.01CH37230), Vancouver, BC, Canada, 17–21 June 2001; Volume 2, pp. 736–741. [Google Scholar] [CrossRef]
- Ardhenta, L.; Subroto, R.K. Feedback Control for Buck Converter—DC Motor Using Observer. In Proceedings of the 2020 12th International Conference on Electrical Engineering (ICEENG), Cairo, Egypt, 7–9 July 2020; pp. 30–33. [Google Scholar] [CrossRef]
- Liceaga-Castro, J.U.; Siller-Alcalá, I.I.; González-San Román, J.D.; Alcántara-Ramírez, R.A. PI Speed Control with Reverse Motion of a Series DC Motor Based on the Noise Reduction Disturbance Observer. Actuators 2022, 11, 117. [Google Scholar] [CrossRef]
- Rahmatullah, R.; Ak, A.; Serteller, N.F.O. SMC Controller Design for DC Motor Speed Control Applications and Performance Comparison with FLC, PID and PI Controllers. In Intelligent Sustainable Systems; Nagar, A.K., Singh Jat, D., Mishra, D.K., Joshi, A., Eds.; Springer: Singapore, 2023; pp. 607–617. [Google Scholar]
- Afifa, R.; Ali, S.; Pervaiz, M.; Iqbal, J. Adaptive Backstepping Integral Sliding Mode Control of a MIMO Separately Excited DC Motor. Robotics 2023, 12, 105. [Google Scholar] [CrossRef]
- Vesović, M.; Jovanović, R.; Trišović, N. Control of a DC motor using feedback linearization and gray wolf optimization algorithm. Adv. Mech. Eng. 2022, 14, 16878132221085324. [Google Scholar] [CrossRef]
- Khasawneh, H.J.; Abdelaal, O.; Saaideh, M.I.A.; Abo-Hammour, Z.S. Optimal Lead Compensator for Two-Loop Control System of Linear DC Motor. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 634–639. [Google Scholar] [CrossRef]
- Slough, J.; Belcher, M.; Tsui, T.; Bhattacharya, S. Modeling and Simulation of Electric Vehicles Using Simulink and Simscape. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Vasca, F.; Iannelli, L. Dynamics and Control of Switched Electronic Systems: Advanced Perspectives for Modeling, Simulation and Control of Power Converters; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Katsioula, A.G.; Karnavas, Y.L.; Boutalis, Y.S. An enhanced simulation model for DC motor belt drive conveyor system control. In Proceedings of the 2018 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Hace, A.; Jezernik, K.; Sabanovic, A. SMC With Disturbance Observer for a Linear Belt Drive. IEEE Trans. Ind. Electron. 2007, 54, 3402–3412. [Google Scholar] [CrossRef]
- Sabanovic, A.; Sozbilir, O.; Goktug, G.; Sabanovic, N. Sliding mode control of timing-belt servosystem. In Proceedings of the 2003 IEEE International Symposium on Industrial Electronics (Cat. No.03TH8692), Rio de Janeiro, Brazil, 9–11 June 2003; Volume 2, pp. 684–689. [Google Scholar] [CrossRef]
- Garelli, F.; Mercedes Ramírez, M.; Ariel Domínguez, C.; Modesto Angulo, A. Simulación de un algoritmo para controlar el nivel en tolva ante alimentación discontinua de caña. Rev. Iberoam. Automática Informática Ind. RIAI 2009, 6, 54–60. [Google Scholar] [CrossRef]
- Mahmoud, M. Robust Control and Filtering for Time-Delay Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar] [CrossRef]
- Antritter, F.; Maurer, P.; Reger, J. Flatness based control of a buck-converter driven DC motor. IFAC Proc. Vol. 2006, 39, 36–41. [Google Scholar] [CrossRef]
- Domański, P.D. Index Ratio Diagram—A New Way to Assess Control Performance. In Proceedings of the 2024 European Control Conference (ECC), Stockholm, Sweden, 25–28 June 2024; pp. 2041–2046. [Google Scholar] [CrossRef]
- Dogruer, T.; Can, M.S. Design and robustness analysis of fuzzy PID controller for automatic voltage regulator system using genetic algorithm. Trans. Inst. Meas. Control 2022, 44, 1862–1873. [Google Scholar] [CrossRef]
- Gurugubelli, V.; Ghosh, A.; Panda, A.K. Droop controlled voltage source converter with different classical controllers in voltage control loop. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 2–5 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Wu, G.; Sun, B.; Ma, F.; Aksun-Guvenc, B.; Guvenc, L. Disturbance Observer-Smith Predictor Compensation-Based Platoon Control with Estimation Deviation. J. Adv. Transp. 2022, 2022, 9866794. [Google Scholar] [CrossRef]
- Yue, L.; Wang, Y.; Xiao, B.; Wang, Y.; Lin, J. Improved active disturbance rejection speed control for autonomous driving of high-speed train based on feedforward compensation. Sci. Prog. 2023, 106, 00368504231208505. [Google Scholar] [CrossRef] [PubMed]
- Orta-Quintana, Á.A.; García-Chávez, R.E.; Silva-Ortigoza, R.; Marciano-Melchor, M.; Villarreal-Cervantes, M.G.; García-Sánchez, J.R.; García-Cortés, R.; Silva-Ortigoza, G. Sensorless Tracking Control Based on Sliding Mode for the “Full-Bridge Buck Inverter–DC Motor” System Fed by PV Panel. Sustainability 2023, 15, 9858. [Google Scholar] [CrossRef]
- Velasco-Muñoz, H.; Candelo-Becerra, J.E.; Hoyos, F.E.; Rincón, A. Speed Regulation of a Permanent Magnet DC Motor with Sliding Mode Control Based on Washout Filter. Symmetry 2022, 14, 728. [Google Scholar] [CrossRef]













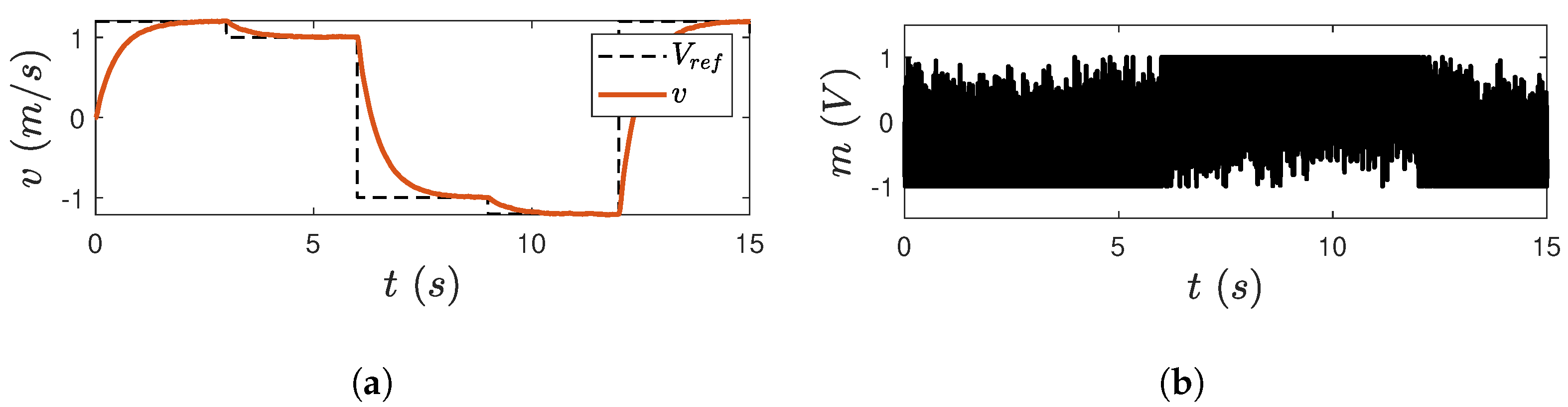
| 1 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 |
| Parameter | Unit | Value |
|---|---|---|
| G | - | 18 |
| kg·m2 | 1 × 10−4 | |
| kg·m2 | 1 × 10−2 | |
| kg·m2 | 1 × 10−2 | |
| R | m | 0.15 |
| 2.5 | ||
| kg | 40 | |
| L | m | 4 |
| A | m | 0.3 |
| 400 | ||
| m | 0.25 | |
| m | 0.25 | |
| 1 | ||
| kg | 120 |
| Parameter | Unit | Value |
|---|---|---|
| J | 6.96 × 10−3 | |
| b | 1.73 × 10−3 | |
| V | 90 | |
| 0.35 | ||
| 0.35 | ||
| mH | 28.44 | |
| 1.27 |
| Parameter | Unit | Value | Percentage |
|---|---|---|---|
| J | 6.54 × 10−3 | −6% | |
| b | 1.76 × 10−3 | +2% | |
| V | 90 | - | |
| 0.320 | −8% | ||
| 0.368 | +5% | ||
| mH | 31.28 | +10% | |
| 1.33 | +5% |
| Parameter | IAE | ISE |
|---|---|---|
| Proposed Scheme 1 | 0.1927 | 0.1814 |
| Proposed Scheme 2 | 0.0888 | 0.0694 |
| Proposed Scheme 3 | 0.0942 | 0.0719 |
| Control Scheme | Reference 1 | Reference 2 | Reference 3 | Reference 4 | Reference 5 |
|---|---|---|---|---|---|
| Proposed Scheme 1 | −22.84 A | - | 33.51 A | - | −40.31 A |
| Proposed Scheme 2 | −59.55 A | 24.61 A | 82.02 A | 20.78 A | −86.52 A |
| Proposed Scheme 3 | −59.55 A | 24.61 A | 82.02 A | 20.78 A | −86.52 A |
| Parameter | IAE |
|---|---|
| Proposed Scheme 1 | 0.3573 |
| Proposed Scheme 2 | 0.7162 |
| Proposed Scheme 3 | 0.7054 |
| Parameter | IAE | ISE |
|---|---|---|
| With Compensator | 0.0533 | 2.9153 |
| Without Compensator | 0.0688 | 3.1454 |
| Work | Motor | Control Scheme | Performance |
|---|---|---|---|
| [12] | A multi-input, multi-output, separately excited DC motor | It combines the advantages of adaptive backstepping and integral sliding mode control (ISMC) to improve the overall robustness of the system. | IAE = 3.086 ISE = 41.36 = 0.477 s |
| [29] | Full-bridge buck inverter–DC motor | The control system performs trajectory tracking of the angular velocity of the DC motor shaft without relying on electromechanical sensors. | Qualitative results for the capability of the control scheme to track Bezier-based velocity trajectories |
| [30] | Permanent magnet DC motor | Sliding mode control method based on a washout filter (SMC-w) for speed control. | s − 0.076 s Output speed overshoot: 0.33% Steady-state error ≈ 0.1 |
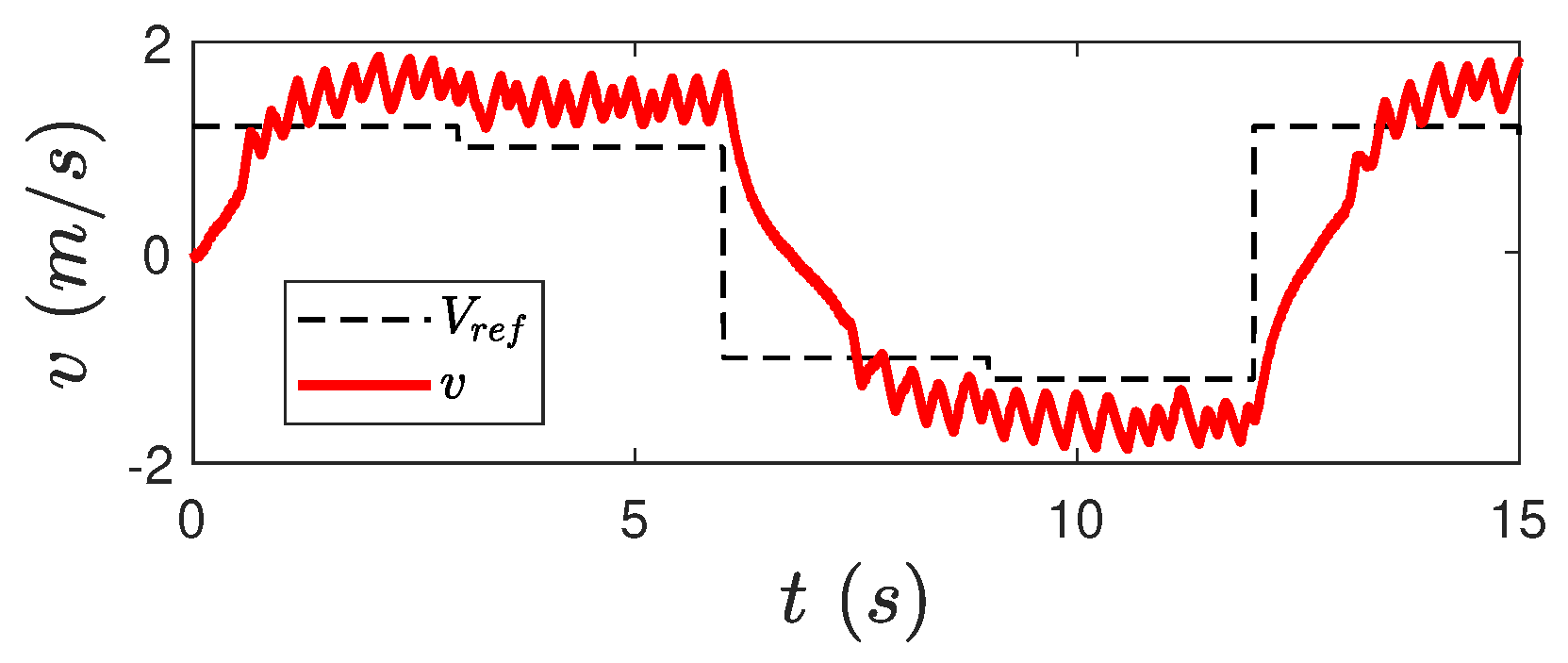
| This work | Full H-bridge power converter used for regulating a permanent magnet DC motor | Based on a PI controller combined with a lead compensator and an external perturbation compensator consisting of a feedforward mechanism with a low-order filter and a state and perturbation observer. | Without changes in the speed reference and abrupt changes in the external perturbation: IAE = 0.0533 and ITE = 2.9153 With changes in the speed reference: IAE = 0.1927 and ITE = 0.1814 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina-Santana, E.; Iturralde Carrera, L.A.; Álvarez-Alvarado, J.M.; Aviles, M.; Rodríguez-Resendiz, J. Modeling and Control of a Permanent Magnet DC Motor: A Case Study for a Bidirectional Conveyor Belt’s Application. Eng 2025, 6, 42. https://doi.org/10.3390/eng6030042
Molina-Santana E, Iturralde Carrera LA, Álvarez-Alvarado JM, Aviles M, Rodríguez-Resendiz J. Modeling and Control of a Permanent Magnet DC Motor: A Case Study for a Bidirectional Conveyor Belt’s Application. Eng. 2025; 6(3):42. https://doi.org/10.3390/eng6030042
Chicago/Turabian StyleMolina-Santana, Ernesto, Luis Angel Iturralde Carrera, José M. Álvarez-Alvarado, Marcos Aviles, and Juvenal Rodríguez-Resendiz. 2025. "Modeling and Control of a Permanent Magnet DC Motor: A Case Study for a Bidirectional Conveyor Belt’s Application" Eng 6, no. 3: 42. https://doi.org/10.3390/eng6030042
APA StyleMolina-Santana, E., Iturralde Carrera, L. A., Álvarez-Alvarado, J. M., Aviles, M., & Rodríguez-Resendiz, J. (2025). Modeling and Control of a Permanent Magnet DC Motor: A Case Study for a Bidirectional Conveyor Belt’s Application. Eng, 6(3), 42. https://doi.org/10.3390/eng6030042










