Manufacturing of Rotational Toroidal Shells in Coin Minting
Abstract
1. Introduction
2. Materials and Methods
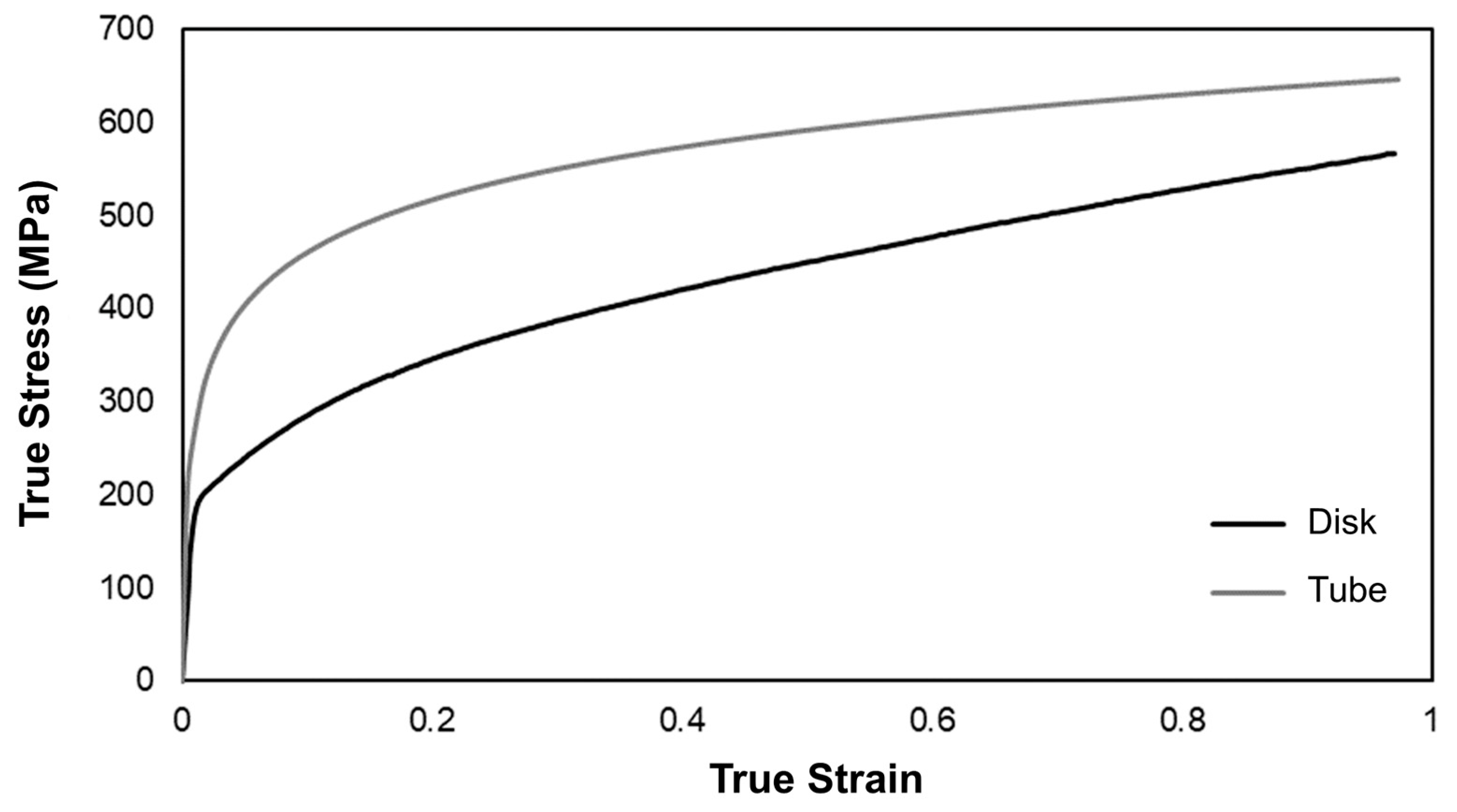
2.1. Stress–Strain Behavior of the Tube and Disk Material
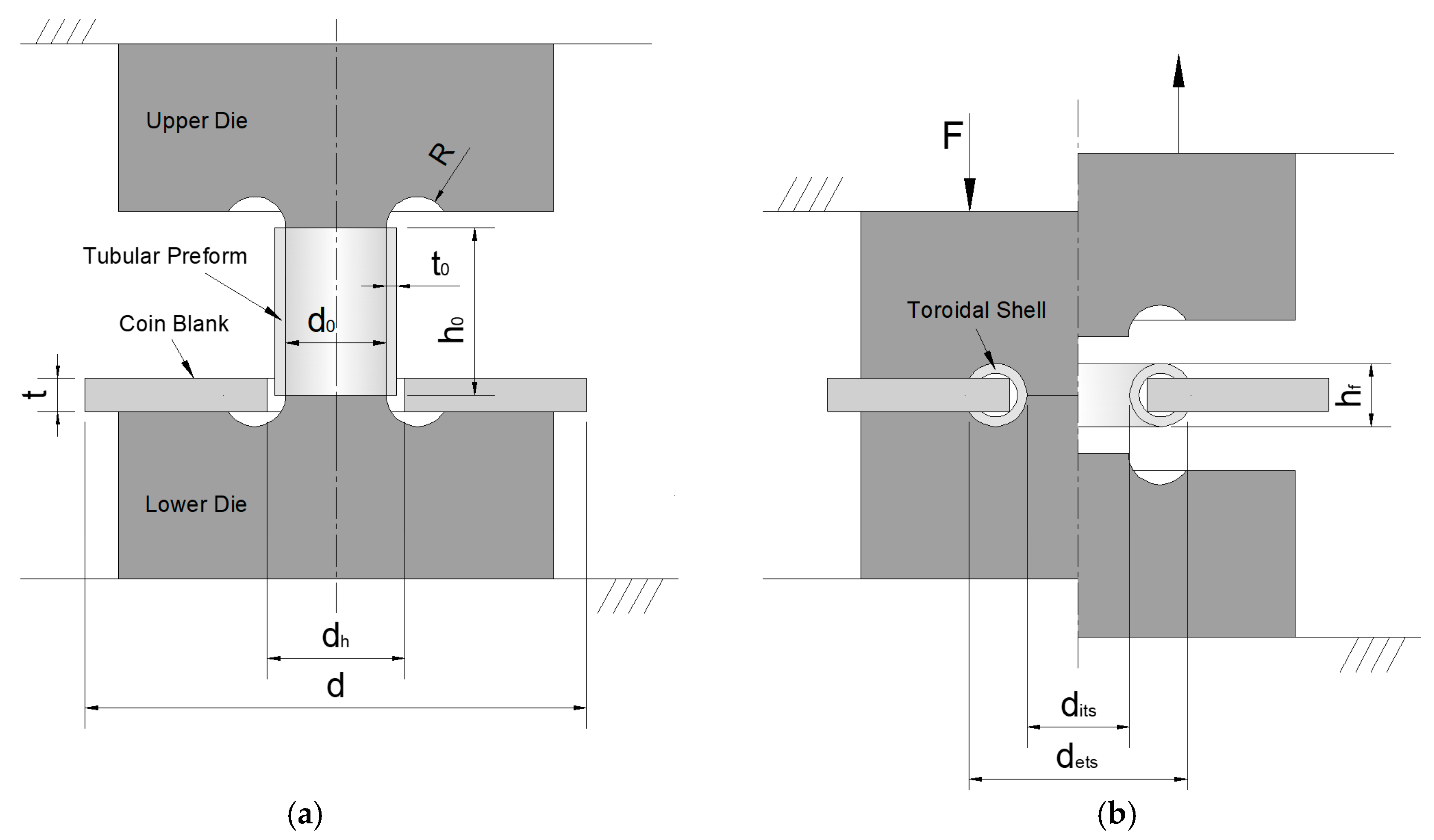
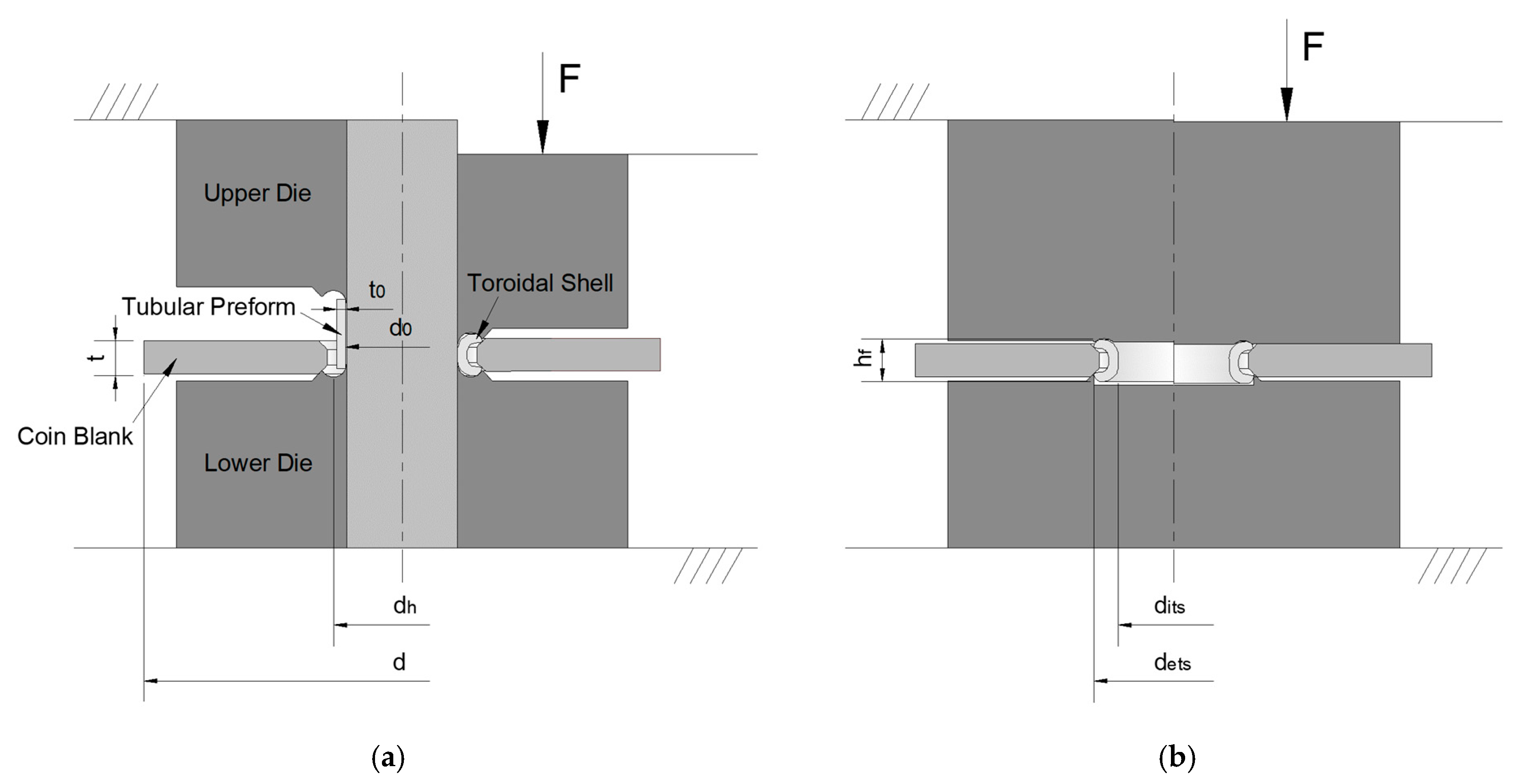
2.2. Forming of Toroidal Shell
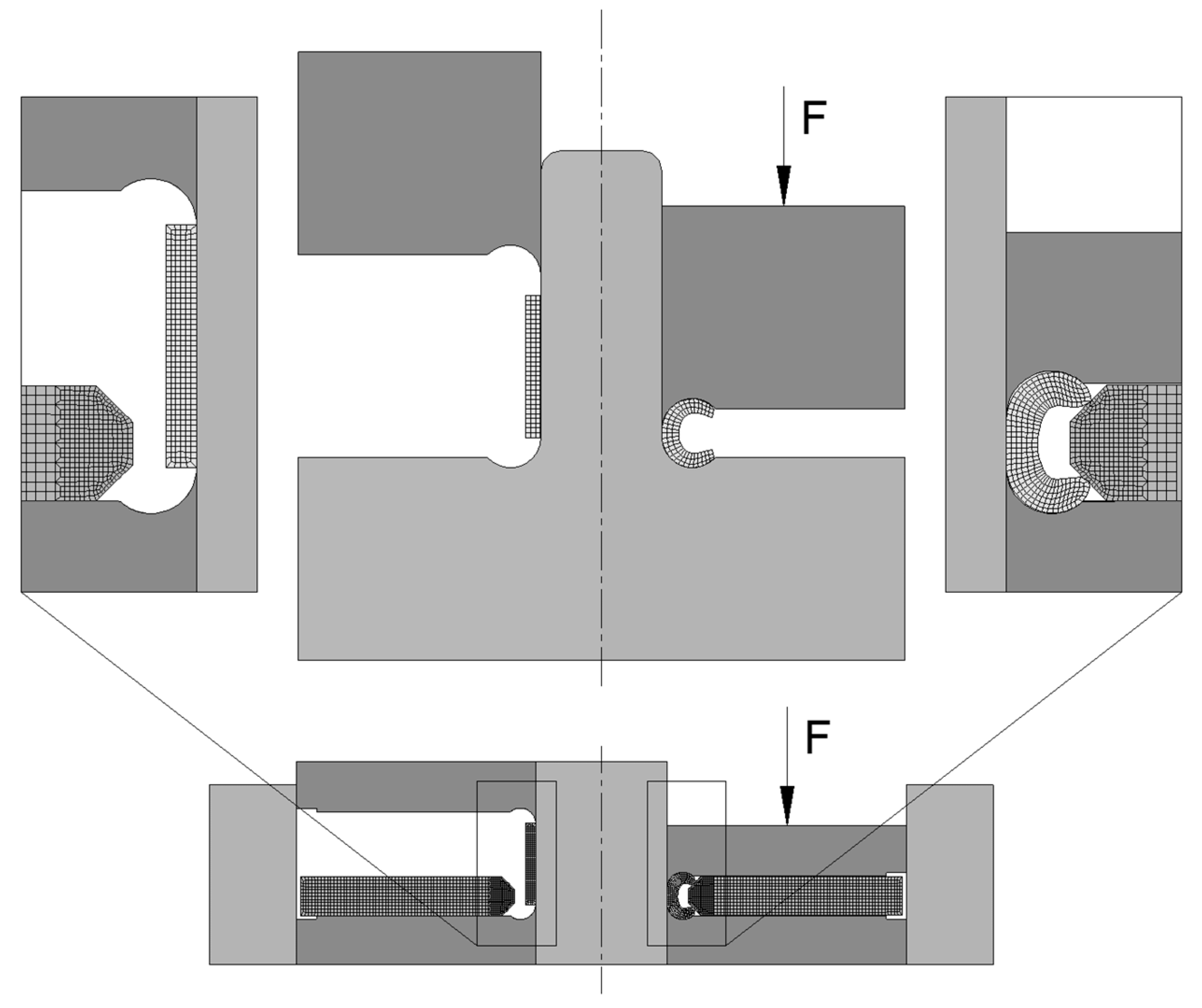
3. Numerical Simulations
4. Results and Discussion
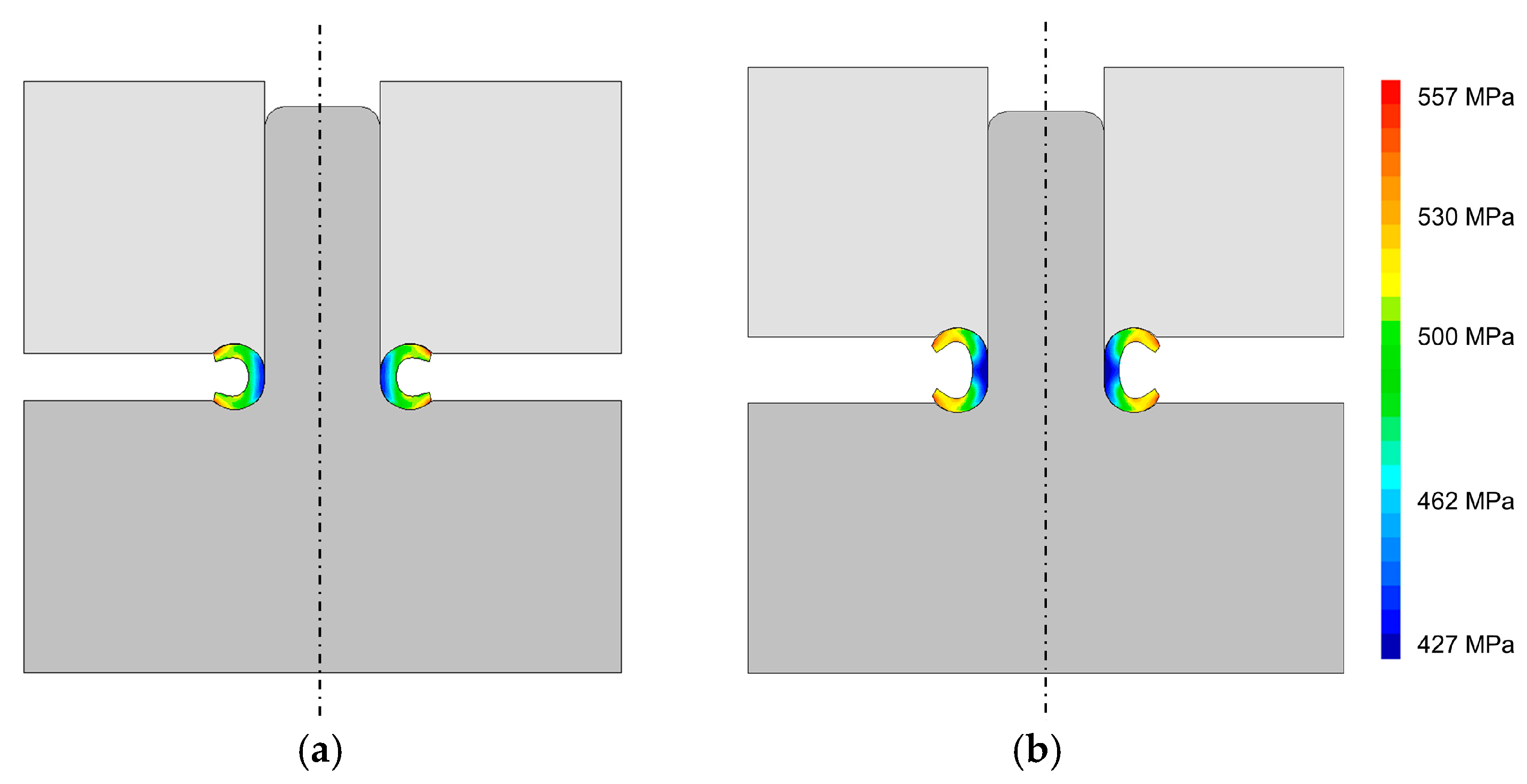
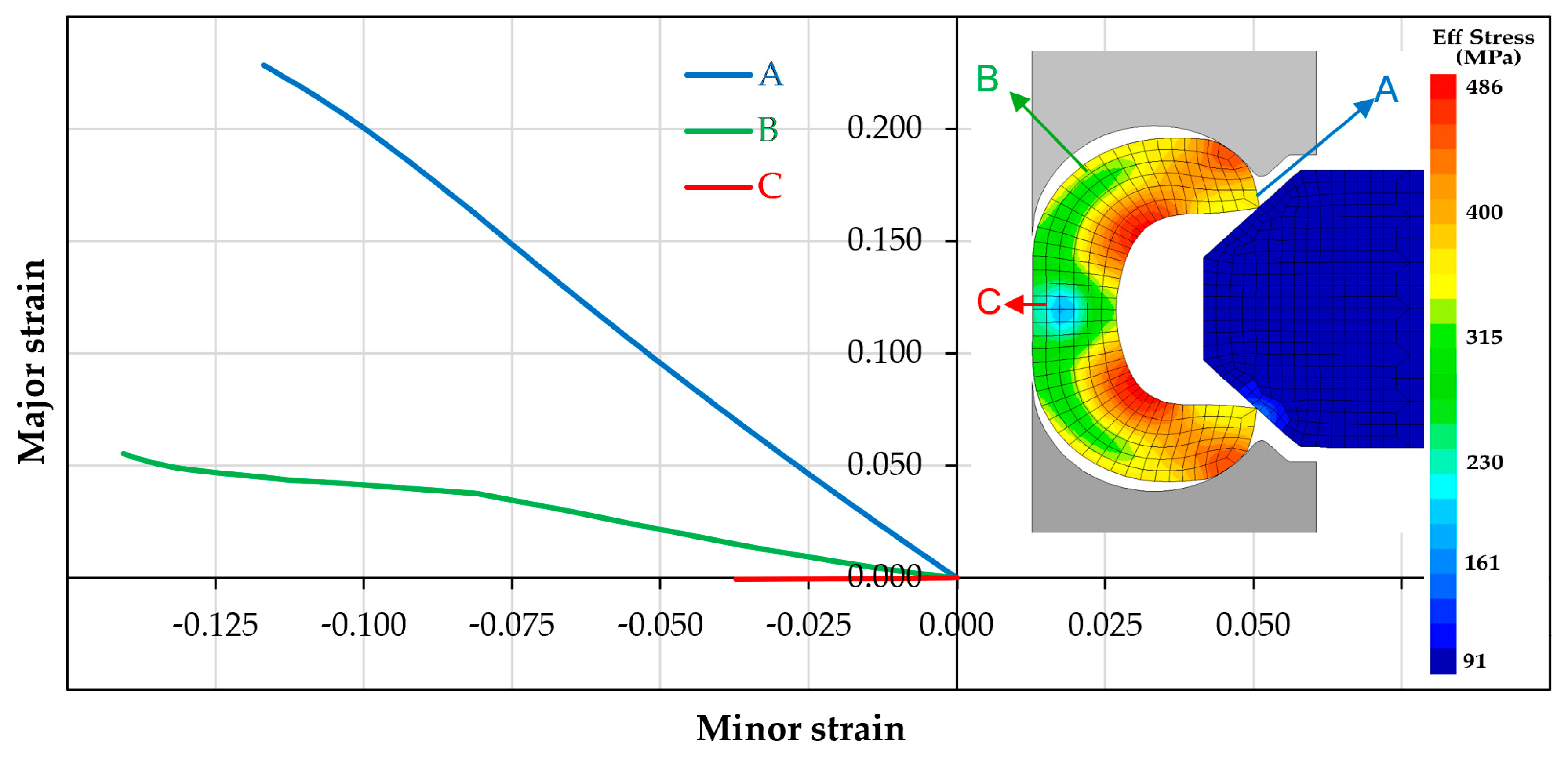
4.1. Forming of a Toroidal Shell of Circular Section
4.2. Forming of a Toroidal Shell of Non-Circular Section
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Afonso, R.M.; Alexandrino, P.; Silva, F.M.; Leitao, P.J.; Alves, L.M.; Martins, P.A. A new type of bi-material coin. Proc. IMechE Part B J. Eng. Manuf. 2019, 233, 2358–2367. [Google Scholar] [CrossRef]
- Bocharov, Y.; Kobayashi, S.; Thomsen, E.G. The mechanics of the coining process. J. Eng. Ind. 1962, 84, 491–501. [Google Scholar] [CrossRef]
- Rosado, P.M.; Sampaio, R.F.; Pragana, J.P.; Bragança, I.M.; Silva, C.M.; Martins, P.A.; Alexandrino, P.; Leitao, P. Joining by forming of bi-material collector coins with rotating elements. J. Adv. Join. Process. 2024, 10, 100265. [Google Scholar] [CrossRef]
- Alexandrino, P.; Leitão, P.; Alves, L.; Martins, P. Numerical and experimental analysis of coin minting. Proc. IMechE Part L J. Mater. Des. Appl. 2017, 233, 842–849. [Google Scholar] [CrossRef]
- Alexandrino, P.; Leitão, P.J.; Alves, L.M.; Martins, P.A. Finite element design procedure for correcting the coining die profiles. Manuf. Rev. 2018, 5, 3. [Google Scholar] [CrossRef]
- Tekkaya, A.E.; Hirsch, J.; Heingärtner, J.; Haase, R. Metal forming beyond the limits: Research and applications in incremental and hybrid technologies. CIRP Ann. 2020, 69, 601–623. [Google Scholar]
- Pragana, J.P.M.; Rosenthal, S.; Bragança, I.M.F.; Silva, C.M.A.; Tekkaya, A.E.; Martins, P.A.F. Hybrid additive manufacturing of collector coins. J. Manuf. Mater. Process. 2020, 4, 115. [Google Scholar] [CrossRef]
- Pragana, J.P.M.; Rosenthal, S.; Alexandrino, P.; Araújo, A.; Bragança, I.M.F.; Silva, C.M.A.; Leitão, P.J.; Tekkaya, A.E.; Martins, P.A.F. Coin minting by additive manufacturing and forming. Proc. IMechE Part B J. Eng. Manuf. 2021, 235, 819–828. [Google Scholar] [CrossRef]
- Gonçalves, A.; Alves, L.M.; Martins, P.A.F. Tube joining by asymmetric plastic instability. J. Mater. Process. Technol. 2014, 214, 132–140. [Google Scholar] [CrossRef]
- Alves, L.M.; Silva, C.M.A.; Martins, P.A.F. Joining tubes by internal mechanical locking. J. Mater. Process. Technol. 2017, 242, 196–204. [Google Scholar] [CrossRef]
- Sekhon, G.S.; Gupta, N.K.; Gupta, P.K. An analysis of external inversion of round tubes. J. Mech. Work. Technol. 2003, 133, 243–256. [Google Scholar] [CrossRef]
- Alves, L.M.; Reis, T.J.; Afonso, R.M.; Martins, P.A. Single-stroke attachment of sheets to tube ends made from dissimilar material. Materials 2021, 14, 815. [Google Scholar] [CrossRef]
- Alves, L.M.; Martins, P.A.F. Forming of thin-walled tubes into toroidal shells. J. Mech. Work. Technol. 2010, 210, 689–695. [Google Scholar] [CrossRef]
- Nielsen, C.V.; Zhang, W.; Alves, L.M.; Bay, N.; Martins, P.A.F. Coupled Finite Element Flow Formulation. In Modelling of Thermo-Electro-Mechanical Manufacturing Processes; Springer: London, UK, 2013; pp. 11–36. [Google Scholar]
- Yin, Y.; Xu, J.; Dong, J.; Li, Y.; Wang, Y.; Zhong, W.; Zhang, Z. CUDA-based parallel dual-grid material point method for simulating bimetallic coining process. Comput. Part. Mech. 2025. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Li, J.; Wang, H. Numerical simulation of metal flow in coin minting using MPM. Materials 2023, 16, 456. [Google Scholar]
- Liu, Y.; Zhang, W.; Wang, Y.; Yin, Y.; Xu, J. A hybrid FEM–MPM approach for high-accuracy modeling of axisymmetric forming processes. Int. J. Mech. Sci. 2023, 236, 107820. [Google Scholar]
- El-Morsy, M.; Mohamed, M.; Eltaib, M.; Attia, H. Experimental and numerical analysis of tubular component deformation using die-based forming. J. Mater. Process. Technol. 2022, 305, 117690. [Google Scholar]
- Gavrilă, C.C.; Lateş, M.T.; Grebenişan, G. Sustainable Approach to Metal Coin Canceling Methods, Using 3D Modeling and Finite Element Method Analysis. Sustainability 2024, 16, 2322. [Google Scholar] [CrossRef]
- Hartl, C. Review on Advances in Metal Micro-Tube Forming. Metals 2019, 9, 542. [Google Scholar] [CrossRef]
- Suntaxi, C.; Ghassemieh, E.; Roy, A. Tube expansion by single point incremental forming. Metals 2021, 11, 1481. [Google Scholar] [CrossRef]
- Alexandrov, S.; Lyamina, E. Analysis of strain-hardening viscoplastic wide sheets subject to bending under tension. Metals 2022, 12, 118. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, R.; Singh, T.P. Finite element analysis of tube hydroforming process for automotive applications. Metals 2021, 11, 1002. [Google Scholar]
- Koç, M.; Altan, T. Process simulation of tube hydroforming: Benchmarking study. J. Mater. Process. Technol. 2002, 125–126, 361–368. [Google Scholar]
- Palumbo, G.; Sorgente, D.; Tricarico, L. Design and manufacturing of titanium cranial prostheses via sheet metal forming. Metals 2022, 12, 293. [Google Scholar] [CrossRef]







| Property | Tensile Strength (MPa) | Elastic Modulus (GPa) | Elongation at Break (%) | Vickers Hardness (HV) | Density (g/cm3) |
|---|---|---|---|---|---|
| Typical Value | 170–350 | 83 | 8–30 | 75–150 | 10.36 |
| (mm) | (mm) | (mm) | (mm) | (mm) | (mm) |
|---|---|---|---|---|---|
| 32.65 ± 0.05 | 1.65 | 8.25 | 7.50 | 0.5 | 4, 6, 7, 9 |
| (mm) | (mm) | (mm) | (mm) | (mm) | (mm) |
|---|---|---|---|---|---|
| 7.5 | 0.75 | 7 (without gap) | 6 | 11.12 | 3.39 |
| 7 (with a gap) | - | - | 3.62 |
| (mm) | (mm) | (mm) | (mm) | (mm) | (mm) |
|---|---|---|---|---|---|
| 7.50 | 0.50 | 4.00 | 6.40 | 9.20 | 2.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alves, L.M.; Alexandrino, P.; Pereira, S. Manufacturing of Rotational Toroidal Shells in Coin Minting. Eng 2025, 6, 155. https://doi.org/10.3390/eng6070155
Alves LM, Alexandrino P, Pereira S. Manufacturing of Rotational Toroidal Shells in Coin Minting. Eng. 2025; 6(7):155. https://doi.org/10.3390/eng6070155
Chicago/Turabian StyleAlves, Luís M., Paulo Alexandrino, and Sónia Pereira. 2025. "Manufacturing of Rotational Toroidal Shells in Coin Minting" Eng 6, no. 7: 155. https://doi.org/10.3390/eng6070155
APA StyleAlves, L. M., Alexandrino, P., & Pereira, S. (2025). Manufacturing of Rotational Toroidal Shells in Coin Minting. Eng, 6(7), 155. https://doi.org/10.3390/eng6070155







