Adherent Moving of Polymers in Spherical Confined Binary Semiflexible Ring Polymer Mixtures

Abstract

Based on the coarse-grained model, we used molecular dynamics methods to calculate and simulate a semiflexible long ring–semiflexible short ring blended polymer system confined in a hard sphere. We systematically studied the distribution and motion characteristics of the long ring chain. The results show that when the short ring is short enough (L_short < 20), the long ring (L_long = 50) is separated from the blend system and then distributed against the inner wall. As the length of the short ring increases (L_short ≥ 20), the long ring can no longer be separated from the blending system. Moreover, we found that the long ring demonstrates a random direction of adherent walking behavior on the inner surface of the hard sphere. The velocity of the long ring decreases with the increase in the short ring length L_short. Specifically for L_short ≥ 20, the system does not undergo phase separation and the speed of the long ring decreases sharply along with the long ring distributed inside the confined bulk. This is related to the inner wall layer moving faster than the inside bulk of the restricted system. Our simulation results can help us to understand the distribution of macromolecules in biological systems in confined systems, including the restricted chromosome partitioning distribution and packing structure of circular DNA molecules.

1. Introduction

Cyclic polymer-restricted systems can be found in biological systems, such as the circular chromosome [1,2], circular DNA of viruses [3,4,5,6] and cyclic peptides [7]. The physical effects of topological constraints and restrictions play an important role in the structure and function of individual genetic material [8,9,10,11,12], such as the shape of chromosomes in elongated bacterial cells [13], the self-organization of DNA (or DNA-actin filament mixing systems) in cell confinement [14], and the drug delivery of spherical vesicles [15,16].

Polymer simulation is an important research method for studying the biosystem, such as the partitioning of chromatin in the nucleus [17], observing the circular DNA of viruses [18,19] and genome folding. Halverson et al. reviewed the research progress and reliability of modeling chromatin folding in eukaryotic cells using topological constraints on the topological constraints of polymers by comparing the latest theories related to simple chains (untangled and unlinked) or chain systems with the latest experiments related to genome folding. Due to the no-ends feature and topological constraints of ring chains, there is territorial segregation in a simulation system composed of 200 unconnected uncommitted uncombusted rings with a chain length of 1600 monomers [18]. This is consistent with experimental results for a partitioning phenomenon in the chromosomal region of fibroblast nuclei [20].

Phase separation is an important phenomenon in biological systems, such as membraneless organelles formed by liquid–liquid phase separation [21], the formation of the bacterial nucleoid due to the segregative phase separation [22] and compartmentalization of conventional nuclei [17]. Abnormal phase-separation mechanisms may even cause diseases, including neurodegenerative diseases, tumors, aging and infectious diseases, etc. Joyeux et al. performed a numerical simulation of the DNA chain inside the confining sphere using a coarse-grained method. They showed that the method has high sensitivity to the dissymmetry of DNA–DNA, DNA–crowder, crowder–crowder repulsive interactions, especially for dumbbells and octahedra crowders. Additionally, the demixing of the DNA coil and non-binding globular macromolecules present in the cytoplasm leads to nucleoid formation [22]. Falk et al. combined Hi-C analysis of inverted rod nuclei with microscopy and polymer simulations. They found that attractions between heterochromatic regions are crucial for establishing both compartmentalization and the concentric shells of pericentromeric heterochromatin, facultative heterochromatin and euchromatin in the inverted nucleus [17].

The semiflexible ring polymer (SRP) is an important model for simulating the study of circular biomolecules, such as circular chromosomes, eukaryotic mitochondrial DNA, circular plasmids and circular structure monosaccharides of E. coli. By introducing the stiffness of the chain, the ring chains stretch into a disk-like ring shape [23,24], similar to molecular structural characteristics. SRPs have been extensively studied theoretically and experimentally [13,22,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. The folding of SRPs in confinement and their interspersing with other SRPs are consistent with the observed biological systems phenomenon. Ostermeir et al. employed a simulation method to investigate the conformations of a single SRP confined in a sphere. By analyzing shape parameters calculated from average simulation data and theoretical analysis, they concluded that the construction of polymer rings causes buckling due to elasticity and entropy [25]. They also discovered and quantified a SRP’s conformational transition to an eight-shaped ring chain confined in a hard sphere [26]. Jeong et al. studied the morphology of SRPs when they were adsorbed on a topographically or chemically structured substrate surface using computational simulation. They found four equilibrium shapes: a round toroidal and a confined elongated shape, as well as two shapes containing bulges. Additionally, there was a cascade of transitions between elongated shapes [27]. Fritsche et al. found that different geometrical constraints can shape the spatial organization of SRP in confined conditions. Elongated, rod-like geometries reduce the number of chain overcrossings and induce ordering. Additionally, there is no preferred orientational axis in the case of spherical confinement. During the simulation process, SRP migrates from the center of the accessible space to the surrounding confined surface, forming a spool-like structure similar to DNA condensation in the capsid [28]. Experimentally, Gómez et al. used X-ray tomography to study the geometrical and topological features of disordered packages of rubber bands in a cylindrical container. For short SRPs, there was a liquid-like disordered structure with a short-range orientational order. However, for longer SRPs, the confinement caused folded configurations, and the bands were interpenetrated and entangled [36].

Biological systems are often complex and diverse, and this paper examines the kinetic behavior of semiflexible circular polymers confined in spheres of blending systems. This study helps us to understand the microscopic mechanisms of folding and movement of biomolecules in confined systems.

In this paper, we constructed a simulation model with a long SRP–short SRP blending system limited to the hard ball and studied the distribution of the long SRP in the binary mixture. We found an instance of phase separation between the long and short SRP, and the long ring is adhered to the wall.

This article consists of the following parts: In Section 2, the model and simulation details are provided. In Section 3, our results on the long ring polymer in spherically confined binary semiflexible ring polymer mixtures are given, and in Section 4, the conclusion is presented. Vesicle-restricted mixed macromolecules can deliver active macromolecules, such as DNA, peptides and some synthetic macromolecules. Our spherical shells can be regarded as vesicles. Furthermore, the simulation results in this paper can help us understand the physical mechanisms of interactions in vesicle-restricted mixed macromolecules.

2. Model and Method

During the simulation process, all ring chains, including long and short chains, are untangled and unconnected structures. We use the classical bead spring model to model the ring polymer chain, which is widely used in polymer simulations, and the simulation results of this model are consistent with the experimental results. Each ring chain is composed of L spherical monomers with a diameter of σ and a mass of m, and the length of the long ring in this article is fixed as L_long = 50, and the length of the short ring ranges from L_short = 5 to L_short = 40. The corresponding potential energy of each chain is given by

$$U=U_{\mathrm{bond}}+U_{\mathrm{angle}}+U_{\mathrm{LJ}}$$

(1)

where adjacent monomers on the chain are connected to each other by finite stretchable nonlinear elasticity (FENE) potentials [41]:

$$U_{\mathrm{bond}}(r)=-\frac{K{R}_0^2}{2}\ln [1-{(\frac{r}{R_0})}^2],r<R_0$$

(2)

where r is the distance between two adjacent monomers on a ring chain. K = 30k_BT/σ² is the spring coefficient, and the finite ductility correlation parameter R₀ = 1.5σ is used to avoid chain crossing.

To describe the rigid property of the semiflexible chains, we introduce the bond angle potential energy between adjacent bonds, as follows [42,43]:

$$U_{\mathrm{angle}}=K_{bending}[1-\cos (\theta -{\theta }_0)]$$

(3)

where θ is the angle between two adjacent bonds and K_bending is the bending energy. Additionally, θ₀ is the equilibrium value of the angle, for different length of rings, θ₀ = [π × (L − 2)]/L, such as for L_long, θ₀ = [π × (50 − 2)]/50 = 0.96π. When K_bending is larger, the chain is more difficult to bend, that is, the chain is rigid. In this paper, the bending energy of the long ring is K_b-long = 100, and the bending energy of the short ring is K_b-short = 50.

To prevent overlap between all monomers, all bonded and non-bonded monomer interactions use the cutoff Lennard–Jones (LJ) potential:

$$U_{\mathrm{L}J}(r)=\left\{\begin{array}{c}4\epsilon [{(\frac{\sigma }{r})}^{12}-{(\frac{\sigma }{r})}^6+\frac{1}{4}],r\le 2^{1/6}\sigma \\ 0,r>2^{1/6}\sigma \end{array}\right.$$

(4)

where r is the distance between two monomers, the truncation radius is r_c = 2^1/6σ—that is, long ring–long ring, short ring–short ring, long ring–short ring, long ring–hard ball and short ring–hard ball interactions are all pure repulsion, and the interaction strength ε = 1.0k_BT.

During the simulation, the binary semiflexible ring hybrid system is confined to a hard ball with a radius of R = 20σ. The spherical surface consists of LJ particles with the same diameter size σ and mass m as the polymer monomer. The velocity Verlet algorithm is used to integrate Newtonian equations of motion with a time step of Δt = 0.006τ₀, where τ₀ = (mσ²/k_BT)^1/2 is the inherent MD unit of time. The units of reduction k_BT = 1, σ = 1, m = 1, τ₀ = (mσ²/k_BT)^1/2 = 1 are units of energy, length, mass and time, respectively. The total particle number density of the binary mixed system is defined by ρ = (L_long ∗ N_long + L_short ∗ N_short)/V, where N_long and N_short are the number of long rings and the number of short rings, L_long and L_short are the long ring chain lengths and short ring lengths, respectively, and V is the volume of the hard ball. According to the results of a previous study, the necessary condition for phase separation in the long-short ring blending system is the high particle number density, and to prevent semiflexible ring deformation, the particle number density in this paper is fixed to ρ = 0.5σ⁻³. In this paper, L_long = 50, N_long = 1 is fixed, N_short can be calculated according to the number of different particles L_short, and the specific values are given in

Table 1. The detailed simulation parameters covered in this paper.

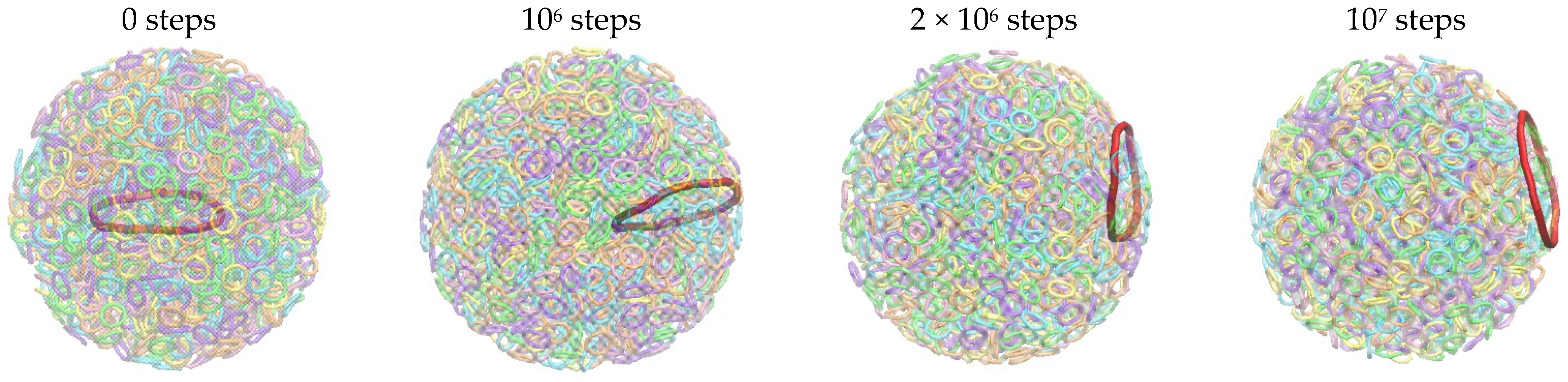
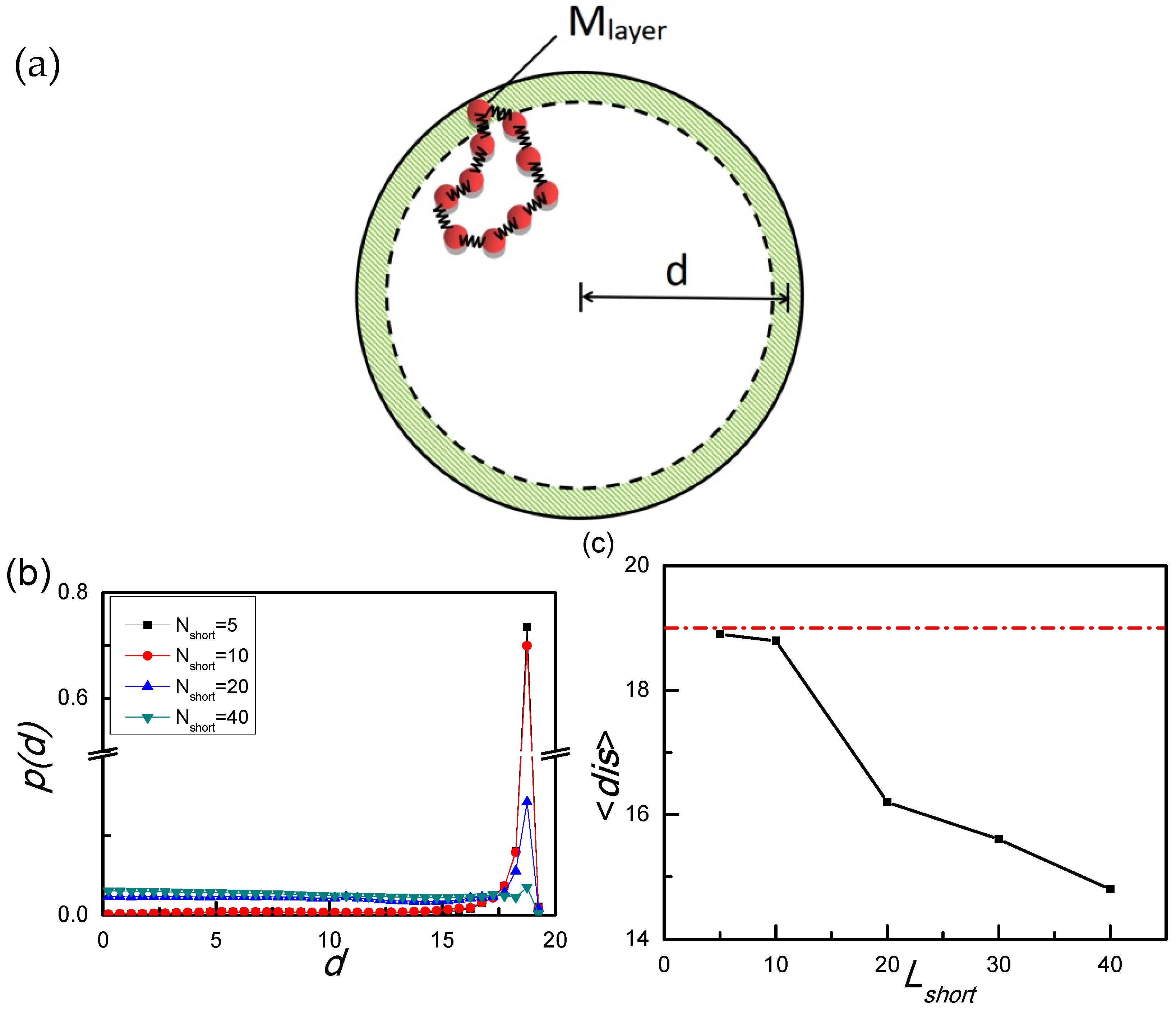
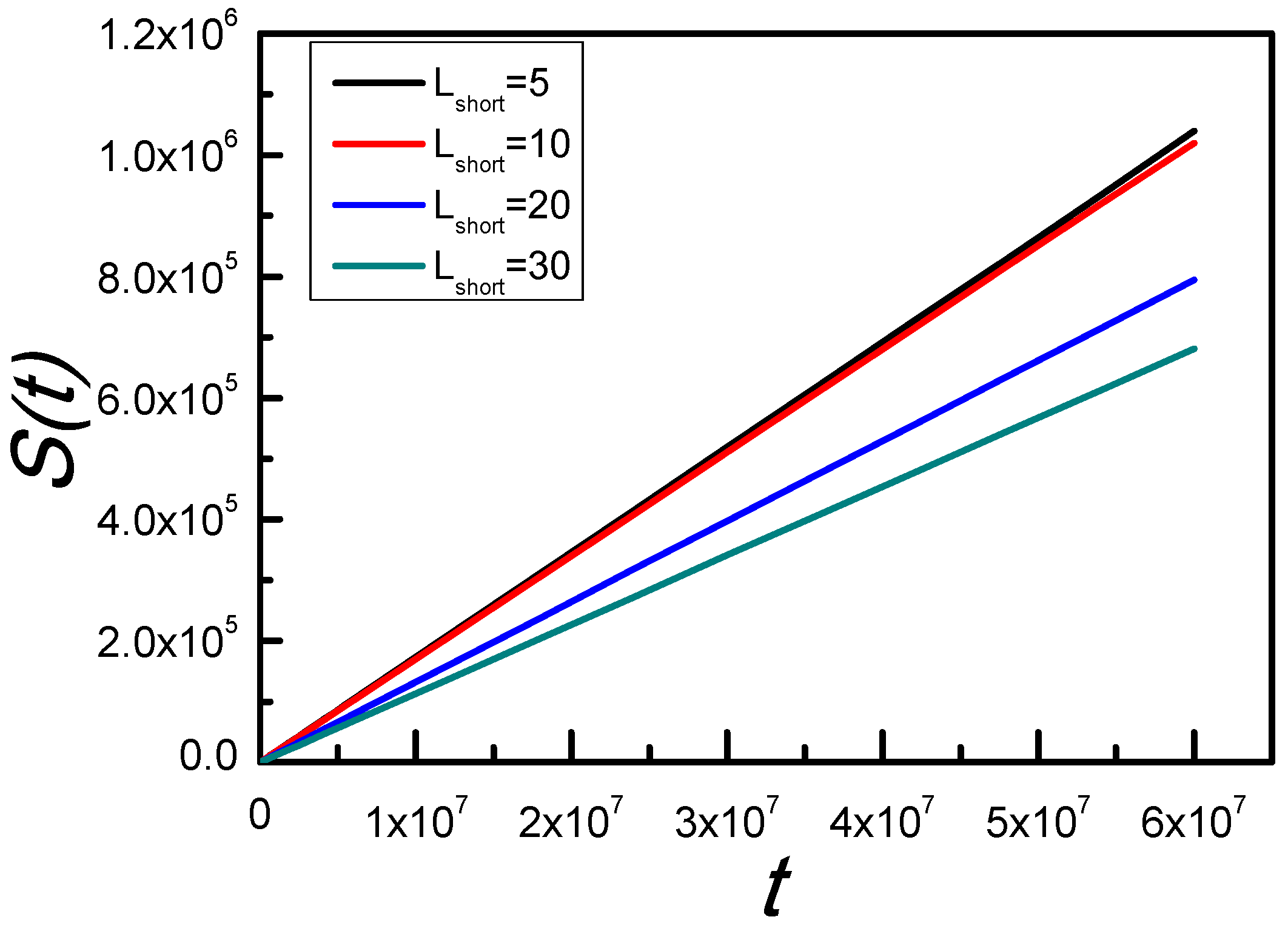
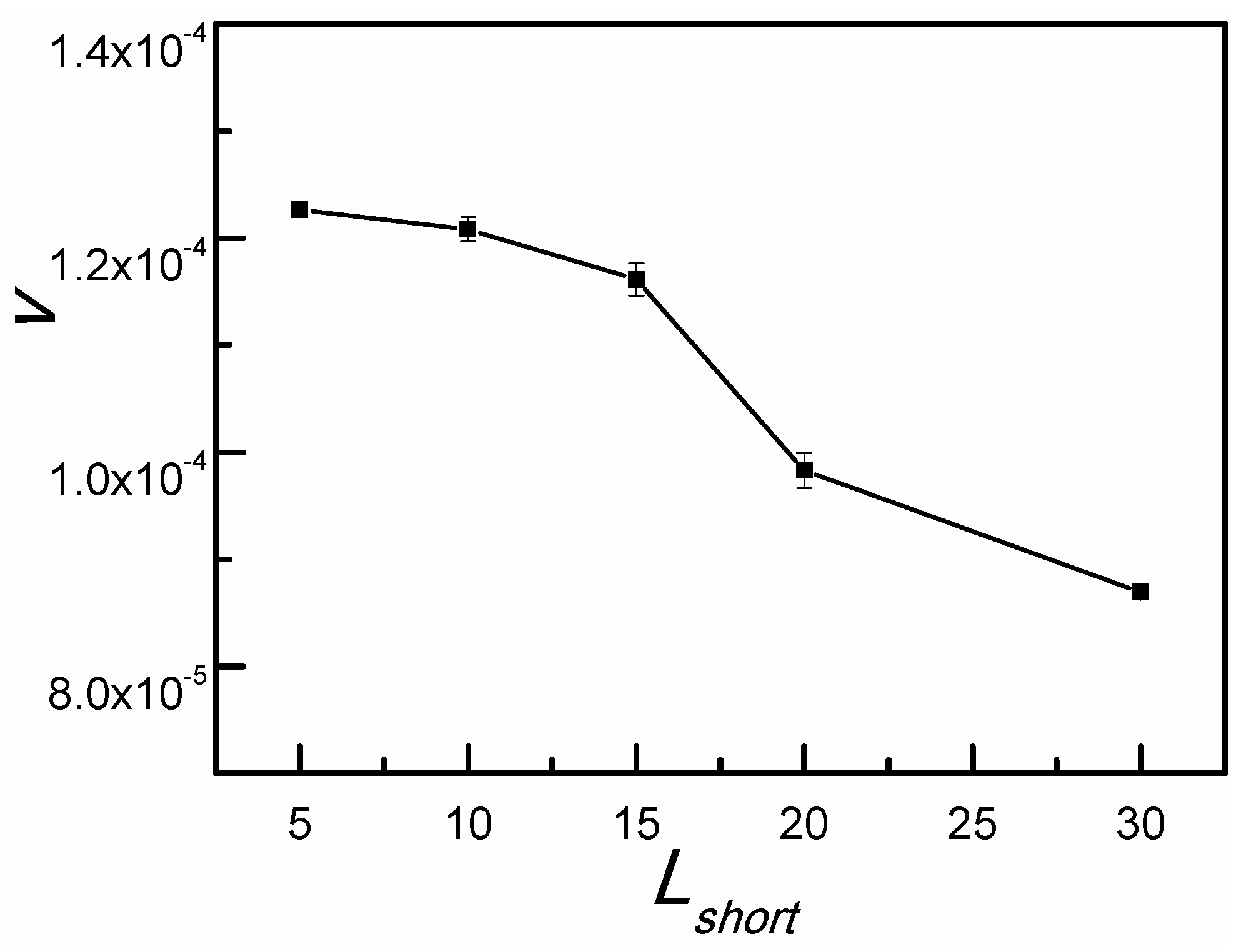
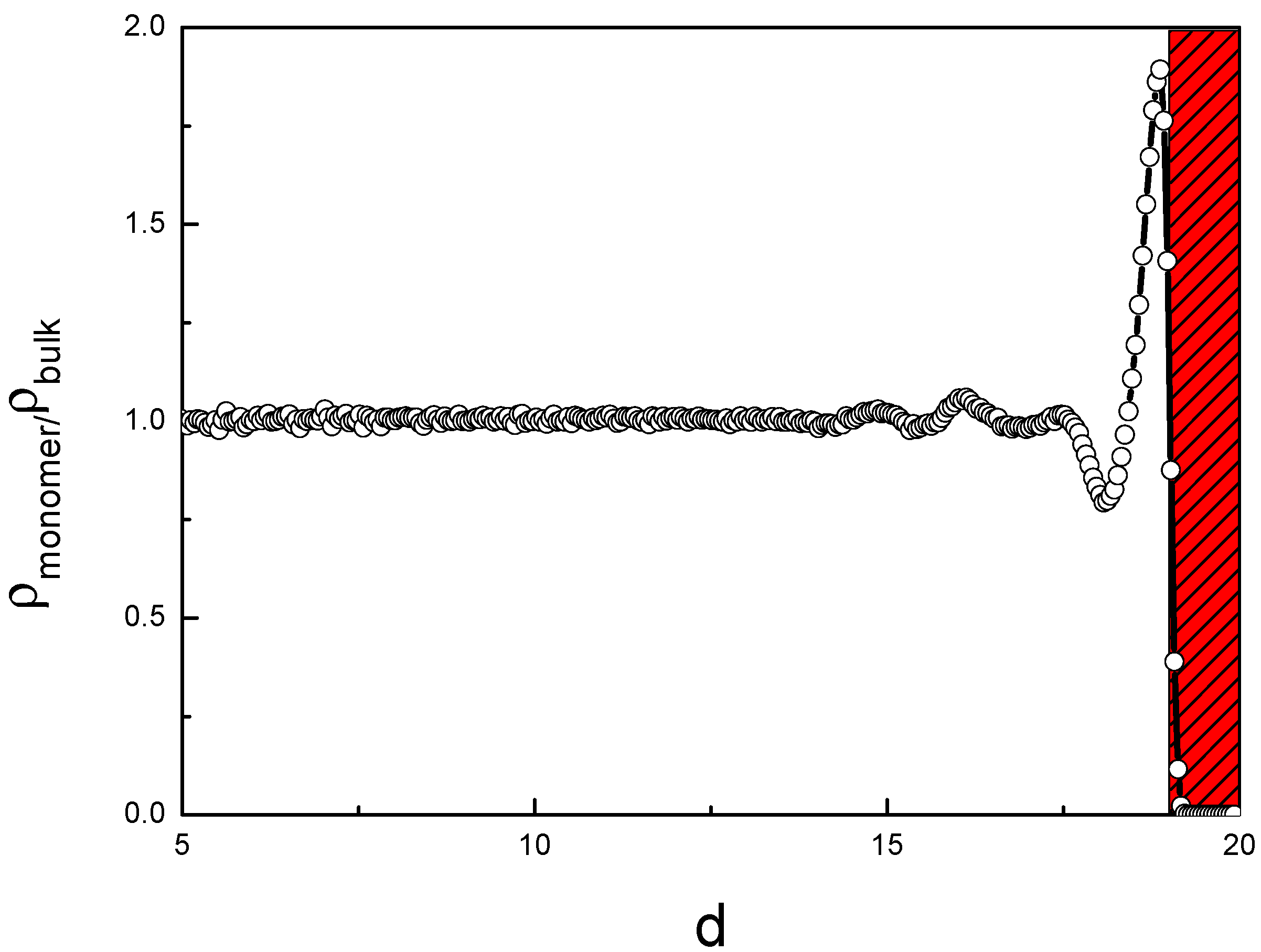
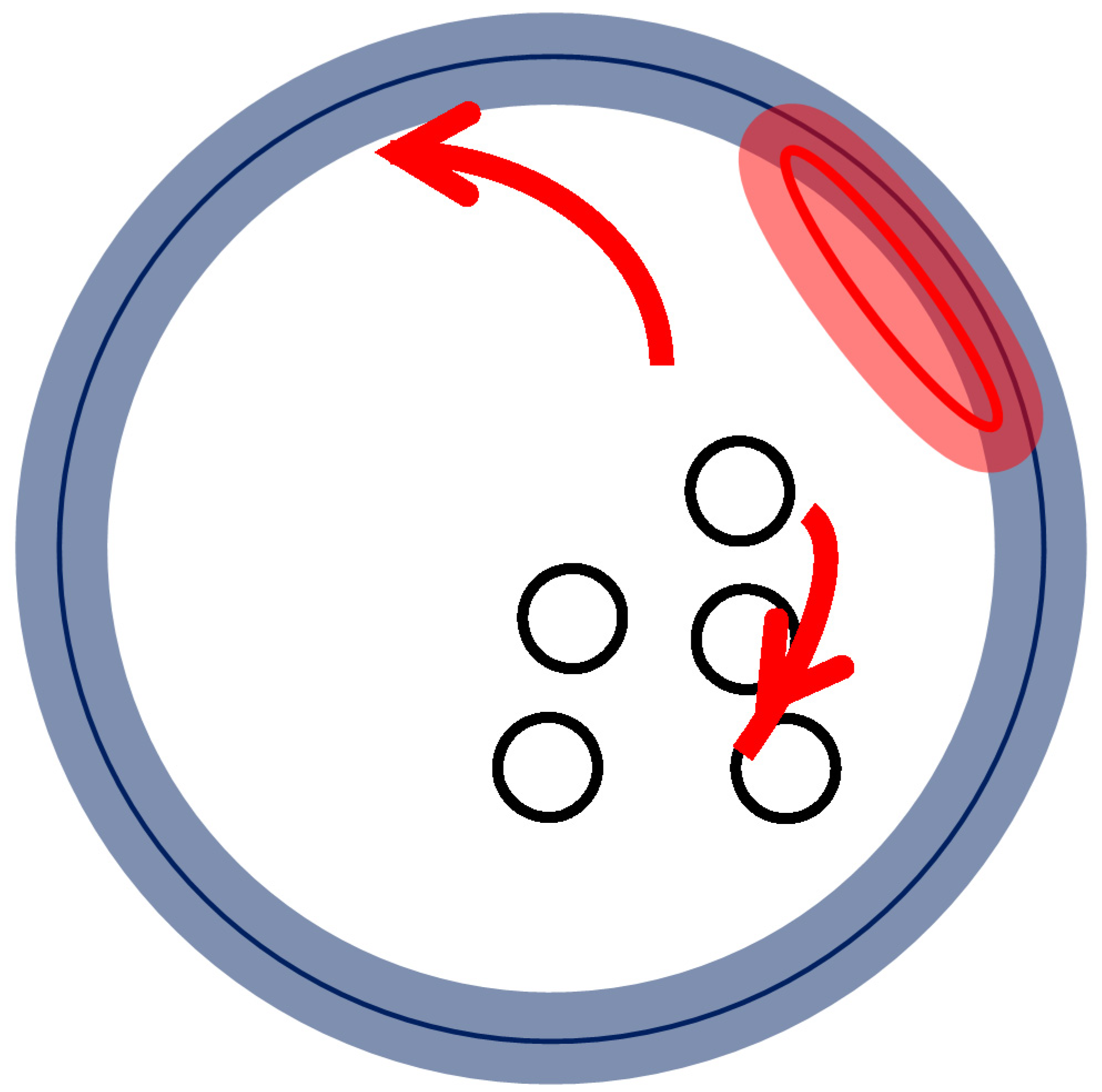
Radius of Sphere	Llong	Nlong	Lshrot	Nshort	Llong ∗ Nlong + Lshort ∗ Nshort
20	50	1	5	2863	14,365
			10	1432
			20	716
			30	477
			40	358

of Section 3.1. Unless otherwise stated, the relevant result is L_long = 50, L_short = 1, L_short = 10.

First, we place all ring chains completely randomly inside the hard ball. All rings remain untangled and unconnected at all times in the simulation with other semiflexible rings. Then, the system is balanced in the NVT ensemble, the total running time is 10⁸ steps, where the first step running time Δt₁ = 10⁷ is used to ensure balance. After Δt₁, data are recorded every 10⁴ steps as a sample. Using a Nosé–Hoover thermostat, the reduction temperature is T* = 1.0 in ε/k_B. All The simulations were performed in the open source molecular dynamics software package LAMMPS [44] (Sandia National Lab, Albuquerque, NM, USA).

3. Results and Discussion

3.1. Distribution of the Binary Mixture

In our system, the radius of the hard ball outside is fixed at R = 20. Since there is a strongly repulsive force for the distance between the monomer of the long SRP and a sphere surface less than d < 1, the distance between the monomer of the long SRP and the sphere center ranges of d is d = 0–19. The length of the long SRP is fixed at L_long = 50, which is commonly used to calculate long SRPs in simulation studies [23,24]. Additionally, the length of the short ring in the bulk involved in this article is in the range of L_short = 5–40, and the corresponding number of short rings can be calculated, and the specific values are given in the following Table 1. Calculation details of the simulation parameters in Table 1 are given in Supplementary Information. A screenshot of the simulation system is shown in Figure 1. The snapshots are after long simulation steps and the system is stable. In general, the system is stable after 10⁷ steps, and 10⁷–10⁹ steps are used for statistics, if we take 10⁴ steps as a data point, there are about 99,000 points per-sample. Additionally, there are N_sample = 50 samples. All calculated results ensemble averaging over many conformations and all SRPs involved.

The rings are initially set as unknotted and unlinked. All chains cannot cross and are preserved during the whole simulation process. To examine the topological state of the system, we calculate the mean square radius of gyration R_g² and the prolateness parameter p, defined, respectively, as

$$R_{{}_g}^2=\frac{1}{N}{\displaystyle \sum _{\mathrm{i}=1}^N}{(r_i-r_c)}^2$$

(5)

Additionally, we analyze the shape of SRPs by calculating the prolateness parameters, which are defined from the radius of the gyration tensor:

$$T_{\alpha \beta }=\frac{1}{N}{\displaystyle \sum _{\mathrm{i}=1}^N(r_{i\alpha }-r_{\alpha cm})(r_{i\beta }-r_{\beta cm})} (\alpha ,\beta =x,y,z)$$

(6)

where N is the chain length, and α and β represent the Cartesian components. The vectors r_i and r_icm are the positions of the monomers and the center-of-mass of the SRPs, respectively. The prolateness parameter p is defined as

$$\mathrm{p}=\frac{(2{\lambda }_1-{\lambda }_2-{\lambda }_3)(2{\lambda }_2-{\lambda }_1-{\lambda }_3)(2{\lambda }_3-{\lambda }_1-{\lambda }_2)}{2{({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2-{\lambda }_1{\lambda }_2-{\lambda }_1{\lambda }_3-{\lambda }_2{\lambda }_3)}^{\frac{3}{2}}}$$

(7)

where λ₁, λ₂, and λ₃ are the three eigenvalues of the tensor with λ₁ ≤ λ₂ ≤ λ₃. For perfectly oblate objects (${\lambda }_1<{\lambda }_2={\lambda }_3$), the prolateness is p = −1. In addition, by taking the average of the stable structures of SRP, we can calculate the average prolateness of the ring chains; the prolateness parameter for a 50-bond ring polymer chain with K_b-long = 100 is <p> = −0.8, and the bracket represents the ensemble averaging over all conformations. For our system, using 10⁷ steps to 10⁸ steps, every 10,000 steps to sample points, and using 50 samples to average, we used a total of 450,000 sample points. Therefore, SRPs can be regarded as disk-like structures and the topological properties of SRPs are completely different from those of flexible ones. In our simulation, $<R_{\mathrm{g}}>=7.9$ for the long SRP, which is close to the radius of the 50-bond circle (r = L_long/2/π = 7.958). Here, b is the bond length, and our simulation result is b = 0.97σ = 0.97, which is widely used in polymer simulation [23,24,38,43]. Thus, the SRPs with K_b,ring = 100 are completely extended and have stiff structures.

As shown in the snapshot in Figure 2, the system reaches equilibrium; the long SRP gradually detaches from the bulk. To avoid the effect of position placement of the long SRP at the initial moment, the long SRP is placed near the center of the ball, as shown in Figure 2. We recorded a typical simulation process in which the rings are distributed at different timesteps, screenshots are shown in Figure 2. As the simulation time increases, the long SRP gradually detaches from the bulk, eventually adheres to the wall distribution and reaches equilibrium.

After reaching equilibrium, we calculated the distribution of long ring beads within the spherical shell, demonstrating that the ring chain is distributed on the inner surface.

To verify the existence of separation structures in a binary hybrid system of short SRPs and a long SRP, we calculated the probability of the occurrence of the long SRP being located in different shells as follows:

$$\mathrm{p}\left(\mathrm{d}\right)=\frac{M_{layer}(d)}{L_{long}}$$

(8)

where M_layer is the monomer number located in the d-th shell, as shown in Figure 3a. As shown in Figure 3b, for L_long > 20, the p(d) curve has no peak and even shows a slight decrease. The distribution of the long SRP is almost uniform throughout the sphere, with a small peak near the wall (d ≈ 19). As L_long decreases to L_long = 5 and L_long = 10, there is a significant peak near the wall; for this condition, the long SRP adheres to the inner surface of the hard sphere, and there is a structure of long-short ring separation in the binary hybrid system with the long-short SRP binary mixture. For L_long > 20 binary hybrid systems, the long SRP and the short SRPs are fully mixed and evenly distributed throughout the confined space, while for the system where L_long is reduced to 5 and 10, the long and short rings are almost completely separated. Experimentally, there exists phase separation for large and small blended particles confined within the sphere.

We also calculated the average distance between the monomer of the long SRP and the sphere center <dis>, defined as:

$$<dis>=\frac{{\displaystyle \sum _{\mathrm{i}=1}^{N_{sample}}{\displaystyle \sum _{j=1}^{L_{long}}di{s}_{ij}}}}{N_{sample}\ast L_{long}}$$

(9)

Figure 3c shows the relationship between the average distance of the long-ring monomer from the center of the sphere <dis> with L_short under different L_short. <dis> decreases as L_short increases. When L_long = 5, 10, <dis> the value reaches above 18, as shown by the dotted line. The results show that most monomers of the long SRP are distributed in the layer closest to the inner surface of the hard sphere, while the short semiflexible ring constitutes the anisotropic matrix inside the sphere.

In fact, in the case of spherical restriction, there is entropy attraction between the long SRP and the spherical shell. This strong entropy attraction causes the long SRP to move towards the spherical shell, eventually forming a separation structure of the long and short rings in the binary semiflexible ring hybrid system.

Yodhet et al. [45,46] studied the separation behavior of binary colloids of different sizes limited to rigid vesicles, and the results showed that this separation structure was formed at a sufficiently high colloid volume fraction. Our system is similar to a binary hardball hybrid system. In a binary hard-ball hybrid system, two larger balls close to each other do not change their interaction energy but increase the space reachable by other particles, causing the system to increase entropy, decrease free energy, and satisfy (3/2) α′∙φ_s∙k_BT [46,47]. Here, α′ is the ratio of the radius of the large ball to the radius of the ball (R_L/R_S), and φ_s is the volume fraction of the ball. Although our binary semiflexible ring system is more complex than the binary hard ball system, there is a similar emptying interaction between the long SRP and the wall, and this entropy attraction also depends on the chain length ratio of the long SRP to the short semiflexible ring, i.e., α = L_long/L_short. The results showed that the shorter the L_short (the larger the α), the stronger the attraction between the long SRP and the wall. If α ≤ 2.5 (i.e., L_short ≥ 20), no significant separation structure can be observed in a binary semiflexible ring hybrid system for all particle densities and long SRP bending energies.

3.2. Adherent Moving of the Long SRP

We found adherent moving of the long SRP in spherically confined binary semiflexible ring polymer mixtures. Figure 4 shows all the regions that the monomers of the long SRP can cover at different times. The time interval is 10⁴ steps. Additionally, the total number of trajectories is 4000. As shown in Figure 4a, for the L_long = 30 simulation system, beads of the long SRP have a high range of motion throughout the space inside the sphere. As can be seen in Figure 4b, for L_long = 10, the range of activity of beads of the long SRP is limited to the inner shell area of the adherent, and the ball formed by the trajectory points is hollow. Therefore, the long SRP-shaped polymer walks against the wall in the blending system.

We further calculated the time-dependent distance S(t) and the average velocity v of long SRPs after equilibrium as follows:

$$S(t)=<{\displaystyle \underset{0}{\overset{t}{\int }}s(t^{\prime })d{t}^{\prime }}>$$

(10)

The distance S(t) we calculated is the total length of the trajectory of the center of mass of the long SRP. For example, when the center of mass of the long SRP moves from t = 0 to position t, S_t(t) is the length of the trajectory that the long SRP passes through during this motion. The distance S_t(t) is the sum of S_t(t) = d₁ + d₂ + d₃ + … + d_t. To investigate the speed of the chain motion in the restricted system, we computed the scalar of the distance and calculated the average velocity v based on the slope of S(t), as shown in Figure 5 and Figure 6. Here, we discuss the distance S(t) instead of the displacement $\overrightarrow{r}(t)$ and the bracket <…> represents ensemble averaging over many conformations. Additionally, velocity V is the ratio of the distance ∆S and the time ∆t, the slope of S(t). As L_short < 20, nearly complete segregation occurs between long and short SRPs, where long SRPs are attached to the sphere surface and only move along the sphere surface. When ρ = 0.5σ⁻³, the average velocity of long SRPs v decreases with the increase in L_short, as shown in Figure 6. As L_short < 20, long SRPs diffuse in a wall-attached shell region with phase separation. With the increase in L_short, i.e., L_short = 20 and 30, long SRPs with low content are immersed in the matrix of short SRPs. Additionally, the inside bulk of the restricted system moves faster than the inner wall layer, and the motion velocity of long SRPs is dominated by the short SRPs matrix and significantly slows down as L_short increases.

For polymer-restricted systems, there is a decrease in system density at the inner layer near the confined surface. There are density oscillations (“layering”) near the inner wall of the sphere, well known for dense fluids near hard walls [48,49,50,51,52,53,54,55,56]. As shown in Figure 7, we calculate reduced polymer number density ρ_monomer/ρ_bulk, where ρ_monomer is the number density of different shell and ρ_bulk is the number density of the inside bulk. This shows that the oscillation of monomer densities fades away for d < 10 by forming layers. The ordered monomers in the nearest inner layer (d = 19) of the sphere help the monomers to be ordered in the second layer (d = 18), and in turn, the third (d = 17) and fourth layers (d = 16) are also formed in a layer-by-layer manner leading to the density oscillations. Additionally, ordering becomes weak as d decreases. Such a layering structure is observed both in polymer systems and in the various confined liquid systems, such as ionic liquids in graphene double layers [57].

Due to the number of possible conformations of polymer chains being limited by an impenetrable object, polymer chains tend to move away from the wall. The monomer density in the closest adherent layer d ≥ 19 is relatively low (region colored in red). Additionally, as the distance from the wall increases, monomers significantly aggregate in the interface layer (d ≈ 18.8), and then the monomer density gradually decreases. Inside part of the sphere with d < 10, the density is stable, ρ_monomer and ρ_bulk are almost equal, and ρ_monomer/ρ_bulk≈1. Chains are affected by the wall’s limitation and the system’s uniform density. That is, the lower density of the polymer chain nearest the wall inevitably increases the chain density of the central area of the bulk, and the increase in the density of the central area of the bulk will in turn produce a force that pushes the chains towards the direction of the wall. Therefore, a lower density layer of is formed nearest the wall surface. The movement speed in the close layer is faster than the internal bulk. When the long ring separates from the blending system, it locates in this adherent layer, where the density is lower and the chain movement speed is faster. Moreover, there is a peak in density immediately left to the minimum, as shown in Figure 7. Additionally, because of the existence of highly dense areas, once the long SRP is distributed in the inner surface layer d≈19, the high-density layer blocks the long SRP from entering the interior. It is difficult for the long SRP to enter the interior d < 19 and then move throughout the inner surface. When L_short ≥ 20, the motion is slower as the ring length increases, and the long ring cannot be separated into the adherent layer and stay in the bulk. Because of the increased length of short chains, the ring movement slows down naturally. Moreover, the long ring cannot be separated from the inside bulk. The long ring distributes both in the interface layer and in the bulk. Combining the above two factors, the average velocity of the long ring v drops significantly for L_short ≥ 20.

All SRPs and the hard ball have repulsive volume, i.e., where other individuals cannot access it. As shown in Figure 8, the shades of red and blue represent the excluded regions of the long SRP and the wall, respectively. When the number of small rings increases, corresponding to the ρ = 0.5σ⁻³ in this article, the large ring is required to adhere to the wall; that is, the exclusion volume of the large ring coincides with the exclusion volume of the spherical monomer, giving the small ring more room for activity so that the entropy of the small ring increases, and the system is oriented to the separation of the two phases of the large ring and the small ring.

When the long SRP moves to the wall, the excluded regions of the long SRP and the wall (shades of red and blue) overlap. The short SRPs’ entropy therefore increases. The reduction in free energy produces an “entropic force” that pushes the long spheres to the inside surface. When the long SRP is moved to a flat wall, moreover, the overlap volume and the free-energy loss are approximately doubled [58]. This phenomenon of entropy leading to the separation of mixed phases is often found in other systems. In binary hard-sphere mixtures, these effects are known to drive the crystallization of large spheres in the bulk [13,59,60] and on flat surfaces.

Furthermore, the shape of the wall can lead to entropic forces in a specific direction along the wall. For example, the larger spheres are locally repelled from an edge cut into the wall [61] and attracted to a corner (i.e., where the “wall” meets the “floor”) [62]. If the wall has a constantly changing radius of curvature, these forces are predicted to act everywhere along it [61]. As shown in Figure 8, when the long SRP is near the wall, the overlap volume depends on the wall’s curvature radius. The large sphere therefore moves in the direction of increasing curvature to minimize the small SRPs’ excluded volume. For our system, the outer surface is spherical, i.e., the curvature of the inner surface is equal everywhere, so the long ring moves in a random direction along the inner surface. The long SRP moves along the wall to maximize the size of the overlap region, as indicated by the arrow.

4. Conclusions

We simulated a long semiflexible ring–short semiflexible ring blending system confined in a sphere, and by changing the length of the short ring, the phase separation results were obtained when the short ring length L_short < 20. The phase separation, related to entropy, coincides with the exclusion volume of the wall when the large ring is attached to the wall, providing more activity space for the small ring, and the entropy of the small ring increases. Additionally, after the large ring is attached to the wall, it moves randomly along the wall in a random direction. By calculating the distance and speed of the long ring, after comparison, we find that as the length of the short ring chain increases, the movement of the long ring gradually slows down, and when there is no more phase separation, the movement of the long ring slows down rapidly. As phase separation disappears, long rings are distributed within the system rather than against the wall. In the restricted sphere, due to the relatively low particle density of the adherent layer, the range of motion space is large, and the internal motion is slower than the motion of the adherent layer. As a result, the movement of the long ring slows down rapidly. Our research helps to understand the separation of macromolecular blending systems in confined biological systems, such as chromosomal partitioning and the self-organization of DNA–actin filament mixing systems with cell confinement.