Abstract
We review the construction and evolution of mathematical models of the Arabidopsis circadian clock, structuring the discussion into two distinct historical phases of modeling strategies: extension and reduction. The extension phase explores the bottom-up assembly of regulatory networks, introducing as many components and interactions as possible to capture the oscillatory nature of the clock. The reduction phase deals with functional decomposition, distilling complex models to their essential dynamical repertoire. Current challenges in this field, including the integration of spatial considerations and environmental influences like light and temperature, are also discussed. The review emphasizes the ongoing need for models that balance molecular detail with practical simplicity.
1. Introduction
In biology, explanations are given by mechanisms: how and why are usually treated as equivalent questions. Mechanisms can be represented through models describing their essential parts and interactions. Moreover, models illustrate how these parts and interactions fit within a system to produce an observed behavior. Consequently, modeling requires the decomposition of the system into parts and identifying those performing the operations giving rise to the phenomenon of interest [1]. This decomposition may proceed in several ways, which will, in turn, modify our understanding of the system’s function [2].
In systems biology, these working units are commonly network motifs [3] or regulatory modules [4] embedded in gene regulatory networks. The main method to probe into mechanisms in a system thus decomposed is through genetic perturbations [4]. Therefore, modeling proceeds iteratively through a constant dialogue between theory and experiment [5]. This iterative cycle establishes a positive feedback loop by which, as more data becomes available, model construction accelerates. The constructed models, in turn, guide further experimental work. Nevertheless, an indefinite continuation of this cycle is neither possible nor desirable for practical and computational reasons. As models become increasingly complex and detailed, they also become less tractable, i.e., harder to develop further, analyze, and manipulate. Arbitrary detail may be obtained by steadily decomposing the system into ever-growing lists of parts, but dynamic mechanistic explanation requires an account of the working parts.
We focus here on the development of mathematical models of the Arabidopsis circadian clock, dividing them into two phases that we have named extension and reduction phases. The extension phase consists of the bottom-up construction of regulatory networks to accurately reproduce the oscillatory behavior of the molecular components of the clock. It is thus concerned with the structural decomposition of the system. The main model lineage is represented by models of ordinary differential equations (ODEs) coming from Andrew Millar’s laboratory at the University of Edinburgh. Several of the models in the expansion phase have already been reviewed in [6]. The reduction phase is instead centered on functional decomposition and (to our knowledge) has not been reviewed so far. In the reduction phase, the constructed models are pruned so that the essential regulatory modules are identified, and the key dynamical features of the model are studied.
In what follows, we review the principal models of the plant circadian clock, classifying them under either the expansion or reduction phase. Finally, we cover recent advances in the field and discuss three of the main challenges ahead for clock models, namely the inclusion of spatial structure in the model or considering the roles of either light or temperature on the properties of the clock.
2. Chronological Development of Arabidopsis Circadian Clock Models: Expansion Phase
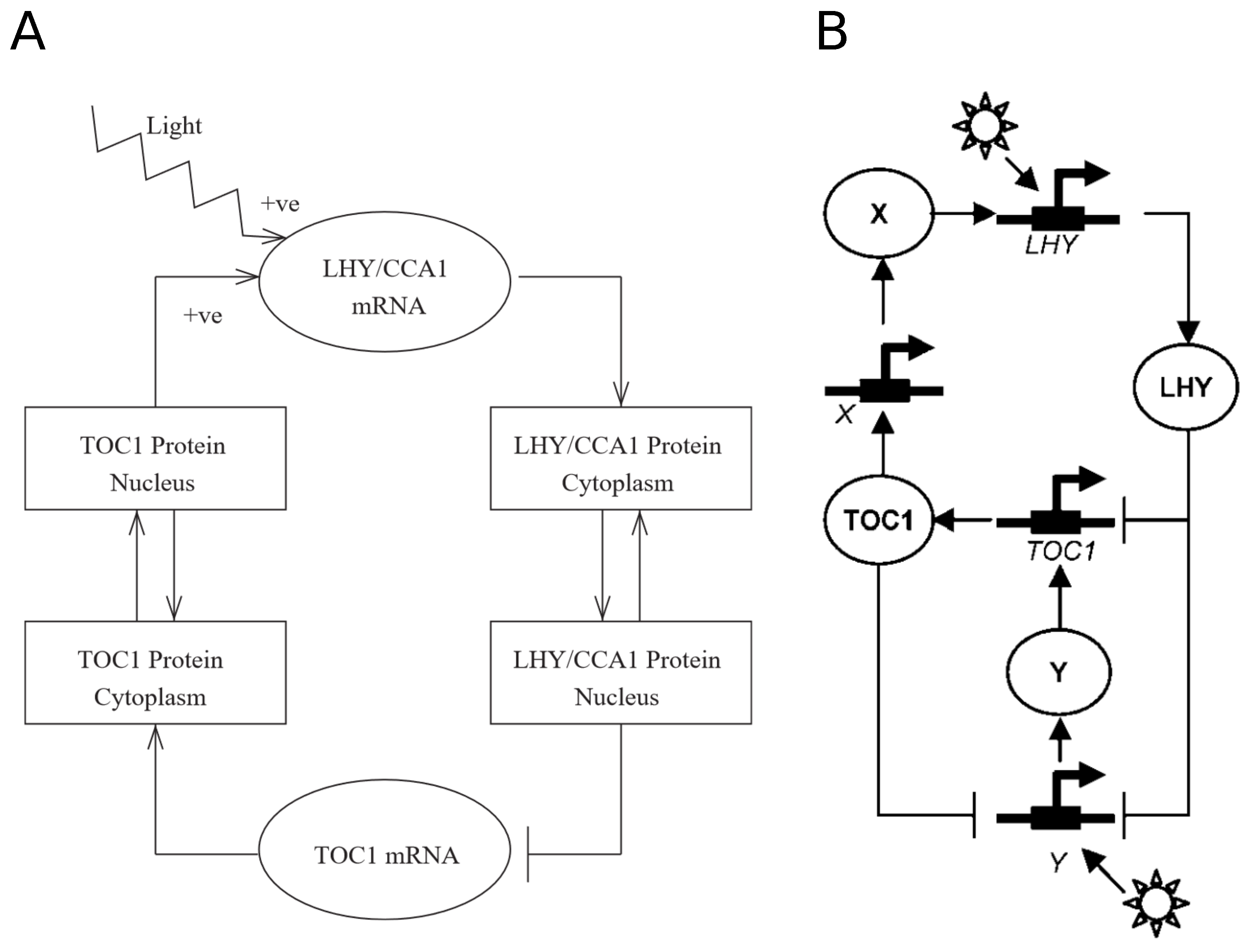
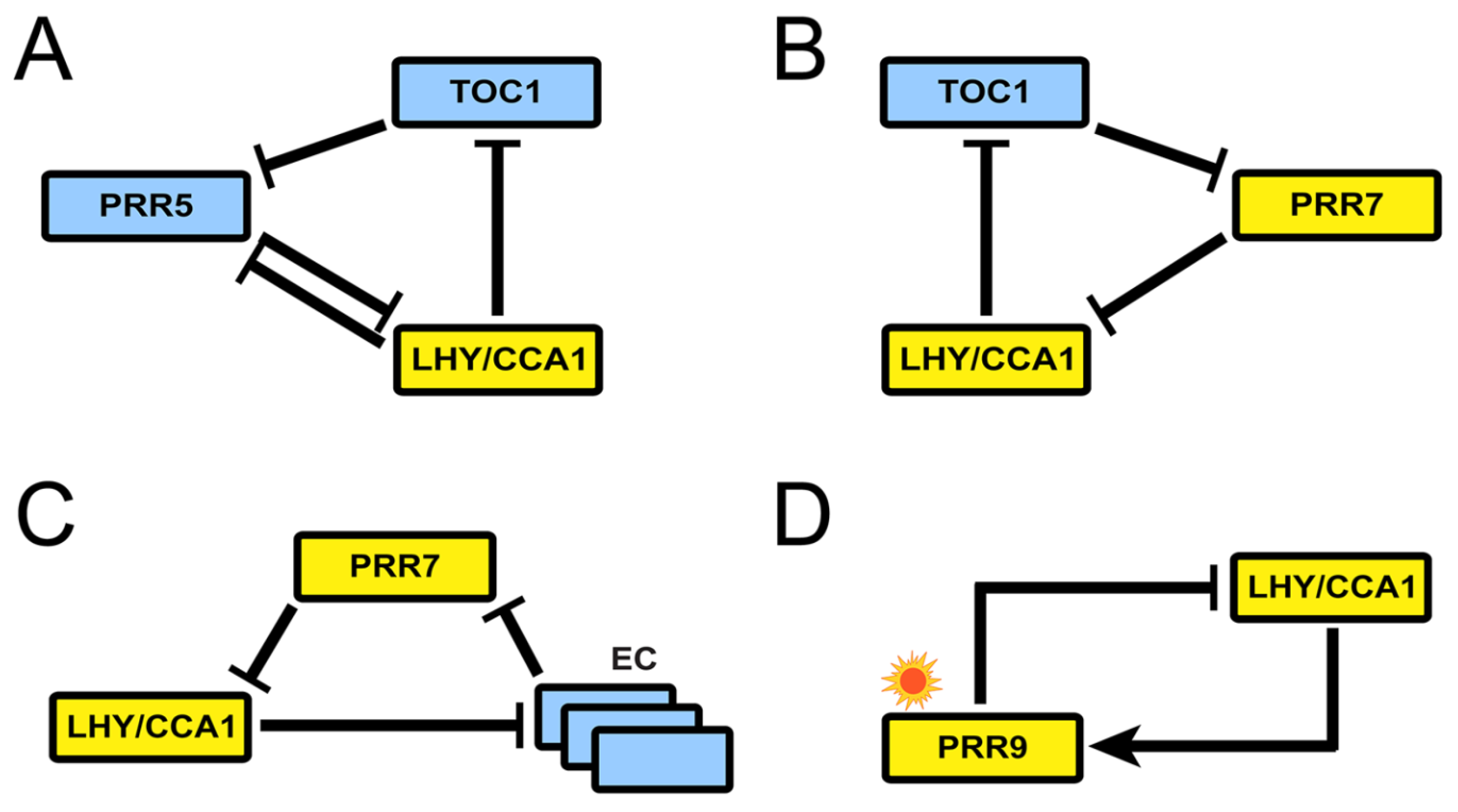
At the roots of Arabidopsis thaliana circadian oscillator modeling is Locke’s 2005 model, henceforth named L2005a. (The convention so far with Arabidopsis clock models has been to name them using the name of the first author and either the year of submission or publication. In what follows, we use the names of the models given by later works citing them.) L2005a [7] is comprised of a single negative feedback loop, the simplest network motif with oscillatory behavior [3]. It is a transcription-translation feedback loop wherein the transcription factors CIRCADIAN CLOCK ASSOCIATED 1 (CCA1) and LATE ELONGATED HYPOCOTYL (LHY), modeled as a single variable because of their partially redundant roles, repress the transcription of TIMING OF CAB EXPRESSION 1 (TOC1), which positively regulates the former (Figure 1A). Entrainment is modeled through light activation on LHY/CCA1 transcription. This makes the network unable to respond to day length, as LHY activation happens only at dawn, rendering the model insensitive to light at the end of the photoperiod.
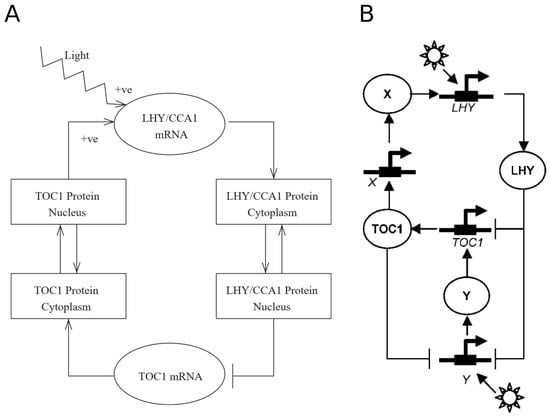
Figure 1.
Structure of the circadian clock in L2005a and L2005b. (A) The circadian clock in L2005a consists of a single feedback loop, where LHY/CCA1 inhibits the expression of TOC1, which activates it. (B) Two new unknown components, X and Y, are included in L2005b to account for experimental data. Reproduced with permission from [7] (A), and with modifications from [8] (B), Creative Commons license.
This system makes for an effective oscillator, but it falls short in predicting most experimental observations. At least two new components are needed: (i) “X”, to explain the delay between TOC1 transcription in the evening and LHY/CCA1 activation in the following morning; and (ii) “Y”, an additional light-responsive component to account for LHY/CCA1-independent entrainment. “X” mediates LHY activation by TOC1 and “Y” forms a feedback loop with TOC1, which explains the oscillatory behavior found in lhy;cca1 double mutants. These two components are added in a new version of the model, which we call L2005b [8]. This interlocked feedback loop (Figure 1B) can account for the experimental data available at the time and shows a robust behavior even upon parameter changes, thus overcoming the weaknesses of the preceding single loop model.
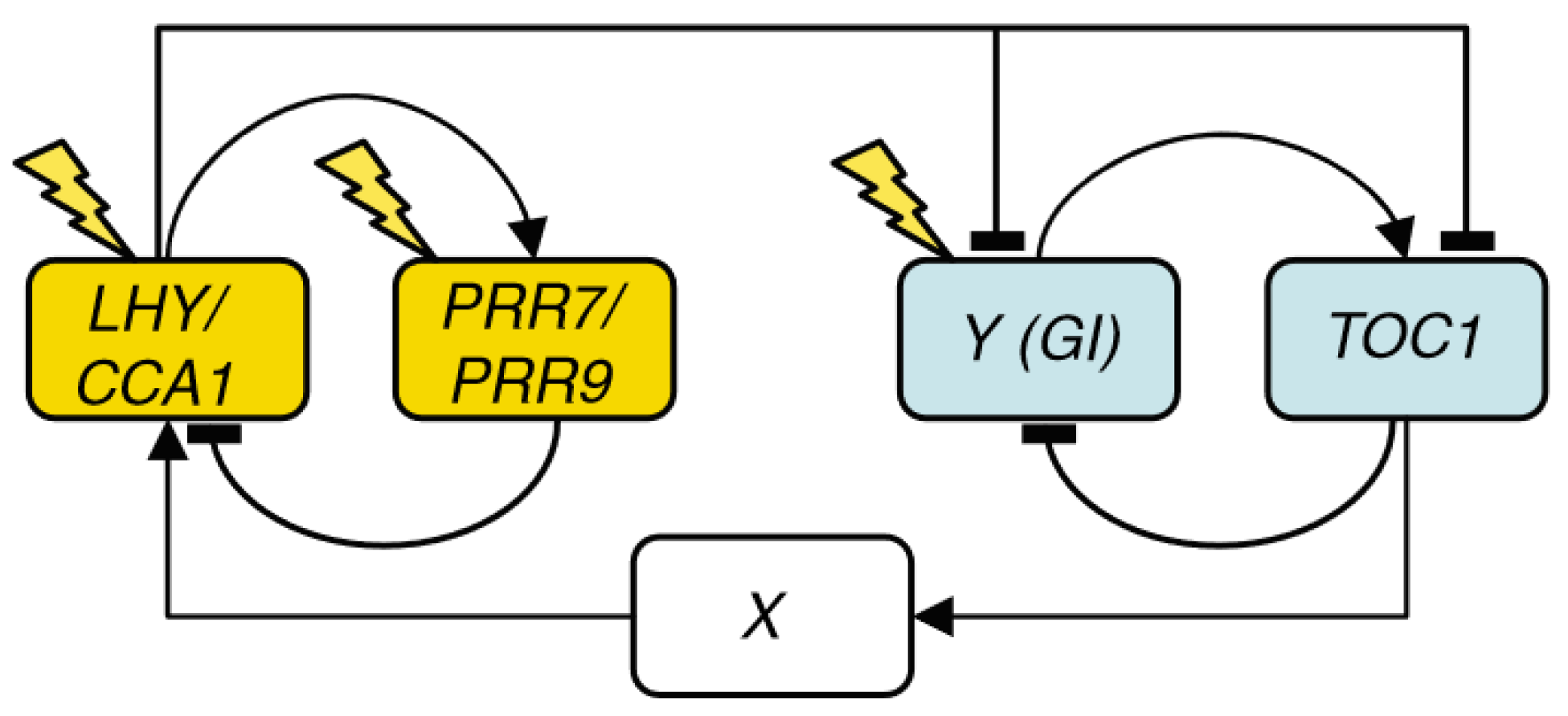
Two models published simultaneously by Zeilinger et al. [9] and Locke et al. [10], henceforth L2006, independently extended L2005b by adding PSEUDO-RESPONSE REGULATOR 7 and 9 (PRR7 and PRR9). In L2006, PRR7 and PRR9 are modeled as a single component that represses LHY/CCA1 and is, in turn, activated by LHY/CCA1. The resulting structure is a three-loop system consisting of two short-period oscillators, the morning (PRR7/9-LHY/CCA1) and evening (TOC1-Y) loops, coupled by the LHY/CCA1-TOC1-X loop (Figure 2). Y is experimentally confirmed to be a component of GIGANTEA (GI), and it is thought to be the light-responsive element of the evening loop, as the lhy/cca1 mutant still maintains entrainable oscillations and TOC1 is not observed to be light-activated.
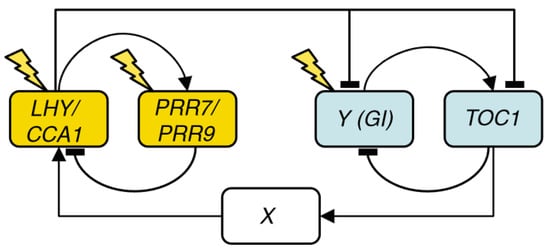
Figure 2.
Structure of the circadian clock in L2006. The clock now consists of three loops: a morning loop (yellow), an evening loop (blue), and an overarching loop that connects both, including LHY/CCA1, TOC1, and the unknown component X. Only genes are shown, and arrows represent regulatory interactions. Reproduced from [10], Creative Commons license.
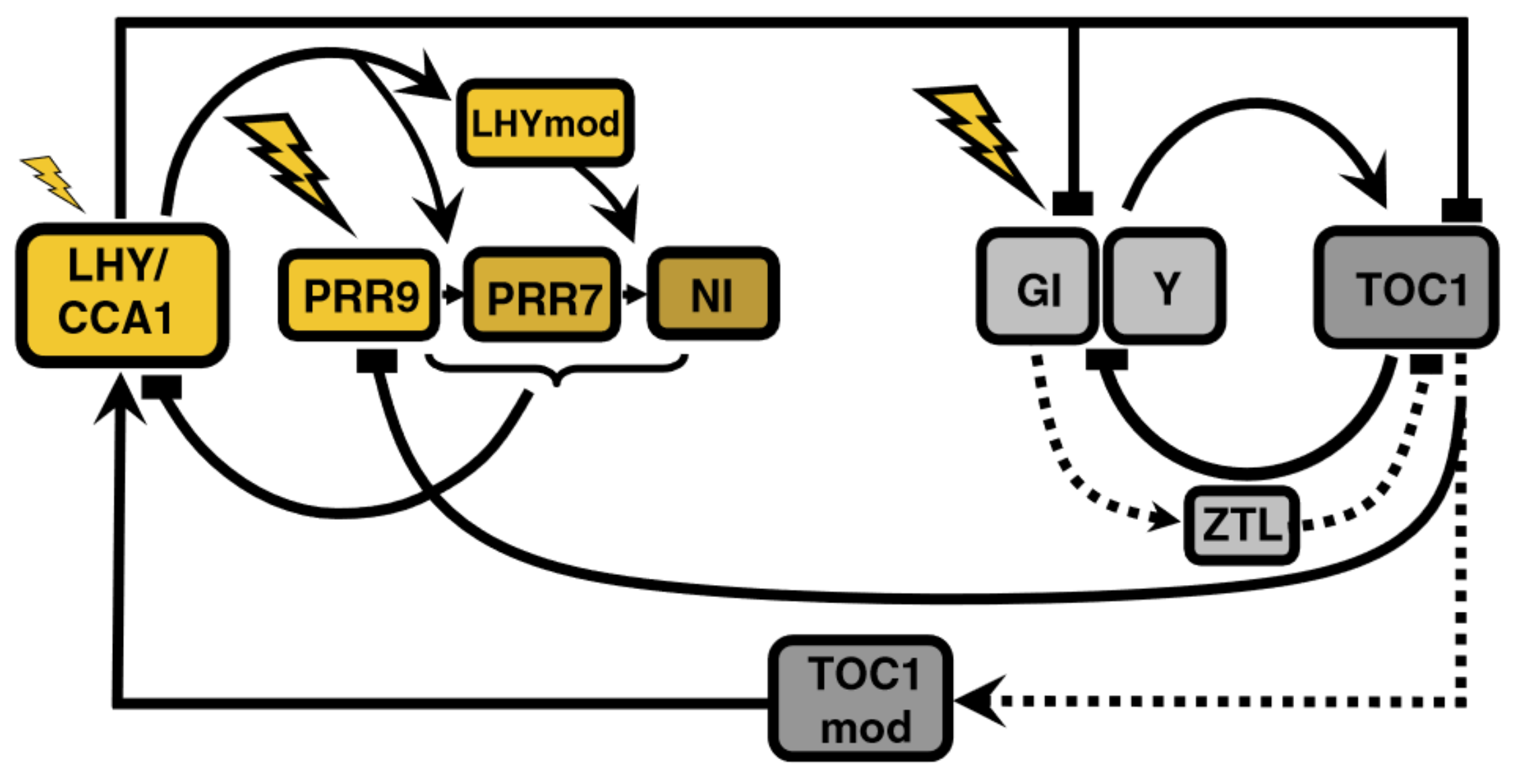
The models so far described are based on transcriptional control and do not include post-transcriptional regulation. Pokhilko’s et al., 2010 model [11], henceforth P2010, is the first model to do so by including ZEITLUPE (ZTL)-induced acceleration of TOC1 protein degradation (Figure 3). ZTL function had been acknowledged in previous models but was not explicitly modeled.
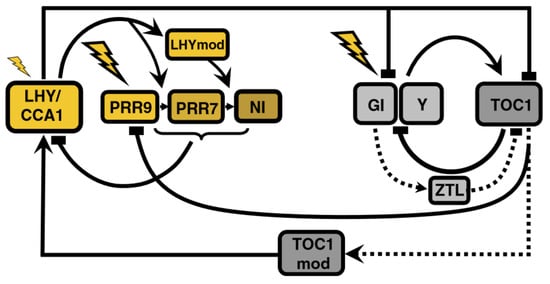
Figure 3.
Structure of the circadian clock in P2010. New components enter the model, both in the morning (NI) and evening (ZTL) loops. Post-transcriptional modification of proteins is included for the first time. Unknown component X is substituted by a TOC1-dependent complex. Modified from [11], Creative Commons license.
High TOC1 mRNA levels in gi mutants bring into question the assumption in L2006 that GI activates TOC1, prompting the separation of GI and Y functions: ZTL stabilization is achieved by GI (observed experimentally) and promotion of TOC1 transcription is due to Y. This regulatory scheme makes up the evening loop.
The morning-evening bridge suffers two modifications: the replacement of X by a TOC1-dependent complex and the addition of TOC1 inhibition of PRR9 expression, which explains the experimentally observed reduction of PRR9 mRNA levels when TOC1 is overexpressed. These interactions describe a coherent type 1 feedforward loop (C1-FFL): TOC1 positively regulates LHY both through TOCmod (see Figure 3) and indirectly via repression of PRR9; LHY then feeds back into TOC1. This network motif buffers noise in input stimuli, acting as a persistence detector [12].
The morning loop is extended by adding a “night inhibitor”, NI, as part of the inhibitor wave: PRR9, PRR7, and NI act sequentially, ensuring that LHY/CCA1 mRNA is kept at very low levels from dawn until the middle of the night. Then, degradation of the components of this inhibitor wave and activation by TOCmod quickly elevates mRNA levels again through the aforementioned C1-FFL. However, the mechanism governing this switch from inhibition to activation is not explained.
In the morning loop, PRR9 is the light-sensitive component, so light initiates the inhibitor wave. In the evening loop, Y becomes the light-sensitive component, positively regulating TOC1. The model also includes stabilization by the light of these components, making this wave dawn-responsive, too, and thus improving the response to changing photoperiods.
The models discussed until now do not allow arrhythmic clocks when performing a loss-of-function mutation in one gene; they only support the speeding up or slowing down of the clock. This theoretical premise is challenged by the observation that knocking out the gene EARLY FLOWERING 4 (ELF4) brings the oscillator to a halt [13]. Following this observation, Kolmos et al. [14] placed ELF4 in the clock model for the first time in 2009, although not mathematically, and hypothesized that it functions as an integrator of the morning and evening loops—the missing piece in P2010.
Arrhythmic mutants exist at another two loci, EARLY FLOWERING 3 (ELF3) and LUX ARRHYTHMO (LUX) [15]. ELF3 and LUX form, together with ELF4, the Evening Complex (EC), which explains the fact that all three mutants have a similar phenotype. Herrero et al. [16] used Linear Time Invariant (LTI) modeling to integrate ELF4 and ELF3 in the L2006 model. LTI modeling not only confirmed already existing connections but also predicted ELF3/ELF4 inhibition by LHY and PRR9/PRR7 inhibition by ELF3/ELF4. An important observation is that ELF3 and LUX overexpression restores rhythm in elf4 mutants, so the rhythmic expression of PRR9 requires both CCA1/LHY-mediated transcriptional activation and cooperative transcriptional repression by the components of the EC.
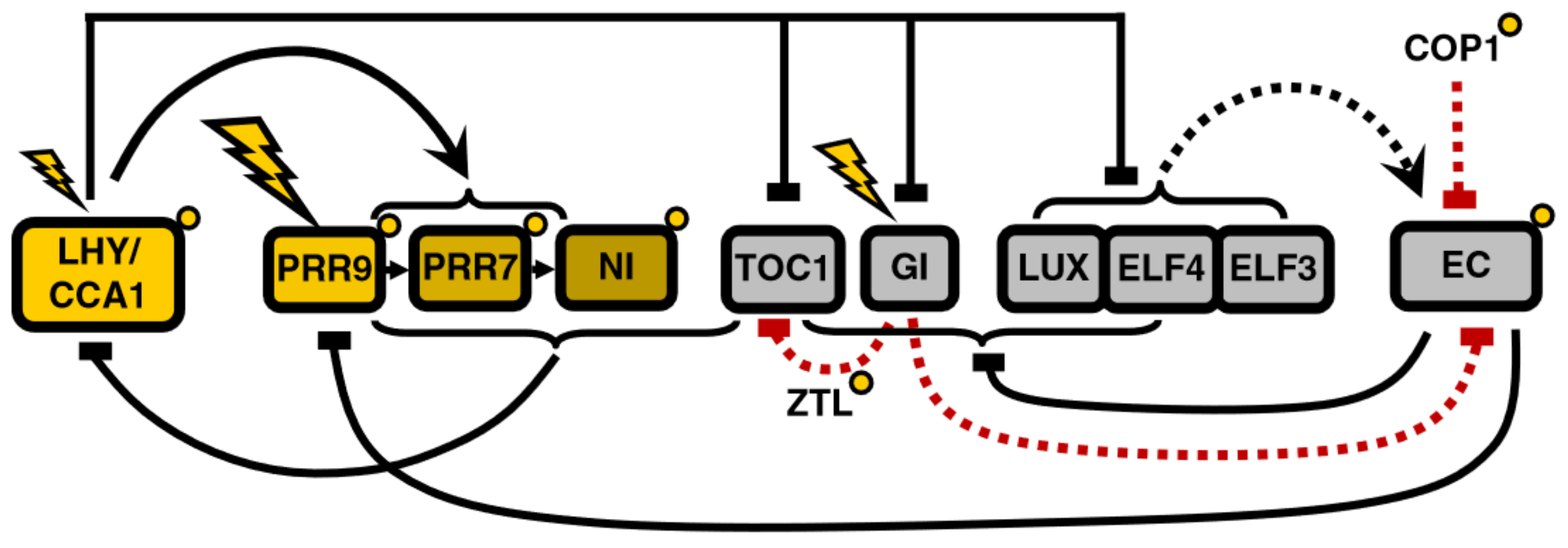
The clock model undergoes significant modifications in the next iteration of Pokhilko’s model, P2011 [17], motivated mainly by the inclusion of the EC (Figure 4). This restructuring of the model starts from the evening loop, now composed of the EC and its separate components—which replace Y. The EC inhibits the expression of both ELF4 and LUX, creating a negative feedback loop, and also represses TOC1. Additionally, the EC is regulated by COP1 [18] and GI in a light-dependent manner: entrainment of the evening loop happens through COP1-mediated degradation of ELF3, and GI acts as a modulator in the evening loop by negatively regulating the EC and thus indirectly activating TOC1 via double inhibition.
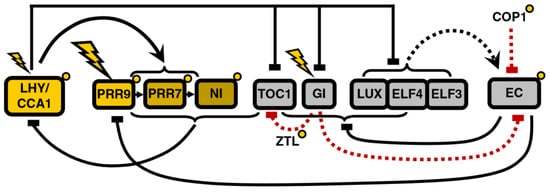
Figure 4.
Structure of the circadian clock in P2011. The main novelty is the introduction of the Evening Complex (EC) into the model, substituting the unknown component Y and changing the relationship between the evening and morning loops. Modified from [17], Creative Commons license.
The morning loop retains its main features—the feedback loop between LHY/CCA1 and the inhibitor wave. However, the role of TOC1 as a regulator of the morning loop is revised: it is no longer an activator but rather a repressor of LHY/CCA1, making it another component of the inhibitor wave. This is consistent with the fact that it also belongs to the PRR gene family. This new role fits better the data from various mutants and eliminates the need for the hypothetical X or TOCmod.
In agreement with experimental findings, the modeling of EC mutants shows a reduction in the amplitude of LHY/CCA1 oscillations. The structure of the model suggests that this is due to the higher level of its EC-regulated inhibitors, TOC1 and PRR9. Repression of both of these LHY/CCA1 inhibitors is required for robust LHY/CCA1 oscillations and thus anticipation of dawn by the clock; the morning loop is unable to support self-sustaining oscillations. This underscores the central role of the EC.
Regulation of the evening loop by the morning loop happens through repression of TOC1, LUX, ELF4, ELF3, and GI expression by LHY/CCA1.
As a result of these modifications, the circadian clock now contains a repressilator [19], consisting of a triad of sequential negative regulation whereby earlier-expressed clock components are repressed by the later ones: LHY/CCA1 represses the EC, which represses the PRRs, which in turn repress LHY/CCA1. The only positive interaction remaining in the model is the LHY/CCA1 promotion of the inhibitor wave.
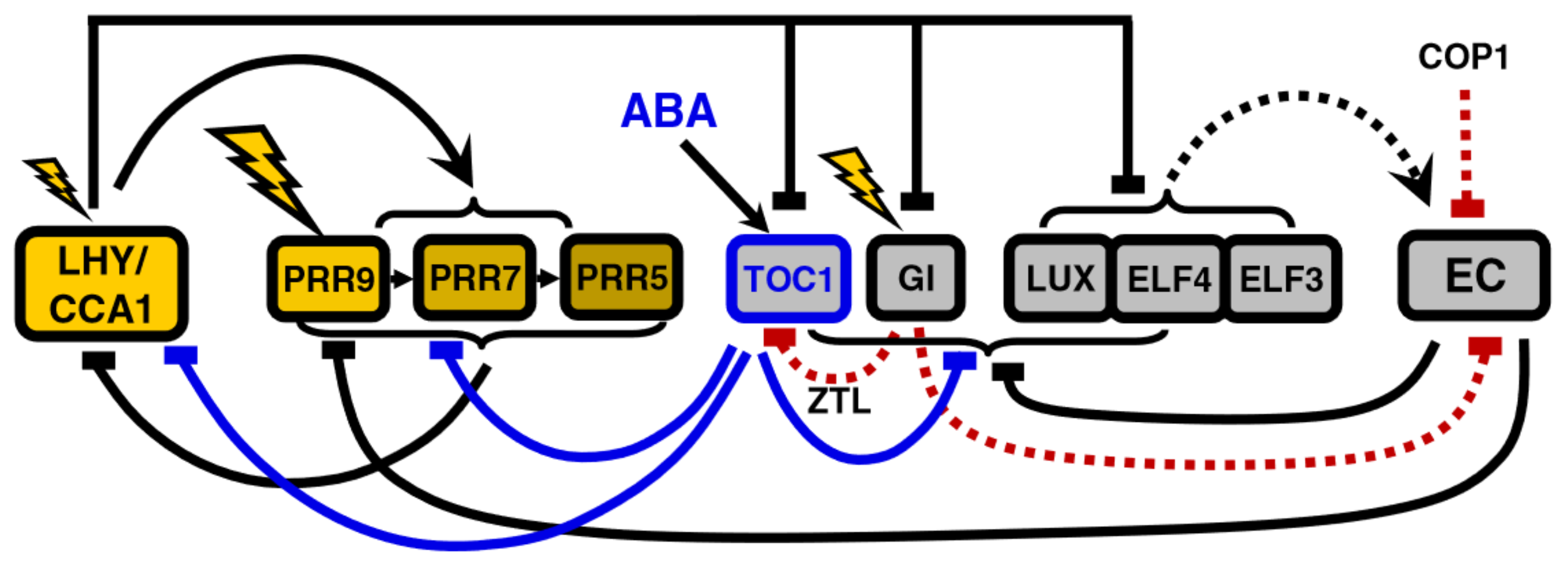
The main theme of the remaining models of the expansion phase is the reinterpretation of direct positive regulation as double inhibition. In this regard, the inhibitory role of TOC1 as a repressor first introduced in P2011 is developed further in the last iteration of Pokhilko’s model, P2012 [20]: TOC1 directly inhibits PRR9, PRR7, PRR5, LUX, ELF4 and GI in addition to LHY/CCA1 (Figure 5).
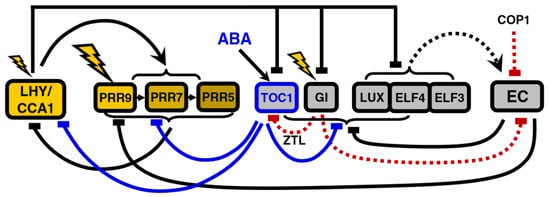
Figure 5.
Structure of the circadian clock in P2012. Note the widespread repressive activity of TOC1, which reflects recent experimental data cited in [20]. The model also includes induction of TOC1 transcription by Abscisic Acid (ABA). Modified from [20], Creative Commons license.
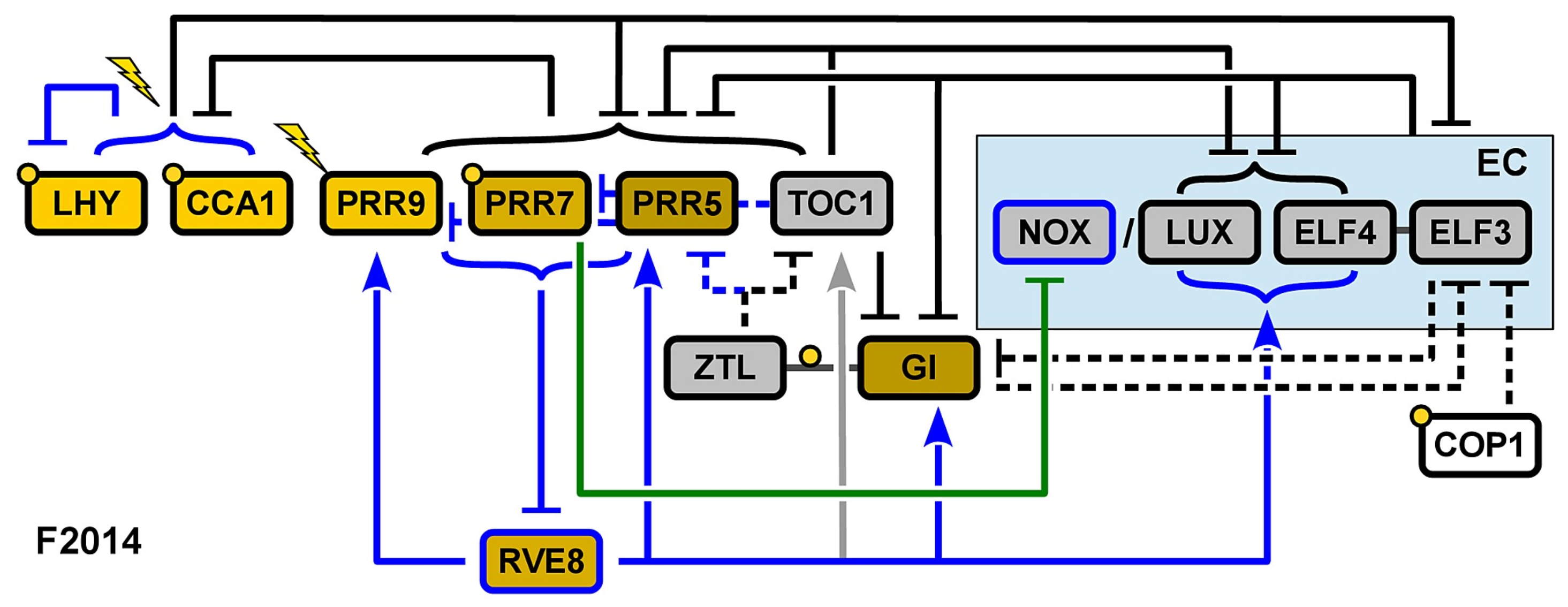
Fogelmark and Troein’s model, henceforth F2014 [21], represents the final model of the expansion phase and is consequently the most intricate of all. The remaining transcriptional activation in previous models is removed in view of the lack of direct experimental data supporting this role in any component of the clock. Instead, a novel component is included, the transcription factor REVEILLE 8 (RVE8), activating the expression of a large portion of clock genes. Another addition is that of the night-expressed transcription factor NOX/BROTHER OF LUX ARRHYTHMO (NOX/BOA).
Five major modifications are made in F2014 (Figure 6). First, the dynamics of the EC are remodeled in view of the recovery of clock function in elf4 mutants via ELF3 overexpression. This had previously been explained by the ability of all the components of the EC to bind to the PRR9 promoter [16]. In F2014, it is proposed that ELF4 enhances the effects of ELF3 through the formation of the ELF3-ELF4 complex, and consequently, ELF3 can play this role, although with reduced efficacy. This way, the activity of the EC is modeled as rate-limited by LUX and NOX on one hand and ELF3-ELF4 on the other; the EC itself no longer has its own variable in the differential equations.
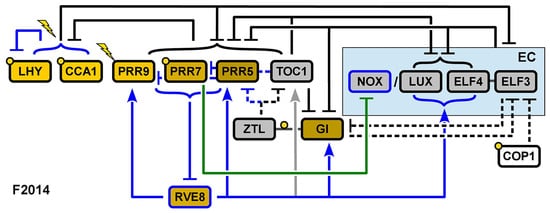
Figure 6.
Structure of the circadian clock in F2014. Two new components are included in the model, RVE8 and NOX. Blue arrows indicate new interactions included in the model. Reproduced from [21], Creative Commons license.
The addition of NOX, a close homolog of LUX, constitutes the second modification. NOX is assumed to act in parallel with LUX, serving as a transcriptional repressor in the EC. This addition enhances the model’s accuracy, particularly in predicting peak timing under constant light conditions.
The third modification involves the inhibitor wave. Earlier models describe PRR activation sequentially, such that PRR9 activates PRR7, which then activates PRR5. This contradicts experiments wherein the loss of function of one of the PRRs leaves the others unaffected. Instead, similarly to the observations that prompted the changes TOC1 underwent in P2012, later PRRs are found to repress the earlier ones.
The fourth adjustment reassesses the role of CCA1 and LHY—now modeled independently. In previous models, they repressed all their targets except for PRR9 and PRR7. However, the inclusion of PRR9 activation by CCA1 and LHY does not improve the fit of the model, so F2014 neither requires nor rules out the activation of PRR9 by CCA1 and LHY.
The fifth and final modification involves the introduction of the transcription factor RVE8. Activation by RVE8 is shown to be dispensable for the clock function, as ascertained by the null effect on the cost of refitting the parameters of the model without including this component. Its inclusion is motivated mainly to explain the effects of the rve mutants.
In parallel to the development of the other models of the expansion phase, Kim et al. published a model that studies how the role of GI depends on its location inside the cell [22]. Nuclear GI acts as a positive regulator of LHY expression, while cytosolic GI negatively regulates LHY. LHY, in turn, inhibits cytosolic GI. These interactions define a spatial network motif, namely a type-3 incoherent feedforward loop [23] between nuclear GI, cytosolic GI, and LHY. The GI loop achieves the same dynamic capabilities as a three-component loop with only two molecular components separated in different compartments. The system shows the generation of strong pulses [23] for which the balance of nuclear and cytosolic GI is shown to be crucial. Additionally, alternative modeling of the network using three distinct components shows that the two-component spatial feedforward loop is more robust against both internal and external noise. In summary, partitioning of the components of a gene regulatory network among intracellular compartments extends its regulatory capabilities, maintaining the number of components involved.
3. Recent Development of Arabidopsis Circadian Clock Models: Reduction Phase
The reduction phase refines the more complex models from the expansion phase, focusing on simplifying mathematics while maintaining the fundamental mechanisms of the clock. This process not only streamlines the models but also enables a more thorough examination of their dynamic characteristics. In addition to its mathematical elegance, model reduction is technically motivated, as exemplified by the sloppy model framework [24,25]. This approach indicates that when a model’s complexity exceeds the available data’s capacity to define its parameters, there are systematic procedures to reduce model size. This process consolidates less-critical processes into a broader, effective dynamic. Hence, leveraging biological insights to formulate simplified models from the outset represents a judicious strategy.
The reduction phase starts with two models published (coincidentally) in the same week of 2016. The first one by Foo et al., MF2015 [26], introduces the notion of kernel to the study of the plant molecular oscillator: a set of minimal regulatory modules that include all molecular components in the system and only the interactions necessary to generate the behavior observed in the wild type. This concept was first introduced in the context of evolutionary developmental biology [27] and has also been defined as the minimal set of nodes inside a gene regulatory network whose regulation ensures the achievement of any attractor state given an initial network state [28]. In the case of circadian clocks, of course, the attractor will be a limit cycle. Foo and collaborators base their analysis on an updated version of P2012 that includes recent experimental findings and removes outdated interactions. Using a heuristic approach, they find that the kernel of the Arabidopsis clock harbors four negative feedback loops labeled A to D (Figure 7). All of them contain at least one PRR and are interlocked by sharing LHY/CCA1. Structurally, loops A to C are repressilators, and loop D is a negative feedback loop.
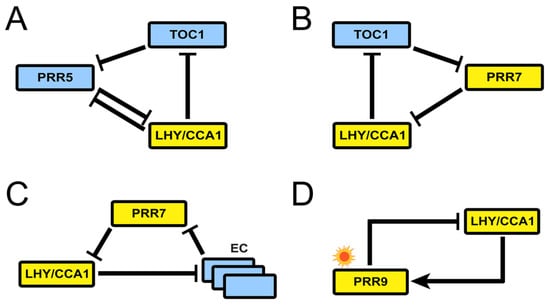
Figure 7.
Structure of the kernel of the circadian clock in MF2015. The kernel consists of four loops, all containing at least one PRR and sharing LHY/CCA1. (A) Loop A, a repressilator involving TOC1, PRR5, and LHY/CCA1. (B) Loop B, a repressilator involving TOC1, PRR7, and LHY/CCA1. (C) Loop C, a repressilator involving the EC, PRR7, and LHY/CCA1. And (D) Loop D, a negative feedback loop between PRR9 and LHY/CCA1. Reproduced from [26], Creative Commons license.
Loop I involves, besides the repressilator structure between LHY/CCA1, TOC1, and PRR5, the inhibition of PRR5 by LHY/CCA1 in a direction opposite to the repressilator’s. This regulatory motif was later named the AC–DC circuit [29] and is able to display rich dynamical behavior. This inhibition slows down the oscillation of the loop, an effect that extends to the whole clock because of the interconnection with the rest of the system. Simulations of the model show that a 20% increase in PRR5 inhibition by LHY/CCA1 lengthens the period by 3.3 h, and decreasing it by the same amount shortens it by 2.9 h. Please note that Loops I and II are not described by previous models, while Loop III echoes the repressilator in P2012.
Foo and collaborators use the kernel decomposition to explore whether any loop is critical to support the oscillations. Separate modeling of each module shows that only loop IV is unable to sustain autonomous oscillations. Meanwhile, loop I can make up for the loss of loops II and III under certain conditions, and loops II and III can buffer the loss of each other. Thus, loop IV has a relatively weak role in free-running rhythm despite it being the only entrainable one. Finally, the kernel decomposition allows the functional study of inhibitory interactions, which are shown to create cuspidate oscillatory profiles, potentially in service of accuracy in the timing of physiological events.
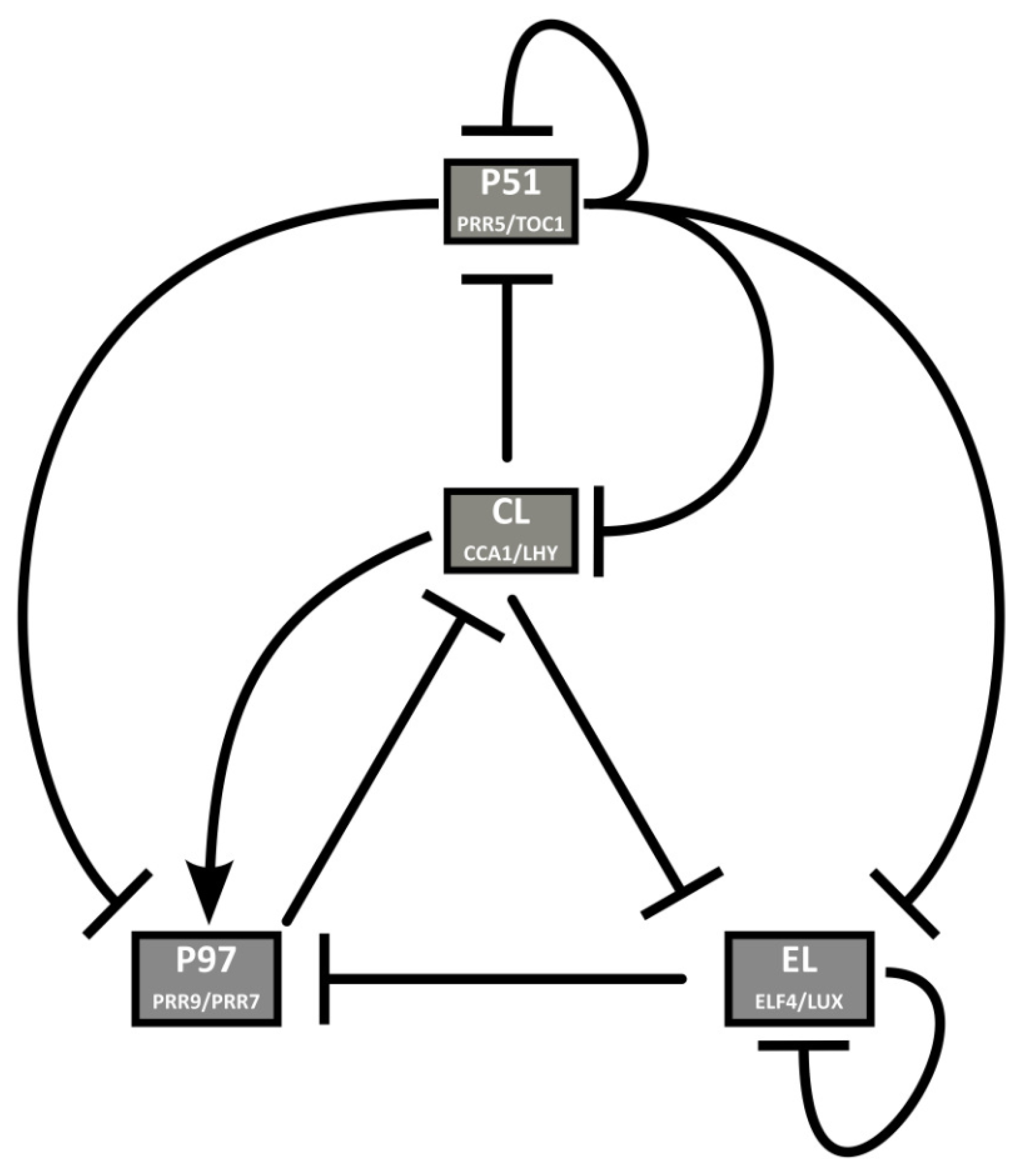
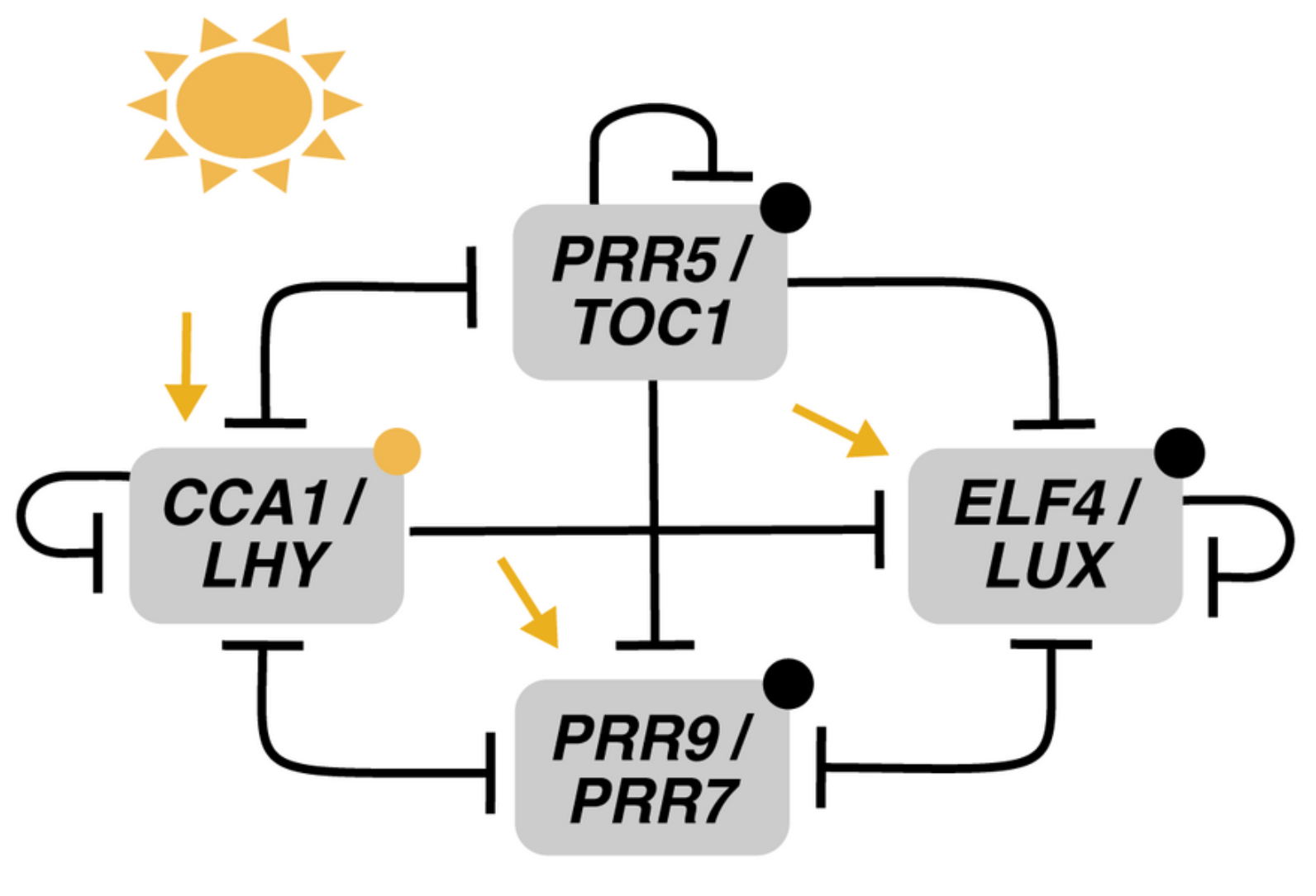
The second model of the reduction phase was published by De Caluwé and collaborators, DC2016 [30]. Their approach is to merge genes that behave similarly in the network to reduce the number of equations. The foregoing networks are reduced to four pairs of genes in view of the large number of clock components and the largely redundant roles some of them have. This way, several sets of almost identical equations are eliminated. In previous models, gene pairs such as LHY and CCA1 (in all models but F2014) or PRR7 and PRR9 (L2006, P2010) are considered single entities. DC2016 applies this strategy to two more pairs of genes, each of which has similar expression profiles, regulators, targets, and defects in loss-of-function mutant lines. The resulting network comprises nine ODEs, representing four nodes: P51 (PRR5/TOC1), CL (CCA1/LHY), P97 (PRR9/PRR7), and EL (ELF4/LUX) (Figure 8). DC2016 retains key qualitative features of the circadian clock and is also able to reproduce how the clock affects hypocotyl growth. Thanks to its simplicity, DC2016 has been the “standard model” used to study the link between the circadian system and physiological and developmental processes, as well as the properties of the clock, such as temperature compensation and entrainment. Some of these studies show the bidirectional relationship between the clock and the processes under its control, such as magnesium metabolism [31], and the role of photosynthetic entrainment [32,33]. DC2016 has also been used for stochastic modeling of the clock [34].
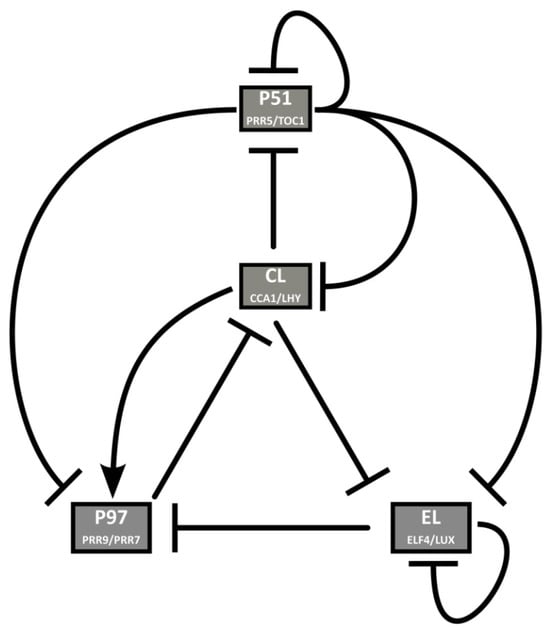
Figure 8.
Structure of the circadian clock in DC2016. Several pairs of genes are combined, thus considerably reducing the complexity of the model. To the previous merging of CCA1/LHY (CL) and PRR9/7 (P97), they add PRR5/TOC1 (P51) and ELF4/LUX (EL). Reproduced from [30], Creative Commons license.
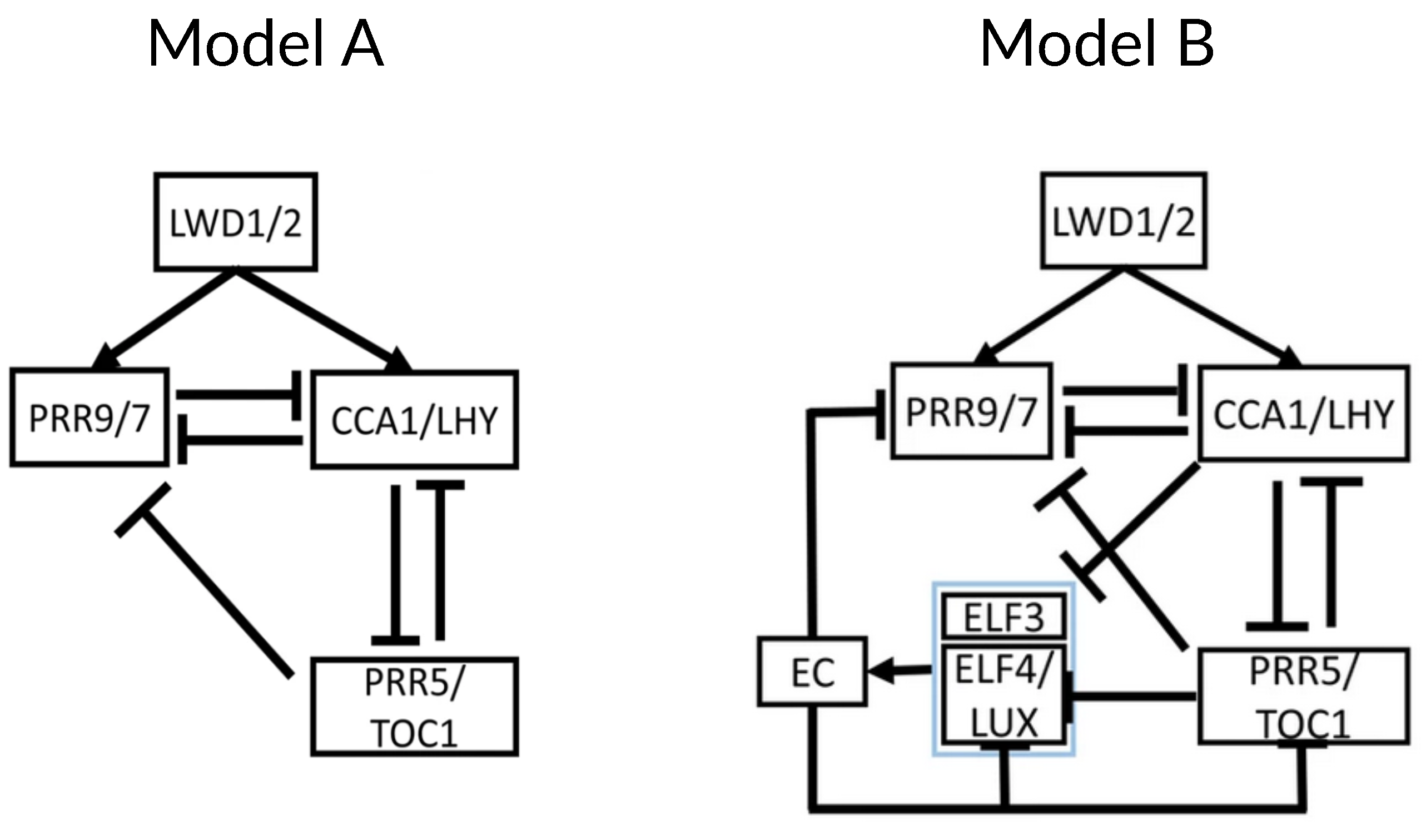
The next model in the reduction phase by Joanito et al., henceforth J2018 [35], decomposes the clock network into compact regulatory modules, providing insights into the robustness and hysteretic behavior of the network. Using the merged gene structure of DC2016, they build a series of simplified models of increasing complexity and compare them, finding that the best description of the available data for both the wild type and several mutants is what they call “Model A” (Figure 9 left). This model is very similar to DC2016 without the EL component, but it only includes inhibitory interactions between CCA1/LHY, TOC1/PRR5, and PRR9/7. As a novelty, J2018 includes positive activation of CCA1/LHY and PRR9/7 by LIGHT-REGULATED WD1 and 2 (LWD1/2).
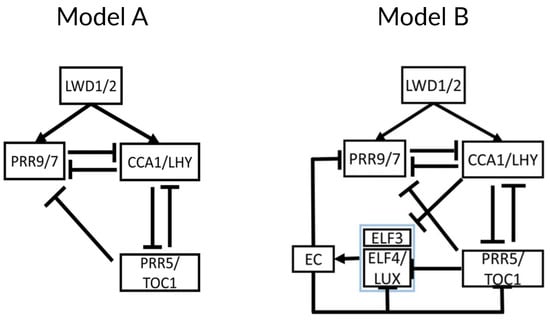
Figure 9.
Structure of the core of the circadian clock in J2018. (Left) Model A is proposed as a core of the circadian clock, including the merged genes CCA1/LHY, PRR5/TOC1, and PRR9/7. As a novelty, the model includes activation by LWD 1/2. (Right) Model B adds the Evening Complex and its components with their respective interactions. This second model better captures the overall behavior of the clock. Modified from [35], Creative Commons license.
Next, Joanito and collaborators explore the different network motifs present in Model A and their functional consequences. They find a repressilator between CCA1/LHY, PRR5/TOC1, and PRR9/7 (also described in DC2016) that must drive the oscillation of the whole clock since Model A contains no other negative feedback loop nor self-oscillating components. Also, Model A contains a positive feedback loop consisting of a double inhibition between CCA1/LHY and PRR5/TOC1. This results in a toggle switch with bistability and hysteresis, where either CCA1/LHY is high, and PRR5/TOC1 is low, or the reverse, depending on the expression of PRR9/7, which acts as the switch. Model A contains another positive feedback loop made of negative interactions between CCA1/LHY and PRR9/7, which does not result in bistable behavior. Finally, Model A also contains three type-2 incoherent feedforward loops [23] between the three components of the model, resulting in a pulse-like expression of PRR9/7 and CCA1/LHY.
J2018 includes an additional model named “Model B” (Figure 9 right). This is an extension of Model A that includes the EC and its components, ELF3 and ELF4/LUX, with their respective regulatory interactions. The presence of the EC adds another repressilator to the system (also present in DC2016), which results in a stronger toggle switch between CCA1/LHY and PRR5/TOC1. Additionally, the EC acts as a nighttime switch for bistable behavior. Model B thus shows a complete alternating behavior between the two stable states: at dawn, CCA1/LHY is high, and PRR5/TOC1 is low. This results in a pulse-like expression of PRR9/7 peaking near noon, which switches the system to the other bistable state at dusk: low CCA1/LHY and high PRR5/TOC1. Low CCA1/LHY results in EC accumulation, which decreases PRR5/TOC1 and eventually switches the system to the other bistable state near dawn. The authors repeat their analyses in P2012 and F2014, observing bistability in both of them, with some caveats: EC does not result in bistability in P2012, and only PRR7 (but not PRR9) shows pulse-like expression in F2014. These results highlight the usefulness of simplified models in studying dynamical behaviors.
Further simplification of the models has been achieved using distributed delays. Using this approach, the number of unknown parameters can be reduced by introducing distributed time delays to substitute interactions whose main dynamical value is delaying the timing of other processes. Distributed delay representations have been applied to L2005a, MF2015, and DC2016 [36], retaining the key dynamical properties of these models while significantly reducing the number of parameters.
4. Current Challenges and Overview
4.1. Spatial Models
The models reviewed so far are mean-field approximations of the molecular behavior across different tissues and plant parts. However, it has been shown that the plant circadian clock has spatially specific functions [37] and consequently, its properties—such as phase, period, and entrainability—and mechanisms are spatially heterogeneous [38]. Two primary considerations arise for effectively incorporating circadian clock models into the broader context of physiology and development. First, the establishment of phase differences among various clocks, which, based on empirical evidence, can arise from differential clock gene expression, variations in molecular clock structures, or differences in signal processing. Second, the nature of inter-clock coupling, with proposed mechanisms including both local and long-distance clock components [38,39].
The spatial model constructed by Greenwood et al., G2022 [40] tries to address these challenges. For the construction of G2022, a conserved clock architecture is assumed: an updated version of DC2016 wherein CL represses P97, CL represses its transcription, and P51 degradation rates in the dark are increased (Figure 10). This network is instantiated in each of the approximately 800 cells, constituting a simplified seedling model segmented into four regions of varying light sensitivities: cotyledon, hypocotyl, root, and root tip. Cell-to-cell coupling is modeled through the sharing of CCA1/LHY mRNA. This mechanism, together with differential light sensitivities, generates the two traveling waves of gene expression—up and down the root—that are experimentally observed [39]. Also, local coupling has a stabilizing effect on individual clock rhythms, buffering noise while maintaining the between-region phase differences. On the other hand, the long-distance coupling is modeled by the apportioning of ELF4 from shoots to roots, which is shown to be non-essential in producing the spatial waves of gene expression. Instead, the model suggests it matches clock periods between different organs.
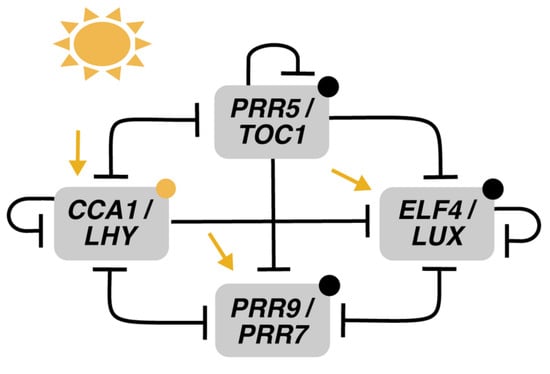
Figure 10.
Structure of the circadian clock in G2022. The model presents an updated version of DC2016. The novelty here is the model of plant structure in hundreds of compartments, each of which has its own set of ODEs. Modified from [40], Creative Commons license.
G2022 is a step towards understanding the plant circadian clock not as a single gene regulatory network embedded in every cell but as a system spanning the whole plant. It is a separable system not just because of its components—which are differentially expressed throughout the plant tissues—but because of what it does—its activity-function [4], namely the proper timing of physiological processes. It also illustrates how bottom-up emergence (molecular oscillations) is sculpted by top-down constraints (tissue-dependent input sensitivities) [41].
4.2. Effects of Light on the Clock
The models presented so far barely deal with the effect of light on the clock. Plants have a wide array of photoreceptors [42] detecting wavelengths from around 280 to 750 nm, i.e., from UV-B to far-red light. These different photoreceptors translate the light signals into molecular actions, in many cases mediated through changes in the clock. In what follows, we discuss works that present mathematical models integrating light intensity and quality (through the inclusion of diverse photoreceptors) with clock models.
Ohara and collaborators [43], O2015, first introduced the effect of light on the clock through a modification of L2005a. They argue that this model captures the core functioning of the clock despite its simplicity. Their modification consists of replacing the light-sensitive protein P of L2005a by including equations for several photoreceptors: phytochromes A and B (phyA and phyB), responsible for detecting red light, and chryptochrome 1 (cry1), responsible for detecting blue light. The molecular concentrations of these photoreceptors are then translated into an “effective light” equation that alters the expression of LHY. O2015 is able to capture the phase response curves of the circadian clock after different pulses of light. In particular, O2015 recovers the atypical phase response curve obtained with a pulse of darkness, in contrast with L2005a or P2011, which predicted an erroneous response.
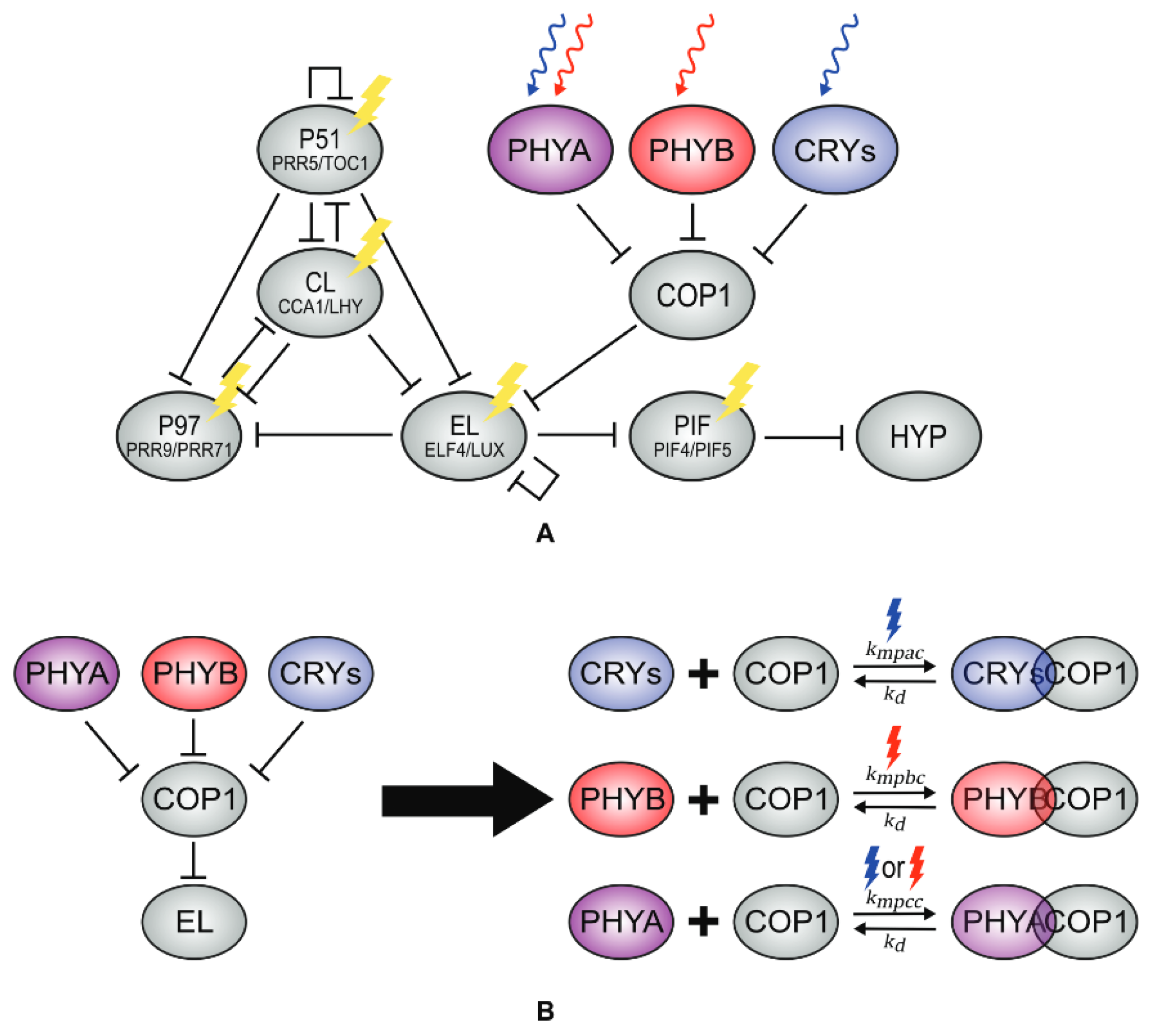
O2015 has recently been updated by Pay and collaborators [44], Pa2022a, who have applied the light functions of O2015 to a modified version of DC2016 to study the effect of light on hypocotyl growth. DC2016 is modified so that the activation of P97 by CL is changed to repression, as in F2014. Pa2022a also includes the competitive binding of COP1 to all photoreceptors, which inactivates them, as well as COP1’s repression of EL and the photoreceptors’ repression of COP1 (Figure 11), ending up with a model of 18 ODEs and 66 parameters. The model is able to qualitatively fit both phase response curves and hypocotyl growth measures under several light environments.
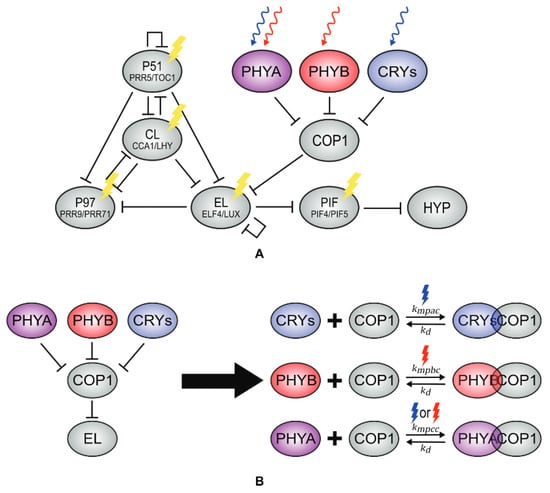
Figure 11.
Structure of the circadian clock in Pa2022a. The model includes the perception of light by different photoreceptors (A) as well as their repression of COP1. The model also incorporates competitive binding between COP1 and phyA, phyB, and cry (B). Reproduced from [44], Creative Commons license.
More recently, Pay et al. [45], Pa2022b, have extended their model in order to study the effect of light on flowering. Notably, this new model includes GI as a regulator of flowering, but downstream of the clock, i.e., GI has no effect on the circadian clock in this model.
Following an alternative route to O2015, Huang et al. [46] have studied the effect of red light on the circadian clock, focusing on the expression patterns of CCA1 through the action of phyB. To build their model, they use a modified version of DC2016, which they complement with the addition of a light-sensitive equation for ELF3 to make the model suitable for red-light environments. Fitting their model to the experimental expression time series of CCA1, they show that a red-light pulse causes a phase shift in CCA1 expression. They also predict that red light can reset both the phase and the period of the clock and study how different red-light dynamic environments alter the parameters of the model and, thus, the dynamical properties of the clock.
De Caluwé and collaborators [47] use a modified version of DC2016 wherein all the clock genes are light-regulated to study the mechanistic basis of entrainment of the clock to changing day lengths. The clock shows diverse behaviors upon exposure to non-24 h light cycles, from frequency demultiplication to chaos. Studying these responses by following Schmal’s theoretical entrainment paradigm [48], they assess the theoretical entrainment range of the clock.
They discuss the change in the limit cycle behind the clock oscillations as day length increases from total darkness to continuous light and find parameter ranges where the behavior of the clock becomes chaotic.
4.3. Effects of Temperature on the Clock
The Arabidopsis circadian clock shows “temperature compensation”, i.e., it is able to maintain a stable period in a broad range of temperatures. Some models have studied the molecular and regulatory basis of this effect.
Gould et al. [49] study the molecular basis of temperature compensation through a combination of experiments and modeling. They show a combined effect of temperature and light quality on temperature compensation. Thus, the clock period is shortened at higher temperatures under white and blue light, and this effect is dependent on cry. Both phyA and phyB also had nonlinear effects on the period at different temperatures, although the effects were small in comparison with those of cry. They also show that the expression of clock-related genes is almost constant over a range of temperatures, but this is also dependent on the presence of cry. To study these effects in detail, they introduce temperature dependence into P2010, resulting in a new model, G02013, which is able to capture their experimental findings and predicts a temperature-dependent change in LHY, a result that was validated experimentally. Notably, their results show that the most important element in temperature compensation is light quality, most importantly cryptochromes through regulating multiple light and temperature-dependent parameters.
More recently, Avello et al. [50] have introduced temperature dependence through Arrhenius equations into DC2016. Although useful for building qualitative insight into temperature effects, such dependence has to be treated with caution. As for plants, there is limited thermodynamic data available, such as activation energies, which would constrain an Arrhenius model. Their model, A2019, is able to reproduce both temperature entrainment and compensation and points to the dependence on the temperature of degradation rates as a driving force behind both processes across a range of temperatures.
In more recent work, Avello and collaborators [51] introduce temperature dependence through Arrhenius equations in several of the models reviewed here: L2005a, L2005b, L2006, P2010, P2011, P2012, F2014, and DC2016. Following the approach by Joanito et al. [35], they analyze the structural patterns of the circadian clock that are behind temperature compensation. By listing all network motifs found in these clock models and studying how the period changes with temperature in each of them, Avello and collaborators are able to conclude that no single network motif is responsible for temperature compensation. Rather, they find that temperature compensation is a global property of the network, where the presence of autoregulation combined with three-node feedback loops, plus a dominance of inhibitory interactions, results in the observed effect. Notably, the presence of these three factors resulted in temperature compensation. This work highlights the use of minimal models as a way to better understand dynamical effects.
5. Conclusions
In the last 20 years, the structure of the clock has been modified and updated as new components and interactions were discovered. In fact, new interactions are continuously being discovered; see, for instance, [52] where new interactions between ELF3 and PRR7 and PRR9 are described. While, in the first phase, mathematical models sought to incorporate as many components and interactions as possible, the last ten years have seen a shift in focus towards minimal models that can be better explored in terms of dynamical properties. In particular, DC2016 has become a golden standard in the field, being used in many subsequent works to study the dynamic properties of the clock, introduce tissue differences, or explore the effect of light and temperature. These recent studies underscore the prevailing trend in the field: experimental testing and mathematical modeling of clock properties across a range of environmental conditions, with an emphasis on intra-plant heterogeneity. The focus is on elucidating underlying mechanisms rather than detailed molecular interactions. This effort aims not only to understand the clock itself but also to explore its influence on clock-dependent phenotypes such as flowering and growth.
The strengths and weaknesses of both the expansion and reduction phases of modeling are evident in their respective contributions to our understanding of the Arabidopsis circadian clock. Expansion phase models excel in their attention to molecular detail and their capability to make specific predictions for individual genes, providing a comprehensive representation of the clock’s regulatory network. However, these models face significant challenges, particularly in the difficulty of unequivocally fitting parameters due to their mathematical complexity and the sheer number of variables involved.
On the other hand, reduction phase models offer notable advantages in terms of mathematical simplicity, allowing for parameters that are better constrained by experimental data. This simplicity enables a clearer understanding of the essential dynamical properties of the clock. Nonetheless, these models also have their limitations, as their parameters are often effective rather than mechanistic, making it challenging to make precise predictions for the dynamics of specific genes.
Looking ahead, future directions in this field should focus on leveraging the strengths of both modeling approaches. Reduced models, which data can better constrain, should serve as foundational templates for developing more complex models. These more intricate models should be capable of being reduced back to the well-tested reduced models, ensuring that they offer reliable insights while also providing detailed predictions for genes or variables of specific interest. This iterative approach will enhance our ability to balance molecular detail with practical simplicity, ultimately leading to a deeper understanding of the circadian clock’s mechanisms and its broader biological implications.
Author Contributions
L.H., P.C. and S.A. contributed to the conception and design of the work. L.H. drafted the manuscript. L.H., P.C. and S.A. edited and revised the manuscript critically for important intellectual content. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MCIN/AEI/10.13039/501100011033 and by “ERDF/EU” through grant PGE, grant numbers PID2022-142185NB-C21 and PID2022-142185NB-C22, to S.A. and P.C.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bechtel, W.; Abrahamsen, A. Dynamic Mechanistic Explanation: Computational Modeling of Circadian Rhythms as an Exemplar for Cognitive Science. Stud. Hist. Philos. Sci. Part A 2010, 41, 321–333. [Google Scholar] [CrossRef]
- Kauffman, S.A. Articulation of Parts Explanation in Biology and the Rational Search for Them. PSA Proc. Bienn. Meet. Philos. Sci. Assoc. 1970, 1970, 257–272. [Google Scholar] [CrossRef]
- Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits, 2nd ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2020. [Google Scholar]
- Jaeger, J.; Monk, N. Dynamical Modules in Metabolism, Cell and Developmental Biology. Interface Focus 2021, 11, 20210011. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Maroto, G.; Catalán, P.; Nieto, C.; Prat, S.; Ares, S. Mathematical Modeling of Photo-and Thermomorphogenesis in Plants. In Thermomorphogenesis: Methods and Protocols; Springer: New York, NY, USA, 2024; pp. 247–261. [Google Scholar]
- Bujdoso, N.; Davis, S.J. Mathematical Modeling of an Oscillating Gene Circuit to Unravel the Circadian Clock Network of Arabidopsis Thaliana. Front. Plant Sci. 2013, 4, 3. [Google Scholar] [CrossRef] [PubMed]
- Locke, J.C.W.; Millar, A.J.; Turner, M.S. Modelling Genetic Networks with Noisy and Varied Experimental Data: The Circadian Clock in Arabidopsis Thaliana. J. Theor. Biol. 2005, 234, 383–393. [Google Scholar] [CrossRef]
- Locke, J.C.W.; Southern, M.M.; Kozma-Bognár, L.; Hibberd, V.; Brown, P.E.; Turner, M.S.; Millar, A.J. Extension of a Genetic Network Model by Iterative Experimentation and Mathematical Analysis. Mol. Syst. Biol. 2005, 1, 2005.0013. [Google Scholar] [CrossRef]
- Zeilinger, M.N.; Farré, E.M.; Taylor, S.R.; Kay, S.A.; Doyle, F.J. A Novel Computational Model of the Circadian Clock in Arabidopsis That Incorporates PRR7 and PRR9. Mol. Syst. Biol. 2006, 2, 58. [Google Scholar] [CrossRef]
- Locke, J.C.W.; Kozma-Bognár, L.; Gould, P.D.; Fehér, B.; Kevei, É.; Nagy, F.; Turner, M.S.; Hall, A.; Millar, A.J. Experimental Validation of a Predicted Feedback Loop in the Multi-oscillator Clock of Arabidopsis thaliana. Mol. Syst. Biol. 2006, 2, 59. [Google Scholar] [CrossRef]
- Pokhilko, A.; Hodge, S.K.; Stratford, K.; Knox, K.; Edwards, K.D.; Thomson, A.W.; Mizuno, T.; Millar, A.J. Data Assimilation Constrains New Connections and Components in a Complex, Eukaryotic Circadian Clock Model. Mol. Syst. Biol. 2010, 6, 416. [Google Scholar] [CrossRef]
- Mangan, S.; Zaslaver, A.; Alon, U. The Coherent Feedforward Loop Serves as a Sign-sensitive Delay Element in Transcription Networks. J. Mol. Biol. 2003, 334, 197–204. [Google Scholar] [CrossRef]
- McWatters, H.G.; Kolmos, E.; Hall, A.; Doyle, M.R.; Amasino, R.M.; Gyula, P.; Nagy, F.; Millar, A.J.; Davis, S.J. ELF4 Is Required for Oscillatory Properties of the Circadian Clock. Plant Physiol. 2007, 144, 391–401. [Google Scholar] [CrossRef] [PubMed]
- Kolmos, E.; Nowak, M.; Werner, M.; Fischer, K.; Schwarz, G.; Mathews, S.; Schoof, H.; Nagy, F.; Bujnicki, J.M.; Davis, S.J. Integrating ELF4 into the Circadian System through Combined Structural and Functional Studies. HFSP J. 2009, 3, 350–366. [Google Scholar] [CrossRef] [PubMed]
- Nusinow, D.A.; Helfer, A.; Hamilton, E.E.; King, J.J.; Imaizumi, T.; Schultz, T.F.; Farré, E.M.; Kay, S.A. The ELF4–ELF3–LUX Complex Links the Circadian Clock to Diurnal Control of Hypocotyl Growth. Nature 2011, 475, 398–402. [Google Scholar] [CrossRef]
- Herrero, E.; Kolmos, E.; Bujdoso, N.; Yuan, Y.; Wang, M.; Berns, M.C.; Uhlworm, H.; Coupland, G.; Saini, R.; Jaskolski, M.; et al. EARLY FLOWERING4 Recruitment of EARLY FLOWERING3 in the Nucleus Sustains the Arabidopsis Circadian Clock. Plant Cell 2012, 24, 428–443. [Google Scholar] [CrossRef]
- Pokhilko, A.; Fernández, A.P.; Edwards, K.D.; Southern, M.M.; Halliday, K.J.; Millar, A.J. The Clock Gene Circuit in Arabidopsis Includes a Repressilator with Additional Feedback Loops. Mol. Syst. Biol. 2012, 8, 574. [Google Scholar] [CrossRef]
- Nieto, C.; Catalán, P.; Luengo, L.M.; Legris, M.; López-Salmerón, V.; Davière, J.M.; Casal, J.J.; Ares, S.; Prat, S. COP1 Dynamics Integrate Conflicting Seasonal Light and Thermal Cues in the Control of Arabidopsis Elongation. Sci. Adv. 2022, 8, eabp8412. [Google Scholar] [CrossRef] [PubMed]
- Elowitz, M.B.; Leibler, S. A synthetic oscillatory network of transcriptional regulators. Nature 2000, 403, 335–338. [Google Scholar] [CrossRef] [PubMed]
- Pokhilko, A.; Mas, P.; Millar, A.J. Modelling the Widespread Effects of TOC1 Signalling on the Plant Circadian Clock and Its Outputs. BMC Syst. Biol. 2013, 7, 23. [Google Scholar] [CrossRef]
- Fogelmark, K.; Troein, C. Rethinking Transcriptional Activation in the Arabidopsis Circadian Clock. PLoS Comput. Biol. 2014, 10, e1003705. [Google Scholar] [CrossRef]
- Kim, Y.; Han, S.; Yeom, M.; Kim, H.; Lim, J.; Cha, J.Y.; Kim, W.Y.; Somers, D.E.; Putterill, J.; Nam, H.G.; et al. Balanced Nucleocytosolic Partitioning Defines a Spatial Network to Coordinate Circadian Physiology in Plants. Dev. Cell 2013, 26, 73–85. [Google Scholar] [CrossRef]
- Mangan, S.; Alon, U. Structure and Function of the Feed-Forward Loop Network Motif. Proc. Natl. Acad. Sci. USA 2003, 100, 11980–11985. [Google Scholar] [CrossRef] [PubMed]
- Gutenkunst, R.N.; Waterfall, J.J.; Casey, F.P.; Brown, K.S.; Myers, C.R.; Sethna, J.P. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 2007, 3, e189. [Google Scholar] [CrossRef] [PubMed]
- Transtrum, M.K.; Machta, B.B.; Brown, K.S.; Daniels, B.C.; Myers, C.R.; Sethna, J.P. Perspective: Sloppiness and emergent theories in physics, biology, and beyond. J. Chem. Phys. 2015, 143, 010901. [Google Scholar] [CrossRef] [PubMed]
- Foo, M.; Somers, D.E.; Kim, P.J. Kernel Architecture of the Genetic Circuitry of the Arabidopsis Circadian System. PLoS Comput. Biol. 2016, 12, e1004748. [Google Scholar] [CrossRef]
- Davidson, E.H.; Erwin, D.H. Gene Regulatory Networks and the Evolution of Animal Body Plans. Science 2006, 311, 796–800. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Park, S.M.; Cho, K.H. Discovery of a Kernel for Controlling Biomolecular Regulatory Networks. Sci. Rep. 2013, 3, 2223. [Google Scholar] [CrossRef] [PubMed]
- Perez-Carrasco, R.; Barnes, C.P.; Schaerli, Y.; Isalan, M.; Briscoe, J.; Page, K.M. Combining a toggle switch and a repressilator within the AC-DC circuit generates distinct dynamical behaviors. Cell Syst. 2018, 6, 521–530. [Google Scholar] [CrossRef] [PubMed]
- De Caluwé, J.; Xiao, Q.; Hermans, C.; Verbruggen, N.; Leloup, J.C.; Gonze, D. A Compact Model for the Complex Plant Circadian Clock. Front. Plant Sci. 2016, 7, 74. [Google Scholar] [CrossRef] [PubMed]
- De Melo, J.R.F.; Gutsch, A.; Caluwé, T.D.; Leloup, J.C.; Gonze, D.; Hermans, C.; Webb, A.A.R.; Verbruggen, N. Magnesium Maintains the Length of the Circadian Period in Arabidopsis. Plant Physiol. 2021, 185, 519–532. [Google Scholar] [CrossRef]
- Ohara, T.; Hearn, T.J.; Webb, A.A.; Satake, A. Gene Regulatory Network Models in Response to Sugars in the Plant Circadian System. J. Theor. Biol. 2018, 457, 137–151. [Google Scholar] [CrossRef]
- Ohara, T.; Satake, A. Photosynthetic Entrainment of the Circadian Clock Facilitates Plant Growth under Environmental Fluctuations: Perspectives from an Integrated Model of Phase Oscillator and Phloem Transportation. Front. Plant Sci. 2017, 8, 1859. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Gonze, D. Stochastic Simulation of a Model for Circadian Rhythms in Plants. J. Theor. Biol. 2021, 527, 110790. [Google Scholar] [CrossRef] [PubMed]
- Joanito, I.; Chu, J.W.; Wu, S.H.; Hsu, C.P. An Incoherent Feed-Forward Loop Switches the Arabidopsis Clock Rapidly between Two Hysteretic States. Sci. Rep. 2018, 8, 13944. [Google Scholar] [CrossRef] [PubMed]
- Tokuda, I.T.; Akman, O.E.; Locke, J.C.W. Reducing the Complexity of Mathematical Models for the Plant Circadian Clock by Distributed Delays. J. Theor. Biol. 2019, 463, 155–166. [Google Scholar] [CrossRef] [PubMed]
- Davis, W.; Endo, M.; Locke, J.C.W. Spatially Specific Mechanisms and Functions of the Plant Circadian Clock. Plant Physiol. 2022, 190, 938–951. [Google Scholar] [CrossRef] [PubMed]
- Nohales, M.A. Spatial Organization and Coordination of the Plant Circadian System. Genes 2021, 12, 442. [Google Scholar] [CrossRef] [PubMed]
- Gould, P.D.; Domijan, M.; Greenwood, M.; Tokuda, I.T.; Rees, H.; Kozma-Bognar, L.; Hall, A.J.; Locke, J.C. Coordination of Robust Single Cell Rhythms in the Arabidopsis Circadian Clock via Spatial Waves of Gene Expression. eLife 2018, 7, e31700. [Google Scholar] [CrossRef] [PubMed]
- Greenwood, M.; Tokuda, I.T.; Locke, J.C.W. A Spatial Model of the Plant Circadian Clock Reveals Design Principles for Coordinated Timing. Mol. Syst. Biol. 2022, 18, e10140. [Google Scholar] [CrossRef] [PubMed]
- Juarrero, A. Context Changes Everything: How Constraints Create Coherence; The MIT Press: Cambridge, MA, USA, 2023. [Google Scholar] [CrossRef]
- Galvão, V.C.; Fankhauser, C. Sensing the light environment in plants: Photoreceptors and early signaling steps. Curr. Opin. Neurobiol. 2015, 34, 46–53. [Google Scholar] [CrossRef]
- Ohara, T.; Fukuda, H.; Tokuda, I.T. An Extended Mathematical Model for Reproducing the Phase Response of Arabidopsis Thaliana under Various Light Conditions. J. Theor. Biol. 2015, 382, 337–344. [Google Scholar] [CrossRef]
- Pay, M.L.; Kim, D.W.; Somers, D.E.; Kim, J.K.; Foo, M. Modelling of Plant Circadian Clock for Characterizing Hypocotyl Growth under Different Light Quality Conditions. In Silico Plants 2022, 4, diac001. [Google Scholar] [CrossRef] [PubMed]
- Pay, M.L.; Christensen, J.; He, F.; Roden, L.; Ahmed, H.; Foo, M. An Extended Plant Circadian Clock Model for Characterising Flowering Time under Different Light Quality Conditions. In Proceedings of the 2022 22nd International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 27 November–1 December 2022; pp. 1848–1853. [Google Scholar] [CrossRef]
- Huang, T.; Shui, Y.; Wu, Y.; Hou, X.; You, X. Red Light Resets the Expression Pattern, Phase, and Period of the Circadian Clock in Plants: A Computational Approach. Biology 2022, 11, 1479. [Google Scholar] [CrossRef] [PubMed]
- De Caluwé, J.; De Melo, J.R.F.; Tosenberger, A.; Hermans, C.; Verbruggen, N.; Leloup, J.C.; Gonze, D. Modeling the Photoperiodic Entrainment of the Plant Circadian Clock. J. Theor. Biol. 2017, 420, 220–231. [Google Scholar] [CrossRef] [PubMed]
- Schmal, C.; Myung, J.; Herzel, H.; Bordyugov, G. A Theoretical Study on Seasonality. Front. Neurol. 2015, 6, 94. [Google Scholar] [CrossRef] [PubMed]
- Gould, P.D.; Ugarte, N.; Domijan, M.; Costa, M.; Foreman, J.; MacGregor, D.; Rose, K.; Griffiths, J.; Millar, A.J.; Finkenstädt, B.; et al. Network Balance via CRY Signalling Controls the Arabidopsis Circadian Clock over Ambient Temperatures. Mol. Syst. Biol. 2013, 9, 650. [Google Scholar] [CrossRef]
- Avello, P.A.; Davis, S.J.; Ronald, J.; Pitchford, J.W. Heat the Clock: Entrainment and Compensation in Arabidopsis Circadian Rhythms. J. Circadian Rhythm. 2019, 17, 5. [Google Scholar] [CrossRef] [PubMed]
- Avello, P.; Davis, S.J.; Pitchford, J.W. Temperature Robustness in Arabidopsis Circadian Clock Models Is Facilitated by Repressive Interactions, Autoregulation, and Three-Node Feedbacks. J. Theor. Biol. 2021, 509, 110495. [Google Scholar] [CrossRef]
- Yuan, L.; Avello, P.; Zhu, Z.; Lock, S.C.; McCarthy, K.; Redmond, E.J.; Davis, A.M.; Song, Y.; Ezer, D.; Pitchford, J.W.; et al. Complex epistatic interactions between ELF3, PRR9, and PRR7 regulate the circadian clock and plant physiology. Genetics 2024, 226, iyad217. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).