Gibbs Free Energy and Enthalpy–Entropy Compensation in Protein Folding

Abstract

The thermodynamic study of protein folding shows the generation of a narrow range of ΔG° values, as a net result of large changes in the ΔH° and TΔS° values of the folding process. The obvious consequence of this narrow range of values is that a linear enthalpy–entropy relationship, showing apparent enthalpy–entropy compensation (EEC), is clearly observed to be associated with the study of protein folding. Herein, we show the ΔH°, TΔS°, and ΔG° values for a set of 583 data from protein folding processes, at various temperatures, as calculated by using the Gibbs–Helmholtz equations. This set of thermodynamic data was calculated from the melting temperature (Tm), the melting enthalpy (ΔHm), and the change in heat capacity (ΔCp°) values, all of them associated with the heat-induced protein unfolding processes and included in the ProTherm Data Base. The average values of enthalpy (ΔH°av), entropy (TΔS°av), and free energy (ΔG°av) for the folding process were calculated within the range of temperature from 0 °C to the average value of Tm. The values and temperature dependency of TΔS°av within this temperature range are practically equal to those corresponding to ΔH°av, while ΔG°av remains small and displaying a curve with a minimum at about 10 °C and a value of ΔG° = −30.9 kJ/mol at the particular temperature of 25 °C. The large negative value of TΔS°av, together with the also large and negative value of ΔCp°av, suggests large conformational changes and important EEC, thus causing the small average value of ΔG° for protein folding, which is enough to guarantee both protein stability and molecular flexibility to allow for adaptation to the chemical potentials of the environment. Our analysis suggests that EEC may be the quantum-mechanical evolutive mechanism to make functional proteins adaptative to environmental temperature and metabolite concentrations. The analysis of protein folding data, compared with those of protein–ligand interaction, allows us to suggest strategies to overcome EEC in the design of new drugs.

1. Introduction

Studies aimed at the design of new drugs or the modification of known molecules to increase their affinity for target molecules are generally faced with the difficulty that an increase in the value of those thermodynamic parameters which are favorable to the interaction is associated with other properties that oppose the positive effect. Isothermal Titration Calorimetry (ITC) provides useful ΔH° values in experiments aimed to the optimization of ligands. The strategy consists of using a panel of ligands constructed by modifying a lead compound to make them interact with the target molecule. ITC experiments render ΔH° values that can give information concerning the kind of modification more convenient to gain affinity for the target molecule. Unfortunately, undesirable negative changes in the entropy change associated with the binding usually oppose the intended gain in affinity. Apparent enthalpy–entropy compensation (EEC) is frequently observed, thus preventing the achievement of more negative values of Gibbs free energy [1,2,3,4,5,6,7,8,9,10,11].

This compensation between ΔH° and TΔS° has been repeatedly observed in studies related to the binding of different structurally related ligands but also when considering the binding of unrelated ligands to different macromolecules [12]. Particularly interesting is the fact that EEC is much more clearly manifested in the thermodynamic study of protein folding, thus emphasizing that it is a phenomenon closely related to the molecular conformation of proteins. Differential Scanning Calorimetry has supplied plenty of data concerning the enthalpy and heat capacity associated with the temperature-induced denaturation of proteins. Herein, we report the results of a statistical analysis of the melting temperature, melting enthalpy, and the corresponding Gibbs free energy for 583 temperature-induced protein unfolding processes from the ProThermDB Data Base [13]. EEC seems to be more extensive in protein folding than in protein–ligand interactions, as deduced from the large decrease in TΔS° and heat capacity values found in the first process. This suggests large conformational changes to achieve functional, folded proteins, resulting in a small value of ΔG°, enough to guarantee protein stability and also a molecular structure flexible enough to allow for adaptation to the chemical potentials of the environment. The EEC in protein–ligand interactions seems to result in much smaller TΔS° and ΔCp° values, suggesting small conformational changes giving as a result the ΔG° values according to the chemical potential of the environmental metabolites. Our results may contribute to explain the apparently small value of ΔG° associated with protein folding at environmental temperature and to suggest some strategies to overcome EEC in the design of new drugs with higher affinity for their protein targets.

2. Methods

Melting temperature (Tm), melting enthalpy (ΔHm), and the increment in heat capacity of melting (ΔCp°), as obtained from the ProThermDB Data Base [13], were used to calculate the ΔH°(T), TΔS°(T), and ΔG°(T) of protein unfolding at different temperatures, according to the Gibbs–Helmholtz equation, by using an Excel spreadsheet from Microsoft 365 (Microsoft Corporation ((1), (2), (3))):

$$\Delta H°\left(T\right)=\Delta Hm-\Delta Cp°(Tm-T)$$

(1)

$$T\Delta S°\left(T\right)=T\Delta Hm/Tm-T\Delta Cp°\mathrm{l}\mathrm{n}(Tm/T)$$

(2)

$$\Delta G°\left(T\right)=\Delta Hm-\Delta Cp°(Tm-T)-T\Delta Hm/Tm+T\Delta Cp°\mathrm{l}\mathrm{n}(Tm/T)$$

(3)

Gaussian distributions were obtained by using ORIGIN 2023, Origin Lab Corporation, Northampton, MA, USA.

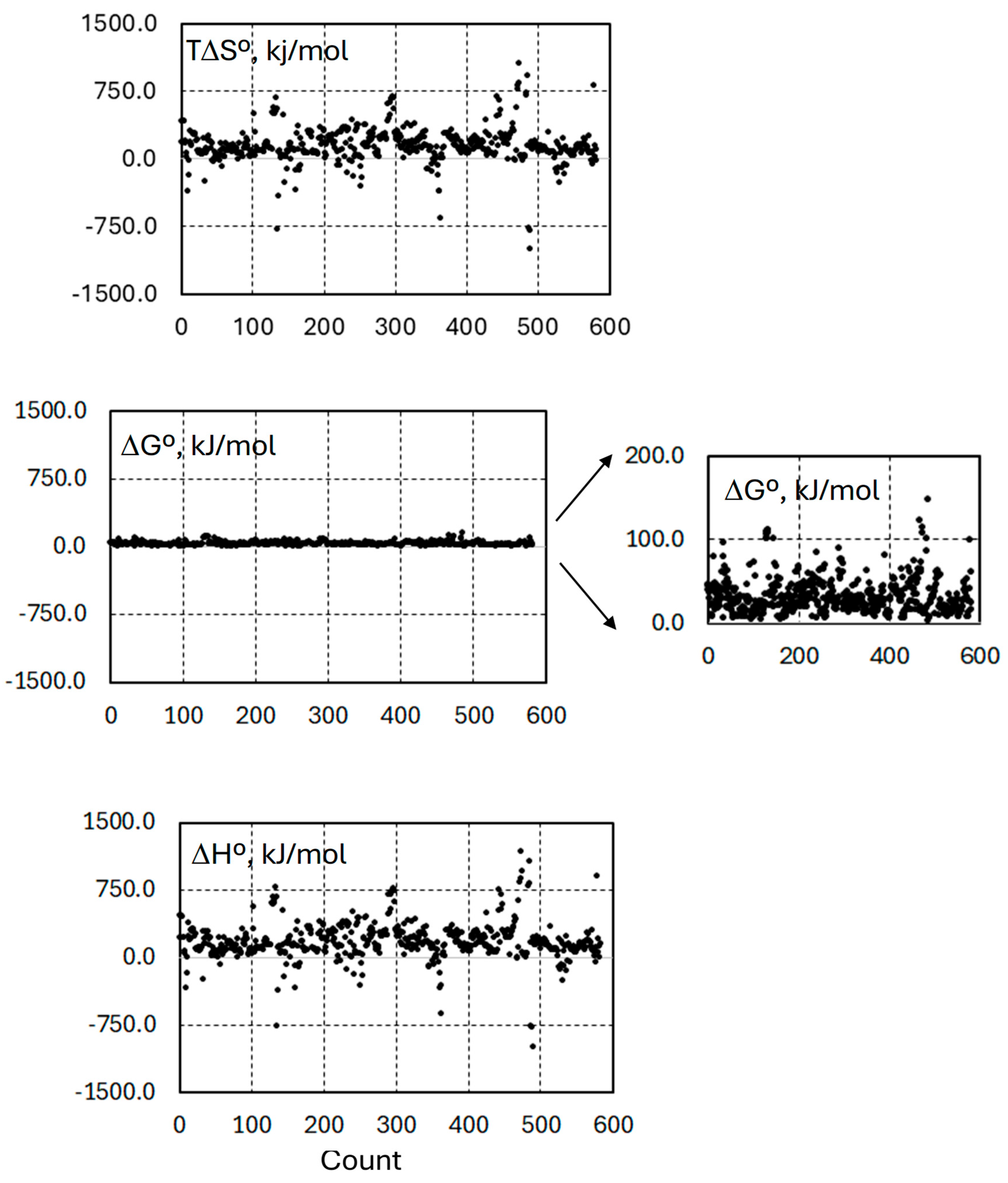
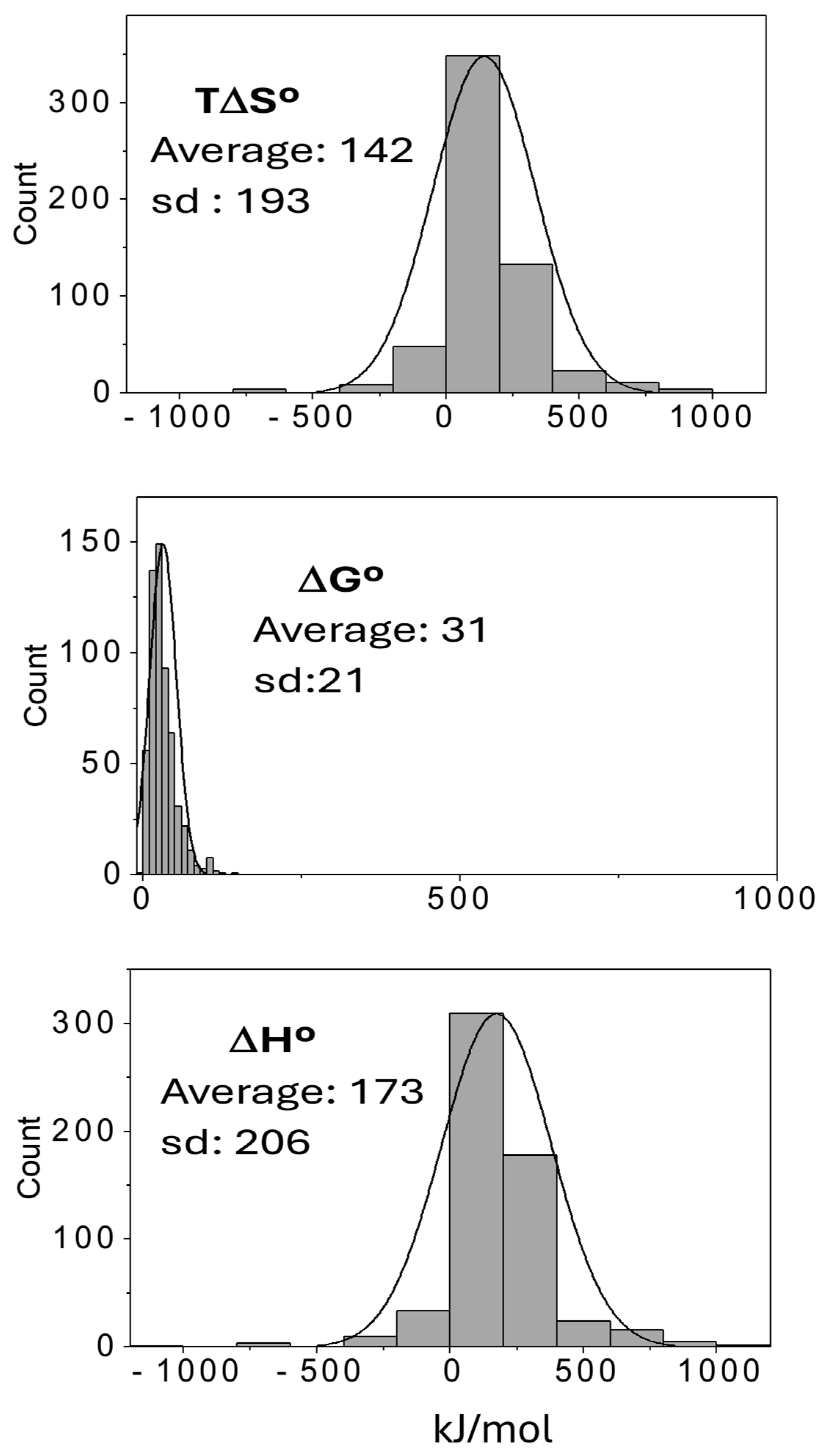
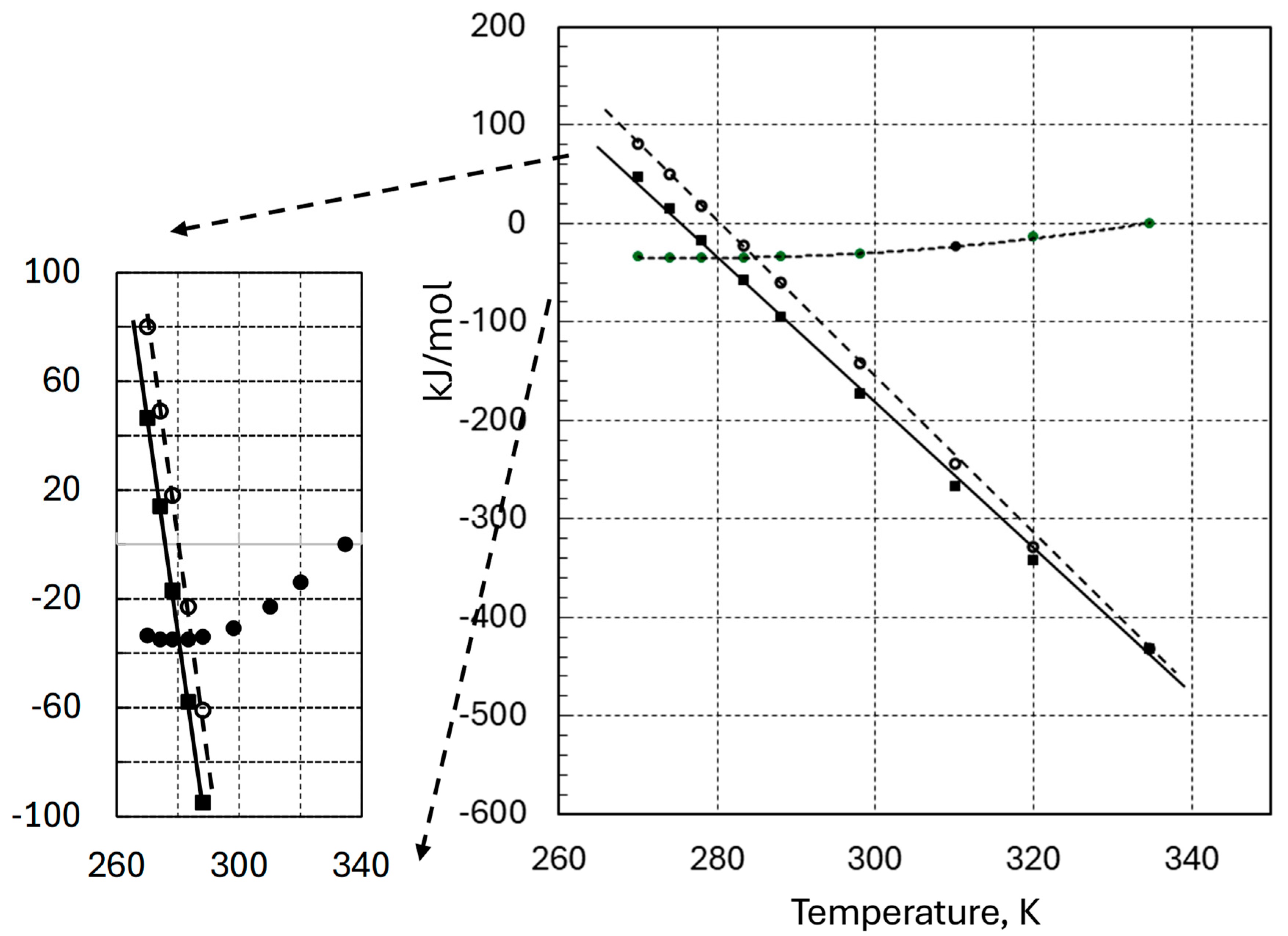
3. Results and Discussion

Figure 1 shows the scattering plots corresponding to the ΔH°, TΔS°, and ΔG° values for a set of 583 protein unfolding processes, at 25 °C, as calculated by using the Gibbs–Helmholtz equations described in Methods. This set of thermodynamic data was calculated from the melting temperature (Tm), the melting enthalpy (ΔHm), and the change in heat capacity (ΔCp°) values, all of them associated with the heat-induced protein unfolding processes and included in the ProTherm Data Base [13]. As can be observed, the range and distribution of the ΔH° values are practically equal to those corresponding to TΔS°, while ΔG° remains within a very narrow range of values, leading us to conclude that most of the heat experimentally detected in the unfolding process (ΔH°) is due to the heat involved in the entropy changes, according to the equation ΔH° = TΔS° + ΔG°.

Figure 2 shows the linear relationship obtained from the plot of ΔH° versus TΔS° values of the same set of data, in agreement with the narrow range of ΔG° values. A similar linear relationship has been previously reported for protein unfolding data [14] and attributed to enthalpy–entropy compensation similar to that repeatedly reported in experiments related to protein–ligand interactions.

The Gaussian distribution of the thermodynamic properties corresponding to the unfolding of the same set of proteins is shown in Figure 3. The average value obtained for ΔG° was 30.9 ± 0.9 kJ/mol. A larger set of ΔG° values obtained by including 342 additional values at 25 °C from the data base showed a similar Gaussian distribution, with an average value of ΔG° = 32 ± 0.9 kJ/mol.

The internal energy of a protein molecule is composed of electronic energy, Ue; vibrational energy, Uv; rotational energy, Ur; and translational energy, Ut. We assume an ideal, diluted protein solution, ignoring intermolecular interactions. The change in internal energy corresponding to a protein folding at constant pressure can be expressed accordingly as

$$\Delta U°=(\Sigma Ue)°+\Delta Us$$

(4)

and the corresponding change in enthalpy is

$$\Delta H°=(\Sigma Ue)°+\Delta Us°+p\Delta V$$

(5)

$(\Sigma Ue)°$ stands for the stoichiometric sum of the electronic energies of unfolded and folded active proteins: electronic energy of folded proteins minus electronic energy of unfolded proteins, both of them at 0 K. Protein folding does not usually involve changes in covalent bonds; therefore, $(\Sigma Ue)°$ includes all kind of weak interactions, such as those derived from salt bridges, Cation-P or Van der Waals forces, and all weak intramolecular interaction contributing to the change in potential energy in the folding process. An important contribution to $(\Sigma Ue)°$ is the energy derived from changes in water molecule reorganization. A vast number of water–protein, water–water, and intramolecular hydrogen bonds have to be involved in the water–protein reorganization associated with folding. All these weak interactions play the same role in protein folding as covalent bonds play in a chemical transformation. On the other hand, $\Delta Us°$ stands for the stoichiometric sums of vibrational, rotational, and translational energy values, ΣUv + ΣUr + ΣUt, corresponding to the difference between the folded and the unfolded forms of the protein. We have grouped ΣUv + ΣUr + ΣUt in the term $\Delta Us°$ because, according to the Boltzmann Distribution Law, at room temperature, the differences in energy values between different quantum levels of vibrational, rotational, and translational energy, at room temperature, are small enough to allow for significant occupation of the different energy levels, thus contributing to the change in the number of quantum states (or configurations) and therefore to the entropy change associated with the protein folding process.

Following the Gibbs free energy definition, G ≡ U + pV − TS, the value of ΔG at constant values of pressure and temperature is given, under standard conditions, by

ΔG° = ΔH° − TΔS°

(6)

The substitution of Equation (5) into (6) yields

$$\Delta G°=(\Sigma Ue)°+\Delta Us°+p\Delta V-T\Delta S°$$

(7)

By defining ΔHs° as

$$\Delta Hs°=\Delta Us°+p\Delta V$$

(8)

we have

$$\Delta G°=(\Sigma Ue)°+\Delta Hs°-T\Delta S°$$

(9)

The difference between the two last terms in Equation (9), ΔHs° − TΔS°, is the contribution to ΔG° by the changes in the energy value of the quantum levels of vibrational, rotational, and translational energies associated with the unfolded-to-folded transformation. Finally, after defining,

$$\Delta Gs°\equiv \Delta Hs°-T\Delta S$$

(10)

we have

$$\Delta G°=(\Sigma Ue)°+\Delta Gs°$$

(11)

Equation (11) may help to follow the hypothesis most frequently used to provide a theoretical basis to EEC. The idea that governs most research on EEC is that whenever $(\Sigma Ue)°$ is negative, as a consequence of weak interactions, the folded structure of the protein becomes more tightened, thus increasing the value of the force constants of all kind of bonds, in turn increasing the vibration frequencies of some of the thousands of vibration modes of the full protein molecule and the corresponding values of the quantum energy levels of those vibrational modes of the protein. Likewise, folding could also produce a decrease in the moments of inertia with a corresponding increase in the value of the rotational levels. Concisely, very negative values of $(\Sigma Ue)°$, which stabilize the molecule, lead to positive values of ΔGs°, which can counteract the final stability supplied by $(\Sigma Ue)°$. Everything can be even more complex if we consider the hydrophobic effect. Protein folding causes a large loss of the water forming part of the protein surface solvation, thus increasing the volume of water available as a solvent to the protein. The energy of the translational levels decreases with the increase in volume, so that the hydrophobic effect associated with protein folding is a negative contribution to ΔGs° [15,16].

In summary, when considering the protein folding process, weak interactions contribute negative values to ΔG° through the $(\Sigma Ue)°$ term, vibrational and rotational energies contribute positive values to ΔG° through the ΔGs° term, and finally, the hydrophobic effect contributes negative values to ΔG° through the ΔGs° term.

Figure 4 shows the results obtained for the average values of ΔG°, ΔH°, and TΔS°, as functions of temperature, corresponding to the 583 examples of protein folding included in the previous figures. As can be observed in Figure 4, the average values of ΔG° form a set of small and almost invariable negative values within the temperature range between approximately 0 °C and 40 °C. At the particular temperature of 25 °C, ΔG° = −30.9 kJ/mol, with a standard deviation of 21 kJ/mol. These values for ΔG° are extraordinarily small compared with the hundreds or even thousands of water–protein and protein–protein hydrogen bonds, van der Waals forces, Cation-P, salt bridges, and some other weak interactions, as well as hydrophobic effects and vibrational–rotational energy changes, involved in the folding of a protein. The energy value of each one of this type of weak interactions ranges from about 0.1–2 kJ/mol for van der Waals forces to about 2–10 kJ/mol for hydrogen bond interactions [17,18,19]. Changes in medium polarity, caused by folding and the nature of amino acid residues themselves, can affect the value of the enormous number of weak interactions, as well as the vibration frequencies and moments of inertia. This complex system, derived from the polymeric and quantum-mechanical nature of proteins, constitutes an extraordinarily sensitive system of folding regulation, always resulting in a value of ΔG° sufficient to maintain the functional structure of the protein in the range of environmental temperature, as well as vibrational frequencies and inertia.

The value of ΔG° at a certain temperature depends on three parameters: the folding temperature, Tm; the enthalpy of folding, ΔHm; and the change in heat capacity, ΔCp°. Simulation of the Gibbs–Helmholtz equations, using different sets of plausible values of Tm, ΔHm, and ΔCp°, shows that proteins having much higher negative values of ΔG° could have been found at different temperatures from those shown in Figure 4. It seems, however, that evolutive stress has selected those sufficiently stable proteins, with the minimum amount of free energy lost in folding, and in the temperature range of the environment. The thermodynamic data included in Figure 4 are the average values for ΔG°, ΔH°, and TΔS° as calculated from the ΔHm, Tm, and ΔCp° values obtained from the ProTherm Data Base. The thermodynamic behavior described by the curves in the figure seems to be similar to that of every individual protein (see [20]).

The value of ΔG° depends on temperature according to the equation

$$d\Delta G/dT=-\Delta S$$

(12)

The temperature value for which ΔS° = 0 for the same set of data used above can be obtained from Equation (2),

$$T\left(\Delta S°=0\right)={\displaystyle \frac{Tm}{\exp \left(\frac{\Delta Hm}{\Delta Cp°Tm}\right)}}=283.4 \mathrm{K}$$

(13)

By using the average values Tm = 334.6 K, ΔHm° = 432.6 k/mol, and ΔCp°m = 7.8 kJ/molK.

The second derivative of ΔG° is given by

$$d2\Delta G°/dT2=-\Delta Cp°/T$$

(14)

The folding of proteins is associated with a negative value of ΔCp, making the second derivative of ΔG° positive. Consequently, the average values of ΔG° must reach a minimum value at 283.4 K, as shown in Figure 4. From this temperature to the melting temperature, Tm, ΔG° increases, and accordingly, TΔS° decreases, as shown in the same figure. This large decrease in the TΔS° term on protein folding must be a consequence of the loss of heat capacity and entropy (Equation (15)) associated with protein folding and due to the increase in the energy values of the vibrational–rotational quantum levels:

$$dT\Delta S°/dT=\Delta Cp°+\Delta S$$

(15)

Protein folding is associated with changes in the quantum-mechanical structure of the vibrational, rotational, and translational energies of the molecule. The weak intramolecular forces causing the decrease in the potential energy responsible for the stability of the folded protein induce the molecular structure to tighten. This tightening is associated with a better-defined molecular structure, an increase in the intramolecular forces, and the consequent increase in the vibrational frequencies of the thousands of modes of molecular vibrations, thus rendering an increase in the energy value of the quantum vibrational levels, which, as a consequence, become more separated, leading to a diminution in the number of quantum states resulting from the distribution of molecules among the energy levels. This is the statistical interpretation of a decrease in entropy. Folding may also cause a decrease in the moment of inertia of the molecule, increasing the rotational energy levels. This means less stacking of energy levels and correspondingly less entropy. Finally, the third important consequence of folding is the hydrophobic effect. Protein folding increases intramolecular protein–protein surface contacts, thus causing an increase in the volume available for molecular translation, leading to lower values of translational energy levels and higher stacking of those levels. This means an increase in entropy [15,16].

The dispersion plots of Figure 1 show how some positive unfolding values of TΔS° and ΔH° display significant deviations from the corresponding average values. Most of the proteins included in the data base are globular in nature, and we have found no correlation with any particular protein function or any class of protein. For example, a complex protein such as Chitinase 40 [21], with a barrel-like fold forming the catalytic domain, displays ΔH° and TΔS° values as large as those corresponding to small molecules such as yeast Phosphoglycerate kinase (about 45,000 MW) [22] or Ribonuclease A (13,700 MW) [23]. Although most of the TΔS° and ΔH° values for the unfolding protein at 25 °C are positive values, negative values can also be found for the unfolding process. Contributions to the change in entropy come from changes in the translational, vibrational, and rotational energy levels. In the unfolding process, the translational energy levels change in the opposite direction to the vibrational–rotational energy levels. In the unfolding process, protein hydration increases, and the available volume decreases, thus causing an increase in the value of translational energy levels with the corresponding decrease in entropy. On the other hand, the unfolding process frequently causes a decrease in the vibrational–rotational energy levels with the corresponding stacking of those levels and the corresponding increase in entropy. According to the results of the scrutiny shown in Figure 1, in most cases, the increasing entropy due to the stacking of the vibrational–rotational levels predominates. However, when hydration is very important in maintaining the folded structure, a negative change in entropy may appear associated with unfolding. This might be the case of Kumamolisin [24], a very stable carboxyl protease displaying a high extent of folding. Positive contributions to the unfolding process are the energies coming from weak interactions $(\Sigma Ue)°$ and those coming from the reversal of the hydrophobic effect. The fact that most folding processes are associated with negative values of $(\Sigma Ue)°$ (associated with weak interactions) and DUt ΔUt (due to the hydrophobic effect) and, on the other hand, positive values of DUv ΔUv and DUr ΔUr reflects the importance of the former in determining the folding energy and of the latter in exerting a compensation effect that determines the final value of ΔG°.

As can be observed in Figure 4, most of the negative enthalpy change (ΔH°) involved in protein folding is due to the heat lost in the negative change in entropy (TΔS°) associated with vast conformational changes in the folding process as reflected in the value of ΔCp°. The average value of ΔG° = − 30.9 kJ/mol at 25 °C for the folding process is the result of the compensation between the negative values included in (ΣUe)° and the positive values corresponding to vibrational–rotational energy increases included in ΔGs° (Equation (11)). Within the range of temperatures showing the negative values of ΔG° for protein folding, the content of entropy is much lower in the folded protein than in the unfolded one. This loss of entropy is due to the large conformational changes induced by $(\Sigma Ue)°$, causing the energy gain of the vibrational–rotational levels included in ΔG°s and the corresponding loss of entropy as a consequence of the loss of energy level stacking.

Figure 5 shows the scattering plots corresponding to the ΔH°, TΔS°, and ΔG° values for a set of 42 protein–ligand interactions reported in a previous publication from our laboratory [9,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. The data of protein folding in Figure 1 have also been included for comparative purposes. As can be observed, the dispersion of the TΔS° and ΔH° values for protein folding is much wider than that for protein–ligand interaction. The average value of the Gibbs free energy of the protein–ligand complex formation of this set of 42 protein–ligand interactions, ΔG° = −29.8 kJ/mol, is surprisingly similar to that reported here for protein folding. The average value for TΔS°, however, is about ten times smaller than that corresponding to protein folding, suggesting that the conformational changes induced by ligand binding are much less significant than those caused by the folding of proteins. This suggestion is confirmed by the much lower value reported for the change in heat capacity for the formation of protein–ligand complexes, ΔCp° = −1.5 kJ/K mol, as the average value of a set of sixteen values of ΔCp for the formation of protein–ligand complexes [43,44]. This ΔCp° value is

$$\begin{gathered} \Delta Cp°=[Cp°\left(PL\right)-Cp°\left(P\right)]-Cp°\left(L\right)=-1.5 \\ Cp°\left(PL\right)-Cp°\left(P\right)=-1.5+Cp°\left(L\right) \end{gathered}$$

(16)

where Cp° (PL), Cp° (P), and Cp° (L) stand for the heat capacities of the protein–ligand complex (PL), the protein (P), and the ligand (L). The heat capacities of ligands of small molecular weight are almost linearly dependent on their molecular weight. Up to a value of about 300 g/mol, the heat capacity values go linearly up to about 0.4 kJ/K mol. According to (16), protein–ligand complex formation is associated with a very small decrease in heat capacity compared with the average value for the change in heat capacity associated with protein folding, ΔCp° = −7.8 kJ/K mol. This observation, together with the small diminution in TΔS°, leads us to conclude that protein–ligand complex formation causes, in general, very small changes in protein conformation and that most of the energy involved in ΔG° comes from $(\Sigma Ue)°$, while the compensation contributed by ΔG°s must be very small.

A different hypothesis has been proposed to provide a theoretical basis to explain the EEC causing the narrow range of unfolding ΔG° values. It has been suggested that these ΔG° values may have an evolutionary origin, although no adaptive goal has been clearly argued [2,7]. Water reorganization, along with some evolutive suggestions, has been considered for years to be associated with EEC [1,14,45,46,47]. However, these theoretical approaches ignore the quantum-mechanical structure of proteins—the vibrational, rotational, and translational energy levels—to evaluate the entropy changes associated with protein unfolding. According to Dragan [48], the increase in entropy associated with the hydrophobic effect might compensate for the enthalpy under the assumption of tightly bound water. By using a model composed of two opposite-charged polymers, Chen and Wang [8] concluded by molecular dynamic calculations that changes in the thermodynamics of water might explain enthalpy–entropy compensation. They argue, however, that the model is too simple and the extent of biomolecular interactions is currently beyond our computational possibilities.

Closer to our proposition here is the idea proposed by Dunitz [49] that the constraints imposed by weak interactions with the consequent tightening of the protein molecule must cause a decrease in TΔS°. This idea could be tested by using a simple model composed of a water molecule bound to a large molecule and a Morse potential. The theoretical calculations proved that the idea was correct whenever low energy values were involved.

We show in this paper that enthalpy–entropy compensation seems to be involved in the narrow range of ΔG° values that guarantees the functionality and stability of folded proteins, as it has been previously suggested [12,49]. Each of these ΔG° values, the average of which is −30.9 kJ/mol, is the net result of a number of contributions of different signs, beside water reorganization, included in Equation (11): (a) A plausibly large number of van der Waals forces, Cation-P, and salt bridges, together with any other weak interaction, contribute negative values to ΔG° through the $(\Sigma Ue)°$ term. (b) Protein folding increases intramolecular protein–protein surface contacts, thus eliminating water molecules from the solvation sphere and causing an increase in the volume available for molecular translation, leading to lower values of translational energy levels and thus contributing negative values to ΔG° through the ΔG°s term [15,16]. (c) The large number of breaking and forming intermolecular and intramolecular hydrogen bonds involved in water reorganization to form the hydration sphere (or spheres) of both the unfolded and the folded protein molecule contribute a net value to ΔG° through $(\Sigma Ue)°$; in this last case, however, the net sign of the resultant is beyond our computational possibilities [8]. (d) The vast number of weak interactions tightens the protein conformation, thus increasing the vibrational frequencies of the thousands of normal modes of vibration and the corresponding value of the quantum levels of vibrational energy. This contributes positive values to ΔG° through the ΔGs° term. Finally, (e) tightening the molecule can also decrease the moment of inertia of the protein molecule, thus increasing the value of the rotational energy levels and contributing positive values to ΔG° through ΔGs°.

It is surprising that this huge group of weak interactions of opposite sign results in an average value of ΔG° as small as −30.9 kJ/mol, which is quite similar to that reported for a set of protein–ligand interactions [12]. In a recent publication [9], we found a similar average value for Gibbs free energy, ΔG° = −36.5 kJ/mol, for a set of more than three thousands protein–ligand interactions. The agreement of this value with the average value for the chemical potential of more than 2500 physiological concentrations of human metabolites led us to suggest that enthalpy–entropy compensation may be the quantum-mechanical mechanism that may have acted over evolution to produce the present functional proteins having the maximal regulatory capacity. Likewise, the average value of −30.9 kJ/mol may be the result of evolutive stress rendering proteins stable with minimal production of free energy, within the current temperature range of liquid water in the environment. The results of the statistical analysis of thermodynamic properties concerning protein folding and protein–ligand interactions suggest that in both processes, enthalpy–entropy compensation is the quantum-mechanical evolutive mechanism to make functional proteins adaptative to environmental temperature and metabolite concentrations. The narrow range of ΔG° values found for protein folding seems to be a consequence of the enthalpy–entropy compensation derived from the intrinsic nature of protein structure. Some mutant forms from the same wild-type protein also form part of the same set of values included in the Gaussian distribution in Figure 3. The set of 583 unfolding data shown here corresponds to different proteins and different mutant forms under different environmental conditions of pH and ionic strength, thus emphasizing the idea that the quantum-mechanical protein structure underlies their evolutionary capacity.

4. Conclusions

Herein, we report the results of a statistical analysis of the melting temperature, melting enthalpy, and the corresponding Gibbs free energy for 583 temperature-induced protein unfolding processes from the ProThermDB data base [13]. We compare the results with those obtained for protein–ligand interactions, reaching the following conclusions: (a) Protein folding renders ΔH° and TΔS° values, as well as heat capacity changes, much higher than those corresponding to protein–ligand interactions. (b) The ΔG° values in both cases are quite similar, equivalent to the energy of about two to three hydrogen bonds. (c) Conformational changes in protein folding are much more extensive than in protein–ligand interactions. (d) The vast number of weak interactions contributing negatively to ΔG°, along with the negative contribution derived from the hydrophobic effect, is strongly compensated by the positive contribution of increasing vibrational and rotational energies derived from the conformational changes associated with the folding process, resulting in the small value of ΔG = −30.9 k/mol; this value is enough, however, to guarantee the folded functional structure of the protein. (e) As deduced from the small values of TΔS°, ΔH°, and ΔCp°, enthalpy–entropy compensation in protein–ligand interaction induces conformational changes much less relevant than those observed in protein folding. Therefore, the free energy of binding (ΔG° = −36.5 kJ/mol) comes mostly directly from the decreasing potential energy contributed by weak interactions. This last observation points to the plausibility that ligands modifications capable of increasing the number and extent of weak interactions with a target protein—for example, hydrogen bonds—may cause a ΔG° decrease without significantly affecting the protein conformation, the vibrational and rotational energy levels, and the corresponding entropic penalty. (f) Our analysis suggests that EEC may be the quantum-mechanical evolutive mechanism to make functional proteins adaptative to environmental temperature and metabolite concentrations.