Quantitative Risk Assessment Methodology for Hydrogen Tank Rupture in a Tunnel Fire
Abstract
:1. Introduction
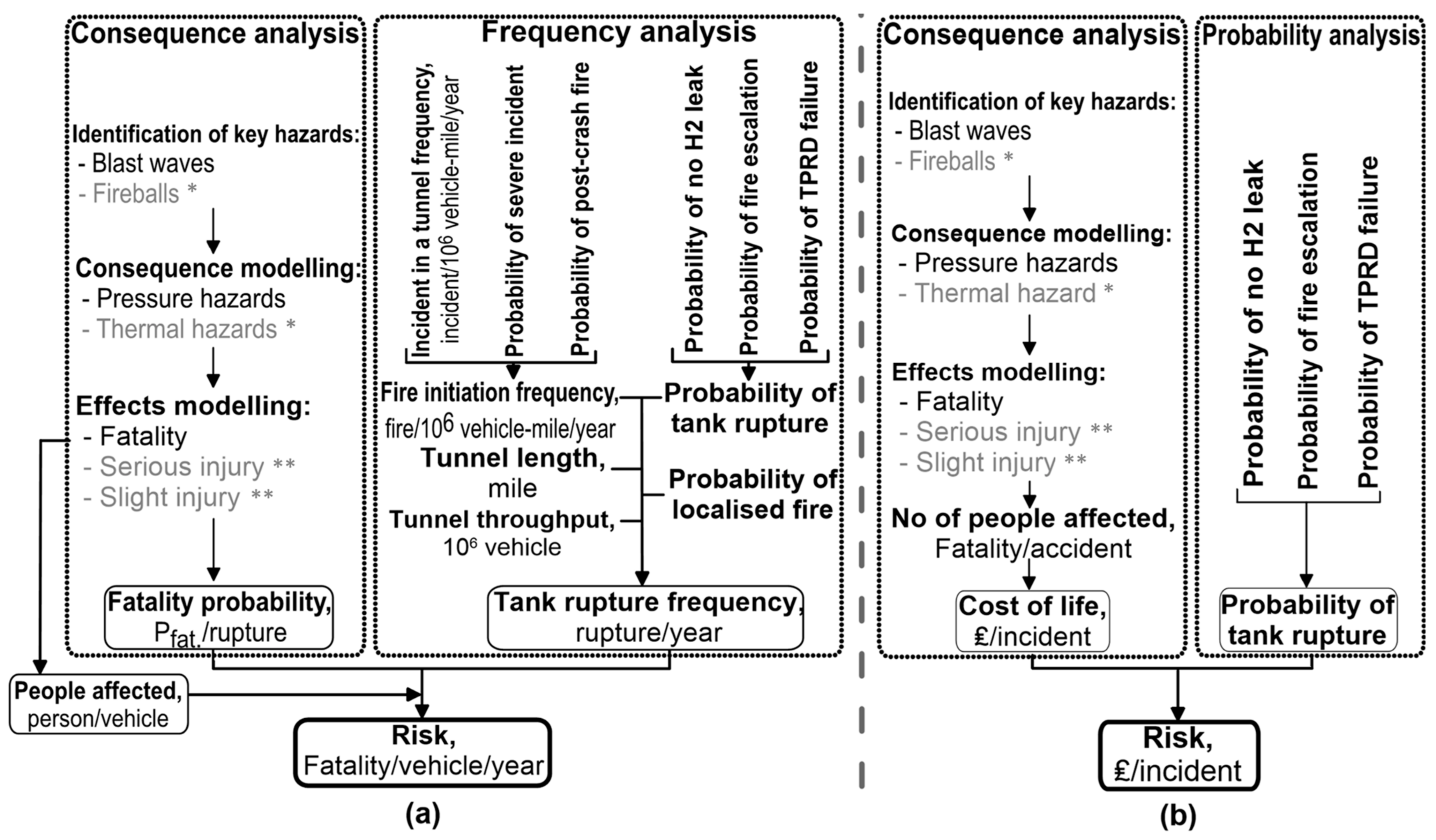
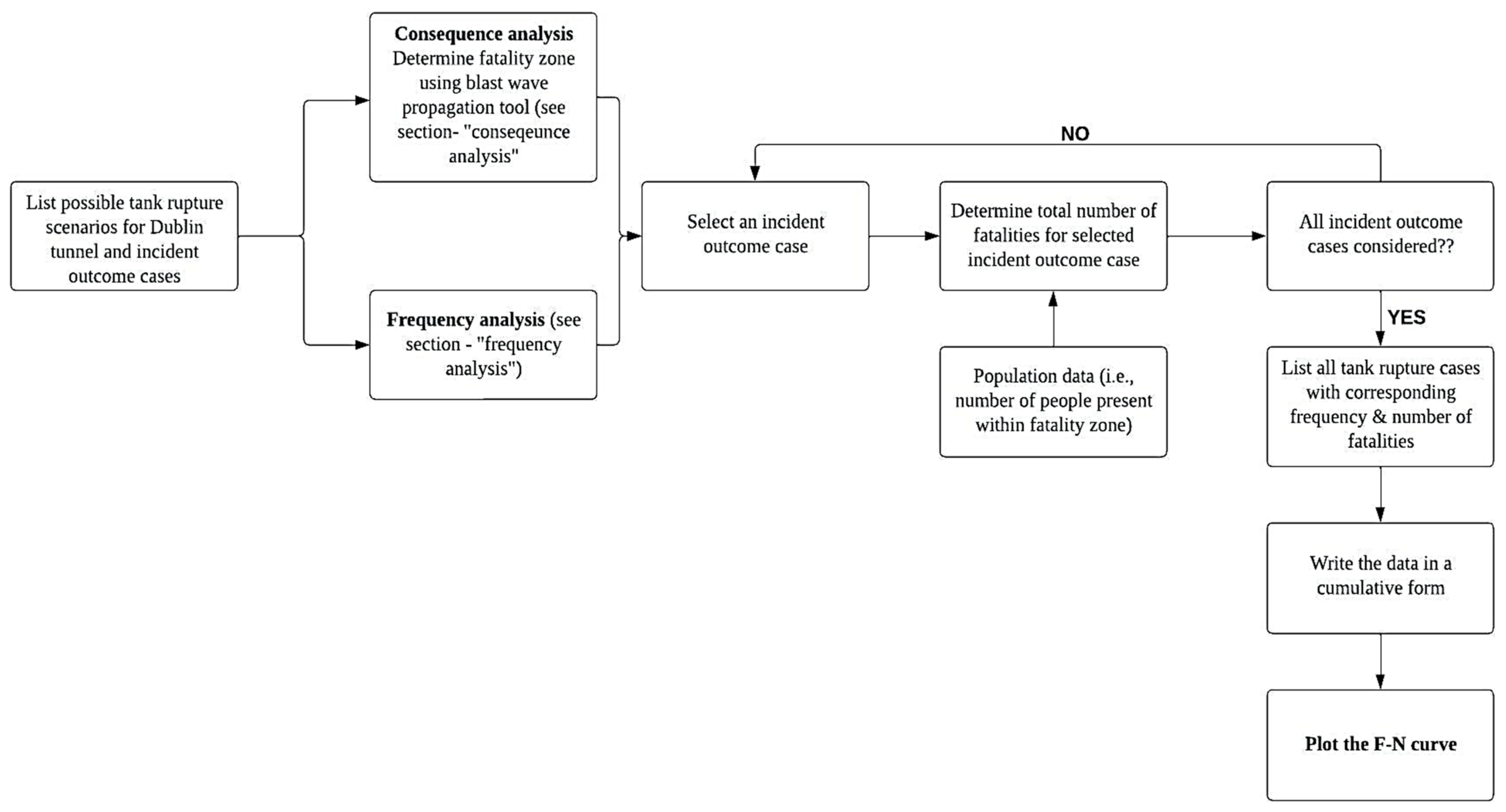
2. QRA Methodology for Hydrogen Tank Rupture in a Tunnel
3. Methodology
- An HFCV is trapped in a severe incident inside the tunnel, that has escalated into a fire. The vehicle has the CHSS consisting of two hydrogen tanks. The bigger tank of 62.4 L volume and NWP = 70 MPa (containing = 2.5 kg of hydrogen) [25] was subject to a fire with a subsequent rupture. The larger tank is chosen for the reason of conservatism. The rupture of one tank is assumed not to provoke the rupture of another tank, i.e., an isolated case of rupture of one tank is considered.
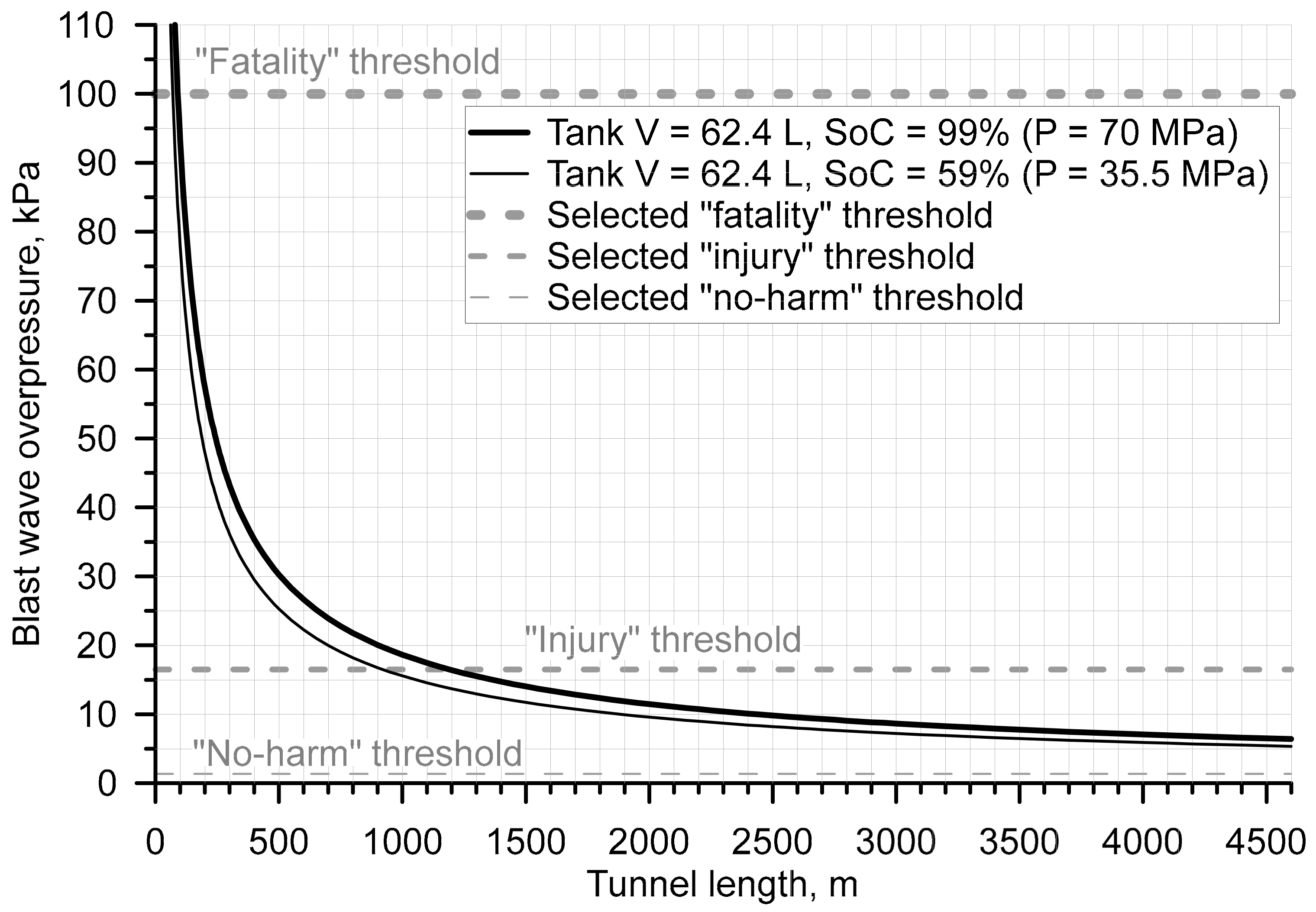
- The blast wave decay in the tunnel is estimated based on the formulation of a stand-alone tank rupture, i.e., no mechanical energy of compressed gas was spent on vehicle destruction and body frame translation [21]. This is justified by the observation that the blast wave strengths after ruptures of stand-alone and under-vehicle tanks are similar in the far-fields [26]. Most of the tunnel length represents a “far-field” distance from the tank rupture location.
- The car incident location is 50 m away from the tunnel tube exit and it blocks both lanes in the tube (as the direction of traffic on both lanes in the tunnel tube is the same). This causes all the vehicles, that have entered the tunnel, to stop inside and be unable to leave the tunnel. This means the affected tunnel length of (4650 − 50) m = 4600 m. There may be several scenarios with many combinations of the incident location and the number of vehicles stopped in the tunnel. An incident could happen in the middle of the tunnel (which is less likely, as per the literature [23,24]), blocking both lanes. Hence, all the vehicles after the incident location will leave the tunnel and only those vehicles inside the tunnel before an incident location are forced to stop and will be affected by the tank rupture consequences. In such cases, twice less of the vehicles/passengers will be in danger, compared to the scenario previously described (and suggested for this paper). Additionally, in order to demonstrate the value of the proposed methodology and risk mitigation strategy, the authors conducted F–N curve analysis using several rupture scenarios, including a rupture at the midway of the Dublin tunnel. It is worth mentioning that the consequences analysis for outside the tunnel is essentially the assessment of the people affected by the tank rupture in the open (similar to the work by authors [6]) and is out of scope of this study.
- Considering that the SoC of CHSS will normally be from 17% to 59% on average before refuelling [12], the value of SoC = 59% (equivalent to 35.5 MPa at 20 °C) is selected for the consequence analysis. The tank filled up to NWP = 70 MPa at 20 °C would have SoC = 99% (the SoC of 100% for such pressure is achieved at hydrogen temperature 15 °C). The SoC = 59% is considered as an attempt to approach a real incident scenario as close as possible.
3.1. Consequence Analysis
- (a)
- Fire due to the car incident;
- (b)
- TPRD failure to operate;
- (c)
- Failure of emergency operation;
- (d)
- Hydrogen tank rupture;
- (e)
- Blast wave.
3.2. Frequency Analysis
3.2.1. Frequency of the Initiating Fire Event
3.2.2. TPRD Failure Probability
3.2.3. Escalation Probability
3.2.4. Probability of a Tank Rupture
3.2.5. Frequency of a Tank Rupture
3.2.6. Risk
4. QRA Results and Discussion
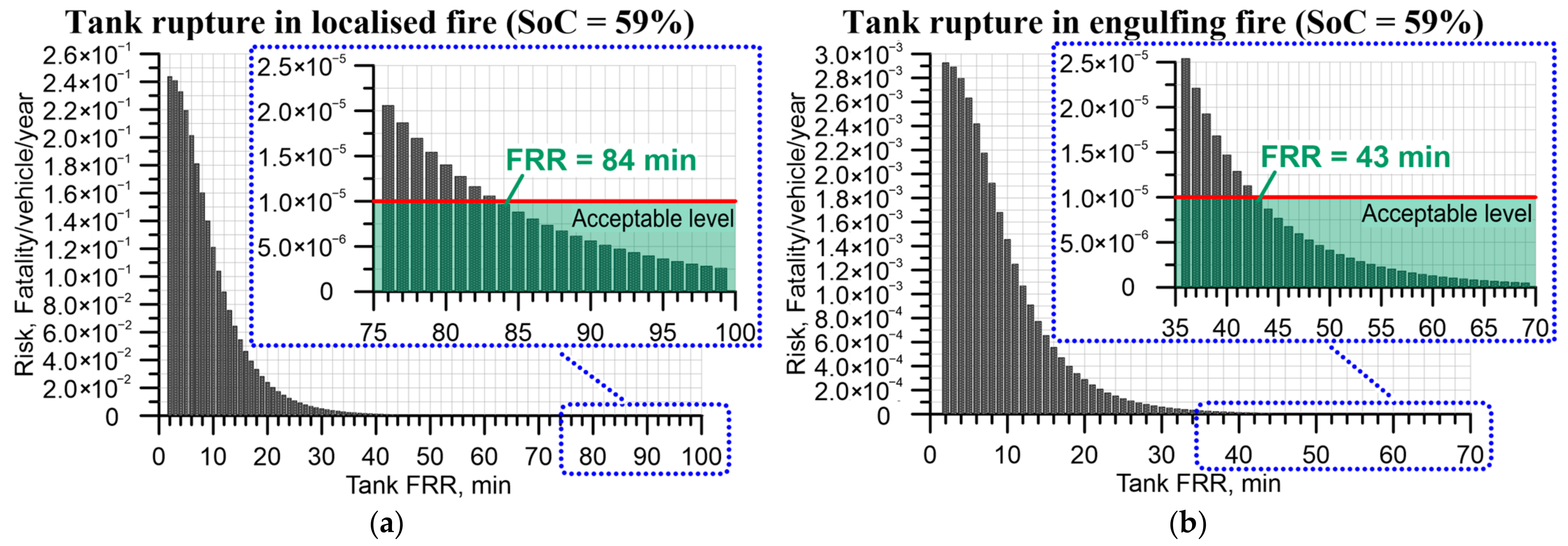
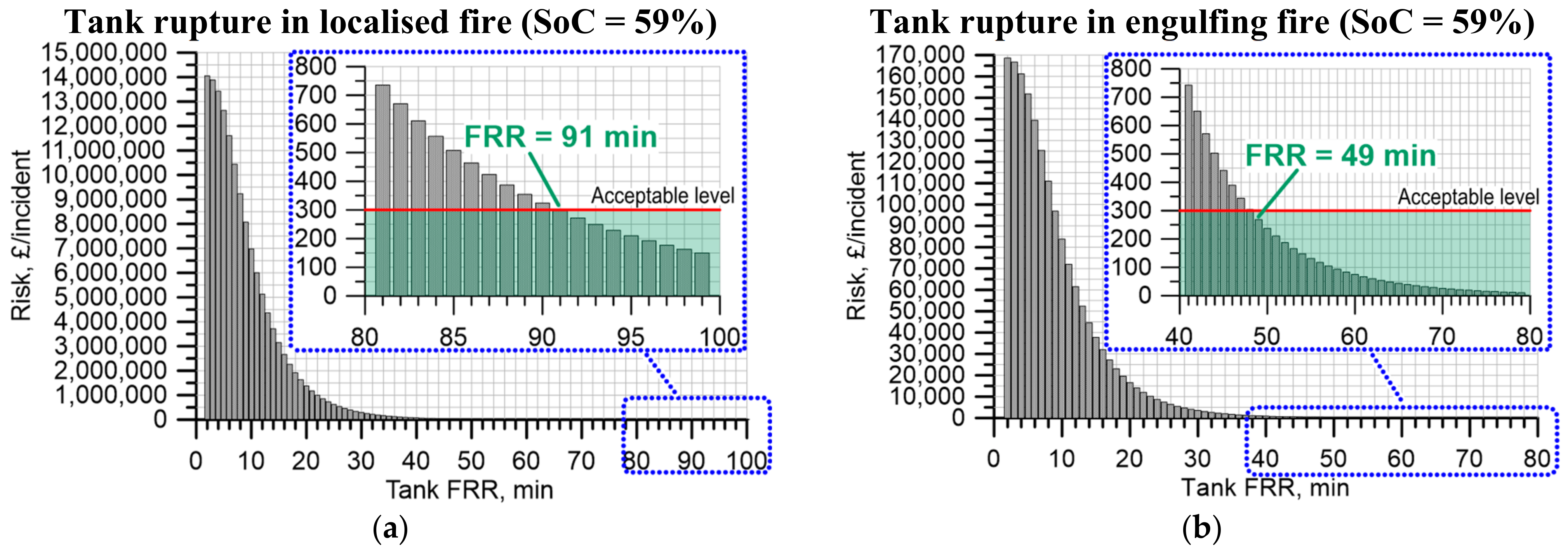
4.1. Effect of Tank FRR on the Risk in Terms of Annual Fatality Rate per Hydrogen-Powered Vehicle
4.2. Effect of Tank FRR on the Risk in Terms of Costs
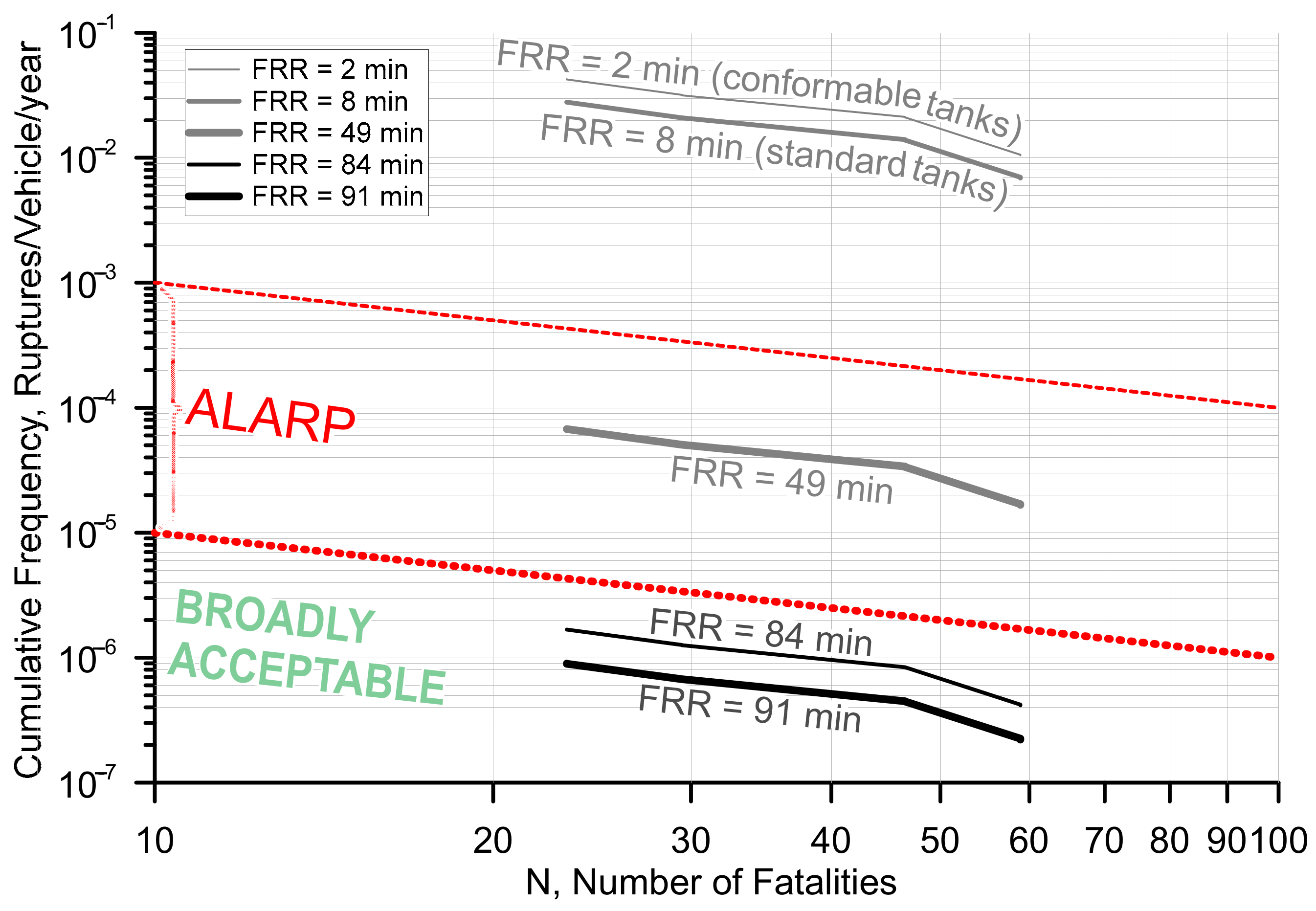
4.3. Societal Risk: F–N Curve Results
4.4. Sensitivity Analysis
4.5. Sensitivity of Tank Rupture Risk—Fire Brigade Response Time
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ingason, H.; Li, Y.Z. Spilled liquid fires in tunnels. Fire Saf. J. 2017, 91, 399–406. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z.; Lönnermark, A. Tunnel Fire Dynamics; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ingason, H.; Hammarström, R. Fire Test with a Front Wheel Loader Rubber Tyre; SP Report 2010:64; SP Technical Research Institute of Sweden: Boras, Sweden, 2010. [Google Scholar]
- Molkov, V.; Dadashzadeh, M.; Kashkarov, S.; Makarov, D. Performance of hydrogen storage tank with TPRD in an engulfing fire. Int. J. Hydrog. Energy 2021, 46, 36581–36597. [Google Scholar] [CrossRef]
- Ehrhart, B.D.; Brooks, D.M.; Muna, A.B.; LaFleur, C.B. Risk Assessment of Hydrogen Fuel Cell Electric Vehicles in Tunnels. Fire Technol. 2020, 56, 891–912. [Google Scholar] [CrossRef]
- Dadashzadeh, M.; Kashkarov, S.; Makarov, D.; Molkov, V. Risk assessment methodology for onboard hydrogen storage. Int. J. Hydrog. Energy 2018, 43, 6462–6475. [Google Scholar] [CrossRef]
- LaChance, J.; Houf, W.; Middletoon, B.; Fluer, L. Analyses to Support Development of Risk-Informed Separation Distances for Hydrogen Codes; SAND2009–0874; Sandia National Laboratories: Albuquerque, NM, USA, 2009. [Google Scholar]
- LaChance, J.; Tchouvelev, A.; Engebo, A. Development of uniform harm criteria for use in quantitative risk analysis of the hydrogen infrastructure. Int. J. Hydrog. Energy 2011, 36, 2381–2388. [Google Scholar] [CrossRef]
- Haugom, G.; Rikheim, H.; Nilsen, S. Hydrogen Applications. Risk Acceptance Criteria and Risk Assessment Methodology. In Proceedings of the European Hydrogen Energy Conference, Grenoble, France, 2–5 September 2003. [Google Scholar]
- UNECE. Global Registry. Addendum 13: Global technical regulation No. 13. In Global Technical Regulation on Hydrogen and Fuel Cell Vehicles; UNECE: Geneva, Switzerland, 2013. [Google Scholar]
- UNECE. Addendum 133–Regulation No. 134. In Uniform Provisions Concerning the Approval of Motor Vehicles and Their Components with Regard to the Safety-Related Performance of Hydrogen Fuelled Vehicles (HFCV); UNECE: Geneva, Switzerland, 2015. [Google Scholar]
- Mattelaer, V. Private Communication; Toyota Europe: Deeside, UK, 2020. [Google Scholar]
- Kashkarov, S.; Makarov, D.; Molkov, V. Performance of Hydrogen Storage Tanks of Type IV in a Fire: Effect of the State of Charge. Hydrogen 2021, 2, 386–398. [Google Scholar] [CrossRef]
- Road Tunnel Association (RTA). UK & Eire Road Tunnel Directory. 2019. Available online: http://www.rtoa.org.uk/Directory.html (accessed on 25 November 2022).
- Lafleur, C.; Bran-Anleu, G.; Muna, A.; Ehrhart, B.; Blaylock, M.; Houf, W. Hydrogen Fuel Cell Electric Vehicle Tunnel Safety Study; Sandia National Lab: Livermore, CA, USA, 2017. [Google Scholar]
- NJ. WATCH: Garbage Truck Explodes in Fireball, Rips Hole in Nearby House. NJCom. 2019. Available online: https://www.nj.com/mercer/2016/01/garbage_truck_explosion_damages_hamilton_house.html (accessed on 5 October 2022).
- Today. Caught on Camera: Natural-Gas Powered Garbage Truck Explodes. Today. 2016. Available online: https://www.today.com/video/caught-on-camera-natural-gas-powered-garbage-truck-explodes-609780803613 (accessed on 5 October 2022).
- A Garbage Truck Explosion Leaves Some Homes Damaged. 2016. Available online: https://www.youtube.com/watch?v=9lxMWxq5zJE (accessed on 5 October 2022).
- Rattigan, W.; Moodie, K.; Molkov, V.; Makarov, D.; Cirrone, D.; Shenstov, V.; Kashkarov, S.; Xu, Z.; Kuznetsov, M.; Venetsanos, A.; et al. Deliverable 4.3 Final Report on Analytical, Numerical and Experimental Studies on Explosions, Including Innovative Prevention and Mitigation Strategies. 2022. Available online: https://hytunnel.net/wordpress/wp-content/uploads/2022/09/HyTunnel-CS_D4.3_Final-report-on-analytical-numerical-and-experimental-studies-on-explosions.pdf (accessed on 6 October 2022).
- Makarov, D.; Cirrone, D.; Shentsov, V.; Kashkarov, S.; Molkov, V.; Xu, Z.; Kuznetsov, M.; Venetsanos, A.G.; Giannissi, S.G.; Tolias, I.C.; et al. Overview of first outcomes of PNR project HyTunnel-CS. In Proceedings of the International Conference on Hydrogen Safety (ICHS2021) “Safe Hydrogen for Net Zero”, Edinburgh, UK, 21–24 September 2021. [Google Scholar]
- Molkov, V.; Dery, W. The blast wave decay correlation for hydrogen tank rupture in a tunnel fire. Int. J. Hydrog. Energy 2020, 45, 31289–31302. [Google Scholar] [CrossRef]
- Kashkarov, S.; Li, Z.; Molkov, V. Blast wave from a hydrogen tank rupture in a fire in the open: Hazard distance nomograms. Int. J. Hydrog. Energy 2020, 45, 2429–2446. [Google Scholar] [CrossRef]
- Bassan, S. Overview of traffic safety aspects and design in road tunnels. IATSS Res. 2016, 40, 35–46. [Google Scholar] [CrossRef] [Green Version]
- Amundsen, F.H.; Ranes, G. Studies on traffic accidents in Norwegian road tunnels. Tunn. Undergr. Space Technol. 2000, 15, 3–11. [Google Scholar] [CrossRef]
- Yamashita, A.; Kondo, M.; Goto, S.; Ogami, N. Development of High-Pressure Hydrogen Storage System for the Toyota “Mirai”. SAE Int. 2015. [Google Scholar] [CrossRef]
- Molkov, V.; Kashkarov, S. Blast wave from a high-pressure gas tank rupture in a fire: Stand-alone and under-vehicle hydrogen tanks. Int. J. Hydrog. Energy 2015, 40, 12581–12603. [Google Scholar] [CrossRef]
- What Are the Average Dimensions of a Car in the UK? 2021. Available online: https://www.nimblefins.co.uk/cheap-car-insurance/average-car-dimensions (accessed on 12 October 2021).
- Average Car and Van Occupancy England 2002–2018 Statistic. Statista n.d. Available online: https://www.statista.com/statistics/314719/average-car-and-van-occupancy-in-england/ (accessed on 12 October 2021).
- Weyandt, N. Vehicle bonfire to induce catastrophic failure of a 5000-psig hydrogen cylinder installed on a typical SUV. In Southwest Research Institute Report for the Motor Vehicle Fire Research Institute; Motor Vehicle Fire Research Institute: Charlottesville, VA, USA, 2006. [Google Scholar]
- Weyandt, N. Analysis of Induced Catastrophic Failure of A 5000 psig Type IV Hydrogen Cylinder. In Southwest Research Institute Report for the Motor Vehicle Fire Research Institute; Motor Vehicle Fire Research Institute: Charlottesville, VA, USA, 2005. [Google Scholar]
- Zheng, J.; Bie, H.; Xu, P.; Chen, H.; Liu, P.; Li, X.; Liu, Y. Experimental and numerical studies on the bonfire test of high-pressure hydrogen storage vessels. Int. J. Hydrog. Energy 2010, 35, 8191–8198. [Google Scholar] [CrossRef]
- Molkov, V.; Cirrone, D.M.C.; Shentsov, V.; Dery, W.; Kim, W.; Makarov, D. Dynamics of blast wave and fireball after hydrogen tank rupture in a fire in the open atmosphere. Int. J. Hydrog. Energy 2021, 46, 4644–4665. [Google Scholar] [CrossRef]
- Shentsov, V.; Cirrone, D.M.C.; Makarov, D.; Molkov, V. Simulation of fireball and blast wave from a hydrogen tank rupture in a fire. In Proceedings of the 7th International Symposium on Non-equilibrium Processes, Plasma, Combustion, and Atmospheric Phenomena, Sochi, Russia, 2–7 October 2016; Torus Press: Sochi, Russia, 2016. [Google Scholar]
- Kudriakov, S.; Studer, E.; Bernard-Michel, G.; Bouix, D.; Domergue, L.; Forero, D.; Gueguen, H.; Ledier, C.; Manicardi, P.; Martin, M.; et al. Full-scale tunnel experiments: Blast wave and fireball evolution following hydrogen tank rupture. Int. J. Hydrog. Energy 2022, 47, 18911–18933. [Google Scholar] [CrossRef]
- UK Health and Safety Executive. Risk Management: Expert Guidance—Cost Benefit Analysis (CBA) Checklist n.d. Available online: https://www.hse.gov.uk/managing/theory/alarpcheck.htm (accessed on 16 September 2022).
- US DOT National Highway Traffic Safety Administration (NHTSA). Traffic Safety Facts 2015: A Compilation of Motor Vehicle Crash Data from the Fatality Analysis Reporting System and the General Estimates System; National Highway Traffic Safety: Washington, DC, USA, 2015.
- Reliability Analysis Center. Non Electronic Parts Reliability Data; Reliability Analysis Center: Rome, NY, USA, 1991. [Google Scholar]
- Saw, J.L.; Flauw, Y.; Demeestere, M.; Naudet, V.; Blanc-Vannet, P.; Hollifield, K.; Wilday, J. The EU FireComp Project and Risk Assessment of Hydrogen Composite Storage Applications using Bow-tie Analysis. In Proceedings of the Hazards, Edinburgh, UK, 24–26 May 2016; Volume 26. [Google Scholar]
- Landucci, G.; Gubinelli, G.; Antonioni, G.; Cozzani, V. The assessment of the damage probability of storage tanks in domino events triggered by fire. Accid. Anal. Prev. 2009, 41, 1206–1215. [Google Scholar] [CrossRef]
- Landucci, G.; Argenti, F.; Tugnoli, A.; Cozzani, V. Quantitative assessment of safety barrier performance in the prevention of domino scenarios triggered by fire. Reliab. Eng. Syst. Saf. 2015, 143, 30–43. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables, and Stochastic Processes, 3rd ed.; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Finney, D.J. Probit Analysis, 3rd ed.; Cambridge University Press: Cambridge, UK, 1971. [Google Scholar]
- Makarov, D.; Kim, Y.; Kashkarov, S.; Molkov, V. Thermal Protection and Fire Resistance of High-Pressure Hydrogen Storage. In Proceedings of the 8th International Seminar on Fire & Explosion Hazards, Hefei, China, 25–28 April 2016. [Google Scholar]
- Halm, D.; Fouillen, F.; Laine, E.; Gueguen, M.; Bertheau, D.; Van Eekelen, T. Composite pressure vessels for hydrogen storage in fire conditions: Fire tests and burst simulation. Int. J. Hydrog. Energy 2017, 42, 20056–20070. [Google Scholar] [CrossRef]
- Molkov, V.; Makarov, D.; Kashkarov, S. Composite Pressure Vessel for Hydrogen Storage. WO 2018/149772 A1 23 August 2018. [Google Scholar]
- Aloqaily, A. Cross Country Pipeline Risk Assessments and Mitigation Strategies; Gulf Professional Publishing: Oxford, UK, 2018. [Google Scholar]
- Burgherr, P.; Hirschberg, S. A Comparative Analysis of Accident Risks in Fossil, Hydro, and Nuclear Energy Chains. Hum. Ecol. Risk Assess. Int. J. 2008, 14, 947–973. [Google Scholar] [CrossRef]
- Freeman, R.A. CCPS guidelines for chemical process quantitative risk analysis. Plant Oper. Prog. 1990, 9, 231–235. [Google Scholar] [CrossRef]
- Zhiyong, L.; Xiangmin, P.; Jianxin, M. Quantitative risk assessment on a gaseous hydrogen refueling station in Shanghai. Int. J. Hydrog. Energy 2010, 35, 6822–6829. [Google Scholar] [CrossRef]
- Kunishima, M.; Horikawa, K. The Fire Disaster in the Tokyo-Nagoya Nihon-zaka Tunnel 11 July 1979. Failure Knowledge Database/100 Selected Cases. 1980. Available online: http://www.shippai.org/fkd/en/hfen/HD1000132.pdf (accessed on 16 September 2022).
- Lacroix, D. The Mont Blanc tunnel fire. What happened and what has been learned. In Proceedings of the Fourth International Conference On Safety In Road And Rail Tunnels, Madrid, Spain, 2–6 April 2001. [Google Scholar]
- Kim, H.K.; Lönnermark, A.; Ingason, H. Effective Firefighting Operations in Road Tunnels; SP Sveriges Tekniska Forskningsinstitut: Borås, Sweden, 2010. [Google Scholar]
- Casey, N. Fire incident data for Australian road tunnels. Fire Saf. J. 2020, 111, 102909. [Google Scholar] [CrossRef]
- Beard, A.; Carvel, R. Handbook of Tunnel Fire Safety; ICE Publishing: London, UK, 2012. [Google Scholar] [CrossRef]
- Maevski, I. Design Fires in Road Tunnels—Transportation Research Board; National Academy of Sciences: Washington, DC, USA, 2011. [Google Scholar]


| Tank SoC, % | Storage Pressure, MPa | |||
|---|---|---|---|---|
| 99 | 70 | 13.6 | 15.6 | 29.2 |
| 59 * | 35.5 * | 8.1 * | 9.3 * | 17.4 * |
| Tunnel and Vehicle Parameters | Values | Units |
|---|---|---|
| Overall tunnel length [14] | 4650 | m |
| Tunnel cross-section area [21] | 39.5 | m2 |
| Tunnel length used in calculations | 4600 | m |
| Tunnel throughput [14] | 5.5 * | 106 vehicle |
| Car length (calculated average from [27]) | 4.5 | m |
| Length of the gap between cars (assumption) | 5 | m |
| The average number of passengers per vehicle [28] | 1.55 | person/vehicle |
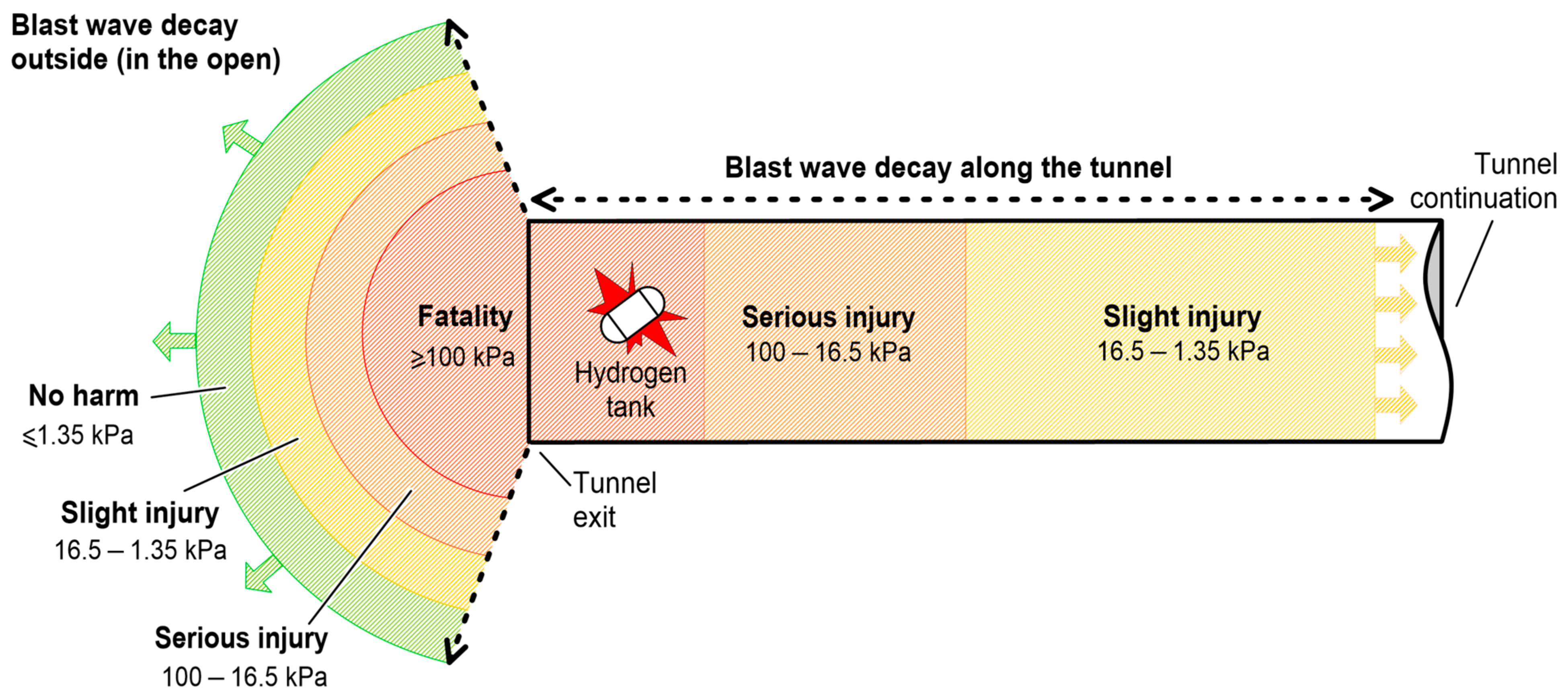
| Harm to People | Blast Wave Hazard Zone for Tank Rupture at Different SoC | |
|---|---|---|
| Tank SoC = 99% (70 MPa, at 20 °C) | Tank SoC = 59% (35.5 MPa, at 20 °C) | |
| Fatality | 0–90 m | 0–70 m |
| Serious Injury | 90–1150 m | 70–900 m |
| Slight Injury | 1150–4600 m (end of the tunnel) | 900–4600 m (end of the tunnel) |
| No harm | Does not exist | Does not exist |
| Tank SoC | Fire Mode | Hydrogen Tank Location |
|---|---|---|
| 59% | Localised fire | At 50 m from the tunnel exit |
| At the tunnel’s midway length | ||
| Engulfing fire | At 50 m from the tunnel exit | |
| At the tunnel’s midway length | ||
| 99% | Localised fire | At 50 m from the tunnel exit |
| At the tunnel’s midway length | ||
| Engulfing fire | At 50 m from the tunnel exit | |
| At the tunnel’s midway length |
| Parameter | Minimum | Base a | Maximum | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Value | FRR, Min b | Value | FRR, Min b | Value | FRR, Min b | ||||
| Loc. Fire | Eng. Fire | Loc. Fire | Eng. Fire | Loc. Fire | Eng. Fire | ||||
| 5.00 × 10−3 | 60 | 26 | 5.94 × 10−2 | 84 | 43 | 1.43 × 10−1 | 94 | 50 | |
| 2.23 × 10−1 | 80 | 41 | 3.17 × 10−1 | 5.55 × 10−1 | 90 | 48 | |||
| c | 2.04 × 106 | 81 | 41 | 2.75 × 106 | 4.38 × 106 | 89 | 47 | ||
| d | 6.00 × 10−2 | 67 | 32 | 3.10 × 10−1 | 8.10 × 10−1 | 95 | 51 | ||
| Group 1 | Group 2 | |||
|---|---|---|---|---|
| No. of data cases (tunnel fires) | 78 incidents | 110 incidents | ||
| Response time distribution | 19% cases | response time under 5 min | 5% cases | response time under 5 min |
| 81% cases | response time under 30 min | 95% cases | response time under 120 min | |
| Hence, failure probability: for 5 min response time—81%, for 30 min response time—19% | Hence, failure probability: for 5 min response time—95%, for 120 min response time—5% | |||
| Calculated probit function values a | 5.88 | —for 5 min | 6.6 | —for 5 min |
| 4.12 | —for 30 min | 3.36 | —for 120 min | |
| The new probit coefficients, and | ||||
| The new | = 7.46 − 0.98 × ln (8) = 5.422 | = 8.3 − 1.03 × ln (8) = 6.158 | ||
| ] = 6.635 × 10−1 | ] = 8.766 × 10−1 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashkarov, S.; Dadashzadeh, M.; Sivaraman, S.; Molkov, V. Quantitative Risk Assessment Methodology for Hydrogen Tank Rupture in a Tunnel Fire. Hydrogen 2022, 3, 512-530. https://doi.org/10.3390/hydrogen3040033
Kashkarov S, Dadashzadeh M, Sivaraman S, Molkov V. Quantitative Risk Assessment Methodology for Hydrogen Tank Rupture in a Tunnel Fire. Hydrogen. 2022; 3(4):512-530. https://doi.org/10.3390/hydrogen3040033
Chicago/Turabian StyleKashkarov, Sergii, Mohammad Dadashzadeh, Srinivas Sivaraman, and Vladimir Molkov. 2022. "Quantitative Risk Assessment Methodology for Hydrogen Tank Rupture in a Tunnel Fire" Hydrogen 3, no. 4: 512-530. https://doi.org/10.3390/hydrogen3040033
APA StyleKashkarov, S., Dadashzadeh, M., Sivaraman, S., & Molkov, V. (2022). Quantitative Risk Assessment Methodology for Hydrogen Tank Rupture in a Tunnel Fire. Hydrogen, 3(4), 512-530. https://doi.org/10.3390/hydrogen3040033







