Modeling of Liquid Hydrogen Tank Cooled with Para-Orthohydrogen Conversion

Abstract

With the accelerating development of liquid-hydrogen storage facilities, the problem of boil-off hydrogen losses becomes very important. A promising method to reduce these losses is to utilize the endothermic para-orthohydrogen conversion of vented hydrogen, which can effectively decrease heat loads on a hydrogen tank. To model such a process, a hybrid computational model has been developed, based on the application of computational fluid dynamics for an ullage space, where knowledge of thermal stratification is important, and reduced-order models for other system elements. The simulation results for a spheroidal tank in selected conditions indicated a 10–25% reduction of boil-off losses due to cooling produced by vented hydrogen undergoing para-ortho-conversion.

1. Introduction

Hydrogen is often considered as a promising energy carrier for the future, since it can be generated using renewable energy sources and does not produce harmful emissions when reacting with oxygen. However, being the lightest substance, gaseous hydrogen has a low energy density [1]. Liquid hydrogen has a much higher energy density, but liquefaction and storage of hydrogen requires cryogenic temperatures, e.g., below 21 K at atmospheric pressure.

During the storage of liquid hydrogen, inevitable heat leaks into cryogenic tanks cause evaporation and require either cooling or venting of some hydrogen [1]. Significant efforts are put into the design and construction of hydrogen tanks to reduce boil-off losses. Multi-layer insulation, vapor shielding and active cooling are some of the means that are applied to counteract heat leaks [2,3,4].

One peculiarity of cryogenic hydrogen is the temperature-dependent content of ortho- and parahydrogen isomers in equilibrium hydrogen. These isomers differ by orientations of spins of hydrogen molecules [5]. At room temperatures, about 75% of hydrogen exists in the ortho-form, while liquid hydrogen is predominantly in the para-form, with the transformation happening mainly below 100 K. The ortho-to-parahydrogen conversion is exothermic, thus requiring additional heat removal during cooling and the application of a catalyst to ensure a high rate of hydrogen conversion prior to liquefaction to reduce the subsequent boil-off, as the natural conversion is a slow process [6,7].

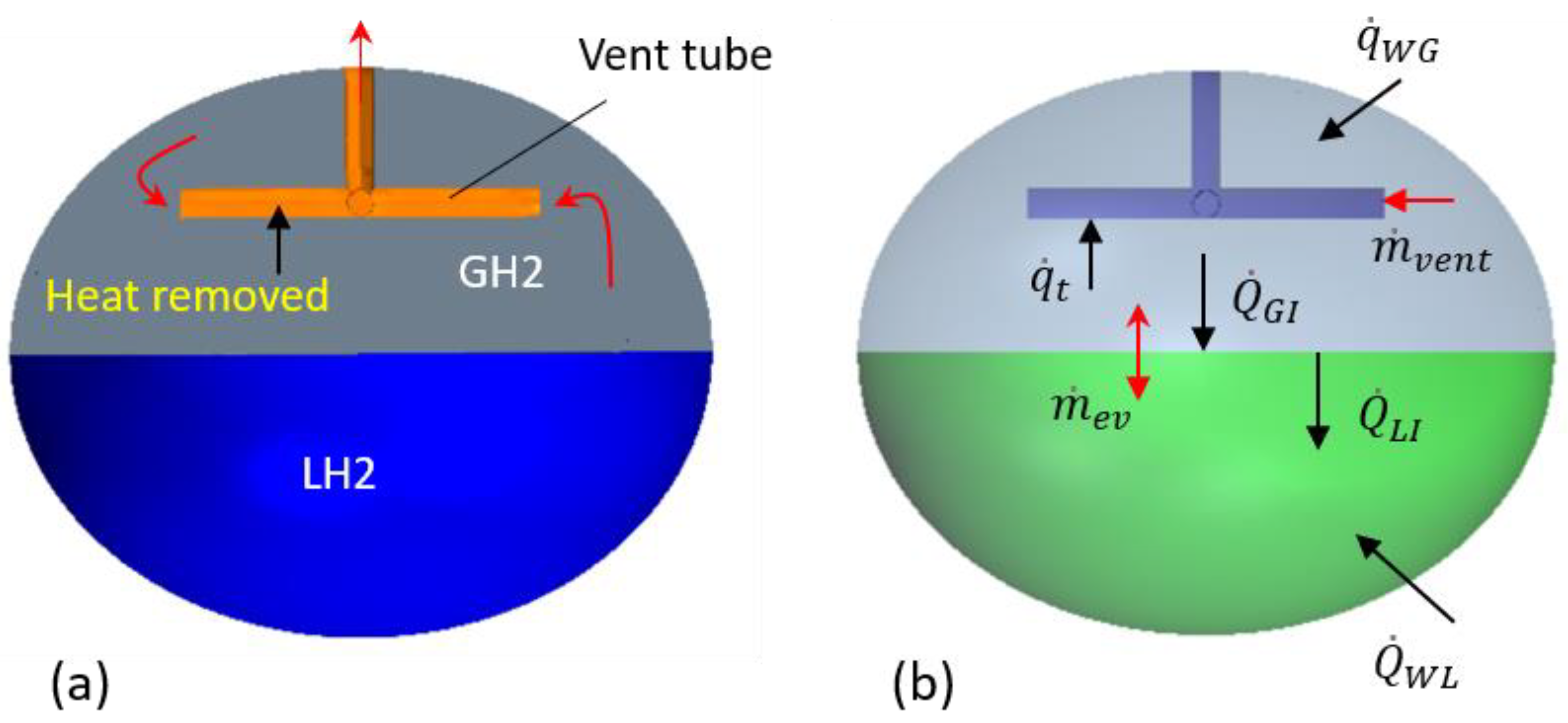
When hydrogen is stored in the liquid form, evaporation occurs due to heat leaks, leading to boil-off losses through venting. There is an opportunity to decrease these losses by converting some vented hydrogen from the para- to ortho-isomer through an endothermic reaction with a magnitude equivalent to the exothermic reaction during liquefaction [8,9,10]. Heat consumed during this process can effectively reduce heat loads on hydrogen stored in a tank. A conceptual illustration of a spheroidal tank (used as model geometry in this study) and a venting tube that absorbs heat is shown in Figure 1a,b. The internal surface of this tube needs to contain a catalyst to make para-to-orthohydrogen conversion effective. In contrast to conventional beds with the catalyst in bulk material form, only a thin layer of catalyst is deposited on the tube’s internal surface, as was demonstrated in previous experiments [9].

The goal of the present study is to demonstrate a computational model that can be used for assessing this type of boil-off reduction. The model is of a hybrid type, having elements of a simplified reduced-order approach and high-fidelity computational fluid dynamics (CFD). It is known that simplified zonal models for hydrogen tanks often cannot achieve a sufficient accuracy [11], while full CFD simulations of the entire tank, including phase-change processes and multi-phase flows, are rather computationally expensive [12]. Hybrid models including both simplified and high-fidelity elements have been used in various forms [13]. In the present study, the ullage space is modeled with CFD, since knowing thermal stratification in the gaseous phase is very important to determine the amount of hydrogen available for conversion and thus its cooling potential, while the liquid hydrogen evolution and the venting-tube cooling effect are estimated using lumped-element sub-models.

2. Modeling Details

For a computationally economical modeling of complex phenomena in LH2 tanks, a hybrid approach has been undertaken. Thermofluid processes in the ullage space are simulated using computational fluid dynamics, while the liquid hydrogen portion, external heat leaks, and venting tube are modeled using lumped-element or other simplified methods. A model schematic with major boundary processes is shown in Figure 1b. CFD simulations are carried out using Star-CCM+ software.

For the ullage gas, the governing continuity, momentum, and energy equations are employed [14]:

$$\frac{\partial \rho }{\partial t}+\frac{\partial \left(\rho u_j\right)}{\partial x_j}=0,$$

(1)

$$\frac{\partial \left(\rho u_i\right)}{\partial t}+\frac{\partial \left(\rho u_i{u}_j\right)}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3}{\delta }_{ij}\frac{\partial u_k}{\partial x_k}\right)\right]+\rho f_j,$$

(2)

$$\frac{\partial \left(\rho E\right)}{\partial t}+\frac{\partial \left(\rho E{u}_j\right)}{\partial x_j}=\frac{\partial }{\partial x_j}\left[-p{\overline{u}}_i{\delta }_{ij}+u_i\left\{\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3}{\delta }_{ij}\frac{\partial u_k}{\partial x_k}\right)\right\}\right]-\frac{\partial q_j}{\partial x_j},$$

(3)

where $u_i$ are the velocity components, $p$ is the pressure, $\rho$ is the gas density, $\mu$ is the viscosity, $E$ is the total energy per unit mass, f is the body force, and $q_j$ are the heat fluxes. Due to small Reynolds numbers, only the laminar flow regime is expected, so no turbulence model was considered. The Redlich–Kwong equation of state (EOS) was used for gaseous hydrogen for faster computations, similar to previous modeling studies with cryogenic hydrogen [15,16]. Other hydrogen properties, such as viscosity, specific heats, and heat conductivity, were tabulated using Refprop data for parahydrogen [17].

A spheroid tank of volume 4.9 m³ is chosen for this study, as some experimental data are available from self-pressurization experiments [18]. The computational domain for the ullage space included a quarter of the actual volume occupied by gas, assuming two symmetry boundaries (Figure 2a,b). The tank wall was treated as a no-slip boundary with a prescribed heat flux. The bottom boundary was approximated as an inlet, with the evaporating hydrogen flow rate and temperature given by an empirical model described below. In simulations including the venting tube, the tube inlets were treated as mass flow outlets for the ullage domain, while the external tube wall acted as a no-slip boundary for the ullage space and the surface heat flux was determined by the amount of para-ortho-conversion.

A numerical mesh, consisting primarily of hexahedral cells, was built in the ullage space, as illustrated in Figure 2c. Several prism layers were arranged near the no-slip walls, and some refinement was added in the bottom of this domain. For the present simulations, which imitated relatively short processes, fixed volumes of the ullage and liquid spaces were utilized, as it was assumed that the associated volume variations had a minor effect. In the mesh-verification study conducted in this work, three grids of different densities were generated, and solutions were utilized to assess numerical uncertainty using Richardson extrapolation [14] and a factor of safety [19]. The uncertainty for numerical results was calculated to be about 2%.

While CFD can provide detailed information about the temperature and flow field in the ullage space, for a simplified modeling of slow temperature evolution in the liquid volume, a lumped-element model is applied:

$$m_L{c}_L\frac{d{T}_L}{dt}={\dot{Q}}_{WL}+{\dot{Q}}_{IL},$$

(4)

where $m_L$ and $c_L$ are the mass and specific heat capacity of the liquid, respectively, which are assumed to be constant in relatively short and slow processes, $T_L$ is the bulk liquid temperature (note that it is different from the interface temperature used below), ${\dot{Q}}_{WL}$ is the heat addition rate from the wall to the liquid domain, and ${\dot{Q}}_{LI}$ is the natural convection heat transfer rate from a thin region near the liquid–gas interface and the bulk of liquid. The latter form of heat transfer is modeled using natural convection correlations, as suggested in previous simplified models for LH2 tanks [20]:

$${\dot{Q}}_{IL}=h_L{A}_I\left(T_I-T_L\right),$$

(5)

$$h_L=c_h\frac{k_L}{R}R{a}^{0.25},$$

(6)

$$Ra=PrGr,$$

(7)

$$Pr=\frac{c_L{\mu }_L}{k_L},$$

(8)

$$Gr=\frac{R^3{\rho }_L^{2}g\beta }{{\mu }_L^2}\left(T_I-T_L\right),$$

(9)

where $h_L$ is the heat-transfer coefficient between the interface and the bulk liquid, $A_I$ is the interface area, $T_I$ is the interface temperature, taken as the saturation temperature at the gas pressure above the interface [20], $c_h$ is an empirical constant depending on a specific configuration, $k_L$ is the thermal conductivity, $R$ is the characteristic vertical dimension, $Ra$ is the Rayleigh number, $Pr$ is the Prandtl number, $Gr$ is the Grashof number, ${\mu }_L$ is the liquid viscosity, $g$ is the gravity, and $\beta$ is the thermal-expansion coefficient of the liquid.

The evaporation (or condensation) rate at the gas–liquid interface is defined by the following expression:

$${\dot{m}}_{ev}=\frac{{\dot{Q}}_{GI}-{\dot{Q}}_{IL}}{h_{ev}},$$

(10)

where $h_{ev}$ is the enthalpy of vaporization, ${\dot{Q}}_{GI}$ is the heat-transfer rate from the gas to the interface (determined from CFD by integrating conduction and convection heat fluxes over the ullage–liquid interface area), and ${\dot{Q}}_{IL}$ is the interface-liquid heat-transfer rate calculated using Equation (5).

The ullage CFD setup together with Equations (4)–(10) can be used to model relevant processes (such as self-pressurization) inside a closed LH2 tank subjected to heat leaks from outside. For the systems with an open vent tube (Figure 1b), the venting mass flow rate ${\dot{m}}_{vent}$ is assigned. If para-orthohydrogen conversion is activated in this tube, another lumped-element-type equation is introduced for the cooling flux ${\dot{q}}_t$ on the external surface of this tube, which is one of the boundaries of the ullage domain:

$${\dot{q}}_t{A}_t={\dot{m}}_{vent}{k}_{op}{y}_o\left(T_t\right)h_{op}-{\dot{m}}_{vent}{c}_p\left(T_{t,in}-T_t\right),$$

(11)

where $A_t$ is the tube surface area, $T_t$ is the effective temperature of hydrogen flowing through this tube (estimated as an average surface temperature of the pipe, assuming a small temperature difference across the pipe wall), $T_{t,in}$ is the temperature at the tube inlet (defined from CFD), $c_p$ is the specific heat of parahydrogen (evaluated by assuming a small difference between $T_{t,in}$ and $T_t$), $y_o\left(T_t\right)$ is the equilibrium concentration of orthohydrogen evaluated at $T_t$ ($y_o\left(T\right)$ function is shown in Figure 3), $k_{op}$ is the fraction of actually converted hydrogen to the maximum possible transformation at the effective tube temperature (taken as one in examples below assuming complete conversion), and $h_{op}$ is the enthalpy of conversion. If empirical data on conversion rates is available for a specific catalyst, one can determine a corresponding value of $k_{op}$. In Equation (11), it is assumed that the hydrogen in the tank is completely in the para-state, although a simple modification of Equation (11) can be made to account for different situations.

The left-hand side of Equation (11) is essentially the additional heat-removal rate from the ullage space. The first term on the right-hand side is the heat consumed in the tube due to orthohydrogen-parahydrogen conversion, while the second term accounts for cooling of hydrogen flowing through the tube. The thermal resistance between $T_t$ and the surrounding ullage space is neglected. In principle, one can apply CFD for both the internal flow in the tube with a conversion reaction and the more sophisticated external flow of a finned tube, but this would make simulations substantially more computationally expensive. In the spirit of the relatively low-cost numerical approach adopted in this study, the vent tube is analyzed here as a simplified cooling source.

3. Results

To validate the applicability of the current modeling approach, experimental data from self-pressurization tests [18] are compared with numerical results. Those tests were conducted in a 4.9-m³ spheroid-type tank (similar to that shown in Figure 1a) at different fill levels of liquid hydrogen and heat leaks. A 49% fill level (by volume) and a wall heat flux (into the tank) of 3.5 W/m² were selected for the present validation study. The initial experimental conditions in the tank corresponded to a 103 kPa absolute pressure and a vertical temperature gradient in the ullage space of about 7.5 K/m.

Computational simulations with these parameters were conducted in the tank without a venting tube, and the pressure evolution in the tank was monitored. Both experimental and numerical results are shown in Figure 4. The observed agreement is considered satisfactory, given assumptions used in the lumped-element portion of the model. Thus, the present computational approach is deemed applicable for approximately estimating boil-off losses and their reduction due to cooling by para-orthohydrogen conversion.

To demonstrate such a process, four scenarios are investigated using the same tank geometry. Two heat-leak fluxes are considered, 3.5 W/m² and 10.5 W/m², while a venting tube is added into the ullage space (as shown in Figure 1 and Figure 2). The heat flux of 3.5 W/m² is the same as in the validation study, whereas the larger heat leak is considered as a higher vent rate; therefore, a more drastic effect of para-orthohydrogen conversion cooling can be expected. (It can be noted that there are tanks with lower heat leaks, depending on insulation materials.)

In these simulations, a hydrogen outflow is imposed through the venting tube to keep pressure constant at about 122 kPa. The venting tube with and without a catalyst is considered so as to illustrate the capability of para-orthohydrogen conversion to provide additional cooling and thus reduce a necessary venting rate.

The venting rate of hydrogen was varied in these four computational scenarios (two heat leaks with and without cooling from the venting-tube surface) to achieve a constant pressure in the tank. The results are summarized in

Table 1. Venting rates of hydrogen required to maintain constant tank pressure.

Heat Leak	Venting Tube	Venting Rate	Boil-off Loss
3.5 W/m2	Non-catalyzed	0.034 g/s	2.9 kg/day
3.5 W/m2	Catalyzed	0.030 g/s	2.6 kg/day
10.5 W/m2	Non-catalyzed	0.121 g/s	10.5 kg/day
10.5 W/m2	Catalyzed	0.094 g/s	8.2 kg/day

, including daily boil-off losses of H₂, which amount to about 1.5% and 6% of hydrogen loss per day for smaller and larger heat leaks, respectively. To maintain constant pressure, the larger heat leak requires about a fourfold larger venting rate. The reduction of boil-off losses due to cooling induced by para-orthohydrogen conversion is about 10% for the tank with a smaller heat leak and close to 25% at a larger heat leak, which results in noticeable savings that can make this technique economically attractive. Moreover, most commercial tanks have cylindrical shapes (rather than spheroidal ones), with larger surface-to-volume ratios. This will produce a larger heat input per volume, thus increasing achievable hydrogen savings.

Illustrations of CFD temperature distributions and velocity fields for the considered scenarios in steady states (reached after about 1.5 h of physical time) are shown in Figure 5. Thermal stratification is clearly visible. Temperature values are greater at a larger heat leak and in the case of a non-catalyzed venting tube without cooling. The high-temperature region is especially pronounced further from the liquid in the top of the tank. It is advantageous to put a catalyzed venting tube in this hotter zone, as the equilibrium fraction of orthohydrogen, and therefore cooling potential of the tube, increases with the temperature. The convection-velocity magnitudes are also more pronounced at a higher heat leak, but the presence of the catalyzed tube only has a minor effect on the flow pattern. The convection vortices have predominantly vertical orientations, and their dimensions become larger with an increasing heat input.

4. Conclusions

A hybrid mathematical model, based on a high-fidelity flow simulation in an ullage space and reduced-order sub-models for liquid hydrogen and a venting tube, has been developed. A novel cooling method, based on endothermic para-orthohydrogen conversion, to cool down the ullage space with the purpose of reducing boil-off losses of hydrogen has been simulated using the present modeling approach. For a selected spheroidal tank, it is found that losses can be decreased by about 10% and 25% at wall heat fluxes of 3.5 and 10.5 W/m², assuming a hydrogen conversion down to an equilibrium value at a local temperature. The model can be further extended to model flow inside a catalyzed venting tube, account for finite hydrogen conversion rates, and include the modeling of heat conduction in the tank wall. The considered cooling method is expected to be even more effective in cylindrical tanks with a larger surface-to-volume ratio.