Next Article in Journal
Association Between Coffee Consumption and Visceral Obesity: A Cross-Sectional Study
Previous Article in Journal
Mechanism of Diabetes Remission or Improvement in Glucose Control Following Roux-en-Y Gastric Bypass Versus Sleeve Gastrectomy: A Systematic Review and Meta-Analysis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Obesities
Volume 5
Issue 1
10.3390/obesities5010015
obesities-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimated Energy Requirement: Comparison Between the 2005 and 2023 Dietary Reference Intakes in Sedentary Adults and Older Adults—A Retrospective Cross-Sectional Study

by
Anderson Matheus Oliveira Haas Verdi
1,
Jaqueline Machado Soares
2,
Jaqueline Fernandes Carneiro
3,
Izadora Oliveira Felez
3,
Dalton Luiz Schiessel
3,
Daniele Gonçalves Vieira
3,
Adriana Masiero Kühl
3,
Daniela Caetano Gonçalves
4 and
Angelica Rocha de Freitas Melhem
3,*
1
Postgraduate Program in Nutrition, Federal University of São Paulo (UNIFESP), Baixada Santista Campus, Santos 11015-020, Brazil
2
Postgraduate Program in Community Development, State University of the Central-West (UNICENTRO), Irati Campus, Irati 11015-020, Brazil
3
Departament of Nutrition, State University of the Central-West (UNICENTRO), CEDETEG Campus, Guarapuava 85040-167, Brazil
4
Department of Biosciences, Federal University of São Paulo (UNIFESP), Baixada Santista Campus, Santos 11015-020, Brazil
*
Author to whom correspondence should be addressed.
Obesities 2025, 5(1), 15; https://doi.org/10.3390/obesities5010015
Submission received: 16 December 2024 / Revised: 14 February 2025 / Accepted: 7 March 2025 / Published: 14 March 2025
Browse Figures
Versions Notes

Abstract

:
Background: Equations for estimating energy expenditure are developed for specific populations and contexts, including clinical settings, body composition variations, and age groups, to enhance precision in nutritional planning and health promotion. Objective: To compare the estimated daily energy requirements using the equations from the 2005 and 2023 Dietary Reference Intakes for Energy in sedentary adults and elderly individuals. Methods: A cross-sectional, retrospective study analyzed data from records at a university outpatient clinic using convenience sampling. Participants included sedentary individuals aged 20 years or older of both sexes. The comparison was conducted using repeated measures Analysis of Variance (rmANOVA). Results: Data from 431 individuals (80% female, mean age 43.57 ± 17.30 years) were analyzed. The 2023 equations provided higher energy estimates compared to the 2005 equations. The rmANOVA revealed a significant difference between the energy estimates (F(1, 429) = 1567.24, p < 0.001, η2 = 0.02), with the 2023 equations consistently yielding higher values. Conclusions: The results indicate that the estimated energy requirements significantly increased in the 2023 equations compared with those of 2005, highlighting their relevance to clinical practice.

Graphical Abstract

1. Introduction

For over a century, the need to estimate individuals’ daily energy requirements has been recognized, taking into account physiological and individual factors such as sex and age [1]. Currently, it is well established that the gold standard for measuring energy expenditure is calorimetry, either direct or indirect, which is frequently used in studies for comparison and validation of new methods [1,2,3]. However, calorimetry presents various challenges for clinical practice, one of which is the high cost of acquisition. This limitation has driven the development of alternatives, such as equations for estimating daily energy requirements, with one of the oldest and most well-known being the one proposed by Harris and Benedict [1]. These equations, frequently used in different clinical contexts, such as clinical and pathological situations [4,5,6,7], variations in body composition [8], and age groups [9,10,11], aim to provide greater specificity in nutritional planning and promote health.
The basal metabolic rate (BMR) accounts for approximately 60 to 75% of an individual’s daily energy needs. It encompasses the maintenance of the body’s thermodynamic homeostasis, including cardiovascular and respiratory functions, cellular synthesis and renewal, among other processes, under standardized conditions of minimal exertion (fasting, physical and mental rest, and a controlled environment in terms of temperature, lighting, and noise) [12,13]. Severe conditions can, in some situations, significantly increase the body’s energy expenditure. A notable example is cancer-associated cachexia, which triggers the activation of non-essential metabolic pathways, leading to energy inefficiency. Another example, though not exclusive, was observed during the COVID-19 pandemic, where severe conditions often resulted in increased energy metabolism, particularly highlighting muscle catabolism [7,14]. Given the complexity of estimating BMR, in clinical practice, resting energy expenditure (REE) is commonly estimated, which is, on average, 10% higher than BMR due to the level of physical activity and the thermic effect of food, which are not considered in this estimate [13].
In response to the complexity of calorimetry and the need for a more accessible estimate, in 2005, the Institute of Medicine proposed the estimated energy requirement (EER) equations as part of the Dietary Reference Intakes (DRIs), which were most recently updated in 2023 [15,16]. The reason for this update is based on the fact that values obtained by the DRI committee, using the doubly labeled water method, showed variations across different life stages. Additionally, other data from systematic reviews and published literature were taken into account [16]. DRIs are a set of reference values that encompass a safe range of intake and provide recommendations for nutrients (energy, carbohydrates, protein, lipids, vitamins, and minerals) [15,16]. Moreover, DRI equations are widely used by health professionals seeking to guide energy balance at both the individual and population levels, as energy intake above necessary levels can lead to weight gain and predispose individuals to obesity [15,16].
The growing concern about the rise in overweight and obesity is justified by the fact that, in 2022, approximately 2.5 billion people were overweight, and 890 million were living with obesity. The global prevalence of obesity more than doubled between 1990 and 2022, highlighting that this is not an issue confined to adults. Children and adolescents were also significantly affected, with a substantial increase in rates during the same period. Moreover, a causal relationship between excess weight and the development of certain types of cancer has already been established. Overweight and obesity largely result from an imbalance between energy intake and daily energy expenditure [17,18,19,20].
Given the impact that the accuracy of EER equations can have on clinical practice, it is essential to understand how differences between the 2005 and 2023 DRI versions can affect energy requirement estimates, particularly in populations with specific characteristics, such as sedentary adults and elderly individuals. Sedentary populations are particularly vulnerable to errors in energy requirement estimation due to the high risk of weight gain and the development of obesity and other associated comorbidities. Therefore, to prevent or treat obesity and other related health conditions, it is essential to accurately determine energy requirements. This ensures adequate intake, preventing both overeating and insufficient consumption [21,22,23]. Comparing the 2005 and 2023 DRI versions will help assess how incorporating new data and measurement methods influences these estimates.
This study aimed to compare the daily energy requirements estimated using the equations proposed in the 2005 and 2023 Dietary Reference Intakes for Energy in a sample of sedentary adults and elderly individuals. The comparisons considered participants’ age range and nutritional status based on Body Mass Index (BMI). By comparing the mean predicted values from each equation, this study seeks to provide health professionals, particularly nutritionists, with a parameter for assessing the influence of different DRI versions on individual energy requirement estimates, aiding in clinical practice.

2. Materials and Methods

2.1. Study Design and Sample

This was a retrospective cross-sectional study carried out at the Nutrition School Clinic (CENUT), under the responsibility of the Department of Nutrition, at the CEDETEG campus of UNICENTRO. The choice of this design was motivated by the advantages of low cost and the lack of need for continuous monitoring, as well as allowing the analysis of different equations within the same population, enabling comparisons between them. This study included patients who were already receiving regular nutritional follow-ups at CENUT and who attended them between 2021 and 2023 through a non-probabilistic (convenience) sampling method. Clinical–nutritional records used during the consultations were analyzed, and data from patients who met the study’s inclusion criteria were collected. It is important to note that no sample size calculation was performed for the conduction of this study.

2.2. Data Collection and Inclusion Criteria

Clinical records were reviewed, and individuals of both sexes who were classified as “sedentary”, aged 20 years or older, and had the necessary data for estimating daily energy needs using DRI equations were included in this study. Those lacking these data were excluded. The collected data included sex (male or female), age (in full years), body weight (in kg), height (in meters or centimeters), and physical activity level (type, frequency, and intensity).

2.3. Classifications: Nutritional Status, Age Group, and Physical Activity Level

Nutritional status was classified using the Body Mass Index (BMI) as a parameter. BMI (Kg/m2) was calculated by dividing weight (in kg) by the square of height (in meters). Classifications followed the World Health Organization (WHO) values [24,25]: underweight (<18.5 kg/m2), normal weight (18.5–24.9 kg/m2), overweight (25.0–29.9 kg/m2), and obesity (≥30.0 kg/m2).
There are various age classifications for distinguishing between adults and elderly individuals. The World Health Organization (WHO), in collaboration with the United Nations (UN), defines elderly individuals as those over 65 years of age in developed countries and over 60 years in developing countries [26]. According to Brazilian legislation, as stated in the Statute of the Elderly [27], elderly individuals are considered to be 60 years or older. Based on these guidelines, individuals were classified as “Adults” if they were under 60 years of age and as “Elderly” if they were 60 years or older.
The “sedentary” classification for physical activity level included light and moderate activities, such as performing household chores, short walks related to daily needs, and predominance of long periods of inactivity, such as watching television [15]. This activity level characterizes individuals who do not engage in structured exercise or physical activities that significantly increase daily energy expenditure, resulting in a predominantly inactive lifestyle with limited impact on cardiovascular and metabolic health.

2.4. Estimation of Daily Energy Requirements

Data used to estimate daily energy needs were tabulated and processed in Microsoft Excel (Office 365). The calculations were performed using formulas directly entered into the software. The equations used for energy estimation are detailed in Table 1.

2.5. Data Analysis

Study variables were initially analyzed using descriptive statistics, with data presented as mean ± standard deviation (confidence interval: lower limit–upper limit). To compare the equations’ progression from 2005 to 2023, a repeated measures Analysis of Variance (rmANOVA) was used due to its ease of application and interpretation. Initially, we evaluated data distribution requirements (normality) and homogeneity of variances (sphericity) using Shapiro-Wilk and Mauchly tests, respectively. Since the data did not show a normal distribution, a logarithmic transformation (LOG10) was applied. It is worth noting that the improper use of rmANOVA, without appropriate corrections for assumption violations, can increase errors and compromise the validity of the results. For this reason, these conditions were carefully evaluated during our analyses, ensuring robustness and statistical adequacy. For multiple comparisons, the post hoc Tukey test was used. The significance level adopted was 5%, and the effect size was estimated using Eta Square (η2). To interpret the effect size of η2, the following classifications were used: small effect = 0.01–0.05; medium effect = 0.06–0.13; large effect ≥ 0.14; η2 values below 0.01 were considered negligible or without effect [28,29]. All statistical tests were conducted using JAMOVI software (version 2.5.6) [30,31,32,33,34].

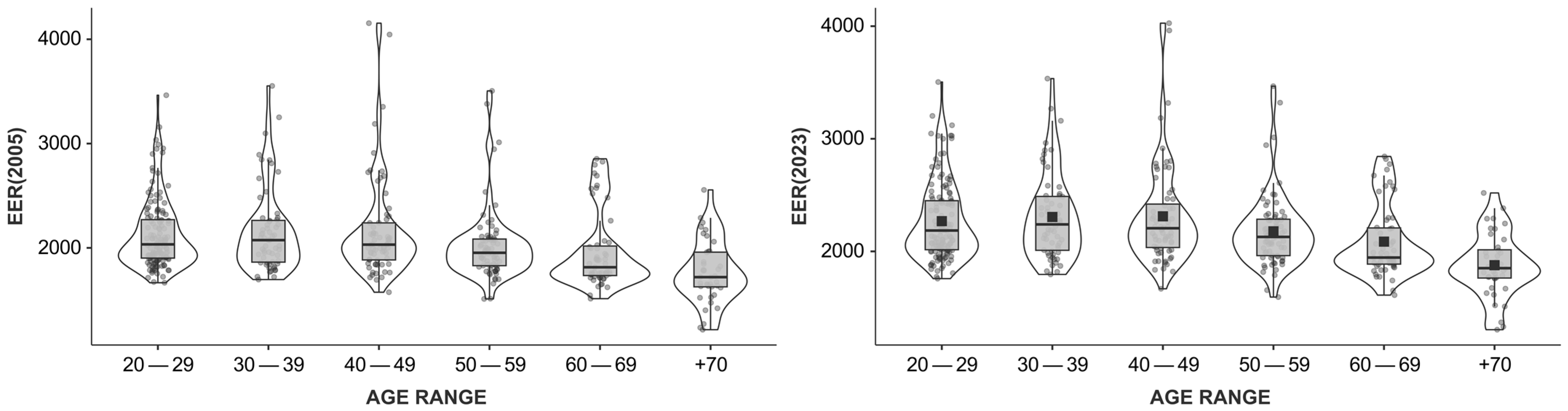
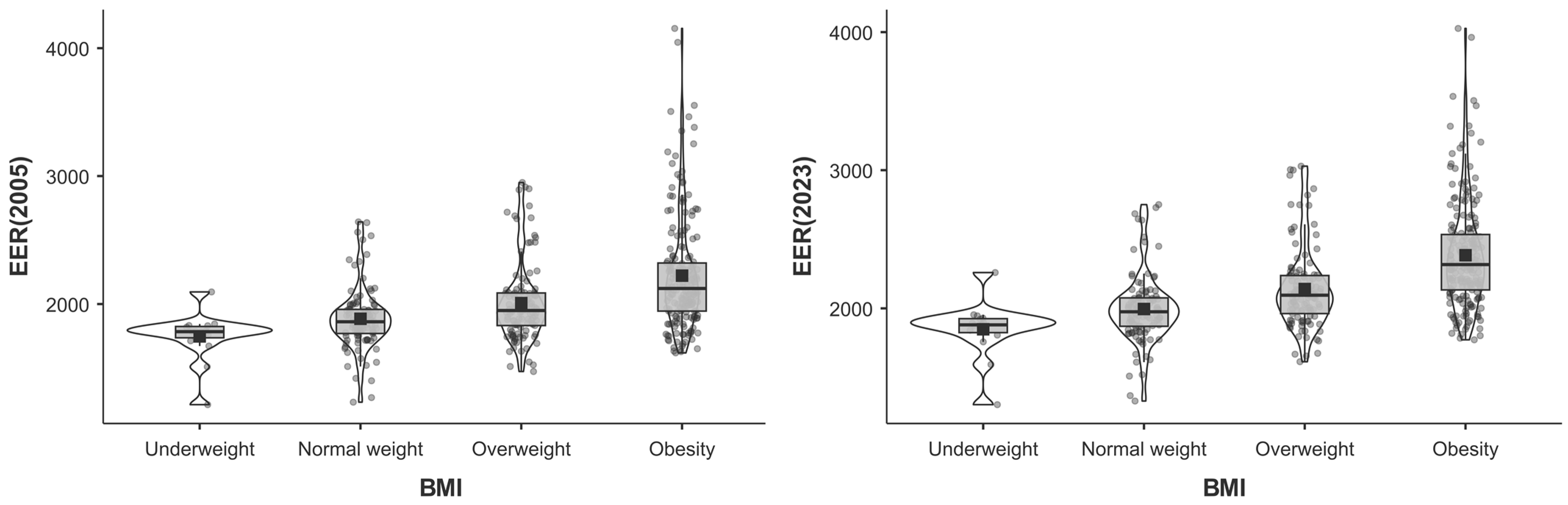
3. Results

In this study, data from 431 sedentary adults and elderly individuals who were treated at CENUT between 2021 and 2023 were analyzed. The sample, predominantly composed of women (80%), had a mean age of 43.57 ± 17.30 years, with a minimum of 20 and a maximum of 85 years. Participants were divided into two age groups: adults (<60 years, n = 346) and elderly (≥60 years, n = 85). Sample description data are presented in Table 2.
Figure 1 shows a boxplot with the EER distribution estimates from 2005 and 2023, separated by age group. A decline in energy needs with advancing age was observed for both equations. Among younger individuals (20–29 and 30–39 years), there was greater data dispersion, indicating more variability in individual energy demands. Additionally, an increase in outliers was noted, suggesting the presence of individuals with energy needs differing from the average. Overall, the comparison between 2005 and 2023 reveals that while the general pattern of declining energy needs with age remains consistent, there may be subtle differences in medians and dispersion between two time points.
Table 3 presents a comparison of energy needs estimates for adults and elderly individuals. In general, the estimated means by the 2023 equation were higher than those of the 2005 equation. The rmANOVA showed a significant effect in the evolution of energy needs estimates between EER-2005 and EER-2023, though with a small effect size (F(1, 429) = 1567.24, p < 0.001, η2 = 0.02), indicating that only 2% of the variation in estimates can be attributed to the change between the two equation sets. Furthermore, comparison between age groups revealed significant differences, with adults having higher EER means than elderly individuals. The effect size was medium (F(1, 429) = 43.1, p < 0.001, η2 = 0.09), indicating that the “age” factor explains 9% of the variability in energy needs estimates. Finally, no significant interaction effect between EER and age group was identified (F(1, 429) = 2.15, p = 0.143), suggesting that the change in EER over time was similar for both adults and the elderly. These results indicate that, regardless of age group, the change in energy needs over time followed a similar pattern. Therefore, DRI equations seem to consistently apply energy needs estimates for adults and elderly individuals without discriminating between age groups in terms of the variation observed over time.
Energy needs estimates for both time points were also investigated concerning nutritional status, with an additional stratification by BMI levels, as the overall BMI average did not adequately represent the sample’s characteristics. As shown in Table 1, the sample majority was classified as obese, followed by overweight, eutrophic, and underweight individuals.
Figure 2 illustrates the data distribution where both time points show similar patterns in EER across BMI categories. The obesity group exhibits the greatest dispersion in EER values, reflecting greater variability among individuals with different degrees of excess weight. Additionally, there is an increase in energy needs as BMI increases, which is expected, given that the EER calculation considers total body mass. This results in higher values for individuals with more body mass, particularly in the obesity group. This observation reflects a mathematical issue inherent in EER equations, which weigh body mass as one of the main energy need determinants. Overall, these results reinforce the importance of considering nutritional status when estimating energy needs, as sample averages may obscure significant variations between different BMI categories.
Table 4 presents the comparisons of energy needs estimates for BMI categories. A significant increase was observed from 2005 to 2023 (F(1, 427) = 1010.3, p < 0.001, η2 = 0.01). However, the effect size is small, indicating that only 1% of the total variability in the model can be attributed to differences between the 2005 and 2023 equations.
When comparing BMI categories with each other, a statistically significant difference was also found (F(3, 427) = 36.7, p < 0.001, η2 = 0.20), with a large effect size, explaining 20% of the variability between BMI groups. Table 5 presents Tukey post hoc results for these multiple comparisons of BMI levels, showing that the Obesity group had a higher EER compared with the others. Additionally, the EER of the overweight group was higher compared to Normal Weight and Underweight individuals. No significant difference was observed between the Normal Weight and Underweight groups. The EER interaction with BMI also resulted in a statistically significant difference (EER ✻ BMI: F(3, 427) = 11.7, p < 0.001, η2 = 0.001), indicating that changes in EER were not the same across all BMI levels. However, the observed effect size was considered negligible.
The interaction between “EER”, “age group”, and “BMI” did not result in a statistically significant difference within subjects (EER ✻ Age group ✻ BMI: F(3, 423) = 0.40, p = 0.752) or between subjects (Age group ✻ BMI: F(3, 423) = 1.30, p = 0.275).

4. Discussion

The comparisons conducted in this study are necessary for healthcare professionals to consider the updates proposed in the 2023 DRI [16]. As noted, the global population has undergone several changes over nearly 20 years, such as increased life expectancy, new dietary habits, and changes in physical activity levels, which needed an update to the equations used to estimate daily energy expenditure. Moreover, technological advancements have allowed for more precise investigations of these factors. Our results confirm that, despite the small effect size, the new equations yield, on average, higher values than the previous version. This difference has significant practical implications, particularly in the management of sedentary populations who are more susceptible to energy imbalance.
Although methods based on calorimetry and the use of doubly labeled water are considered the gold standard for accurately estimating energy requirements, their application in clinical practice is not always feasible due to high costs and the need for specialized professionals to ensure proper implementation. Furthermore, the high cost of the doubly labeled water method often results in studies with small sample sizes, typically fewer than 30 participants, which limits the ability of these samples to address key scientific questions in the field of nutrition. Therefore, seeking updated and accurate equations, such as the one proposed in the 2023 DRI, which is based on a larger sample using doubly labeled water, is an effective strategy to minimize errors in energy requirement estimation across diverse populations [35,36].
The results of this study also showed that adult individuals had higher average estimated values compared with older individuals, as it is well known that with advancing age, there is a reduction in the amount of metabolically active tissue, especially skeletal muscle [37]. This condition is occasionally associated with sarcopenia, which is exclusively related to aging [38]. Cooper and colleagues [39] conducted a longitudinal study in which they evaluated resting metabolic rate at two distinct time points: the first assessment was conducted in 1999 and the second in 2006, using indirect calorimetry. The study observed that, from 1999 to 2006, male individuals exhibited statistically significant reductions in resting metabolic rate measured by calorimetry, while females showed only numerical reductions. These findings are particularly interesting, as reductions in resting metabolic rate with aging may increase the risk of obesity (including sarcopenic obesity) in sedentary individuals consuming a high-calorie diet.
It is equally important to emphasize the relevance of the equations proposed by the DRIs, as previously noted by Macena et al. [40]. In their systematic review with meta-analysis, these authors sought to identify which predictive equations for resting energy expenditure, and total energy expenditure exhibited the least bias and greatest accuracy in overweight and obese adults. This is because not all equations are suitable for use in this population, given the risk of providing inaccurate estimates. Among the various equations evaluated, the one proposed by the Institute of Medicine stood out as having the least bias in estimating total energy expenditure.
Additionally, Macena and colleagues [40] identified that estimation equations that include body composition variables (lean mass and fat mass) in their formulas tended to underestimate resting energy expenditure. The authors hypothesized that the heterogeneity of the methods used to estimate these variables could explain this issue. One example is bioelectrical impedance, which has many requirements for proper execution. Therefore, all these factors should be considered when choosing the predictive equation for energy expenditure, and it is expected that the new proposed equations will be useful tools in clinical practice.
Our results must be interpreted with caution. This study included a heterogeneous sample but was predominantly white and female. For nutritional status, it only considered BMI levels without stratifying based on body composition or the participants’ age. Another variable not considered was the clinical status of the participants. The presence of chronic or acute diseases, with or without the use of medications, can influence the results, compromising the accuracy of energy requirement estimations—although the population served at CENUT does not present such severe clinical profiles. We recommend that future evaluations and research include these variables and adopt an approach with probabilistic sampling, appropriate sample size calculation, and balanced stratifications (1:1) by sex, age group, BMI, race and ethnicity. This would enable the generation of results with greater external validity and broader applicability to larger populations.

5. Conclusions

This study demonstrates that there was a significant increase in energy requirement estimates from 2005 to the 2023 DRI equations for sedentary individuals, although the effect size was small. In the comparison between groups, we showed that adults have higher EER than elderly individuals (medium effect size). Additionally, obese individuals have higher EER than those who are overweight, of normal weight, and underweight, while overweight individuals have higher EER than those of normal and underweight status (large effect size).
The absence of significant interaction between EER and age group suggests that the variation in energy requirement estimates is consistent between adults and the elderly over time. Although the 2005 and 2023 EER equations presented a significant interaction regarding BMI, this variation does not translate into a practically relevant impact, given the null effect size. Lastly, the interaction between EER, age group, and BMI also did not show a statistically significant difference, reinforcing that the combined influence of these factors does not meaningfully alter the EER. Considering the evolution of the population described in the DRIs and the results of this study, it is recommended that professionals update their clinical protocols, using updated equations to estimate energy requirements with greater accuracy.

Author Contributions

Conceptualization, A.R.d.F.M.; formal analysis, A.M.O.H.V. and J.M.S.; investigation, J.F.C. and I.O.F.; methodology, A.M.O.H.V. and J.M.S.; project administration, A.R.d.F.M.; software, A.M.O.H.V. and J.M.S.; supervision, D.C.G. and A.R.d.F.M.; visualization, D.C.G.; writing—original draft, A.M.O.H.V. and J.M.S.; Writing—review and editing, A.M.O.H.V., J.M.S., J.F.C., I.O.F., D.L.S., D.G.V., A.M.K., D.C.G. and A.R.d.F.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study was conducted in accordance with the Declaration of Helsinki and approved by the Research Ethics Committee of the State University of the Midwest (UNICENTRO), an interdisciplinary and independent body (protocol code 6916255 (CAE 80824224.4.0000.0106).

Informed Consent Statement

Data collection was carried out retrospectively, using medical records of patients who no longer attend the institution. Due to the impossibility of identifying and contacting the patients and because the analysis was conducted in an aggregated manner, the Research Ethics Committee waived the requirement for the Informed Consent Form (ICF) in accordance with Resolution CNS No. 466/2012. All information that could identify the participants was removed, leaving only the variables sex, age, height, weight, and physical activity level classification. The anonymized data are under the responsibility of the principal investigator and are securely stored in compliance with the General Data Protection Law.

Data Availability Statement

The data presented in this study are available upon reasonable request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Harris, J.A.; Benedict, F.G. A Biometric Study of Human Basal Metabolism. Proc. Natl. Acad. Sci. USA 1918, 4, 370. [Google Scholar] [CrossRef] [PubMed]
  2. Frankenfield, D.; Roth-Yousey, L.; Compher, C. Comparison of Predictive Equations for Resting Metabolic Rate in Healthy Nonobese and Obese Adults: A Systematic Review. J. Am. Diet. Assoc. 2005, 105, 775–789. [Google Scholar] [CrossRef] [PubMed]
  3. Bendavid, I.; Lobo, D.N.; Barazzoni, R.; Cederholm, T.; Coëffier, M.; de van der Schueren, M.; Fontaine, E.; Hiesmayr, M.; Laviano, A.; Pichard, C.; et al. The centenary of the Harris–Benedict equations: How to assess energy requirements best? Recommendations from the ESPEN expert group. Clin. Nutr. 2021, 40, 690–701. [Google Scholar] [CrossRef]
  4. Mifflin, M.; St Jeor, S.; Hill, L.; Scott, B.; Daugherty, S.; Koh, Y. A new predictive equation for resting energy expenditure in healthy individuals. Am. J. Clin. Nutr. 1990, 51, 241–247. [Google Scholar] [CrossRef]
  5. Kawase, F.; Masaki, Y.; Ozawa, H.; Imanaka, M.; Sugiyama, A.; Wada, H.; Kobayashi, S.; Tsukahara, T. New prediction equations for resting energy expenditure in older hospitalized patients: Development and validation. Nutrition 2023, 115, 112188. [Google Scholar] [CrossRef]
  6. Almajwal, A.M.; Abulmeaty, M.M.A. New Predictive Equations for Resting Energy Expenditure in Normal to Overweight and Obese Population. Int. J. Endocrinol. 2019, 2019, 5727496. [Google Scholar] [CrossRef]
  7. Niederer, L.E.; Miller, H.; Haines, K.L.; Molinger, J.; Whittle, J.; MacLeod, D.B.; McClave, S.A.; Wischmeyer, P.E. Prolonged progressive hypermetabolism during COVID-19 hospitalization undetected by common predictive energy equations. Clin. Nutr. ESPEN 2021, 45, 341–350. [Google Scholar] [CrossRef]
  8. Tinsley, G.M.; Graybeal, A.J.; Moore, M.L. Resting metabolic rate in muscular physique athletes: Validity of existing methods and development of new prediction equations. Appl. Physiol. Nutr. Metab. 2019, 44, 397–406. [Google Scholar] [CrossRef]
  9. Porter, J.; Ward, L.C.; Nguo, K.; Ward, A.; Davidson, Z.; Gibson, S.; Prentice, R.; Neuhouser, M.L.; Truby, H. Development and validation of age-specific predictive equations for total energy expenditure and physical activity levels for older adults. Am. J. Clin. Nutr. 2024, 119, 1111–1121. [Google Scholar] [CrossRef]
  10. Kajale, N.; Khadilkar, A.; Oza, C.; Gondhalekar, K.; Khadilkar, V. Resting metabolic rate and its association with body composition parameters in 9- to 18-year-old Indian children and adolescents. Nutrition 2022, 99–100, 111652. [Google Scholar] [CrossRef]
  11. United Nations University; World Health Organization; Food and Agriculture Organization of the United Nations. Human Energy Requirements. Report of a Joint FAO/WHO/UNU Expert Consultation; FAO Food and Nutrition Technical Report Series 1; FAO: Rome, Italy, 2001. [Google Scholar]
  12. Miles-Chan, J.L.; Harper, M.E. Deconstructing interindividual variability in energy metabolism: Implications for metabolic health. Am. J. Physiol. Endocrinol. Metab. 2023, 325, E107–E112. [Google Scholar] [CrossRef] [PubMed]
  13. Carvalho, F.G.D.; Monteiro, B.d.A.; Goulart-de-Andrade, D.E.; Bronzi, É.d.S.; Oliveira, M.R.M.d. Métodos de Avaliação de Necessidades Nutricionais e Consumo de Energia em Humanos. Rev. Simbiol. 2012, 5, 99–120. [Google Scholar]
  14. Argilés, J.M.; López-Soriano, F.J.; Stemmler, B.; Busquets, S. Cancer-associated cachexia—Understanding the tumour macroenvironment and microenvironment to improve management. Nat. Rev. Clin. Oncol. 2023, 20, 250–264. [Google Scholar] [CrossRef] [PubMed]
  15. Institute of Medicine. Dietary Reference Intakes for Energy, Carbohydrate, Fiber, Fat, Fatty Acids, Cholesterol, Protein, and Amino Acids; National Academies Press: Washington, DC, USA, 2005. [Google Scholar] [CrossRef]
  16. National Academies of Sciences. Dietary Reference Intakes for Energy; National Academies Press: Washington, DC, USA, 2023. [Google Scholar] [CrossRef]
  17. World Health Organization. Obesity and Overweight. 2024. Available online: https://www.who.int/news-room/fact-sheets/detail/obesity-and-overweight (accessed on 20 January 2025).
  18. Pearson-Stuttard, J.; Zhou, B.; Kontis, V.; Bentham, J.; Gunter, M.J.; Ezzati, M. Worldwide burden of cancer attributable to diabetes and high body-mass index: A comparative risk assessment. Lancet Diabetes Endocrinol. 2018, 6, e6–e15. [Google Scholar] [CrossRef]
  19. Safizadeh, F.; Mandic, M.; Hoffmeister, M.; Brenner, H. Colorectal Cancer and Central Obesity. JAMA Netw. Open 2025, 8, e2454753. [Google Scholar] [CrossRef]
  20. Phelps, N.H.; Singleton, R.K.; Zhou, B.; Heap, R.A.; Mishra, A.; Bennett, J.E.; Paciorek, C.J.; Lhoste, V.P.; Carrillo-Larco, R.M.; Stevens, G.A.; et al. Worldwide trends in underweight and obesity from 1990 to 2022: A pooled analysis of 3663 population-representative studies with 222 million children, adolescents, and adults. Lancet 2024, 403, 1027–1050. [Google Scholar] [CrossRef]
  21. Pureza, I.R.d.O.M.; Macena, M.L.; Silva, A.E.; Praxedes, D.R.S.; Vasconcelos, L.G.L.; Florêncio, T.M.M.T.; Bueno, N.B. Agreement between equations-estimated resting metabolic rate and indirect calorimetry-estimated resting metabolic rate in low-income obese women. Arch. Endocrinol. Metab. 2020. [CrossRef]
  22. Lin, Y.R.; Chen, P.C.; Li, W.T.; Huang, M.H.; Huang, S.F.; Wang, C.J.; Chien, Y.W.; Kao, A.W.; Shan, Y.S. The relationship between caloric intake and clinical outcomes in critically ill patients: A retrospective study. Clin. Nutr. ESPEN 2025, 65, 9–15. [Google Scholar] [CrossRef]
  23. Moonen, H.P.F.X.; Beckers, K.J.H.; van Zanten, A.R.H. Energy expenditure and indirect calorimetry in critical illness and convalescence: Current evidence and practical considerations. J. Intensive Care 2021, 9, 8. [Google Scholar] [CrossRef]
  24. World Health Organization (WHO). Physical Status: The Use and Interpretation of Anthropometry; WHO Technical Report Series n. 854; World Health Organization: Geneva, Switzerland, 1995. [Google Scholar]
  25. World Health Organization (WHO). Surveillance of Chronic Disease Risk Factors: Country Level Data and Comparable Estimates; World Health Organization: Geneva, Switzerland, 2005; Available online: https://iris.who.int/handle/10665/43190 (accessed on 16 October 2024).
  26. United Nations Department of Economic; Social Affairs; Population Division. World Population Ageing 2019; United Nations: New York, NY, USA, 2019. [Google Scholar]
  27. BRASIL. Lei No 14.423. 2022. Available online: https://www.planalto.gov.br/ccivil_03/_Ato2019-2022/2022/Lei/L14423.htm (accessed on 1 December 2024).
  28. Lenhard, W.; Lenhard, A. Computation of Effect Sizes. 2022. Available online: https://www.psychometrica.de/effect_size.html (accessed on 1 December 2024). [CrossRef]
  29. Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: New York, NY, USA, 1988. [Google Scholar]
  30. Jamovi (2.6.13), The Jamovi Project. 2024.
  31. R Core Team.  R: A Language and Environment for Statistical Computing. 2023. [Google Scholar]
  32. Fox, J.; Weisberg, S. CAR: Companion to Applied Regression; [R Package]. 2023. [Google Scholar]
  33. Lenth, R. emmeans: Estimated Marginal Means, aka Least-Squares Means; [R Package]. 2023. [Google Scholar]
  34. Singmann, H. AFEX: Analysis of Factorial Experiments; [R Package]. 2023. [Google Scholar]
  35. Holdy, K.E. Monitoring Energy Metabolism with Indirect Calorimetry: Instruments, Interpretation, and Clinical Application. Nutr. Clin. Pract. 2004, 19, 447–454. [Google Scholar] [CrossRef]
  36. Speakman, J.R.; Pontzer, H.; Rood, J.; Sagayama, H.; Schoeller, D.A.; Westerterp, K.R.; Wong, W.W.; Yamada, Y.; Loechl, C.; Murphy-Alford, A.J. The International Atomic Energy Agency International Doubly Labelled Water Database: Aims, Scope and Procedures. Ann. Nutr. Metab. 2019, 75, 114–118. [Google Scholar] [CrossRef] [PubMed]
  37. Gaillard, C.; Alix, E.; Sallé, A.; Berrut, G.; Ritz, P. Energy requirements in frail elderly people: A review of the literature. Clin. Nutr. 2007, 26, 16–24. [Google Scholar] [CrossRef] [PubMed]
  38. Cruz-Jentoft, A.J.; Bahat, G.; Bauer, J.; Boirie, Y.; Bruyère, O.; Cederholm, T.; Cooper, C.; Landi, F.; Rolland, Y.; Sayer, A.A.; et al. Sarcopenia: Revised European consensus on definition and diagnosis. Age Ageing 2019, 48, 16–31. [Google Scholar] [CrossRef] [PubMed]
  39. Cooper, J.A.; Manini, T.M.; Paton, C.M.; Yamada, Y.; Everhart, J.E.; Cummings, S.; Mackey, D.C.; Newman, A.B.; Glynn, N.W.; Tylavsky, F.; et al. Longitudinal change in energy expenditure and effects on energy requirements of the elderly. Nutr. J. 2013, 12, 73. [Google Scholar] [CrossRef]
  40. de Lima Macena, M.; da Costa Paula, D.T.; da Silva Júnior, A.E.; Praxedes, D.R.S.; de Oliverira Maranhão Pureza, I.R.; de Melo, I.S.V.; Bueno, N.B. Estimates of resting energy expenditure and total energy expenditure using predictive equations in adults with overweight and obesity: A systematic review with meta-analysis. Nutr. Rev. 2022, 80, 2113–2135. [Google Scholar] [CrossRef]
Obesities 05 00015 g001
Figure 1. Boxplot showing the mean and median of estimated energy requirements for adults and the elderly separated by age range. Figure description: The data are presented as mean ± SD (median). EER (2005): 20–29: 2129.3 ± 333.6 (2033.6) | 30–39: 2161.2 ± 401.8 (2074.3) | 40–49: 2166.9 ± 487.6 (2031.1) | 50–59: 2020.5 ± 349.4 (1952.9) | 60–69: 1961.8 ± 363.0 (1814.3) | +70: 1764.1 ± 297.6 (1719.5); EER (2023): 20–29: 2268.3 ± 342.9 (2185.2) | 30–39: 2305.5 ± 381.9 (2239.6) | 40–49: 2311.2 ± 440.6 (2205.4) | 50–59: 2178.0 ± 324.8 (2128.4) | 60–69: 2086.6 ± 315.4 (1945.1) | +70: 1877.3 ± 278.1 (1850.8).
Figure 1. Boxplot showing the mean and median of estimated energy requirements for adults and the elderly separated by age range. Figure description: The data are presented as mean ± SD (median). EER (2005): 20–29: 2129.3 ± 333.6 (2033.6) | 30–39: 2161.2 ± 401.8 (2074.3) | 40–49: 2166.9 ± 487.6 (2031.1) | 50–59: 2020.5 ± 349.4 (1952.9) | 60–69: 1961.8 ± 363.0 (1814.3) | +70: 1764.1 ± 297.6 (1719.5); EER (2023): 20–29: 2268.3 ± 342.9 (2185.2) | 30–39: 2305.5 ± 381.9 (2239.6) | 40–49: 2311.2 ± 440.6 (2205.4) | 50–59: 2178.0 ± 324.8 (2128.4) | 60–69: 2086.6 ± 315.4 (1945.1) | +70: 1877.3 ± 278.1 (1850.8).
Obesities 05 00015 g001
Obesities 05 00015 g002
Figure 2. Boxplot showing the mean and median of estimated energy requirements separated by BMI levels. Figure description: The data are presented as mean ± SD (median). EER (2005): Underweight: 1747.68 ± 189.35 (1784.66) | Normal weight: 1885.20 ± 244.77 (1861.99) | Overweight: 2007.59 ± 309.93 (1949.65) | Obesity: 2221.50 ± 441.47(2121.55); EER (2023): Underweight: 1848.83 ± 203.19 (1880.82) | Normal weight: 1995.32 ± 248.73 (1975.30) | Overweight: 2139.73 ± 293.57 (2095.07) | Obesity: 2383.87 ± 393.34 (2316.35).
Figure 2. Boxplot showing the mean and median of estimated energy requirements separated by BMI levels. Figure description: The data are presented as mean ± SD (median). EER (2005): Underweight: 1747.68 ± 189.35 (1784.66) | Normal weight: 1885.20 ± 244.77 (1861.99) | Overweight: 2007.59 ± 309.93 (1949.65) | Obesity: 2221.50 ± 441.47(2121.55); EER (2023): Underweight: 1848.83 ± 203.19 (1880.82) | Normal weight: 1995.32 ± 248.73 (1975.30) | Overweight: 2139.73 ± 293.57 (2095.07) | Obesity: 2383.87 ± 393.34 (2316.35).
Obesities 05 00015 g002
Table 1. Energy estimation equations according to the DRIs (2005 and 2023).
Table 1. Energy estimation equations according to the DRIs (2005 and 2023).
2005 EQUATIONS (≥19 years)
MaleEER = 662 − (9.53 × Age [Y]) + PA × (15.91 × Weight [Kg] + 539.6 × Height [M])
FemaleEER = 354 − (6.91 × Age [Y]) + PA × (9.36 × Weight [Kg] + 726 × Height [M])
2023 EQUATIONS (≥19 years)
MaleEER = 753.07 − (10.83 × Age [Y]) + (6.50 × Height [Cm]) + (14.10 × Weight [Kg])
FemaleEER = 584.90 − (7.01 × Age [Y]) + (5.72 × Height [Cm]) + (11.71 × Weight [Kg])
Notes: Y = years; Kg = kilograms; M = meters; Cm = centimeters.
Table 2. Sample characterization (n = 431).
Table 2. Sample characterization (n = 431).
Sex (Female)345 (80.00%)
Age (Y)43.57 ± 17.30
(CI95%: 41.93–45.21)
Adults (<60 years old)346 (80.30%)
   20–29 (years old)136 (39.31%)
   30–39 (years old)60 (17.34%)
   40–49 (years old)68 (19.65%)
   50–59 (years old)72 (20.81%)
Elderly (≥60 years old)85 (19.70%)
   60–69 (years old)45 (64.70%)
   +70 (years old)40 (47.05%)
Height (M)1.62 ± 0.08
(CI 95%: 1.62–1.63)
Weight (Kg)79.52 ± 21.72
(CI 95%: 77.47–81.58)
Overall BMI (Kg/m2)30.08 ± 7.55
(CI 95%: 29.36–30.79)
   Underweight (n = 15; 3.5%)17.1 ± 1.02
(CI 95%: 16.50–17.70)
   Normal weight (n = 106; 24.6%)22.2 ± 1.88
(CI 95%: 21.00–22.60)
   Overweight (n = 113; 26.2%)27.7 ± 1.42
(CI 95%: 27.50–28.00)
   Obesity (n = 197; 45.7%)36.6 ± 5.46
(CI 95%: 35.90–37.40)
Notes: Continuous data are presented as mean ± SD (95% CI: lower limit–upper limit), and categorical data are presented as proportions. Y = years; M = meters; Kg = kilograms; BMI = Body Mass Index; SD = standard deviation; CI 95% = confidence interval; n = sample.
Table 3. Comparison of estimated energy requirements for adults and the elderly.
Table 3. Comparison of estimated energy requirements for adults and the elderly.
Overall (Kcal)Adults (Kcal)Elderly (Kcal)Within-Subjects EffectBetween-Subjects Effect
F (df)p (ES)F (df)p (ES)
EER, 20052066.22 ± 391.43
(CI 95%: 2029.16–2103.28)		2113.83 ± 386.62
(CI 95%: 2072.94–2154.71)		1872.44 ± 350.86
(CI 95%: 1796.76–1948.12)		1567.24
(1, 429)		<0.001
(η2 = 0.02)		43.1
(1, 429)		<0.001
(η2 = 0.09)
EER, 20232205.68 ± 374.78
(CI 95%: 2170.20–2241.16)		2259.16 ± 368.86
(CI 95%: 2220.15–2298.16)		1987.99 ± 316.98
(CI 95%: 1919.62–2056.36)
Notes: Continuous data are presented as mean ± SD (95% CI: lower limit–upper limit). The adult group refers to individuals under 60 years of age, and the elderly group refers to individuals over 60 years of age. EER = estimated energy requirements; df = degrees of freedom; ES = effect size; SD = standard deviation; CI 95% = confidence interval.
Table 4. Comparison of estimated energy requirements for BMI levels.
Table 4. Comparison of estimated energy requirements for BMI levels.
Underweight
(Kg/m²)		Normal Weight
(Kg/m²)		Overweight
(Kg/m²)		Obesity
(Kg/m²)		Within-Subjects EffectBetween-Subjects Effect
F (df)p (ES)F (df)p (ES)
EER, 20051747.68 ± 189.35
(CI 95%: 1642.82–1852.54)		1885.20 ± 244.77
(CI 95%: 1838.06–1932.35)		2007.59 ± 309.93
(CI 95%: 1949.82–2065.36)		2221.50 ± 441.47
(CI 95%: 2159.47–2283.53)		1010.3
(1, 427)		<0.001
(η2 = 0.01)		36.7
(3, 427)		<0.001
(η2 = 0.20)
EER, 20231848.83 ± 203.18
(CI 95%: 1736.31–1961.35)		1995.32 ± 248.73
(CI 95%: 1947.42–2043.22)		2139.73 ± 293.57
(CI 95%: 2085.02–2194.45)		2383.87 ± 393.34
(CI 95%: 2328.60–2439.13)
Notes: Continuous data are presented as mean ± SD (95% CI: lower limit–upper limit). EER = estimated energy requirements; df = degrees of freedom; ES = effect size; SD = standard deviation; CI 95% = confidence interval.
Table 5. Tukey’s post hoc test for the comparison of estimated energy requirements for BMI levels.
Table 5. Tukey’s post hoc test for the comparison of estimated energy requirements for BMI levels.
BMI BMIMDSEdftp Tukey
Underweight-Normal weight−0.0320.018427−1.820.266
-Overweight −0.0600.018−3.410.004
-Obesity−0.1040.017−6.00<0.001
Normal weight-Overweight −0.0280.009−3.220.008
-Obesity−0.0710.008−9.19<0.001
Overweight -Obesity−0.0430.008−5.69<0.001
Notes: BMI = Body Mass Index; df = degrees of freedom; MD = mean difference; SE = standard error.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Verdi, A.M.O.H.; Soares, J.M.; Carneiro, J.F.; Felez, I.O.; Schiessel, D.L.; Vieira, D.G.; Kühl, A.M.; Gonçalves, D.C.; Melhem, A.R.d.F. Estimated Energy Requirement: Comparison Between the 2005 and 2023 Dietary Reference Intakes in Sedentary Adults and Older Adults—A Retrospective Cross-Sectional Study. Obesities 2025, 5, 15. https://doi.org/10.3390/obesities5010015

AMA Style

Verdi AMOH, Soares JM, Carneiro JF, Felez IO, Schiessel DL, Vieira DG, Kühl AM, Gonçalves DC, Melhem ARdF. Estimated Energy Requirement: Comparison Between the 2005 and 2023 Dietary Reference Intakes in Sedentary Adults and Older Adults—A Retrospective Cross-Sectional Study. Obesities. 2025; 5(1):15. https://doi.org/10.3390/obesities5010015

Chicago/Turabian Style

Verdi, Anderson Matheus Oliveira Haas, Jaqueline Machado Soares, Jaqueline Fernandes Carneiro, Izadora Oliveira Felez, Dalton Luiz Schiessel, Daniele Gonçalves Vieira, Adriana Masiero Kühl, Daniela Caetano Gonçalves, and Angelica Rocha de Freitas Melhem. 2025. "Estimated Energy Requirement: Comparison Between the 2005 and 2023 Dietary Reference Intakes in Sedentary Adults and Older Adults—A Retrospective Cross-Sectional Study" Obesities 5, no. 1: 15. https://doi.org/10.3390/obesities5010015

APA Style

Verdi, A. M. O. H., Soares, J. M., Carneiro, J. F., Felez, I. O., Schiessel, D. L., Vieira, D. G., Kühl, A. M., Gonçalves, D. C., & Melhem, A. R. d. F. (2025). Estimated Energy Requirement: Comparison Between the 2005 and 2023 Dietary Reference Intakes in Sedentary Adults and Older Adults—A Retrospective Cross-Sectional Study. Obesities, 5(1), 15. https://doi.org/10.3390/obesities5010015

Article Metrics

Back to TopTop