Abstract
Aims: The accurate prediction of blood glucose (BG) levels is critical for managing Type-1 Diabetes (T1D) in pediatric patients, where variability due to factors like physical activity and developmental changes presents significant challenges. Methods: This work explores the application of foundational models, particularly the encoder–decoder model TimeGPT, for BG forecasting in T1D pediatric patients. Methods: The performance of TimeGPT is compared against state-of-the-art models, including ARIMAX and LSTM, and multilayer perceptron (MLP) architectures such as TiDE and TSMixer. The models were evaluated using continuous glucose monitoring (CGM) data and exogenous variables, such as insulin intake. Results: TimeGPT outperforms or achieves comparable accuracy to the state of the art and MLP models in short-term predictions (15 and 30 min), with most predictions falling within the clinically safe zones of the Clarke Error Grid. Conclusions: The findings suggest that foundational models like TimeGPT offer promising generalization capabilities for medical applications and can serve as valuable tools to enhance diabetes management in pediatric T1D patients.
1. Introduction
In recent years, the development and proliferation of large language models (LLMs) and transformer-based generative models, along with the attention mechanism, have revolutionized the state of the art in Natural Language Processing (NLP) tasks [1]. These models are often pre-trained on vast amounts of data and made publicly available, accelerating further advancements in various fields [2,3]. Drawing inspiration from the success of large pre-trained models in text and vision tasks [4,5], time series forecasting is also experimenting with a universal prediction paradigm [6]. In this new paradigm, a single large pre-trained model can address a wide range of time series prediction tasks.
However, developing such a model presents significant challenges, particularly due to the diverse and complex nature of time series data, especially in the medical context [7]. Medical time series data encompass a wide range of physiological variables, each with unique characteristics and complexities. The related measured signals, such as electrocardiograms (ECG), electroencephalograms (EEG), and the blood glucose (BG) curve, require precise models to accurately capture their temporal dynamics. For instance, time series forecasting models have been employed to predict patient vitals in intensive care units (ICUs) and monitor chronic conditions such as diabetes [8,9].
The prediction of BG levels in patients with Type-1 Diabetes (T1D) is particularly challenging due to its high variability and numerous influencing factors, including diet, physical activity, and insulin therapy [10]. T1D is a significant global health concern, affecting children, adolescents, and adults. According to the International Diabetes Federation (IDF) 2022 Atlas Report [11], there are 8.75 million people living with T1D worldwide, with 1.52 million being under 20 years old. The incidence of T1D is particularly high in children, necessitating accurate and timely predictions of BG levels to manage the disease effectively. Pediatric patients with T1D require precise glycemic control to prevent complications such as hyperglycemia and hypoglycemia, which can have severe health implications [12].
In this paper, we explore, for the first time to our knowledge, the adoption of encoder–decoder models based on the attention mechanism, such as TimeGPT with different settings [13], for predicting the BG levels in pediatric patients with T1D. We compare these models with encoder–decoder models without attention, such as the Time-series Dense Encoder (TiDE) [14], with Multilayer Perceptron (MLP) models, such as Time-Series Mixer (TSMixer) [15], as well as with state-of-the-art non-attention-based deep learning models, for BG forecasting. We evaluate their performance and effectiveness in a medical context, analyzing whether foundational models can be integrated into the variety of available ICT tools and devices to predict BG levels.
Related Works
Extensive research has been conducted on predicting BG levels in individuals with T1D [16], leading to the development of numerous models over the years, driven by the widespread adoption of Continuous Glucose Monitoring (CGM) systems, which enable the collection of large volumes of CGM readings. Traditional approaches primarily rely on autoregressive (AR) models, which use past BG values to predict future levels. These models are often extended with moving average (ARMA) integrated components (ARIMA) to handle non-stationary data, and exogenous variables (ARIMAX). ARIMAX models have been used to predict BG by incorporating external factors like insulin dosage and carbohydrate intake, enhancing prediction accuracy [17]. While effective at capturing glucose dynamics, these classical models are limited by their linear assumptions. Support Vector Regression (SVR) has also been widely utilized, leveraging the capabilities of support vector machines to capture underlying trends and variability in BG data. Additionally, methods such as regression trees, random forests, logistic regression, and Extreme Gradient Boosting (XGBoost) have been applied to predict BG levels and identify patterns leading to hypoglycemia and hyperglycemia [18].
Deep learning has significantly advanced BG prediction models for T1D. Early efforts with artificial neural networks (ANNs), particularly feed-forward neural networks (FFNNs), demonstrated substantial improvements over traditional models by capturing complex non-linear relationships in BG data. Recurrent neural networks (RNNs) and Long Short-Term Memory (LSTM) networks further advanced the field by retaining memory of past predictions, enabling more accurate and context-aware forecasts [19,20,21]. Other notable models, such as Extreme Learning Machines (ELMs) and one-dimension convolutional neural networks (CNNs-1D), have been adapted to time series data, improving prediction accuracy by capturing spatial dependencies in BG data [18,22]. Additionally, some studies have integrated exogenous variables like basal insulin, boluses, meal information, and physical activity into predictive models. This integration of CGM data with other physiological and behavioral inputs has been crucial in developing comprehensive models that adapt to individual variability in T1D management. While BG prediction has been extensively studied in adults with T1D, research in pediatric populations, especially using deep learning models, remains limited [18,23].
Pediatric patients present unique challenges due to their unplanned physical activity and developmental variations that affect insulin sensitivity and glucose dynamics. Marx et al. [23] investigated the performance of deep learning methods in predicting BG levels in children with T1D participating in a supervised sports camp, collecting time series measurements of BG levels, carbohydrate intake, insulin dosing, and physical activity. The results indicated that while integrating static patient characteristics improved short-term prediction accuracy, the performance of these models significantly declined for longer-term predictions. This highlights the unique challenges in pediatric populations, where factors such as physical activity and developmental stage play a significant role. Another relevant study by D’Antoni et al. [16] optimized a CNN and a LSTM network using BG and insulin data from ten virtual pediatric patients. Their findings indicated that both models effectively predicted BG levels in pediatric patients with good analytical and clinical accuracy. The implementation of these models on edge computing devices demonstrated the feasibility of real-time BG forecasting in practical applications.
Recent developments in encoder–decoder models [24] have introduced pre-trained solutions for time-series forecasting, offering greater flexibility compared to deep learning models such as LSTM and CNN. These models have been applied in various domains (e.g., electricity, weather), but their application in the medical domain, particularly in BG forecasting for adult and pediatric patients, remains limited [25]. TimeGPT is a foundational model that achieved optimal results in the literature in forecasting across diverse domains, including finance, web traffic, IoT, weather, demand, and electricity [26,27]. ForecastPFN leverages pre-training on synthetic time series for zero-shot forecasting applications, which is especially useful in scenarios with limited data; it demonstrated a strong performance in predicting the seasonal incidence of flu cases [28]. Lag-LLaMA, building on the LLaMA architecture, incorporates lagged time series features and achieves strong results in weather forecasting [29]. However, both ForecastPFN and Lag-LLaMA do not support exogenous variables such as insulin boluses or meals, which is a significant limitation in the context of diabetes, where such information is crucial for accurate forecasting.
Additionally, other models in the literature employ encoder–decoder architectures but are not based on attention mechanisms. For instance, TiDE, designed for long-term forecasting, is design to capture complex dependencies in the time-series data while maintaining computational efficiency, outperforming traditional models in domains such as electricity and weather forecasting [14]. Recently, other MLP-based models have been developed for time-series forecasting. An example is TSMixer, which employs a mixer-style architecture tailored for time-series data. TSMixer is able to process high-dimensional and multivariate time series, achieving impressive results across various domains, including electricity and traffic, and surpassing the performance of several other models [15]. Nevertheless, despite these advances, the application of encoder–decoder architectures and new MLP-based models in BG prediction remains limited.
2. Materials and Methods
2.1. Data and Preprocessing
The dataset consists of fifteen pediatric patients, aged 4 to 19 years (nine males and six females), who had already been treated at the Diabetes Unit of Bambino Gesù Children’s Hospital in Rome, Italy, as shown in Table 1. These patients were monitored using the Dexcom G6 CGM system (San Diego, CA, USA), which provides glucose readings every five minutes [30], for an average of 52 days (±26.9 days standard deviation). Data on basal insulin, bolus insulin, and carbohydrate intake (CO) were also collected, with CO representing the quantity and glycemic load distribution of the ingested carbohydrates. Among the participants, eleven were receiving Automated Hybrid Closed-Loop (AHCL) therapy, while four were on Sensor-Augmented Pump (SAP) therapy. AHCL therapy combines a CGM system with an insulin pump that automatically adjusts basal insulin delivery based on real-time glucose levels. In contrast, SAP therapy also uses a CGM and insulin pump, but insulin delivery is manually controlled by the patient.

Table 1.
Study participants’ characteristics at enrollment. Summary statistics are presented as frequency or mean ± standard deviation.
The pediatric patients were categorized into four groups based on their age and pubertal stage, according to hospital guidelines. These groups include children aged 8–11 years at Tanner Stages 1 or 2 (prepubertal or early pubertal) and adolescents aged 12–17 years at a Tanner Stage greater than 2 (mid to late pubertal) [31,32]. This classification aids in tailoring treatment to the specific developmental and physiological needs of each group.
The preprocessing procedures were divided into four steps. First, BG values outside the [40–500 mg/dL] measurement range were adjusted, with values above 500 mg/dL capped at 500 mg/dL and values below 40 mg/dL raised to 40 mg/dL. The second step involved handling missing data. Linear interpolation was used to estimate values for gaps up to 90 min; gaps longer than 90 min were left as missing. Although more advanced techniques, such as the Kalman filter, are available for imputing BG curves, they are not feasible in real-time contexts because they require future data, which involves knowledge of future values.
In the third step, exogenous variables were longitudinally aligned with the CGM time series for each patient. Basal insulin injections were matched to the nearest CGM time point. A similar approach was applied to bolus insulin. If no bolus insulin event was temporally close to a CGM measurement, a value of zero was assigned, indicating periods when no insulin boluses were administered.
Finally, initial correlation analyses revealed that the carbohydrate fraction (CO) was highly correlated with bolus insulin, with an average correlation coefficient of 0.71. Since highly correlated variables can negatively impact model performance due to multicollinearity, we decided to retain only basal insulin and bolus insulin as exogenous variables.
2.2. Models Development
We explored the application of the encoder–decoder TimeGPT model with different settings for BG forecasting using CGM data and exogenous variables. These models were compared with state-of-the-art models, namely ARIMAX, XGBoost, and LSTM, as well as MLP-based models, including a baseline Shallow-MLP network, TiDE, and TSMixer.
The training and testing paradigm was applied to all models except the base TimeGPT model, which was already pre-trained. To build the training set for each patient, we first identified the longest time series of BG data that was free of missing values for every patient. Once these segments were identified for all patients, we then determined the shortest duration that was consistently available across all of these segments. This ensured that every model was trained on a uniform and complete set of data for each patient, allowing for fair comparisons across the models.
Regarding the test set, we followed a similar approach, taking the second-longest time series without missing values. A time window of 146 points and different time horizons of 15, 30, and 60 min were used in these experiments, as shown in Figure 1 and Figure 2. The 146-point time window was specifically chosen as the minimum required by a fine-tuned version of TimeGPT, as outlined in Section 2.2.3.
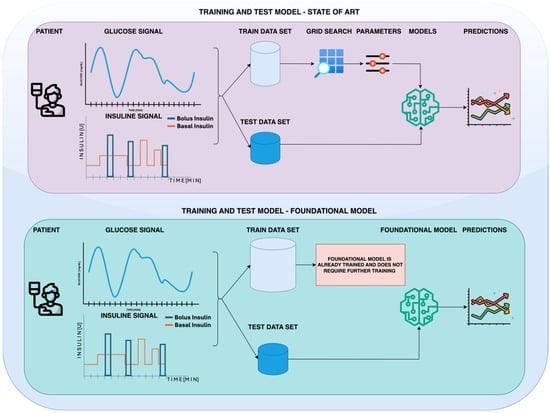
Figure 1.
Comparison of state-of-the-art and foundational model approaches for forecasting glucose levels using glucose and insulin signals. The upper panel depicts a conventional workflow, where a training dataset is used to train multiple models, which are then validated on a separate test dataset to generate predictions. In contrast, the lower panel illustrates the foundational model approach, where a pre-trained foundational model is used directly for predictions, bypassing the need for an additional training phase.
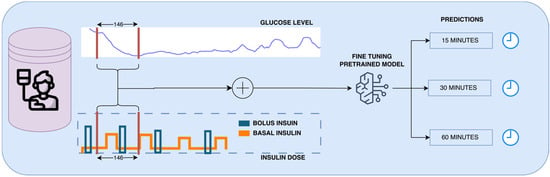
Figure 2.
Schematic of the fine-tuning process for a pre-trained model using continuous glucose monitoring and insulin data to predict future glucose levels at 15, 30, and 60 min forecasting horizons.
As regards models requiring a training phase, an extensive grid search was conducted separately on each patient’s training time series data to identify the optimal hyperparameters, as detailed in the following. For models that did not require a training phase, such as TimeGPT, we applied the hyperparameters recommended by the authors in the documentation [26].
Additionally, we explored a multi-patient training strategy for models with a large number of parameters, i.e., TiDE and TSMixer, to compare them with TimeGPT. Specifically, models were trained on a dataset containing data from patients (resulting in the TiDE-MM and TSMixer-MM models) using a leave-one-patient-out approach on the training data. The testing phase, however, followed the same method as previously described.
Finally, we employed the Friedman test and Wilcoxon signed-rank test to evaluate the statistical differences between the models. All analyses were conducted on a 2019 Apple Mac mini with 32 GB of RAM and an Intel Core i5 processor.
2.2.1. State-of-the-Art Models
The ARIMAX model captures the relationships between an observation and several lagged observations (p parameter), the number of differences required to make the time series stationary (d parameter), and the relationship between an observation and the residual errors from a moving average model applied to lagged observations (q parameter). During our grid search, we varied the p and q parameters from 1 to 10, while the d parameter was automatically determined using the optimization algorithm provided by the pmdarima Python package.
Recent approaches have increasingly focused on machine learning and deep learning techniques, such as XGBoost, LSTM, and CNNs. XGBoost is a machine learning algorithm that constructs an ensemble of decision trees sequentially, with each tree correcting the errors made by the previous ones. Key parameters of XGBoost include the maximum depth of a tree (varied in our grid search from 3 to 9), the minimum sum of instance weights needed in a child node (from 1 to 5), the regularization term (from 0 to 0.3), the number of trees in the model (from 500 to 2000), and the learning rate, which scales the contribution of each tree (from 0.01 to 0.2).
In contrast, LSTM networks are a subclass of RNNs designed to learn long-term dependencies. They feature a distinctive architecture with memory cells and three types of gates—input, forget, and output gates—that regulate the flow of information within the memory cell. This gating mechanism helps LSTMs to overcome the vanishing gradient problem, allowing them to preserve relevant information over extended periods, which is particularly advantageous for sequential data tasks. We used the hyperbolic tangent as the activation function and explored various parameter settings to optimize the LSTM model, including the number of LSTM layers (1, 2, or 3), the number of units in the LSTM layers (ranging from 30 to 100), the batch size (from 16 to 64), and the number of epochs (10, 20, or 50), adopting the Adam optimization algorithm. The number of epochs for the LSTM model were chosen based on the latest research in the literature [33,34,35], which indicates that using a high number of epochs in complex model like LSTM can degrade performance. This is because excessive epochs may lead to overfitting and stability issues in the network.
CNNs-1D are designed to process data with a grid-like structure. They take one-dimensional time-series data as the input, transform the data through a series of hidden layers, and output class scores. In our grid search, we explored several configurations to optimize the network, including varying the number of convolutional layers (1 to 3), the number of filters in the convolutional layers (32, 64, or 128), and the activation function (rectified linear unit or hyperbolic tangent). We also tested different batch sizes (16, 32, or 64), different convolutional kernel sizes (2, 3, or 5), and different numbers of epochs (10, 20, or 50), adopting the Adam optimization algorithm.
2.2.2. Multilayer Perceptron-Based Models
An MLP is a type of neural network composed of neurons arranged in multiple layers. Each neuron processes input vectors, weights, and biases, which are adjusted during training to minimize the error between actual and predicted outcomes. In this study, we implemented a baseline MLP-based model, named Shallow-MLP, with two layers and optimized it through a grid search. The hyperparameters we tuned included the number of neurons in the hidden layers (50, 100, or 150), the batch sizes (10, 20, or 30), the number of training epochs (50, 100, or 150), and the choice of optimizer (Adam or RMSprop).
Next, we considered more advanced MLP-based architectures such as TiDE and TSMixer. TiDE utilizes an encoder–decoder architecture with dense MLP layers for both encoding and decoding processes. The encoder transforms past time series data and covariates into a dense representation, while the decoder uses this representation to generate future predictions. Key components of TiDE include feature projection, where dynamic covariates are mapped into a lower-dimensional space using residual blocks, and a temporal decoder that combines encoded vectors with future covariates to produce the final predictions. We optimized TiDE through a grid search across various hyperparameters, including the number of encoder layers (1, 2, or 3) and decoder layers (1, 2, or 3), the decoder output dimension (10, 20, or 30), and the hidden size (50, 100, or 150). Additionally, we explored the temporal width of past data used by the model (0, 5, or 10), the number of epochs (10, 20, or 50), and various dropout rates (0.1, 0.2, or 0.5).
On the other hand, TSMixer employs a distinct approach by alternating between time-mixing and feature-mixing MLP layers to capture both temporal dependencies and cross-variate interactions in the time series data. Time-mixing MLPs process each feature independently across all time steps to capture temporal patterns, while feature-mixing MLPs manage interactions between different variables at each time step. Additionally, TSMixer includes a temporal projection layer that maps the processed time-series data from the input sequence length to the forecast sequence length. This design allows the TSMixer to model both temporal and cross-variate interactions effectively without relying on a traditional encoder–decoder framework. To optimize TSMixer, we performed a grid search across key parameters, including the hidden layer size (50, 100, or 150), the size of the first feed-forward layer (100, 200, or 300), and the number of mixer blocks (1, 2, or 3). We also explored different activation functions (rectified linear unit, hyperbolic tangent, or sigmoid), various dropout rates (0.1, 0.2, or 0.5), different batch sizes (32 or 64), and different numbers of training epochs (50 or 100).
2.2.3. Foundational Models
TimeGPT is a time series forecasting model built on the transformer architecture, originally designed for natural language processing (NLP). Central to TimeGPT is the self-attention mechanism, which dynamically assesses the importance of different time points within an input sequence. This mechanism is crucial for capturing long-term dependencies and relationships in time series data, thereby enhancing forecast accuracy. By computing a weighted sum of input features, self-attention enables the model to focus on the most relevant parts of the time series, making it particularly effective for identifying complex patterns.
The architecture of TimeGPT follows the typical transformer design, comprising an encoder–decoder structure. The encoder processes historical time series data, converting it into encoded representations that capture underlying patterns and essential information, such as trends, seasonality, and other temporal dynamics, from the input sequence. The decoder then uses these encoded representations, along with positional information about future time points, to generate forecasts. The final forecasted values are produced by passing the decoder’s output through a linear layer.
TimeGPT also incorporates positional encoding within the encoder to maintain the sequential order of data points. This encoding is added to the input embeddings, helping the model to distinguish between different positions in the sequence and better understand temporal relationships.
Key parameters in TimeGPT include the time horizon (h), which specifies how far into the future the model predicts (e.g., 15, 30, or 60 min in our experiments), and the sampling frequency (freq), which determines the intervals at which the time series data are sampled (in our case, the data are sampled every 5 min, corresponding to the CGM sampling frequency). A detailed explanation is provided in the Supplementary Materials.
A notable advantage of TimeGPT is its pre-trained nature, which allows for immediate deployment without additional training, thereby saving both time and computational resources. However, for scenarios that require customization—such as when adapting the model for individual patients in healthcare applications—fine-tuning is available. We used this fine-tuning option to develop the TimeGPT fine-tuned (TimeGPT-FT) model. Nevertheless, the model could not be tuned using one validation time series and then evaluated on a different test series due to constraints related to its export capabilities. Therefore, to build the TimeGPT-FT model, we used a window of 146 data points—identified as the minimum required for this parameter by the model—preceding each BG test point to be predicted, as illustrated in Figure 2.
Additionally, there was the option to utilize a long-horizon variant of TimeGPT (TimeGPT-LH), specifically designed for predicting time series over extended durations (a minimum of 72 timestamps). To ensure a fair comparison between the different models, we also employed a window of 146 data points in TimeGPT-LH.
2.3. Evaluation Metrics
For the assessment of the proposed BG forecasting models, we employed a combination of standard indicators commonly used in the literature, evaluating prediction accuracy in both analytical and clinical terms.
For the analytical evaluation, we utilized the Root Mean Square Error (RMSE) and the Mean Absolute Error (MAE). These metrics provide a quantitative measure of prediction error at the same scale as the BG values (mg/dL), with lower values indicating better performance. The formulas for RMSE and MAE are presented in Equations (1) and (2), respectively, where n denotes the length of the BG time series, yi represents the actual BG value for the i-th observation, and ŷi is the predicted BG value for the same observation. RMSE quantifies the average deviation of the model’s predictions from the actual values, with larger errors having a greater impact due to the squaring of differences before averaging. In contrast, MAE reflects the average absolute difference between the actual and predicted values, treating all errors equally regardless of their size. While MAE offers a straightforward representation of average error and is less sensitive to outliers, it does not emphasize large errors as RMSE does.
However, since RMSE and MAE do not provide any insight into the clinical implications of prediction errors, we also applied the Clarke Error Grid Analysis (EGA) [36]. EGA is a non-parametric graphical method that interprets the relationship between BG measurements and their corresponding predictions based on the severity of the potential harm caused by prediction errors. The grid is divided into five zones: Zone A represents the area where the difference between actual and predicted BG values is less than 20%, leading to accurate clinical decisions based on the prediction. Zone B indicates incorrect but non-critical clinical decisions. In Zone C, prediction errors could result in inappropriate treatment, though without dangerous consequences. Zone D errors fail to trigger necessary corrections in cases of hypoglycemia or hyperglycemia, and Zone E errors are the most dangerous, as they could lead to the treatment of hypoglycemia instead of hyperglycemia, or vice versa.
3. Results
3.1. Glucose Data Analysis
Considering the entire monitoring period, after applying linear interpolation for gaps up to 90 min, the BG time series exhibited an average of 2.07% (±1.95%) missing data across all patients. Regarding glycemic control, patients spent an average of 70.98% (±14.69%) of their time within the 70–180 mg/dL range (TIR), consistent with the last International Society for Pediatric and Adolescent Diabetes (ISPAD) Consensus Guidelines [37]. The average Time Above Range (TAR), which includes both TAR Level-1 (the percentage of BG readings in the range of 181–250 mg/dL) and TAR Level-2 (the percentage of BG readings above 250 mg/dL), was 24.87%. The average Time Below Range (TBR), which combines both TBR Level-1 (the percentage of BG readings in the range of 54–69 mg/dL) and TBR Level-2 (the percentage of BG readings below 54 mg/dL), was 4.15%.
In the training data, each patient’s time series included 5 days, 21 h, and 50 min of continuous measurements, with the test time series lasting 14 h and 40 min, both without gaps. The stacked bars in Figure 3 show that the average distribution of time spent below, above, and within this range is comparable between the training and test sets, as well as with the original dataset, with no statistically significant differences. In the training set, the average TIR was 71.18%, with TAR and TBR average values of 26.23% and 2.59%, respectively. In the test set, the average TIR was 70.6%, with TAR and TBR average values of 27.23% and 2.17%, respectively.
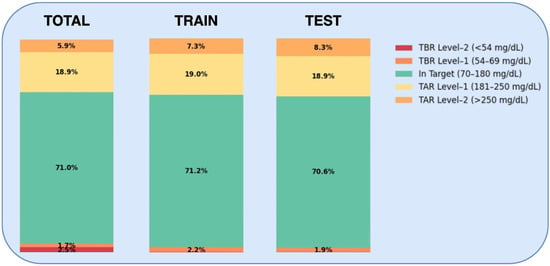
Figure 3.
Distribution of average time spent in different glycemic bands considering the entire dataset (left), the training set (middle), and the test set (right). Each stacked bar shows the percentage of time spent within various glucose ranges: Time Severely Above Range (TAR Level-2), Time Slightly Above Range (TAR Level-1), Time In Range (TIR), Time Slightly Below Range (TBR Level-1), and Time Severely Below Range (TBR Level-2). For ease of interpretation, the same colors as those used in the Advanced Technologies & Treatments for Diabetes (ATTD) consensus report [38] are applied in the figure.
While the average CGM-related metrics aligned with the ISPAD targets for safe glycemic control, four patients (26.67%) in the training set and five patient (33.33%) in the test set had considerably lower average TIR (<70%) and higher TAR (>25%) values than recommended. Of these, three patients were consistent across both the training and test sets. These patients showed also a high glycemic variability, with an average Standard Deviation (SD) greater than 70 mg/dL and an average coefficient of variation (CV) greater than the ≤36% ISPAD recommended target.
3.2. Models Performances
3.2.1. Statistical Evaluation
From the RMSE and MAE boxplots displayed in Figure 4 and Figure 5, it can be observed that the TimeGPT model is comparable to, or outperforms, all state-of-the-art and MLP-based models trained individually on patients for both the 15 min and 30 min forecasting horizons.
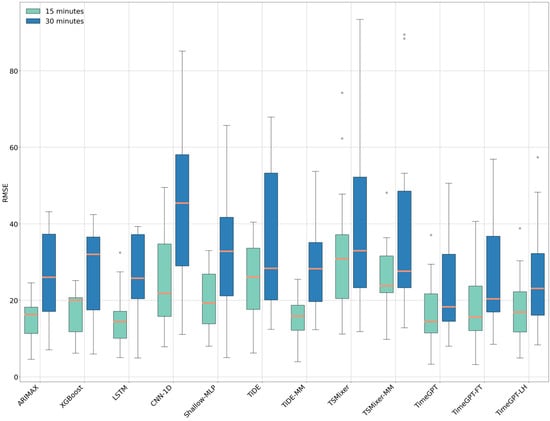
Figure 4.
Boxplot of Root Mean Square Error (RMSE) values across different models for 15 min (in green) and 30 min (in blue) forecasting horizons. The horizontal orange line within each box represents the median RMSE.
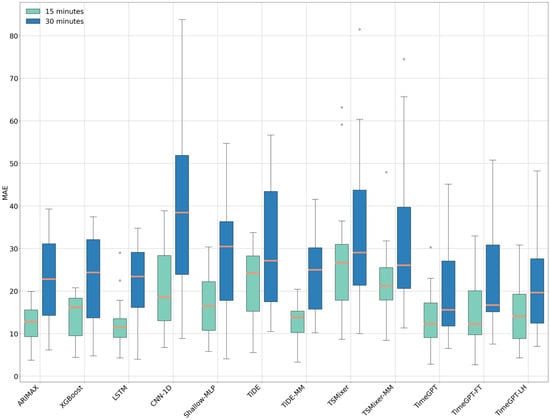
Figure 5.
Boxplot of Mean Absolute Error (MAE) values across different models for 15 min (in green) and 30 min (in blue) forecasting horizons. The horizontal orange line within each box represents the median MAE.
Specifically, for the 15 min forecasting horizon, the median RMSE of the TimeGPT model (14.40 mg/dL ± IQR 10.18 mg/dL) is comparable to that of the LSTM model (14.41 mg/dL ± IQR 7.07 mg/dL) and the TiDE-MM model (15.86 mg/dL ± IQR 6.55 mg/dL). However, a Wilcoxon signed-rank test and Tukey HSD test revealed a statistically significant difference in the case of TiDE-MM. Regarding MAE, the LSTM model shows a slightly better median performance than the TimeGPT model (11.53 mg/dL vs. 12.29 mg/dL, respectively), while TiDE-MM has a higher median MAE (13.77 mg/dL). However, these differences were not statistically significant. TimeGPT also demonstrates marginally better performance compared to the TimeGPT-FT and TimeGPT-LH models, though these differences are not significant.
For the 30 min forecasting horizon, TimeGPT achieves the best median RMSE (18.26 mg/dL ± IQR 17.57 mg/dL) and median MAE (15.59 mg/dL ± IQR 15.29 mg/dL), with statistically significant differences compared to TimeGPT-FT and TiDE-MM.
Additionally, it can be observed that MLP-based models, such as TiDE and TSMixer, trained on individual patients, have a reduced performance compared to when they are trained on multiple patients. Nevertheless, statistical analysis confirms that TimeGPT’s RMSE values show significant differences when compared to TiDE and TSMixer models, regardless of whether they were trained on individual or multiple patients across both forecasting horizons.
The poorest-performing model in terms of RMSE and MAE for the 15 min forecasting horizon was TSMixer, with an RMSE of 30.89 mg/dL (±IQR 16.73 mg/dL) and an MAE of 26.67 mg/dL (±IQR 13.14 mg/dL). For the 30 min forecasting horizon, the CNN-1D model showed the lowest performance among all models, with an RMSE of 45.41 mg/dL (±IQR 29.11 mg/dL) and an MAE of 38.43 mg/dL (±IQR 27.96 mg/dL).
The Supplementary Materials provide further analysis for the 60 min forecasting horizon, where TimeGPT also achieved lower RMSE and MAE values than the other models used for this task.
To highlight the robustness of the models with respect to the therapy administered to pediatric patients, we compared the performance of the models between those treated with AHCL therapy and those treated with SAP therapy. A Mann–Whitney U test was conducted to assess the statistical significance of the differences in model performance between the two groups. The results indicated that no significant differences were observed for any of the models, suggesting that the predictive models, particularly TimeGPT, are robust across both therapy types.
3.2.2. Clinical Evaluation
Table 2 and Table 3 summarize the performance of the models based on the EGA for 15 min and 30 min forecasting, respectively.

Table 2.
Clarke Error Grid average values of different models for the 15 min forecasting horizon.

Table 3.
Clarke Error Grid average values of different models for the 30 min forecasting horizon.
For the 15 min forecasting horizon, as detailed in Table 2, the ARIMAX model achieved the highest percentage of predictions in Zone A (91.33%), followed by TiDE-MM (87.11%) and LSTM (86.44%). TimeGPT also had a good performance, with 85.56% of predictions in Zone A, comparable to the results of TimeGPT-FT and TimeGPT-LH models (84.89% and 81.11% in Zone A, respectively). The TSMixer model shows the lowest EGA quality, with fewer than 60% of predictions in Zone A and 40.88% in Zone B.
For the 30 min forecasting horizon, as shown in Table 3, TimeGPT had the highest percentage of predictions in Zone A (74%), followed by TimeGPT-LH (69.56%) and TimeGPT-FT (68.22%). However, overall EGA quality decreases compared to the 15 min forecasting horizon, with some predictions falling into Zone C and particularly in Zone E, which was empty in the 15 min horizon. ARIMAX, LSTM, and XGBoost exhibited a similar performance, with approximately 61% of predictions in Zone A. CNN-1D and TSMixer-MM models showed the lowest performance, with around 45% of predictions in Zone A and a significant dispersion of points in Zones B and D.
For the 60 min forecasting horizon, as presented in Supplementary Table S1, TimeGPT had the highest performance in Zone A (64%), consistent with the fine-tuned version of TimeGPT, while the long-horizon version of TimeGPT followed closely, with 60.89% of predictions in Zone A. Other models showed a notable decline in the percentage of predictions falling in Zone A. The CNN-1D and TiDE models performed particularly poorly, with 44.67% and 37.78% of points in Zone A, respectively, and significant percentages of predictions falling into Zones C and D.
4. Discussion
In this exploratory study, we compared foundational generative models, particularly TimeGPT, with current state-of-the-art models for predicting BG levels. It is important to note that although TimeGPT was not specifically trained on our dataset, it was pre-trained on various datasets from diverse fields, including economics, energy, and medicine. However, the specific type of medical data used during its pre-training were not disclosed by the authors.
Our initial analysis revealed that the average CGM-related metrics generally aligned with ISPAD targets for safe glycemic control. However, five out of fifteen patients (33.33%) exhibited a significantly lower average TIR (<70%) and higher TAR (>25%) in the test time series. Additionally, while the overall average SD in the test set was 46.07 mg/dL (±19.71 mg/dL), these five patients had a higher average SD of 70.01 mg/dL (±19.20 mg/dL) compared to the others, with a peak SD of 83.54 mg/dL and a coefficient of variation (CV) of 39.95% in one patient. This high glycemic variability impacted the models’ performance.
Our findings suggest that TimeGPT, with its context-based architecture, can effectively predict glycemic behavior across a variety of patients, even without specific training on their data. Remarkably, it achieved comparable or lower RMSE values at both the 15 and 30 min forecasting horizons when compared to state-of-the-art models and MLP-based approaches. The absence of statistically significant performance differences between TimeGPT and models such as ARIMAX, XGBoost, and LSTM—despite these models being trained on individual patient data—highlights TimeGPT’s ability to generalize across diverse pediatric T1D patient profiles. Additionally, its consistent performance across different therapies, such as AHCL and SAP, further emphasizes its robustness and flexibility.
We also assessed the models’ clinical performances using EGA. TimeGPT demonstrated high performances, with 98% of its predictions falling into clinically safe Zones A and B, and only 1.78% falling into Zone D. Similar outcomes were observed with other TimeGPT-based models, as well as ARIMAX, XGBoost, and LSTM models, although the XGBoost model had a lower percentage of predictions in Zone A within the 15 min forecasting horizon compared to the others.
In contrast, models like TiDE and TSMixer, which rely on MLP architectures with hundreds of thousands of parameters, underperformed when trained on individual patient data, likely due to overfitting. Notably, the results from the TiDE-MM models showed that training on a larger dataset (using a leave-one-patient-out strategy) significantly improved their ability to predict BG levels, as these models require more data than ARIMAX, LSTM, and XGBoost to reach optimal performances.
For the 60 min forecasting horizon, as detailed in the Supplementary Materials, most models experienced a general decline in accuracy, highlighting the challenges of medium-term predictions in T1D. Nevertheless, TimeGPT still achieved results that were comparable to or better than those of other models.
Among the different variants of TimeGPT—pre-trained (TimeGPT), pre-trained and fine-tuned (TimeGPT-FT), and pre-trained for long horizons (TimeGPT-LH)—the pre-trained model slightly outperformed the other two. However, this may be attributed to the study’s design limitations. Specifically, we were unable to tune the TimeGPT model using a specific validation time series and then test it on a different time series, as the model cannot currently be exported. Consequently, we decided to fine-tune the model using the 146 points preceding each test point, which is the minimum allowed value for this parameter, though this may not have been optimal for this context. For the long-horizon version, which is designed to predict time series progression over extended periods (at least 72 timestamps), we used the same 146-points time window to ensure a fair comparison. Despite this, TimeGPT still outperformed TimeGPT-LH.
A key limitation of the study is the small sample size, which may affect the generalizability of the results. The research included only 15 pediatric patients with Type 1 Diabetes treated at the Diabetes Unit of Bambino Gesù Children’s Hospital, Rome, Italy. This limited sample is due to challenges in accessing T1D pediatric patient data, particularly given the ethical constraints and the complexities involved in obtaining consent for clinical data collection. To partially address this limitation, we also applied the TimeGPT model—using the same configuration—on the OhioT1DM 2018 dataset [39], which contains data from six adult T1D patients with CGM and insulin records. We compared its performance with ARIMAX and LSTM, the models that performed best on our pediatric dataset. On the OhioT1DM data, TimeGPT achieved a median RMSE of 10.79 mg/dL and a median MAE of 9.36 mg/dL for 15 min forecasts. For longer intervals, TimeGPT reported a median RMSE of 19.26 mg/dL and a median MAE of 15.84 mg/dL, as indicated in the Supplementary Materials. Furthermore, the Wilcoxon test showed no significant differences between TimeGPT and the patient-specific models (LSTM and ARIMAX).
We acknowledge that this study is exploratory; however, it offers valuable insights into the potential of foundational models for predicting glycemic levels in pediatric T1D populations.
In addition, the computational cost analysis shows that ARIMAX is the most efficient model, with a computation time of just 12 s, making it significantly faster than more complex architectures, such as LSTM (1.242 s), CNN-1D (2.840 s), and others. Despite its simplicity, ARIMAX demonstrated its effectiveness, with a relatively low RMSE compared to more complex models like CNN-1D and XGBoost. However, transitioning to multi-patient training leads to a substantial increase in computational time, with an average augmentation of 1746%. This rise in training time is accompanied by a notable improvement in model performance, with an approximate 30% reduction in RMSE for 15 min forecasting and a 12% reduction in RMSE for 30 min forecasting. These findings illustrate that while larger datasets can significantly enhance model accuracy, they also result in a considerable increase in computational demands, which can be challenging in a real-world scenario.
5. Conclusions
This study explored the effectiveness of foundational models, with a particular focus on TimeGPT, in predicting glycemic levels among pediatric patients with T1D. We compared TimeGPT to state-of-the-art and MLP models. TimeGPT consistently matched or outperformed other models in short-term predictions (15 and 30 min) in both analytical and clinical assessments. Notably, it demonstrated strong generalization abilities without requiring patient-specific training.
Overall, foundational models demonstrate potential for medical predictive analytics and could play a crucial role in future medical devices, such as artificial pancreas systems. However, the application of these models in medical tasks—such as using TimeGPT for glucose forecasting or employing chatbots like ChatGPT to address clinical questions—requires thorough investigation [40,41]. Identifying and addressing limitations, especially regarding the transparency and quality of training data, is crucial for improving their effectiveness in patient care [42,43,44].
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/diabetology5060042/s1, Figure S1: Boxplot of Root Mean Square Error (RMSE) values across different models for 60 min forecasting horizons; Figure S2: Boxplot of Mean Absolute Error (MAE) values across different models for 60 min forecasting horizons; Figure S3: Boxplot of Root Mean Square Error (RMSE) values for different models at 15 min and 30 min forecasting horizons on the OhioT1DM 2018 dataset; Figure S4: Boxplot of Mean Absolute Error (MAE) values for different models at 15 min and 30 min forecasting horizons on the OhioT1DM 2018 dataset; Table S1: Clarke Error Grid average values of different models for the 60 min forecasting horizon.
Author Contributions
Conceptualization, S.R., P.B. and R.B.; methodology, S.R., P.B., R.B. and L.S.; software, S.R. and P.B.; validation, L.S., C.T. and R.S.; data curation, A.D., R.S., P.A.M. and C.T.; writing—original draft preparation, S.R. and P.B.; writing—review and editing, R.B. and C.T.; supervision, R.B. and C.T.; funding acquisition, R.B. and C.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the National Recovery and Resilience Plan (NRRP), Mission 4, Component 2, Investment 1.1, Call for tender No. 104 published on 2 February 2022 by the Italian Ministry of University and Research (MUR), funded by the European Union—NextGenerationEU—Project Title “Adaptive Personalised Safe Artificial Pancreas for children and adolescents (APS-AP)”—CUP F53D23000720006—Grant Assignment Decree No. 960 adopted on 30 June 2023 by the Italian Ministry of University and Research (MUR). The research was also funded by the Project “Hub Life Science—Digital Health (LSH-DH) PNC-E3-2022-23683267—Progetto DHEAL-COM—CUP”, funded by the Piano Complementare Ecosistema Innovativo della Salute-CUI: PNC-E.3. This publication reflects only the authors’ views, and the Italian Ministry of Health is not responsible for any use that may be made of the information it contains.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of Bambino Gesù Children’s Hospital, Rome, Italy.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to legal reasons.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zubiaga, A. Natural Language Processing in the Era of Large Language Models. Front. Artif. Intell. 2024, 6, 1350306. [Google Scholar] [CrossRef] [PubMed]
- Kalyan, K.S. A Survey of GPT-3 Family Large Language Models Including ChatGPT and GPT-4. Nat. Lang. Process. J. 2023, 6, 100048. [Google Scholar] [CrossRef]
- Touvron, H.; Lavril, T.; Izacard, G.; Martinet, X.; Lachaux, M.-A.; Lacroix, T.; Rozière, B.; Goyal, N.; Hambro, E.; Azhar, F.; et al. LLaMA: Open and Efficient Foundation Language Models. arXiv 2023, arXiv:2302.13971. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models Are Few-Shot Learners. arXiv 2020, arXiv:2005.14165. [Google Scholar]
- Woo, G.; Liu, C.; Kumar, A.; Xiong, C.; Savarese, S.; Sahoo, D. Unified Training of Universal Time Series Forecasting Transformers. arXiv 2024, arXiv:2402.02592. [Google Scholar]
- Clusmann, J.; Kolbinger, F.R.; Muti, H.S.; Carrero, Z.I.; Eckardt, J.-N.; Laleh, N.G.; Löffler, C.M.L.; Schwarzkopf, S.-C.; Unger, M.; Veldhuizen, G.P.; et al. The Future Landscape of Large Language Models in Medicine. Commun. Med. 2023, 3, 141. [Google Scholar] [CrossRef]
- Shickel, B.; Tighe, P.J.; Bihorac, A.; Rashidi, P. Deep EHR: A Survey of Recent Advances in Deep Learning Techniques for Electronic Health Record (EHR) Analysis. IEEE J. Biomed. Health Inform. 2018, 22, 1589–1604. [Google Scholar] [CrossRef]
- Rajkomar, A.; Oren, E.; Chen, K.; Dai, A.M.; Hajaj, N.; Hardt, M.; Liu, P.J.; Liu, X.; Marcus, J.; Sun, M.; et al. Scalable and Accurate Deep Learning with Electronic Health Records. npj Digit. Med. 2018, 1, 18. [Google Scholar] [CrossRef]
- van Doorn, W.P.T.M.; Foreman, Y.D.; Schaper, N.C.; Savelberg, H.H.C.M.; Koster, A.; van der Kallen, C.J.H.; Wesselius, A.; Schram, M.T.; Henry, R.M.A.; Dagnelie, P.C.; et al. Machine Learning-Based Glucose Prediction with Use of Continuous Glucose and Physical Activity Monitoring Data: The Maastricht Study. PLoS ONE 2021, 16, e0253125. [Google Scholar] [CrossRef]
- IDF Diabetes Atlas. Available online: https://diabetesatlas.org/atlas/t1d-index-2022/ (accessed on 1 August 2024).
- Ogle, G.D.; Wang, F.; Gregory, G.A.; Maniam, J. Type 1 Diabetes Numbers in Children and Adults Authors. Available online: https://diabetesatlas.org/idfawp/resource-files/2022/12/IDF-T1D-Index-Report.pdf (accessed on 3 September 2024).
- Liao, W.; Porte-Agel, F.; Fang, J.; Rehtanz, C.; Wang, S.; Yang, D.; Yang, Z. TimeGPT in Load Forecasting: A Large Time Series Model Perspective. arXiv 2024, arXiv:2404.04885. [Google Scholar]
- Das, A.; Kong, W.; Leach, A.; Mathur, S.; Sen, R.; Yu, R. Long-Term Forecasting with TiDE: Time-Series Dense Encoder. arXiv 2024, arXiv:2304.08424. [Google Scholar]
- Chen, S.-A.; Li, C.-L.; Yoder, N.; Arik, S.O.; Pfister, T. TSMixer: An All-MLP Architecture for Time Series Forecasting. arXiv 2023, arXiv:2303.06053. [Google Scholar]
- D’Antoni, F.; Petrosino, L.; Sgarro, F.; Pagano, A.; Vollero, L.; Piemonte, V.; Merone, M. Prediction of Glucose Concentration in Children with Type 1 Diabetes Using Neural Networks: An Edge Computing Application. Bioengineering 2022, 9, 183. [Google Scholar] [CrossRef]
- Assessment of Seasonal Stochastic Local Models for Glucose Prediction without Meal Size Information under Free-Living Conditions. Available online: https://pubmed.ncbi.nlm.nih.gov/36433278/ (accessed on 3 September 2024).
- De Bois, M.; Yacoubi, M.A.E.; Ammi, M. GLYFE: Review and Benchmark of Personalized Glucose Predictive Models in Type 1 Diabetes. Med. Biol. Eng. Comput. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Iacono, F.; Magni, L.; Toffanin, C. Personalized LSTM-Based Alarm Systems for Hypoglycemia and Hyperglycemia Prevention. Biomed. Signal Process. Control 2023, 86, 105167. [Google Scholar] [CrossRef]
- Stacked LSTM Based Deep Recurrent Neural Network with Kalman Smoothing for Blood Glucose Prediction. BMC Medical Informatics and Decision Making. Available online: https://bmcmedinformdecismak.biomedcentral.com/articles/10.1186/s12911-021-01462-5 (accessed on 3 September 2024).
- Aiello, E.M.; Lisanti, G.; Magni, L.; Musci, M.; Toffanin, C. Therapy-Driven Deep Glucose Forecasting. Eng. Appl. Artif. Intell. 2020, 87, 103255. [Google Scholar] [CrossRef]
- Nguyen, B.P.; Pham, H.N.; Tran, H.; Nghiem, N.; Nguyen, Q.H.; Do, T.T.T.; Tran, C.T.; Simpson, C.R. Predicting the Onset of Type 2 Diabetes Using Wide and Deep Learning with Electronic Health Records. Comput. Methods Programs Biomed. 2019, 182, 105055. [Google Scholar] [CrossRef]
- Marx, A.; Di Stefano, F.; Leutheuser, H.; Chin-Cheong, K.; Pfister, M.; Burckhardt, M.-A.; Bachmann, S.; Vogt, J.E. Blood Glucose Forecasting from Temporal and Static Information in Children with T1D. Front. Pediatr. 2023, 11, 1296904. [Google Scholar] [CrossRef]
- Seq Miller, J.A.; Aldosari, M.; Saeed, F.; Barna, N.H.; Rana, S.; Arpinar, I.B.; Liu, N. A Survey of Deep Learning and Foundation Models for Time Series Forecasting. arXiv 2024, arXiv:2401.13912. [Google Scholar]
- Tan, M.; Merrill, M.A.; Gupta, V.; Althoff, T.; Hartvigsen, T. Are Language Models Actually Useful for Time Series Forecasting? arXiv 2024, arXiv:2406.16964. [Google Scholar]
- Tang, H.; Zhang, C.; Jin, M.; Yu, Q.; Wang, Z.; Jin, X.; Zhang, Y.; Du, M. Time Series Forecasting with LLMs: Understanding and Enhancing Model Capabilities. arXiv 2024, arXiv:2402.10835. [Google Scholar]
- Deforce, B.; Baesens, B.; Asensio, E.S. Time-Series Foundation Models for Forecasting Soil Moisture Levels in Smart Agriculture. arXiv 2024, arXiv:2405.18913. [Google Scholar]
- Dooley, S.; Khurana, G.S.; Mohapatra, C.; Naidu, S.; White, C. ForecastPFN: Synthetically-Trained Zero-Shot Forecasting. arXiv 2023, arXiv:2311.01933. [Google Scholar]
- Rasul, K.; Ashok, A.; Williams, A.R.; Ghonia, H.; Bhagwatkar, R.; Khorasani, A.; Bayazi, M.J.D.; Adamopoulos, G.; Riachi, R.; Hassen, N.; et al. Lag-Llama: Towards Foundation Models for Probabilistic Time Series Forecasting. arXiv 2024, arXiv:2310.08278. [Google Scholar]
- Dexcom G6 CGM System. Available online: https://www.dexcom.com/en-us/g6-cgm-system (accessed on 1 August 2024).
- Marshall, W.A.; Tanner, J.M. Variations in the Pattern of Pubertal Changes in Boys. Arch. Dis. Child. 1970, 45, 13–23. [Google Scholar] [CrossRef]
- Marshall, W.A.; Tanner, J.M. Variations in Pattern of Pubertal Changes in Girls. Arch. Dis. Child. 1969, 44, 291–303. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Namin, A.S. Forecasting Economics and Financial Time Series: ARIMA vs. LSTM. Available online: https://arxiv.org/abs/1803.06386 (accessed on 3 September 2024).
- Komatsuzaki, A. One Epoch Is All You Need. arXiv 2019, arXiv:1906.06669. [Google Scholar]
- Koparanov, K.A.; Georgiev, K.K.; Shterev, V.A. Lookback Period, Epochs and Hidden States Effect on Time Series Prediction Using a LSTM Based Neural Network. In Proceedings of the 2020 28th National Conference with International Participation (TELECOM), Sofia, Bulgaria, 29–30 October 2020; pp. 61–64. [Google Scholar]
- Clarke, W.L. The Original Clarke Error Grid Analysis (EGA). Diabetes Technol. Ther. 2005, 7, 776–779. [Google Scholar] [CrossRef]
- de Bock, M.; Codner, E.; Craig, M.E.; Huynh, T.; Maahs, D.M.; Mahmud, F.H.; Marcovecchio, L.; DiMeglio, L.A. ISPAD Clinical Practice Consensus Guidelines 2022: Glycemic Targets and Glucose Monitoring for Children, Adolescents, and Young People with Diabetes. Pediatr. Diabetes 2022, 23, 1270–1276. [Google Scholar] [CrossRef]
- Battelino, T.; Danne, T.; Bergenstal, R.M.; Amiel, S.A.; Beck, R.; Biester, T.; Bosi, E.; Buckingham, B.A.; Cefalu, W.T.; Close, K.L.; et al. Clinical Targets for Continuous Glucose Monitoring Data Interpretation: Recommendations From the International Consensus on Time in Range. Diabetes Care 2019, 42, 1593–1603. [Google Scholar] [CrossRef] [PubMed]
- Marling, C.; Bunescu, R. The OhioT1DM Dataset for Blood Glucose Level Prediction: Update 2020. CEUR Workshop Proc. 2020, 2675, 71–74. [Google Scholar] [PubMed]
- Huang, J.; Yeung, A.M.; Kerr, D.; Klonoff, D.C. Using ChatGPT to Predict the Future of Diabetes Technology. J. Diabetes Sci. Technol. 2023, 17, 853–854. [Google Scholar] [CrossRef] [PubMed]
- Sng, G.G.R.; Tung, J.Y.M.; Lim, D.Y.Z.; Bee, Y.M. Potential and Pitfalls of ChatGPT and Natural-Language Artificial Intelligence Models for Diabetes Education. Diabetes Care 2023, 46, e103–e105. [Google Scholar] [CrossRef]
- Contreras, I.; Vehi, J. Artificial Intelligence for Diabetes Management and Decision Support: Literature Review. J. Med. Internet Res. 2018, 20, e10775. [Google Scholar] [CrossRef]
- Guan, Z.; Li, H.; Liu, R.; Cai, C.; Liu, Y.; Li, J.; Wang, X.; Huang, S.; Wu, L.; Liu, D.; et al. Artificial Intelligence in Diabetes Management: Advancements, Opportunities, and Challenges. Cell Rep. Med. 2023, 4, 101213. [Google Scholar] [CrossRef]
- Lombrozo, T. Learning by Thinking in Natural and Artificial Minds. Trends Cogn. Sci. 2024; online ahead of print. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).