Implementing Artificial Intelligence in Chaos-Based Image Encryption Algorithms ^†

Abstract

This paper presents a modification of an image encryption algorithm combining chaos and the Fibonacci matrix by integrating artificial intelligence via a Generative Pre-Trained Transformer (GPT). The goal is to improve the robustness of the algorithm by dynamically adapting the parameters of the chaotic system and generating cryptographic keys based on image characteristics. The proposed methodology includes two main innovations: the implementation of GPT for automated generation of the initial parameters of the chaotic system, which allows for greater variability and security in encryption, and the use of GPT for dynamic determination of the Fibonacci Q-matrix, which provides additional complexity and increased resistance to attacks. The method is realized in the MATLAB (R2023a) environment through integration with OpenAI API and the MATLAB–Python interface for requesting GPT models. The efficiency and reliability of the modified algorithm are compared with those of standard chaotic encryption algorithms, and its robustness to various cryptographic attacks is also studied.

1. Introduction

The implementation of artificial intelligence in mobile smart devices has gained immense popularity in recent years. Features like photo tools, voice assistants, predictive text, as well as music and facial recognition have been staples for years. The standard user of such a device uses the AI implemented in their device mostly through applications for capturing and processing images. According to statistical studies by Canalys, approximately 1.94 trillion photos were taken in 2024, or 5.3 billion photos daily, with 94% of them being taken with a smartphone, and 14 billion images are shared daily on social media. This spectacular volume of generated digital information invariably raises the issue of ensuring its protection.

Sharing personal digital information has become an everyday occurrence for a large part of the population. However, to what extent can the integrity of the created digital content be guaranteed? Widespread platforms for sharing digital content are working increasingly hard to maintain certain levels of protection from unauthorized access. And if on these platforms digital information is shared intentionally and with the aim of reaching a wide audience, this is not the case with the transmission of sensitive information relating to medical conditions, corporate data, the location of objects of strategic importance, etc. This is precisely what has caused the increased scientific interest in the field of protected data transmission in recent years.

Artificial intelligence is rapidly entering every aspect of new technologies. Its application is wide and diverse and covers areas such as automotive manufacturing [1,2,3], industrial and power electronics [4,5,6], medicine [7,8,9,10,11,12], chemistry [13,14], communications [15,16,17,18,19,20,21], etc. One of the most current trends in the field of communications is precisely the secure transmission of data, which determines the study of various possibilities for implementing AI in image encryption algorithms.

There are many different algorithms for image encryption. They can be mainly divided into symmetric [22], asymmetric [23], chaotic [24], fractal [25], and hybrid algorithms [26]. Some of the more common image encryption algorithms are based on classical approaches, such as OTP algorithms [27,28], while others rely on eccentric approaches, such as implementing chaotic synchronization schemes [29,30,31]. Recently, innovative approaches in image encryption, such as implementing AI, have gained particular popularity.

Currently, MATLAB does not have built-in tools for working with large language models, so implementing GPT (Generative Pre-Trained Transformer) in MATLAB is not completely straightforward. However, there are several approaches to implementing GPT in MATLAB: Using OpenAI: One of the easiest ways to use GPT in MATLAB is through OpenAI API. MATLAB supports sending HTTP requests via webwrite and webread, which allows calling GPT models via OpenAI API. MATLAB–Python interface: MATLAB allows the execution of Python code, so the OpenAI library from Python (3.13) can be used. This method gives more flexibility when working with more complex queries. Local execution of a GPT model in MATLAB: This approach involves the simultaneous use of the MATLAB Deep Learning Toolbox, a pre-trained model from Hugging Face Transformers (via Python), and the MATLAB–Python interface to access a local model.

This paper proposes a modification of an image encryption algorithm based on chaos and the Fibonacci Q-matrix [32]. The modification introduces AI functionality in the form of a GPT implementation into several modules of the encryption algorithm.

The main contributions of the paper can be summarized as follows:

• A general architecture is proposed for implementing AI functionalities in image encryption algorithms based on chaotic systems;
• A modified version of an existing algorithm, which combines a chaotic system and a Fibonacci matrix with AI capabilities, is presented. The modification leads to improved performance compared to the classical algorithm;
• A security analysis of the modified algorithm implemented in a MATLAB environment is conducted, demonstrating an increased level of protection.

The modified algorithm is implemented in a Matlab environment, and how the use of GPT affects the efficiency and robustness of the algorithm is investigated.

2. Mathematical Foundations

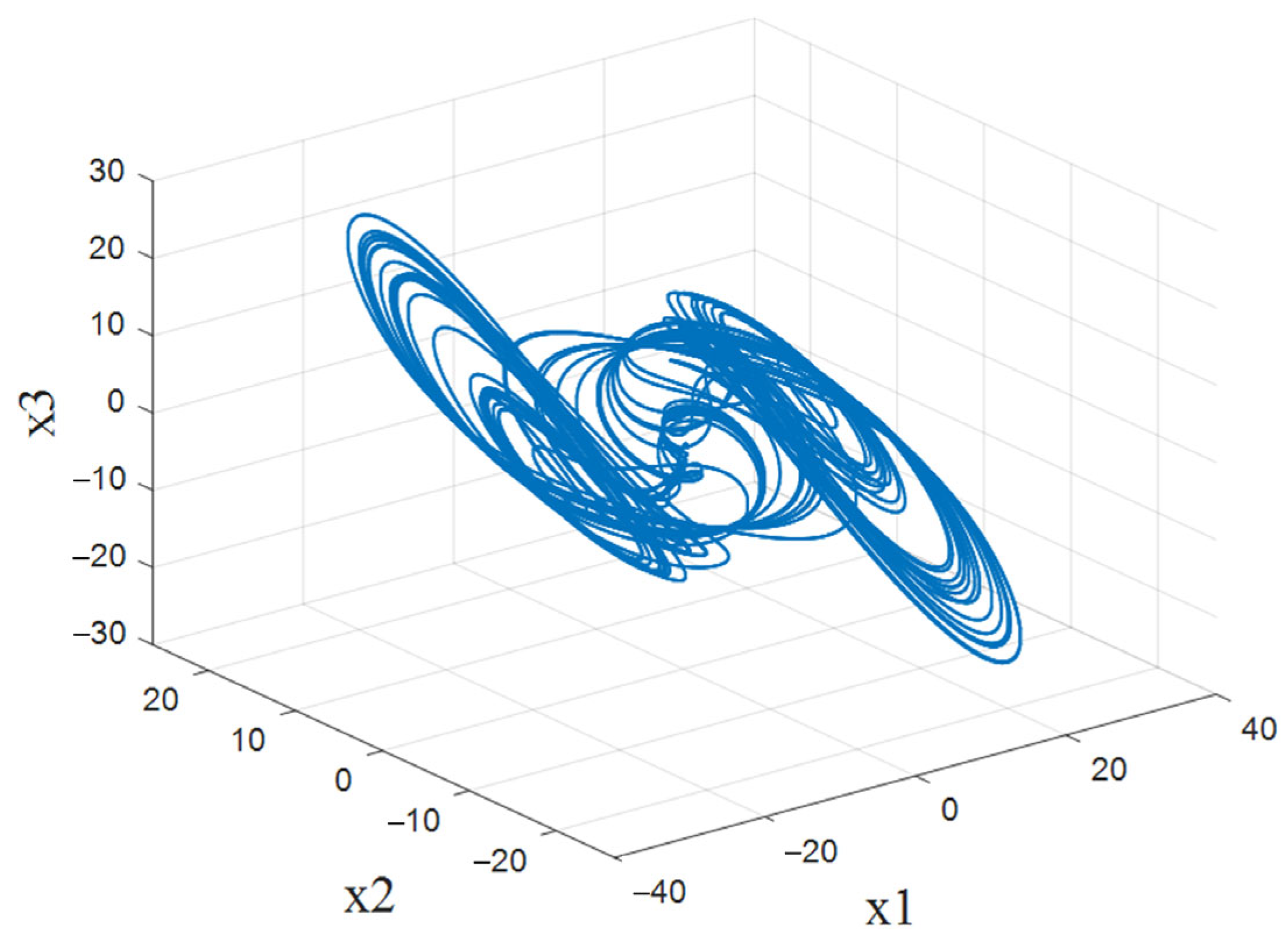
2.1. Chaotic Model

In 2024, Shukur et al. proposed a model of a third-order chaotic system with specific nonlinearity [33]:

$$\left\{\begin{array}{l}{\dot{x}}_1=x_2 \\ {\dot{x}}_2=x_3 \\ {\dot{x}}_3={ax}_1-b{x}_2-c{x}_3-d{x}_1\left|x_1\right|\end{array}\right.$$

(1)

where the values of the system parameters are $a=1.8;b=1.4;c=0.43;\mathrm{a}\mathrm{n}\mathrm{d} d=0.1$. The graphical interpretation of the chaotic attractor of the system (Figure 1) was simulated under the following randomly chosen initial conditions: ${\mathbf{x}}_0={\left[\begin{array}{ccc}0& 0& -1\end{array}\right]}^T$.

2.2. Fibonacci Q-Matrix

In mathematics, the Fibonacci sequence is a sequence in which each element is the sum of the two elements that precede it [34]. The sequence is closely related to the golden ratio and has been studied in various scientific fields for hundreds of years.

The Fibonacci Q-matrix is the matrix defined by

$$Q=\left[\begin{array}{cc}{F}_2& F_1\\ F_1& F_0\end{array}\right]=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right],$$

(2)

where F_n is a Fibonacci number. Then,

$$Q^n=\left[\begin{array}{cc}{F}_{n+1}& F_n\\ F_n& F_{n-1}\end{array}\right],$$

(3)

The Q-matrices immediately give a number of important Fibonacci identities [34], including

$$\left|Q^n\right|={\left|Q\right|}^n,$$

(4)

which gives

$$F_{n-1}{F}_{n+1}-F_n^2={\left(-1\right)}^n,$$

(5)

$$Q^{n+1}{Q}^n=Q^{2n+1},$$

(6)

therefore

$$Q^n=\left[\begin{array}{cc}{F}_{n+2}& F_{n+1}\\ F_{n+1}& F_n\end{array}\right]\left[\begin{array}{cc}{F}_{n+1}& F_n\\ F_n& F_{n-1}\end{array}\right]=\left[\begin{array}{cc}{F}_{2n+2}& F_{2n+1}\\ F_{2n+1}& F_{2n}\end{array}\right],$$

(7)

and

$$Q^m{Q}^{n-1}=Q^{n+m-1},$$

(8)

which gives

$$Q^n=\left[\begin{array}{cc}{F}_{m+1}& F_m\\ F_m& F_{m-1}\end{array}\right]\left[\begin{array}{cc}{F}_{n+1}& F_n\\ F_n& F_{n-1}\end{array}\right]=\left[\begin{array}{cc}{F}_{m+n}& F_{m+n-1}\\ F_{m+n-1}& F_{m+n-2}\end{array}\right]$$

(9)

The inverse matrix Q⁽⁻ⁿ⁾ has the following form:

$$Q^{-n}=\left[\begin{array}{cc}{F}_{n-1}& {-F}_n\\ -F_n& F_{n+1}\end{array}\right],$$

(10)

3. Modification of the Encryption Algorithm

3.1. Introducing a Modified Algorithm Based on Chaos and the Fibonacci Q-Matrix

The algorithm is based on a signal from a hyperchaotic system and the Fibonacci Q-matrix. The basic algorithm, along with a detailed presentation of the method, is provided in [32].

Encryption is carried out in two main stages: confusion and diffusion. During the confusion process, the arrangement of pixels is altered, while in the diffusion process, their values are modified. This method utilizes a novel third-order chaotic system. At first, the system’s initial state is computed based on the original image. Then, through iterations of the chaotic system, a new vector (x₁, x₂, and x₃) is generated. This vector is sorted, and the positions of the sorted values are used to confuse the original image.

Once the confusion stage is complete, the diffusion process is applied to obtain the encrypted image. In the current algorithm, diffusion is implemented using the Fibonacci Q-matrix. The scrambled image is divided into blocks of size 2 × 2, with each block being transformed using the Fibonacci Q-matrix. To ensure a higher level of security, the confusion and diffusion stages are performed twice.

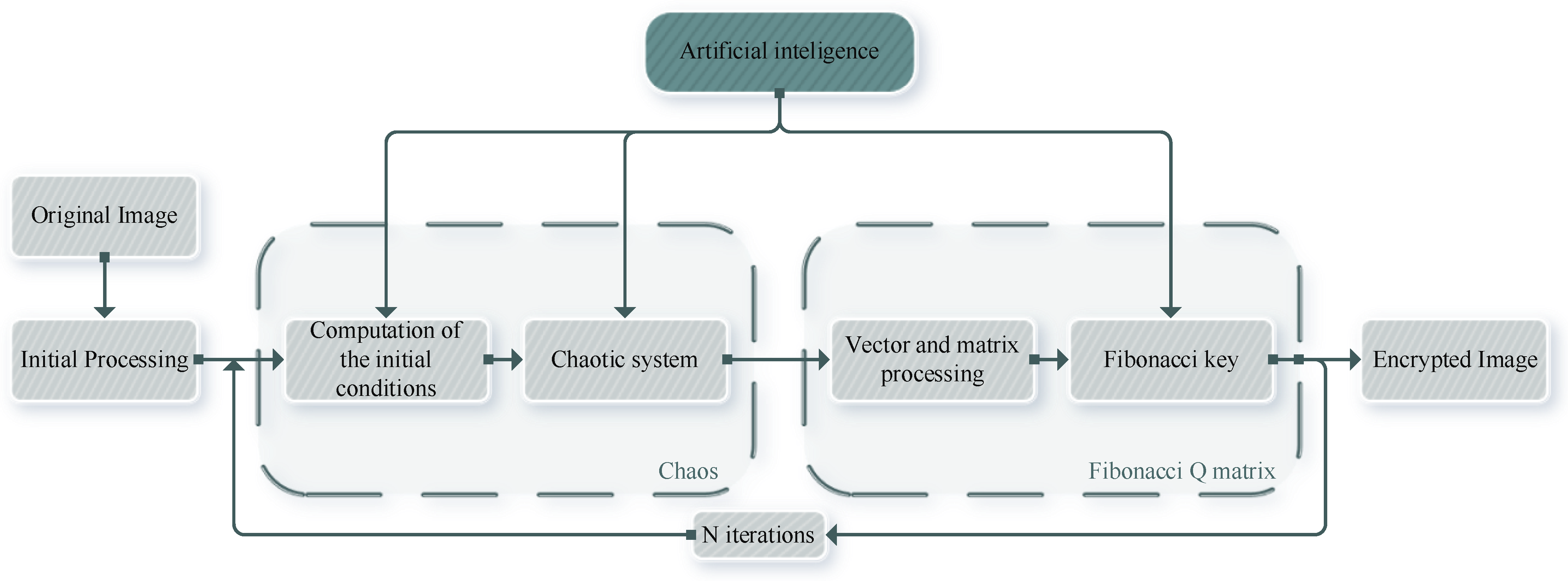
3.2. Structure of the Modified Algorithm with AI Functionalities

Algorithms of this type offer a high level of security but also have certain drawbacks, primarily consolidated in the generation of the encryption key. The use of artificial intelligence will enhance the qualities of the encoding scheme under consideration, making it more flexible and efficient when working with color images.

The modification of the algorithm includes the use of AI in determining the parameters of the chaotic system, its initial conditions, and the Fibonacci matrix, based on the properties of the encoded image. This gives these steps in the encoding process a dynamic nature. In addition to the implementation of AI, the algorithm is also modified by incorporating a third-order chaotic system, which was described and analyzed in the previous section.

Figure 2 shows a block diagram of the modified algorithm.

The considered images for encryption are color images with dimensions $M\times N$. At the beginning of the encryption process, the initial conditions and parameter initialization are determined. This process includes validation of the image, verification of the valid number of encoding iterations, as well as ensuring the correct input of the OpenAI API key. The image dimensions are extracted, and due to the use of the Fibonacci Q-matrix, an even number of rows and columns is ensured.

The iterative encoding process begins with converting the image into a matrix of double-type numbers.

The next step is obtaining the parameters for the chaotic system, as well as the initial conditions for the state vector. The validation of the generated parameters and initial conditions is performed in the core part of the algorithm. The validation is characterized by the following:

• No parameters have been received from the AI—In this case, the request is resent, but no more than three times. If the request fails after the third attempt, it is assumed that there is no internet access, and default values are used.
• The parameter values are out of range—A check is performed to ensure that the values do not exceed predefined limits, which determine the chaotic nature of the system. It is desirable that the parameters acting as bifurcation points for the system do not vary widely, but their modification is crucial, as they ensure the key sensitivity condition of the algorithm.
• Initial conditions of the state vector—Due to the characteristic sensitivity of chaotic systems to initial conditions, these are chosen within specific areas of attraction of the attractor, with the aim of ensuring the desired dynamics.

The next step in the encoding process is obtaining two arrays of values derived from solving the system with the obtained parameters and initial conditions. The method used for solving is the Dormand–Prince method. This method integrates the system of differential equations $y^{\prime }=f\left(t,y\right) \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} t_0={\displaystyle \frac{0.9865 \times M \times N}{3}}$, thus producing an output array, Y, with values greater than $M\times N$ or each of the variables in the state vector.

The array, Y, is used to form a new array, L, with dimensions $M\times N\times 3$ of the double type, which includes the values for x₁, x₂, and x₃ of the chaotic system. The use of a higher-order chaotic system is not optimal, as the algorithm requires the use of three variables. Different values for these variables can be ensured through the use of AI, while a more complex system would require more time to solve.

The matrix, L, is sorted in descending order, and the result is stored in a new array, S. From this array, a permutated vector is formed using the relationship $R=P\left(Si\right)$. This vector is then transformed into a matrix, R_s, with dimensions $N\times M$, essentially reconstructing an image from it.

Following this procedure comes the third point where AI is utilized—specifically, for generating the dynamic Fibonacci Q-matrix. The Fibonacci transformation using this matrix generally involves dividing $R_s$ into individual 2 × 2, blocks, where each block is scrambled using the Fibonacci Q-matrix. This process is iterative and is repeated ${\displaystyle \frac{M\times N}{4}}$ times. As a result, the encoded matrix, C, is obtained.

In the final stage of the encoding process, a modular operation is applied between the input image and the encoding matrix, C. If this is not the final iteration, the result is passed to matrix P, and the steps are repeated from the beginning. If it is the final encoding iteration, the resulting matrix represents the final encrypted image.

The decoding process generally follows the reverse order, with the key difference being the use of the inverse Fibonacci matrix.

3.3. Implementation and Integration of AI Functionality in the Modified Algorithm

The integration of AI functionality, as previously mentioned, is implemented in two critical modules of the algorithm: the parameters of the chaotic system and the initial Fibonacci matrix. The use of AI—specifically OpenAI’s GPT—is organized into subprograms: one for generating the chaotic system parameters and another for generating the Fibonacci matrix. The structure of these subprograms is uniform, as the same approach is used in both cases, namely, an HTTP request.

The structure of the subprograms includes several stages:

Determining Image Properties—Key features such as entropy, average brightness, contrast, histogram, or even the entire image are analyzed. However, using the full image may significantly increase processing time, so it is recommended to use a fragment of the image with a size of 64x64 pixels. This also increases the algorithm’s key space, enhancing security.

Defining the Working Prompts—When working with GPT, a prompt represents the entry point to the model. Essentially, it is the instruction or message in text format sent to the model in the appropriate structure. The prompt used for generating the chaotic system parameters has the following format in MATLAB:

• prompt = sprintf([‘Generate optimized chaotic encryption parameters (a, b, c, d) for a Shukur system based on image entropy %.2f, mean intensity %.2f, and contrast %.2f. Output only four floating point numbers separated by spaces.’], entropy_value, mean_intensity, contrast).

For generating the Fibonacci matrix, the prompt is as follows:

• prompt = sprintf([‘Generate a 2 × 2 matrix based on Fibonacci numbers, suitable for use as a Q-matrix in dynamic system modeling. Base the values on image entropy %.2f, mean intensity %.2f, and contrast %.2f. Output only four floating point numbers (Fibonacci-based) in row-major order separated by spaces.’], entropy_value, mean_intensity, contrast).

Each prompt must necessarily end with a request for result formatting, as the final output requires numerical values. Otherwise, a parser function must be implemented to extract the values from the response.

Creating a JSON Structure—The entire request is organized into what is known as a JSON structure. This structure includes various parameters and options. It starts by adding a system message that defines the model’s role. This message is treated as a system prompt with content like the following: ‘You are an AI that provides optimized chaotic encryption parameters.’

The model type, maximum number of tokens, and temperature are selected and set. In the current implementation, the model chosen is ‘gpt-4’, with a maximum token limit of no more than 50, which is sufficient for the purpose. These two parameters mainly influence the cost, response time, and performance. The temperature is a parameter that determines the randomness of the generated response. The higher the value, the more random the response will be for the same input data. The allowable values for temperature range between 0 and 2. In the specific implementation, the temperature value is set to 1.2. To further control GPT’s output variability, several key parameters are utilized. The n parameter, which enables the generation of multiple chat completions for a single input prompt, is set to 1 in this case. Another important parameter is max_tokens, which defines the maximum number of tokens allowed in a generated completion. This is considered a good practice for managing computational costs. However, it should be noted that if this value is set excessively high, it may be ignored due to the model’s overall token limit, which includes both the input and the generated output. In this implementation, max_tokens is set to 50. Additional optional parameters, such as function, function_call, and stream, are not utilized in this setup.

Formulating the Final Request and Sending It—Before sending the request, it is checked for proper JSON formatting, and any necessary adjustments are made to ensure it is correctly structured. Once the formatting is verified, the request is closed. Various HTTP request options are then defined, such as the API key, timeout, and request method. The final request is sent to OpenAI using the webwrite function.

Extracting the Response from GPT—Despite the formatting in the main prompt, the response from GPT is returned as text. This text must be converted into a numerical array. A check is then performed to validate the correctness of the extracted data. If the returned values are not valid parameters, default values are selected. The same procedure is followed if the request cannot be executed, for example, if there is no internet access. Unlike the parameters for the chaotic system, the default values for the Fibonacci matrix can be functionally tied to the numerical expressions of the image properties.

4. Results and Analysis

To test the modified algorithm, various standard color images from freely accessible databases were used. To evaluate the quality and level of image encryption, several widely used statistical and numerical analyses were employed, namely, histograms, correlation functions, information entropy, NPCR, and UACI.

4.1. Main Results

The main test image chosen is “Lena.” The original, encrypted, and decrypted images are presented in Figure 3a–c, followed by the graphically represented histograms ((d) and (e)) and correlations ((f) and (g)) of the original and encrypted images.

The histogram of the encrypted image is stable, smooth, and evenly distributed, which demonstrates a high level of image encryption. This indicates that the resulting encrypted image does not provide any statistical information about the corresponding input image. Regarding the analysis of the correlation model, the degree of correlation between the original and encrypted images is extremely low, further confirming the high level of encryption achieved.

Table 1. Numerical results.

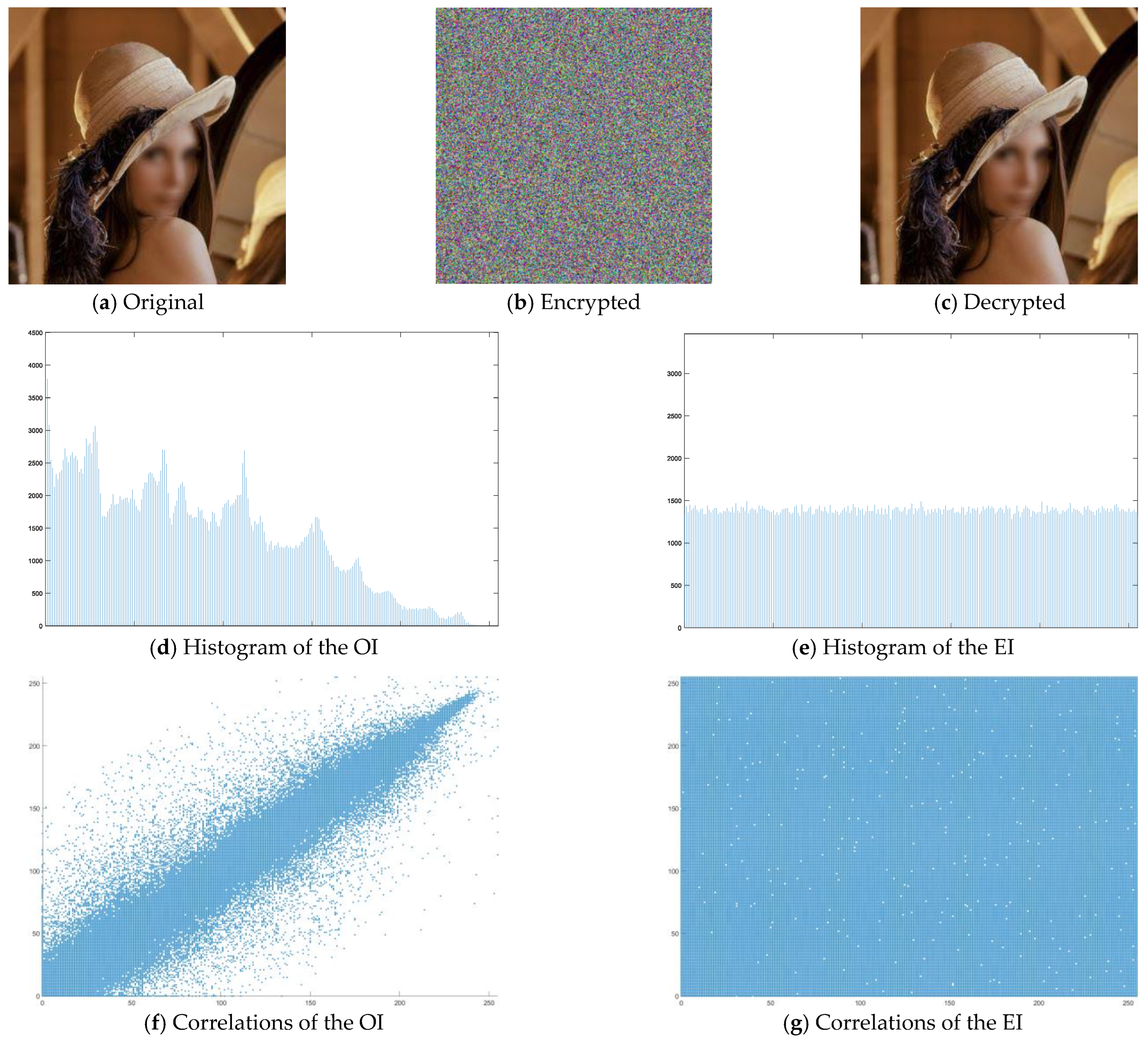
	Entropy	Correlation	NPCR	UACI
Input image	7.3283	0.9864	-	-
Encrypted image	7.9995	0.0037	99.6217	33.4463

presents the numerical results for information entropy, NPCR, and UACI coefficients.

The presented numerical results indicate that the values of information entropy and NPCR are close to the theoretical maximum, while the correlation coefficient is significantly lower than that of the original image.

Table 2. Comparison of original and modified algorithms with grayscale Lena image.

	Entropy	Correlation	NPCR	UACI
Input image	7.3283	0.9864	-	-
Original method [32]	7.9993	0.0069	99.6174	33.4226
Modified	7.9995	0.0037	99.6217	33.4463

presents a comparison of the original algorithm based on a sixth-order hyperchaotic system and the Fibonacci Q-matrix [32] and the presented modification. The comparison was made based on the digital results obtained from encrypting the grayscale Lena image.

From the presented data, it can be concluded that the modifications introduced in the algorithm increase the information entropy and NPCR coefficients and significantly improve the correlation coefficient.

4.2. Additional Results

In addition, the modified algorithm based on chaos, GPT, and the Fibonacci Q-matrix has been tested with four additional standard test images. The obtained results are presented in

Table 3. Numerical results for the additional images.

Entropy	OI	3.6779	7.6288	7.8471	7.7563
	EI	7.9707	7.9992	7.9993	7.9994
Correlation	OI	0.9365	0.9747	0.9394	0.9829
	EI	0.0172	0.0012	−0.0014	−0.0018

below.

The obtained results for the set of additional test images confirm the statement related to the previous point. The correlation and information entropy coefficients have values close to the theoretical maximum, which demonstrates the robustness of the algorithm against brute force attacks.

4.2.1. Differential Attacks

One of the characteristic properties of encryption algorithms that are resistant to differential attacks is their exceptional sensitivity to even slight changes in the encoded image. The ability of the encryption algorithm to withstand differential attacks can be evaluated by analyzing the algorithm’s performance using the Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI) tests.

Table 4. Differential attack—numerical results.

	Lena	MRI	Parrots	Koala	Flower
NPCR	99.6217	98.7732	99.6005	99.6180	99.5985
UACI	33.4463	34.9041	32.9957	33.2955	33.2622

presents the values of the NPCR and UACI coefficients for the set of test images.

The achieved high level of resistance to differential attacks is confirmed by the exceptionally high values of the NPCR and UACI coefficients.

4.2.2. Brute Force Attacks

The key space refers to the full range of potential key combinations that an encryption algorithm can employ. A sufficiently large key space—typically greater than $2^{100}$—is essential to prevent brute force attacks.

For the algorithm under consideration, the key space depends on the initial conditions of the chaotic system variables, $x_1, x_2, \mathrm{a}\mathrm{n}\mathrm{d} x_3$, as well as on the system parameters, $a, b, c, \mathrm{a}\mathrm{n}\mathrm{d} d$, in combination with the values of the Q-matrix. Assuming that only the system parameters and the initial state, ${\mathbf{x}}_0$, are used as the shared secret key—which is common practice in chaos-based encryption algorithms—the resulting keyspace is at a minimum equal to ${\mathbf{x}}_0\times 2^{212}$. This value significantly exceeds the threshold required to resist brute force attacks, thereby ensuring a high degree of security.

4.2.3. Resistance to Noise and Data Loss

To assess the algorithm’s resistance to noise attacks, “Salt and Pepper” noise with varying density is added to the encrypted image. Subsequently, the affected images must be successfully decrypted. Additionally, it is necessary to evaluate the algorithm’s ability to decrypt an encrypted image that has missing segments of varying sizes. To quantitatively determine the quality of encryption algorithms when decrypting a corrupted image, the PSNR (Peak Signal-to-Noise Ratio) metric is used.

Table 5. PSNR for “Salt and Pepper” noise and data cut attack.

	Lena	MRI	Parrots	Koala	Flower
S&P noise level 0.002	22.6550	20.7806	23.6613	23.4391	22.8415
S&P noise level 0.005	18.9475	16.7527	19.6873	19.6417	19.0693
Data cut—6%	16.8817	14.9539	17.7199	17.5721	17.0821
Data cut—12%	11.6756	10.2426	12.4800	12.3592	11.7835

presents the PSNR coefficient results for “Salt and Pepper” noise with densities of 0.002 and 0.005, as well as for image integrity violations with losses of 6% and 12%, for the entire set of test images.

4.2.4. Run-Time Performance Analysis

When estimating the computational complexity of the algorithm using O(…) notation, it becomes evident that the overall complexity primarily depends on the size of the input image. In other words, the algorithm has a complexity of O(NxM). However, a more practical insight into the computational cost and execution time can be obtained through the use of MATLAB’s Run-Time Profiler, as the algorithm is implemented and tested within the MATLAB environment.

To evaluate the execution time, the main program records the time required for sending and receiving responses from the AI model, as well as the time taken for encryption and decryption. The results for images of size 256 × 256 and 512 × 512 are summarized in

Table 6. MATLAB run-time performance results.

Image Size	Using AI	Encrypt	Decrypt	Total Time
256 × 256	1.615 s	0.721 s	0.066 s	4.7415 s
512 × 512	2.062 s	2.395 s	0.252 s	7.584 s

.

The obtained results clearly indicate that the method used to send the request to the GPT model is not a determining factor. Instead, the execution time primarily depends on the network bandwidth, latency, endpoint load, and any possible rate limiting applied at the endpoint. Regarding the encryption process, the majority of the time required is consumed by the subroutine that solves the system of differential equations of the chaotic system. For example, this computation takes approximately 0.663 s for a 256 × 256 image and around 2.137 s for a 512 × 512 image, accounting for roughly 90% of the total encryption time. The decryption process, on the other hand, is significantly faster since the differential system does not need to be solved again. The total execution time also includes numerous auxiliary operations such as figure creation and manipulation, image visualization, file handling, and others. When the durations of these additional processes are excluded, it can be concluded that the theoretical time complexity expressed with O(…) notation is indeed confirmed.

5. Conclusions

The presented article proposes an approach for integrating artificial intelligence into an image encryption algorithm based on chaos and the Fibonacci matrix. By using the GPT model, a subroutine is implemented within the main algorithm, which, based on properties of the input image, generates unique values for the parameters of the chaotic system as well as for the Fibonacci matrix. This approach aims to achieve a higher degree of security, as well as a certain level of abstraction in generating the encryption key, since the process does not require human intervention, and the encryption key remains concealed. The obtained results demonstrate that the modification enhances the qualities of the encryption scheme. The conducted experiments reinforce the algorithm’s resistance to some known cryptographic attacks.