Abstract
Nowadays, floating point multiplier (FPM) plays an essential role in computers. The IEEE 754 norm for floating point numbers is the most widely recognized portrayal for real numbers on today’s PCs. Addition, multiplication, subtraction, and division are the four important functions of single precision floating arithmetic, amongst which multiplication has the most extensive use in every algorithm. Fast multipliers are of critical need in modern high-performance applications, especially in digital signal processing, because DSP involves many important multiplication-based operations, e.g., fast Fourier transform (FFT) and convolution. These speedy computations can be implemented on field programmable gate arrays (FPGAs), because they can provide a high speed and a large number of on-board digital resources. FPGAs are involved in many modern applications such as cryptography and communication computations, arithmetic and scientific computation, digital image and signal processing, etc. There are many forms of FPM available. This paper describes an efficient way to implement single precision FPM in IEEE 754 standard format, where Verilog hardware description language (VHDL) is used to implement the design for Xilinx Spartan 6 FPGA. Here, the 32-bit number will be divided into three parts: sign bit, exponent, and mantissa. This paper is implemented by using different types of adders, which includes carry increment adder (CIA), carry select adder (CSA), ripple carry adder (RCA), and carry look-ahead adder (CLA). Carry save array (CSA) multiplication is used for performing the mantissa multiplication.
1. Introduction
There are many different methods to express real numbers in binary format on computers. Floating point representation is the most effective way to represent real numbers in binary form, e.g., 9876543.21 could be represented as 9.87654321 × 106 [1]. Decimal interchange and binary interchange are the two distinct customary formats available in IEEE 754 for floating point (FP). Booth’s multiplier algorithm uses standard add shift operations, ultimately reducing the number of partial products, therefore achieving a speed advantage [2]. Wallace’s tree algorithm, using a tree of carry save adders, implemented a new way to add the partial component bits in parallel [3]. Vedic multiplier is based on Sutra of Vedic multiplication and reduces the hardware requirement. Sutra of Urdhava–Triyakbhayam multiplier is used for high-speed performance [4].
The proposed paper focuses on single precision multiplication only. This paper presents comparative investigation on SPFPM, and it is undertaken using carry save array multiplier and different adders such as carry skip, carry save, CLA, CIA, carry select, and RCA for calculating the addition of mantissa and for adding partial products.
2. Representation and Calculation of Floating Point in IEEE-754 Standard
According to this format, a floating point number N is represented as follows.
For 32-bit SPFP-numbers, the IEEE-754 norm has following three parts [5] and representation is shown in Table 1:
Table 1.
Representation of SPFP number [1].
- i.
- The sign of the FP number is represented by the most significant bit (MSB): 0 for a positive number and 1 for a negative number. By taking the XOR of sign bit of multiplier and multiplicand, the sign-bit is consequently determined.
S = S1 ⊕ S2
- ii.
- Bit (30-23) is used to express a biased exponent (E). E = e + 127, where e is the actual exponent, and 127 is the bias value for single precision. We add the exponents of two numbers using a different type of 8-bit full adder. After adding the exponents of two inputs, the bias is subtracted from this using a 9-bit subtractor (to cater the carry of addition) to obtain the final output.
E = (E1 + E2) − bias
- iii.
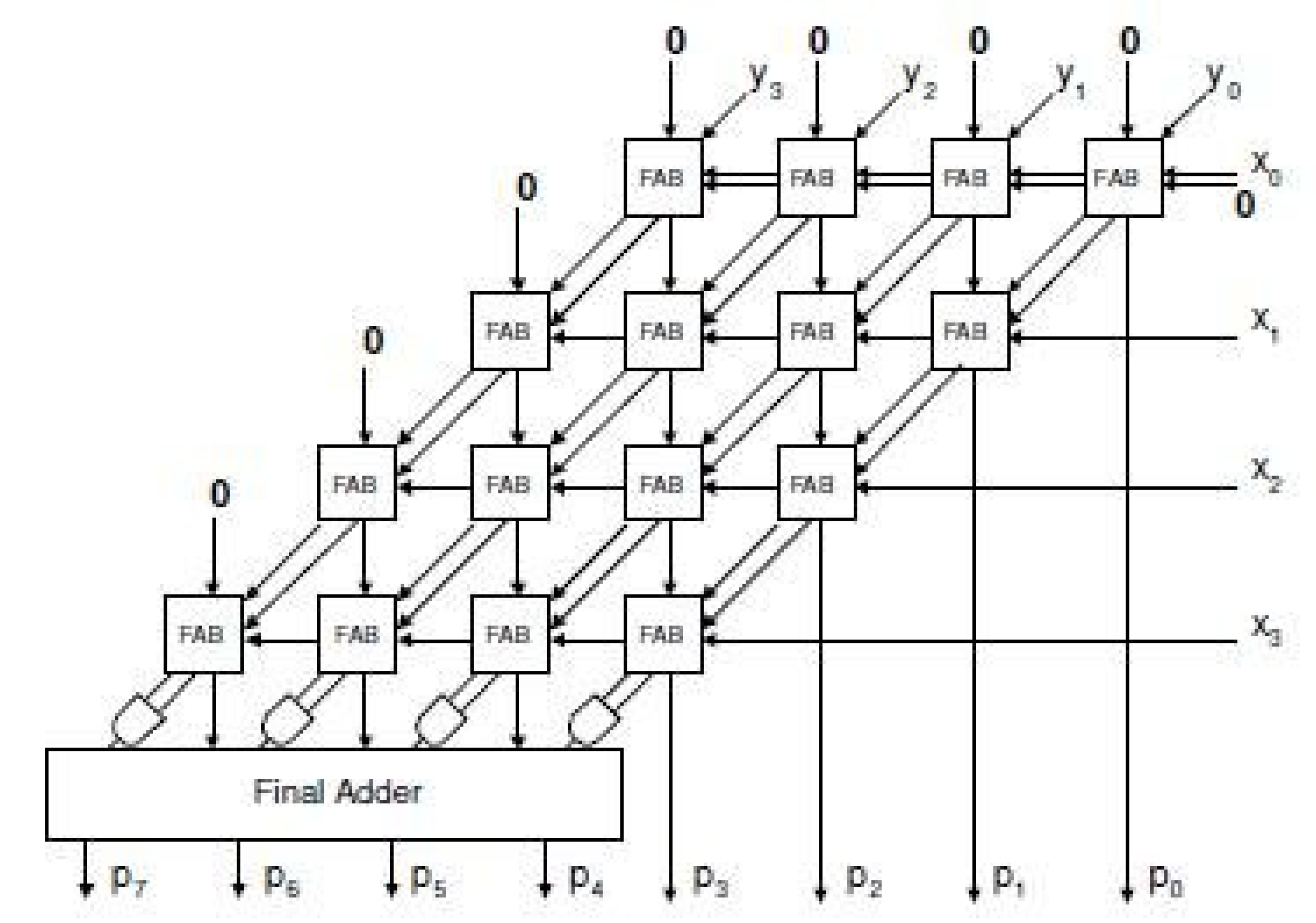
- The mantissa/significand for a binary number is represented by 0 to 22 bits as shown in Table 1. Here, we are using array multiplier for this purpose as shown in Figure 1. This involves the multiplication of 24-bit (23 fraction bits and one hidden bit) mantissas of two input numbers and results a 48-bit mantissa, which is then truncated to 24 bits.
Figure 1. Block diagram of carry save array multiplier [4].
M = M1 ∗ M2
- iv.
- As mentioned earlier, IEEE-754 standard floating point numbers always have one ‘1’ to the left of the binary point. We ignored the binary point while multiplying the mantissa. Therefore, the lower 46 bits are placed to the left of the binary point in the result. In this case, we have two possibilities, i.e., the binary point could be in 47th or 46th place.
- In the first case, no normalization is required if the leading ‘1’ bit is in 46th place (i.e., there is just one bit ‘1’ on the left), because the result is already normalized.
- In the second case, normalization is needed if the leading ‘1’ bit is at 47th place (i.e., it occurs one bit away from the binary point). So, mantissa needs to be shifted one unit left, and consequently, the exponent also requires normalization, which is done by adding one to it.
In the final product, the output should be of 23 bits only, so we round off over the result. So, in the first case, we select [45:23], and in the second case, [46:24].
3. Adders for Comparison
3.1. Carry Look Ahead Adder (CLA)
This is just another kind of adder that contains carry propagation that, depending on the input signal, can calculate the carry in advance. This adder can perform faster addition than ripple carry adder, and it can also reduce the time delay [6].
3.2. Carry Skip Adder (CSA/CBA)
This adder is also known as carry bypass adder. It improves the ripple carry adder by reducing the delay. In this method for the propagation of carry, skip logic is used. The basic logic to propagate carry is that bit position remains unchanged for different values of A1, B1 [7].
3.3. Carry Increment Adder (CIA)
Incremental circuit and ripple carry adders (RCA) are used in the layout of carry increment adder (CIA). Half adders (HA) are used in making the design of incremental circuit of CIA. Firstly, the total number of bits is split up into groups of 4 bits, and afterwards, addition is accomplished by respective RCA [8].
4. Results
For simulation purposes, data flow and gate level modeling is selected in the Xilinx, and the design is a composite, using Xilinx ISIM tool, Family Spartan6, device XC6SLX45, and package CSG324. Two 32-bit numbers were multiplied using FPM, and the desired result was obtained.
4.1. Comparison with the Literature
The proposed technique using different adders was compared with different research papers, in which different adders and multipliers are used as shown in Table 2. The given literature is compared with time delay, number of LUTs, and number of occupied slices of below-mentioned techniques.
Table 2.
Comparison with literature.
4.2. Device Utilization Summary
Carry select adder (CSA) and carry increment adder (CIA) use minimum time delay, 81.716 ns, to perform the floating point multiplication. Moreover, CIA occupies minimum number of slices, and CSA uses minimum number of slice LUTs as shown in Table 3.
Table 3.
Device utilization summary.
5. Conclusions and Future Work
The major focus of this paper is to perform a 32-bit floating point multiplier that supports IEEE 754 format; the multiplier performs significands multiplication, thus normalizing the mantissa to obtain a 32-bit accurate output. The design may be implemented on intel’s Stratix10NX, Heterogeneous FPGA in the future to obtain fastest multiplication for higher bit numbers [11].
Author Contributions
Conceptualization by M.A.; Methodology by H.A. and Z.A.; Software by H.A. and H.R.; Formal Analysis by Z.A. and H.R.; Investigation by M.A. and H.A.; Resources by M.A.; Data curation by H.A.; writing original draft preparation by H.R. and Z.A.; writing review and editing by M.A. and H.A.; Visualization by H.A.; Supervision by M.A.; project administration by H.A.; funding acquisition by H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Acknowledgments
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Floating Point Number. 754-2008 IEEE Standard for Floating-Point Arithmetic. 2008, pp. 1–70. Available online: https://steve.hollasch.net/cgindex/coding/ieeefloat.html (accessed on 20 April 2021).
- Manolopoulos, K.; Reisis, D.; Chouliaras, V.A. An efficient multiple floating point multiplier. In Proceedings of the 2011 18th IEEE International Conference on Electronics, Circuits, and Systems, Beirut, Lebanon, 11–14 December 2011; pp. 153–156. [Google Scholar]
- Weste, N.H.E.; Harris, D. CMOS VLSI Design: A Circuits and Systems Perspective, 3rd ed.; Pearson Education: London, UK, 2005; pp. 345–356. [Google Scholar]
- Digital Multipliers. Available online: https://www.ijemr.net/DOC/DigitalMultipliers-AReview(220-223)8aa5905d-5da5-4b50-8b2e-f0bd850becb7.pdf (accessed on 17 May 2021).
- Mangalath, N.S.; Priya, R.; Malathi, P. An efficient universal multi-mode floating point multiplier using Vedic mathematics. In Proceedings of the IEEE 2014 International Conference on Advances in Communication and Computing Technologies (ICACACT), Mumbai, India, 10–11 August 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Raahemifar, K.; Ahmadi, M. Fast carry-look-ahead adder. In Proceedings of the Engineering Solutions for the Next Millennium. 1999 IEEE Canadian Conference on Electrical and Computer Engineering (Cat. No.99TH8411), Edmonton, AB, Canada, 9–12 May 1999. [Google Scholar]
- Jom, S.; Asha, J. Hybrid Variable Latency Carry Skip Adder. In Proceedings of the International Conference on Circuits and Systems in Digital Enterprise Technology (ICCSDET), Kottayam, India, 21–22 December 2018; pp. 1–6. [Google Scholar]
- Devi, A.B.; Kumar, M.; Laishram, R. Design and Implementation of an Improved Carry Increment Adder. Int. J. VLSI Des. Commun. Syst. 2016, 7, 21–27. [Google Scholar] [CrossRef]
- Ramya, V.; Seshasayanan, R. Low power single precision BCD floating–point Vedic multiplier. Microprocess. Microsyst. 2020, 72, 102930. [Google Scholar] [CrossRef]
- Krishnan, T.; Saravanan, S. Design of Low-Area and High Speed Pipelined Single Precision Floating Point Multiplier. In Proceedings of the IEEE 2020 6th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, India 6–7 March 2020; pp. 1259–1264. [Google Scholar] [CrossRef]
- McNamaraField, D. Programmable Gate Arrays Accelerate Applications from the Cloud to the Edge; Intel Corporation: Santa Clara, CA, USA, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).