Analytical and Experimental Investigation of a Triangular-Channeled Solar Water Heater ^†

Abstract

Utilization of solar energy is increasing in different states of the world, and the sun is regarded as the largest source of continuous and coherent energy. In the present study, a novel configuration of a v-corrugated solar collector with triangular channels for domestic water heating has been analytically investigated. A mathematical model based on effectiveness-NTU method is established to thermally examine the collector. Additionally, the heat losses from the body of the collector, useful energy from the collector and solar efficiency have been calculated analytically over different operating parameters. The effects of mass flow rate and solar heat flux on water outlet temperature are evaluated analytically and compared with the experimental results. Moreover, the study includes the experimental and theoretical investigation of the heat exchange effectiveness and thermal efficiency of the proposed absorber. The study shows that high temperature and high performance can be obtained from this collector as more heat energy can be collected by using triangular channels because all the three sides of these channels are exposed to solar radiations at the same time. Therefore, these channels will enhance the collector exposed surface area and thereby increase the solar efficiency and overall performance of the system.

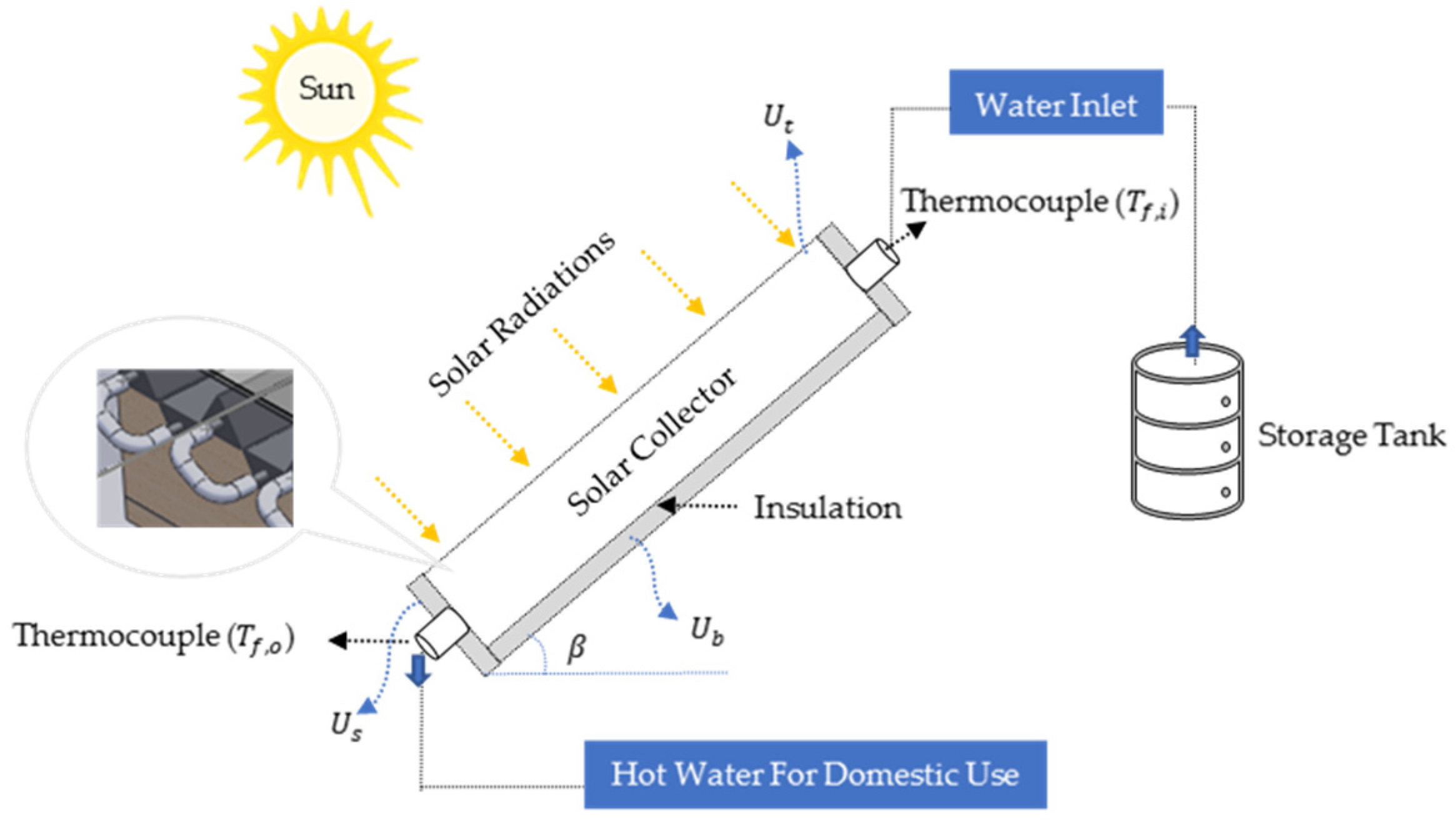
1. Introduction

The most common type of solar water absorbers is the flat plate solar collector (FPSC). It behaves as a heat exchanger and transmits the radiant solar energy to the sensible heat of the working fluid (air or water), and it is used for domestic water and space heating purposes worldwide. During the last fifty years, different scientists from all over the world have been trying to build and test various types of liquid FPSCs [1,2,3,4]. The main purpose of this research was to convert as much solar energy as possible into a useful form with little investment in labor and materials. The FPSC can be used for domestic water heating applications where a maximum temperature of 60 °C is required [5].

To the best of the authors’ knowledge, no work has been reported on triangular-channeled collectors with an inverted configuration. The development and testing of this triangular-channeled collector have been performed by Khan et al. [6], in which the effect of water flow rate on its outlet temperature was investigated for domestic water heating. The proposed configuration takes the advantage of a more exposed surface for heat transfer than that of the existing available FPSCs. The present study uses analytical modelling to investigate the performance of the proposed triangular-channeled solar water heater based on the effectiveness NTU method. The advantage of this formulation is simplicity and the ability of prediction for water collectors with any geometry. The effects of mass flow and solar flux on water outlet temperature are investigated analytically and compared with the experimental results of Khan et al. [6]. Moreover, the study includes the experimental and theoretical investigation of the heat exchange effectiveness and thermal efficiency of the proposed absorber.

2. Mathematical Model of Triangular-Channeled Solar Water Heater

The detailed specifications and the operating parameters of the designed triangular-channeled solar collector are given here. The collector, shown in Figure 1, is oriented in a south-facing position and it is exposed to solar irradiation at Swabi, Pakistan (latitude 34°7′ and longitude 72°28′), with an angle of 45° from the horizontal, chosen according to the location. In the presence of sunlight, solar irradiation fall on the top surface of the collector with instantaneous solar flux $I_F$ (range: 0–900 W/m²), and solar energy $q_s$ is absorbed inside the body of the collector. The cold water from the storage tank will enter the collector at its inlet, with a certain value of flow rate, $m_f$ (range: 0.1–0.5 L/min), and at a certain temperature, $T_{f,i}$ (range: 23–32 °C), and will flow through these channels under gravity. A part of this absorbed solar energy is used to increase its temperature during its circulation through the channels, and it leaves the collector at its outlet, whose temperature will be $T_{f,o}$. At a given time, the absorber, triangular channels, connecting pipes, and back and side surfaces are at the same mean temperature ($T_{mp}$). The thermophysical properties of water (${\mu }_f$ = 855 × 10⁻⁶ Pa-s, $k_f$ = 0.613 W/m-K) are considered to be constant. Water flow through the channels is assumed to be homogeneous (no phase-change is considered). Steady state heat transfer is considered. As the back and side surfaces are well-insulated ($k_i$ = 0.043 W/m-K), convection and radiation through these surfaces are considered negligible.

Energy balance of the entire collector can be written as:

$$\mathrm{Incident}\mathrm{energy}\left(q_s\right)=\mathrm{Useful}\mathrm{collector}\mathrm{energy}\left(q_u\right)+\mathrm{Energy}\mathrm{loss}\mathrm{from}\mathrm{collector} \left(q_L\right)$$

(1)

Heat loses from the body of the collector to its surroundings through its top, bottom, and side surfaces are given by Equations (2), (4) and (5) as follows:

$$U_t=\frac{1}{\frac{N{T}_{mp}}{C{\left\{\left(T_{mp}-T_{amb}\right)/\left(N+f\right)\right\}}^e}+\frac{1}{h_{wi}}}+\frac{\sigma \left(T_{mp}{}^2+T_{amb}{}^2\right)\left(T_{mp}+T_{amb}\right)}{\frac{1}{d}+\frac{2N+f-1}{{\epsilon }_g}+g-N}$$

(2)

where $\sigma$ is the Stefan–Boltzmann constant, ${\epsilon }_g$ is the emissivity of glass cover, 0.9, and $C$, $f$, $e$, $d$ and $g$ are constants and functions, and these are proposed by Malhotra and Garg [7].

The empirical relation for the wind heat transfer coefficient between the glazing and surrounding proposed by Watmuff et al. [1] is:

$$h_{wi}=2.8+3.0V_{wi}[\mathrm{for}{V}_{wi}>0.15\mathrm{m}/\mathrm{s}]$$

(3)

As heat transfer from back and side surfaces is assumed to be one dimensional conduction, so loss coefficients for these surfaces can be obtained respectively as [1]:

$$U_b=\frac{k_i}{l_i}$$

(4)

$$U_s=\frac{\left(l_1+l_2\right)l_3{k}_i}{l_1{l}_2{l}_i}$$

(5)

where the insulation thermal conductivity is represented as $k_i$. Thus, the overall loss coefficient is the heat loss combination from the top, bottom, and side surfaces and can be used for total heat loss from collector to surrounding as follows:

$$q_L=U_L{A}_g\left(T_{mp}-T_{amb}\right)$$

(6)

The useful energy from the collector can be calculated as:

$$q_f=h_f{A}_f\Delta T_m$$

(7)

where $h_f$ is the heat transfer coefficient for fluid (water) and $\Delta T_m$ is the logarithmic mean temperature difference and can be obtained as:

$$\Delta T_m=\frac{T_{f,i}-T_{f.o}}{\ln \left[\frac{T_{mp}-T_{f.o}}{T_{mp}-T_{f,i}}\right]}$$

(8)

$T_{f.o}$ can be calculated from effectiveness of the heat exchanger (collector) as:

$${\epsilon }_f=1-\exp \left[-\frac{h_f{A}_f}{m_f{C}_{p,f}}\right]$$

(9)

$h_f$ can be calculated using the Nusselt Number correlation as follows:

$$N_u=3.66+\frac{0.0668\left(D_h/L\right)R_e{P}_r}{1+0.04{\left[\left(D_h/L\right)R_e{P}_r\right]}^{2/3}}$$

(10)

where the $R_e$ and $P_r$ represents Reynolds number and Prandtl number. Therefore, the useful energy from the collector will be:

$$q_u={\epsilon }_f{m}_f{C}_{p,f}\left(T_{mp}-T_{f,i}\right)$$

(11)

The ratio of the useful energy absorbed by the working fluid to the total irradiated energy on the collector surface is known as collector thermal efficiency:

$$\eta =\frac{q_u}{q_s}=\frac{{\epsilon }_f{m}_f{C}_{p,f}\left(T_{mp}-T_{f,i}\right)}{I_F{A}_g}\times 100$$

(12)

3. Results and Discussion

Figure 2a shows the trend of theoretical results of water outlet temperature, $T_{f,o }$(at 0.1 L/min), which are compared with the experimental of Khan et al. [6]. $T_{f,o}$ increases gradually, having a maximum value at 14:00, and then decreases in the afternoon. This is because of the solar flux, which increases with the increase in intensity of solar radiation and then decreases and forms a bell shape curve ($T_{f,o}$ follows this).

Figure 2b shows the theoretical results of $T_{f,o}$ at different mass flow rates from 0.1 to 0.5 L/min, which have been performed experimentally by Khan et al. [6]. The theoretical results are different from experimental results and are overlapping because these are plotted at the same mean surface temperature ($T_{mp}$) as in the case of 0.1 L/min. If actual values of $T_{mp}$ are taken for all the flow rates, then there will be a difference between these values of temperature. At a high flow rate, the given amount of water passes quickly through the collector, and it takes less time for heat transfer compared to a lower flow rate. Therefore, at lower flow rates, the absorbers give higher temperature values at the outlet. Experimentally, it can be said that the momentum diffusivity is greater than the thermal diffusivity at higher flow rates (value of Prandtl number increasers). Therefore, it gives a high temperature at low flow rates.

Figure 3 shows the trends of experimental and theoretical values of the thermal efficiency ($\eta$) of the absorber. At the start, its value was low because useful energy was lower. During 12:00 to 16:00 h, the thermal efficiency increases gradually with the increase in useful energy and solar flux. After 16:00 h, there is a sudden increase in the solar efficiency because, during this time, the solar flux decreases abruptly due to the absence of solar radiation, whereas heat is transferred to water. Experimental results show that the main reason for higher values of useful energy is that the large amount of heat energy was entrapped in the collector body during the presence of solar radiation. Therefore, by reducing heat losses, these absorbers can provide a more useful output.

4. Conclusions

In the present study, a mathematical model has been developed for the investigation of a triangular-channeled solar water heater using the effectiveness-NTU approach. The analytical results of the model are in-line with the experimental results and, therefore, this proposed model can be used for the prediction of the performance of the solar collector.