Analytical Subdomain Model for Double-Stator Permanent Magnet Synchronous Machine with Surface-Mounted Radial Magnetization †
Abstract
:1. Introduction
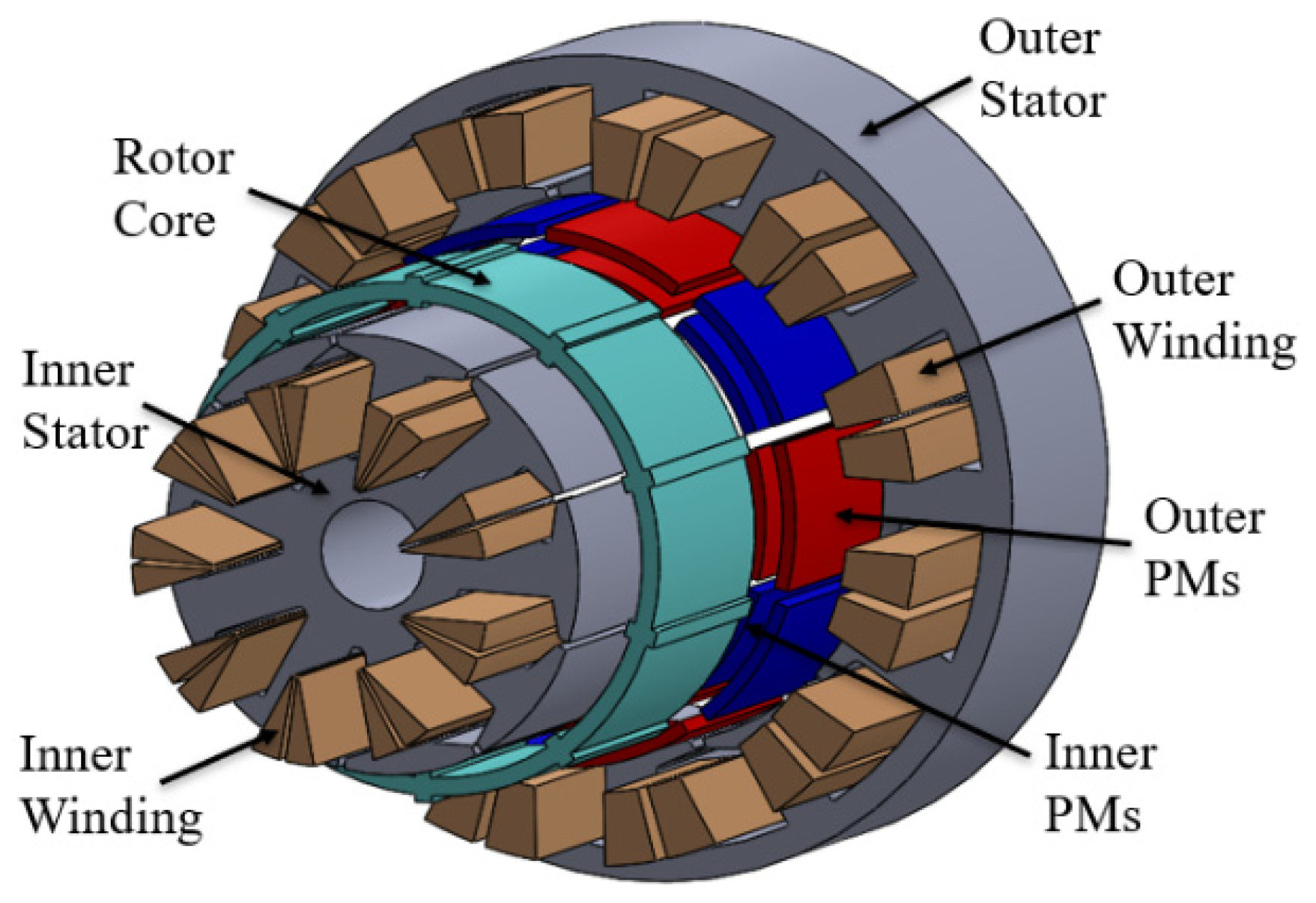
2. Motor Geometry
3. Analytical Formulations and Field Solutions
4. Results and Discussion
5. Conclusions
Acknowledgments
References
- Wang, Z.; Liu, B.; Guan, L.; Zhang, Y.; Cheng, M.; Zhang, B.; Xu, L. A dual-channel magnetically integrated EV chargers based on double-stator-winding permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2019, 55, 1941–1953. [Google Scholar] [CrossRef]
- Gul, W.; Gao, Q.; Lenwari, W. Optimal design of a 5-mw double-stator single-rotor pmsg for offshore direct drive wind turbines. IEEE Trans. Ind. Appl. 2020, 56, 216–225. [Google Scholar] [CrossRef]
- Zhu, X.; Cheng, M. Design and analysis of 10 MW Class HTS exciting double stator direct-drive wind generator with stationary seal. IEEE Access 2019, 7, 51129–51139. [Google Scholar] [CrossRef]
- Kiani, M.; Wang, W.; Gu, L.; Fahimi, B. PM-assist double stator synchronous machine. IEEE Int. Symp. Ind. Electron. 2017, 7, 342–347. [Google Scholar]
- Mohamed, M.R.; Ishak, D. Optimization of surface-mounted permanent magnet brushless AC motor using analytical model and differential evolution algorithm. J. Electr. Eng. 2019, 70, 208–217. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, M.S.; Ishak, D.; Leong, T.T.; Mohamed, M.R. Optimization of double stator PMSM with different slot number in inner and outer stators using genetic algorithm. Int. J. Power Electron. Drive Syst. 2021, 12, 726–735. [Google Scholar] [CrossRef]
- Tiang, T.L.; Ishak, D.; Jamil, M.K.M. Complete subdomain model for surface-mounted permanent magnet machines. In Proceedings of the IEEE Conference on Energy Conversion 2014, Johor Bahru, Malaysia, 13–14 October 2014; pp. 140–145. [Google Scholar]
- Ling, P.P.; Ishak, D.; Tiang, T.L. Influence of magnet pole arc variation on the performance of external rotor permanent magnet synchronous machine based on finite element analysis. In Proceedings of the International Conference Power Energy 2016, Bangkok, Thailand, 28–29 November 2016; pp. 552–557. [Google Scholar]


| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Outer Stator Slot Number, Nos | 12 | Stack Length, ls (mm) | 40 |
| Inner Stator Slot Number, Nis | 9 | Outer Airgap Length, log (mm) | 1 |
| Rotor Pole Number, 2p | 10 | Inner Airgap Length, lig (mm) | 1 |
| Outer Stator Outer Radius, Roso (mm) | 90 | Outer Magnet Thickness, hom (mm) | 3 |
| Outer Stator Inner Radius, Rosi (mm) | 60 | Inner Magnet Thickness, him (mm) | 3 |
| Inner Stator Outer Radius, Riso (mm) | 48 | Magnet Remanence, Br (T) | 1.12 |
| Inner Stator Inner Radius, Risi (mm) | 12 | Saturation Flux density, Bmax (T) | 1.6 |
| Rotor Outer Radius, Rro (mm) | 56 | Relative Recoil Permeability, µr | 1.05 |
| Rotor Inner Radius, Rri (mm) | 52 | Rated Speed, rm (rpm) | 600 |
| Outer Magnet Radius, Rom (mm) | 59 | Outer Winding Turns per coil, Noc | 114 |
| Inner Magnet Radius, Rim (mm) | 49 | Inner Winding Turns per coil, Nic | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.S.; Ishak, D.; Leong, T.T.; Mohamed, M.R. Analytical Subdomain Model for Double-Stator Permanent Magnet Synchronous Machine with Surface-Mounted Radial Magnetization. Eng. Proc. 2021, 12, 37. https://doi.org/10.3390/engproc2021012037
Ahmad MS, Ishak D, Leong TT, Mohamed MR. Analytical Subdomain Model for Double-Stator Permanent Magnet Synchronous Machine with Surface-Mounted Radial Magnetization. Engineering Proceedings. 2021; 12(1):37. https://doi.org/10.3390/engproc2021012037
Chicago/Turabian StyleAhmad, Mohd Saufi, Dahaman Ishak, Tiang Tow Leong, and Mohd Rezal Mohamed. 2021. "Analytical Subdomain Model for Double-Stator Permanent Magnet Synchronous Machine with Surface-Mounted Radial Magnetization" Engineering Proceedings 12, no. 1: 37. https://doi.org/10.3390/engproc2021012037
APA StyleAhmad, M. S., Ishak, D., Leong, T. T., & Mohamed, M. R. (2021). Analytical Subdomain Model for Double-Stator Permanent Magnet Synchronous Machine with Surface-Mounted Radial Magnetization. Engineering Proceedings, 12(1), 37. https://doi.org/10.3390/engproc2021012037






