Modelling Ocean Waves and an Investigation of Ocean Wave Spectra for the Wave-to-Wire Model of Energy Harvesting †
Abstract
:1. Introduction
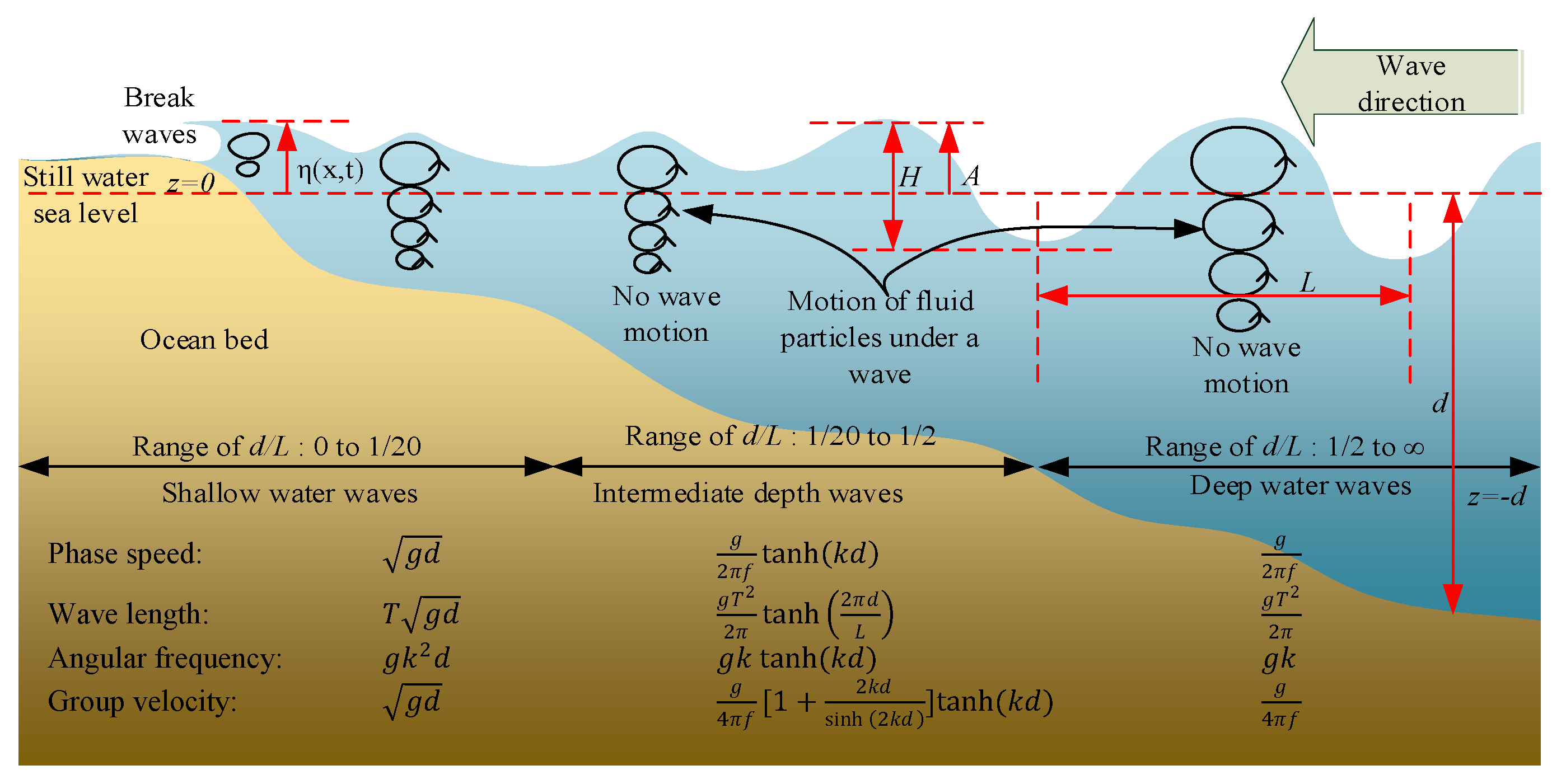
2. Modelling Ocean Waves
Linear Wave Theory
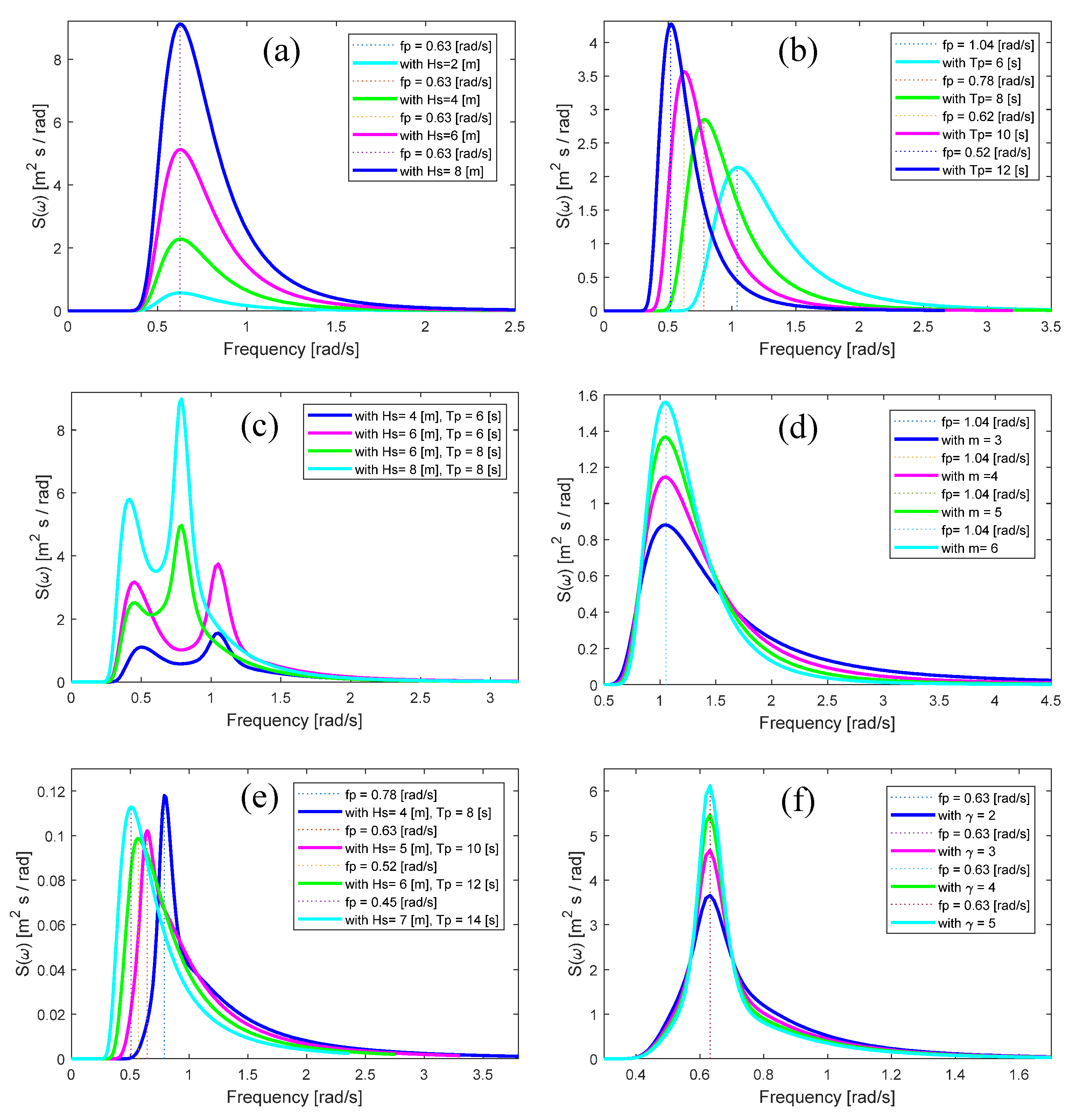
3. Parametric Wave Spectra
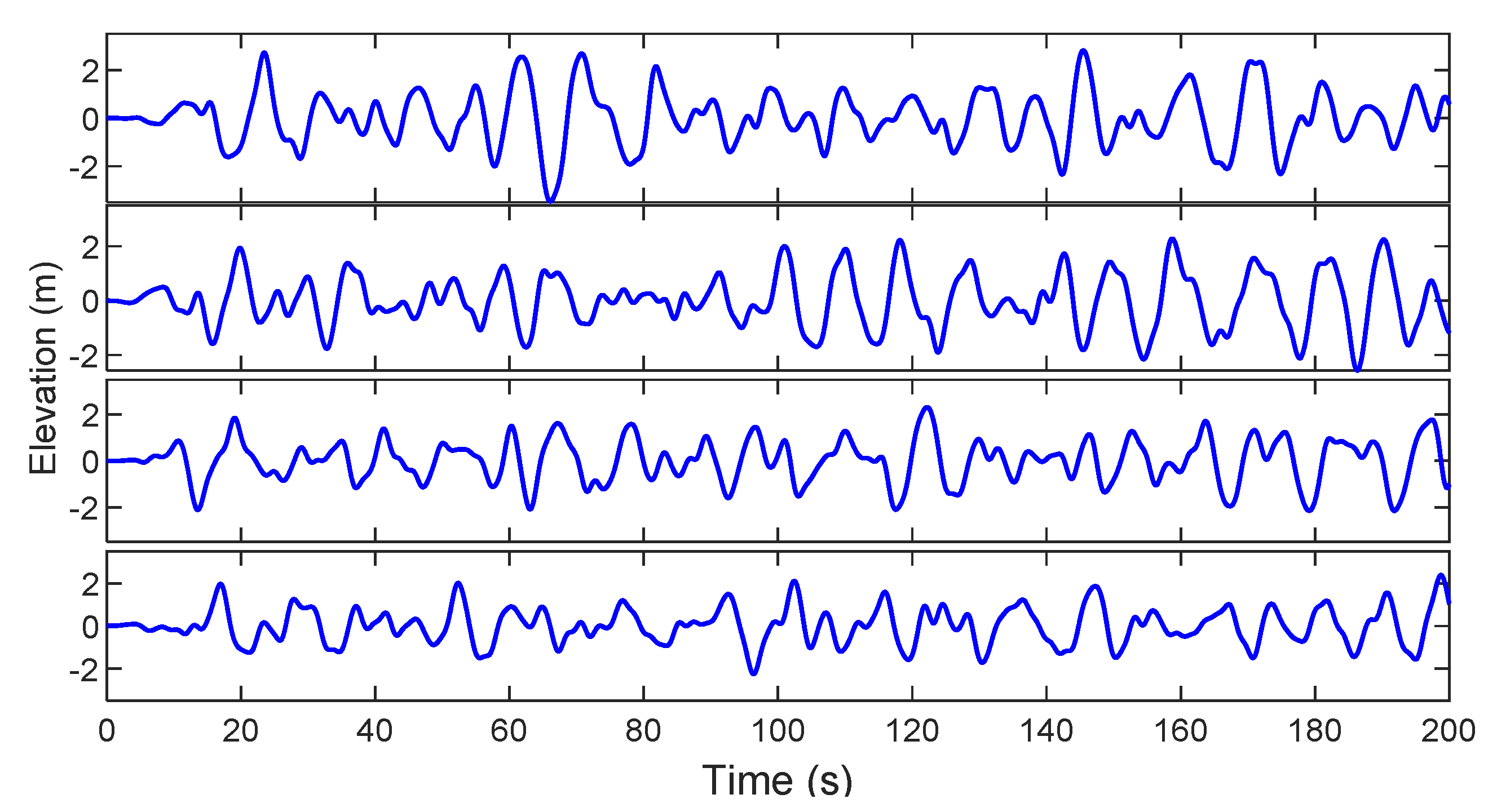
4. Results and Discussions
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Melikoglu, M. Current status and future of ocean energy sources: A global review. Ocean Eng. 2018, 148, 563–573. [Google Scholar] [CrossRef]
- Rasool, S.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. The Grid Connection of Linear Machine-Based Wave Power Generators. In Advanced Linear Machines and Drive Systems; Springer: Singapore, 2019; pp. 303–341. [Google Scholar]
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.; Rheem, C.-K.; Koh, K.K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Gunn, K.; Stock-Williams, C. Quantifying the global wave power resource. Renew. Energy 2012, 44, 296–304. [Google Scholar] [CrossRef]
- Rasool, S.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. Coupled Modeling and Advanced Control for Smooth Operation of a Grid-Connected Linear Electric Generator Based Wave-to-Wire System. IEEE Trans. Ind. Appl. 2020, 56, 5575–5584. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, UK, 2002; ISBN 9780511754630. [Google Scholar]
- Rasool, S.; Muttaqi, K.M.; Sutanto, D. Modelling of a wave-to-wire system for a wave farm and its response analysis against power quality and grid codes. Renew. Energy 2020, 162, 2041–2055. [Google Scholar] [CrossRef]

| Wave Spectrum | Relation | Wave Spectrum | Relation |
|---|---|---|---|
| Bretschneider | Wallops | ||
| Pierson–Moskowitz | TMA | ||
| Torsethaugen | JONSWAP |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasool, S.; Muttaqi, K.M.; Sutanto, D. Modelling Ocean Waves and an Investigation of Ocean Wave Spectra for the Wave-to-Wire Model of Energy Harvesting. Eng. Proc. 2021, 12, 51. https://doi.org/10.3390/engproc2021012051
Rasool S, Muttaqi KM, Sutanto D. Modelling Ocean Waves and an Investigation of Ocean Wave Spectra for the Wave-to-Wire Model of Energy Harvesting. Engineering Proceedings. 2021; 12(1):51. https://doi.org/10.3390/engproc2021012051
Chicago/Turabian StyleRasool, Safdar, Kashem M. Muttaqi, and Danny Sutanto. 2021. "Modelling Ocean Waves and an Investigation of Ocean Wave Spectra for the Wave-to-Wire Model of Energy Harvesting" Engineering Proceedings 12, no. 1: 51. https://doi.org/10.3390/engproc2021012051
APA StyleRasool, S., Muttaqi, K. M., & Sutanto, D. (2021). Modelling Ocean Waves and an Investigation of Ocean Wave Spectra for the Wave-to-Wire Model of Energy Harvesting. Engineering Proceedings, 12(1), 51. https://doi.org/10.3390/engproc2021012051






