Sliding Mode Control Based on Backstepping Approach for Microsatellite Attitude Pointing †
Abstract
:1. Introduction
2. Spacecraft Attitude Model
- is the state vector;
- is the control matrix;
- is the observation matrix;
- is the control input torque.
3. Backstepping Control Design
3.1. Step 1
3.2. Step 2
4. Sliding Mode Control Design
4.1. Choice of Sliding Surface
4.2. Convergence and Existence Conditions
4.3. Establishment of the Control Law
5. Backstepping–Sliding Mode Control Design
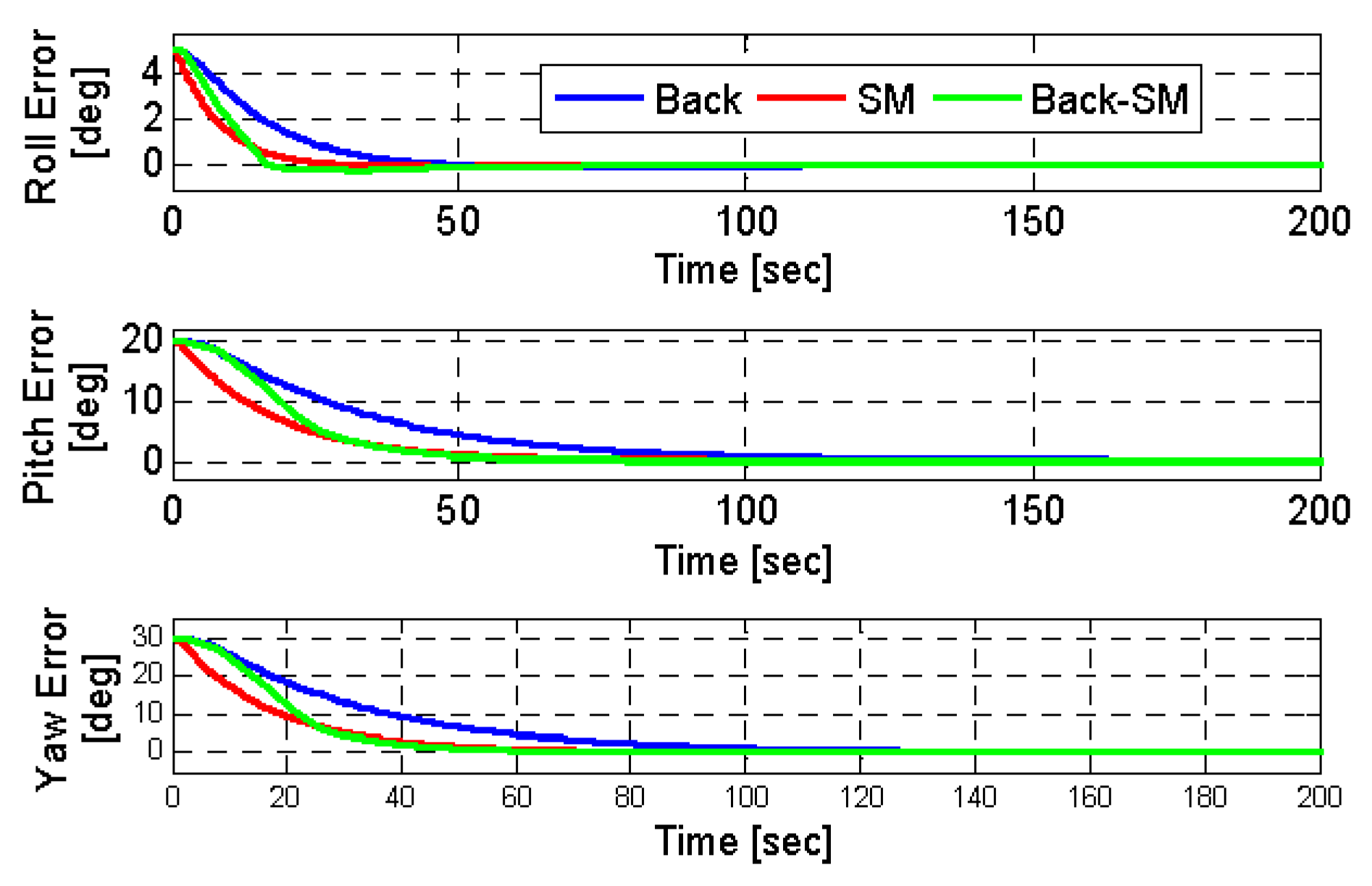
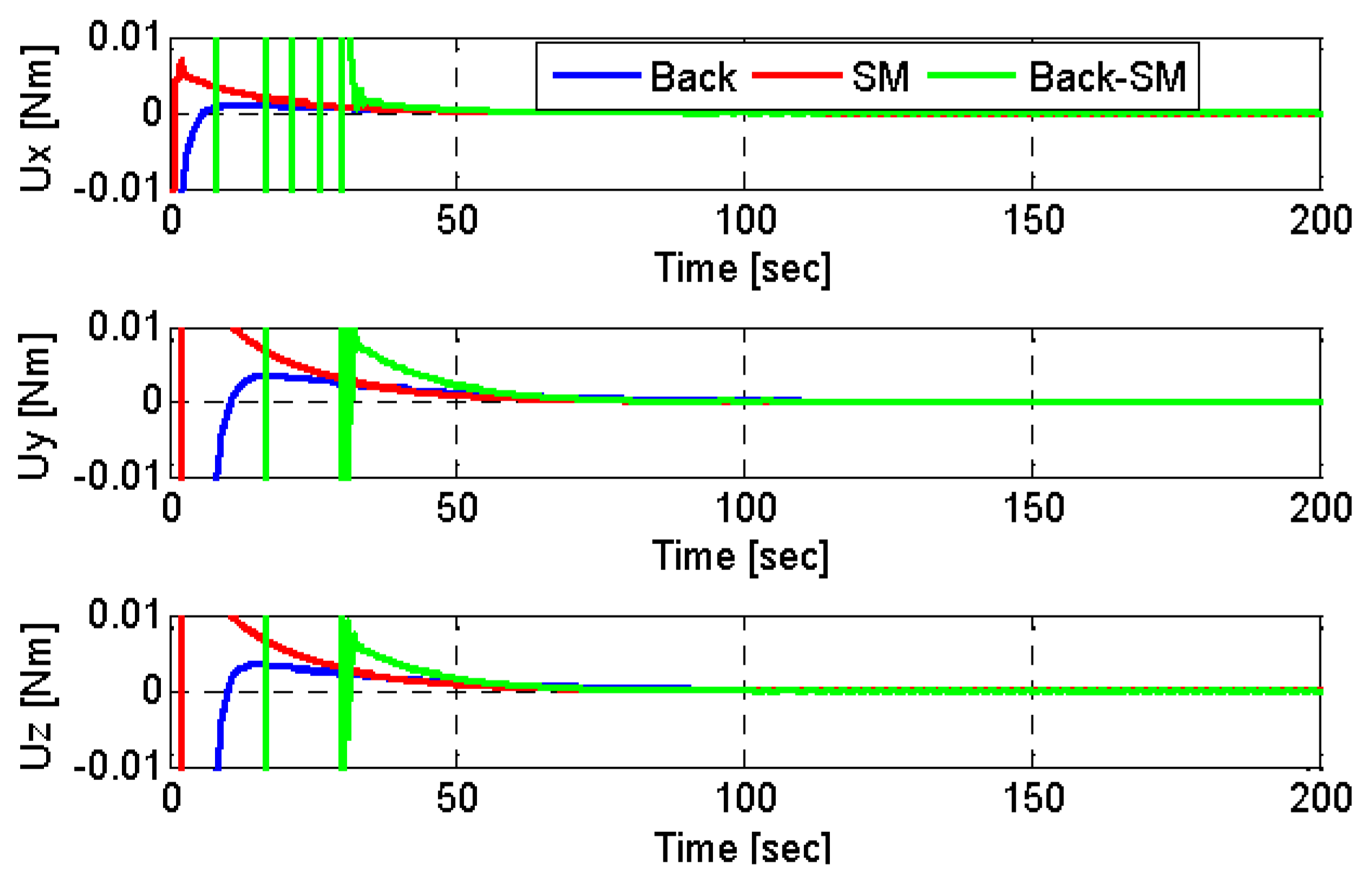
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohammed, M.A.S.; Boussadia, H.; Bellar, A.; Adnane, A. Adaptive backstepping control for three axis microsatellite attitude pointing under actuator faults. In Proceedings of the 13th European Workshop on Advanced Control and Diagnosis (ACD 2016), Lille, France, 17–18 November 2016. [Google Scholar]
- Boskovic, J.D.; Li, S.M.; Mehra, M.K. Robust adaptive variable structure control of spacecraft under input saturation. J. Guid. Control Dyn. 2001, 24, 14–22. [Google Scholar] [CrossRef]
- Lu, K.; Xia, Y.; Zhu, Z.; Basin, M.V. Sliding mode attitude tracking of rigid spacecraft with disturbance. J. Frankl. Inst. 2012, 349, 413–440. [Google Scholar] [CrossRef]
- Zou, A.; Kumar, K.D. Adaptive fuzzy fault-tolerant attitude control of spacecraft. Control Eng. Pract. 2011, 19, 10–21. [Google Scholar] [CrossRef]
- Costic, B.T.; Dawson, D.M.; Queiroz, M.S.; Kapila, V. Quaternion based attitude tracking control without velocity measurements. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000. [Google Scholar]
- Wong, H.; de Queiroz, M.S.; Kapila, V. Adaptive tracking control using synthesized velocity from attitude measurements. Automatica 2001, 37, 947–953. [Google Scholar] [CrossRef]
- Boussadia, H.; Mohammed, A.S.; Boughanmi, N.; Bellar, A. Adaptive Backstepping control for Microsatellite under Inertia Uncertainties. In Proceedings of the 39th IEEE Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 19–22 June 2017. [Google Scholar]
- Krstié, M.; Tsiotras, P. Inverse optimale stabilization of a rigid spacecraft. IEEE Trans. Autom. Control 1999, 44, 1014–1027. [Google Scholar]
- Liu, Y.C.; Zhang, T.; Song, J.Y. Attitude controller design for larger angle maneuver based on similar skew-symmetric structure. J. Astronaut. 2009, 30, 1017–1023. [Google Scholar]
- Doruk, R.Ö.; Kocaoğlan, E. Satellite attitude control by integrator backstepping with internal stabilization. Aircr. Eng. Aerosp. Technol. 2008, 80, 3–10. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Vadali, S.R.; Markley, F.L. Optimal Tracking of Spacecraft Using Variable-Structure Control. In Proceedings of the Flight Mechanics/Estimation Theory Symposium, NASA-Goddard Space Flight Center, NASA/CP-1999-209235, Greenbelt, MD, USA, 18–20 May 1999; pp. 201–214. [Google Scholar]
- Hu, Q.; Xie, L.; Wang, Y. Sliding Mode Attitude and Vibration Control of Flexible Spacecraft with Actuator Dynamics. In Proceedings of the IEEE International Conference on Control and Automation, Guangzhou, China, 30 May–1 June 2007. [Google Scholar]
- Mohammed, A.M.S. Three Axis Attitude Control Using Sliding Mode Based on the Artificial Neural Network for Low Earth Orbit Microsatellite. Int. J. Syst. Appl. Eng. Dev. 2012, 6, 223–233. [Google Scholar]
- Azza El-S, I.; Tobal, A.M.; Sultan, M.A. Satellite Attitude Maneuver using Sliding Mode Control under Body Angular Velocity Constraints. Int. J. Comput. Appl. 2012, 975, 8887. [Google Scholar]
- Bouadi, H.; Bouchoucha, M.; Tadjine, M. Sliding Mode Control based on Backstepping Approch for an UAV Type-Quadrotor. World Acad. Sci. Eng. Technol. 2007, 26, 22–27. [Google Scholar]
- Wertz, J.R. Spacecraft Attitude Determination and Control; D. Reidel Publishing Company: Boston, MA, USA, 1986. [Google Scholar]
- Sidi, M. Spacecraft Dynamics and Control; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kanellakopoulos, I.; Kokotovic, P.V.; Morse, A.S. Systematic Design of Adaptive Controllers for Feedback Linearizable Systems. IEEE Trans. Autom. Control 1991, 36, 1241–1253. [Google Scholar] [CrossRef] [Green Version]
- Young, K.; Utkin, V.; Özgüner, Ü. A control engineer’s guide to sliding mode control. IEEE Trans. Autom. Control 1999, 7, 328–342. [Google Scholar] [CrossRef] [Green Version]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice-Hall Inc.: Hoboken, NJ, USA, 1991. [Google Scholar]

| Parameter | Value |
|---|---|
| Inertia [kgm2] | |
| Orbit [km] | 686 |
| Inclination [deg] | 98 |
| Initial attitude [deg] | |
| Initial angular rate [deg/sec] | |
| External Torques [N.m] |
| Sliding Mode Prameters | Backstepping Prameters | Sliding Mode-Backstepping Prameters | ||||
|---|---|---|---|---|---|---|
| 0.06eye(3) | 200eye(3) | 0.01eye(3) | 8eye(3) | 0.08eye(3) | 110eye(3) | 3eye(3) |
| Sliding Mode | Backstepping | Hybrid | |
|---|---|---|---|
| RMS errors [deg] | 0.0013 | 0.00068 | 0.0007 |
| Convergence time [sec] | |||
| Power consumption | 2.45 × 10−5 | 2.46 × 10−5 | 0.065 |
| Maximum reaction wheel velocity | 233.29 | 526.64 | 729.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boussadia, H.; Si Mohammed, A.M.; Boughanmi, N.; Meche, A. Sliding Mode Control Based on Backstepping Approach for Microsatellite Attitude Pointing. Eng. Proc. 2022, 14, 24. https://doi.org/10.3390/engproc2022014024
Boussadia H, Si Mohammed AM, Boughanmi N, Meche A. Sliding Mode Control Based on Backstepping Approach for Microsatellite Attitude Pointing. Engineering Proceedings. 2022; 14(1):24. https://doi.org/10.3390/engproc2022014024
Chicago/Turabian StyleBoussadia, Halima, Arezki Mohamed Si Mohammed, Nabil Boughanmi, and Abdelkrim Meche. 2022. "Sliding Mode Control Based on Backstepping Approach for Microsatellite Attitude Pointing" Engineering Proceedings 14, no. 1: 24. https://doi.org/10.3390/engproc2022014024
APA StyleBoussadia, H., Si Mohammed, A. M., Boughanmi, N., & Meche, A. (2022). Sliding Mode Control Based on Backstepping Approach for Microsatellite Attitude Pointing. Engineering Proceedings, 14(1), 24. https://doi.org/10.3390/engproc2022014024






